Ортоцентр – это точка пересечения высот треугольника.
Рассмотрим остроугольный треугольник ABC:
O – ортоцентр,
∠ BAC = a,
∠ ABC = b,
∠ ACB = c.
Утверждения.
1. Треугольник ABC подобен треугольнику, образованному вершиной B и основанием двух высот:
Δ ABC ∼ Δ H3BH2,
коэффициент подобия:
H3B / AB = H2B / CB = H3H2 / AC = cos b.
2. Соотношение отрезков, на которые ортоцентр делит высоту, можно вычислить по формуле:
BO / OH1 = cos b / (cos a * cos c).
3. Высоты треугольника можно вычислить по формуле:
BH1 = AC * sin a * sin c / sin b.
4. Расстояние от ортоцентра до вершины треугольника:
OB = AC / tg b.
5. 1 / BH1 + 1 / CH2 + 1 / AH3 = 1 / r,
r – радиус вписанной окружности.
Докажем эти утверждения.
1. 
В треугольнике ABC проведены высоты BD и CE.
Докажем, что треугольник ABC подобен треугольнику ADE.
Решение.
Рассмотрим Δ ABD:
cos A = AD / AB.
Рассмотрим Δ ACE:
cos A = AE / AC.
Таким образом,
cos A = AD / AB = AE / AC.
Значит, Δ ABC ∼ Δ ADE по двум сторонам и углу между ними.
2. 
Диагонали трапеции ABCD пересекаются под прямым углом.
CH – высота, проведенная к большему основанию AD.
∠ CAD = a,
∠ ACD = c,
∠ ADC = d.
Найдем отношение, в котором диагональ трапеции делит высоту CH.
Решение.
Пусть K – точка пересечения диагоналей трапеции,
O – точка пересечения диагонали BD и высоты CH.
Найдем соотношение CO / OH.
Δ BOC подобен Δ DOH по двум углам,
так как ∠ BCO = ∠ DHO = 90,
∠ BOC = ∠ DOH как вертикальные.
Значит,
CO / OH = BC / DH. (*)
Рассмотрим Δ CKD:
KC = CD * cos c.
Рассмотрим Δ BCK:
BC = KC / cos a = (CD * cos c) / cos a.
Рассмотрим Δ CHD:
HD = CD * cos d.
Из (*) и последних трех равенств получаем:
CO / OH = BC / DH =
( (CD * cos c) / cos a ) : (CD * cos d) = 
Таким образом, мы нашли соотношение отрезков, на которые ортоцентр O треугольника ABD делит высоту CH:
3.
Найдем расстояние от ортоцентра треугольника до его вершины, и высоту, проведенную из этой вершины, если известны углы треугольника и противолежащая сторона.
Решение.
Рассмотрим треугольник ABC.
O – ортоцентр.
∠ BAC = a,
∠ ABC = b,
∠ ACB = с,
также известна величина стороны AC.
Найдем BH и OB.
Обозначим AH за x, тогда HC = AC – x.
Рассмотрим Δ AHB:
BH = x * tg a.
Рассмотрим Δ CHB:
BH = (AC – x) * tg c.
Таким образом,
BH = x * tg a = (AC – x) * tg c. 
Рассмотрим Δ AHB:
Таким образом высоту можно вычислить по формуле, 
4.
Найдем теперь расстояние от вершины B до ортоцентра.
Так как BH = BO + OH, получаем: 
Выражаем из уравнения (1) OH и подставляем в уравнение (2): 
Значит, расстояние от ортоцентра до вершины можно вычислить по формуле: 
5.
1 / BH1 + 1 / CH2 + 1 / AH3 = 1 / r.
Площадь треугольника ABC можно вычислить по формуле:
S = ½ * AC * BH1 = ½ * AB * CH2 = ½ * BC * AH3,
Значит,
BH1 = 2S / AC
CH2 = 2S / AB
AH3 = 2S / BC
1 / BH1 = AC / 2S
1 / CH2 = AB / 2S
1 / AH3 = BC / 2S
1 / BH1 + 1 / CH2 + 1 / AH3 = (AC + BC + AB) / 2S = p / S, (*)
где p – полупериметр.
Еще одна формула площади треугольника:
S = p * r,
откуда r = S / p
1 / r = p / S.
Из (*) и последнего равенства получаем нужное нам равенство.
Содержание 👉
A simple polygon having three sides and three vertices are called a triangle. The intersection point of the three altitudes of a triangle is called the “orthocenter of a triangle,” and it is generally represented by the letter “H.” An altitude of a triangle is a line segment drawn from each vertex to the opposite side that is perpendicular to its opposite side. As a triangle has three vertices and three sides, it has three altitudes, and the point of intersection of these three sides is called the orthocenter.

For every triangle, the position of the orthocenter varies; i.e; for an equilateral triangle, the orthocenter, circumcenter, incenter, and centroid are the same, but in the case of the other triangles,, the position will be different.
- In the case of an acute-angled triangle, the orthocenter lies inside the triangle.
- In the case of an obtuse-angled triangle, the orthocenter lies outside the triangle.
- In the case of a right-angled triangle, the orthocenter lies on the vertex of the right angle.

Determining the orthocenter of a triangle
Let’s consider a triangle ABC to determine the orthocenter of a triangle. AD, BE, and CF are the perpendiculars drawn from the vertices A (x1, y1), B (x2, y2), and C (x3, y3) to their respective opposite sides BC, AC, and AB and “H” is the point of their intersection.
Step 1: Calculate the slopes of the sides of the triangle ABC using the slope formula;
m = (y2 – y1)/(x2 – x1)
Let the slope of the AB be mAB.
mAB = (y2 – y1)/(x2 – x1)
Let the slope of the BC be mBC
So, mBC = (y3 – y2)/(x3 – x2)
Step 2: Using the slopes of the sides of a triangle, find the slopes of altitudes.
We know that the altitude is perpendicular to the side.
Product of slopes of two perpendicular slopes lines = m1 × m2 = -1
So, the slope of the altitude = -1/slope of the side = -1/m
Now, the slopes of the respective altitudes CF and AD are,
mCF = -1/mAB
mAD = -1/mBC
Step 4: With the help of the point-slope form equation, find the equations of the altitudes using the slopes and the coordinates of the opposite vertices.
The equation of CF is (y – y3) = mCF(x – x3)
The equation of AD is (y – y1) = mAD(x – x1)
Step 4: Solve the equations of any two altitudes and the values of x and y obtained by solving both equations are the coordinates of the orthocenter of the triangle.
Sample Problems
Problem 1: Determine the coordinates of the orthocenter of a triangle whose vertices are A (3, 1), B (-5, 2), and C (0, 4).
Solution:
Given,
The vertices of a triangle are A (x1, y1) = (3,1), B (x2, y2) = (-5,2) and C (x3, y3) = (0,4)
Now, the slope of the side AB = (y2 – y1)/(x2 – x1)
⇒ mAB = (2 – 1)/(-5 -3) = -(1/8)
The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = 8
So, the equation of the line CF with point C (0,4) and slope = 8 is y – y3 = m(x – x3) [point-slope form]
⇒ y – 4 = 8 (x – 0)
⇒ y – 4 = 8x
⇒ 8x – y = -4 ⇢ (1)
Slope of the side BC = (y3 – y2)/(x3 – x2)
⇒ mBC = (4 – 2)/(0 – (-5)) = 2/5
Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = -(5/2)
So, the equation of the line AD with point A (3,1) and slope = -(5/2) is y – y1 = m(x – x1) [point slope form]
⇒ y – 1 = -(5/2) (x – 3)
⇒ 2(y – 1) = -5(x – 3)
⇒ 2y – 2 = -5x + 15
⇒ 5x + 2y = 17 ⇢ (2)
Now, multiply the equation (1) with “2” on both sides and add both equations (1) and (2).
16x – 2y = -8
5x + 2y = 17
21x = 9 ⇒ x = 3/7
Now, substitute the value of x = 3/7 in equation (1)
⇒ 8(3/7) – y = -4
⇒ y = 24/7 + 4 = 52/7
Hence, the coordinates of the orthocenter (H) are (3/7, 52/7).
Problem 2: Determine the coordinates of the orthocenter of a triangle whose vertices are A (5, -3), B (7, 0), and C (4, 9).
Solution:
Given,
The vertices of a triangle are A (x1, y1) = (5, -3), B (x2, y2) = (7, 0) and C (x3, y3) = (4, 9).
Now, the slope of the side AB = (y2 – y1)/(x2 – x1)
⇒ mAB = (0 – (-3))/(7 – 5) = 3/2
The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = -(2/3)
So, the equation of the line CF with point C (4, 9) and slope = -(2/3) is y – y3 = m(x – x3) [point-slope form]
⇒ y – 9 = -(2/3) (x – 4)
⇒ 3(y – 9) = -2(x – 4)
⇒ 3y – 27 = -2x + 8
⇒ 2x + 3y = 35 ⇢ (1)
Slope of the side BC = (y3 – y2)/(x3 – x2)
⇒ mBC = (9 – 0)/(4 – 7) = -(9/3) = -3
Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = 1/3
So, the equation of the line AD with point A (5, -3) and slope = 1/3 is y – y1 = m(x – x1) [point slope form]
⇒ y – (-3) = (1/3) (x – 5)
⇒ 3(y + 3) = x – 5
⇒ 3y + 9 = x – 5
⇒ x – 3y = 14 ⇢ (2)
Now, add equations (1) and (2)
2x + 3y = 35
x – 3y = 14
3x = 49 ⇒ x =49/3
Now, substitute the value of x = 49/3 in equation (2)
⇒ 49/3 – 3y = 14 ⇒ 3y = -1
⇒ y =7/9
Hence, the coordinates of the orthocenter (H) are (49/3, 7/9).
Problem 3: Find the orthocenter of a triangle whose vertices are A (2, -7), B (6, 3), and C (-8, 0).
Solution:
Given,
The vertices of a triangle are A (x1, y1) = (5, -3), B (x2, y2) = (7, 0) and C (x3, y3) = (4, 9)
Now, the slope of the side AB = (y2 – y1)/(x2 – x1)
⇒ mAB = (3 – (-7))/(6 – 2) = 10/4 = 5/2
The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = -(2/5)
So, the equation of the line CF with point C (-8, 0) and slope = -(2/5) is y – y3 = m(x – x3) [point-slope form]
⇒ y – 0 = -(2/5) (x – (-8))
⇒ 5y = -2(x + 8)
⇒ 5y = -2x -16
⇒ 2x + 5y = -16 ⇢ (1)
Slope of the side AC = (y3 – y1)/(x3 – x1)
⇒ mAC = (0 – (-7))/(-8 – 2) = -(7/10)
Now, the slope of the line perpendicular to AC i.e., the slope of BE = -(1/slope of AC) = 10/7
So, the equation of the line BE with point B (6, 3) and slope = 10/7 is y – y2 = m(x – x2) [point slope form]
⇒ y – 3 = (10/7) (x – 6)
⇒ 7(y – 3) = 10(x – 6)
⇒ 7y – 21 = 10x – 60
⇒ 10x – 7y = 39 ⇢ (2)
Multiply equation (1) with “5” on both sides and subtract both equations.
10x + 25y = -80
10x – 7y = 39
(-) (+) (-)
——————
32y = -119 ⇒ y = – 119/32
Now, substitute the value of y = -119/32 in equation (1)
2x + 5(-119/32) = -16
⇒ 2x – 595/32 = -16 ⇒ 2x = 595/32 – 16
⇒ 2x = 83/32 ⇒ x = 83/64
Hence, the coordinates of the orthocenter (H) are (83/64, -119/32).
Problem 4: Find the orthocenter of a triangle whose vertices are A (6, 2), B (1, 1), and C (-4, 7).
Given,
The vertices of a triangle are A (x1, y1) = (6, 2), B (x2, y2) = (1, 1) and C (x3, y3) = (-4, 7).
Now, the slope of the side AC = (y3 – y1)/(x3– x1)
⇒ mAC = (7 – 2)/(-4 – 6) = -(5/10) = -1/2
The slope of the line perpendicular to AC i.e., slope of BE = -(1/slope of AC) = 2
So, the equation of the line BE with point B (1,1) and slope = 2 is y – y2 = m(x – x2) [point-slope form]
⇒ y – 1 = 2(x – 1)
⇒ y – 1 = 2x – 2
⇒ 2x – y = 1 ⇢ (1)
Slope of the side BC = (y3 – y2)/(x3 – x2)
⇒ mBC =(7 – 1)/(-4 – 1) = -(6/5)
Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = 5/6
So, the equation of the line BE with point A (6, 2) and slope = 10/7 is y – y1 = m(x – x1) [point slope form]
⇒ y – 2 = (5/6) (x – 6)
⇒ 6(y – 2) = 5(x – 6)
⇒ 6y – 12 = 5x – 30
⇒ 5x – 6y = 18 ⇢ (2)
Now, multiply equation (1) with “6” on both sides and subtract both equations.
12x – 6y = 6
5x – 6y = 18
(-) (+) (-)
——————
7x = -12 ⇒ x = -12/7
Now, substitute the value of x = -12/7 in equation (1)
2(-12/7) – y = 1
⇒ y = -24/7 – 1 ⇒ y = -31/7
Hence, the coordinates of the orthocenter (H) are (-12/7, -31/7).
Problem 5: Determine the coordinates of the orthocenter of a triangle whose vertices are A (0,-5), B (3,-2), and C (-6, 0).
Given,
The vertices of a triangle are A (x1, y1) = (3,1), B (x2, y2) = (-5,2) and C (x3, y3) = (0,4)
Slope of the side BC = (y3 – y2)/(x3 – x2)
⇒ mBC =(0 – (-2))/(-6 – 3) = -(2/9)
Now, the slope of the line perpendicular to BC i.e., the slope of AD = -(1/slope of BC) = (9/2)
So, the equation of the line AD with point A (3,1) and slope = (9/2) is y – y1 = m(x – x1) [point slope form]
⇒ y – (-5) = (9/2) (x – 0)
⇒ 2(y + 5) = 9x
⇒ 2y + 10 = 9x
⇒ 9x – 2y = 10 ⇢ (1)
Now, the slope of the side AB = (y2 – y1)/(x2 – x1)
⇒ mAB = (-2 – (-5))/(3 – 0) = 3/3 = 1
The slope of the line perpendicular to AB i.e., slope of CF = -(1/slope of AB) = -1
So, the equation of the line CF with point C (-6, 0) and slope = -1 is y – y3 = m(x – x3) [point-slope form]
⇒ y – 0 = (-1)(x – (-6))
⇒ y = -(x + 6)
⇒ y = -x – 6
⇒ x + y = -6 ⇢ (2)
Now, multiply equation (2) with “2” on both sides and add both equations.
9x – 2y = 10
2x + 2y = -12
11x = -2 ⇒ x = -2/11
Now, substitute the value of x = -2/11 in equation (2)
⇒ -2/11 + y = -6
⇒ y = -6 + 2/11 ⇒ y = -64/11
Now, by solving the equations of the lines AD and CF we get the coordinates of the orthocenter (H) are (-2/11, -64/11).
Содержание
$newcommand{updownarrows}{uparrow!downarrow}$
$newcommand{tg}{mathop{rm tg}nolimits}$
$newcommand{ctg}{mathop{rm ctg}nolimits}$
$newcommand{sign}{mathop{rm sign}nolimits}$
$newcommand{arctg}{mathop{rm arctg}nolimits}$
$newcommand{arcctg}{mathop{rm arcctg}nolimits}$
$newcommand{deg}{^circ}$
$newcommand{a}{angle}$
$newcommand{archat}{arcbuildrel,,frownover}$
$newcommand{Vec}{overrightarrow}$
Ортоцентр
Теорема об ортоцентрической системе точек
Если в четвёрке точек $A, B, C, H$ точка $H$ является точкой
пересечения высот треугольника $ABC$, то и любая из четырёх точек
является ортоцентром треугольника, образованного тремя остальными
точками.
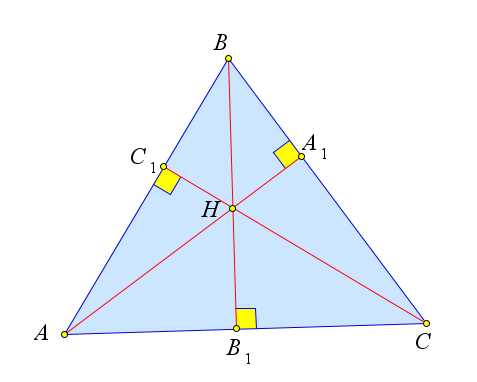

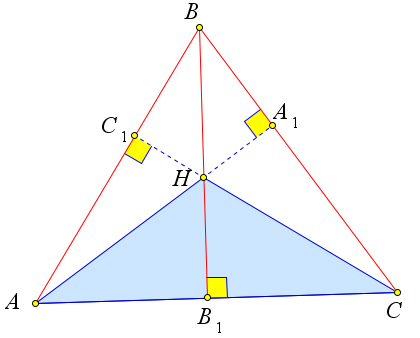
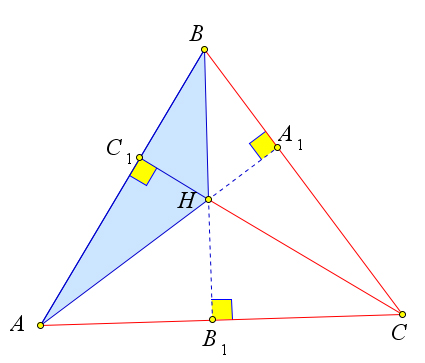
Доказательство
Рассмотрим треугольник $ABC$, в котором $AA_1, BB_1, CC_1$ – это
высоты, точка $H$ – это ортоцентр.
Докажем, что точка $A$ – это ортоцентр треугольника $BCH$.
Действительно, для треугольника $BCH$ высотами являются $BC_1, HA_1$
и $B_1C$.
А прямые, содержащие эти отрезки, пересекаются в точке $A$.
Аналогично точки $B$ и $C$ являются ортоцентрами для треугольников $ACH$ и $ABH$ соответственно.
Теорема
Радиусы окружностей, проходящих через любые три точки
ортоцентрической системы, равны.
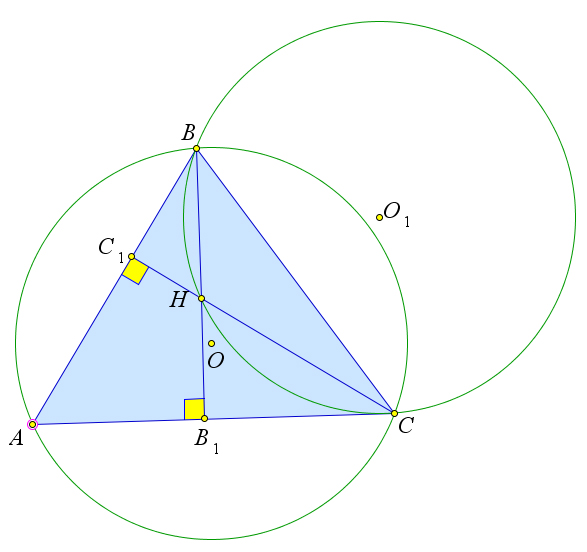
Доказательство
Рассмотрим треугольник $ABC$, в котором высоты $BB_1$ и $CC_1$ пересекаются в точке $H$.
Докажем, что радиусы окружностей $omega$ и $omega_1$, описанных соответственно около треугольников $ABC$ и $BCH$, равны.
В четырёхугольнике $AC_1HB_1$ углы $C_1$ и $B_1$ прямые.
А так как сумма углов четырёхугольника равна $360^circ$, то $angle CHB=180^circ-angle A$, и, следовательно, синусы этих углов равны.
Радиусы рассматриваемых окружностей выражаются по формулам $R=dfrac{BC}{2sin{angle A}}, R_1=dfrac{BC}{2sin{angle CHB}}$.
Но так как синусы $angle A$ и $angle CHB$ равны, то и радиусы $R$ и $R_1$ равны.
Теорема
В остроугольном треугольнике $ABC$ с высотами $AA_1, BB_1, CC_1$
выполняются следующие соотношения:
-
$angle A_1AC=angle B_1BC,$
-
$angle C_1CB=angle A_1AB,$
-
$angle B_1BA=angle C_1CA.$
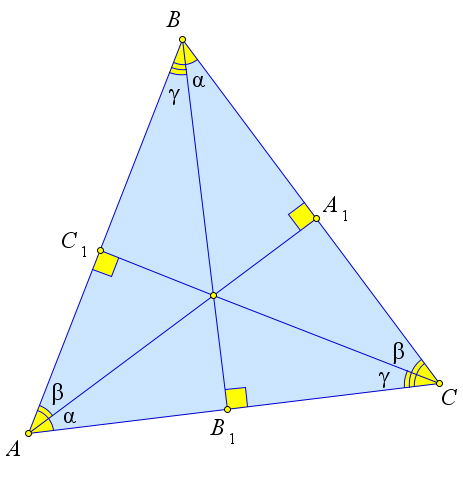
Доказательство
Рассмотрим треугольник $ABC$ с высотами $AA_1, BB_1, CC_1$.
В прямоугольных треугольниках $AA_1C$ и $BB_1C$ острый угол $C$
является общим, поэтому другие острые углы равны: $angle A_1AC=angle B_1BC$.
Аналогично в треугольниках $A_1AB$ и $C_1CB$ есть общий острый угол $B$, а в треугольниках $B_1BA$ и $C_1CA$ есть общий острый угол $A$.
Следовательно, другие острые углы в этих парах треугольников равны между собой: $angle C_1CB=angle A_1AB, angle B_1BA=angle C_1CA.$
Теорема
В остроугольном треугольнике $ABC$ с высотами $AA_1, BB_1, CC_1$ и
ортоцентром $H$ выполняются следующие соотношения:
-
$angle A=angle B_1HC=angle C_1HB=angle B_1A_1C=angle C_1A_1B,$
-
$angle B=angle A_1HC=angle C_1HA=angle C_1B_1A=angle A_1B_1C,$
-
$angle C=angle B_1HA=angle A_1HB=angle B_1C_1A=angle A_1C_1B.$
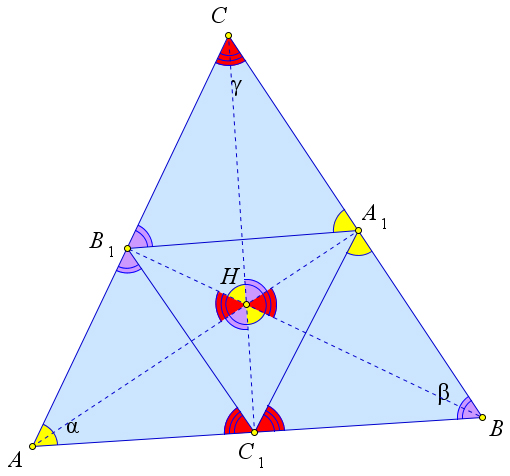
Доказательство
Обозначим $alpha=angle A, beta=angle B, gamma=angle C$.
В прямоугольных треугольниках $ACC_1$ и $CB_1H$ есть общий острый угол $angle ACC_1$,
следовательно, другие острые углы в этих треугольниках равны: $angle
A=angle B_1HC=alpha$.
Кроме того $angle C_1HB=angle B_1HC=alpha$, как
вертикальные.
Заметим, что $angle CAA_1=angle B_1BC$.
Выпишем синусы этих углов из прямоугольных треугольников $CAA_1$ и $BB_1C$:
$sin{angle CAA_1}=dfrac{A_1C}{AC}$, $sin{angle B_1BC}=dfrac{B_1C}{BC}$.
Значит, $dfrac{A_1C}{AC}=dfrac{B_1C}{BC}$ или $dfrac{A_1C}{B_1C}=dfrac{AC}{BC}$.
Тогда $triangle A_1B_1Csimtriangle ABC$ по второму признаку подобия (угол $C$ – общий, а стороны $CA_1$ и $CB_1$ пропорциональны сторонам $CA$ и $CB$).
Тогда углы этих треугольников, лежащие напротив пропорциональных сторон, равны: $angle
CA_1B_1=angle A=alpha, angle CB_1A_1=angle B=beta$.
Аналогично из подобия треугольников $A_1BC_1$ и $ABC$ получаем $angle BA_1C_1=angle A=alpha, angle BC_1A_1=angle C=gamma$.
Таким образом $angle A=angle B_1HC=angle C_1HB=angle B_1A_1C=angle C_1A_1B$.
Аналогично можно получить и остальные соотношения.
Теорема
В остроугольном треугольнике $ABC$ с высотами $AA_1, BB_1, CC_1$ и
ортоцентром $H$ выполняются следующие соотношения:
-
$angle B_1BC=angle CC_1A_1=angle CC_1B_1=angle A_1AC$,
-
$angle BAA_1=angle C_1B_1B=angle A_1B_1B=angle C_1CB$,
-
$angle ABB_1=angle C_1A_1A=angle AA_1B_1=angle ACC_1$.
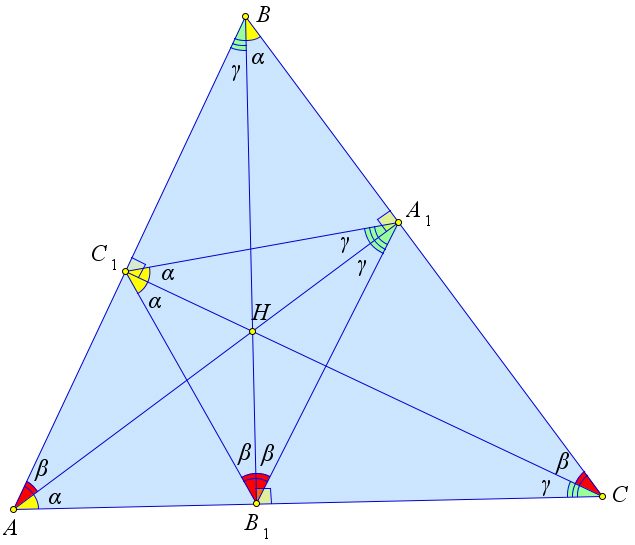
Доказательство
Рассмотрим треугольник $ABC$, в котором проведены высоты $AA_1,
BB_1, CC_1$, а точка $H$ является ортоцентром.
Заметим, что $angle AC_1B_1=angle BC_1A_1=angle C$.
Тогда, так как $angle CC_1A=90^circ$, то $angle CC_1B_1=90^circ-angle C=angle A_1C_1C$.
C другой стороны, из прямоугольного треугольника $AA_1C$ получаем, что $angle
A_1AC=90^circ-angle C$.
Значит, $angle A_1AC=angle CC_1B_1=angle CC_1A_1$.
Аналогично можно получить и остальные соотношения.
Следствие
Высоты треугольника являются биссектрисами его ортотреугольника
(следовательно, ортоцентр остроугольного треугольника является
центром окружности, вписанной в его ортотреугольник).
Теорема
Пусть $AA_1, BB_1$ и $CC_1$ – высоты треугольнике $ABC$, а $H$ –
ортоцентр этого треугольника. Тогда
-
$triangle ABC simtriangle AC_1B_1simtriangle BC_1A_1simtriangle CB_1A_1$.
-
-
$triangle BCH simtriangle B_1C_1H$
-
$triangle ABHsimtriangle A_1B_1H$
-
$triangle ACHsimtriangle A_1C_1H$
-
-
-
$triangle BC_1H simtriangle B_1CHsimtriangle BAB_1simtriangle CC_1A$
-
$triangle BA_1Hsimtriangle AB_1Hsimtriangle BB_1Csimtriangle AA_1C$
-
$triangle AC_1Hsimtriangle A_1HCsimtriangle ABA_1simtriangle CC_1B$
-
Доказательство
С учётом первого признака подобия треугольников первый пункт теоремы
напрямую следует из теоремы ref{108b}, а второй пункт теоремы
напрямую следует из теоремы ref{108c}.
В третьем пункте теоремы $triangle BCHsimtriangle B_1CH$ по второму признаку подобия, так как $angle HBC_1=angle B_1CH$ по теореме ref{108a}, а $angle C_1HB=angle
B_1HC$, как вертикальные.
Подобие прямоугольных треугольников $BC_1H$ и $ABB_1$ следует из того, что острый угол $ABB_1$ для этих треугольников является общим.
Остальные подобия доказываются аналогично.
Теорема
Точки, симметричные ортоцентру треугольника относительно его сторон,
лежат на описанной окружности.
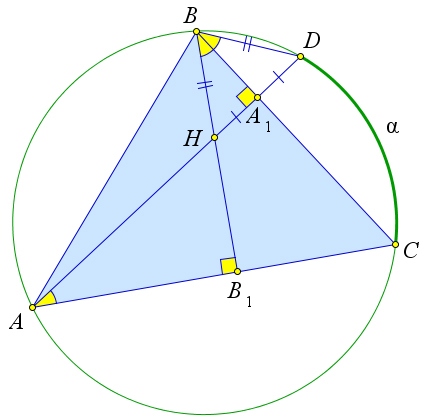
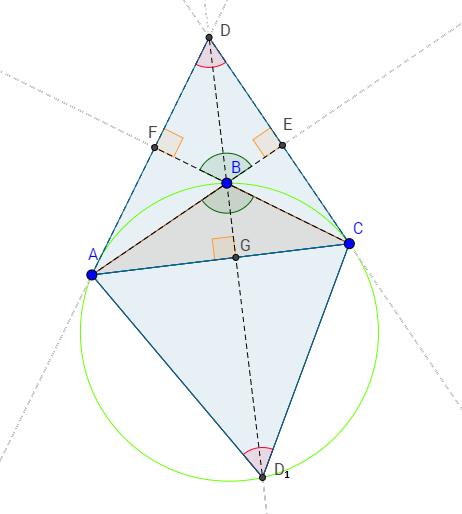
Доказательство
Первый случай: остроугольный треугольник
Рассмотрим треугольник $ABC$, в котором высоты $BB_1$ и $AA_1$
пересекаются в точке $H$.
Пусть прямая $AA_1$ пересекает окружность, описанную около треугольника $ABC$, в точке $D$.
Докажем, что точка $D$ симметрична точке $H$ относительно стороны $BC$.
Так как $HDperp BC$, то достаточно доказать, что $HA_1=A_1D$.
Пусть $buildrel,,frownover{DC}=alpha$.
Тогда $angle DAC=angle DBC=frac{alpha}{2}$, так как это вписанные углы.
Кроме того, так как в прямоугольных треугольниках $AHB_1$ и $BHA_1$ острые углы $angle AHB_1$ и $angle BHA_1$ равны, то другие острые углы тоже равны, то есть $angle HAC=angle
HBC=frac{alpha}{2}$.
Тогда в треугольнике $HBD$ отрезок $BA_1$ является биссектрисой и высотой, значит, $triangle BHD$ – равнобедренный, а $BA_1$ не только высота и биссектриса, но и медиана, то есть $HA_1=A_1D$.
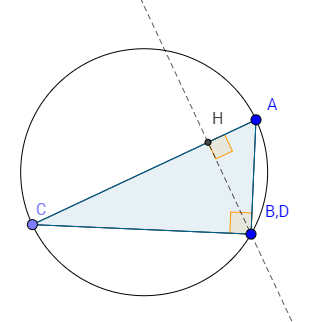
Второй случай: тупоугольный треугольник
Рассмотрим треугольник $ABC$, в котором высоты $AE, BG, CF$
пересекаются в точке $D$.
Докажем, что точка $D_1$, симметричная точке $D$ относительно точки $G$ стороны $AC$, лежит на
окружности, описанной около треугольника $ABC$.
Найдем чему равен $angle AD_1C$.
Пусть $angle ABC= α $ , тогда $angle EBC= α$, так как они вертикальны. $angle EDF= 180^circ – α$ следует из того, что сумма углов в четырехугольнике равна $360^circ$, а $angle DEB= angle DFB = 90^circ$.
Треугольники $ADC$ и $AD_1C$ равны, так как каждый из которых состоит из двух треугольников, которое в свою очередь равны соответствующему треугольнику по двум сторонам и углу ($angle G= 90^circ, DG= D_1G$, $AC$ – общая). Из этого следует, что $angle ADC= angle AD_1C = 180^circ – α$.
Предположим противное, что точка $D_1$ не лежит на окружности. Тогда существует точка $D_2$, которая лежит на окружности и на продолжении $DG$.
Докажем, что $angle AD_2C =180^circ – α$. $angle B =α$ и опирается на дугу $AD_2C$. Эта дуга равна $2α$. Тогда дуга $ABC= 360^circ -2α$, и из того, что $angle AD_2C$ опирается на дугу $ABC$, следует: $angle AD_2C= 180^circ -α$.
Есть два варианта расположения точки $D_1$. Либо внутри окружности, либо за ее пределами.
Если точка $D_1$ находится внутри окружности, то получается, что $angle D_1=angle D_2 = α = α- angle D_1AD_2 -angle D_1CD_2$, где $angle D_1AD_2≠0 $ и $angle D_1CD_2≠0$. Такого не возможно, противоречие.
Если точка $D_1$ находится за пределами окружности, то получается, что $angle D_1=angle D_2 = α = α + angle D_1AD_2 + angle D_1CD_2$, где $angle D_1AD_2≠0 $ и $angle D_1CD_2≠0$. Такого тоже не возможно, противоречие.
Из противоречия следует, что точка $D_2$ равна точке $D_1$, то есть точка $D_1$ лежит на окружности.
Третий случай:прямоугольный треугольник
Рассмотрим треугольник $ABC$. Его высоты пересекаются в точке $B$.
То есть точка $D$, симметричная точке $B$ относительно точки $B$ стороны $AC$, это и есть точка $B$, которая в любом случае лежит на около описанной окружности.
Теорема
Точки, симметричные ортоцентру треугольника относительно середин
сторон, также лежат на описанной окружности и совпадают с точками,
диаметрально противоположными соответствующим вершинам.
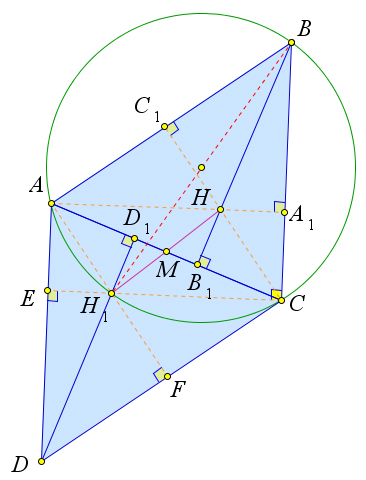
Доказательство
Рассмотрим треугольник $ABC$, в котором высоты $AA_1, BB_1, CC_1$
пересекаются в точке $H$.
Докажем, что точка $H_1$, симметричная точке $H$ относительно середины $M$ стороны $AC$, лежит на
окружности, описанной около треугольника $ABC$, при этом $H_1B$ –
это диаметр.
Рассмотрим центральную симметрию треугольника $ABC$ относительно точки $M$.
Пусть точка $D$ – это образ точки $B$ при такой симметрии, тогда треугольник $ABC$ отображается в треугольник
$CAD$, а точка $H$, ортоцентр треугольника $ABC$, отображается в
точку $H_1$, ортоцентр треугольника $CAD$.
Нужно доказать, что точка $H_1$ лежит на окружности, описанной около треугольника $ABC$.
Углы $B$ и $D$ равны (так как симметричные треугольники $ABC$ и $CAD$ равны).
Кроме того, так как в четырёхугольнике $DEH_1F$ углы $E$ и $А$ прямые, то $angle AH_1F=180^circ-angle D=180^circ-angle B$.
Таким образом $angle AH_1C+angle B=180^circ$.
Таким образом в четрёхугольнике $ABCH_1$ сумма противоположных углов равна $180^circ$, а значит, он
является вписанным, то есть точка $H_1$ лежит на окружности.
Докажем, что $H_1B$ – диаметр.
Так как треугольник $ABC$ отображается в треугольник $CAD$, то $angle EAC=angle ACB$.
Но из прямоугольного треугольника $ACE$ имеем $angle EAC+angle ACE=90^circ$.
Тогда $angle ACB+angle ACE=angle H_1CB=90^circ$.
А так как вписанный прямой угол опирается на диаметр, то $H_1B$ – это диаметр.
Теорема
Центр описанной около треугольника окружности служит ортоцентром
треугольника с вершинами в серединах сторон данного треугольника.
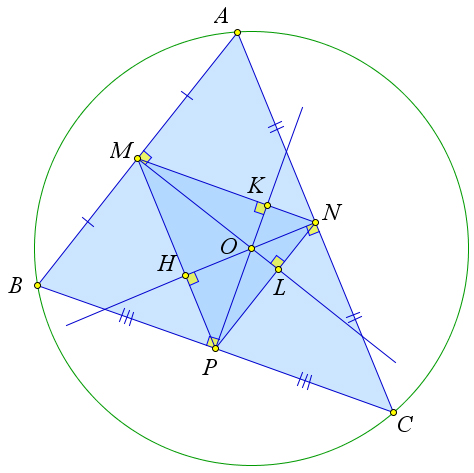
Доказательство
Рассмотрим треугольник $ABC$, в котором точки $M, N, P$ – это
середины сторон $AB, AC, BC$, а точка $O$ – центр описанной
окружности.
Докажем, что $O$ – ортоцентр треугольника $MNP$.
Так как центр описанной окружности лежит на серединных перпендикулярах к сторонам треугольника, то, например, $POperp BC$.
А так как $MN$ средняя линия, и, следовательно, $MNparallel BC$, то
$POperp MN$.
Таким образом $PK$ – это высота треугольника $MNP$.
Аналогично $ML$ и $NH$ – высоты треугольника $MNP$.
Таким образом точка $O$ является ортоцентром треугольника $MNP$.
Следствие
Точки $Z$, $O$ и $H$ лежат на одной прямой, причем $H_{Z}^{-0,5}(H)=O$, в частности, $overrightarrow{ZH} = -2cdotoverrightarrow{ZO}$.
Теорема
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем
расстояние от центра описанной окружности до противоположной
стороны.
Доказательство
Рассмотрим треугольник $ABC$, в котором точка $H$ – это ортоцентр,
а точка $O$ – это центр описанной окружности.
Докажем, что расстояние от точки $O$ до стороны $BA$ (обозначим его $BD$) вдвое
меньше отрезка $CH$.
Основываясь на следствии ref{sle96-1}, построим треугольник $MNP$, для которого треугольник $ABC$ будет
серединным.
Тогда по следствию ref{sle96-2} точка $H$ является центром окружности, описанной около $tri MNP$.
Таким образом отрезок $CH$ в треугольнике $MNP$ соответствует отрезку $OD$ в
треугольнике $ABC$.
А так как по следствию ref{sle96-1} эти треугольники подобны с коэффициентом $2$, получаем, что $CH=2OD$.
Теорема
Если $O$ – центр описанной окружности $triangle ABC$, то
$overrightarrow{OH}=overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}$.
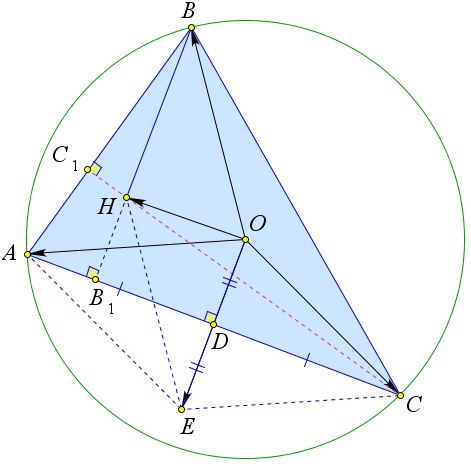
Доказательство
Рассмотрим треугольник $ABC$, в котором точка $O$ – центр описанной
окружности, точка $H$ – ортоцентр, $D$ – середина стороны $AC$,
$BB_1$ – высота.
Отложим на серединном перпендикуляре $OD$ точку $E$ так, чтобы $DE=OD$.
Тогда $AOCE$ – параллелограмм (так как диагонали точкой пересечения делятся пополам), а, следовательно,
$overrightarrow{OA}+overrightarrow{OC}=overrightarrow{OE}$.
Кроме того прямые $BH$ и $OE$ перпендикулярны стороне $BC$, следовательно $BHparallel OE$.
Кроме того по теореме ref{117} $BH=2OD=OE$.
Следовательно, $BOEH$ – параллелограмм, а значит $overrightarrow{OB}+overrightarrow{OE}=overrightarrow{OH}$.
Таким образом $overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}=overrightarrow{OH}$.
Теорема
$OH=sqrt{9R^2-(a^2+b^2+c^2)}$ , где $R$ – радиус описанной
окружности; $a,b,c$ – длины сторон треугольника.
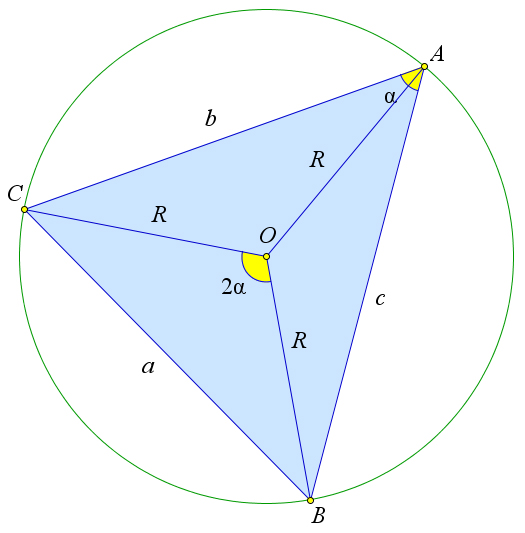
Доказательство
Рассмотрим остроугольный треугольник $ABC$, около которого описана окружность с
центром $O$. Центральный угол $BOC$ и вписанный угол $BAC$ опираются
на дугу $BC$, поэтому $angle BAC=2cdotangle BOC$. Кроме того по
обобщённой теореме синусов верны соотношения $a=2Rsin{A},
b=2Rsin{B}, c=2Rsin{gamma}$. Учитывая эти соотношения, а так же
теорему ref{119}, получаем
$OH^2=overrightarrow{OH}^2=(overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC})^2=$
$=OA^2+OB^2+OC^2+2overrightarrow{OA}cdotoverrightarrow{OB}+2overrightarrow{OA}cdot overrightarrow{OC}+2overrightarrow{OB}cdot overrightarrow{OC}=$
$=3R^2+2R^2cos{2A}+2R^2cos{2B}+2R^2cos{2C}=$
$=3R^2+2R^2(1-2sin^2{A})+2R^2(1-2sin^2{B})+2R^2(1-2sin^2{C})=$
$=9R^2-(4R^2sin^2{A}+4R^2sin^2{B}+4R^2sin^2{C})=9R^2-(a^2+b^2+c^2).$
Если треугольник тупоугольный с тупым углом $angle A$, то $angle BAC=360^circ-2cdotangle BOC$, но доказательства это не меняет, так как $ cos{(360^circ-2x)} = cos{2x}$.
Если треугольник прямоугольный с прямым углом $angle A$, то $angle BOC = 180^circ = 2cdot angle A$, и доказательство не меняется.
Следствие
$OZ = dfrac{1}{3}sqrt{9R^2-(a^2+b^2+c^2)}$
$ZH = dfrac{2}{3}sqrt{9R^2-(a^2+b^2+c^2)}$
Теорема
$HC = ABcdot|ctg{gamma}|$.
Доказательство
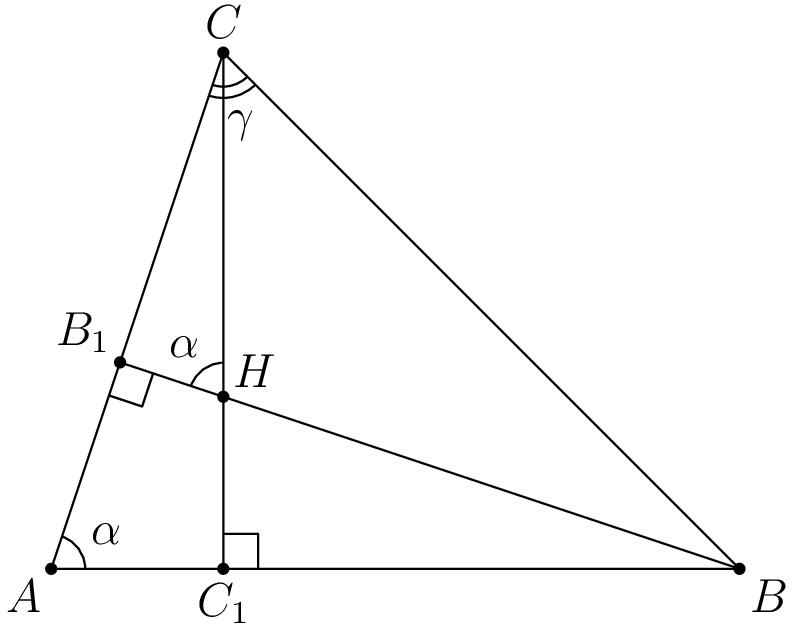
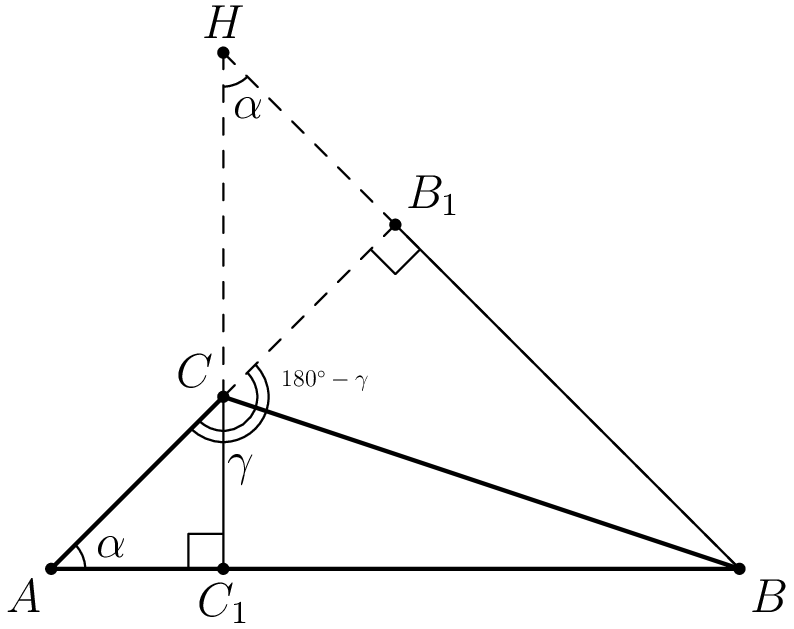
Рассмотрим треугольник $ABC$, с высотами $BB_1$ и $CC_1$.
$HC = dfrac{B_1C}{sin{alpha}}=dfrac{BCcdot|cos{gamma}|}{sin{alpha}} = dfrac{ABcdot|cos{gamma}|}{sin{gamma}} = ABcdot|ctg{gamma}| $
Первое равенство следует из треугольника $B_1HC$, второе – из треугольника $BB_1C$, а третье из теоремы синусов для треугольника $ABC$. Модуль появляется из-за случая, когда $angle С=gamma$ – тупой.
Ссылки
https://math.stackexchange.com/questions/1767751/distance-between-incentre-and-orthocentre
$$sqrt{2r^2-4R^2cos Acos Bcos C}$$
here $r$ is inradius and $R$ is circumradius. I considered $triangle A P I(P$ is orthocentre and $I$ is incentre). I
could find $A P=2 R cos A, A I=4 R sin frac{B}{2} sin frac{C}{2}$ and $angle P A I=angle frac{B-C}{2}$
So applying cosine rule I got
$begin{align}&small PI^2=4R^2color{red}{cos^2A}+16R^2sin^2frac{B}{2}sin^2frac{C}{2} -16R^2cos Asinfrac{B}{2}sinfrac{C}{2}Bigg(cosfrac{B}{2}cosfrac{C}{2}+sinfrac{B}{2}sinfrac{C}{2}Bigg)\&small=4R^2left(cos^2A+4sin^2frac{B}{2}sin^2frac{C}{2} -4cos Asinfrac{B}{2}sinfrac{C}{2}Bigg(cosfrac{B}{2}cosfrac{C}{2}+sinfrac{B}{2}sinfrac{C}{2}Bigg)right)\&small=4R^2left(cos^2A+4sin^2frac{B}{2}sin^2frac{C}{2}-cos Acdot color{green}{2sinfrac{B}{2}cosfrac{B}{2}cdot 2sinfrac{C}{2}cosfrac{C}{2}}-4cos Asin^2frac{B}{2}sin^2frac{C}{2}right)\&small=4R^2left(cos^2A+8sin^2frac{B}{2}sin^2frac{C}{2}cdot color{blue}{frac 12left(1-cos Aright)}-cos Acolor{green}{sin Bsin C}right)\&small=4R^2left(cos^2A+8color{blue}{sin^2frac A2}sin^2frac{B}{2}sin^2frac{C}{2}-cos Asin Bsin Cright)\&small=4R^2left(8sin^2frac A2sin^2frac{B}{2}sin^2frac{C}{2}+cos A(cos A-sin Bsin C)right)\&small=4R^2left(8sin^2frac A2sin^2frac{B}{2}sin^2frac{C}{2}+cos A(cos(180^circ-(B+C))-sin Bsin C)right)\&small=4R^2left(8sin^2frac A2sin^2frac{B}{2}sin^2frac{C}{2}-cos Acos Bcos Cright)\&small =2left(4Rsin frac A2sin frac B2sinfrac C2right)^2-4R^2cos Acos Bcos C\&small=2r^2-4R^2cos Acos Bcos Cend{align}$
Теорема (расстояние между ортоцентром и инцентром)
$$HI = sqrt{4R^2-dfrac{a^3+b^3+c^3+abc}{2p}}.$$
Доказательство
Чтобы центр масс треугольника попал в инцентр $I$ вершины $A, B, C$ нужно загрузить массами $a, b, c$ соответственно.
Тогда для любой точки $X$ будет верно равенство $$overrightarrow{XI} = dfrac{a}{a+b+c}overrightarrow{XA}+dfrac{b}{a+b+c}overrightarrow{XB}+dfrac{c}{a+b+c}overrightarrow{XC}.$$
Тогда можно взять вместо точки $X$ ортоцентр $H$:
$$overrightarrow{HI} = dfrac{1}{2p}left(acdot overrightarrow{HA}+bcdot overrightarrow{HB}+ccdot overrightarrow{HC}right)$$
Вспомним, что $HA = actg{alpha}$. Тогда
$HI^2 = dfrac{1}{4p^2}left(acdot overrightarrow{HA}+bcdot overrightarrow{HB}+ccdot overrightarrow{HC}right)^2 = $
$ = dfrac{1}{4p^2}left(a^2 overrightarrow{HA}^2+b^2 overrightarrow{HB}^2+c^2 overrightarrow{HC}^2+2aboverrightarrow{HA}cdotoverrightarrow{HB}+2bcoverrightarrow{HB}cdotoverrightarrow{HC}+2acoverrightarrow{HA}cdotoverrightarrow{HC}right)$
Лемма 0
$$cos{alpha}cos{beta}cos{gamma} = dfrac{sin^2{alpha}+sin^2{beta}+sin^2{gamma}}{2}-1 = dfrac{a^2+b^2+c^2}{8R^2}-1$$
Лемма 1
$a^2 overrightarrow{HA}^2+b^2 overrightarrow{HB}^2+c^2 overrightarrow{HC}^2 = $
$= a^4ctg^2{alpha}+b^4ctg^2{beta}+c^4ctg^2{gamma} = $
$= 16R^4sin^4{alpha}ctg^2{alpha}+16R^4sin^4{beta}ctg^2{beta}+16R^4sin^4{gamma}ctg^2{gamma} = $
$= 16R^4(sin^2{alpha}cos^2{alpha}+sin^2{beta}cos^2{beta}+sin^2{gamma}cos^2{gamma}) = $
$= 16R^4(sin^2{alpha}-sin^4{alpha}+sin^2{beta}-sin^4{beta}+sin^2{gamma}-sin^4{gamma}) = $
$= 16R^4left(dfrac{a^2}{4R^2}+dfrac{b^2}{4R^2}+dfrac{c^2}{4R^2}-dfrac{a^4}{16R^4}-dfrac{b^4}{16R^4}-dfrac{c^4}{16R^4}right) = $
$=4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)$
Лемма 2
$2aboverrightarrow{HA}cdotoverrightarrow{HB}+2bcoverrightarrow{HB}cdotoverrightarrow{HC}+2acoverrightarrow{HA}cdotoverrightarrow{HC} = $
$ = +2a^2b^2ctg^2{alpha}ctg^2{beta}cos{(180^circ-gamma)} + 2b^2c^2ctg^2{beta}ctg^2{gamma}cos{(180^circ-alpha)} + 2a^2c^2ctg^2{alpha}ctg^2{gamma}cos{(180^circ-beta)} = $
$ = -2a^2b^2ctg^2{alpha}ctg^2{beta}cos{gamma} – 2b^2c^2ctg^2{beta}ctg^2{gamma}cos{alpha} – 2a^2c^2ctg^2{alpha}ctg^2{gamma}cos{beta} = $
$ = -2cos{alpha}cos{beta}cos{gamma}left(dfrac{a^2b^2}{sin{alpha}sin{beta}}+dfrac{b^2c^2}{sin{beta}sin{gamma}}+dfrac{a^2c^2}{sin{alpha}sin{gamma}}right) = $
$ = -2cos{alpha}cos{beta}cos{gamma}left(4R^2ab+4R^2bc+4R^2acright) = $
$ = -2left(dfrac{a^2+b^2+c^2}{8R^2}-1right)4R^2left(ab+bc+acright) = $
$ = 4R^2left(2ab+2bc+2acright)-(a^2+b^2+c^2)(ab+bc+ac)$
продолжение доказательства
Тогда
$HI^2 = dfrac{1}{4p^2}left(a^2 overrightarrow{HA}^2+b^2 overrightarrow{HB}^2+c^2 overrightarrow{HC}^2+2aboverrightarrow{HA}cdotoverrightarrow{HB}+2bcoverrightarrow{HB}cdotoverrightarrow{HC}+2acoverrightarrow{HA}cdotoverrightarrow{HC}right) =$
$= dfrac{1}{4p^2}left(4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)+4R^2left(2ab+2bc+2acright)-(a^2+b^2+c^2)(ab+bc+ac)right) = $
$= dfrac{1}{4p^2}left(4R^2(a^2+b^2+c^2+2ab+2bc+2ac)-(a^4+b^4+c^4+(a^2+b^2+c^2)(ab+bc+ac))right) = $
$= dfrac{1}{4p^2}left(4R^2(a+b+c)^2-(a^4+b^4+c^4+a^3b+a^2bc+a^3c+ab^3+b^3c+b^2ac+abc^2+bc^3+ac^3)right) = $
$= dfrac{1}{4p^2}left(16R^2p^2-(a^4+a^3b+a^3c+ab^3+b^4+cb^3+ac^3+bc^3+c^4+a^2bc+ab^2c+abc^2)right)=$
$= dfrac{1}{4p^2}left(16R^2p^2-(a^3(a+b+c)+b^3(a+b+c)+c^3(a+b+c)+abc(a+b+c))right) =$
$= dfrac{1}{4p^2}left(16R^2p^2-(a^3+b^3+c^3+abc)2pright) =$
$= 4R^2-dfrac{a^3+b^3+c^3+abc}{a+b+c}$
Теорема
$$HI_a=sqrt{4R^2-dfrac{-a^3+b^3+c^3-abc}{2(p-a)}}$$
Доказательство
Лемма 3
$-2aboverrightarrow{HA}cdotoverrightarrow{HB}+2bcoverrightarrow{HB}cdotoverrightarrow{HC}-2acoverrightarrow{HA}cdotoverrightarrow{HC} = $
$ = -2a^2b^2ctg^2{alpha}ctg^2{beta}cos{(180^circ-gamma)} + 2b^2c^2ctg^2{beta}ctg^2{gamma}cos{(180^circ-alpha)} – 2a^2c^2ctg^2{alpha}ctg^2{gamma}cos{(180^circ-beta)} = $
$ = 2a^2b^2ctg^2{alpha}ctg^2{beta}cos{gamma} – 2b^2c^2ctg^2{beta}ctg^2{gamma}cos{alpha} 2a^2c^2ctg^2{alpha}ctg^2{gamma}cos{beta} = $
$ = -2cos{alpha}cos{beta}cos{gamma}left(-dfrac{a^2b^2}{sin{alpha}sin{beta}}+dfrac{b^2c^2}{sin{beta}sin{gamma}}-dfrac{a^2c^2}{sin{alpha}sin{gamma}}right) = $
$ = -2cos{alpha}cos{beta}cos{gamma}left(-4R^2ab+4R^2bc-4R^2acright) = $
$ = -2left(dfrac{a^2+b^2+c^2}{8R^2}-1right)4R^2left(-ab+bc-acright) = $
$ = 4R^2left(-2ab+2bc-2acright)-(a^2+b^2+c^2)(-ab+bc-ac)$
продолжение доказательства
Тогда
$HI^2_a = dfrac{1}{4(p-a)^2}left(a^2 overrightarrow{HA}^2+b^2 overrightarrow{HB}^2+c^2 overrightarrow{HC}^2-2aboverrightarrow{HA}cdotoverrightarrow{HB}+2bcoverrightarrow{HB}cdotoverrightarrow{HC}-2acoverrightarrow{HA}cdotoverrightarrow{HC}right) =$
$=dfrac{1}{4(p-a)^2}left(4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)+4R^2left(-2ab+2bc-2acright)-(a^2+b^2+c^2)(-ab+bc-ac)right)$
$=dfrac{1}{4(p-a)^2}left(4R^2(a^2+b^2+c^2-2ab+2bc-2ac)-((a^4+b^4+c^4)+(a^2+b^2+c^2)(-ab+bc-ac))right)$
$=dfrac{1}{4(p-a)^2}left(4R^2(-a+b+c)^2-(a^4 – a^3 b – a^3 c
+ b^4 – a b^3 + b^3 c
+ c^4 – a c^3 + b c^3
+ a^2 b c – a b^2 c – a b c^2)right)$
$=dfrac{1}{4(p-a)^2}left(4R^2(-a+b+c)^2-(
– a^3(-a+b+c)
+ b^3(-a+b+c)
+ c^3(-a+b+c)
– abc(-a+b+c)right)$
$=dfrac{1}{4(p-a)^2}left(16R^2(p-a)^2-2(p-a)(
– a^3+ b^3+ c^3- abc)right)$
$=4R^2-dfrac{-a^3+b^3+c^3-abc}{2(p-a)}$
| Ортоцентр | |
|---|---|
 Высоты и ортоцентр |
|
| Барицентрические координаты |
 |
| Трилинейные координаты |
 |
| Код ЭЦТ | X(4) |
| Связанные точки | |
| Изогонально сопряженная | центр описанной окружности |
| Дополнительная[es] | центр описанной окружности |
| Антидополнительная[es] | точка де Лоншама[en] |
Ортоцентр (от др.-греч. ὀρθός «прямой») — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой 
Свойства[править | править код]
- Если в четвёрке точек
,
,
,
точка
является точкой пересечения высот треугольника
, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек (см. рис.).
- Более того, при любом разбиении множества ортоцентрической системы точек
на две пары, например,
и
или при любом другом подобном разбиении, всегда перпендикулярны образующиеся два отрезка прямых с концами в данных точках множеств (в нашем случае
перпендикулярно
) независимо от выбора этих двух пар
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона.
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
- Более того, при любом разбиении множества ортоцентрической системы точек

Точки, симметричные ортоцентру относительно сторон, лежат на описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности (см. рисунок)[1].
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если
— центр описанной окружности
, то
.
- При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью, всегда делится окружностью Эйлера пополам. Это следует из того, что ортоцентр есть центр гомотетии этих двух окружностей с коэффициентом
.
- Четыре попарно пересекающиеся прямые, никакие три из которых не проходят через одну точку (четырёхсторонник), при пересечении образуют четыре треугольника. Их ортоцентры лежат на одной прямой (на прямой Обера).
- Если считать, что ортоцентр треугольника делит первую высоту на части длиной
и
, вторую высоту на части длиной
и
, третью высоту на части длиной
и
, тогда
[4][5].
- Цепочка уравнений в последнем пункте:
по сути означает, что три пары отрезков, на которые ортоцентр разделяет три высоты остроугольного треугольника, подчиняются правилу хорд, пересекающихся внутри окружности, например:
. Отсюда автоматически следует то, что через четыре конца любых двух высот остроугольного треугольника всегда можно провести окружность (высоты в ней будут пересекающимися хордами). Оказывается, это утверждение сохраняет силу и для тупоугольного, и прямоугольного треугольников.
- Расстояние от стороны до центра описанной окружности равно половине расстояния от противоположной ей вершины до ортоцентра[6][7].
- Сумма квадратов расстояний от вершин до ортоцентра плюс сумма квадратов сторон равна двенадцати квадратам радиуса описанной окружности[8].
- Три основания высот остроугольного треугольника или три проекции ортоцентра на стороны треугольника образуют ортотреугольник.

Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра
- Трилинейной полярой ортоцентра является ортоцентрическая ось
(Orthic axis) (см. рис.)
- Четыре ортоцентра четырёх треугольников, образованных четырьмя попарно пересекающимися прямыми, никакие три из которых не проходят через одну точку, лежат на одной прямой (Прямая Обера четырёхугольника). Здесь используются те же четыре треугольника, что и при построении точки Микеля.
- Существует формула Карно[9]:
,
- где
,
,
— расстояния от центра описанной окружности соответственно до сторон
,
,
треугольника,
,
,
— расстояния от ортоцентра соответственно до вершин
,
,
треугольника.

В ортоцентрической системе 4 точек любая точка является ортоцентром треугольника, образованного 3 остальными точками.
- Ортоцентрическая система. Здесь O1, O2, O3 и O4 — центры окружностей четырех возможных треугольников, образованных из ортоцентрических точек A1, A2, A3 и A4 (см. рис.). Три из них вершины исходного треугольника, а четвертая — его ортоцентр. Радиусы всех четырех окружностей равны. Центры трех из четырех окружностей (кроме описанной исходного треугольника) образуют вершины треугольника, равного исходному, со сторонами, попарно параллельными сторонам исходного треугольника.
Ортоцентрическая система. Здесь O1, O2, O3 и O4 — центры окружностей четырех возможных треугольников, образованных из ортоцентрических точек A1, A2, A3 и A4.
- *Если прямая ℓ ортополюса P проходит через ортоцентр Q треугольника, то точка, расположенная на продолжении отрезка PQ, соединяющего ортополюс с ортоцентром, по другую сторону на расстоянии, равном PQ, лежит на окружности Эйлера этого треугольника.[10]
История[править | править код]
Утверждение: «Все 3 высоты треугольника пересекаются в одной точке», называемой теперь ортоцентром, в «Началах» Евклида отсутствует. Ортоцентр впервые в греческой математике использован в «Книге лемм» Архимеда, хотя явного доказательства существования ортоцентра Архимед не привёл.
Часть историков приписывает это утверждение Архимеду и называют его теоремой Архимеда[11]. До середины девятнадцатого века, ортоцентр нередко называли архимедовой точкой[12].
В явном виде это утверждение («Все 3 высоты треугольника пересекаются в одной точке») встречается у Прокла (410—485) — комментатора Евклида[13].
Другие историки математики считают автором первого доказательства Уильяма Чеппла (англ.) (рус. (Miscellanea Curiosa Mathematica, 1749 год)[14].
Термин ортоцентр впервые был использован У. Х. Безантом (англ.) (рус. в работе «Конические сечения, исследованные геометрически (1869)» ([15])[16].
См. также[править | править код]
- Высота треугольника
- Высота (геометрия)
- Замечательные точки треугольника
- Центр вписанной окружности
- Ортотреугольник
- Ортоцентроидная окружность
- Центроид
Примечания[править | править код]
- ↑ Honsberger, 1995, p. 18.
- ↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers»,
Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html Архивная копия от 28 апреля 2021 на Wayback Machine - ↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
- ↑ Altshiller-Court, 2007, p. 94.
- ↑ Honsberger, 1995, p. 20.
- ↑ Altshiller-Court, 2007, p. 99.
- ↑ Honsberger, 1995, p. 17, 23.
- ↑ Altshiller-Court, 2007, p. 102.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд. — М.: Учпедгиз, 1962. — С. 120—125 (задача), параграф 57, с. 73.
- ↑ College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. Nathan Altshiller-Court. (Параграф: G. The Orthopole. Пункт. 699. Теорема. Fig. 156. С.290-291). Mineola, New York: Dover Publication, Inc., 2012. 292 p.
- ↑ Ефремов Д. Новая геометрия треугольника. Одесса, 1902. С. 9, п. 16. Высоты треугольника. Теорема Архимеда.
- ↑ Maureen T. Carroll, Elyn Rykken. Geometry: The Line and the Circle. Дата обращения: 10 апреля 2020.
- ↑ Nathan Altshiller-Court. «College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle». Second Edition. Mineola, New York: Dover Publications, Inc. 2007. P. 298, § 175.
- ↑ Bogomolny, Alexander, A Possibly First Proof of the Concurrence of Altitudes, <https://www.cut-the-knot.org/triangle/Chapple.shtml>. Проверено 17 ноября 2019. Архивная копия от 7 мая 2021 на Wayback Machine
- ↑ Conic Sections Treated Geometrically, 1869. Ссылка: 1895: Conic sections treated geometrically Архивная копия от 18 апреля 2018 на Wayback Machine from Cornell University Historical Math Monographs.
- ↑ Nathan Altshiller-Court. «College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle». Second Edition. Mineola, New York: Dover Publications, Inc. 2007. § 176, p. 94; § 176, p. 298
Литература[править | править код]
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 37—39. — ISBN 5-94057-170-0.
- Nathan Altshiller-Court. College geometry : an introduction to the modern geometry of the triangle and the circle. — Dover Publications, Inc., 2007. — ISBN 0-486-45805-9.
- Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Mathematical Association of America, 1995. — Vol. 37. — P. 17—26. — (New Mathematical Library). — ISBN 0-88385-639-5 (Vol. 37). — ISBN 0-88385-600-X (complete set).
Ссылки[править | править код]
- Живой чертёж
- Weisstein, Eric W. Orthocenter (англ.) на сайте Wolfram MathWorld.
- Bernard Gibert Circumcubic K006 (недоступная ссылка)
- Clark Kimberling, «Encyclopedia of triangle centers».
- Weisstein, Eric W. «Orthocentric System.» From MathWorld–A Wolfram Web Resource. [1]
Чтобы найти ортоцентр треугольника, можно воспользоваться калькулятором, где следует внести координаты. В автоматическом режиме с помощью формул произведется расчет. Можно также все расчеты произвести самостоятельно.
Например, имеются следующие данные точек:
А – 4,3;
В – 0,5;
С – 3,-6.
Первое , что необходимо найти наклон сторон, который обозначается – m , используется формула :
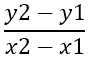
Из этого следует:
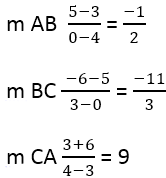
Далее необходимо найти наклон перпендикулярных сторон, для этого используется формула:
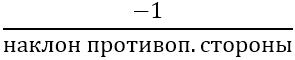
Имеем:
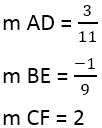
Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:
y-y1 = m(x-x1) y-3 = 3/11(x-4)
С помощью упрощения, имеем: 3х – 11у=-21
Для линии ВЕ, где точка 0,5, а наклон -1/9, имеем 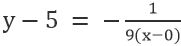
Упрощение дает: х+9у=45.
И последние линии CF, где точка 3, -6, а наклон 2, имеем уравнение y+6 = 2(x-3).
И упрощение, 2x — y = 12.
Если решить два из трех уравнений будут найдены значения х и у. Для данного примера:
Значение х = 8,05263;
Значение у = 4,10526.
Которые в данном случае являются координатами искомого Ортоцентра.

