Как найти подобные треугольники в трапеции

Рассмотрим базовые задачи на подобные треугольники в трапеции.

I. Точка пересечения диагоналей трапеции  — вершина подобных треугольников.

Рассмотрим треугольники AOD и COB.

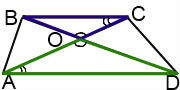
Визуализация облегчает  решение задач на подобие. Поэтому подобные треугольники в трапеции выделим разными цветами.

1) ∠AOD=∠COB (как вертикальные);

2)∠DAO=∠BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).

Следовательно, треугольники AOD и COB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

Задача.

Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.

Решение:

AO=9 см, CO=5 см, BD=28 см. BO =?, DO- ?

Доказываем подобие треугольников AOD и COB. Отсюда

   

Выбираем нужные отношения:

   

Пусть BO=x см, тогда DO=28-x см. Следовательно,

   

   

   

   

BO=10 см, DO=28-10=18 см.

Ответ: 10 см, 18 см.

 Задача

Известно, что О — точка пересечения диагоналей трапеции ABCD (AD ∥  BC). Найти длину отрезка BO, если AO:OC=7:6 и BD=39 см.

Решение:

Аналогичн0, доказываем подобие треугольников AOD и COB и

   

Пусть BO=x см, тогда DO=39-x см. Таким образом,

   

   

   

Ответ: 18 см.

II. Продолжения боковых сторон трапеции пересекаются в точке.

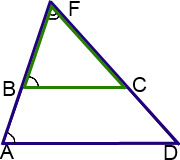
Аналогично задаче I, рассмотрим треугольники AFD и BFC:

1) ∠F — общий;

2)∠ DAF=∠CBF (как соответственные углы при BC ∥ AD и секущей AF).

Следовательно, треугольники AFD и BFC подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

Задача

Продолжения боковых сторон AB и CD  трапеции ABCD пересекаются в точке F. Меньшее основание BC равно 4 см, BF=5 см, AB=15 см. Найти большее основание трапеции.

Решение:

Доказываем, треугольники AFD и BFC — подобны.

Следовательно,

   

   

   

   

   

Ответ: 16 см.

В следующий раз рассмотрим задачи на отношение площадей подобных треугольников.

Узнать ещё

Знание — сила. Познавательная информация

Подобные треугольники в трапеции

Рассмотрим базовые задачи на подобные треугольники в трапеции.

I. Точка пересечения диагоналей трапеции — вершина подобных треугольников.

Рассмотрим треугольники AOD и COB.

Визуализация облегчает решение задач на подобие. Поэтому подобные треугольники в трапеции выделим разными цветами.

1) ∠AOD= ∠ COB (как вертикальные);

2) ∠DAO= ∠ BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).

Следовательно, треугольники AOD и COB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.

AO=9 см, CO=5 см, BD=28 см. BO =?, DO- ?

Доказываем подобие треугольников AOD и COB. Отсюда

Выбираем нужные отношения:

Пусть BO=x см, тогда DO=28-x см. Следовательно,

BO=10 см, DO=28-10=18 см.

Ответ: 10 см, 18 см.

Известно, что О — точка пересечения диагоналей трапеции ABCD (AD ∥ BC). Найти длину отрезка BO, если AO:OC=7:6 и BD=39 см.

Аналогичн0, доказываем подобие треугольников AOD и COB и

Пусть BO=x см, тогда DO=39-x см. Таким образом,

II. Продолжения боковых сторон трапеции пересекаются в точке.

Аналогично задаче I, рассмотрим треугольники AFD и BFC:

2) ∠ DAF= ∠ CBF (как соответственные углы при BC ∥ AD и секущей AF).

Следовательно, треугольники AFD и BFC подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке F. Меньшее основание BC равно 4 см, BF=5 см, AB=15 см. Найти большее основание трапеции.

Доказываем, треугольники AFD и BFC — подобны.

В следующий раз рассмотрим задачи на отношение площадей подобных треугольников.

Основания BC и AD трапеции

Рассмотрим еще одну задачу на подобие треугольников.

Основания BC и AD трапеции ABCD равны соответственно 9 и 36, BD=18. Доказать, что треугольники CBD и BDA подобны.

Дано : ABCD — трапеция, AD ∥ BC,

Рассмотрим треугольники и BDA.

1) ∠CBD=∠BDA (как внутренние накрест лежащие при AD ∥ BC и секущей BD)

Диагонали трапеции

Свойства диагоналей трапеции

1. Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
2. Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения – подобны
3. Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции – равновеликие (имеют одинаковую площадь)
4. Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
5. Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
6. Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b – основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Свойства треугольников, образованных диагоналями трапеции

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Свойства трапеции, достроенной до треугольника

• Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
• Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Свойства отрезка, параллельного основаниям трапеции

• Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
• Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Формулы нахождения диагоналей трапеции через высоту

Примечание. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа – задайте вопрос на форуме.

Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам – AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16

Задача .
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение .
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая – то обозначим длину AM = a, длину KD = b ( не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK – прямоугольник.

Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 – b

Треугольники DBM и ACK – прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

h 2 + (24 – a) 2 = (5√17) 2
и
h 2 + (24 – b) 2 = 13 2

Учтем, что a = 16 – b , тогда в первом уравнении
h 2 + (24 – 16 + b) 2 = 425
h 2 = 425 – (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 – (8 + b) 2 + (24 – b) 2 = 169
-(64 + 16b + b) 2 + (24 – b) 2 = -256
-64 – 16b – b 2 + 576 – 48b + b 2 = -256
-64b = -768
b = 12

Таким образом, KD = 12
Откуда
h 2 = 425 – (8 + b) 2 = 425 – (8 + 12) 2 = 25
h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b – основания трапеции, h – высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2

Ответ: площадь трапеции равна 80 см 2 .

[spoiler title=”источники:”]

http://profmeter.com.ua/communication/learning/course/course7/lesson181/

[/spoiler]

Диагонали трапеции пересекаются в точке. Что можно сказать об образовавшихся  треугольниках, прилежащих к основаниям?

Утверждение.

Если диагонали трапеции пересекаются в точке, то образованные при этом прилежащие к основаниям треугольники подобны.

Дано:  ABCD — трапеция,

   

   

Доказать:

   

Доказательство:

В треугольниках AOD и COB

1) ∠AOD=∠COB (как вертикальные)

2) ∠DAO=∠BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).

Следовательно, треугольники AOD и COB подобны (по двум углам).

Что и требовалось доказать.

Задача.

Одна из диагоналей трапеции равна 14 см и делит другую диагональ на отрезки длиной  см и см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.

Дано: ABCD — трапеция,

   

   

AC=14 см, DO=20 см, BO=8 см.

Найти: AO, CO.

Решение:

   

(доказали в утверждении выше).

Из подобия треугольников следует пропорциональность их соответствующих сторон:

   

Пусть CO=x см, тогда AO=(14-x) см. Отсюда

   

   

   

   

   

   

Значит, CO=4 см, AO=14-4=10 см.

Ответ: 4 см, 10 см.

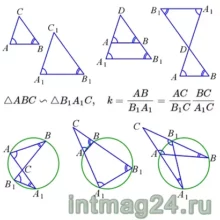Подобные треугольники — это треугольники, у которых  отношения всех их соответствующих сторон равны. Отношение k соответствующих сторон подобных треугольников называется коэффициентом подобия этих треугольников.
На рисунке:  △ABC∽△A₁B₁C₁ ⇔ AB/A₁B₁=AC/A₁C₁=BC/B₁C₁; k=AB/A₁B₁=AC/A₁C₁=BC/B₁C₁.

Свойство углов подобных треугольников

Если треугольники подобны, то все их соответствующие углы равны.
На рисунке: △ABC∽△A₁B₁C₁ ⇒ ∠A=∠A₁, ∠B=∠B₁, ∠C=∠C₁.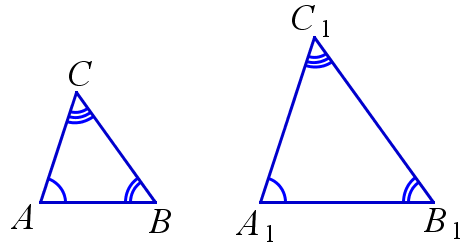

Признаки подобия треугольников

Отношения для подобных треугольников

• Отношение любых двух соответствующих линейных элементов (стороны, медианы, радиус, периметр) подобных треугольников равно коэффициенту подобия этих треугольников.
• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

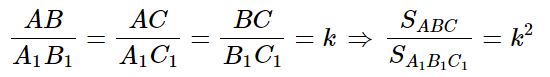
Параллельные прямые и подобие треугольников

Если стороны двух треугольников лежат на соответственно параллельных или совпадающих прямых, то такие треугольники подобны. В частности, параллельные прямые отсекают от угла, либо вертикальных углов, подобные треугольники. На рисунке: AB||A₁B₁, AC||A₁C₁, BC||B₁C₁.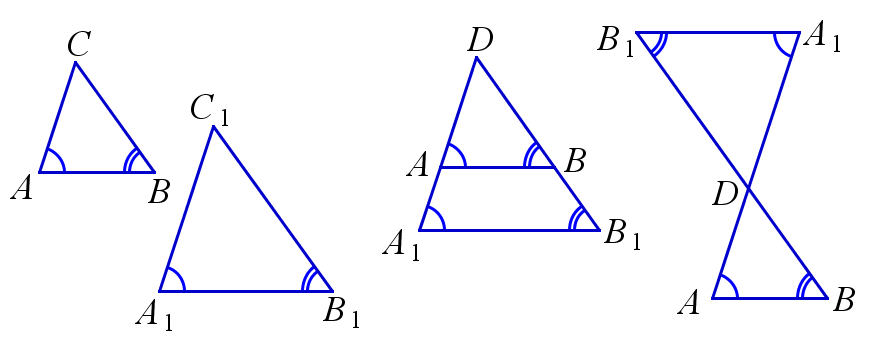 

При пересечении диагоналей трапеции, а также продолжений её боковых сторон, образуются подобные треугольники, прилежащие к основаниям трапеции. Коэффициент подобия в обоих случаях равен отношению оснований трапеции. На рисунке: k=AD/BC; k=AD/BC.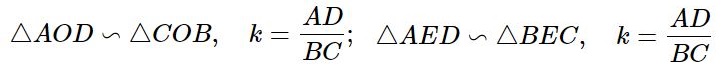 
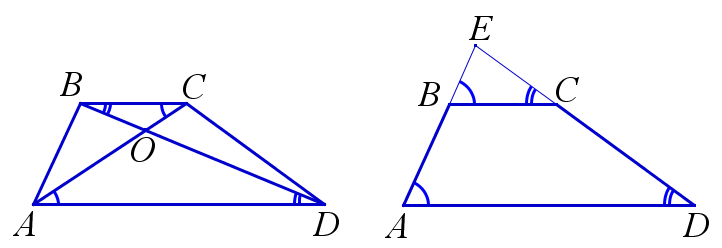
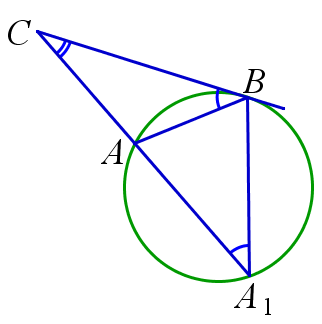
При пересечении двух прямых с окружностью образуются подобные треугольники. На рисунке: k=AB/B₁A₁=AC/B₁C*BC/A₁C.

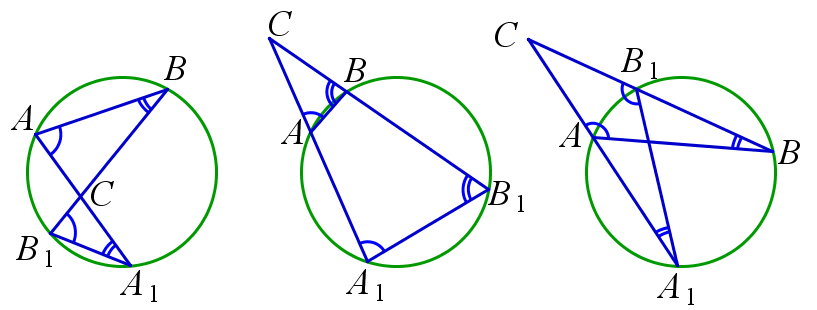
Касательная к окружности и подобные треугольники.
Пусть к окружности проведена касательная CB и секущая CA, пересекающая окружность во второй раз в точке A1. Тогда △ABC∽△BA₁C. На рисунке: △ABC∽△BCA₁, k=AB/BA₁=AC/BC * BC/A₁C.