Задачи по статистике с решениями: Мода и медиана
Задания по статистике по структурным средним
К структурным средним относятся медиана и мода.
Задача №1. Нахождение моды и медианы для интервального ряда
Рассчитать моду по данным таблицы. Решение приведем ниже. Сначала выберем модальный интервал, максимальная частота в нашем случае равна 10. Таким образом, получаем:
|
Группы предприятий по стоимости ОПФ, у.е. |
Число предприятий, f |
Середина интервалов, х |
Накопленная частота, S |
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 19 21 22 |
2 8 18 22 25 |
|
Итого: |
25 |
– |
1) По максимальной частоте найдем модальный интервал: Fmax=10 → I = 18-20
2) По соответствующей формуле (формулы моды и медианы приведены ниже)
Мода =18+2(10-6)/(10-6)(10-4)=18,33 млн. руб. – наиболее часто встречающаяся стоимость ОПФ среди 25 предприятий.
Вычислим медиану по приведенным исходным данным.
Как найти медиану? В данной задачи нам даны интервалы.
1) Найдем медианный интервал по накопленной частоте. Нужная накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n +1/2 или n/2.
Для нечетного ряда (25+1)/2= 13→S= 18 →18-20- медианный интервал.
2) По соответствующей формуле (формулы моды и медианы приведены ниже)
Медиана Ме =18+2[(25+1)/2 – 8/10]=18,9 млн.руб. Из 25 малых предприятий региона 12 пр. имеют стоимость ОПФ менее 18 млн.руб., а 12 пр. более.
Задача №2. Нахождение моды и медианы для дискретного ряда.
|
тарифный разряд, Xi |
Число рабочих f |
Частость, w |
Накопленная частота, S |
|
2 |
1 |
0,05 |
1 |
|
3 |
5 |
0,25 |
6 |
|
4 |
8 |
0,4 |
14 |
|
5 |
4 |
0,2 |
18 |
|
6 |
2 |
0,1 |
20 |
|
Итого: |
20 |
1,0 |
20 |
Распределение рабочих 5 участков по их квалификации (тарифному разряду)
Найти моду по приведенным данным.
Решение:
По максимальной частоте найдем соответствующую группу и варианту: f max=8 → Мода=4 разряд. Наиболее часто встречающийся разряд рабочих 4.
Определить медиану по данным таблицы.
Как рассчитать медиану? Прежде всего найдем медианный интервал по накопленной частоте. Нужная накопленную частоту. Накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n+1/2 или n/2.
Для четного ряда 20/2= 10→S= 14 → Ме =4 разряд. Половина всех рабочих имеет тарифный разряд меньше 4, другая половина больше 4.
Теория для решения данных задач. Формулы для расчета моды и медианы
Модой в статистике называется величины признака (варианта), которая чаще всего встречается в данной совокупности.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.
Распределительные средние – мода и медиана, их сущность и способы исчисления.
Данные показатели относятся к группе распределительных средних и используются для формирования обобщающей характеристики величины варьирующего признака.
Мода  – это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:
– это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:

где:  – нижняя граница модального интервала;
– нижняя граница модального интервала;
 – величина модального интервала;
– величина модального интервала;
 – частота модального интервала;
– частота модального интервала;
 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным;
– частота интервала, следующего за модальным;
Медиана (Ме) – это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:

где:  – нижняя граница медианного интервала;
– нижняя граница медианного интервала;
 – величина медианного интервала;
– величина медианного интервала;
 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
 – частота медианного интервала;
– частота медианного интервала;
Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:
| №п/п | Товарооборот, млн. руб. | Число фирм |
| 1 | до 5 | 20 |
| 2 | 5-10 | 26 |
| 3 | 10-15 | 20 |
| 4 | 15-20 | 14 |
| 5 | 20-25 | 10 |
| 6 | 25 и более | 10 |
| Итого | – | 100 |
Определите:
а) средний размер месячного товарооборота на одну фирму;
б) модальное и медианное значение месячного товарооборота;
в) сделайте выводы о характере данного распределения.
Решение:
а) Рассчитаем средний размер товарооборота на одну фирму.
В данном ряду варианты усредняемого признака (товарооборот) представлены не одним числом, а в виде интервала «от – до». Причём первый и последний – интервалы открытые.
В таких рядах условно принимается, величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей. Таким образом, товарооборот первой группы от 0 до 5 млн. руб., товарооборот последней – от 25 до 30 млн. руб. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
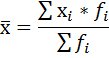
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так для первой группы дискретная величина х будет равна: (0 + 5) / 2 = 2,5. Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной:
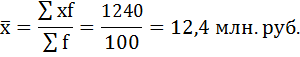
Исходные и расчётные данные представим в таблице:
| Товарооборот, млн. руб. | Число фирм, f | Середина интервала, х | xf | Сумма накопленных частот |
| 0-5 | 20 | 2,5 | 50 | 20 |
| 5-10 | 26 | 7,5 | 195 | 46 |
| 10-15 | 20 | 12,5 | 250 | 66 |
| 15-20 | 14 | 17,5 | 245 | – |
| 20-25 | 10 | 22,5 | 225 | – |
| 25-30 | 10 | 27,5 | 275 | – |
| Итого | 100 | – | 1240 | – |
б) Определим модальное и медианное значение месячного товарооборота.
В интервальных рядах распределения с равными интервалами мода определяется по формуле:
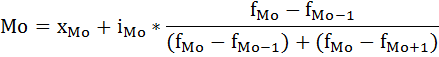
xMo – начальное значение интервала, содержащего моду;
iMo – величина модального интервала,
fMo – частота модального интервала,
f(Mo-1) – частота интервала, предшествующего модальному,
f(Mo+1) – частота интервала, следующего за модальным.
Наибольшее число фирм (26) имеют величину товарооборота от 5 до 10 млн. руб. Следовательно, этот интервал является модальным интервалом ряда распределения. Введём следующие обозначения:
xMo=5, iMo=5, fMo=26, f(Mo-1)=20, f(Mo+1)=20.
Подставим эти значения в формулу моды и произведём вычисления:
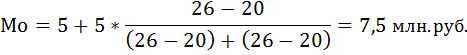
Следовательно, наибольшее число фирм имеет товарооборот 7,5 млн. руб.
Медиана интервального вариационного ряда распределения определяется по формуле:
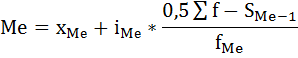
где xMе – начальное значение интервала, содержащего медиану;
iMе – величина медианного интервала;
Σf – сумма частот ряда;
S(Me-1) – сумма накопленных частот, предшествующих медианному интервалу;
fMe – частота медианного интервала.
Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (66), соответствует интервалу 10 – 15. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если:
xMе=10, iMе=5, Σf=100, S(Me-1)=46, fMe=20:
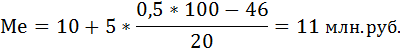
Таким образом, половина фирм имеет товарооборот менее 11 млн. руб., а остальные фирмы – более 11 млн. руб.
в) В симметричных рядах распределения значения моды и медианы совпадают со средней величиной, а в умеренно ассиметричных они соотносятся таким образом:
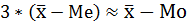
Соотношение характеристик центра распределения товарооборота свидетельствует об умеренной асимметрии:
3(12,4-11) ≈12,4-7,5
Цель урока: сформировать у учащихся
представление о медиане набора чисел и умение
вычислять ее для несложных числовых наборов,
закрепление понятия среднего арифметического
набора чисел.
Тип урока: объяснение нового материала.
Оборудование: доска, учебник под ред. Ю.Н
Тюрина “Теория вероятностей и статистика”,
компьютер с проектором.
Ход урока
1. Организационный момент.
Сообщить тему урока и сформулировать его цели.
2. Актуализация прежних знаний.
Вопросы учащимся:
- Что называется средним арифметическим набора
чисел? - Где располагается среднее арифметическое
внутри набора чисел? - Что характеризует среднее арифметическое
набора чисел? - Где часто применяется среднее арифметическое
набора чисел?
Устные задачи:
Найти среднее арифметическое набора чисел:
- 1, 3, 5, 7, 9;
- 10, 12, 18, 20
Проверка домашнего задания с помощью проектора
(Приложение 1):
Учебник: :№12(б,г), №18(в,г)
3. Изучение нового материала.
На предыдущем уроке мы познакомились с такой
статистической характеристикой как среднее
арифметическое набора чисел. Сегодня мы посвятим
урок еще одной статистической характеристике –
медиане.
Не только среднее арифметическое показывает,
где на числовой прямой располагаются числа
какого-либо набора и где их центр. Другим
показателем является медиана.
Медианой набора чисел называется такое число,
которое разделяет набор на две равные по
численности части. Вместо “медиана” можно было
бы сказать “середина”.
Сначала на примерах разберем, как найти
медиану, а затем дадим строгое определение.
Рассмотрим следующий устный пример с
применением проектора (Приложение
2)
В конце учебного года 11 учеников 7-го класса
сдали норматив по бегу на 100 метров. Были
зафиксированы следующие результаты:
|
Ученик |
Результат в секундах |
| Данила |
15,3 |
| Петя |
16,9 |
| Лена |
21,8 |
| Катя |
18,4 |
| Стас |
16,1 |
| Аня |
25,1 |
| Оля |
19,9 |
| Боря |
15,5 |
| Паша |
14,7 |
| Наташа |
20,2 |
| Миша |
15,4 |
После того как ребята пробежали дистанцию, к
преподавателю подошел Петя и спросил, кокой у
него результат.
“Самый средний результат: 16,9 секунды”, –
ответил учитель
“Почему?” – удивился Петя. – Ведь среднее
арифметическое всех результатов – примерно 18,3
секунды, а я пробежал на секунду с лишним лучше. И
вообще, результат Кати (18,4) гораздо ближе к
среднему, чем мой”.
“Твой результат средний, так как пять человек
пробежали лучше, чем ты, и пять – хуже. То есть ты
как раз посередине”, – сказал учитель. [ 2 ]
Далее предложить учащимся самостоятельно
рассмотреть по учебнику примеры 1,2,3 и
сформулировать алгоритм нахождения медианы
набора чисел.
Записать алгоритм нахождения медианы
набора чисел:
- Упорядочить числовой набор (составить
ранжированный ряд). - Одновременно зачеркиваем “самое большое” и
“самое маленькое” числа данного набора чисел до
тех пор пока не останется одно число или два
числа. - Если осталось одно число, то оно и есть медиана.
- Если осталось два числа, то медианой будет
среднее арифметическое двух оставшихся чисел.
Предложить учащимся самостоятельно
сформулировать определение медианы набора
чисел, затем прочитать в учебнике два
определения медианы ( стр. 50), далее разобрать
примеры 4 и 5 учебника (стр.50-52)
Замечание:
Обратить внимание учащихся на важное
обстоятельство: медиана практически не
чувствительна к значительным отклонениям
отдельных крайних значений наборов чисел. В
статистике это свойство называется
устойчивостью. Устойчивость статистического
показателя – очень важное свойство, оно страхует
нас от случайных ошибок и отдельных
недостоверных данных.
4. Закрепление изученного материала.
Решение номеров из учебника к п.11 “Медиана”.
№ 1(а)
Набор чисел: 1,3,5,7,9
![]() =( 1+3+5+7+9):5=25:5=5
=( 1+3+5+7+9):5=25:5=5
Ме = 5
![]() = Ме
= Ме
№1(б)
Набор чисел: 1,3,5,7,14.
![]() =( 1+3+5+7+14):5=30:5=6
=( 1+3+5+7+14):5=30:5=6
Ме = 5
![]() > Ме
> Ме
№5
а) Набор чисел: 3,4,11,17,21
Ме=11
б) Набор чисел: 17,18,19,25,28
Ме=19
в) Набор чисел:25, 25, 27, 28, 29, 40, 50
Ме = 28
Вывод : медиана набора чисел, состоящего из
нечетного числа членов равна числу, стоящему
посередине.
№ 6
а) Набор чисел:2, 4, 8, 9.
Ме = (4+8):2=12:2=6
б) Набор чисел:1,3,5,7,8,9.
Ме = (5+7):2=12:2=6
Медиана набора чисел, содержащего четное число
членов равна полусумме двух чисел, стоящих
посередине.
Задача 1.
Ученик получил в течении четверти следующие
оценки по алгебре:
5, 4, 2, 5, 5, 4, 4, 5, 5, 5.
Найдите средний балл и медиану этого набора. [ 3 ]
- Найдем средний балл, то есть среднее
арифметическое: - Найдем медиану этого набора чисел:
![]() = ( 5+4+2+5+5+4+4+5+5+5): 10=44:10 =
= ( 5+4+2+5+5+4+4+5+5+5): 10=44:10 =
4,4
Упорядочим набор чисел: 2,4,4,4,5,5,5,5,5,5
Всего 10 чисел, чтобы найти медиану надо взять
два средних числа и найти их полусумму.
Ме = (5+5):2 = 5
Вопрос к учащимся: Если бы вы были учителем,
какую бы вы поставили оценку за четверть этому
ученику? Ответ обоснуйте.
Задача 2.
Президент компании получает зарплату 300000 руб.
три его заместителя получают по 150000 руб., сорок
служащих – по 50000 руб. и зарплата уборщицы
составляет 10000 руб. Найдите среднее
арифметическое и медиану зарплат в компании.
Какую из этих характеристик выгоднее
использовать президенту в рекламных целях?
![]() = (
= (
300000+3·150000+40·50000+10000):(1+3+40+1) = 2760000:45![]() 61333,33 (руб.)
61333,33 (руб.)
Ме = 50000 руб.
В рекламных целях выгоднее использовать
среднее арифметическое зарплат, т.к. она выше.
Задача 3. (Предложить учащимся решить
самостоятельно, задачу спроецировать с помощью
проектора)
В таблице показан примерный объем воды
крупнейших озер и водохранилищ России в куб. км. (Приложение 3) [ 4 ]
|
Водоем |
Объем воды в куб. км |
| Ладожское озеро | 900 |
| Онежское озеро | 290 |
| Озеро Байкал | 23000 |
| Рыбинское водохранилище | 30 |
| Куйбышевское водохранилище | 60 |
| Цимлянское водохранилище | 20 |
| Саяно-Шушенское водохранилище | 30 |
| Волгоградское водохранилище | 30 |
| Красноярское водохранилище | 60 |
| Братское водохранилище | 170 |
А) Найдите средний объем воды в данных водоемах
(среднее арифметическое);
Б) Найдите объем воды в среднем по величине
водоеме (медиану данных);
В) По вашему мнению, какая из этих характеристик
– среднее арифметическое или медиана – лучше
описывает объем типичного крупного водоема
России? Ответ объясните.
Ответ :
а) 2459 куб. км
б) 60 куб. км
в) Медиана, т.к. данные содержат значения сильно
отличающиеся от всех прочих.
Задача 4. Устно.
А) Сколько чисел в наборе, если его медианой
служит ее девятый член?
Б) Сколько чисел в наборе, если его медианой
служит среднее арифметическое 7-го и 8-го членов?
В) В наборе из семи чисел наибольшее число
увеличили на 14. Изменится ли при этом и как
среднее арифметическое и медиана ?
Г) Каждое из чисел набора увеличили на 3. Что
произойдет со средним арифметическим и медианой?
Задача 5.
Конфеты в магазине продают на вес. Чтобы узнать,
сколько конфет содержится в одном килограмме,
Маша решила найти вес одной конфеты. Она взвесила
несколько конфет и получила следующие
результаты:
12, 13, 14, 12, 15, 16, 14, 13, 11.
Решение.
![]() = 13,33
= 13,33
Ме = 13
Для оценки веса одной конфеты пригодны обе
характеристики, т.к. они не сильно отличаются
друг от друга.
Итак, для характеристики статистической
информации используют среднее арифметическое и
медиану. Во многих случаях какая-то из
характеристик может не иметь никакого
содержательного смысла( например, имея сведения
о времени дорожно-транспортных происшествий,
вряд ли имеет смысл говорить о среднем
арифметическом этих данных).
- Домашнее задание :пункт 11, № 3,4,9,11.
- Итоги урока. Рефлексия.
Литература:
- Ю.Н. Тюрин и др. “Теория вероятностей и
статистика”, Издательство МЦНМО, ОАО
“Московские учебники”, Москва 2008. - Е.А. Бунимович, В.А. Булычев “Основы статистики и
вероятность”, ДРОФА, Москва 2004. - Газета “Математика” №23, 2007 год.
- Демоверсия контрольной работы по теории
вероятностей и статистике для 7 класса, 2007/2008 уч.
год.
Структурные средние – мода, медиана, квантиль, дециль
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода – величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
– величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили –
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили – на 100
частей.
Медиана –
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
– нижняя граница медианного интервала
– величина медианного интервала
– сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили – это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% –
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
– накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1.5 |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд – значения дохода жильцов распределены по возрастанию.
Мода
– наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
– такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
– значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% – между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
|
Удельный вес вкладов, % |
5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода – варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
–
начало модального интервала
–
величина интервала
–
частота модального интервала
–
частота интервала, предшествующего модальному
–
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана – варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина – более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 | 0.2 |
| 12-15 | 0.05 |
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:

(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:
 (8.17 – формула Медианы)
(8.17 – формула Медианы)
где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:

Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):

Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
![]() Загрузка…
Загрузка…
