Рассмотрим фигуру ниже:
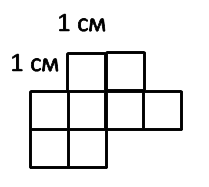
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см2.
Площадь всей фигуры 8 см2.
Запомните!
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м2); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см2).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
Рассмотрим квадрат со стороной 1 см.
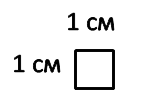
Его площадь равна:
S = 1 см · 1 см = 1см2
Рассмотрим квадрат со стороной 1 м.
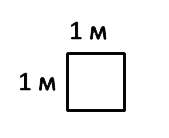
Его площадь равна:
S = 1 м · 1 м = 1 м2
Известно, что: 1 м = 100 см
1 м2 = 1 м · 1 м = 100 см · 100 см = 10 000 см2
Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.
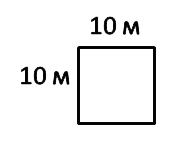
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м2
Чтобы выразить ар в cм2, вспомним, что 1 м2 = 10 000 см2.
Значит: 1 ар (сотка) = 100 м2 = 100 · 10 000 см2 = 1 000 000 см2
Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.
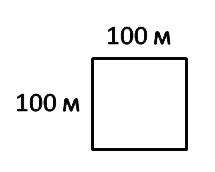
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м2
Теперь определим, сколько в одном гектаре аров.
1 ар = 100 м2
Значит: 10 000 м2 : 100 м2 = 100 (ар)
1 га = 100 ар
Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км2.
1 км = 1000 м
1 км2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
| га | ар | м2 | cм2 | |
|---|---|---|---|---|
| 1 км2 | 100 га | 10 000 ар | 1 000 000 м2 | 1 000 000 000 cм2 |
| 1 га | 1 га | 100 ар | 10 000 м2 | 100 000 000 cм2 |
| 1 ар | 0,01 га | 1 ар | 100 м2 | 1 000 000cм2 |
| 1 м2 | 0,000 1 га | 0,01 ар | 1 м2 | 10 000 cм2 |
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
12 сентября 2018 в 20:57
Дмитрий Мозговой
Профиль
Благодарили: 0
Сообщений: 1
Дмитрий Мозговой
Профиль
Благодарили: 0
Сообщений: 1
Внутри большего квадрата расположен меньший квадрат площади 73. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?
0
Спасибо
Ответить
14 октября 2018 в 20:45
Ответ для Дмитрий Мозговой
Дарья Тихая
Профиль
Благодарили: 0
Сообщений: 1
Дарья Тихая
Профиль
Благодарили: 0
Сообщений: 1
146
0
Спасибо
Ответить
21 октября 2018 в 15:44
Ответ для Дмитрий Мозговой
Владимир Шварцман
Профиль
Благодарили: 0
Сообщений: 1
Владимир Шварцман
Профиль
Благодарили: 0
Сообщений: 1
Пусть отрезки большего квадрата a и в. Тогда а2 + в2 =73 Сумма двух чисел нечётна если одно чёт., а второе нечёт. Это 1,9,25,49 и 4, 16,36.64 Легко видеть, что это числа 9 и 64.Т.е. а=3 и в=8 Пл. большого квадрата=112 =121
0
Спасибо
Ответить
12 ноября 2018 в 3:31
Ответ для Дмитрий Мозговой
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Неверно.
0
Спасибо
Ответить
22 июня 2016 в 20:17
Клара Чукаева
Профиль
Благодарили: 0
Сообщений: 1
Клара Чукаева
Профиль
Благодарили: 0
Сообщений: 1
д вечер. у меня вопрос: как найти площадь таблички размером 50 см на 75 см? если перемножить, как нам предлагает школьная программа, то получается 3750 см2, разве это возможно? я ошибаюсь? напишите формулу для расчета пожалуйста?
0
Спасибо
Ответить
24 июня 2016 в 12:18
Ответ для Клара Чукаева
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Здравствуйте! Все верно.
Формула площади прямоугольника S=a · b
(a)50 · (b)75=3750 см2
Может вы спутали с периметром? Периметр будет равен 250 см
a ·2+b · 2
0
Спасибо
Ответить
16 января 2016 в 18:29
Надюша Бисерова
Профиль
Благодарили: 0
Сообщений: 1
Надюша Бисерова
Профиль
Благодарили: 0
Сообщений: 1
ширина прамоугольника 23 см. на сколько увеличиться площадь прамоугольника, если его длину увеличить на 3 см?
подскажите решение пожалуйста
0
Спасибо
Ответить
21 января 2016 в 16:17
Ответ для Надюша Бисерова
Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
на 3 см квадратных
если я не ошибаюсь взависимости от длины
0
Спасибо
Ответить
24 января 2016 в 13:50
Ответ для Надюша Бисерова
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
увеличится на 69
0
Спасибо
Ответить
12 октября 2015 в 17:22
Мося Мося
Профиль
Благодарили: 0
Сообщений: 1
Мося Мося
Профиль
Благодарили: 0
Сообщений: 1
найди площадь квадрата периметр которого 280см
0
Спасибо
Ответить
1 июля 2016 в 14:20
Ответ для Мося Мося
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для нахождения площади квадрата в данном случае нам понадобятся две формулу, а именно:
1) Формула периметра квадрата P=4a. Подробно про периметр читаем здесь http://math-prosto.ru/?page=pages/perimeter/perimeter.php
2) Формула площади квадрата S=a2. Подробно читать здесь http://math-prosto.ru/?page=pages/area/area_figures.php
Приступим к решению. Выразим сторону квадрата из формулы периметра:
P=4a
a=P: 4
a= 280: 4 = 70 (см)
Теперь воспользуемся формулой площади квадрата:
S=a2
S=702=4900 (см2)
Ответ: площадь квадрата равна 4900 см2
0
Спасибо
Ответить
4 сентября 2015 в 15:44
Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Площадь прямоугольника64мс2, одна из сторон 16см. Надо найти соседнюю сторону
0
Спасибо
Ответить
1 сентября 2016 в 10:18
Ответ для Игорь Винников
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Площадь прямоугольника рассчитывается по формуле S=a · b. Подставим значения в формулу и вычислим вторую сторону:
64=16 · b
b=64/16=4
вторая сторона равна 4.
проверка: 16 · 4 = 64.
Ответ: Соседняя сторона прямоугольника равна 4 см.
0
Спасибо
Ответить
6 июля 2015 в 17:48
Дмитрий Рыжков
Профиль
Благодарили: 0
Сообщений: 2
Дмитрий Рыжков
Профиль
Благодарили: 0
Сообщений: 2
Посмотрите, у вас не первый раз перепутаны буквы в примерах.Например посмотрите нм тему: площадь сложных фигур.там же треугольник обозначен одними буквами, а написано в примере другими совершенно. Никто не ответил по предыдущей теме.спасибо.
0
Спасибо
Ответить
12 июля 2015 в 13:31
Ответ для Дмитрий Рыжков
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Здравствуйте, Дмитрий.
Благодарим Вас за указанное замечание.
Пожалуйста, укажите, более конкретно место ошибки.
В уроке «Площадь сложных фигур» мы не нашли ошибку, о которой Вы написали.
0
Спасибо
Ответить
17 мая 2015 в 10:59
Соня Кизилова
Профиль
Благодарили: 0
Сообщений: 1
Соня Кизилова
Профиль
Благодарили: 0
Сообщений: 1
Самостоятельная работа.
Задание 3.
На сколько частей разбивают плоскость 4 прямые, пересекающиеся в одное точке?
Задание 2.
Начертите угол MON. Отметьте точку K, лежащую внутри этого угла, и точку L, лежащую на отрезке NK.
Задание 4.
Постройте треугольник ABC со стороной AB= 6см,?ABC= 45градусов, ?BAC= 75 градусов.Помогите пожалуйста
…
0
Спасибо
Ответить
17 мая 2015 в 12:57
Ответ для Соня Кизилова
Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
1.8 частей
0
Спасибо
Ответить
Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.
Формула площади квадрата.
Площадь квадрата обозначается буквой – S.
Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.
Обычно сторону обозначают буквой – “a”
Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.
Либо может встречаться вот такая формулировка площади квадрата:
Площадь квадрата равна произведению стороны квадрата на себя.
S = a²
Где S – площадь квадрата,
a – длина одной из сторон.
Пример подсчета площади квадрата
Как вычислить площадь квадрата?
Для того, чтобы найти площадь квадрата – нужно знать длину стороны квадрата.
Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!
Пусть это будет 10см.
Условие задачи :
Сколько будет площадь квадрата со стороной 10см.
Решение задачи – найти площадь квадрата:
Как вы помните из правила высчитывания площади квадрата – нужно сторону квадрата умножить на себя или возвести во вторую степень.
S = a²
Умножаем сторону квадрата 10, на себя, на 10 :
10 * 10 = 100см2
Ответ :
Площадь квадрата со стороной 10см, будет равна 100см2
100см2
Как найти площадь квадрата если известен периметр!?
Условие задачи : найдите площадь квадрата, если известен периметр = 32см.
Решение задачи – найти площадь квадрата:
Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:
P = 4a
Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.
И далее по формуле площади квадрата узнаем его площадь :
S = a² = 4² = 16см²
Ответ задачи :
Квадрат, у которого периметр 32 см, площадь равна 16см²
Как найти площадь квадрата если известна диагональ!?
Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.
Решение задачи – найти площадь квадрата:
Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :
a² + a² = d²
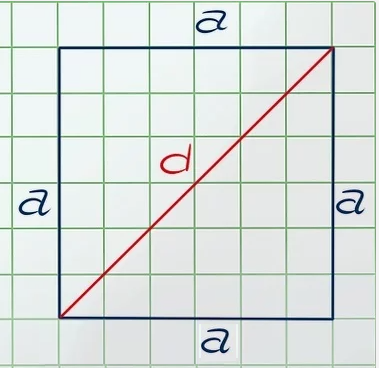
Немного нужно преобразовать :
a² + a² = d² -> 2a² = d² -> a² = d²/2
А если S = a², то S = d²/2
И далее нам нужно подставить нашу диагональ :
S = 8²/2 = 64/2 = 32см².
Ответ :
Если диагональ квадрата равна – 8см, То площадь квадрата равна – 32см².
Какая единица измерения площади квадрата!?
После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : “площадь квадрата почему см2“.
Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?
Мы можем рассказать… о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?
Единица измерения площади квадрата
Единица измерения площади квадрата – может быть, любая мера длины в квадрате.
Если мера длины сантиметр, то площадь будет сантиметр в квадрате – см².
Если мера длины метр, то площадь будет метр в квадрате – м².
Если мера длины километр, то площадь будет километр в квадрате – км². и т.д…
Почему единица измерения площади квадрата пишется с двойкой
Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!
Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?
Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения… то мы увидим откуда берется двойка…
Давайте покажем на примере…
Пусть надо найти площадь квадрата со стороной 12 см.
Так и записываем в формулу :
S = 12см * 12см
Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :
12*12(см*см) = 12²см² = 144см²
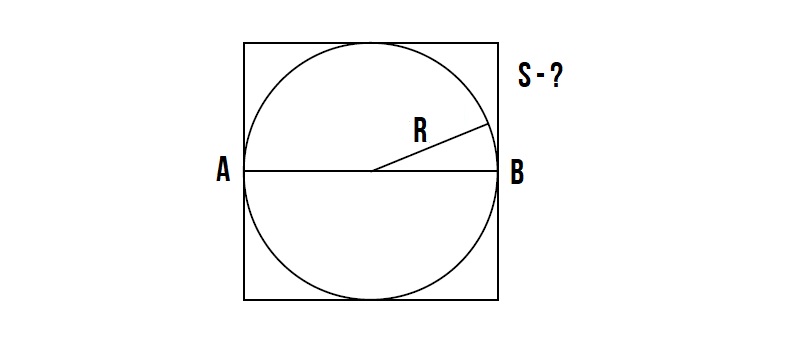
Как найти площадь квадрата зная радиус вписанной окружности!?
Задача :
Как найти площадь квадрата зная радиус вписанной окружности!?
Это очень простая задача!
Диаметр вписанной окружности равна стороне квадрата.
Диаметр окружности равен 2R.
Значит сторона квадрата равна 2R.
Далее вспоминаем формулу площади квадрата – S = a², где a – сторона квадрата, которая равна = 2R.
Значит площадь квадрата равна S = (2R)²
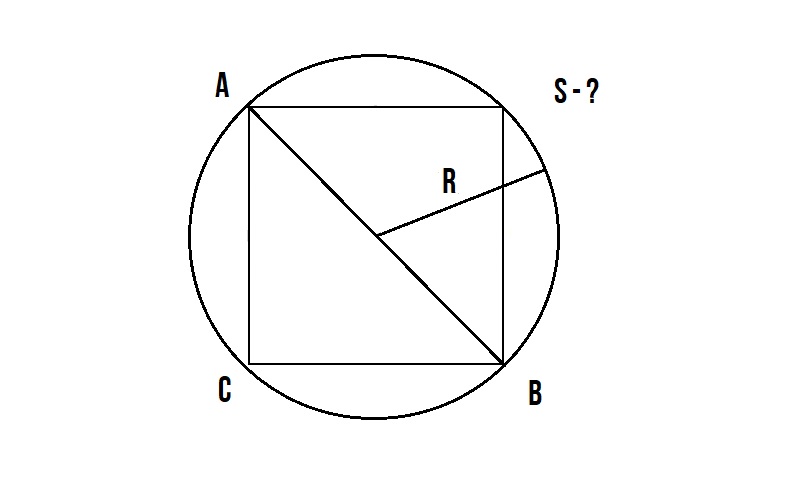
Как найти площадь квадрата зная радиус описанной окружности!?
Задача :
Как найти площадь квадрата зная радиус описанной окружности!?
Данная задача такая же простая, как и выше описанная!
У нас известен радиус окружности описанной вокруг квадрата.
Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.
По диагонали квадрата мы уже один раз высчитывали площадь здесь -> S = d²/2
Далее подставляем S = (2R)²/2
Найти площадь квадрата онлайн
Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :
Сторона квадрата – заполнить значением стороны квадрата.
И нажать кнопку посчитать.
Загрузить PDF
Загрузить PDF
Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см2) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.
-
1
Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.[1]
-
2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
-
3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее “в квадрат” или “во вторую степень”), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама
-
1
Найдите площадь круга по формуле: S = π × r2. Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
-
2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
-
3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
-
4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
-
5
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
-
6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама
-
1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
-
2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
-
3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама
Об этой статье
Эту страницу просматривали 153 899 раз.
Была ли эта статья полезной?
План урока:
Понятие площади многоугольника
Свойство аддитивности площади
Площадь квадрата
Соотношение между единицами измерения площадей
Площадь прямоугольника
Понятие площади многоугольника
Понятие площади уже знакомо нам из младших классов и повседневной жизни. Эта величина, которая, грубо говоря, характеризует размер плоских фигур. Она показывает, какую часть плоскости занимает та или иная фигура. Исторически понятие площади многоугольника считалось неопределяемым, так же как понятия точка, прямая, плоскость и т. д. Основная же задача геометров (а именно так называют математиков, специализирующихся на геометрии) сводилась к измерению площади.
Как известно, для проведения любых измерений должна существовать некоторая единица измерения. Так, массу измеряют в килограммах, длину – в метрах и т. д. При этом единицы измерения разных величин могут быть связаны друг с другом. С практической точки зрения удобно принять в качестве единицы измерения площади квадрат, сторона которого равна 1 метру. Принимается, что площадь такого квадрата равна 1 квадратному метру (обозначается символом м2):
Аналогично можно определить такие величины, как квадратный сантиметр (см2), квадратный километр (км2), квадратный миллиметр (мм2) и т.д.:
Как мы знаем, иногда в задачах единицу измерения длины не указывают вовсе. Например, говорят, что сторона квадрата равна единице. В таких случаях и площадь является безразмерной величиной. Принимается, что площадь квадрата со стороной, равной единице, также равна единице. Такой квадрат называется единичным.
Общепринято, что площадь фигуры обозначается буквой S.
Свойство аддитивности площади
Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:
Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.
В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:
Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.
Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.
Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.
Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:
В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:
Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:
Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.
Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут. Равносоставленные же фигуры могут и не накладываться друг на друга.
Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны. Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:
С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.
Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.
Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:
Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство
Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:
- площадь квадрата со стороной 1 равна единице:
- равносоставленные фигуры имеют равную площадь.
Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.
Площадь квадрата
Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.
Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:
Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.
Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:
В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:
Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.
Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:
Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:
В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине
Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».
Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I2<S (случай, когда I2>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что
Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:
Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):
из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.
Задание. Найдите площадь квадрата, если его сторона равна
Задание. Площадь квадрата равна 25. Найдите длину его стороны.
Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:
Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:
Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.
Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.
Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:
По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:
Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.
Ответ: 16 см2.
Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2. Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.
Соотношение между единицами измерения площадей
Площадь измеряется в «квадратных» величинах: м2, см2, км2 и т.д. Как связаны эти единицы измерения? Для ответа на этот вопрос построим квадрат со стороной 1 см и разобьем каждую его сторону на отрезки длиной 1 мм. Естественно, что таких отрезков будет 10, ведь, в 1 см равен 10 мм. Далее разобьем большой квадрат на маленькие, их число будет равно 102 = 100:
Площадь большого квадрата равна 1 см2, а площадь маленьких составляет 1 мм2. Так как большой квадрат состоит из 100 маленьких, мы можем записать:
Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:
В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:
Задание. Площадь окружности равна 24 см2. Выразите эту величину в мм2 и м2.
Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см2 равен 100 мм2:
Площадь прямоугольника
Ещё из младшей школы известно, что площадь прямоугольника равна произведению его сторон. Докажем этот факт, используя только свойства площади и выведенную нами ранее формулу площади квадрата.
Возьмем произвольный прямоугольник со сторонами a и b. Далее достроим его до квадрата со стороной (а + b):
С одной стороны, площадь большого квадрата (со стороной а + b) равна величине (а + b)2. С другой стороны, он состоит из 4 фигур, а потому его площадь равна сумме
Итак, мы доказали следующее утверждение:
Задание. Найдите площадь прямоугольника со сторонами 5 и 8 см?
Решение. Просто перемножаем эти числа:
Задание. Найдите площадь фигуры, изображенной на рисунке:
Решение. Необходимо разбить фигуры на несколько прямоугольников:
Далее считаем площадь каждого отдельного прямоугольника:
Задание. Полкомнаты необходимо покрыть паркетом. Длина и ширина комнаты равны 6 и 5,5 метрам, а каждая дощечка паркета имеет габариты 30х5 см. Сколько дощечек паркета необходимо купить для ремонта?
Решение. В таких задачах прежде всего следует все длины выразить в одних единицах измерения. Перепишем габариты комнаты:
Важно убедиться, что пол можно полностью покрыть целым числом дощечек, не используя какие-либо дощечки наполовину. Для этого габариты дощечки должны быть кратны габаритам комнаты. Это условие соблюдается:
Получается, что для покрытия пола дощечки необходимо разместить их в 20 рядов, в каждом из которых будет 110 досок. Тогда общее количество досок будет равно
Задание. Площадь прямоугольника равна 64, а одна из его сторон имеет длину 16. Найдите вторую сторону прямоугольника.
Решение. Запишем формулу площади прямоугольника:
Задание. Найдите стороны прямоугольника, если площадь равна 500, а одна из сторон в 5 раз больше другой стороны.
Решение. Обозначим меньшую сторону переменной х. Тогда большая сторона будет в 5 раз больше, то есть она равна 5х. Площадь прямоугольника будет вычисляться как произведение этих чисел
Мы получили два значения х, 10 и (– 10). Естественно, длина отрезка не может выражаться отрицательным числом, поэтому нам подходит только значение 10. Это длина меньшей стороны. Большая же сторона в 5 раз длиннее, то есть ее длина равна
Задание. Одна сторона прямоугольника длиннее другой на 5 см, а площадь прямоугольника равна 150 см2. Вычислите обе стороны прямоугольника.
Решение. Снова обозначим длину меньшей стороны буквой х, тогда большая сторона будет иметь длину х + 5 см. По условию произведение этих сторон равно 150:
Это обычное квадратное уравнение, решаемое с помощью:
Снова получили два корня, из которых только один является положительным. Итак, меньшая сторона равна 10 см. Тогда большая сторона буде равна
Задание. Периметр прямоугольника равен 16 см, а площадь составляет 15 см2. Каковы стороны этого прямоугольника?
Решение. Обозначим смежные стороны буквами a и b. Тогда и две другие стороны также будут равны а и b. Так как периметр (его обозначают буквой Р) по определению является суммой длин всех сторон, то для прямоугольника он будет равен:
Если сюда вместо S подставить 15, а вместо а выражение 8 – b, то получим такое уравнение:
Оба полученных корня являются положительными числами, то есть устраивают нас. Зная b, легко найдем и a:
В первом случае получается, что стороны равны 3 и 5 см. Во втором случае получились те же числа, только в другом порядке: 5 и 3 см. То есть эти два ответа, по сути, идентичны друг другу.
Ответ: 5 см; 3 см.
Площадь квадрата онлайн
С помощю этого онлайн калькулятора можно найти площадь квадрата. Для нахождения площади квадрата, введите известные данные в ячейку и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Площадь квадрата. Определение
Определение 1. Площадь квадрата − это величина той части плоскости, которую занимает квадрат.
Единицы измерения площади квадрата
За единицу измерения площадей применяют квадрат, сторона которого равна единице измерения отрезков. В качестве единицы измерения площадей принимают квадраты со сторонами 1мм, 1см, 1дм, 1м и т.д (Рис.1). Такие квадраты назыают квадратным миллиметром, квадратным сантиметром, квадратным дециметром, квадратным метром и т.д., соответственно. Обозначаются они мм2, см2, дм2, м2 и т.д., соответственно.
Если выбрана единица измерения, то площадь измеряемого объекта (квадрата, треугольника, прямоугольника, многоугольника и т.д.)определяется положительным числом, которая определяет сколько раз единица измерения и ее части укладываются в данном объекте.
Для измерения отдельных плоских фигур используются специальные формулы. В данной статье мы выведем формулу для вычисления площади квадрата.
Площадь квадрата. Доказательство
Теорема 1. Площадь S квадрата со стороной a равна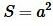 
.
Доказательство. Пусть n целое неотрицательное число и пусть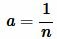 
. Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим 
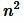маленьких квадратов состоронами 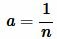. Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:
а поскольку 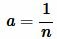, то имеем:
Пусть теперь a является конечной десятичной дробью, содержащую n знаков после запятой. (Если n=0, то a будет целым числом). Тогда a можно представить в виде обыкновенной дроби, умножив и делив на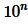 
:
откуда
где m − целое число.
Возьмем квадрат со стороной a и разделим его по горизонлали и вертикали на m ровных частей. Получим m2 маленьких квадратов (Рис.3).
Тогда, учитывая (2), сторона каждого квадрата равна:
По формуле (1) площадь маленького квадрата равна:
Следовательно, площадь квадрата со стороной a равна:
Пусть, далее, число a представляет собой бесконечную десятичную дробь. Рассмотрим число an которая получается из a отбрасыванием всех десятичных знаков после запятой, начиная с (n+1)-го. Поскольку a отличается от an не более, чем на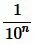 
, то имеем:
откуда
Из неравенства (4) следует, что площадь S квадрата со стороной a заключена между площадью квадрата со стороной an и площадью квадрата со стороной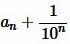 
(Рис.4), т.е.
При неограниченном увеличении числа n, число 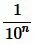будет становиться сколь угодно малым и, следовательно, число 
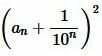будет сколь угодно мало отличаться от 
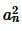. Тогда из неравенства (5) следует, что число S будет мало отличаться от числа 
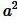. Следовательно они равны, т.е. .
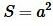Площадь квадрата по стороне
Из вышеизложенного доказательства получили, что площадь квадрата равна:
где ( small a ) сторона квадрата.
Пример 1. Сторона квадрата равна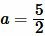 
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (6). Подставляя 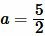в (6), получим:
Ответ: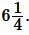 
Площадь квадрата по диагонали
Пусть известна диагональ ( small d ) квадрата (Рис.5). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Для этого воспользуемся теоремой Пифагора:
Подставляя (7) в (6), получим:
то есть площадь квадрата по диагонали вычисляется из следующей формулы:
Пример 2. Диагональ квадрата равна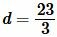 
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (8). Подставляя 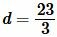в (8), получим:
Ответ: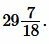 
Площадь квадрата по радиусу вписанной окружности
Пусть известен ( small r ) радиус окружности вписанной в квадрат (Рис.6). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Нетрудно заметить, что радиус ( small r ) равна половине стороны ( small a ) квадрата, т.е.
Подставляя (9) в (6), получим:
или
Пример 3. Радиус вписанной в квадрат окружности равен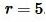 
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (10). Подставляя 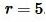в (10), получим:
Ответ: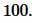 
Площадь квадрата по радиусу описанной окружности
Пусть известен ( small R ) радиус окружности описанной около квадрата (Рис.7). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Восрользуемся теоремой Пифагора:
Подставляя (11) в (6), получим:
Пример 4. Радиус описанной окружности равен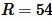 
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (12). Подставляя 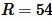в (12), получим:
Ответ: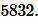 
Площадь квадрата по периметру
Пусть известен периметр ( small P ) квадрата. Найдем площадь квадрата. По периметру можно найти сторону квадрата:
Подставляя (13) в (6), получим:
то есть площадь квадрата через периметр равна:
Пример 5. Периметр квадрата равен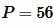 
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (14). Подставляя 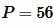в (14), получим:
Ответ: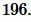 
Смотрите также:
- Квадрат. Онлайн калькулятор
