Значение области допустимых значений в математике: способы нахождения
Содержание:
- Допустимые и недопустимые значения переменных
- Что такое ОДЗ
-
Как найти ОДЗ: примеры, решения
- Общие принципы нахождения области допустимых значений
- Примеры нахождения ОДЗ
- Почему важно учитывать ОДЗ при проведении преобразований
-
Функции, для которых важна ОДЗ
- ОДЗ обратной зависимости
- ОДЗ степенной функции
- ОДЗ показательной функции
- ОДЗ логарифмической функции
- ОДЗ тригонометрических функций
Допустимые и недопустимые значения переменных
Перед тем, как вводить понятие области допустимых значений функции, необходимо определиться с самим термином «допустимое значение».
Допустимое значение переменной — такое значение переменной, при котором зависимая от нее функция имеет смысл. Это значит, что, подставив данное значение переменной в выражение функции, можно получить конкретный результат. Сама функция в алгебре — это уравнение, в котором каждому значению x соответствует одно значение y.
Например, для функции обратной пропорциональности (y=frac1x) допустимыми значениями для переменной x будут: 1; 2,7; -5, (sqrt{126}), — в общем, все действительные числа. При подстановке их на место x, функция принимает конкретное значение. Исключениями из этого перечня будут 0, (-infty )и (+infty), так как когда x принимает такие значения, функция не имеет смысла.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Что такое ОДЗ
Область допустимых значений (область определения) функции — совокупность всех значений переменных, при которых функция имеет смысл, то есть решается. Для примера из предыдущего пункта, (y=frac1x), область допустимых значений будет иметь следующий вид: ((-infty;;0)cup(0;;+infty)). Это значит, что в область определения функции ( y=frac1x) входят все числа в промежутках от минус бесконечности до нуля и от нуля до плюс бесконечности.
У записи области определения есть некоторые особенности, которые важно иметь в виду. Круглые скобки — () — применяются, когда область допустимых значений заканчивается на данном числе, причем оно не входит в ОДЗ. Квадратные скобки — [] — применяются в ситуациях, когда в область определения входит число, на котором она заканчивается. Знак объединения — (cup) — по сути означает союз «и». Он используется, когда ОДЗ является системой из нескольких числовых промежутков.
Как найти ОДЗ: примеры, решения
Чтобы найти область допустимых значений для какой-либо функции, не имеет смысла перебирать все числа, при подстановке которых ее можно решить. Рациональнее найти те значения, при которых функция не имеет смысла и исключить их из всего множества чисел.
Общие принципы нахождения области допустимых значений
- деление на 0. Практически во всех стандартных математических выражениях такая операция не имеет смысла. У этого действия есть конкретный результат только при нахождении предела последовательности или функции. Пример бессмысленных выражений: (y=frac50;)
- извлечение корня из отрицательного числа. При работе с действительными числами, найти корень любой степени отрицательного числа невозможно. Эта операция приобретает смысл только при переходе к комплексным числам. Пример: (y=sqrt{-11};)
- возведение в степень. У данного действия есть свои ограничения: нельзя возводить 0 в отрицательную и нулевую степень, отрицательные числа в положительную дробную степень и неположительные (отрицательные и 0) в дробную степень со знаком минус. Примеры: (y=0^{-3};;y=0^0;;y=({-7}^{textstylefrac32});;y=({-6}^{-{textstylefrac17}});)
- нахождение логарифма. Так как логарифм равняется степени, в которую необходимо возвести основание, чтобы получить логарифмируемое число, некоторые операции не имеют смысла. К ним относятся логарифмирование неположительного числа, положительного числа по отрицательному основанию или единице. Примеры:( y=log_3left(-9right);;y=log_2left(0right);;y=log_{-4}left(64right);;y=log_1left(5right);)
- тригонометрические функции. Для синуса, косинуса, арктангенса и арккотангенса никаких ограничений нет. Но для тангенса, котангенса, арксинуса и арккосинуса они появляются, исходя из их формул. Так как тангенс является частным при делении синуса на косинус, последний не может равняться нулю. То же самое справедливо и для котангенса, но там уже синус не должен принимать значение 0.
Арксинус и арккосинус могут быть определены только в промежутке от -1 до 1 включительно — (lbrack-1;;1rbrack.)
Примеры нахождения ОДЗ
Пример №1. Найти область определения функции (y=sqrt{1-x^2})
Из обозначенных выше принципов следует, что подкоренное выражение не может быть отрицательным, значит 1-x^2geq0. Приведем данное неравенство к общему виду: (1-x^2geq0Rightarrow1geq x^2Rightarrow x^2leq1)
Вычислим квадратный корень для обеих частей неравенства:
(x^2leq1Rightarrowsqrt{x^2}leqsqrt1Rightarrowleft|xright|leq1)
Раскроем модуль согласно правилу:
(left|xright|leq1Rightarrow-1leq xleq1)
Из этого следует, что область допустимых значений функции (y=sqrt{1-x^2}) лежит в пределах между -1 и 1, включая эти числа. Таким образом, ОДЗ данной функции: (xinlbrack-1;;1rbrack)
Пример №2. Найти ОДЗ функции (y=lgleft(xright))
(lgleft(xright)) является краткой формой записи десятичного логарифма (log_{10}left(xright)). Так как 10 — положительное число, не равное единице, единственным условием остается x>0. Таким образом, область определения функции (y=lgleft(xright)) будет включать в себя все числа в промежутке от нуля до (+infty). Так как неравенство x>0 — строгое, ОДЗ будет иметь следующий вид: (xin(0;;+infty)).
Почему важно учитывать ОДЗ при проведении преобразований
Тождественные преобразования могут приводить к расширению или сужению области допустимых значений. В этом случае значение, подходящее к изначальной функции, после преобразования может оказаться вне области определения. Поэтому стоит избегать сужающих ОДЗ преобразований или находить область допустимых значений уже после них.
Функции, для которых важна ОДЗ
Сама по себе область допустимых значений — важная характеристика для всех функций. Чтобы правильно решать математические задачи, следует всегда находить ее. При этом, для многих, если не большинства, функций она включает в себя все множество действительных чисел. Например, линейная (y=kcdot x+b) или квадратичная (y=acdot x^2+bcdot x+c) функции. Рассмотрим некоторые функции, для которых это не так.
ОДЗ обратной зависимости
Функция обратной пропорциональности (y=frac kx) уже упоминалась выше. Ее область определения содержит все действительные числа, за исключением нуля: (xin(-infty;;0)cup(0;;+infty).)
ОДЗ степенной функции
Для степенной функции y=x^n следует учитывать обозначенные выше принципы нахождения ОДЗ, справедливые для возведения в степень и извлечения корня. Рассмотрим области определения переменной x в зависимости от значения n:
- при n>0 и (ninmathbb{Z}), то есть n — целое положительное число: ( xin(-infty;;+infty);)
- для n>0, причем n — дробное число: ( xinlbrack0;;+infty);)
- для n=0:( xin(-infty;0)cup(0;;+infty);)
- при n<0 и (ninmathbb{Z}: xin(-infty;;0)cup(0;;+infty);)
- для n<0, причем n — дробное число: (xin(0;;+infty).)
ОДЗ показательной функции
Показательная функция y=a^x очень похожа на степенную, но, в отличие от нее, здесь переменная не в основании, а в степени. Область допустимых значений для нее определяется по тем же правилам, что и для степенной функции:
- для a>0: (xin(-infty;;+infty);)
- для a=0: (xin(0;;+infty);)
- для a<0: (xin(-infty;;+infty)), причем x должен быть целым числом.
ОДЗ логарифмической функции
Логарифмическая функция (y=log_aleft(xright)) является обратной для показательной. Согласно свойствам логарифмирования, область определения такой функции будет включать все положительные числа: (xin(0;;+infty).)
ОДЗ тригонометрических функций
Как уже упоминалось выше, для синуса, косинуса, арктангенса и арккотангенса область допустимых значений включает в себя все действительные числа: (xin(-infty;;+infty)). Рассмотрим ОДЗ еще четырех тригонометрических функций:
- тангенс: (xin(-infty;;frac{mathrmpi}2+mathrmpicdotmathrm n)cup(frac{mathrmpi}2+mathrmpicdotmathrm n;;+infty), где ninmathbb{Z};)
- котангенс: (xin(-infty;;mathrmpicdotmathrm n)cup(mathrmpicdotmathrm n;;+infty), где ninmathbb{Z};)
- арксинус и арккосинус: (xinlbrack-1;;1rbrack.)
Для многих учащихся, тема “Графики” и все что с ними связано, очень сложна и почти все как один говорит, что не понимает их. А на самом деле, все легко. Достаточно уметь выполнять простые арифметические действия. Если сравнивать задания из второй части ОГЭ по математике, то решить текстовую задачу, чаще бывает сложнее, чем построить график и ответить на вопрос. Сложность заключается в том, что задача требует размышления, правильного прочтения текста, и составление математической модели. При выполнения заданий на построение графиков, нужно всего лишь следовать алгоритму построения. Что можно описать конкретными шагами, то всегда легко.
Разберем построение следующего графика функции и определим шаги для выполнения таких заданий.
Напишем алгоритм построения:
1) Находим ОДЗ функции, т.е. находим такие значения, при которых знаменатель дроби может превратится в ноль.
Как видим, функция не может принимать значения при х=0, х=2/9 и х=-2/9.
2) Упрощаем дробное выражение:
В итоге мы получаем простую функцию, которая называется – обратная пропорциональная зависимость (гипербола).
3) Применяем свойство модуля.
Когда мы выполнили раскрытие модуля, содержащего в функции, и нашли координаты точек для построения графика, можем уже построить график на координатной плоскости.
4) Строим график функции
Если на графике не будут указаны выколотые точки (черные пустые точки на графике), то график будет считаться не верным
5) Отвечаем на вопрос задания, находим параметр по графику. В данном задании нужно было ответить на следующий вопрос:
Поскольку график функции y=kx, это график прямой пропорциональности, то он проходит через координату (0;0). Что бы прямая y=kx не имела с нашим графиком общих точек, то она должна проходить через выколотые точки, как это показано на рисунке красными линиями
Осталось найти значения параметра K. Для этого, в прямую y=kx подставим координаты выколотых точек (2/9; -9/2) и (-2/9; -9/2).
В ответе получаем три значения параметра К. Третье значение К=0 соответствует прямой которая совпадает с осью Ох.
Итак, в алгоритме у нас получилось 5 шагов:
1) Находим ОДЗ функции.
2) Упрощаем дробное выражение функции
3)Раскрываем модуль по его свойству и находи точки для построения графика.
4) Строим график по точкам, которые нашли в пункте 3.
5) Находим параметр.
Так же разбор этого задания, вы можете посмотреть ниже:
Спасибо, что прочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Область допустимых значений (ОДЗ) – это все значения переменной, при которых не нарушаются правила математики.
Например:
– если в выражении (frac{x}{x-1}) значение переменной будет равно 1, нарушается правило: на ноль делить нельзя. Поэтому здесь (x) не может быть единицей и ОДЗ записывается так: (xneq1);
– если в выражении (sqrt{x-2}) значение переменной равно (0), нарушается правило: подкоренное выражение не должно быть отрицательно. Значит, здесь (x) не может быть (0), а также (1, -3, -52,7) и т.д. То есть, икс должен быть больше или равен 2 и ОДЗ будет: (xgeq2);
– а вот в выражение (4x+1) мы можем подставить любое число вместо икса, и никакие правила нарушены не будут. Поэтому область допустимых значений здесь – вся числовая ось. В таких случаях ОДЗ не записывают, потому что оно не несет в себе полезной информации.
Как найти ОДЗ?
Если переменная (икс) в уравнении или неравенстве стоит в знаменателе, логарифме, под корнем, в тангенсе или котангенсе ОДЗ записать нужно.

В квадратных и линейных уравнениях
(неравенствах) ОДЗ писать не нужно. В иррациональных, дробно-рациональных, логарифмических, а также тригонометрических
с тангенсом
и котангенсом
– ОДЗ обязательно. В уравнениях с синусом и косинусом – если нет знаменателей или других «отягощающих» функций – ОДЗ не записывают.
Чтобы осознать важность ОДЗ, давайте сравним два решения уравнения: с ОДЗ и без ОДЗ.
Пример: Решить уравнение (frac{x^2-x}{x+3}=frac{12}{x+3})
Решение:
| Без ОДЗ: | С ОДЗ: | |
| (frac{x^2-x}{x+3}=frac{12}{x+3}) | (frac{x^2-x}{x+3}=frac{12}{x+3}) | |
|
ОДЗ: (x+3≠0) (⇔) (x≠-3) |
||
| (x^2-x=12) | (x^2-x=12) | |
| (x^2-x-12=0) | (x^2-x-12=0) | |
| (D=(-1)^2-4·1·(-12)=49) | (D=(-1)^2-4·1·(-12)=49) | |
| (x_1=)(frac{-(-1) + sqrt{49}}{2·1})(=4) | (x_2=)(frac{-(-1) + sqrt{49}}{2·1}) (=4) | |
| (x_1=)(frac{-(-1) – sqrt{49}}{2·1})(=-3) | (x_2=)(frac{-(-1) – sqrt{49}}{2·1})(=-3) – не подходит под ОДЗ | |
| Ответ: (4; -3) | Ответ: (4) |
Видите разницу? В первом решении у нас в ответе появился неверный, лишний корень! Почему неверный? А давайте попробуем подставить его в исходное уравнение.
(frac{(-3)^2-(-3)}{(-3)+3})(=)(frac{12}{(-3)+3})
(frac{12}{0})(=)(frac{12}{0})
Видите, у нас получились и слева, и справа невычислимые, бессмысленные выражения (ведь на ноль делить нельзя). И то, что они одинаковы уже не играет роли, поскольку эти значения – не существуют. Таким образом, “(-3)” – неподходящий, посторонний корень, а область допустимых значений оберегает нас от таких серьезных ошибок.
Именно поэтому за первое решение вы получите двойку, а за второе – пятерку. И это не занудные придирки учителя, ведь неучет одз – не мелочь, а вполне конкретная ошибка, такая же как потерянный знак или применение не той формулы. В конце концов, итоговый ответ-то неверен!
Нахождение области допустимых значений часто приводит к необходимости решать системы неравенств или уравнений, поэтому вы должны уметь это делать хорошо.
Пример: Найдите область определения выражения (sqrt{5-2x}+)(frac{1}{sqrt{14+5x-x^{2}}})
Решение: В выражении два корня, один из которых в знаменателе. Кто не помнит ограничения, накладывающиеся в этом случае, тот смотрит таблицу. Кто помнит, записывает, что выражение под первым корнем больше или равно нулю, а под вторым – больше нуля. Понимаете, почему ограничения именно такие?
| (begin{cases}5-2xgeq0\14+5x-x^{2} > 0end{cases}) |
Дело за малым, нужно решить систему неравенств. |
| (begin{cases}-2xgeq-5\x^{2}-5x-14 < 0end{cases}) |
Поделим первое неравенство на (-2). |
| (begin{cases}xleq2,5\(x-7)(x+2) < 0end{cases}) |
Отметим все корни первого неравенства на числовой оси. |

|
Запишем общий ответ для системы – это и есть допустимые значения для икса. |
Ответ: ((-2;2,5])
Скачать статью
ОДЗ (Область допустимых значений) — подробнее
Давай разберем пример, наглядно показывающий, что такое ОДЗ:
Решим уравнение ( displaystyle sqrt{2x+3}=x).
Все очень просто, если ты уже освоил тему «Иррациональные уравнения».
Возводим левую и правую части уравнения в квадрат:
( displaystyle 2x+3={{x}^{2}}text{ }Leftrightarrow text{ }{{x}^{2}}-2{x}-3=0).
Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл, что это такое, – посмотри тему «Квадратные уравнения»).
Получаем корни:
( displaystyle left[ begin{array}{l}x=3\x=-1end{array} right.)
Вроде все? А давай-ка теперь сделаем проверку – подставим полученные значения в начальное уравнение:
( displaystyle x=3:text{ }sqrt{2cdot 3+3}=3text{ }Leftrightarrow text{ }sqrt{9}=3) – все верно.
( displaystyle x=-1:text{ }sqrt{2cdot left( -1 right)+3}=-1text{ }Leftrightarrow text{ }sqrt{1}=-1) – неверно! А все почему?
Да потому, что мы не учли ОДЗ!
По определению квадратный корень из любого числа не может быть отрицательным.
Значит, глядя на уравнение ( displaystyle sqrt{2x+3}=x) мы должны сразу же написать:
( displaystyle left{ begin{array}{l}xge 0;\2x+3ge 0.end{array} right.)
Если помнишь тему «Иррациональные уравнения», ты сразу скажешь, что второе условие в этой системе писать необязательно. И правда, мы ведь потом возведем все в квадрат, и получится, что ( displaystyle 2x+3={{x}^{2}}), а значит – автоматически неотрицательно.
Итак, с помощью этих рассуждений приходим к такой области допустимых значений:
( displaystyle xge 0).
Тогда сразу становится ясно, что корень ( displaystyle x=-1) не подходит. И остается единственный ответ ( displaystyle x=3).
Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они со своими ОДЗ в удобной табличке.
Как найти область допустимых значений выражения
Определение
Область ОДЗ – это множество простых числовых значений, которые допустимы, для любого данного выражения.
Ограничение области определения:
Область ограничения действительных чисел может быть от [(0 ;+infty)].
Например: [[-4 ; 1) cup[5,7)].
Область определения может указывать на следующие характеристики:
- деление функции как [y=x+frac{2 cdot x}{x^{4}-1}]
- корень четной степени и переменная под корнем:
[=sqrt{x+1} text { или } y=sqrt[n]{2^{2 cdot x+1}} text {; }] - переменная в основании степенного значения
[y=3 cdot(x+1)^{-2}, y=-2+x^{frac{1}{3}} ; y=left(x^{4}-x+2right)sqrt{4}] - логарифмическая переменная [y=ln frac{x^{4}+x}{8} ; quad y=2+].
Значения основания должно быть положительным. Также как и логарифмическое значение. - переменная тангенса и котангенса в виде следующего уравнения: [y=arcsin (x+4)+4 cdot x^{2}]
Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.
Пример 1: [y=frac{x^{4}+2 x-x+2}{4}+2 frac{2}{3} cdot x], в данном множестве нет переменной, поэтому и решается оно иначе.
Пример 2: [y=frac{3}{x-1}], нужно вычислить область определения. Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено.
Следовательно получаем следующее действие: [frac{3}{x-1}].
Область значения не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах [(-infty, 1) cup(1,+infty)].
Область допустимых значений для уравнения
Чтобы правильно уметь определять данную область, нужно знать следующие утверждения:
если функция вычисляется, при помощи суммы: [f_{1}+f_{2}+ldots f_{n} text { или } mathrm{y}=f_{1}+f_{2}+ldots f_{n}].
Область определения будет следующего вида: [mathrm{D}(mathrm{f})=mathrm{D}left(f_{1}right)left(f_{2}right) ldotsleft(f_{n}right)]
Пример суммы числовых значений:
Возьмем уравнение: [y=x^{7}+x+5+operatorname{tg} x]
Решение: уравнение представлено в виде суммы нескольких значений, где степень равна семи, показатель один.
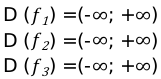
Области определения tg характерны все действительные числа.
Ответ: для заданной функции относится пересечение областей или количество действительных чисел кроме [pi / 2+pi cdot mathrm{n} . mathrm{n} in z]
Пример разности значений:
[y=log _{3} x-4 cdot 2^{x}]
Решение:
[f_{1}(mathrm{x})=log _{3} text { и } f_{2}(mathrm{x})=4 cdot 2^{x}]
Область определения функции разности будет: [(0,+infty)] это для [f_{1} ; text { для } f_{2}(-infty .+infty)]
[y=log _{3} x-4 cdot 2^{x} Rightarrow Dleft(f_{1}right)=(0 ;+infty), quad Dleft(f_{2}right)=(-infty ;+infty)]
Ответ: [(0 ;+infty)].
Пример произведения чисел:
[y=3 cdot operatorname{arctg} x cdot ln x]

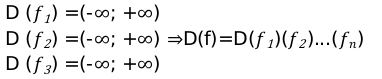
Область допустимых значений для функции
Сложная функция имеет следующий вид: [mathrm{y}=f_{1}left(f_{2}(mathrm{k})right)]
D (f) — множество значений;
Пересечение двух множеств и будет являться областью определения функции сложного типа.
[mathrm{k} in Dleft(f_{2}right) text { и } D f_{2}(x) in Dleft(f_{1}right)]
Пример
[y=ln x^{2}]
Представим функцию в виде: [mathrm{y}=f_{1}left(f_{2}(mathrm{k})right)]
[f_{1}] — логарифм с заданным основанием;
[f_{1}] — степень со значением 2.
Используем изученные в данном уроке области определения:
[Dleft(f_{1}right)=(0 ;+infty)]
[Dleft(f_{2}right)=(-infty ;+infty)]
Исходя из этого получаем систему неравенства: [x in Dleft(f_{2}right) ; f_{2} k in Dleft(f_{1}right) Leftrightarrow k in(-infty ;+infty) k^{2} in(0 ;+infty) Leftrightarrow k in(-infty ;+infty)k^{2}>0 Leftrightarrow k in(-infty ;+infty)]
[ k in(-infty ; 0) cup(0 ;+infty) . Leftrightarrow k in(-infty ; 0) cup(0,+infty)]
Ответ: все действительные числа, кроме нуля.
Область определения функции в виде дробного алгебраического значения
Когда функция задается выражение в виде дроби. Переменная значений находится в знаменателе. Следовательно, область определения являются действительные числа. Исключением служит число, которое приведет знаменатель к нулевому значению.
Пример №1: [y=frac{x-4}{x+4}]. Решив уравнение, определим искомое значение области определения. Которое является [-infty ;-4 cup-4 ;+infty]
Пример №2: [y=frac{1}{x^{2^{2}} 1} ;]
[x^{2-} 1=0 Rightarrow x^{2} Rightarrow x_{1}=-1 x_{2}=1]
Искомая область : [text { — ]- } infty ;-1[cup]-1 ; 1[cup] 1 ;+infty[.]
Пример №3: [y=cos x+frac{3}{x^{2}-4}].
Первое слагаемое имеет область определения множество действительных чисел. Второе — также все числа, кроме -2 и 2, они приведут знаменатель к нулю. Область определения должна соответствовать условиям двух слагаемых и равняться действительным числам, кроме -2 и 2.
Область определения показательной и логарифмической функции
Показательная функция записывается как: [y=k^{x}]
где значение x — показатель степени; k — число, которое обязательно больше нуля и не равно единице. Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
Область определения, для этих функций, записывается следующим образом: [(-infty,+infty)].
Логарифмическая функция выражается как: [y=log n^{k}], где значение n , имеет значение больше нуля и не менее единицы.
Определение
Область определения логарифма и логарифмической функции — это множество положительных значений и действительных чисел.
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1:
[y=ln x], определить область определения натурального логарифма.
[D(y)=(0 ;+infty)]
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
[y=ln x=frac{1}{x}]
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
[lim _{x rightarrow 0+0} ln x=ln (0+0)=-infty]
[lim _{x rightarrow infty} ln x=ln (+infty)=+infty .]
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Определения области допустимых значений функции
На примерах рассмотрим, как определить области значений функции.
Первоначально, необходимо определить значения непрерывной функции y=f(x).
Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.
Пример №1 :
Необходимо вычислить область значений уравнения [y=x^{4}-5 x^{3}+6 x^{2}] на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
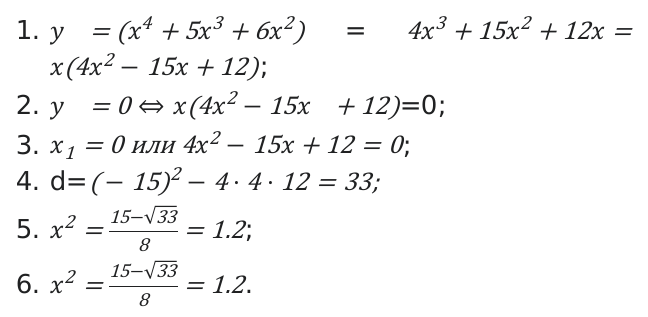
Следующим шагом будет определение значений функции в конечной и начальной точках.
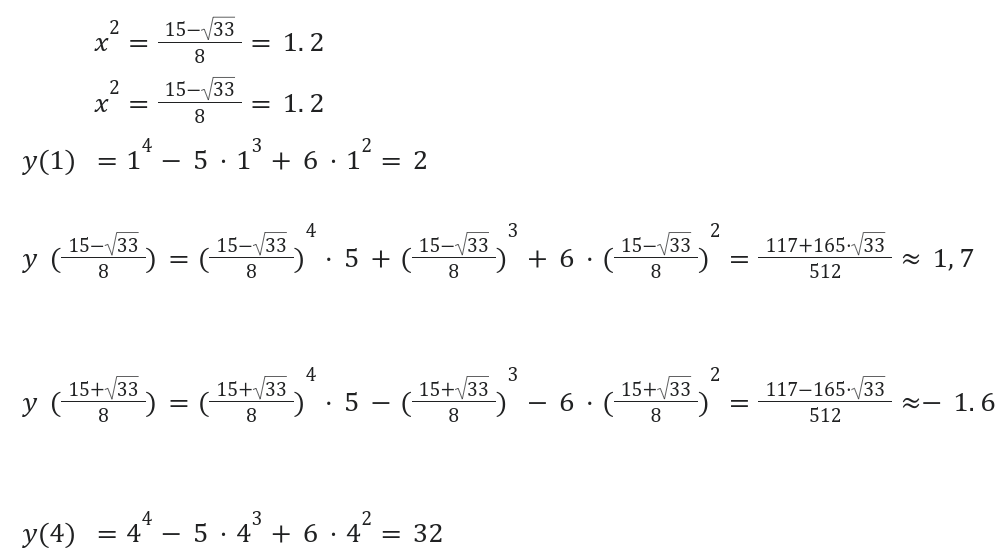
Ответ: [left(frac{117-165 cdot sqrt{33}}{512} ; 32right)].
Нет времени решать самому?
Наши эксперты помогут!
Пример №2.
На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.
Для этого, первоначально вычислим:
- наименьшее и наибольшее значение;
- определим промежуток возрастания и убывания функции;
- односторонние пределы;
- предел бесконечности.
Решение:
Для решения возьмем функцию [y=frac{1}{x^{2}-4}] и вычислим область значений на промежутке (-2;2).
Находим наименьшее и наибольшее значение функции на заданном отрезке.
[y=frac{1}{x^{2}-4}=frac{-2 x}{left(x^{2}-4right)^{2}}]
[mathrm{y}=0 Leftrightarrow frac{-2 x}{left(x^{2}-4right)^{2}}=0 Leftrightarrow x=0 in(-2 ; 2)]
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.
А именно: [y(0)=frac{1}{0^{2}-4}=-frac{1}{4}]
[-frac{1}{4}] — будет являться наибольшим значение заданной функции.
Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).
В алгебре иными словами эти значения называют односторонними пределами.
Решение выглядит следующим образом.
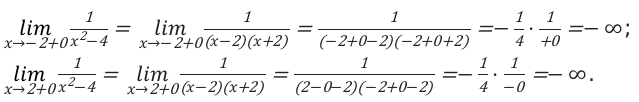
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать от [-infty text { до }-frac{1}{4}]. Если аргумент меняется, от 0 до то наоборот будет убывать к [-infty].
Следовательно, необходимое множество значений будет на интервале [-infty text { до }-frac{1}{4}]
Ответ: [left(-infty-frac{1}{4}right)].
Пример №3:
Данная функция имеет определенное значение, только при положительных значениях. [mathrm{D}(mathrm{y})=(0 ;+infty)]
Производная будет иметь следующий вид: [y=(ln x)=frac{1}{x}].
Так как функция имеет положительное значение, то всем промежутке будет наблюдаться ее возрастание. От [-infty text { до } +infty]
Поэтому область значения — это множество всех натуральных значений.
Пример №4:
У функции [y=frac{9}{z^{2}-1}]
Если значение z имеет положительное значение, то функция будет считаться определенной.
Вычислим наибольшее и наименьшее значение, а также промежутки возрастания и убывания.
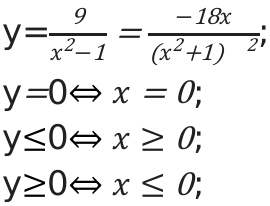
Если значение x будет больше, либо равным 0,то функция будет убывать.
Если значение x будет меньше либо равным нулю , функция будет возрастать.
Затем рассмотрим поведение функции и ее значения на бесконечной прямой.
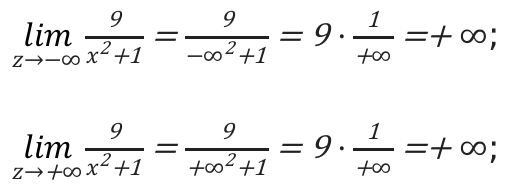
Вывод: если аргумент изменяется от [-infty] до 0, тогда значение функции увеличиваются от 0 до 9 . Когда значения аргумента меняются от 0 до [+infty], значения функции будут уменьшаться от 9 до 0.
Пример №5:
Определить область значений [y=frac{x}{x-2}];
По правилам математики. знаменатель не может равняться нулю. Поэтому: [D(y)=(-infty ; 2)(+infty ; 2)].
Определим множества на первом отрезке. [(-infty ; 2)]. На этом отрезке функция будет убывающей и значение отрицательным.
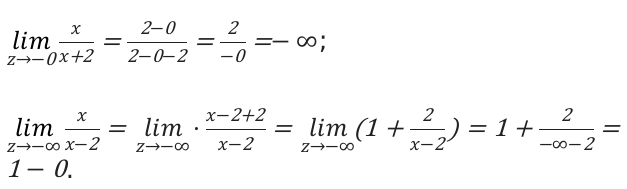
Функция ассиметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.
Определим множества на втором отрезке. [(+infty ; 2)]. На этом отрезке функция будет также убывающей.
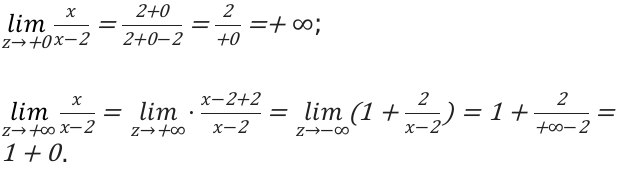
Вывод: [E(y)=(+infty ; 1) cup(1 ;+infty)].

