Правило сложения дисперсий
Пример решения задачи
Задача
Имеются
данные о фонде месячной заработной платы и средней зарплаты одного рабочего по
трем цехам.
| Цех |
Средняя месячная зарплата одного рабочего (у.е.) |
Фонд зарплаты (у.е.) |
СКО по зарплате (у.е.) |
| 1 | 148 | 41200.7 | 3000 |
| 2 | 150 | 51290.4 | 2100 |
| 3 | 151 | 41530.5 | 4900 |
Требуется:
- Определить среднюю зарплату одного рабочего по предприятию в целом.
- Общую дисперсию по зарплате.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычисление средней
1)
Среднюю заработную плату вычислим по формуле средней гармонической:
где
– фонд заработной платы в
цехе
– средняя заработная плата в
цехе
Вычисление средней внутригрупповой и межгрупповой дисперсий
2)
Вычислим общую дисперсию, пользуясь правилом сложения дисперсий:
Внутригрупповые
дисперсии найдем как квадрат среднего квадратического отклонения (СКО) по
зарплате:
Вычислим
количество рабочих в цеху, разделив фонд заработной платы на среднюю месячную
заработную плату по цеху:
Средняя
из внутригрупповых дисперсий:
Рассчитаем
межгрупповую дисперсию:
Согласно
правилу сложения дисперсий:
Вывод к задаче
Таким
образом средняя заработная плата по трем цехам составила 149,685 у.е. при общей
дисперсии заработной платы
.
Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей | Число семей сотрудников по подразделениям | ||
|---|---|---|---|
| первое | второе | третье | |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | – |
Вычислить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
Проверьте правильность произведения расчётов с помощью правила сложения дисперсий.
Решение:
Совокупность семей сотрудников финансовой корпорации разбита на три группы по количеству детей.
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле:
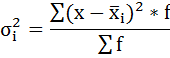
Нахождению внутригрупповой дисперсии предшествует расчёт средней арифметической по каждой группе.
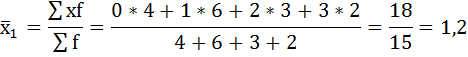
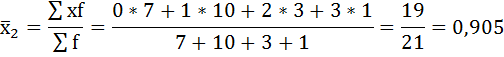
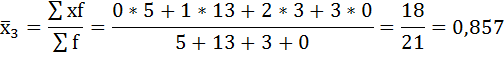
Рассчитаем внутригрупповые дисперсии:
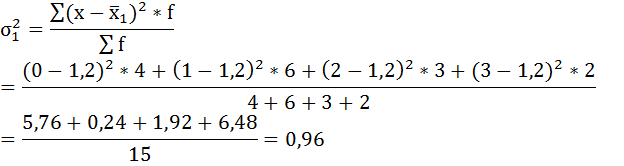
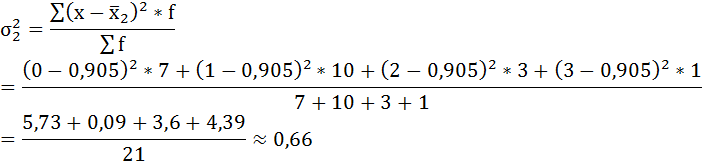
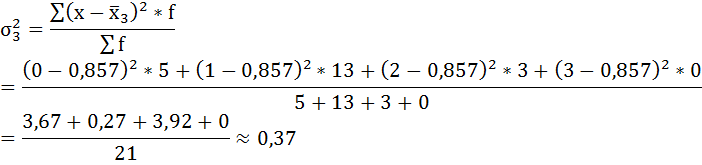
б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых:
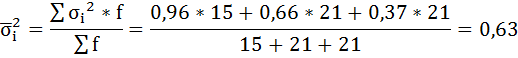
в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней:
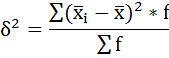
Для её расчета необходимо вычислить общую среднюю:
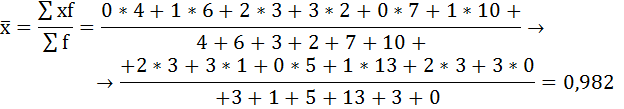
Определим межгрупповую дисперсию:
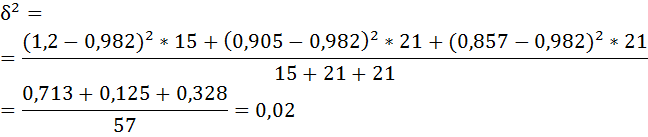
Вычислим общую дисперсию обычным способом:
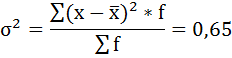
Проверим полученный результат, исчислив общую дисперсию по правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
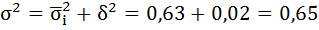
Пусть некоторая
совокупность объема
разбита на части – на
непересекающихся групп, не обязательно
одинаковых по объему. Группы называются
непересекающимися, если каждый вариант
принадлежит только одной группе. Для
каждой группы вариантов можно вычислить
средние, которые называются групповыми
средними
(![]()
).
Пусть
![]()
– количество вариант соответственно в
1-ой, 2-ой, …,
-ой
группах;
– количество вариант всей совокупности;
![]()
– объемы данных групп.
![]()
Групповая средняя
![]()
– ой группы (![]()
)
вычисляется по формуле

(17)
Общей средней
называется средняя арифметическая всей
совокупности:

(18)
Общую
среднюю можно выразить через групповые
средние:

, (19)
где
![]()
– объем
-ой
группы.
Если численности
всех групп одинаковые, то общая средняя
может быть получена и как простая средняя
из групповых средних

(20)
Дисперсия для
распределения вариантов
-ой
группы относительно их групповой средней
называется групповой
дисперсией
![]()
и
вычисляется по формуле:

, (21)
где
– номер группы,
– значения вариант группы (![]()
),
– частоты значений
,
– групповая средняя
-ой
группы,
– объем
-ой
группы.
Дисперсия по этому
же признаку всей совокупности относительно
общей средней называется общей
средней
(![]()
).
Групповые средние
(
)
могут не совпадать с общей средней (
).
Мерой колеблемости
групповых средних (
)
вокруг общей средней (
)
является межгрупповая
дисперсия
(![]()
),
которая вычисляется по формуле:

. (22)
Межгрупповая
дисперсия характеризует систематическую
вариацию, которая возникает под влиянием
фактора, признака, положенного в основе
группировки.
Для характеристики
среднего рассеяния признака внутри
групп из групповых дисперсий может быть
найдена их средняя арифметическая,
взвешенная по объемам групп, которая
называется внутригрупповой
дисперсией
(![]()
)
и вычисляется по формуле:

. (23)
Внутригрупповая
дисперсия характеризует случайную
вариацию в каждой отдельной группе. Она
возникает под влиянием других,
неучитываемых факторов и не зависит от
условий (или признака-фактора), положенных
в основу группировки.
Общей дисперсией
(![]()
)
называют дисперсию значений признака
всей совокупности относительно общей
средней:

, (24)
где
– частота значения
,
– общая средняя,
– объем всей совокупности.
Между общей
дисперсией, внутригрупповой и межгрупповой
дисперсией существует связь, определяемая
теоремой.
Теорема (правило
сложения дисперсий).
Если
совокупность состоит из нескольких
групп, то общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий.
![]()
(25)
Пример 3.
Дано распределение рабочих предприятия
по заработной плате в разрезе цехов:
Таблица №6
|
Заработная плата (в тыс. руб.) |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
|
Цех 1 |
7 |
12 |
15 |
6 |
0 |
0 |
|
Цех 2 |
1 |
5 |
9 |
18 |
12 |
5 |
|
Цех 3 |
0 |
0 |
4 |
8 |
32 |
16 |
Вычислить средние
заработные платы рабочих в каждом цехе
и по предприятию. Вычислить дисперсии
по цехам (групповые дисперсии) и по
предприятию (общую дисперсию). Проверить
правило сложения дисперсий.
Решение.
-
Найдем
объемы групп

и объем всей совокупности
и частоты
для значений
относительно всей совокупности (столбец
«Всего»).
![]()
;
![]()
;
![]()
;
![]()
.
-
Найдем
значенияпредставителей интервалов по формуле:
![]()
,
где
![]()
– начало интервала,
![]()
– конец интервала.
![]()
;![]()
;
![]()
;![]()
;
![]()
;![]()
.
Число
вариант в каждой группе
![]()
.
-
Вычислим
групповые средние (формула (17)) и общую
среднюю (формулы (18) и (19)).
Число
вариант в каждой группе
.

;

;

;
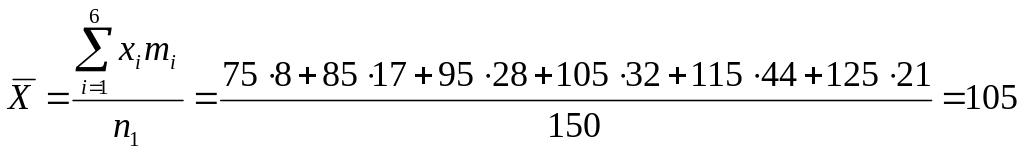
;

.
-
Вычислим
групповые дисперсии (формула (21)) и общую
дисперсию (формула (24)):

![]()

![]()

![]()
![]()
;

![]()
![]()
-
Вычислим
внутригрупповую (формула (23)), межгрупповую
(формула (22)) и общую (формула (25)) дисперсии:


![]()
;
![]()
.
Этапы решения задачи оформим в виде
расчетных таблиц №7 и №8(все расчеты
выполним в табличном процессоре Excel):
Таблица №7
|
Заработная (в |
Цех 1 ( |
Цех 2 ( |
Цех 3 ( |
Всего |
(цех |
(цех |
(цех |
(вся |
||
|
70,00 |
||||||||||
|
80,00 |
7,00 |
1,00 |
0,00 |
8,00 |
75,00 |
13,13 |
1,50 |
0,00 |
4,00 |
|
|
90,00 |
12,00 |
5,00 |
0,00 |
17,00 |
85,00 |
25,50 |
8,50 |
0,00 |
9,63 |
|
|
100,00 |
15,00 |
9,00 |
4,00 |
28,00 |
95,00 |
35,63 |
17,10 |
6,33 |
17,73 |
|
|
110,00 |
6,00 |
18,00 |
8,00 |
32,00 |
105,00 |
15,75 |
37,80 |
14,00 |
22,40 |
|
|
120,00 |
0,00 |
12,00 |
32,00 |
44,00 |
115,00 |
0,00 |
27,60 |
61,33 |
33,73 |
|
|
130,00 |
0,00 |
5,00 |
16,00 |
21,00 |
125,00 |
0,00 |
12,50 |
33,33 |
17,50 |
|
|
Всего |
40,00 |
50,00 |
60,00 |
150,00 |
90,00 |
105,00 |
115,00 |
105,00 |
||
|
|
|
|
|
|
|
|||||
|
Таблица №8 |
||||||||||
|
|
|
|
|
|
||||||
|
39,38 |
18,00 |
0,00 |
48,00 |
97,33 |
100,00 |
197,33 |
||||
|
7,50 |
40,00 |
0,00 |
45,33 |
|||||||
|
9,38 |
18,00 |
26,67 |
18,67 |
|||||||
|
33,75 |
0,00 |
13,33 |
0,00 |
|||||||
|
0,00 |
24,00 |
0,00 |
29,33 |
|||||||
|
0,00 |
40,00 |
26,67 |
56,00 |
|||||||
|
90 |
140 |
66,67 |
197,33 |
|||||||
|
|
|
|
Задача 3. Трое
рабочих изготовляли одинаковые детали.
Каждый из них изготовил по 70 деталей.
Для контроля составлены распределения
изготовленных каждым рабочим деталей
по их размеру. Точность измерения 0,01.
Поле допуска 50,04-50,28мм. Сравнением
распределений выяснить, какой рабочий
работает лучше.
Таблица №9
|
Интервалы |
I |
II |
III |
|
50-50,04 |
2 |
0 |
3 |
|
50,04-50,08 |
6 |
2 |
8 |
|
50,08-50,12 |
9 |
5 |
16 |
|
50,12-50,16 |
26 |
9 |
9 |
|
50,16-50,2 |
14 |
14 |
4 |
|
50,2-50,24 |
7 |
19 |
13 |
|
50,24-50,28 |
5 |
8 |
11 |
|
50,28-50,32 |
1 |
5 |
4 |
|
50,32-50,36 |
0 |
5 |
2 |
|
50,36-50,4 |
0 |
2 |
0 |
|
50,4-50,44 |
0 |
1 |
0 |
|
Всего |
70 |
70 |
70 |
Все расчеты
выполнить в табличном процессоре Excel
и оформить в виде расчетных таблиц.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти дисперсию?
Понравилось? Добавьте в закладки
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Понравилось? Добавьте в закладки
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.
Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
![]()
Эмпирическую функцию распределения определим по формуле
![]()
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
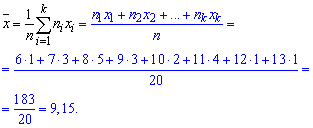
Выборочную дисперсию находим по формуле
![]()
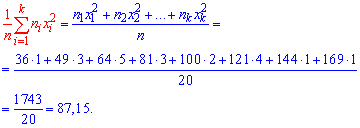
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
![]()
Подправленную дисперсию вычисляем согласно формулы
![]()
Выборочное среднее квадратичное отклонение вычисляем по формуле
![]()
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
![]()
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
![]()
Медиану находим по 2 формулам:
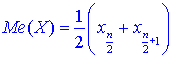 если число n – четное;
если число n – четное;
![]() если число n – нечетное.
если число n – нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
![]()
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
![]()
Квантильное отклонение находят по формуле
![]()
где ![]() – первый квантиль,
– первый квантиль, ![]() – третий квантиль.
– третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
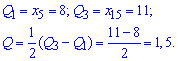
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
![]()
Коэффициент асимметрии находим по формуле
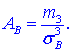
Здесь 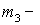 центральный эмпирический момент 3-го порядка,
центральный эмпирический момент 3-го порядка,
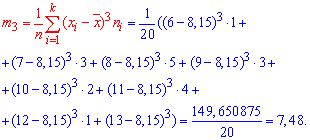
Подставляем в формулу коэффициента асимметрии
![]()
Эксцессом ![]() статистического распределения выборки называется число, которое вычисляют по формуле:
статистического распределения выборки называется число, которое вычисляют по формуле:
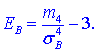
Здесь m4 центральный эмпирический момент 4-го порядка. Находим момент
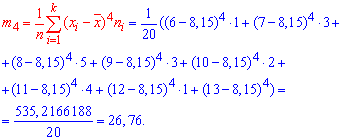
а далее эксцесс![]()
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья – Построение уравнения прямой регрессии Y на X
