В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
-
3. Полная площадь
- Примеры задач
Формула вычисления площади конуса
1. Боковая поверхность
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.
Sбок. = πRl

Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
Основанием конуса является круг, площадь которого вычисляется так:
Sосн. = πR2
Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:
Sосн. = π(d/2)2
3. Полная площадь
Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:
Sполн. = πRl + πR2 = πR(l + R)
Примеры задач
Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.
Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см2.
Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l2 = (4 см)2 + (3 см)2 = 25 см2.
l = 5 см.
Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см2.
Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
|
Рис. (1). Конус |
Площадь боковой поверхности конуса вычисляется по формуле: где (R) — радиус конуса, (l) — образующая конуса. Площадь основания конуса вычисляется по формуле S(круга) = Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = 13⋅H⋅ S(круга) = πR2⋅H3 |
Площадью боковой поверхности конуса является площадь её развёртки.
Развёрткой боковой поверхности конуса является круговой сектор.
|
Рис. (2). Развёртка конуса |
α
— градусная мера центрального угла. Радиус этого сектора — образующая конуса (AK = KB = l)
|
Источники:
Рис. 1. Конус. © Якласс
Рис. 2. Развёртка конуса. © Якласс
Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
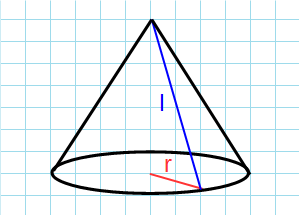
Формула боковой поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Боковая поверхность через радиус и высоту
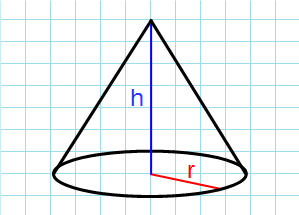
Формула боковой поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Площадь поверхности конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности конуса
Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Площадь боковой поверхности конуса
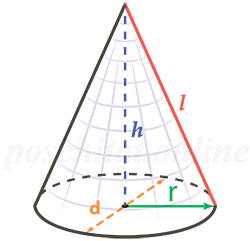
=
=
Sб.пов =
0
Округление числа π: Округление ответа:
Площадь полной поверхности конуса
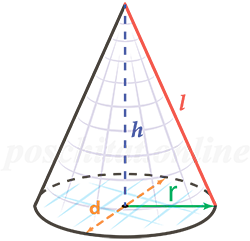
=
=
Sп.пов =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Площадь боковой поверхности конуса через образующую
Чему равна площадь боковой поверхности конуса Sб.пов, если образующая l, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ l
через диаметр:
Sб.пов = π ⋅ l ⋅ d⁄2
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sб.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²
Площадь боковой поверхности конуса через высоту
Чему равна площадь боковой поверхности конуса Sб.пов, если высота h, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ √r² + h²
через диаметр:
Sб.пов = π ⋅ d⁄2 ⋅ √(d/2)² + h²
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sб.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²
Площадь полной поверхности конуса через образующую
Чему равна площадь полной поверхности конуса Sп.пов, если образующая l, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + l)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + l)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sп.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²
Площадь полной поверхности конуса через высоту
Чему равна площадь полной поверхности конуса Sп.пов, если высота h, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + √r² + h²)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + √(d/2)² + h²)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sп.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²
См. также
Площадь поверхности конуса
Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

Формула площади боковой поверхности конуса: S = π r l ,
где r – радиус основания, l – образующая.
Формула площади полной поверхности конуса: S = π r (r + l) ,
где r – радиус основания, l – образующая.
Калькулятор пощади поверхности конуса позволяет найти площадь боковой поверхности конуса и полную площадь поверхности конуса.
Поделиться страницей в социальных сетях:
