Как найти радиус вписанной сферы тетраэдра

Тетраэдр.

Тетраэдр – это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Правильный тетраэдр – это один из 5-ти правильных многогранников.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

– Каркасный тетраэдр — тетраэдр, который таким условиям:

• есть сфера, которая касается каждого ребра,
• суммы длин ребер, что скрещиваются равны,
• суммы двугранных углов при противоположных ребрах равны,
• окружности, которые вписаны в грани, попарно касаются,
• каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
• перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.

– Соразмерный тетраэдр, бивысоты у него одинаковы.

– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

где h – высота тетраэдра, a – ребро тетраэдра.

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

где V – объем тетраэдра, a – ребро тетраэдра.

Основные формулы для правильного тетраэдра:

Где S – Площадь поверхности правильного тетраэдра;

h – высота, опущенная на основание;

r – радиус вписанной в тетраэдр окружности;

Радиус вписанной сферы тетраэдра

Свойства

Зная радиус сферы, вписанной в тетраэдр, нужно сначала найти ребро тетраэдра, а также можно без хитрых преобразований рассчитать сразу радиус сферы, описанной около тетраэдра. a=2√6 r_1 R_1=3r_1

Зная ребро тетраэдра через радиус вписанной сферы, можно рассчитать периметр тетраэдра, равный длине всех шести его ребер, площадь одной грани и площадь полной поверхности тетраэдра, состоящей из четырех таких граней. P=12√6 r_1 S_1=6√3 〖r_1〗^2 S_(п.п.)=4S_1=24√3 〖r_1〗^2

Кроме радиусов вписанной и описанной около тетраэдра сфер, у него есть также радиусы вписанной и описанной окружностей около грани, являющейся основанием, которые можно вычислить через радиус вписанной сферы. r=√2 r_1 R=2√2 r_1

Высота и апофема тетраэдра располагаются под прямым углом к основанию с той лишь разницей, что высота падает в центр основания, являющийся по совместительству центром для вписанной и описанной окружностей основания, а апофема опускается по боковому ребру в центр стороны основания. h=4r_1 l=3√2 r_1

Чтобы вычислить объем тетраэдра через радиус сферы, вписанной в него, нужно возвести радиус в третью степень и умножить его на восемь корней из трех. V=8√3 〖r_1〗^3

Сфера, вписанная в пирамиду

Биссекторная плоскость. Основное свойство биссекторной плоскости

Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

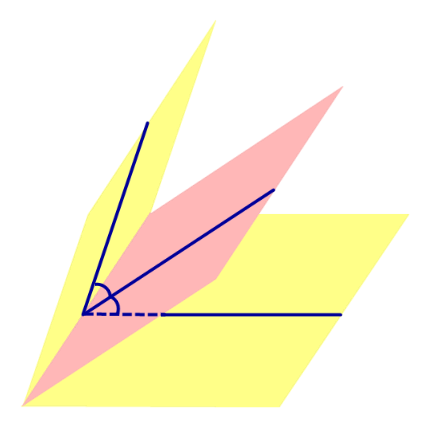
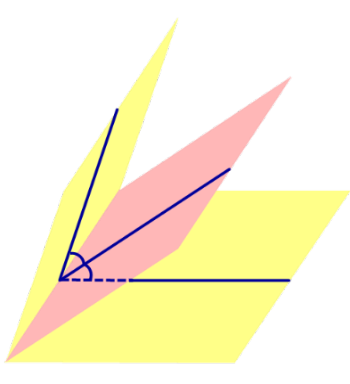
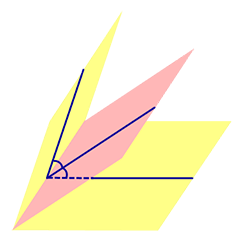
Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).

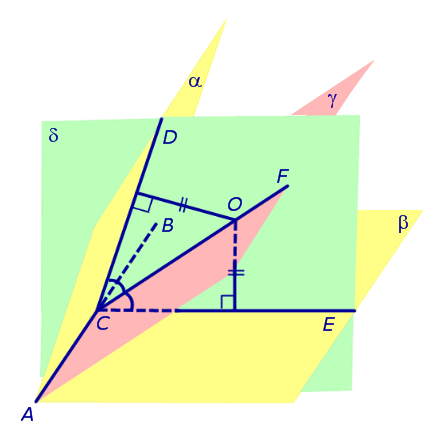
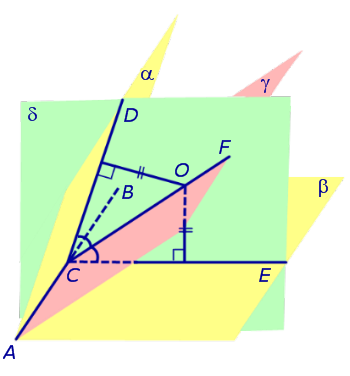
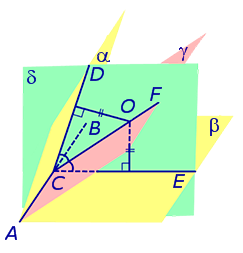
Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .

Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.

Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

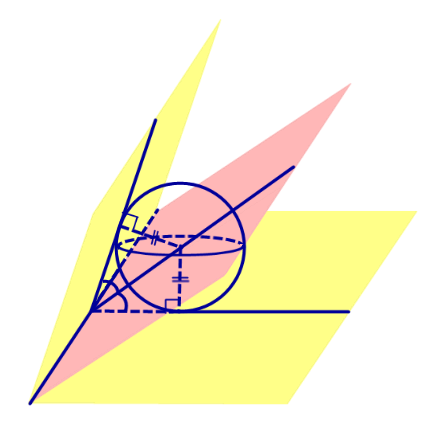
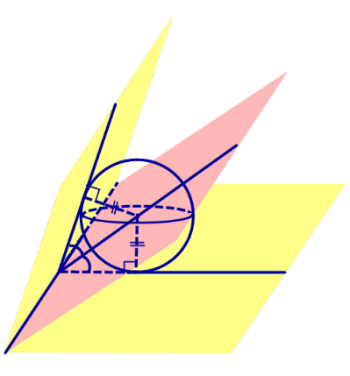
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

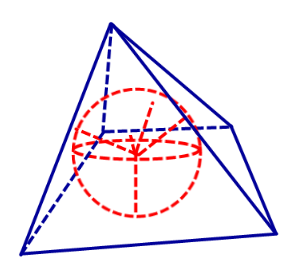
Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

Утверждение 2. Если у пирамиды SA₁A₂ . A_n основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A₁A₂ . A_n , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA₁A₂ и проведем в ней высоту SB (рис. 5).

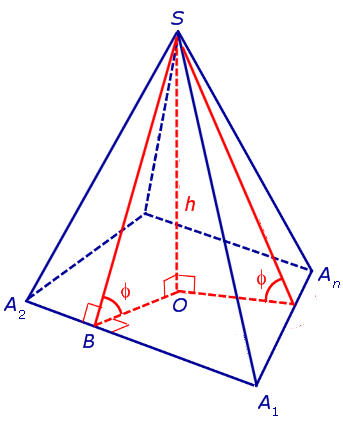
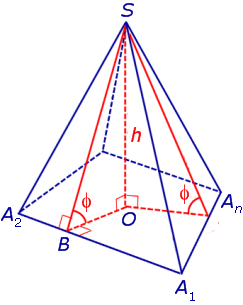
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A₁A₂ . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA₁A₂ и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).

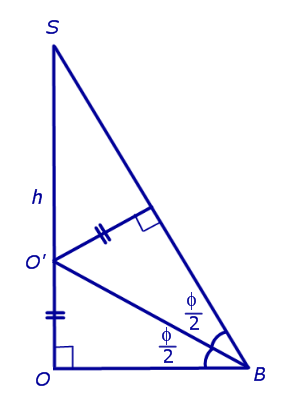
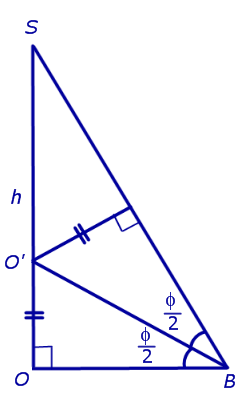
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле

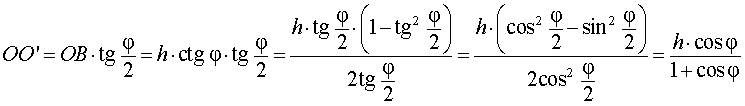
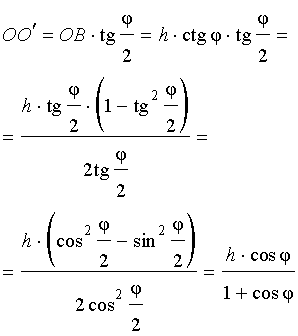
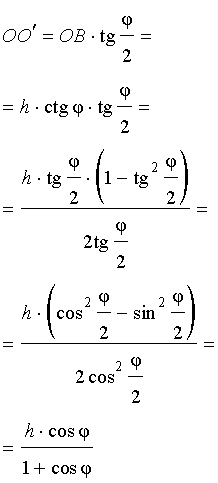
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.

Доказательство утверждения 2 завершено.

Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле

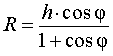(1)

Радиус сферы, вписанной в правильную n – угольную пирамиду

Решение. Рассмотрим правильную n – угольную пирамиду SA₁A₂ . A_n и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).

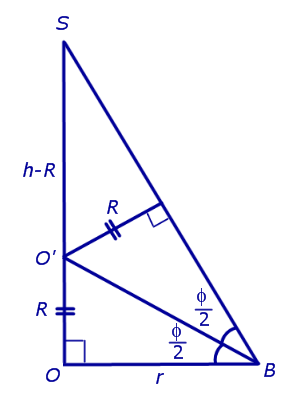
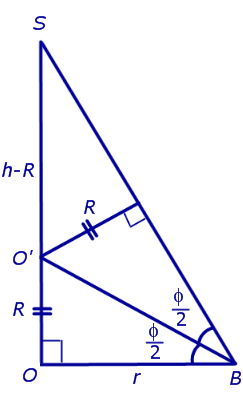
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

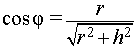(2)

В силу следствия 2 из формул (1) и (2) получаем

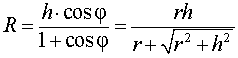
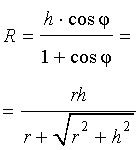
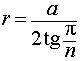
из формулы (3) получаем соотношение

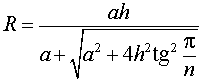
Ответ.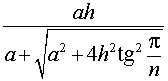

Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен

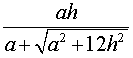
Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен

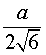
Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен

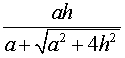
Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен

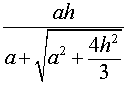
Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы

Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).

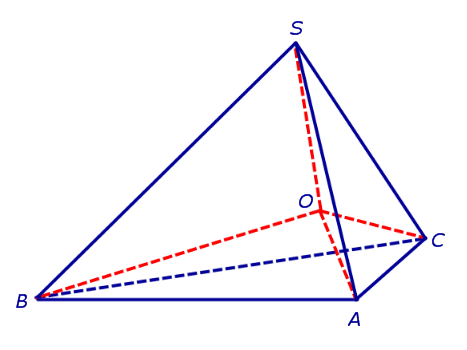
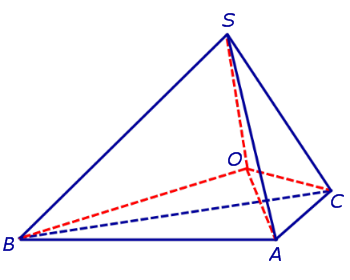
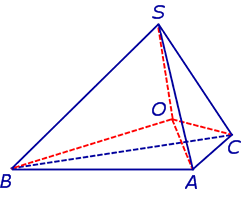
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами

а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами

то справедливы следующие равенства:

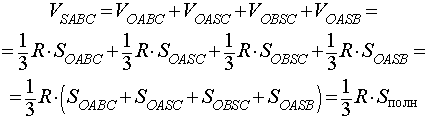
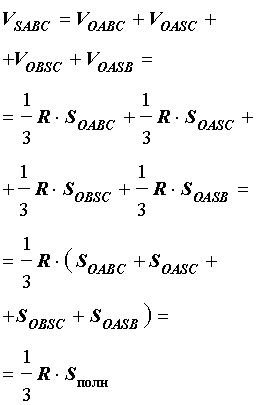
где символом S_полн обозначена площадь полной поверхности пирамиды SABC.

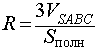
Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы

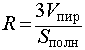
где символами V_пир и S_полн обозначены объем и площадь полной поверхности пирамиды соответственно.

[spoiler title=”источники:”]

http://geleot.ru/education/math/geometry/calc/tetrahedron/radius_inscribed_sphere

http://www.resolventa.ru/spr/stereometry/sphere_piramide.htm

[/spoiler]

Зная радиус сферы, вписанной в тетраэдр, нужно сначала найти ребро тетраэдра, а также можно без хитрых преобразований рассчитать сразу радиус сферы, описанной около тетраэдра.
a=2√6 r_1
R_1=3r_1

Зная ребро тетраэдра через радиус вписанной сферы, можно рассчитать периметр тетраэдра, равный длине всех шести его ребер, площадь одной грани и площадь полной поверхности тетраэдра, состоящей из четырех таких граней.
P=12√6 r_1
S_1=6√3 〖r_1〗^2
S_(п.п.)=4S_1=24√3 〖r_1〗^2

Кроме радиусов вписанной и описанной около тетраэдра сфер, у него есть также радиусы вписанной и описанной окружностей около грани, являющейся основанием, которые можно вычислить через радиус вписанной сферы.
r=√2 r_1
R=2√2 r_1

Высота и апофема тетраэдра располагаются под прямым углом к основанию с той лишь разницей, что высота падает в центр основания, являющийся по совместительству центром для вписанной и описанной окружностей основания, а апофема опускается по боковому ребру в центр стороны основания.
h=4r_1
l=3√2 r_1

Чтобы вычислить объем тетраэдра через радиус сферы, вписанной в него, нужно возвести радиус в третью степень и умножить его на восемь корней из трех.
V=8√3 〖r_1〗^3

Правильные многогранники

Существует всего пять правильных многогранников:

• Тетраэдр
• Куб (Гексаэдр)
• Октаэдр
• Икосаэдр
• Додекаэдр

Если какое-то из этих названий звучит для тебя как древний эльфийский язык, обязательно прочитай эту статью!

Давай посмотрим, как они выглядят, и разберем основные формулы – площади поверхности, объема, радиусов вписанной и описанной сферы.

А также решим задачу №8.

О том, как рисовать пространственные фигуры на плоскости, можно прочитать в нашей статье: «Изображение пространственных фигур. Визуальный гид».

Поехали!

Правильные многогранники — подробнее

Многогранник называется правильным, если:

• он выпуклый;
• все его грани являются правильными многоугольниками;
• в каждой его вершине сходится одинаковое число его ребер.

Пять правильных многогранников

Тетраэдр

Тетраэдр состоит из четырёх равносторонних треугольников.

Фигура имеет 4 грани, 4 вершины и 6 ребер(a).

Площадь поверхности тетраэдра:

( displaystyle S={{a}^{2}}sqrt{3})

Объем тетраэдра:

( displaystyle V=frac{{{a}^{3}}}{12}sqrt{2})

Радиус описанной вокруг тетраэдра сферы:

( displaystyle R=frac{a}{4}sqrt{6})

Радиус вписанной в тетраэдр сферы:

( displaystyle R=frac{a}{12}sqrt{6})

Куб (Гексаэдр)

Куб состоит из шести квадратов.

 Фигура имеет 6 граней, 8 вершин и 12 ребер (a).

Площадь поверхности куба:

( displaystyle S=6{{a}^{2}})

Объем куба:

( displaystyle V={{a}^{3}})

Радиус описанной вокруг куба сферы:

( displaystyle R=frac{a}{2}sqrt{3})

Радиус вписанной в куб сферы:

( displaystyle r=frac{a}{2})

Октаэдр

Октаэдр составлен из восьми равносторонних треугольников.

Фигура имеет 8 граней, 6 вершин и 12 ребер (a).

Площадь поверхности октаэдра:

( displaystyle S=2{{a}^{2}}sqrt{3})

Объем октаэдра:

( displaystyle V=frac{{{a}^{3}}}{3}sqrt{2})

Радиус описанной вокруг октаэдра сферы:

( displaystyle R=frac{a}{2}sqrt{2})

Радиус вписанной в октаэдр сферы:

( displaystyle r=frac{a}{6}sqrt{6})

Икосаэдр

Икосаэдр составлен из двадцати равносторонних треугольников.

Фигура имеет 20 граней, 12 вершин и 30 ребер (a).

Площадь поверхности икосаэдра:

( displaystyle S=5{{a}^{2}}sqrt{3})

Объем икосаэдра:

( displaystyle V=frac{5{{a}^{3}}}{12}left( 3+sqrt{5} right))

Радиус описанной вокруг икосаэдра сферы:

( displaystyle R=frac{a}{4}sqrt{2left( 5+sqrt{5} right)})

Радиус вписанной в икосаэдр сферы:

( displaystyle r=frac{a}{4sqrt{3}}left( 3+sqrt{5} right))

Додекаэдр

Додекаэдр составлен из двенадцати равносторонних пятиугольников.

Фигура имеет 12 граней, 20 вершин и 30 ребер (a).

Площадь поверхности додекаэдра:

( displaystyle S=3{{a}^{2}}sqrt{5left( 5+2sqrt{5} right)})

Объем додекаэдра:

( displaystyle V=frac{{{a}^{3}}}{4}left( 15+7sqrt{5} right))

Радиус описанной вокруг додекаэдра сферы:

( displaystyle R=frac{a}{4}left( 1+sqrt{5} right)sqrt{3})

Радиус вписанной в додекаэдр сферы:

( displaystyle r=frac{a}{4}sqrt{10+frac{22}{sqrt{5}}})

Решение задачи №8 на тему «Правильные многогранники»

Задача:

В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) с ребром ( displaystyle sqrt{12}) найдите ( displaystyle A{{C}_{1}}).

Решение:

( displaystyle d=asqrt{3}),

где ( displaystyle d) – диагональ куба,( displaystyle a) – сторона куба.( displaystyle A{{C}_{1}}) – это и есть диагональ куба.

Тогда ( displaystyle A{{C}_{1}}=asqrt{3}=sqrt{12}cdot sqrt{3}=sqrt{36}=6).

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
• отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

2023-02-18   

Найдите радиус сферы, вписанной в правильный тетраэдр с ребром $a$.

Решение:

Первый способ. Пусть $ABCD$ – правильный тетраэдр с ребром $a$, $M$ – центр грани $ABC$, $L$ – середина $BC$, $Q$ – центр вписанной сферы, $r$ – её радиус.
Поскольку $DLperp BC$ и $LMperp BC$, линейный угол искомого двугранного угла между плоскостями $ABC$ и $DBC$ – это угол $DLM$. Обозначим его $beta$. Так как $DM$ – высота тетраэдра, то треугольник $DLM$ – прямоугольный. В нём известно, что $DL=frac{asqrt{3}}{2}$, $LM=frac{asqrt{3}}{6}$. Следовательно,

$cosbeta=cosangle DLM=frac{LM}{DL}=frac{frac{asqrt{3}}{6}}{frac{asqrt{3}}{2}}=frac{1}{3},~sinbeta=frac{2sqrt{2}}{3}.$

Поскольку сфера вписана в двугранный угол, образованный плоскостями $ABC$ и $DBC$, её центр $Q$ лежит в биссекторной плоскости этого угла.
Проведём сечение тетраэдра плоскостью, проходящей через ребро $AD$ и середину $L$ противоположного ему ребра $BC$. Получим треугольник $ALD$, стороны $AL$ и $AD$ которого касаются окружности радиуса $r$ с центром $Q$ на высоте $DM$. Из прямоугольного треугольника $LMQ$ находим, что

$r=QM=LMtgangle QKM=frac{asqrt{3}}{6}cdot tgfrac{beta}{2}=frac{asqrt{3}}{6}cdotfrac{sinbeta}{1+cosbeta}=frac{asqrt{3}}{6}cdotfrac{frac{2sqrt{2}}{3}}{frac{4}{3}}=frac{asqrt{6}}{12}.$

Второй способ. Пусть $ABCD$ – правильный тетраэдр с ребром $a$, $r$ – искомый радиус вписанной сферы. Центр сферы, вписанной в правильный тетраэдр, лежит на каждой из четырёх высот тетраэдра. Высоты правильного тетраэдра являются его медианами, а медианы любой треугольной пирамиды пересекаются в одной точке и делятся ею в отношении $3:1$, считая от вершины. Значит, центр вписанной сферы совпадает с точкой пересечения высот правильного тетраэдра, а радиус равен $frac{1}{4}$ высоты тетраэдра. Следовательно,

$r=frac{1}{4}asqrt{frac{2}{3}}=frac{asqrt{6}}{12}.$

Третий способ. Пусть $r$ – радиус сферы, вписанной в правильный тетраэдр с ребром $a$, $V$ – объём тетраэдра, $S$ – полная поверхность. Тогда

$r=frac{3V}{S}=frac{frac{3a^{3}sqrt{2}}{12}}{a^{2}sqrt{3}}=frac{asqrt{6}}{12}.$

Площади граней тетраэдра при вершине с прямыми плоскими углами равны 270, 360, 600. Сфера касается всех плоскостей, содержащих грани тетраэдра. Чему равен радиус сферы? бонус за лучший ответ (выдан): 20 кредитов Нам необходимо найти радиус вписанной в тетраэдр сферы, который определяется как отношение утроенного объема тетраэдра к площади полной его поверхности, то есть Для начала найдем боковые ребра а, b и с. Согласно условию {ab/2 = 270; {bc/2 = 360; {ас/2 = 600. Разделив первое уравнение на второе, получим а = 0,75с. Подставив данное выражение в третье уравнение, получаем с = 40, тогда а = 0,75*40 = 30, b = 360*2/40 = 18. Объем пирамиды можно вычислить, умножив треть высоты на площадь основания. Поскольку по условию углы при вершине прямые, Vпир = 30*360/3 = 18*600/3 = 40*270/3 = 3600. Используя т. Пифагора, можно легко найти стороны треугольника, являющегося основанием тэтраэдра: √(18² + 30²) = √1224, √(18² + 40²) = √1924, √(40² + 30²) = 50. Зная стороны треугольника, можно вычислить его площадь по ф. Герона. где а, b, c – стороны тр-ка, а р – его полупериметр. И в нашей задаче площадь основания получилась равной 750. Тогда Sполн = (270 + 360 + 600 + 750) = 1980, а искомый радиус R = 3*3600/1980 = 60/11 = 5,(45). система выбрала этот ответ лучшим bezde­lnik [34.1K] 3 года назад  В комментарии к ответу Георг­ия22 я написал, что задача может иметь несколько решений, если принять площади граней МВА и МВС равными между собой,а площадь основания тетраэдра Sт равной 600. Рисунок Георгия дополним двумя перпендикулярами ВК и МК к стороне АС. В треугольнике АВС АВ=АС/√2, ВК=АК=АС/2 как стороны расположенные против равных углов 45 градусов. 600=АС*ВК/2, 1200=АС*ВК, , 1200=АС^2/2, АС^2=2400, АС=√2400. Такие решения излагаю ниже, их не два, а даже три, если площади указанных граней считать попарно равными 270, 360 и 600 квадратным единицам. Площадь треугольника определяется по формуле S=L*h/2, где L- длина стороны, h – высота треугольника опущенная на эту сторону. Поскольку треугольники МВА и МВС прямоугольные, то общая высота у них будет равна длине грани МВ. Объём пирамиды V=S*H/3, Радиус вписанного шара r=3V/S. 1)Рассмотрим решение для S1=270=АВ*МВ1/2, МВ1=540/АВ=540*√2/АС­=540*√2/√2400. V1=600*540*√2/3√2400­= 200*540*√2/√2400=108­000*√2/√2400. r1=3*108000*√2/600√2­400=540√2400,r1=11… 2)Для S2=360=АВ*МВ2/2=600*­720*√2/√2400. V2=432000√2/√2400, r2=3*432000√2/600√24­00=720√2/√2400=20,78.­… 3)Для V3=600=АВ*МВ3/2=600*­1200*√2/√2400= 720000*√2/√2400. r3=3*720000*√2/600√2­400=3600*√2/√2400=103­,9… Для прямоугольного тетраэдра верна обобщенная теорема Пифагора: S²о = Sa² + Sb² +Sс². Откуда, So = 750. Таких сфер, как в условии, у тетраэдра может быть от пяти до восьми. Всегда существуют вписанная сфера и четыре вневписанных, касающихся одной из граней с внешней стороны. Радиус вписанной сферы легко находится, как верно указала Светлана0202: R = 3V/Sp = 3V/(So + Sa + Sb + Sc). Радиус вневписанной сферы, касающейся грани с площадью Sa, также легко найти, он равен: Ra = 3V/(Sp − 2Sa). Аналогично находятся Rb, Rc, Ro. У нашего тетраэдра еще есть три сферы, вневписанные в “корытца” при ребрах. Радиус сферы, вневписанной в “корытце” при ребре, образованном гранями с площадями Sa и Sb, равен: Rab = 3V/(Sp − 2Sa − 2Sb). Аналогично находим Rac и Rbc. bezde­lnik [34.1K] 3 года назад  Поскольку по условию задачи площади разные, то надо рассматривать общий случай тетраэдра. В общем случае тетраэдр имеет 4 грани в виде треугольников, 6 ребер и 4 вершины, в каждой из которых сходятся по три грани. Все рёбра тетраэдра равны между собой, поэтому все грани есть равносторонние правильные треугольники и их площади равны между собой. Условие задачи ошибочно. Но можно найти радиус сферы вписанный в правильный тетраэдр. Площадь любого треугольника S=h*L/2, где h – высота треугольника, L – его основание, или в данном случае длина грани. Обозначим вершины треугольника А,В,С. Высоты равносторонних треугольников h = (L√3)/2. Точку пересечения всех высот в нём обозначим О, тогда ОА=ОВ=ОС равны радиусу вписанной окружности r=h/3=(L√3)/6. Четвёртую вершину тетраэдра обозначим Р. ОР будет высотой тетраэдра Н=L(√2/3). Радиус сферы касающейся всех граней R=L/2√6. √6=2,449… , если принять длину граней равной √6 или примерно 2,45, то R будет примерно равен 1/2. Георг­ий22 [403] 3 года назад  Площади граней тетраэдра при вершине с прямыми плоскими углами равны 270, 360, 600. Сфера касается всех плоскостей, содержащих грани тетраэдра. Решение задачи: ovro1 [96.5K] 3 года назад  Используя онлайн-калькуятор >>>>>>>>>>> , через полную площадь граней тетраэдра можно вычислить радиусы вписанной и описанной сфер. В данном случае это будут цифры 6,902 и 20,705 соответственно. Методика расчета представлена внизу сайта. Знаете ответ?

Смотрите также: ОГЭ математика 5, годовая 4 по алгебре и 4 по геометрии, что в аттестат? ОГЭ математика 4. Годовая алгебра 4, геометрия 3. Что будет в аттестате? Математика 6, 5, 2 класс. Где скачать ответы на задачи в 2017? Задача о разделении школьников на кружки по математике поровну. Как решить? Как решить задачу: в школе мальчики составляют 57 % (см)? Как объяснить ребенку задачи на скорость, время, расстояние? 4 класс. Как решить задачу: Алёша решил в 3 раза больше задач, чем Боря (см.)? Вы помните каких учителей вы не любили в школе? За что? Задача. Если сегодня вторник, какой день недели будет через 150 дней? Задачи экологического характера для 1 класса, какие придумать?