Запросы «sin» и «синус» перенаправляются сюда; у терминов sin и синус есть также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.

Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Тригонометри́ческие фу́нкции — элементарные функции[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
- прямые тригонометрические функции:
- синус (
);
- косинус (
);
- производные тригонометрические функции:
- тангенс
;
- котангенс
;
- секанс
;
- косеканс
;
- обратные тригонометрические функции:
- арксинус, арккосинус и т. д.
В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются 


Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках 

Графики тригонометрических функций показаны на рис. 1.
Способы определения[править | править код]
Определение для любых углов[править | править код]

Рис. 2.
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически[3]. В декартовой системе координат на плоскости построим окружность единичного радиуса (






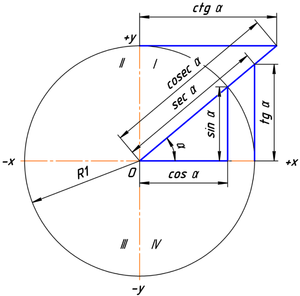
Синусом угла 






Косинусом угла 






Тангенсом угла 


Котангенсом угла 


Таким образом, определения тригонометрических функций выглядят следующим образом:
Нетрудно видеть, что такое определение также основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак (

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в 






Наконец, определим тригонометрические функции вещественного числа 

Определение для острых углов[править | править код]

Рис. 4.
Тригонометрические функции острого угла

Определение тангенса. Марка СССР 1961 года
В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника[5]. Пусть 



Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Определение как решений дифференциальных уравнений[править | править код]
Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:
То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения
с дополнительными условиями:


Определение как решений функциональных уравнений[править | править код]
Функции косинус и синус можно определить[7]
как решения (


при дополнительных условиях:




Определение через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также равенствами 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов[править | править код]
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («
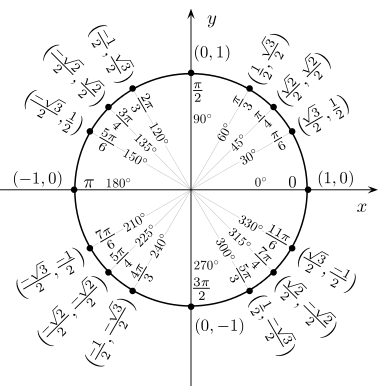
Значения косинуса и синуса на окружности
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций нестандартных углов[править | править код]
| Радианы | 
|

|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций для некоторых других углов
Свойства тригонометрических функций[править | править код]
Простейшие тождества[править | править код]
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности (
Это соотношение называется основным тригонометрическим тождеством.
Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:
Из определения тангенса и котангенса следует, что
Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для 
| sin | cos | tg | ctg | sec | cosec | |
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Непрерывность[править | править код]
Чётность[править | править код]
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность[править | править код]
Функции 




Формулы приведения[править | править код]
Формулами приведения называются формулы следующего вида:
Здесь 



или что то же самое:
Некоторые формулы приведения:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Интересующие формулы приведения так же могут легко быть получены рассмотрением функций на единичной окружности.
Формулы сложения и вычитания[править | править код]
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов[править | править код]
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для гамма-функции.
Из формулы Муавра можно получить следующие общие выражения для кратных углов:
где ![[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)


Формулы половинного угла:
Произведения[править | править код]
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени[править | править код]

Иллюстрация равенства
Суммы[править | править код]
Существует представление:
где угол 
Универсальная тригонометрическая подстановка[править | править код]
Все тригонометрические функции можно выразить через тангенс половинного угла:






Исследование функций в математическом анализе[править | править код]
Разложение в бесконечные произведения[править | править код]
Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:
Эти соотношения выполняются при любом значении 
Непрерывные дроби[править | править код]
Разложение тангенса в непрерывную дробь:
Производные и первообразные[править | править код]
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:






Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом[8]:






Тригонометрические функции комплексного аргумента[править | править код]
Определение[править | править код]
Формула Эйлера:
Формула Эйлера позволяет определить тригонометрические функции от комплексных аргументов через экспоненту по аналогии с гиперболическими функциями, или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x:
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики[править | править код]
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
|
|
|
|
|
|

|

|

|

|

|

|
История названий[править | править код]
Линия синуса (линия 
Современные краткие обозначения 

Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Интегральный секанс
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература[править | править код]
- Бермант А. Ф., Люстерник Л. А. Тригонометрия. — М.: Наука, 1967.
- Тригонометрические функции — статья из Большой советской энциклопедии. — М.: Советская энциклопедия, 1977. — Т. 26. — С. 204—206.
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 www.alleng.ru/d/math/math42.htm
- Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
- Кожеуров П. А. Тригонометрия. — М.: Физматгиз, 1963.
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — И. М. Виноградов. Тригонометрические функции // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В. (гл. ред.), Савин А. П. и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. — ISBN 5-7155-0218-7 (С. 342, 343 — таблицы тригонометрических функций 0°-90°, в том числе в радианах)
- Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с.
Ссылки[править | править код]
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Trigonometric Functions (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций (в том числе нахождение углов треугольника по сторонам)
- Интерактивная карта значений тригонометрических функций
- Тригонометрические таблицы (0° — 360°)
- «Синус и косинус — это проценты» — перевод статьи How To Learn Trigonometry Intuitively | BetterExplained (англ.)
Примечания[править | править код]
- ↑ Справочник: Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с. Архивная копия от 19 января 2015 на Wayback Machine относит их к специальным функциям.
- ↑ Знак математический. // Большая советская энциклопедия. 1-е изд. Т. 27. — М., 1933.
- ↑ Справочник по элементарной математике, 1978, с. 282—284.
- ↑ Шахмейстер А. Х. Определение основных тригонометрических функций // Тригонометрия : [рус.] : книга / А. Х. Шахмейстер; под ред. Б. Г. Зива. — 3-е изд., стереотипное. — М. : Издательство МЦНМО ; СПб. : «Петроглиф» : «Виктория плюс», 2013. — С. 11, 14, 18, 20. — 752 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-4439-0050-6. — ISBN 978-5-98712-042-2. — ISBN 978-5-91673-097-5.
- ↑ Справочник по элементарной математике, 1978, с. 271—272.
- ↑ Латинско-русский словарь. Дата обращения: 9 апреля 2023.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — М.: Наука, 1998. — ISBN 5-02-015231-5.
- ↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования
, вообще говоря, различны для различных интервалов непрерывности.
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z – любое целое число.
Изобразим данные формулы на рисунке:
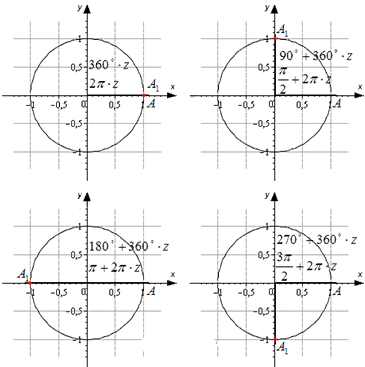
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
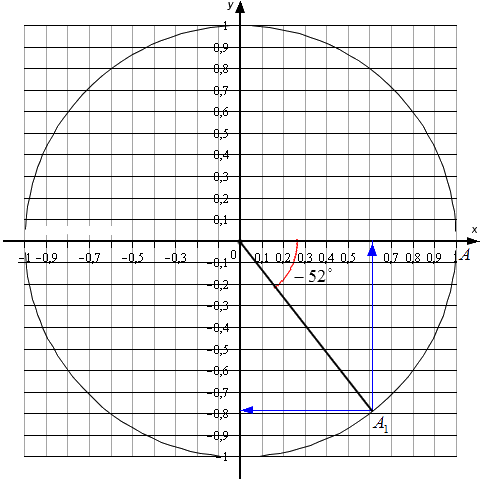
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( – 52 ° ) ≈ – 0 , 78 и cos ( – 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( – 52 ° ) ≈ – 0 , 78 0 , 62 ≈ – 1 , 26 и c t g ( – 52 ° ) ≈ 0 , 62 – 0 , 78 ≈ – 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
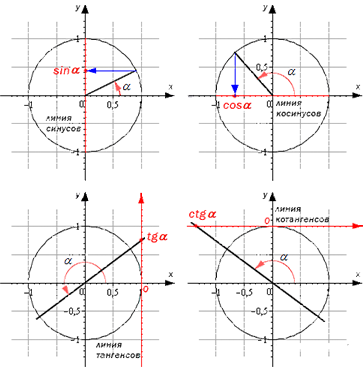
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 – 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
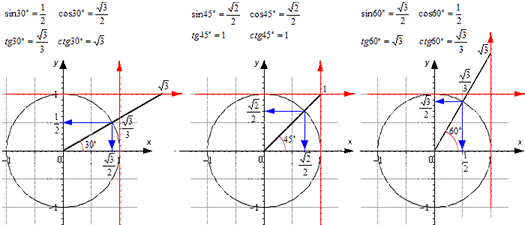
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 – 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 – 1 = 2 + 1 ( 2 – 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 – 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 – 2 2 · ( 2 + 2 ) · ( 2 – 2 ) = = 2 – 2 2 · ( 2 2 – ( 2 ) 2 ) = 2 – 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 – 2 4 = 2 – 2 2 . sin π 8 = 2 – 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = – sin 30 ° = – 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° – 60 ° ) = – cos 60 ° = – 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 – cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 – cos π 4 1 + cos π 4 = 1 – 2 2 1 + 2 2 = 2 – 2 2 + 2 = = ( 2 – 2 ) 2 ( 2 + 2 ) · ( 2 – 2 ) = ( 2 – 2 ) 2 2 2 – ( 2 ) 2 = ( 2 – 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 – 2 ) 2 2 = 2 – 2 2 = 2 – 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Узнать ещё
Знание — сила. Познавательная информация
Синус 1, sin 2, sin 3
Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.
Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.
Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.
Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здесь ), то для нахождения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6 достаточно определить значение y в точках 1, 2, 3, 4, 5 и 6 радиан.
Поскольку синус — это y, то вверху, над осью x, синус принимает положительные значения. Поэтому sin 1>0, sin 2>0, sin 3>0.
Соответственно внизу синус отрицателен: sin 4 sin4, ведь любое положительное число больше любого отрицательного.
Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.
Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:
Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:
Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
0 °
30 °
45 °
60 °
90 °
sin α
0
1 2
2 2
3 2
1
cos α
1
3 2
2 2
1 2
0
tg α
0
3 3
1
3
нет
ctg α
нет
3
1
3 3
0
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
[spoiler title=”источники:”]
[/spoiler]
тригонометрическая функция угла
| Синус | |
|---|---|
 |
|
| Основные характеристики | |
| Четность | нечетное |
| Домен | (- ∞, + ∞) |
| Кодомен | [−1, 1] |
| Период | 2π |
| Конкретные значения | |
| В нуле | 0 |
| Максимум | (2kπ + π / 2, 1) |
| Минимум | (2kπ – π / 2, −1) |
| Особенности | |
| Корень | kπ |
| Критическая точка | kπ + π / 2 |
| Перегиб точка | kπ |
| Фиксированная точка | 0 |
|
В математике синус – это тригонометрическая функция угла угла. Синус острого угла определяется в контексте прямоугольного треугольника : для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны. треугольника (гипотенуза ). Для угла x { displaystyle x}

В более общем смысле определение синуса ( и другие тригонометрические функции) могут быть расширены до любого действительного значения с точки зрения длины определенного линейного сегмента в единичной окружности . Более современные определения выражают синус как бесконечный ряд или как решение некоторых дифференциальных уравнений, что позволяет их расширить до произвольных положительных и отрицательных значений и даже до комплексных чисел.
Синусоидальная функция обычно используется для моделирования периодических явлений, таких как звук и световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность светового дня, а также изменения средней температуры на всем протяжении год.
Функциональный синус можно проследить до функций jyā и koṭi-jyā, используемых в период Гупта Индийская астрономия (Aryabhatiya, Сурья Сиддханта ), путем перевода с санскрита на арабский, а затем с арабского на латинский. Слово «синус» (латинское «синус») произошло от латинского неправильного перевода Робертом Честерским арабского джиба, который является транслитерацией санскрита. слово для половины хорды, джья-ардха.
Содержание
- 1 Определение прямоугольного треугольника
- 2 Определение единичного круга
- 3 Тождества
- 3.1 Взаимное
- 3.2 Обратное
- 3.3 Исчисление
- 3.4 Другие тригонометрические функции
- 3.5 Функция квадрата синуса
- 4 Свойства, относящиеся к квадрантам
- 5 Определение ряда
- 5.1 Непрерывная дробь
- 6 Фиксированная точка
- 7 Длина дуги
- 8 Закон синусов
- 9 Особые значения
- 10 Связь с комплексными числами
- 10.1 Синус с комплексным аргументом
- 10.1.1 Разложение комплексного синуса на частичную дробь и произведение
- 10.1.2 Использование комплексного sine
- 10.2 Сложные графы
- 10.1 Синус с комплексным аргументом
- 11 История
- 11.1 Этимология
- 12 Программные реализации
- 12.1 Реализации на основе поворотов
- 13 См. также
- 14 Цитаты
- 15 Ссылки
- 16 Внешние ссылки
прямоугольный треугольник определение угла
 Для угла α функция синуса дает отношение длины противоположной стороны к длине гипотенузы.
Для угла α функция синуса дает отношение длины противоположной стороны к длине гипотенузы.
Чтобы определить функцию синуса острого угла α, начните с прямоугольный треугольник, содержащий угол измерения α; на сопроводительном рисунке угол α в треугольнике ABC представляет собой интересующий угол. Три стороны треугольника названы следующим образом:
- Противоположная сторона – это сторона, противоположная интересующему углу, в данном случае сторона a.
- Гипотенуза – это сторона, противоположная прямому углу, в эта сторона дела h. Гипотенуза всегда является самой длинной стороной прямоугольного треугольника.
- Соседняя сторона – это оставшаяся сторона, в данном случае сторона b. Он образует сторону (и примыкает) как к интересующему углу (углу A), так и к прямому углу.
После выбора такого треугольника синус угла равен длине противоположной стороны, деленное на длину гипотенузы:
- sin (α) = противоположная гипотенуза { displaystyle sin ( alpha) = { frac { textrm {Against}} { textrm {hypotenuse}}}}
Остальные тригонометрические функции угла можно определить аналогично; например, косинус угла – это отношение между соседней стороной и гипотенузой, а касательная дает отношение между противоположной и смежной сторонами.
Как указано, значение sin (α) { displaystyle sin ( alpha)}
Определение единичной окружности
В тригонометрии, единичная окружность – это окружность радиуса 1 с центром в начале координат (0, 0) в Декартова система координат.
 Единичная окружность: окружность с радиусом один
Единичная окружность: окружность с радиусом один
Пусть прямая, проходящая через начало координат, пересекает единичную окружность, составляя угол θ с положительной половиной оси x. Координаты x и y этой точки пересечения равны cos (θ) и sin (θ) соответственно. Это определение согласуется с определением синуса и косинуса в прямоугольном треугольнике, когда 0 ° < θ < 90°: because the length of the hypotenuse of the unit circle is always 1, sin (θ) = противоположная гипотенуза = противоположная точка 1 = противоположная { displaystyle sin ( theta) = { tfrac { textrm {напротив}} { textrm {гипотенуза}}} = { tfrac { textrm {напротив}} {1}} = { textrm {напротив}}}


Использование определения единичной окружности имеет то преимущество, что угол может быть расширен до любого действительного аргумента. Этого также можно добиться, потребовав определенные симметрии, и чтобы синус был периодической функцией.

Анимация, показывающая, как функция синуса (красным) y = sin (θ) { displaystyle y = sin ( theta)}
строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.
Идентификаторы
Точные идентификаторы (с использованием радиан ):
Они применяются для всех значений θ { displaystyle theta}
- sin (θ) знак равно соз (π 2 – θ) = 1 csc (θ) { displaystyle sin ( theta) = cos left ({ frac { pi} {2}} – theta right) = { frac {1} { csc ( theta)}}}
Взаимное
, обратное синуса – косеканс, т. е. обратное значение sin (A) это csc (A) или cosec (A). Косеканс дает отношение длины гипотенузы к длине противоположной стороны:
- csc (A) = 1 sin (A) = гипотенуза напротив = h a. { displaystyle csc (A) = { frac {1} { sin (A)}} = { frac { textrm {hypotenuse}} { textrm {напротив}}} = { frac {h} { a}}.}
Обратный
 Обычные главные значения функции arcsin (x), построенные на декартовой плоскости. Arcsin – это функция, обратная sin.
Обычные главные значения функции arcsin (x), построенные на декартовой плоскости. Arcsin – это функция, обратная sin.
обратная функция синуса – это arcsine (arcsin или asin) или обратный синус (sin). Поскольку синус не является инъективным, это не точная обратная функция, а частичная обратная функция. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0 и т. Д. Отсюда следует, что функция арксинуса многозначна: arcsin (0) = 0, но также arcsin (0) = π, arcsin (0) = 2π и т. д. Когда требуется только одно значение, функция может быть ограничена ее главной ветвью. С этим ограничением для каждого x в домене выражение arcsin (x) будет оценивать только одно значение, называемое его главным значением.
- θ = arcsin (противоположная гипотенуза) = sin – 1 (ah). { displaystyle theta = arcsin left ({ frac { text {напротив}} { text {hypotenuse}}} right) = sin ^ {- 1} left ({ frac {a} { h}} right).}
где (для некоторого целого числа k):
- sin (y) = x ⟺ y = arcsin (x) + 2 π k, или y = π – arcsin ( Икс) + 2 π К { Displaystyle { begin {align} sin (y) = x iff y = arcsin (x) +2 pi k, { text {или}} \ y = pi – arcsin (x) +2 pi k end {align}}}
Или в одном уравнении:
- sin (y) = x ⟺ y = (- 1) k arcsin (x) + π К { displaystyle sin (y) = x iff y = (- 1) ^ {k} arcsin (x) + pi k}
По определению, арксинус удовлетворяет уравнению:
- sin (arcsin (x)) знак равно x { displaystyle sin ( arcsin (x)) = x !}
и
- arcsin (sin (θ)) = θ для – π 2 ≤ θ ≤ π 2. { displaystyle arcsin ( sin ( theta)) = theta quad { text {for}} – { frac { pi} {2}} leq theta leq { frac { pi} {2}}.}
Исчисление
Для функции синуса:
- f (x) = sin (x) { displaystyle f (x) = sin (x)}
Производная:
- f ‘(x) = cos (x) { displaystyle f’ (x) = cos (x)}
Первообразная:
- ∫ f (x) dx = – cos (x) + C { displaystyle int f (x) , dx = – cos (x) + C}
где C обозначает постоянную интегрирования.
Другие тригонометрические функции
 Функции синуса и косинуса связаны множеством способов. Две функции сдвинуты по фазе на 90 °:
Функции синуса и косинуса связаны множеством способов. Две функции сдвинуты по фазе на 90 °:
sin (π / 2 – x) { displaystyle sin ( pi / 2-x)}

cos (x) { displaystyle cos (x)}

Любую тригонометрическую функцию можно выразить через любую другую (до знака плюс или минус или с помощью функции знака ).
В следующей таблице показано, как синус может быть выражен в терминах других общих тригонометрических функций :
| f θ | Использование плюса / минуса (±) | Использование функции знака (sgn) | |||||
|---|---|---|---|---|---|---|---|
| f θ = | ± на квадрант | f θ = | |||||
| I | II | III | IV | ||||
| соз | грех (θ) { displaystyle sin ( theta)} |
= ± 1 – cos 2 (θ) { displaystyle = pm { sqrt {1- cos ^ {2 } ( theta)}}} |
+ | + | − | − | = sign (соз (θ – π 2)) 1 – соз 2 (θ) { displaystyle = operatorname {sgn} left ( cos left ( theta – { frac { pi} {2}} right) right) { sqrt {1- cos ^ {2} ( theta)}}} |
cos (θ) { displaystyle соз ( theta)} |
= ± 1 – грех 2 (θ) { displaystyle = pm { sqrt {1- sin ^ {2} ( theta)}}} |
+ | − | − | + | = sgn (грех (θ + π 2)) 1 – грех 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} вправо) вправо) { sqrt {1- sin ^ {2} ( theta)}}} |
|
| кроватка | грех (θ) { displaystyle sin ( theta)} |
= ± 1 1 + детская кроватка 2 (θ) { displaysty le = pm { frac {1} { sqrt {1+ cot ^ {2} ( theta)}}}} |
+ | + | − | − | = sgn (детская кроватка (θ 2)) 1 1 + детская кроватка 2 (θ) { displaystyle = operatorname {sgn} left ( cot left ({ frac { theta} {2}} right) right) { frac {1} { sqrt {1+ кроватка ^ {2} ( theta)}}}} |
детская кроватка (θ) { displaystyle cot ( theta)} |
= ± 1 – sin 2 (θ) sin (θ) { displaystyle = pm { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}} |
+ | − | − | + | = sgn (sin (θ + π 2)) 1 – грех 2 (θ) грех (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) справа) { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}} |
|
| tan | грех (θ) { displaystyle sin ( theta)} |
= ± загар (θ) 1 + загар 2 (θ) { displaystyle = pm { frac { tan ( theta)} { sqrt {1+ tan ^ { 2} ( theta)}}}} |
+ | − | − | + | = sign (tan (2 θ + π 4)) tan (θ) 1 + tan 2 (θ) { displaystyle = operatorname {sgn} left ( tan left ({ frac {2 theta + pi} {4}} right) right) { frac { tan ( theta)} { sqrt {1+ tan ^ {2 } ( theta)}}}} |
загар (θ) { Displaystyle загар ( theta)} |
= ± грех (θ) 1 – грех 2 (θ) { displaystyle = pm { frac { sin ( theta)} { sqrt {1- sin ^ {2} ( theta)}}}} |
+ | − | − | + | = sgn (sin (θ + π 2)) sin (θ) 1 – sin 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { frac { sin ( theta)} { sqrt { 1- sin ^ {2} ( theta)}}}} |
|
| сек | грех (θ) { displaystyle sin ( theta)} |
= ± sec 2 (θ) – 1 сек (θ) { displaystyle = pm { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}} |
+ | − | + | − | = sgn ( сек (4 θ – π 2)) сек 2 (θ) – 1 сек (θ) { displaystyle = operatorname {sgn} left ( sec left ({ frac {4 theta – pi } {2}} right) right) { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}} |
сек (θ) { displaystyle sec ( theta)} |
= ± 1 1 – грех 2 (θ) { displaystyle = pm { frac {1} { sqrt {1- sin ^ {2} ( тета)}}}} |
+ | − | − | + | = знак (грех (θ + π 2)) 1 1 – грех 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( th eta + { frac { pi} {2}} right) right) { frac {1} { sqrt {1- sin ^ {2} ( theta)}}}} |
Для всех уравнения, которые используют плюс / минус (±), результат будет положительным для углов в первом квадранте.
Основное соотношение между синусом и косинусом также может быть выражено как тригонометрическое тождество Пифагора :
- cos 2 (θ) + sin 2 (θ) = 1 { displaystyle cos ^ {2} ( theta) + sin ^ {2} ( theta) = 1 !}
где sin (x) означает (sin (x)).
Функция синус-квадрата
 Синусоидальная функция синим цветом и функция синус-квадрата красным. Ось Y находится в радианах.
Синусоидальная функция синим цветом и функция синус-квадрата красным. Ось Y находится в радианах.
На графике показаны как функция синуса, так и функция в квадрате синуса, причем синус отображается синим цветом, а синус в квадрате – красным. Оба графика имеют одинаковую форму, но с разными диапазонами значений и разными периодами. Синус в квадрате имеет только положительные значения, но в два раза больше периодов.
Функция квадрата синуса может быть выражена как модифицированная синусоида из тождества Пифагора и уменьшения мощности – с помощью формулы двойного угла косинуса:
- sin 2 (θ) = 1 – sin (2 θ + π 2) 2 { displaystyle sin ^ {2} ( theta) = { frac {1- sin (2 theta + { tfrac { pi} {2}})} {2} } }
Свойства, относящиеся к квадрантам
 Четыре квадранта декартовой системы координат
Четыре квадранта декартовой системы координат
В таблице ниже показаны многие ключевые свойства синусоидальной функции (знак, монотонность, выпуклость), упорядоченные по квадрантам аргумента. Для аргументов, не указанных в таблице, можно вычислить соответствующую информацию, используя периодичность sin (α + 360 ∘) = sin (α) { displaystyle sin ( alpha +360 ^ { circ}) = sin ( alpha)}
| Квадрант | Градусы | Радианы | Значение | Знак | Монотонность | Выпуклость |
|---|---|---|---|---|---|---|
| 1-й квадрант | 0 ∘ < x < 90 ∘ {displaystyle 0^{circ } |
0 < x < π 2 {displaystyle 0 |
0 < sin ( x) < 1 {displaystyle 0<sin(x)<1} |
+ { displaystyle +} |
увеличение | вогнутый |
| 2-й квадрант | 90 ∘ < x < 180 ∘ {displaystyle 90^{circ } |
π 2 < x < π {displaystyle {frac {pi }{2}} |
0 < sin ( x) < 1 {displaystyle 0<sin(x)<1} |
+ { displaystyle +} |
уменьшение | вогнутый |
| 3-й квадрант | 180 ∘ < x < 270 ∘ {displaystyle 180^{circ } |
π < x < 3 π 2 {displaystyle pi  |
– 1 < sin ( x) < 0 {displaystyle -1<sin(x)<0} |
– { displaystyle -} |
уменьшение | выпуклый |
| 4-й квадрант | 270 ∘ < x < 360 ∘ {displaystyle 270^{circ } |
3 π 2 < x < 2 π {displaystyle {frac {3pi }{2}} |
– 1 < sin ( x) < 0 {displaystyle -1<sin(x)<0} |
– { displaystyle -} |
увеличение | выпуклое |
 Квадранты единичной окружности и sin (x) с использованием декартовой системы координат
Квадранты единичной окружности и sin (x) с использованием декартовой системы координат
В следующей таблице приведены основная информация на границе квадрантов.
| Градусы | Радианы | грех (x) { displaystyle sin (x)} |
Тип точки |
|---|---|---|---|
0 ∘ { displaystyle 0 ^ { circ}} |
0 { displaystyle 0} |
0 { displaystyle 0} |
Корень, Inflection |
90 ∘ { displaystyle 90 ^ { circ}} |
π 2 { displaystyle { frac { pi} {2}}} |
1 { displaystyle 1} |
Максимум |
180 ∘ { displaystyle 180 ^ { circ}} |
π { displaystyle pi} |
0 { displaystyle 0} |
Корень, перегиб |
270 ∘ { displaystyle 270 ^ { circ}} |
3 π 2 { displaystyle { frac {3 pi } {2}}} |
– 1 { displaystyle -1} |
Минимум |
Определение ряда
 Синусоидальная функция (синий цвет) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного цикла с центром в начале координат.
Синусоидальная функция (синий цвет) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного цикла с центром в начале координат.  Эта анимация показывает, как включение все большего и большего числа членов в частичную сумму своего ряда Тейлора приближается к синусоиде.
Эта анимация показывает, как включение все большего и большего числа членов в частичную сумму своего ряда Тейлора приближается к синусоиде.
Использование только геометрии и свойств ограничивает, можно показать, что производная синуса является косинусом, и что де Производная косинуса является отрицательной величиной синуса.
Использование отражения из вычисленного геометрического вывода синуса с (4n + k) -й производной в точке 0:
- sin (4 n + k) (0) = {0 когда k = 0 1, когда k = 1 0, когда k = 2 – 1, когда k = 3 { displaystyle sin ^ {(4n + k)} (0) = { begin {cases} 0 { text {when} } k = 0 \ 1 { text {when}} k = 1 \ 0 { text {when}} k = 2 \ – 1 { text {when}} k = 3 end {cases}} }
Это дает следующее разложение в ряд Тейлора при x = 0. Затем можно использовать теорию ряда Тейлора, чтобы показать, что следующие тождества выполняются для всех действительных чисел x ( где x – угол в радианах):
- sin (x) = x – x 3 3! + х 5 5! – х 7 7! + ⋯ знак равно ∑ N знак равно 0 ∞ (- 1) N (2 N + 1)! Икс 2 N + 1 { Displaystyle { begin {align} sin (x) = x – { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} { 5!}} – { frac {x ^ {7}} {7!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} x ^ {2n + 1} \ [8pt] end {align}}}
Если бы x был выражен в градусах, тогда ряд содержал бы факторы, включающие степени π / 180: если x – количество градусов, количество радианов равно y = πx / 180, поэтому
- sin (xdeg) = sin (yrad) = π 180 x – (π 180) 3 х 3 3! + (π 180) 5 х 5 5! – (π 180) 7 х 7 7! + ⋯. { displaystyle { begin {align} sin (x _ { mathrm {deg}}) = sin (y _ { mathrm {rad}}) \ = { frac { pi} {180}} x- left ({ frac { pi} {180}} right) ^ {3} { frac {x ^ {3}} {3!}} + left ({ frac { pi} { 180}} right) ^ {5} { frac {x ^ {5}} {5!}} – left ({ frac { pi} {180}} right) ^ {7} { frac {x ^ {7}} {7!}} + cdots. end {align}}}
Формулы ряда для синуса и косинуса определяются однозначно, с точностью до выбора единицы для углов, согласно требованиям, что
- sin (0) = 0 и sin (2 x) = 2 sin (x) cos (x) cos 2 (x) + sin 2 (x) = 1 и соз (2 Икс) знак равно соз 2 (Икс) – грех 2 (Икс) { Displaystyle { begin {align} sin (0) = 0 { text {и}} sin (2x) = 2 sin (x) cos (x) \ cos ^ {2} (x) + sin ^ {2} (x) = 1 { text {and}} cos (2x) = cos ^ {2} (x) – sin ^ {2} (x) \ end {align}}}
Радиан – это единица, которая приводит к разложению с ведущим коэффициентом 1 для синуса и определяется дополнительное требование:
- sin (x) ≈ x, когда x ≈ 0. { displaystyle sin (x) приблизительно x { text {when}} x a pprox 0.}
Коэффициенты для серий синуса и косинуса, следовательно, могут быть получены путем подстановки их разложений в тождества пифагора и двойного угла, принимая ведущий коэффициент для синуса равным 1 и согласовывая остальные коэффициенты.
В общем, математически важные отношения между функциями синуса и косинуса и экспоненциальной функцией (см., Например, формулу Эйлера ) существенно упрощаются, когда углы выражаются в радианах, а не в градусах, градусах или других единицах. Поэтому в большинстве разделов математики, выходящих за рамки практической геометрии, считается, что углы выражаются в радианах.
Аналогичный ряд – это ряд Грегори для arctan, который получается путем опускания факториалов в знаменателе.
Непрерывная дробь
Функция синуса также может быть представлена как обобщенная непрерывная дробь :
- sin (x) = x 1 + x 2 2 ⋅ 3 – x 2 + 2 ⋅ 3 x 2 4 ⋅ 5 – x 2 + 4 ⋅ 5 x 2 6 ⋅ 7 – x 2 + ⋱. { displaystyle sin (x) = { cfrac {x} {1 + { cfrac {x ^ {2}} {2 cdot 3-x ^ {2} + { cfrac {2 cdot 3x ^ { 2}} {4 cdot 5-x ^ {2} + { cfrac {4 cdot 5x ^ {2}} {6 cdot 7-x ^ {2} + ddots}}}}}}}}.}
Представление непрерывной дроби может быть получено из формулы непрерывной дроби Эйлера и выражает вещественное число, как рациональное, так и иррациональное синусоидальной функции.
Фиксированная точка
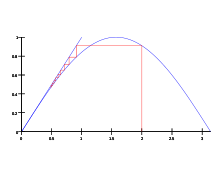 Итерация с фиксированной точкой x n + 1 = sin (x n) с начальным значением x 0 = 2 сходится к 0.
Итерация с фиксированной точкой x n + 1 = sin (x n) с начальным значением x 0 = 2 сходится к 0.
Ноль – единственная действительная фиксированная точка синусоидальной функции; другими словами, единственное пересечение синусоидальной функции и тождественной функции – это sin (0) = 0.
Длина дуги
Длина дуги синусоидальной кривой между a { displaystyle a}


Длина дуги для полного периода равна 4 2 π 3 Γ (1/4) 2 + Γ (1/4) 2 2 π = 7.640395578 … { Textstyle { frac {4 { sqrt {2 pi ^ {3}}}} { Gamma (1/4) ^ {2}}} + { frac { Gamma (1/4) ^ {2}} { sqrt {2 pi}}} = 7.640395578 ldots}

Длина дуги синусоидальной кривой от 0 до x равна приведенному выше числу, деленному на 2 π { displaystyle 2 pi}

- 1,21600672 x + 0,10317093 sin (2 x) – 0,00220445 sin (4 x) + 0,00012584 sin (6 x) – 0,00001011 sin (8 x) + ⋯ { displaystyle 1.21600672x + 0.10317093 sin (2x) -0.00220445 sin (4x) +0.00012584 sin (6x) -0.00001011 sin (8x) + cdots}
Главный член в приведенном выше уравнении и предел отношение длины дуги к расстоянию определяется следующим образом:
- π 2 + 2 Γ (3 4) 4 2 π 3/2 Γ (3 4) 2 { displaystyle { frac { pi ^ {2} +2 Гамма left ({ frac {3} {4}} right) ^ {4}} {{ sqrt {2}} pi ^ {3/2} Gamma left ({ frac {3} { 4}} right) ^ {2}}}}
Закон синусов
Закон синусов гласит, что для произвольного треугольника со сторонами a, b и c и углы, противоположные этим сторонам A, B и C:
- sin A a = sin B b = sin C c. { displaystyle { frac { sin A} {a}} = { frac { sin B} {b}} = { frac { sin C} {c}}.}
Это эквивалентно равенство первых трех выражений ниже:
- a sin sin A = b sin B = c sin C = 2 R, { displaystyle { frac {a} { sin A}} = { frac { b} { sin B}} = { frac {c} { sin C}} = 2R,}
где R – описанный радиус треугольника.
Это можно доказать, разделив треугольник на два правильные и используя приведенное выше определение синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая в триангуляции, методе определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.
Особые значения
 Некоторые общие углы (θ) показаны на единичной окружности . Углы указаны в градусах и радианах вместе с соответствующей точкой пересечения на единичной окружности (cos (θ), sin (θ)).
Некоторые общие углы (θ) показаны на единичной окружности . Углы указаны в градусах и радианах вместе с соответствующей точкой пересечения на единичной окружности (cos (θ), sin (θ)).
Для некоторых целых чисел x градусов, значение sin (x) особенно просто. Таблица некоторых из этих значений приведена ниже.
| x (угол) | sin (x) | ||||
|---|---|---|---|---|---|
| Градусы | Радианы | Градианы | Повороты | Точное значение | Десятичное число |
| 0° | 0 | 0 | 0 | 0 | 0 |
| 180 ° | π | 200 | 1/2 | ||
| 15 ° | 1 / 12π | 16+2/3 | 1/24 | 6 – 2 4 { displaystyle { frac {{ sqrt {6}} – { sqrt {2}}} {4}}} |
0,258819045102521 |
| 165 ° | 11 / 12π | 183 + 1/3 | 11/24 | ||
| 30 ° | 1 / 6π | 33+1/3 | 1/12 | 1/2 | 0,5 |
| 150 ° | 5 / 6π | 166+2/3 | 5/12 | ||
| 45 ° | 1 / 4π | 50 | 1/8 | 2 2 { displaystyle { frac { sqrt {2}} {2}}} |
0,707106781186548 |
| 135 ° | 3 / 4π | 150 | 3/8 | ||
| 60 ° | 1 / 3π | 66 + 2/3 | 1/6 | 3 2 { displaystyle { frac { sqrt {3}} {2}}} |
0,866025403784439 |
| 120 ° | 2 / 3π | 133+1/3 | 1/3 | ||
| 75 ° | 5 / 12π | 83 + 1/3 | 5/24 | 6 + 2 4 { displaystyle { frac {{ sqrt {6}} + { sqrt {2}}} {4}}} |
0,965925826289068 |
| 105 ° | 7 / 12π | 116 + 2/3 | 7/24 | ||
| 90 ° | 1 / 2π | 100 | 1/4 | 1 | 1 |
с шагом 90 градусов:
| x в градусах | 0° | 90 ° | 180 ° | 270 ° | 360 ° |
| x в радианах | 0 | π / 2 | π | 3π / 2 | 2π |
| x в углах | 0 | 100 | 200 | 300 | 400 |
| x по очереди | 0 | 1/4 | 1/2 | 3/4 | 1 |
| sin x | 0 | 1 | 0 | -1 | 0 |
Другие значения, не указанные выше:
- sin (π 60) знак равно грех (3 ∘) знак равно (2–12) 5 + 5 + (10–2) (3 + 1) 16 { displaystyle sin left ({ frac { pi} {60}} right) = sin (3 ^ { circ}) = { frac {(2 – { sqrt {12}}) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10} } – { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019812
- грех (π 30) = грех (6 ∘) = 30 – 180 – 5 – 1 8 { displaystyle sin left ({ frac { pi} {30}} right) = sin (6 ^ { circ}) = { frac {{ sqrt {30 – { sqrt {180}}}} – { sqrt {5}} – 1} {8}}}
OEIS : A019815
- грех (π 20) знак равно грех (9 ∘) = 10 + 2-20-80 8 { displaystyle sin left ({ frac { pi} {20}} right) = sin (9 ^ { circ}) = { frac {{ sqrt {10}} + { sqrt {2}} – { sqrt {20 – { sqrt {80}}}}} {8}}}
OEIS : A019818
- грех (π 15) = грех (12 ∘) = 10 + 20 + 3-15 8 { displaystyle sin left ({ frac { pi} {15}} right) = sin (12 ^ { circ}) = { frac {{ sqrt {10 + { sqrt {20}}}} + { sqrt {3}} – { sqrt {15}}} {8}}}
OEIS : A019821
- грех (π 10) = грех (18 ∘) = 5 – 1 4 = 1 2 φ – 1 { displaystyle sin left ({ frac { pi} {10}} right) = sin (18 ^ { circ}) = { frac {{ sqrt {5}} – 1} {4}} = { tfrac {1} {2}} varphi ^ {- 1}}
OEIS : A019827
- sin (7 π 60) = sin (21 ∘) = (2 + 12) 5-5 – (10 + 2) (3-1) 16 { displaystyle sin left ({ frac {7 pi} {60}} right) = sin (21 ^ { circ}) = { frac {(2+ { sqrt {12}}) { sqrt {5 – { sqrt {5}}}} – ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} – 1)} {16}}}
OEIS : A019830
- грех (π 8) = грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 – { sqrt {2}}}} {2}}}
- грех (2 π 15) = грех (24 ∘) = 3 + 15 – 10 – 20 8 { displaystyle sin left ({ frac {2 pi} {15}} right) = sin (24 ^ { circ}) = { frac {{ sqrt { 3}} + { sqrt {15}} – { sqrt {10 – { sqrt {20}}}}} {8}}}
OEIS : A019833
- грех (3 π 20) знак равно грех (27 ∘) = 20 + 80-10 + 2 8 { displaystyle sin left ({ frac {3 pi} {20}} right) = sin (27 ^ { circ}) = { frac {{ sqrt {20 + { sqrt {80}}}} – { sqrt {10}} + { sqrt {2}}} {8}}}
OEIS : A019836
- грех (11 π 60) = грех (33 ∘) = (12–2) 5 + 5 + (10–2) (3 + 1) 16 { displaystyle sin left ({ frac {11 pi} {60}} right) = sin (33 ^ { circ}) = { frac {({ sqrt {12}} – 2) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10}} – { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019842
- грех (π 5) = грех (36 ∘) = 10-20 4 { displaystyle sin left ({ frac { pi} {5}} справа) = sin (36 ^ { circ}) = { frac { sqrt {10 – { sqrt {20}}}} {4}}}
OEIS : A019845
- грех (13 π 60) = грех (39 ∘) = (2–12) 5–5 + (10 + 2) (3 + 1) 16 { displaystyle sin left ({ frac {13 число Пи } {60}} right) = sin (39 ^ { circ}) = { frac {(2 – { sqrt {12}}) { sqrt {5 – { sqrt {5}}}} + ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019848
- грех (7 π 30) знак равно грех (42 ∘) = 30 + 180 – 5 + 1 8 { displaystyle sin left ({ frac {7 pi} {30}} right) = sin ( 42 ^ { circ}) = { frac {{ sqrt {30 + { sqrt {180}}}} – { sqrt {5}} + 1} {8}}}
OEIS : A019851
Связь с комплексными числами
 Иллюстрация комплексной плоскости. мнимые числа расположены на вертикальной координатной оси.
Иллюстрация комплексной плоскости. мнимые числа расположены на вертикальной координатной оси.
Синус используется для определения мнимой части комплексного числа , заданного в полярных координатах. (г, φ):
- Z знак равно р (соз (φ) + я грех (φ)) { Displaystyle Z = г ( соз ( varphi) + я грех ( varphi))}
мнимая часть:
- Im (z) = r sin (φ) { displaystyle operatorname {Im} (z) = r sin ( varphi)}
r и φ представляют собой величину и угол комплексного числа соответственно. i – это мнимая единица. z – комплексное число ..
Несмотря на то, что мы имеем дело с комплексными числами, параметр синуса в этом случае по-прежнему является действительным числом. Синус также может принимать в качестве аргумента комплексное число.
Синус с комплексным аргументом

sin (z) { displaystyle sin (z)}

 sin (z) как векторное поле
sin (z) как векторное поле 
sin (θ) { displaystyle sin ( theta)}

ei θ { displaystyle e ^ {i theta}}

Определение синусоидальной функции для комплексных аргументов z:
- sin (z) = ∑ n = 0 ∞ (- 1) n ( 2 п + 1)! z 2 N + 1 знак равно eiz – е – iz 2 i = sinh (iz) i { displaystyle { begin {align} sin (z) = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} z ^ {2n + 1} \ = { frac {e ^ {iz} -e ^ {- iz}} { 2i}} \ = { frac { sinh left (iz right)} {i}} end {align}}}
где i = −1, а sinh – гиперболический синус. Это целая функция. Кроме того, для чисто вещественного x
- sin (x) = Im (e i x). { displaystyle sin (x) = operatorname {Im} (e ^ {ix}).}
Для чисто мнимых чисел:
- sin (i y) = i sinh (y). { displaystyle sin (iy) = i sinh (y).}
Также иногда полезно выразить сложную синусоидальную функцию в терминах действительной и мнимой частей ее аргумента:
- sin (x + iy) = sin (x) cos (iy) + cos (x) sin (iy) = sin (x) cosh (y) + i cos (x) sinh (y). { Displaystyle { begin {align} sin (x + iy) = sin (x) cos (iy) + cos (x) sin (iy) \ = sin (x) cosh (y) + i cos (x) sinh (y). end {align}}}
Разложение на частичную дробь и произведение комплексного синуса
Использование техники разложения на частичную дробь в комплексный анализ, можно найти, что бесконечный ряд
- ∑ n = – ∞ ∞ (- 1) nz – n = 1 z – 2 z ∑ n = 1 ∞ (- 1) nn 2 – z 2 { displaystyle { begin {align} sum _ {n = – infty} ^ { infty} { frac {(-1) ^ {n}} {zn}} = { frac {1} {z} } -2z sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n}} {n ^ {2} -z ^ {2}}} end {выровнено}}}
сходятся и равны π sin (π z) { textstyle { frac { pi} { sin ( pi z)}}}
- π 2 sin 2 (π z) = ∑ n = – ∞ ∞ 1 (z – n) 2. { displaystyle { begin {align} { frac { pi ^ {2}} { sin ^ {2} ( pi z)}} = sum _ {n = – infty} ^ { infty} { frac {1} {(zn) ^ {2}}}. end {align}}}
Используя технику расширения произведения, можно вывести
- sin (π z) = π z ∏ n = 1 ∞ (1 – z 2 n 2). { displaystyle { begin {align} sin ( pi z) = pi z prod _ {n = 1} ^ { infty} left (1 – { frac {z ^ {2}} {n ^{2}}}right).end{aligned}}}
Alternatively, the infinite product for the sine can be proved using complex Fourier series.
| Proof of the infinite product for the sine |
|---|
|
Using complex Fourier series, the function cos ( zx) {displaystyle cos(zx)}
Setting x = π {displaystyle x=pi }
Therefore we get
The function π cot ( π z) {displaystyle pi cot(pi z)}
Exponentiating gives
Since lim z → 0 sin ( π z) z = π {textstyle lim _{zto 0}{frac {sin(pi z)}{z}}=pi }
for some open and connected subset of C {displaystyle mathbb {C} } |
Usage of complex sine
sin(z) is found in the functional equation for the Gamma function,
- Γ ( s) Γ ( 1 − s) = π sin ( π s), {displaystyle Gamma (s)Gamma (1-s)={pi over sin(pi s)},}
which in turn is found in the functional equation for the Riemann zeta-function,
- ζ ( s) = 2 ( 2 π) s − 1 Γ ( 1 − s) sin ( π s / 2) ζ ( 1 − s). {displaystyle zeta (s)=2(2pi)^{s-1}Gamma (1-s)sin(pi s/2)zeta (1-s).}
As a holomorphic function, sin z is a 2D solution of Laplace’s equation :
- Δ u ( x 1, x 2) = 0. {displaystyle Delta u(x_{1},x_{2})=0.}
The complex sine function is also related to the level curves of pendulums.
Complex graphs
 |
 |
 |
| real component | imaginary component | magnitude |
.
 |
 |
 |
| real component | imaginary component | magnitude |
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Rom Египет (90–165 гг. н. э.).
Функцию синуса и версин (1 – косинус) можно проследить до функций jyā и koṭi-jyā, используемых в период Гупты (320–550 гг. Н. Э.) Индийская астрономия (Арьябхатия, Сурья Сиддханта ) посредством перевода с санскрита на арабский, а затем с арабского на латинский.
Все шесть используемых в настоящее время тригонометрических функций были известны в исламской математике к 9 веку, как и закон синусов, использовавшийся в решении треугольников. За исключением синуса (который был заимствован из индийской математики), арабскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс. Аль-Хваризми (ок. 780–850) составил таблицы синусов, косинусов и тангенсов. Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыл взаимные функции секанса и косеканса и создал первую таблицу косекансов. для каждой степени от 1 ° до 90 °.
Первое опубликованное использование сокращений sin, cos и tan принадлежит французскому математику 16 века Альбер Жирар ; в дальнейшем они были обнародованы Эйлером (см. ниже). Opus palatinum de triangulis Георга Иоахима Ретикуса, ученика Коперника, вероятно, был первым в Европе, который определил тригонометрические функции непосредственно в терминах прямоугольных треугольников, а не окружностей, с таблицами для все шесть тригонометрических функций; эта работа была закончена учеником Ретикуса Валентином Отоном в 1596 году.
В статье, опубликованной в 1682 году, Лейбниц доказал, что sin x не является алгебраической функцией x Роджер Котес вычислил производную синуса в своей Harmonia Mensurarum (1722). Введение Леонарда Эйлера в анализ бесконечности (1748) в основном отвечало за установление аналитического подхода к тригонометрическим функциям. в Европе, также определяя их как бесконечные серии и представляя «формулу Эйлера », а также почти современные сокращения sin., cos., tang., cot., sec. и cosec.
Этимология
| Найдите sine в Wiktionary, бесплатном словаре. |
Этимологически слово синус происходит от санскрита слово, обозначающее аккорд, jiva * (jya – его более популярный синоним). Это было транслитерировано на арабском как jiba جيب, что, однако, не имеет смысла на этом языке и сокращается как jb جب. Поскольку арабский язык написан без коротких гласных, «jb» интерпретировалось как слово jaib جيب, что означает «грудь». Когда в XII веке арабские тексты были переведены на латинский Герардом Кремонским, он использовал латинский эквивалент слова «лоно», sinus (что означает « лоно »или« гнедой »или« складкой »). Джерард, вероятно, был не первым ученым, использовавшим этот перевод; Роберт Честерский, кажется, предшествовал ему, и есть свидетельства более раннего использования. Английская форма синуса была введена в 1590-х годах.
Программные реализации
Не существует стандартного алгоритма для вычисления синуса. IEEE 754-2008, наиболее широко используемый стандарт для вычислений с плавающей запятой, не касается вычисления тригонометрических функций, таких как синус. Алгоритмы вычисления синуса могут быть сбалансированы с учетом таких ограничений, как скорость, точность, переносимость или диапазон принимаемых входных значений. Это может привести к разным результатам для разных алгоритмов, особенно для особых обстоятельств, таких как очень большие входные данные, например sin (10).
Некогда распространенная оптимизация программирования, особенно используемая в трехмерной графике, заключалась в предварительном вычислении таблицы значений синуса, например, одно значение на градус. Это позволяло искать результаты в таблице, а не рассчитывать их в реальном времени. С современной архитектурой ЦП этот метод не может дать никаких преимуществ.
Алгоритм CORDIC обычно используется в научных калькуляторах.
Функция синуса, наряду с другими тригонометрическими функциями, широко доступна для разных языков и платформ программирования. В вычислениях это обычно сокращается до sin.
Некоторые архитектуры ЦП имеют встроенную инструкцию для синуса, включая FPU Intel x87 начиная с 80387.
В языках программирования sinобычно либо встроенная функция, либо находится в стандартной математической библиотеке языка.
Например, стандартная библиотека C определяет синусоидальные функции в пределах math.h : sin (double ), sinf (float )и sinl (long double ). Параметром каждого из них является значение с плавающей запятой, определяющее угол в радианах. Каждая функция возвращает тот же тип данных , который принимает.Множество других тригонометрических функций также определены в math.h, например, для косинуса, арксинуса и гиперболического синуса (sinh).
Аналогично, Python определяет math.sin (x)во встроенном модуле math. Сложные синусоидальные функции также доступны в Модуль cmath, например, cmath.sin (z). Математические функции CPython вызывают библиотеку C mathи используют Формат с плавающей запятой двойной точности.
.
Реализации на основе поворотов
Некоторые программные библиотеки предоставляют реализации синусоиды с использованием входного угла в половину- оборотов, где пол-оборота составляет угол 180 градусы или π { displaystyle pi}
| Окружение | Название функции | Угловые единицы |
|---|---|---|
| MATLAB | sinpi |
полуобороты |
| OpenCL | sinpi |
полуобороты |
| R | sinpi |
полуобороты |
| Julia | sinpi |
полуобороты |
| CUDA | sinpi |
полуобороты |
| ARM | sinpi |
полуобороты |
Преимущество точности проистекает из способности идеально представлять ключевые углы, такие как полный оборот, полуоборот и четверть оборота, без потерь в двоичной системе с плавающей запятой или с фиксированной запятой. Напротив, представляя 2 π { displaystyle 2 pi}


Повороты также имеют преимущество в точности и эффективности для вычисления по модулю до одного периода. Вычисление по модулю 1 оборот или по модулю 2 полуоборотов может выполняться без потерь и эффективно как с плавающей, так и с фиксированной точкой. Например, вычисление по модулю 1 или 2 для значения с фиксированной запятой, масштабированного по двоичной точке, требует только битового сдвига или операции побитового И. Напротив, вычисление по модулю π 2 { displaystyle { frac { pi} {2}}}

Для приложений, связанных с датчиками угла, датчик обычно обеспечивает угловые измерения в форме, напрямую совместимой с поворотами или полуоборотами. Например, датчик угла может отсчитывать от 0 до 4096 за один полный оборот. Если полуворота используются в качестве единицы измерения угла, тогда значение, предоставляемое датчиком, напрямую и без потерь отображается в тип данных с фиксированной точкой с 11 битами справа от двоичной точки. Напротив, если радианы используются в качестве единицы для хранения угла, то неточности и стоимость умножения необработанного целого числа датчика на приближение к π 2048 { displaystyle { frac { pi} {2048}}}
См. Также
- таблицу синусов Рьябханы
- Формула аппроксимации синуса Бхаскары I
- Дискретное синусоидальное преобразование
- Формула Эйлера
- Обобщенная тригонометрия
- Гиперболическая функция
- Закон синусов
- Список периодических функций
- Список тригонометрических тождеств
- Серия Мадхав
- Таблица синусов Мадхавы
- Теорема оптического синуса
- Полярный синус – обобщение на углы вершин
- Доказательства тригонометрических тождества
- функция Sinc
- преобразования синуса и косинуса
- интеграл синуса
- квадрант синуса
- волна синуса
- уравнение синуса – Гордона
- синусоидальная модель
- тригонометрические функции
- тригонометрический интеграл
Цитаты
Ссылки
- Траупман, доктор философии, Джон К. (1966), Латинский и английский словарь Нью-колледжа, Торонто: Bantam, ISBN 0-553-27619-0
- Седьмой новый университетский словарь Вебстера, Спрингфилд: G. C. Merriam Company, 1969
Внешние ссылки
 СМИ, связанные с функцией синуса на Wikimedia Commons
СМИ, связанные с функцией синуса на Wikimedia Commons
| Найдите sine в Wiktionary, бесплатном словаре. |
Преломление света.
-
Закон преломления (частный случай).
-
Обратимость световых лучей.
-
Закон преломления (общий случай).
-
Полное внутреннее отражение.
-
Разберем задачи ЕГЭ по теме: Преломление света.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.
На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление – свет, переходя в другую среду, меняет направление своего распространения.
Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда – читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет – во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.
к оглавлению ▴
Закон преломления (частный случай).
Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.
Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.
 |
| Рис. 1. Преломление луча на границе “воздух–среда” |
В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль)
к поверхности среды. Луч
, как и раньше, называется падающим лучом, а угол
между падающим лучом и нормалью – углом падения. Луч
– это преломлённый луч; угол
между преломлённым лучом и нормалью к поверхности называется углом преломления.
Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла
, а для воды
. Вообще, у любой среды
; показатель преломления равен единице только в вакууме. У воздуха
, поэтому для воздуха с достаточной точностью можно полагать в задачах
(в оптике воздух не сильно отличается от вакуума).
Закон преломления (переход “воздух–среда”).
1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:
. (1)
Поскольку из соотношения (1) следует, что
, то есть
– угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.
Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме:
. И вот оказывается,что
. (2)
Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):
. (3)
Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.
к оглавлению ▴
Обратимость световых лучей.
Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.
Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.
Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.
 |
| Рис. 2. Преломление луча на границе “среда–воздух” |
Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла к синусу угла
по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол
стал углом падения, а угол
– углом преломления.
В любом случае, как бы ни шёл луч – из воздуха в среду или из среды в воздух – работает следующее простое правило. Берём два угла – угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.
Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.
к оглавлению ▴
Закон преломления (общий случай).
Пусть свет переходит из среды 1 с показателем преломления в среду 2 с показателем преломления
. Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.
Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .
Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:
Оказывается, оба этих случая охватываются одной формулой – общим законом преломления, справедливым для любых двух прозрачных сред.
Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:
. (4)
Нетрудно видеть, что сформулированный ранее закон преломления для перехода “воздух–среда” является частным случаем данного закона. В самом деле, полагая в формуле (4) , мы придём к формуле (1).
Вспомним теперь, что показатель преломления – это отношение скорости света в вакууме к скорости света в данной среде: . Подставляя это в (4), получим:
. (5)
Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.
к оглавлению ▴
Полное внутреннее отражение.
При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление – полное внутреннее отражение. Давайте разберёмся, что это такое.
Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).
 |
| Рис. 5. Полное внутреннее отражение |
Луч падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч
) и частично отражается назад в воду (луч
). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.
Угол падения луча больше. Этот луч также разделяется на два луча – преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч
будет тусклее, чем луч
(то есть получит меньшую долю энергии), а отражённый луч
– соответственно ярче, чем луч
(он получит большую долю энергии).
По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая – преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!
Это исчезновение происходит при достижении угла падения , которому отвечает угол преломления
. В данной ситуации преломлённый луч
должен был бы пойти параллельно поверхности воды, да идти уже нечему – вся энергия падающего луча
целиком досталась отражённому лучу
.
При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.
Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение – все такие лучи целиком отражаются назад в воду. Угол
называется предельным углом полного отражения.
Величину легко найти из закона преломления. Имеем:
.
Но , поэтому
,
откуда
.
Так, для воды предельный угол полного отражения равен:
.
Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности – вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.
Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.
к оглавлению ▴
Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления
Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.
Дано:
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла
Тогда угол падения луча на плоское зеркало будет равен
То есть угол падения равен .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.
Ответ: 1,15
Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.
Так как источник света расположен на расстоянии то
Тогда формула тонкой линзы (1) примет вид следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.
Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.
Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:
Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:
В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и
.
и
Так как правые части этих уравнений равны, то
Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.
Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.
Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.
| Угол преломления | Скорость света в стекле |
Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.
Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение
так же будет уменьшаться. Поэтому угол преломления уменьшится.
Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.
Ответ: 23.
Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с в вещество с
?
Решение.

Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.
Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.
При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления . С учетом того, что
уравнение (1) примет вид:
Ответ: 0,8.
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.
- Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$ - Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$ - Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$ - Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$ - Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$ - Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$ - Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$ - Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$ - Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$ - Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$ - Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$ - Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$ - Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$ - Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$ - Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$ - Формулы приведения можно найти в отдельной статье
Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Основное тригонометрическое тождество
$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)
Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус – это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$
Ответ: (4.)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.
Основные связи тригонометрических функций
А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:
$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$
Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.
Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).
Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$
Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)
Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$
Вывод связи тангенса с косинусом и котангенса с синусом
Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство – формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).
Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$
Формулы суммы и разности тригонометрических функций
- Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$ - Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$ - Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$ - Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$
Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.
Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:
Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).
Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$
Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:
Пример 4
Найдите значение (sin(15^o)=?)
(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.
Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Пример 5
Найдите значение (cos(75^o)=?)
(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.
Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Мы не будем выводить эти формулы – это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.
Формулы двойного угла
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)
Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)
Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$
Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)
Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$
Формулы тройного угла
Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$
Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$
Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$
Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.
Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.
Формулы половинного угла (двойного аргумента)
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$
Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$
Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$
Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$
Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$
Формулы понижения степени
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Формулы понижения второй степени на самом деле дублируют формулы половинного угла.
Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.
Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.
Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:
$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$
Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.
Аналогично выводятся все остальные формулы.
Пример 10
Вычислить (sin(165)+sin(75)=?)
(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$
Преобразование произведения тригонометрических функций
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.
Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:
$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.
Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.
Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)
Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$














































![sin(nalpha)=sum_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}cos^{n-2k-1}alpha,sin^{2k+1}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![cos(nalpha)=sum_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}cos^{n-2k}alpha,sin^{2k}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![mathrm{tg}(nalpha)=frac{sin(nalpha)}{cos(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{tg}^{2k+1}alpha}}{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{tg}^{2k}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![mathrm{ctg}(nalpha)=frac{cos(nalpha)}{sin(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{ctg}^{n-2k}alpha}}{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{ctg}^{n-2k-1}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)








































































![{ displaystyle { begin {align} sin (x) = x - { frac {x ^ {3}} {3!}} + { Frac {x ^ {5}} {5!}} - { frac {x ^ {7}} {7!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} x ^ {2n + 1} \ [8pt] end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/def345e147219a7892eb8140dfeb1c77b29dce38)


















 can be decomposed as
can be decomposed as![{ displaystyle cos (zx) = { frac {z sin ( pi z)} { pi}} displaystyle sum _ {n = - infty} ^ { infty} { frac {(-1) ^ {n} , e ^ {inx}} {z ^ { 2} -n ^ {2}}}, , z in mathbb {C} setminu s { mathbb {Z} }, , x in [- pi, pi].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f892c035938064b0ca52b732ef6265e86a052f)
 yields
yields

 is the derivative of ln ( sin ( π z)) + C 0 {displaystyle ln(sin(pi z))+C_{0}}
is the derivative of ln ( sin ( π z)) + C 0 {displaystyle ln(sin(pi z))+C_{0}} . Furthermore, if d f d z = z z 2 − n 2 {textstyle {frac {df}{dz}}={frac {z}{z^{2}-n^{2}}}}
. Furthermore, if d f d z = z z 2 − n 2 {textstyle {frac {df}{dz}}={frac {z}{z^{2}-n^{2}}}} , then the function f {displaystyle f}
, then the function f {displaystyle f} , which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that
, which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that

 and lim z → 0 ∏ n = 1 ∞ ( 1 − z 2 n 2) = 1 {textstyle lim _{zto 0}prod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)=1}
and lim z → 0 ∏ n = 1 ∞ ( 1 − z 2 n 2) = 1 {textstyle lim _{zto 0}prod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)=1} , we have e C = π {displaystyle e^{C}=pi }
, we have e C = π {displaystyle e^{C}=pi } . Hence
. Hence
 . Let a n ( z) = − z 2 n 2 {displaystyle textstyle {a_{n}(z)=-{frac {z^{2}}{n^{2}}}}}
. Let a n ( z) = − z 2 n 2 {displaystyle textstyle {a_{n}(z)=-{frac {z^{2}}{n^{2}}}}} . Since ∑ n = 1 ∞ | a n ( z) | {displaystyle textstyle {sum _{n=1}^{infty }|a_{n}(z)|}}
. Since ∑ n = 1 ∞ | a n ( z) | {displaystyle textstyle {sum _{n=1}^{infty }|a_{n}(z)|}} converges uniformly on any closed disk, ∏ n = 1 ∞ ( 1 + a n ( z)) {displaystyle textstyle {prod _{n=1}^{infty }(1+a_{n}(z))}}
converges uniformly on any closed disk, ∏ n = 1 ∞ ( 1 + a n ( z)) {displaystyle textstyle {prod _{n=1}^{infty }(1+a_{n}(z))}} converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on C {displaystyle mathbb {C} }
converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on C {displaystyle mathbb {C} } , which completes the proof. ◼ {displaystyle blacksquare }
, which completes the proof. ◼ {displaystyle blacksquare }



