В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора
| Для плоских задач | AB = {Bx – Ax; By – Ay} |
| Для трехмерных задач | AB = {Bx – Ax; By – Ay; Bz – Az} |
| Для n-мерных векторов | AB = {B1 – A1; B2 – A2; … Bn – An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Содержание:
- Формула
- Примеры нахождения координат вектора
Формула
Чтобы найти координаты вектора $overline {A B}$, если заданы координаты его начала и конца,
необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно
координаты $Aleft(x_{A} ; y_{A}right)$ и $Bleft(x_{B} ; y_{B}right)$, то координаты вектора $overline {A B}$ вычисляются по формуле:
$$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A}right)$$
Если точки заданы в пространстве и имеют координаты
$Aleft(x_{A} ; y_{A} ; z_{A}right)$ и $Bleft(x_{B} ; y_{B} ; z_{B}right)$ соответственно, то координаты вектора
$overline {A B}$ вычисляются по следующей формуле:
$$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}right)$$
Примеры нахождения координат вектора
Пример
Задание. Даны точки
$A(5 ; 1)$ и $B(4 ;-3)$. Найти координаты векторов
$overline {A B}$ и
$overline {B A}$
Решение. Точки заданны на плоскости, поэтому координаты вектора
$overline {A B}$ вычислим по формуле:
$$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A}right)$$
Подставляя координаты заданных точек, получим:
$$overline{A B}=(4-5 ;-3-1)=(-1 ;-4)$$
Для нахождения вектора $overline {B A}$ исходная формула примет вид:
$$overline{B A}=left(x_{A}-x_{B} ; y_{A}-y_{B}right)$$
то есть
$$overline{B A}=(5-4 ; 1-(-3))=(1 ; 4)$$
Ответ. $overline{A B}=(-1 ;-4), overline{B A}=(1 ; 4)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны точки
$A(4 ; 3 ; 2)$, $B(-3 ; 2 ;-1)$ и $C(-1 ; 0 ; 1)$ . Найти координаты вектора
$overline {A B}$,
$overline {C B}$ .
Решение. Точки заданны в пространстве, поэтому для нахождения координат искомых векторов будем пользоваться формулой
$overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}right)$
Подставляя заданные координаты, получим:
$$overline{A B}=(-3-4 ; 2-3 ;-1-2)=(-7 ;-1 ;-3)$$
Для вектора $overline {C B}$ имеем:
$overline{C B}=left(x_{B}-x_{C} ; y_{B}-y_{C} ; z_{B}-z_{C}right)$
$overline{C B}=(-3-(-1) ; 2-0 ;-1-1)=(-2 ; 2 ;-2)$
Ответ. $overline{A B}=(-7 ;-1 ;-3), overline{C B}=(-2 ; 2 ;-2)$
Читать дальше: как найти направляющие косинусы вектора.
Как найти координаты вектора
ФОРМУЛА
Чтобы найти координаты вектора
(
overline{A B}
) , если заданы координаты его начала и конца, необходимо вычесть соответствующие координаты начала из координат конца. Если точки установлены на плоскости и имеют соответственно координаты (
Aleft(x_{A} ; y_{A}right) quad{и}quad Bleft(x_{B} ; y_{B}right)
), то координаты вектора (
overline{A B}
) рассчитываются по формуле:
(
overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A}right)
)
Если точки заданы в пространстве и имеют координаты (
Aleft(x_{A} ; y_{A} ; z_{A}right)
) и (
Bleft(x_{B} ; y_{B} ; z_{B}right)
) соответственно, то координаты вектора (
overline{A B}
) вычисляются по следующей формуле: (
overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}right)
)
ПРИМЕРЫ РАСПОЛОЖЕНИЯ ВЕКТОРНЫХ КООРДИНАТ
ПРИМЕР
A(5 ; 1) quad{и}quad B(4 ;-3)
) . Найти координаты векторов (
overline{A B} quad{и}quad overline{B A}
)
overline{A B}
)вычисляются по формуле:
(
overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A}right)
)
Подставляя координаты заданных точек, получаем:
(
overline{A B}=(4-5 ;-3-1)=(-1 ;-4)
)
Чтобы найти вектор (
overline{B A}
) , оригинальная формула принимает вид:
(
overline{B A}=left(x_{A}-x_{B} ; y_{A}-y_{B}right)
)
т.е.
(
overline{B A}=(5-4 ; 1-(-3))=(1 ; 4)
)
overline{A B}=(-1 ;-4), overline{B A}=(1 ; 4)
)
ПРИМЕР
A(4 ; 3 ; 2), B(-3 ; 2 ;-1) quad{и}quad C(-1 ; 0 ; 1)
). Найти координаты вектора (
overline{A B}, overline{C B}
)
(
overline{A B}=left(x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}right)
)
Подставляя заданные координаты, получаем:
(
overline{A B}=(-3-4 ; 2-3 ;-1-2)=(-7 ;-1 ;-3)
)
Для вектора (
overline{C B}
)имеем:
(
overline{C B}=left(x_{B}-x_{C} ; y_{B}-y_{C} ; z_{B}-z_{C}right)
)
(
overline{C B}=(-3-(-1) ; 2-0 ;-1-1)=(-2 ; 2 ;-2)
)
overline{A B}=(-7 ;-1 ;-3), overline{C B}=(-2 ; 2 ;-2)
)
Задачи с векторами только на первый взгляд кажутся сложными, особенно если задача связана с трехмерным пространством. Но не стоит пугаться ведь если разобраться по-лучше в данной тематике задачи решаются в два счета. Так например в данной статье мы разберем тематику определения координат вектора, исходными данными для которого известны координаты начальной и конечной точки.
Для того чтобы определить координаты некоторого вектора MN⃗vec{MN}, зная координаты начала и конца, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Задача 1
Рассмотрим первый вариант задачи. Вектор задан в двухмерном пространстве {x,y}. Тогда у каждой точки вектора существует две координаты, соответственно относящиеся к оси ОХ и ОУ. Формула для определения координаты вектора в таком случае принимает вид:
MN⃗=Mx−Nx;My−Ny.vec{MN}={M_x{-N}_x;M_y{-N}_y}.
Рассмотрим на примере: На некоторой плоскости заданы точки M и N, координаты которых равны соответственно (1,2) и (3,5). Необходимо найти координаты вектора MN⃗vec{MN}
Решение
Возьмем некоторую плоскость ОХУОХУ и отметим точки ММ и NN. Затем соединим исходные точки и рассчитаем координаты полученного вектора. MN⃗={3−1;5−2}=2;3.vec{MN}=left{3-1;5-2right}={2;3}.
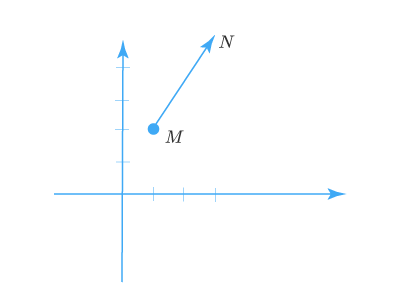
Вот так вот мы получили простое решение искомой задачи. Вариация таких задач может сочетать в себе нахождение не только координат вектора, но и отдельных координат исходных точек вектора.
Но у меня задача может быть не только одно- или двухмерное, но также трехмерное или как мы будем называть их n-мерное. Формула тогда в таком случае немного изменит вид, но смысл не меняется.
Задача 2
Сформулируем формулу для определения координат вектора расположенного в n-мерном пространстве.
Такое пространство подразумевает координаты точек в виде M(M1;M2;M3;..;Mn)M(M_1;M_2{;M}_3;..{;M}_n) и формула примет вид:
MN⃗=Mx−Nx;My−Ny;..;Mn−Nn.vec{MN}={M_x{-N}_x;M_y{-N}_y{;..;M}_n{-N}_n}.
Рассмотрим задачу на примере 5-мерного пространства. Необходимо найти координаты точки N вектора
MN⃗={3,8,4,1,7}vec{MN}={3,8,4,1,7}, если известны координаты точки M(1,9,6,7,4).M(1,9,6,7,4).
Решение
Не стоит пугаться при виде слов 5-мерное пространство, т.к. рисовать данную систему координат не обязательно. Стоит лишь правильно понимать и применять формулу которую мы рассмотрели выше. Перепишем ее еще раз для нашего случая.
MN⃗={M1−N1;M2−N2;M3−N3;M4−N4;M5−N5}.vec{MN}= {M_1{-N}_1;M_2{-N}_2{;M_3{-N}_3{;M}_4{-N}_4;M}_5{-N}_5}.
Тогда рассмотрим систему:
{1−N1=39−N2=86−N3=47−N4=14−N5=7begin{cases}1-N_1=3 \
9-N_2=8 \
6-N_3=4\
7-N_4=1\
4-N_5=7end{cases}
и решив данную систему, получим
{N1=−2N2=1N3=2N4=6N5=−3begin{cases}N_1=-2\
N_2=1\
N_3=2\
N_4=6\
N_5=-3\ end{cases}
Тогда получим ответ на задачу N(−2,1,2,6,−3).N(-2,1,2,6,-3).
Вспомним для начала основные понятия и формулы.
Пусть даны две точки: А(x1; x2) и B(y1; y2). Рассмотрим отрезок AB.
Длина отрезка АВ – это расстояние между точками A и B, его величина вычисляется по следующей формуле:
![]()
Рассмотрим теперь вектор AB. Напомню, что вектор – это направленный отрезок, то есть для него указано, какая из двух точек A и B является началом, а какая – концом. На рисунке ниже слева изображен отрезок AB, а справа – вектор AB с началом в точке A и концом в точке B.
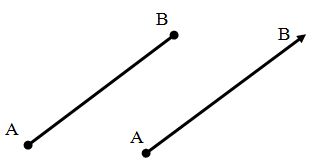
Координаты вектора AB вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора. Например, для нашего вектора AB это будет выглядеть так: AB(x2 – x1; y2 – y1).
Замечу, что модулем вектора AB называется длина отрезка AB.
Вспомним как найти координаты середины отрезка AB. Для этого есть простая формула:
x = (x1 + x2)/2, y = (y1 + y2)/2.
До этого момента мы рассматривали координаты на плоскости, а что, если речь пойдет о пространстве? Тут, оказывается, тоже все просто.
Пусть даны две точки A(x1; x2; x3) и B(y1; y2; y3).
Формула для вычисления длины отрезка AB, расположенного в пространстве будет выглядеть так:
![]()
А координаты середины отрезка AB найдем по формуле
x = (x1 + x2)/2, y = (y1 + y2)/2, z = (z1 + z2)/2.
И еще одна полезная формула: если вектор задан своими координатами, например, MN(x1; x2; x3), то его модуль вычисляется по формуле:
![]()
Чтобы сложить два или более векторов, нужно сложить их соответствующие координаты, например,
(x1; x2; x3) + (y1; y2; y3) = (x1 + y1; x2 + y2; x3 + y3).
Чтобы умножить вектор на число, нужно умножить каждую его координату на это число, например,
5 · (x1; x2; x3) = (5 · x1; 5 · x2; 5 · x3).
Скалярным произведением двух векторов а и b называется число
a · b = |a”b| · сos (a, b),
Чтобы вычислить скалярное произведение векторов, заданных координатами, например, MN(x1; x2; x3) и PK(y1; y2; y3), можно воспользоваться следующей формулой:
MN · PK = x1 · y1 + x2 · y2 + x3 · y3.
Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
На практике коллинеарность векторов (x1; x2) и (y1; y2) проще всего проверить, используя следующее свойство: коллинеарные векторы имеют пропорциональные координаты, то есть существует число p, такое, что (x1; x2) = p · (y1; y2).
Существуют также такие понятия, как сонаправленные векторы и противоположно направленные векторы. Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону, соответственно, противоположно направленные векторы – это коллинеарные векторы, которые направлены в разные стороны.
Теперь давайте рассмотрим несколько задач на эту тему.
Задача 1.
Доказать, что треугольник с вершинами A(6; -4; 2), B(3; 2; 3) и C(3; -5; -1) прямоугольный.
Решение.
Вполне очевидно, что для доказательства этой задачи достаточно показать, что один из углов треугольника ABC равен 90 градусов. Вспомним формулу для вычисления скалярного произведения через модули соответствующих векторов и косинус угла между ними, преобразуем ее и воспользуемся для нахождения угла.
сos (a, b) = a · b/|a”b|.
Для начала нам понадобятся координаты всех векторов, задающих стороны треугольника, их модули и всевозможные скалярные произведения. Вычисляем их.
Координаты векторов:
AB(3 – 6; 2 – (-4); 3 – 2) = AB(-3; 6; 1);
BC(3 – 3; -5 – 2; -1 – 3) = BC(0; -7; -4);
CA(6 – 3; -4 – (-5); 2 – (-1)) = CA(3; 1; 3).
Модули:
|AB| =
![]()
|BC| =
![]()
|CA| =
![]()
Скалярные произведения:
AB · BC = (-3) · 0 + 6 · (-7) + 1 · (-4) = 0 – 42 – 4 = -46;
BC · CA = 0 · 3 + (-7) · 1 + (-4) · 3 = 0 – 7 – 12 = -19;
AB · CA = (-3) · 3 + 6 · 1 + 1 · 3 = -9 + 6 + 3 = 0.
Теперь легко заметить, что угол между векторами AB и CA равен 90 градусов, так как
сos (AB, CA) = AB · CA / |AB”CA| = 0.
А, значит, угол А треугольника ABC равен 90 градусов, то есть треугольник ABC – прямоугольный, что и требовалось доказать.
Задача 2.
Даны точки А(0; 1; 2), B(1; 2; 4), C(-1; -1; 3) и D(1; 0; 0). Точки M и N – середины отрезков AC и BD. Найдите вектор MN и его модуль.
Решение.
Для начала найдем координаты точек M и N.
M((0 – 1)/2; (1 – 1)/2; (2 + 3)/2) = M(-1/2; 0; 5/2);
N((1 + 1)/2; (2 + 0)/2; (4 + 0)/2) = N(1; 1; 2).
Теперь найдем координаты вектора MN:
MN(1 – (-1/2); 1 – 0; 2 – 5/2) = MN(3/2; 1; -1/2).
Осталось найти модуль вектора MN.
|MN| =
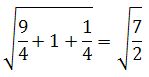
Задача 3.
При каких значениях x векторы (x3 – 1)a и 2xa сонаправлены, где a – вектор, не равный нулевому вектору?
Решение.
Для того чтобы данные векторы были сонаправлены, необходимо, чтобы коэффициенты (x3 – 1) и 2x имели одинаковый знак, а значит, чтобы выполнялось следующее неравенство: (x3 – 1) · 2x > 0. Решим его методом интервалов и найдем соответствующие x.
Получим x € (-∞; 0) U (1; +∞).
Если бы в задаче требовалось узнать, при каких x данные векторы будут противоположно направлены, мы бы потребовали, чтобы у коэффициентов (x3 – 1) и 2x были различные знаки.
Задача 4.
Даны координаты вершин четырехугольника: A(2; -2), B(-3; 1), C(7; 7) и D(7; 1). Доказать, что ABCD – трапеция.
Решение.
Так как трапеция – это четырехугольник, у которого одна пара противолежащих сторон параллельна, то для доказательства нам достаточно показать, что векторы BC и AD – коллинеарны, то есть лежат на параллельных прямых. Найдем для начала их координаты.
BC(7 – (-3); 7 – 1) = BC(10; 6);
AD(7 – 2; 1 – (-2)) = AD(5; 3).
Заметим, что координаты векторов пропорциональны: (10; 6) = 2 · (5; 3). Это и указывает на то, что данные векторы коллинеарны, а, значит, ABCD – трапеция.
Остались вопросы? Не знаете, как выполнять действия над векторами?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
