Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем  , умноженный на плотность его материала
, умноженный на плотность его материала  (см. таблицы плотностей):
(см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой  обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
 Объем параллелепипеда:
Объем параллелепипеда:  , где
, где  — длина,
— длина,  — ширина,
— ширина,  — высота.
— высота.
Тогда масса:

2. Масса цилиндра
 Объем цилиндра:
Объем цилиндра:  , где
, где  — диаметр основания,
— диаметр основания,  — высота цилиндра.
— высота цилиндра.
Тогда масса:

3. Масса шара
 Объем шара:
Объем шара:  , где
, где  — диаметр шара.
— диаметр шара.
Тогда масса:

4. Масса сегмента шара
 Объем сегмента шара:
Объем сегмента шара:  , где
, где  — диаметр основания сегмента,
— диаметр основания сегмента,  — высота сегмента.
— высота сегмента.
Тогда масса:

5. Масса конуса
 Объем любого конуса:
Объем любого конуса:  , где
, где  — площадь основания,
— площадь основания,  — высота конуса.
— высота конуса.
Для круглого конуса:  , где
, где  — диаметр основания,
— диаметр основания,  — высота конуса.
— высота конуса.
Масса круглого конуса:

6. Масса усеченного конуса
 Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями  и
и  :
:  , где
, где  ,
,  . После никому не интересных алгебраических преобразований получаем:
. После никому не интересных алгебраических преобразований получаем:
 , где
, где  — диаметр большего основания,
— диаметр большего основания,  — диаметр меньшего основания,
— диаметр меньшего основания,  — высота усеченного конуса.
— высота усеченного конуса.
Отсюда масса:

7. Масса пирамиды
 Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)):
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)):  , где
, где  — площадь основания,
— площадь основания,  — высота пирамиды.
— высота пирамиды.
Для пирамиды с прямоугольным основанием:  , где
, где  — ширина,
— ширина,  — длина,
— длина,  — высота пирамиды.
— высота пирамиды.
Тогда масса пирамиды:

8. Масса усеченной пирамиды
 Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями  и
и  :
:  , где
, где  ,
,  .
.
Исчеркав половину тетрадного листа, получаем:  , где
, где  ,
,  — ширина и длина большего основания,
— ширина и длина большего основания,  ,
,  — ширина и длина меньшего основания,
— ширина и длина меньшего основания,  — высота пирамиды.
— высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим:  .
.
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием ( ,
,  ) формула выглядит проще:
) формула выглядит проще:


Некоторые приложения тройного интеграла
Объем тела
Объем области  выражается формулой
выражается формулой 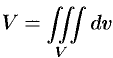 или
или
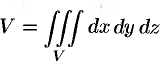 — в декартовых координатах,
— в декартовых координатах,
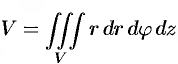 — в цилиндрических координатах,
— в цилиндрических координатах,
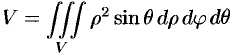 — в сферических координатах.
— в сферических координатах.
Масса тела
Масса тела 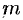 при заданной объемной плотности
при заданной объемной плотности 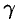 вычисляется с помощью тройного интеграла как
вычисляется с помощью тройного интеграла как
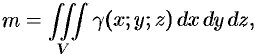
где 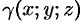 — объемная плотность распределения массы в точке
— объемная плотность распределения массы в точке 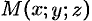 .
.
Статические моменты
Моменты 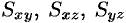 тела относительно координатных плоскостей
тела относительно координатных плоскостей 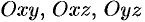 вычисляются по формулам
вычисляются по формулам
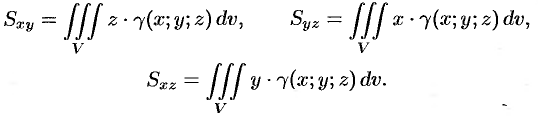
Центр тяжести тела
Координаты центра тяжести тела  находятся по формулам
находятся по формулам
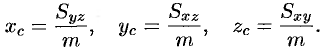
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
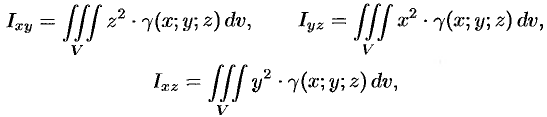
а моменты инерции относительно координатных осей:
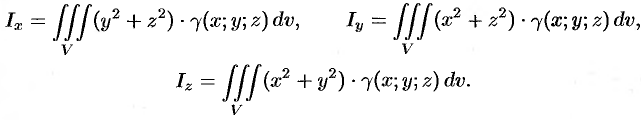
Пример №54.4.
Найти объем тела, ограниченного поверхностями 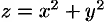 и
и 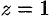 .
.
Решение:
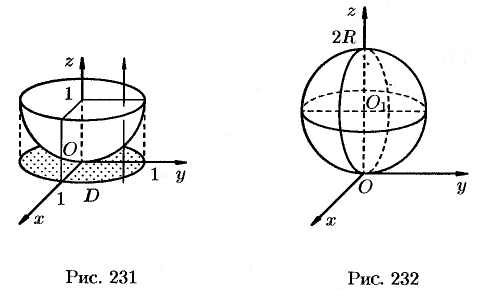
Данное тело ограничено сверху плоскостью 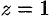 , снизу — параболоидом
, снизу — параболоидом 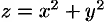 (см. рис. 231). Объем тела находим, используя цилиндрические координаты:
(см. рис. 231). Объем тела находим, используя цилиндрические координаты:
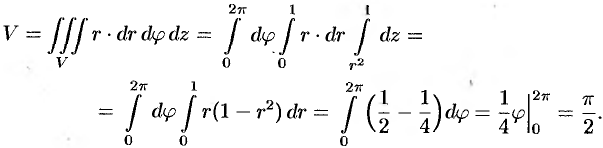
Пример №54.5.
Найти массу шара 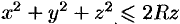 , если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
Решение:
Уравнение сферы 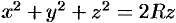 можно записать так:
можно записать так: 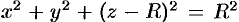 . Центр шара расположен в точке
. Центр шара расположен в точке 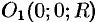 (см. рис. 232). Пусть
(см. рис. 232). Пусть 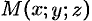 — произвольная точка шара. Тогда, по условию, плотность
— произвольная точка шара. Тогда, по условию, плотность 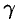 определяется формулой
определяется формулой
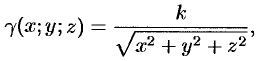
где 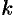 — коэффициент пропорциональности,
— коэффициент пропорциональности, 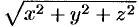 — расстояние от точки
— расстояние от точки  до начала координат.
до начала координат.
Итак, 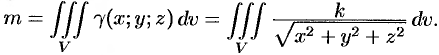
Вычислять интеграл будем в сферических координатах. Уравнение сферы 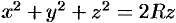 примет вид
примет вид  , т. е.
, т. е. 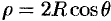 .
.
Поэтому сферические координаты будут изменяться в следующих пределах: 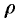 — от 0 до
— от 0 до 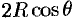 ;
; 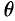 — от 0 до
— от 0 до 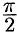 ;
; 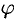 — от 0 до
— от 0 до 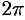 . Подынтегральная функция примет вид
. Подынтегральная функция примет вид 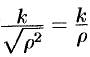 . Поэтому
. Поэтому
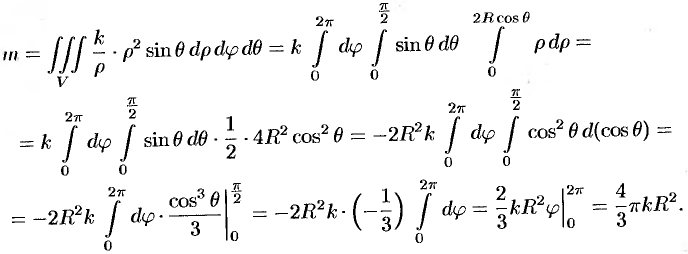
Из соображений симметрии следует, что 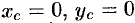 ; вычислив интеграл
; вычислив интеграл 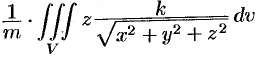 , найдем
, найдем 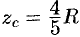 . Итак, координаты центра тяжести
. Итак, координаты центра тяжести 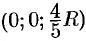 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:

Лучший ответ
Маргоша
Мастер
(1973)
10 лет назад
разделить вес на 9,8 (или 10) Вес это Р=mg, а g=9,8 (округленно 10)
Остальные ответы
snigivas
Профи
(801)
10 лет назад
вес (Н) = масса (кг) х ускорение свободного падения (м/с2)
constanta
Профи
(872)
10 лет назад
наведите пример
вот я так понимаю
P-вес
Р=m*ж ж=9,8 м/с^2
m=….считайте
Валентин Беляев
Оракул
(71418)
10 лет назад
Вес разделить на ускорение свободного падения тела в данной местности.
Формула: P=mg,отсюда m=P/g.
Я ещё в детсаду проходил
Типичный Тохофаг
Ученик
(206)
10 лет назад
P – это вес. P=gm, значит m=P/g. g=9,8Н/кг – коэф-т ускорения свободного падения.
Вес измеряется в ньютонах, а масса – в киллограммах.
Как найти массу тела
Массу тела обычно определяют экспериментально. Для этого берут груз, ставят его на весы и получают результат измерения. Но при решении физических задач, приведенных в учебниках, измерение массы по объективным причинам невозможно, зато имеются те или иные данные о теле. Зная эти данные, можно определить массу тела косвенно путем расчета.
Инструкция
В школьных курсах физики, химии, астрономии можно встретить понятие массы. По массе тела находят обратные величины – объем, плотность, силу. Масса – количественный показатель вещества, поэтому в задачах по химии количество вещества находят, исходя из массы. Масса зависит от свойств вещества, из которого состоит тело, а также от количества этого вещества.Существует несколько основных методов расчета массы. Выбирают их в зависимости от того, какие другие физические величины заданы в задаче. Рассмотрим каждый случай по отдельности.
Самый распространенный способ нахождения массы тела – это ее расчет на основании объема и плотности. Правда, в ряде задач перед определением массы приходится рассчитывать сам объем, руководствуясь иными геометрическими характеристиками тела. Например, для цилиндра с известными площадью основания и высотой, изготовленного из вещества с известной плотностью, масса будет равна:m=?*V=?*S*h, где Vцил.=S*h, ? – плотность, S – площадь основания цилиндра, h – высота цилиндра.Если же объем указан в задаче прямо, для нахождения массы его достаточно просто умножить на плотность:m=?*V
Другой раздел физики, где приходится рассчитывать массу – динамика. Обычно в нем изучается взаимодействие между телами, действие внешних сил на тела, состояние тел при равномерном движении. Любое тело силой F получает ускорение при взаимодействии с другим телом. При этом, оно некоторую массу m. Массы связана с силой следующим соотношением:F=m*a, где a – ускорение заданного тела; m -масса телаОтсюда можно узнать массу тела:m=F/a
В учебниках по химии мы встречаются понятия количества вещества и молярной массы. Через эти две величины также можно выразить массу вещества. Поскольку количество вещества – это физическая величина, пропорциональная числу частиц, из которых состоит вещество, а молярная масса – масса одного моля вещества, рассчитать массу заданного количества этого вещества можно следующим образом:mв=Mв*nв, где Mв – молярная масса, nв -количество вещества
Видео по теме
Полезный совет
Пример задачи по нахождению массы тела.
Допустим, дан небольшой железный шарик радиусом R=5 см. Определить массу шарика, если известно, что p жел.= 7,8 мг/м^3.
Первоначально найдите объем шара. Он равен:
V=4πR^2=4*3,14*25=314 см^3
Масса рассчитывается следующим образом:
m=p*V=7,8*314=24,492 г
Источники:
- как определить массу тела
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Теоретическая выкладка
Ещё в Древней Греции учёные знали формулу определения объема вещей в зависимости от массы и плотности. Так Архимед открыл закон, названный его именем. Почему же ведро с водой поднять заметно легче, чем с песком? Всё объясняется различной плотностью веществ. В единице объёма песка больше вещества, чем в воде, значит, он плотнее жидкой субстанции.
Структура практически всех окружающих субстанций неравномерна, а значит, и концентрация массы в единице веществ отличается, но незначительно. В задачах этой разницей пренебрегают.
Плотностью называется величина, получаемая вследствие разделения массы объекта на занимаемое им пространство. В физике имеет вид:
ρ = m/V, ρ – читается как «ро».
В системе СИ измеряется в кг/м³, на практике применяются кратные и дольные единицы измерения, например, см/кг3.
В физике существует несколько трактовок или типов плотностей:
- объёмная – рассматриваемая величина;
- поверхностная – отношение веса к площади;
- линейная – указывает на обратную пропорциональность массы к длине, применяется в двухмерных вычислениях;
- плотность электрического заряда.
Относительно к газам формула видоизменяется:
ρ = M / Vm, здесь, M и Vm – молярные масса с объёмом соответственно.
Видео
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой тяжести (Ft) избранного тела:
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Что характеризует, каким прибором измеряют
Выделяют два вида массы:
- инертная;
- гравитационная.
Инертная масса показывает инертность тел и выражена во втором законе Ньютона.
Гравитационная масса характеризует силу, с которой тело взаимодействует с полями тяготения и какое гравитационное поле создает само. Входит в закон всемирного тяготения.
Согласно экспериментам на Земле, разницы между гравитационной массой и инертной нет, так что их можно считать равными и объединять в общее краткое понятие. Как правило, они также имеют общее обозначение m.
Масса измеряется в килограммах (кг). Для того, чтобы ее измерить, используют специальный прибор – весы.
Весы измеряют массу тела, а не его вес. Но в повседневном сознании эти понятия считают синонимичными.
Если к телу приложена сила с ускорением 1м/с2,а сила при этом равна 1 Н, то масса такого тела равна 1 кг.
В Международном бюро мер и весов находится эталон массы в 1 кг. С 2018 года им является цилиндр диаметром и высотой в 39,17 мм. Цилиндр состоит из сплава, состоящего на 90% из платины и на 10% из иридия.
Примеры решения задач
Пример
Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света). При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц до соударения равны m.
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна: $$E^{prime}=M c^{2}(1.1)$$
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией. По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики: $$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$
где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде: $$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна: $$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут! Узнать стоимость
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу: $$m=rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 cdot 2=17800$ (кг)
Ответ. $m=8900 cdot 2=17800$ (кг)
