Как показывают
наблюдения и расчеты, звезды движутся
в пространстве с большими скоростями
вплоть до сотен километров в секунду.
Скорость, с которой звезда движется в
пространстве, называется пространственной
скоростью
этой звезды.
Пространственная
скорость V
звезды разлагается на две составляющие:
лучевую
скорость
звезды относительно Солнца Vr
(она
направлена по лучу зрения) и тангенциальную
скорость Vt
(направлена
перпендикулярно лучу зрения). Поскольку
Vr
и Vt
взаимно перпендикулярны, пространственная
скорость звезды равна
|
|
(6.1) |
Направление же
пространственной скорости звезды
задается углом
к лучу зрения, который можно определить
как
|
|
(6.2) |
Лучевая скорость
звезды определяется по доплеровскому
смещению линий в спектре звезды. Но
непосредственно из наблюдений можно
найти лучевую скорость относительно
Земли vr
:
|
|
(6.3) |
где
![]()
есть относительное смещение линий в
спектре, с — скорость света. Зная
теперь vr,
можно рассчитать лучевую скорость
звезды относительно Солнца Vr
(в км/с):
|
Vr |
(6.4) |
где
и
—
эклиптические долготы соответственно
звезды и Солнца,
— эклиптическая широта звезды (см. §
1.9). Соотношение (6.3) указывает на то, что
для нахождения Vr
необходимо
из скорости vr
исключить
проекцию скорости обращения Земли
вокруг Солнца v
= 29,8 км/с
на направление к звезде.
Наличие тангенциальной
скорости
звезды Vt
приводит к угловому смещению звезды по
небу. Смещение звезды на небесной сфере
за год называется собственным
движением
звезды .
Оно выражается в секундах дуги в год.
Собственные
движения у разных звезд различны по
величине и направлению. Только несколько
десятков звезд имеют собственные
движения больше 1″ в год. Самое большое
известное собственное движение
= 10”,27 (у “летящей” звезды Барнарда).
Громадное же большинство измеренных
собственных движений у звезд составляют
сотые и тысячные доли секунды дуги в
год. Из-за малости собственных движений
изменение видимых положений звезд не
заметно для невооруженного глаза.
Выделяют две
составляющие собственного движения
звезды: собственное движение по прямому
восхождению
и собственное движение по склонению
.
Собственное же движение звезды
вычисляется по формуле
|
|
(6.5) |
Если известно
собственное движение звезды
и ее параллакс ,
то можно определить тангенциальную
скорость звезды
Vt
(в км/с)
по формуле
|
|
(6.6) |
Зная обе составляющие
Vr
и Vt,
можно определить величину и направление
пространственной скорости звезды V.
Анализ измеренных
пространственных скоростей звезд
позволяет сделать следующие выводы.
-
Наше Солнце
движется относительно ближайших к нам
звезд со скоростью около 20 км/с
по направлению к точке, расположенной
в созвездии Геркулеса. Эта точка
называется апексом
Солнца. -
Кроме этого, Солнце
вместе с окружающими звездами движется
со скоростью около 220 км/с
по направлению к точке в созвездии
Лебедя. Это движение есть следствие
вращения
Галактики вокруг собственной оси.
Если подсчитать время полного оборота
Солнца вокруг центра Галактики, то
получается примерно 250 млн лет. Этот
промежуток времени называется
галактическим
годом.
Вращение Галактики
происходит по часовой стрелке, если
смотреть на Галактику со стороны ее
северного полюса, находящегося в
созвездии Волосы Вероники. Угловая
скорость вращения зависит от расстояния
до центра и убывает по мере удаления от
него.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
The true velocity of the star is called the space velocity and tangential velocity is the part of a star’s total velocity which is perpendicular to the line of sight. Given below is the rotational velocity of star formula which is based on the space velocity and tangential velocity. Take the square of space and tangential velocity and subtract these both. Then, taking the square root of the resultant value, you will get the rotational velocity of star.
Formula:
Rotational Velocity (Rv)= √(a2 – b2)
Where,
a = Space Velocity
b = Tangential Velocity
Related Calculator:
Rotational velocity of star formula is defined as √(a2-b2). Also, you can navigate to the online calculator provided above for ease calculations.
Какие способы оценки скорости звезд существуют
Все звезды в Галактике движутся вокруг ее центра по почти круговым орбитам, а также обладают собственным движением под действием сил притяжения других звезд (рис. 11.12). Собственные движения звезд – величины очень маленькие, поэтому обнаружить собственное движение возможно, наблюдая звезды в течение длительного промежутка времени (порядка 100 лет и более). Собственное движение звезды – это ее видимое угловое перемещение по небесной сфере в среднем за год. Собственные движения звезд определяются из наблюдений изменения их экваториальных координат.
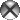
Вверху – за 100 000 лет до наших дней; в центре – наши дни; внизу – через 100 000 лет
Изучение собственных движений, а также проекций пространственных скоростей звезд на луч зрения позволяет определить направление и скорость движения Солнца в пространстве, а также обнаружить вращение Галактики.
Пространственные скорости звезд определяются из наблюдений. Пространственная скорость звезды V состоит из двух компонент – ее касательной или тангенциальной скорости Vt и лучевой скорости Vr (рис. 11.13).
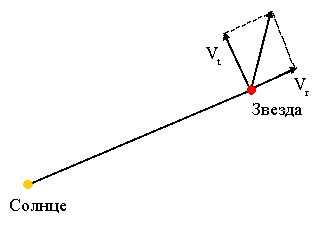
Тангенциальная скорость Vt определяется по формуле Vt = μ/p а. е. в год, где μ – собственное движение звезды, p – ее параллакс; а лучевая скорость определяется по величине красного смещения линий в спектре звезды, вызванного эффектом Доплера. Тогда полная скорость звезды определится по формуле:
Источник
Эффект Доплера и определение лучевых скоростей звёзд.
Лучевые скорости определяют по спектрам звёзд. При этом используется явление, которое называют эффектом Доплера. Суть эффекта Доплера состоит в том, что линии в спектре источника, приближающегося к наблюдателю, смещены к фиолетовому концу спектра, а линии в спектре удаляющегося источника — к красному концу спектра (по отношению к положению линий в спектре неподвижного источника).
 Этот рисунок объясняет, что происходит при этом.
Этот рисунок объясняет, что происходит при этом.
ВЫДЕЛЕННОЕ ЖЕЛТЫМ ЦВЕТОМ ПРОЧИТАТЬ(можно не записывать.
Почему же меняется частота излучения, воспринимаемая наблюдателем? Пусть расстояние от источника до наблюдателя равно c∙t (где с — скорость света, t — время, за которое свет преодолевает расстояние до наблюдателя). За время t источник испускает v0t волн (v0 — частота излучения). Если источник неподвижен, то на отрезке c t как раз и укладывается v0t волн. Но если источник движется (например, удаляется со скоростью ?r), то число волн v0t уложится на отрезке, длина которого ct + ?rt. Перейдём от частоты к длинам волн (рис. 88). Длина волны, которую принимает наблюдатель от неподвижного источника, 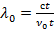 (или известное вам из физики соотношение
(или известное вам из физики соотношение 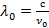 ), а длина волны, которую наблюдатель принимает от удаляющегося источника,
), а длина волны, которую наблюдатель принимает от удаляющегося источника,
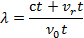
Тогда смещение, равное ∆ 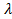 =
= 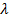 —
— 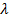 0, то есть
0, то есть
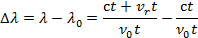
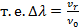 , или
, или 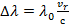 откуда
откуда
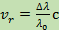 (9)
(9)
Это формула для вычисления лучевых скоростей. Из неё видно, что для определения ?r нужно измерить сдвиг спектральной линии, т. е. сравнить положение данной линии в спектре звезды с положением этой же линии в спектре неподвижного (например, наблюдаемого в лаборатории) источника света. Лучевая скорость удаляющегося источника получается со знаком плюс, а приближающегося — со знаком минус.
К настоящему времени рассчитаны лучевые скорости и собственные движения многих звёзд. Измерение лучевых скоростей проще и быстрее, чем измерение собственных движений.
Задача.. В спектре звезды линия, соответствующая длине волны 5,5 ∙10 −4 мм, смещена к фиолетовому концу спектра на 5,5 ∙10 −8 мм.  Определите лучевую скорость звезды.
Определите лучевую скорость звезды.

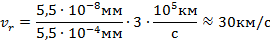
Ответ: ?r ≈ 30 км/с. Поскольку смещение происходит к фиолетовому концу спектра, то звезда приближается к наблюдателю, т. е. ?r ≈ −30 км/с.
Пространственные скорости звёзд относительно Солнца (или Земли) составляют, как правило, десятки километров в секунду
Изучение собственных движений и лучевых скоростей показало, что Солнечная система движется относительно ближайших звёзд со скоростью около 20 км/с в направлении созвездия Геркулеса. Точка небесной сферы, куда направлена эта скорость, называетсяапексомСолнца.
Анализ собственных движений и лучевых скоростей звёзд по всему небу показал, что они движутся вокруг центра Галактики. Это движение звёзд воспринимается как вращение нашей звёздной системы, которое подчиняется определённой закономерности: угловая скорость вращения убывает по мере удаления от центра, а линейная возрастает, достигая максимального значения на том расстоянии, на котором находится Солнце, а затем практически остаётся постоянной.
Звёзды, газ и другие объекты, составляющие галактический диск, движутся по орбитам, близким к круговым. Солнце вместе с близлежащими звёздами обращается вокруг центра Галактики со скоростью около 220 км/с, совершая один оборот примерно за 220 млн лет. Расстояние от Солнца до центра Галактики составляет 23—28 тыс. св. лет (7—9 тыс. пк). Скорость обращения Солнца практически совпадает со скоростью, с которой на данном расстоянии от центра Галактики движутся спиральные рукава. Эта область Галактики получила название коротационной окружности (от англ, corotation — совместное вращение).
Вопросы и задания для самоконтроля
1. Что нужно знать, чтобы определить пространственную скорость звезды? 2. Что нужно знать, чтобы определить тангенциальную скорость звезды? 3. В чём заключается эффект Доплера? 4. Что нужно знать, чтобы определить лучевую скорость звезды?
Источник
Измерение скорости звезды
Заметить периодические колебания звезды можно не только по изменению ее видимого положения на небе, но и по изменению расстояния до нее. Вновь рассмотрим систему Юпитер — Солнце, имеющую отношение масс 1:1000. Поскольку Юпитер движется по орбите со скоростью 13 км/с, скорость движения Солнца по его собственной небольшой орбите вокруг центра масс системы составляет V = 13 м/с. Для удаленного наблюдателя, расположенного в плоскости орбиты Юпитера, Солнце с периодом около 12 лет меняет свою скорость с амплитудой 13 м/с.
Для точного измерения скоростей звезд астрономы используют эффект Доплера. Он проявляется в том, что в спектре звезды, движущейся относительно земного наблюдателя, изменяется длина волны всех линий: если звезда приближается к Земле, линии смещаются к синему концу спектра, если удаляется — к красному. При нерелятивистских скоростях движения эффект Доплера чувствителен лишь к лучевой скорости звезды, т. е. к проекции полного вектора ее скорости на луч зрения наблюдателя (прямую, соединяющую наблюдателя со звездой). Поэтому скорость движения звезды, а значит, и масса планеты определяются с точностью до множителя cos α, где α — угол между плоскостью орбиты планеты и лучом зрения наблюдателя. Вместо точного значения массы планеты (М) доплеровский метод дает лишь нижнюю границу ее массы (М•cos α).
Обычно угол а неизвестен. Лишь в тех случаях, когда наблюдаются прохождения планеты по диску звезды, можно быть уверенным, что угол α близок к нулю. Но у доплеровского метода есть два важных преимущества: он работает на любых расстояниях (разумеется, если удается получить спектр), и его точность почти не зависит от расстояния. В табл. 6.3 показаны характерные значения доплеровской скорости и углового смещения Солнца под влиянием каждой из планет. Плутон здесь присутствует как прототип планет-карликов.
Как видим, влияние планеты вызывает движение звезды со скоростью в лучшем случае метры в секунду. Можно ли заметить перемещение звезды с такой скоростью? До конца 1980-х гг. ошибка измерения скорости оптической звезды методом Доплера составляла не менее 500 м/с. Но затем были разработаны принципиально новые спектральные приборы, позволившие повысить точность до 10 м/с. Например, в прецизионном спектрометре Европейской южной обсерватории Ла-Силья (Чили) свет звезды пропускается сквозь кювету с парами йода, находящуюся в термостатированном помещении. Фиксируя относительное положение спектральных линий звезды и йода, удается очень точно измерять скорость звезды. Новая техника сделала возможным открытие экзопланет, определение их орбитальных параметров и масс.
Источник
Методы измерения скорости света

МЕТОДЫ ИЗМЕРЕНИЯ СКОРОСТИ СВЕТА
1. Основные этапы измерения скорости света. 4
2. Методы измерения скорости света. 7
2.1 Астрономические измерения. 7
2.2 Времяпролетные эксперименты. 9
2.3 Электромагнитные постоянные. 12
2.4 Применение резонаторов. 13
2.5 Интерферометрия. 14
3. Прочие эксперименты. 15
3.1 Распространение света в среде. 15
3.2 Максимальная скорость света. 17
Список используемой литературы. 20
Скорость света является одной из фундаментальных величин и играет важную роль в физике. Она характеризует величину скорости распространения электромагнитных волн в вакууме и относится к постоянным, которые характеризуют не только отдельные тела и поля, но и геометрию пространства-времени в целом. На сегодняшний день, скорость света в вакууме является предельной скоростью движения частиц и распространения взаимодействий. Численно её значение равно 299 792,458 км/с.
В природе со скоростью света распространяются собственно видимый свет и любое другое электромагнитное излучение и, предположительно, гравитационные волны, если таковые существуют.
Массивные частицы могут иметь сколь угодно большие скорости, но всегда заведомо меньше скорости света. Такими частицами, движущимися с околосветовыми скоростями, являются, например, частицы в ускорителях или космические лучи.
Скорость света не зависит от движения источника и наблюдателя и является инвариантом во всех инерциальных системах отсчёта. Такая инвариантность постулируется в специальной теории относительности и подтверждается множеством экспериментов.
1. ОСНОВНЫЕ ЭТАПЫ ИЗМЕРЕНИЯ СКОРОСТИ СВЕТА
Античные мыслители полагали, что скорость света бесконечна, используя в качестве аргумента аналогию полёта стрелы: её траектория тем прямее, чем больше скорость. Платон был сторонником теории зрительных лучей, «ощупывающих пространство». Демокрит и Аристотель настаивали в свою очередь на истечении атомов предметов, которые проникают в зрительные органы человека. Однако, геометрическая интерпретация распространения света, разработанная в работах Евклида, практически сделала обе точки зрения эквивалентными.
Но уже в Новое время факт бесконечности скорости света ставился под сомнения такими учёными как Галилей и Гук, допускавшими, что скорость света конечна, хотя и очень велика. В это время как Кеплер, Декарт и Ферма продолжали настаивать на её бесконечности.
Декарт выдвинул идею о распространении света с бесконечной скоростью посредством давления в среде. Гук первый предложил волновую теорию света: свет есть волновое движение в однородной среде. Эта теория была развита впоследствии Гюйгенсом в его работах. Ньютон старался не высказываться про скорость света, но явно придерживался корпускулярных воззрений на счёт света.
Первая астрономическая оценка скорости света была получена в 1676 году Рёмером. Он заметил, что когда Земля и Юпитер находятся по разные стороны от Солнца затмения спутника Юпитера Ио происходят с запаздыванием в 22 мин. Отсюда было получено первая оценка скорости света – 220 000 км/c. Вскоре Брэдли, в 1728 году, используя явления аберрации света, подтвердил конечность скорости света и уточнил её значение до 308 000 км/с.
Впервые измерить скорость света в земных условиях за счёт прохождения светом известного расстояния удалось в 1849 Физо. Свет преодолевал расстояние около 9 км, а его регистрация была осуществлена с помощью «метода прерываний». Значение скорости света, полученное в ходе измерений, составило 312 000 км/с.
Несколько иной подход («метод вращающегося зеркала») был использован Фуко в 1862. Суть метода заключалась в измерении малых промежутков времени с помощью быстро вращающегося зеркала. Измерения дали значение 298 000 ± 500 км/c. Длина базы в опыте Фуко была небольшой. Впоследствии техника данного эксперимента была значительно улучшена, и уже в 1926 в эксперименте Майлькельсона погрешность была снижена до 4 км/c при измеренной величине скорости света 299 796 км/с. База при этом составляла 35 км!
Дальнейшее развитие методов измерения скорости было связано с изобретением квантовых генераторов (лазеров), дающие высоко когерентное излучение, позволившие определять скорость света одновременным измерением длины волны и частоты излучения. К началу 1970-х величина погрешности таких измерения приблизилась к 1 м/c. Так, на XV Генеральной конференции мер и весов в 1975 году скорость света в вакууме была принята равной 299 792 458 м/с с абсолютной погрешностью 1,2 м/с.
Следует отметить, что последующее повышении точности было затруднено из-за точности определения метра. Исходя из этого, на XVII Генеральной конференции мер и весов скорость света в вакууме была зафиксирована, а метр было рекомендовано определять как расстояние, которое проходит свет за 1/299 792 458 секунды.
Таблица 1. Прогресс в измерении скорости света
Источник
Как измеряли скорость света?

Действительно, как? Как измерить самую высокую скорость во Вселенной в наших скромных, Земных условиях? Нам уже не нужно ломать над этим голову – ведь за несколько веков столько людей трудилось над этим вопросом, разрабатывая методы измерения скорости света. Начнем рассказ по порядку.
Скорость света – скорость распространения электромагнитных волн в вакууме. Она обозначается латинской буквой c. Скорость света равняется приблизительно 300 000 000 м/с.
Сначала над вопросом измерения скорости света вообще никто не задумывался. Есть свет – вот и отлично. Затем, в эпоху античности, среди ученых философов господствовало мнение о том, что скорость света бесконечна, то есть мгновенна. Потом было Средневековье с инквизицией, когда главным вопросом мыслящих и прогрессивных людей был вопрос «Как бы не попасть в костер?» И только в эпохи Возрождения и Просвещения мнения ученых расплодились и, конечно же, разделились.
Так, Декарт, Кеплер и Ферма были того же мнения, что и ученые античности. А вот Галилео Галилей считал, что скорость света конечна, хоть и очень велика. Собственно, он и произвел первое измерение скорости света. Точнее, предпринял первую попытку по ее измерению.
Опыт Галилея
Опыт Галилео Галилея был гениален в своей простоте. Ученый проводил эксперимент по измерению скорости света, вооружившись простыми подручными средствами. На большом и известном расстоянии друг от друга, на разных холмах, Галилей и его помощник стояли с зажженными фонарями. Один из них открывал заслонку на фонаре, а второй должен был проделать то же самое, когда увидит свет первого фонаря. Зная расстояние и время (задержку перед тем, как помощник откроет фонарь) Галилей рассчитывал вычислить скорость света. К сожалению, для того, чтобы этот эксперимент увенчался успехом, Галилею и его помощнику нужно было выбрать холмы, которые находятся на расстоянии в несколько миллионов километров друг от друга. Хотелось бы напомнить, что вы можете заказать эссе, оформив заявку на сайте.
 Галилео Галилей
Галилео Галилей
Опыты Рёмера и Брэдли
Первым удачным и на удивление точным опытом по определению скорости света был опыт датского астронома Олафа Рёмера. Рёмер применил астрономический метод измерения скорости света. В 1676 он наблюдал в телескоп за спутником Юпитера Ио, и обнаружил, что время наступления затмения спутника меняется по мере отдаления Земли от Юпитера. Максимальное время запаздывания составило 22 минуты. Посчитав, что Земля удаляется от Юпитера на расстояние диаметра земной орбиты, Рёмер разделил примерное значение диаметра на время запаздывания, и получил значение 214000 километров в секунду. Конечно, такой подсчет был очень груб, расстояния между планетами были известны лишь примерно, но результат оказался относительно недалек от истины.
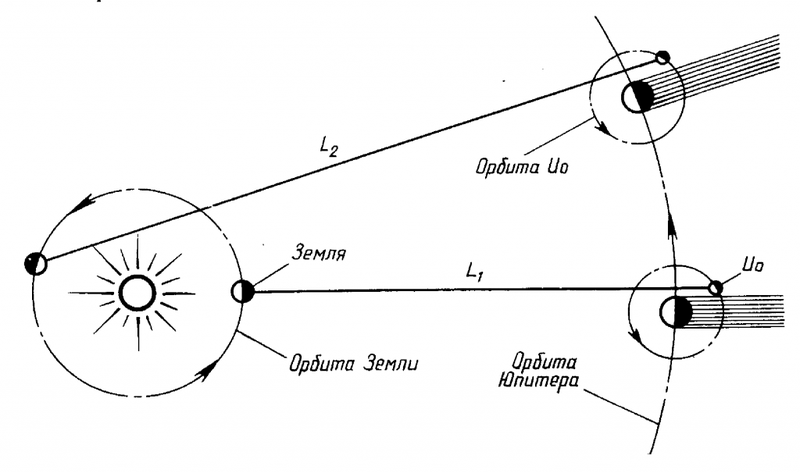 К измерению скорости света Рёмером
К измерению скорости света Рёмером
Опыт Брэдли. В 1728 году Джеймс Брэдли оценил скорость света наблюдая абберацию звезд. Абберация – это изменение видимого положения звезды, вызванное движением земли по орбите. Зная скорость движения Земли и измерив угол абберации, Брэдли получил значение в 301000 километров в секунду.
Опыт Физо
К результату опыта Рёмера и Брэдли тогдашний ученый мир отнесся с недоверием. Тем не менее, результат Брэдли был самым точным на протяжении сотни с лишним лет, аж до 1849 года. В тот год французский ученый Арман Физо измерил скорость света методом вращающегося затвора, без наблюдений за небесными телами, а здесь, на Земле. По сути, это был первый после Галилея лабораторный метод измерения скорости света. Приведем ниже схему его лабораторной установки.
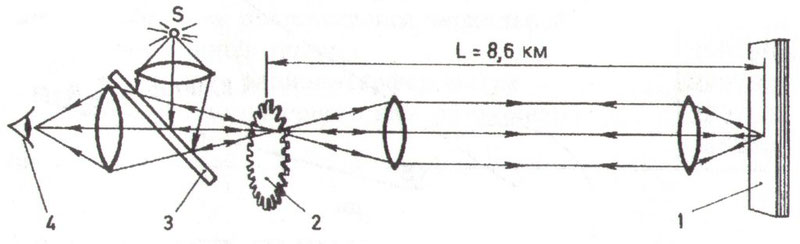 Установка Физо
Установка Физо
Свет, отражаясь от зеркала, проходил через зубья колеса и отражался от еще одного зеркала, удаленного на 8,6 километров. Скорость колеса увеличивали до того момента, пока свет не становился виден в следующем зазоре. Расчеты Физо дали результат в 313000 километров в секунду. Спустя год подобный эксперимент с вращающимся зеркалом быо проведен Леоном Фуко, получившим результат 298000 километров в секунду.
С появлением мазеров и лазеров у людей появились новые возможности и способы для измерение скорости света, а развитие теории позволило также рассчитывать скорость света косвенно, без проведения прямых измерений.
 Арман Ипполит Луи Физо
Арман Ипполит Луи Физо
Самое точное значение скорости света
Человечество накопило огромный опыт по измерению скорости света. На сегодняшний день самым точным значением скорости света принято считать значение 299 792 458 метров в секунду, полученное в 1983 году. Интересно, что дальнейшее, более точное измерение скорости света, оказалось невозможным из-за погрешностей в измерении метра. Сейчас значение метра привязано к скорости света и равняется расстоянию, которое свет проходит за 1 / 299 792 458 секунды.
Напоследок, как всегда, предлагаем посмотреть познавательное видео. Друзья, даже если перед Вами стоит такая задача, как самостоятельное измерение скорости света подручными средствами, Вы можете смело обратиться за помощью к нашим авторам. Заказать контрольную работу онлайн вы можете оформив заявку на сайте Заочника. Желаем Вам приятной и легкой учебы!
Источник
![]()
![]()
![]()
![]()
![]()
![]()
Глава VII
Математические основы
§10. Движения звезд
Скорость любой звезды относительно Земли изменяется непрерывно с периодом в один сидерический год. Причина этого в том, что вектор скорости Земли относительно Солнца за это время успевает повернуться на 360°. На рис.67 показано, как изменяются положение и скорость Земли за полгода.
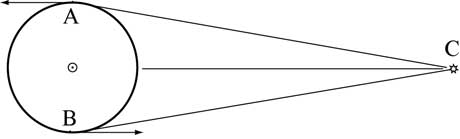
Рис.67.
Если звезда находится в плоскости земной орбиты и неподвижна относительно Солнца, то относительно Земли она удаляется со скоростью 30 км/с в случае А и приближается с такой же скоростью – в случае В. Для исключения подобного изменения скорости звезды её определяют относительно Солнца, вводя соответствующую поправку в значение скорости относительно Земли.
Различают лучевую и тангенциальную скорости звезды, рис.68.
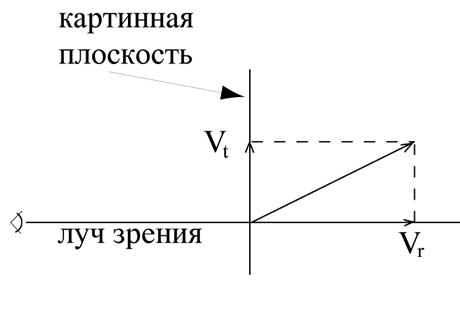
Рис.68.
Лучевая скорость (Vr) – это проекция полной скорости звезды на луч, проведенный от Солнца к звезде (луч зрения). Эта скорость считается большей нуля, если звезда удаляется от Солнца. Чтобы найти лучевую скорость, исследуют доплеровское смещение линий в спектре. Соответствующая формула имеет вид:
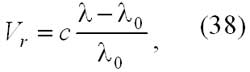
где с – скорость света, l и l0 – длины волн одной и той же линии в спектре звезды и лабораторного источника соответственно.
Тангенциальная скорость (Vt) – это проекция полной скорости на картинную плоскость. Картинной называют плоскость, проходящую через звезду перпендикулярно лучу зрения. Очевидно, полная скорость определяется по теореме Пифагора:
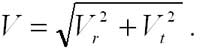
При этом тангенциальную скорость находят по формуле:
![]()
где m – собственное движение, выраженное в секундах дуги за год, и r – расстояние, выраженное в парсеках (скорость получается в км/с).
Собственное движение m – это угловое смещение звезды на небе, вызванное её движением в пространстве. Для подавляющего большинства звёзд m<0,1″ в год и ни у одной звезды не превышает 11″ в год. Сравнивая два снимка одной и той же области неба, полученных с интервалом времени в 25-100 лет (в одно и то же время года), измеряют угловое смещение l данной звезды относительно гораздо более далёких звёзд или ядер галактик. Собственное движение
находят по формуле:
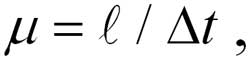
где Dt – интервал времени от первого снимка до второго. При этом определяют не только величину собственного движения, но и его направление.
Расстояние до звезды определяют прямым или косвенным методом. Один из прямых методов основан на использовании годичного параллакса, p. Так называют выраженный в секундах дуги угол, под которым от звезды видели бы средний радиус земной орбиты, перпендикулярный лучу зрения. Связь между параллаксом и расстоянием имеет вид:r=(1″/p) пк. Для нахождения параллакса фотографируют данную звезду (на фоне гораздо более далёких
звёзд) по крайней мере дважды в течение
года, когда Земля находится вблизи точек А и В (см. рис.67).
Угол между направлениями АС и ВС на рис.67 равен удвоенному годичному параллаксу звезды С. Зная этот угол (по смещению звезды С на фоне гораздо более далёких звёзд) и расстояние между точками А и В (примерно 300 млн .км), можно определить расстояние до звезды.
Как найти скорость самого Солнца? Пусть Vi – вектор скорости i – той звезды (i=1,2,…,N) относительно Солнца. Здесь рассматриваются звёзды какого-то определённого вида (например, наблюдаемые невооружённым глазом или какие-то другие) внутри сферы радиуса R с центром в Солнце. Скорость центроида этих звёзд (геометрического центра их совокупности) может быть определена из равенства:
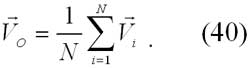
Скорость Солнца относительно совокупности рассматриваемых звёзд, очевидно удовлетворяет условию: Vc–V0. Если рассматривать только звёзды солнечного типа, то есть с почти такими же, как у Солнца, массами, светимостями и спектральными классами, то относительно них скорость нашего светила составит около 36 км/с. Вектор этой скорости направлен к созвездию Лира. Но относительно ближайших звёзд, наблюдаемых невооруженным глазом, скорость
равна 20 км/с и она направлена к созвездию Геркулес в точку с экваториальными координатами
альфа=18h и дельта=+30°. Эту точку называют апексом движения Солнца.
Для каждой звезды можно, в принципе, определить остаточную (пекулярную) скорость: vt=Vt–V0. Это – скорость звезды относительно центроида. Для выборки звёзд со сходными физическими характеристиками распределение остаточных скоростей в проекции на некоторое направление l(vt) подчиняется нормальному закону (как и в случае молекул газа):
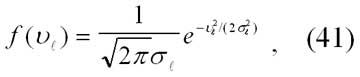
где f(vt) – плотность вероятности и s2t – дисперсия скоростей vt. В отличие от того, что наблюдается для частичек газа (атомов или молекул), значение st зависит от выбранного направления.
Данные наблюдений свидетельствуют, что наибольшее значение st получается в направлении приблизительно на центр Галактики, наименьшее в направлении, перпендикулярном к плоскости галактического экватора. Для звёзд с разными физическими свойствами значения st изменяются от 510 км/с до 100-200 км/с.
Скорости звезд изменяются со временем под действием притяжении других звёзд, звёздных скоплений и облаков пыли и газа. При этом растёт дисперсия скоростей.
Выше шла речь о звёздах, не принадлежащих к звёздным скоплениям и кратным системам. В первом случае при случайных сближениях звёзд также дисперсия скоростей постепенно увеличивается, что в конце концов приводит к распаду скоп ления. Во втором случае обычно структура системы обеспечивает её существование на протяжении многих миллиардов лет.
![]()
![]()
![]()
![]()
![]()
Звёздная кинематика — раздел астрономии, изучающий кинематику или движение звёзд в пространстве. Предметом исследования кинематики звёзд включает в себя измерение скоростей звёзд Млечного Пути и его галактик-спутников наряду с измерением внутренней кинематики более далёких галактик. Определение кинематических свойств звёзд в различных компонентах Млечного Пути, включая тонкий диск, толстый диск, балдж и звёздное гало, предоставляет важную информацию о формировании и эволюции Галактики. Данные о кинематике также помогают обнаружить такие экзотические объекты, как гиперскоростные звёзды, наличие которых обычно объясняют результатом гравитационного взаимодействия двойной звезды и сверхмассивной чёрной дыры, Sgr A* в центре Галактики.
Звёздная кинематика связана (хотя и отличается) с предметом звёздной динамики, использующей теоретическое изучение или моделирование движений звёзд под действием гравитации. Модели звёздной динамики таких систем, как галактики или звёздные скопления, часто сопоставляют с кинематическими данными для исследования эволюции и распределения массы, а также для выявления наличия тёмной материи или сверхмассивных чёрных дыр по их гравитационному влиянию на орбиты звёзд.
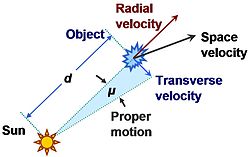
Пространственная скорость[править | править код]
Соотношение между собственным движением и компонентами скорости объекта. В момент испускания излучения объект находился на расстоянии d от Солнца и двигался с угловой скоростью μ радиан/с, то есть μ = vt/d, где vt = трансверсальная (тангенциальная) компонента скорости по отношению к лучу зрения. (Схема показывает угол μ в виде сектора, заметаемого за единицу времени тангенциальной скоростью vt.)
Компонента движения звезды к или от Солнца, известная как лучевая скорость, может быть измерена по смещению линий в спектре вследствие эффекта Доплера. Трансверсальную компоненту (или собственное движение) можно определить по серии определений положения объекта относительно более далёких объектов. При определении расстояния до звезды астрометрическими методами (такими как определение параллакса) можно определить пространственную скорость.[1] При этом мы получим оценку движения звезды относительно Солнца или местного стандарта покоя. Местный стандарт покоя определяют как точку около современного положения Солнца, движущуюся по круговой орбите вокруг центра Галактики со скоростью, равной среднему значению для ближайших к Солнцу звёзд с малой дисперсией скоростей.[2] Движение Солнца относительно МСП называется пекулярным движением Солнца.
Компоненты пространственной скорости Млечного Пути в галактической системе координат обычно обозначаются как U, V и W и измеряются в км/с, причём U положительно в направлении на центр Галактики, V положительно в направлении вращения Галактики, W положительно в направлении северного полюса Галактики.[3] Пекулярное движение Солнца относительно МСП равно[4]
- (U, V, W) = (11,1, 12,24, 7,25) км/с,
со статистической неопределённостью (+0,69−0,75, +0,47−0,47, +0,37−0,36) км/с и систематической неопределённостью (1, 2, 0,5) км/с. (Заметим, что V на 7 км/с превышает оценку, полученную в 1999 году Дененом (англ. Dehnen) и коллегами[5]).
Звёзды Млечного Пути можно разделить на два типа населения в соответствии с металличностью или долей элементов тяжелее гелия. Среди ближайших звёзд было обнаружено, что население первого типа, то есть звёзды с большей металличностью, обладают меньшими радиальными скоростями, чем более старые представители второго типа населения. Последние находятся на эллиптических орбитах, наклонённых к плоскости Млечного Пути.[6] Сравнение кинематических характеристик ближайших звёзд привело к обнаружение звёздных ассоциаций. Вероятно это группы звёзд, имеющих общее место рождения в гигантском молекулярном облаке.[7]
В Млечном Пути существуют три основных кинематических компонента: диск, гало и балдж (с перемычкой). Эти компоненты тесно связаны со звёздными населениями Млечного Пути, образуя сильную корреляцию между параметрами движения и химическим составом. Гало можно разделить на внутреннее и внешнее, при этом внутреннее гало будет обладать упорядоченным движением в ту же сторону, что и вращение Млечного Пути, а внешнее гало будет обладать ретроградным движением.[8]
Звёзды с высокими скоростями[править | править код]
В зависимости от определения к звёздам с высокой скоростью относят звезды, двигающиеся со скоростью, на 65-100 км/с превышающей среднюю скорость звёзд в окрестности Солнца. Иногда скорость определяют как сверхзвуковую относительно окружающей межзвёздной среды. Существует три типа звёзд с высокими скоростями: убегающие звёзды, звёзды гало и гиперскоростные звёзды.
Убегающие звезды[править | править код]

Четыре убегающие звезды, движущиеся сквозь области плотного межзвёздного газа и создающие яркие ударные волны и хвосты светящегося газа. Данные звёзды, изображения которых получены телескопом «Хаббл», являются одними из 14 молодых убегающих звёзд, выявленных камерой «Advanced Camera for Surveys» с октября 2005 года по июль 2006 года.
Убегающей звездой является звезда, двигающаяся в пространстве с крайне высокой скоростью относительно окружающей межзвёздной среды. Собственное движение убегающей звезды зачастую указывает прямо от звёздной ассоциации, к которой раньше принадлежала убегающая звезда.
Существуют два возможных механизма образования убегающей звезды:
- в первом сценарии тесное сближение двух двойных звёзд может привести к разрушению обеих систем, при этом некоторые звёзды могут быть выброшены с высокими скоростями;
- во втором сценарии вспышка сверхновой в кратной звёздной системе может привести к движению оставшихся компонентов с большими скоростями.[9][10]
Хотя возможны оба механизма, но астрономы обычно рассматривают механизм возникновения убегающих звёзд при вспышках сверхновых.
Одним из примеров множества убегающих звёзд может служить случай AE Возничего, 53 Овна и мю Голубя, которые удаляются друг от друга со скоростями более 100 км/с (для сравнения, Солнце движется в Млечном Пути со скоростью, на 20 км/с превышающей среднюю местную скорость). Прослеживание движений данных звёзд в обратную сторону показало, что их траектории пересекались вблизи туманности Ориона около 2 миллионов лет назад. Петля Барнарда считается остатком сверхновой, приведшей к ускорению остальных звёзд.
Другим примером является рентгеновский источник Паруса X-1, в котором фотоцифровые технологии выявили наличие типичной сверхзвуковой ударной волны.
Звёзды гало[править | править код]
Звёзды с высокими скоростями являются очень старыми звёздами, чьё движение сильно отличается от солнечного или от движения звёзд в солнечной окрестности, находящихся на схожих круговых орбитах вокруг центра Млечного Пути. Высокоскоростные звёзды обычно двигаются по эллиптическим орбитам вне плоскости Млечного Пути. Хотя полные скорости этих звёзд могут не превышать скорость Солнца, разница орбит приводит к высоким относительным скоростям.
Типичными примерами являются звёзды гало, проходящие сквозь диск Млечного Пути под большим углом. Одна из 45 ближайших звёзд, звезда Каптейна, является высокоскоростной звездой. Её наблюдаемая лучевая скорость равна −245 км/с, компоненты пространственной скорости равны U = 19 км/с, V = −288 км/с, W = −52 км/с.
Гиперскоростные звёзды[править | править код]
Гиперскоростные звёзды (англ. Hypervelocity stars, HVS или HV) являются звёздами со скоростями, существенно отличающимися от ожидаемых для звезды при нормальном распределении звёзд в галактике. Подобные звёзды могут обладать настолько большими скоростями, что превосходят скорость убегания для галактики.[11] Обычные звёзды Млечного Пути обладают скоростями порядка 100 км/с, а гиперскоростные звёзды, особенно вблизи центра Млечного Пути, обладают скоростями порядка 1000 км/с.
На существование гиперскоростных звёзд впервые указал Джек Хиллс в 1988 году,[12] а затем их существование подтвердили Уоррен Браун, Маргарет Геллер, Скотт Кеньон и Майкл Курц в 2005 году.[13] По состоянию на 2008 год было известно 10 несвязанных гиперскоростных звёзд, одна из которых считается происходящей из Большого Магелланова Облака.[14] В дальнейшем измерения показали, что эта звезда всё же принадлежит Млечному Пути.[15] Вследствие неопределённости распределения массы в Млечном Пути определение связанности гиперскоростной звезды затруднено. Пять дополнительно известных гиперскоростных звёзд могут не быть гравитационно связанными с Млечным Путём, 16 же считаются связанными. Ближайшая к Солнцу известная гиперскоростная звезда (HVS2) расположена на расстоянии 19 кпк от Солнца.
Считается, что около 1000 гиперскоростных звёзд существует в Млечном Пути.[16]
Причины возникновения гиперскоростных звёзд[править | править код]
Считается, что гиперскоростные звёзды возникают при тесных сближениях двойных звёзд со сверхмассивной чёрной дырой в центре Млечного Пути. Один из двух компонентов захватывается чёрной дырой, а другой вылетает с высокой скоростью. Захваченный компонент может перейти на орбиту вокруг чёрной дыры. Однако, это может происходить только в том случае, если двойная звезда падает прямо на чёрную дыру с очень далёкого расстояния, в других случаях звезда не наберёт необходимую скорость.
Гиперскоростные звёзды, созданные вспышками сверхновых, также могут существовать, однако более редко. В данном сценарии гиперскоростные звёзды выбрасываются из тесной двойной системы в результате вспышки сверхновой звезды-компаньона. Скорости выбросов достигают 770 км/с относительно галактической системы покоя, что возможно для поздних B-звёзд.[17] Данный механизм может объяснить причины возникновения высокоскоростных звёзд, выбрасываемых из диска Галактики.
Известные гиперскоростные звёзды являются звёздами главной последовательности с массами, в несколько раз превышающими солнечную. Гиперскоростные звёзды меньших масс также могут существовать, а кандидаты в гиперскоростные звёзды, являющиеся G/K-карликами уже были обнаружены.
Предполагалось, что гиперскоростные звёзды Млечного Пути являются результатом прохождения вращающейся карликовой галактики вблизи Млечного Пути. Когда карликовая галактика проходит наиболее близко к центру Млечного Пути, она испытывает сильное гравитационное возмущение. Энергия некоторых звёзд при этом меняется настолько сильно, что они освобождаются от карликовой галактики и улетают в свободное пространство.[18]
Некоторые нейтронные звёзды могут двигаться с похожими скоростями. Они могут быть связаны со гиперскоростными звёздами и механизмом их выброса. Нейтронные звёзды представляют собой остатки вспышек сверхновой, а их экстремально высокие скорости, вероятно, являются результатом асимметричной вспышки сверхновой или потери компаньона при вспышке сверхновой. Нейтронная звезда RX J0822-4300, чья скорость по измерениям 2007 года составляет рекордные 1500 км/с (0,5 % c), вероятно была образована первым способом.[19]
Некоторые типы сверхновых, как считается, возникают в случае, если белый карлик сталкивается со звездой-компаньоном и поглощает внешнее вещество звезды-компаньона. При этом обе звезды имеют очень высокие орбитальные скорости. Потеря массы белым карликом во время вспышки сверхновой приводит к тому, что звезда-компаньон покидает орбиту с прежней высокой скоростью в несколько сотен км/с, становясь гиперскоростной звездой. Остаток сверхновой превращается в быстро двигающуюся нейтронную звезду. Вероятно, данный механизм является наиболее вероятной причиной возникновения большей части гиперскоростных звёзд и быстрых нейтронных звёзд.
Примеры гиперскоростных звёзд[править | править код]
По состоянию на 2014 год было известно 20 гиперскоростных звёзд:[20][21]
- HVS 1 — (SDSS J090744.99+024506.8) — первая открытая гиперскоростная звезда,[13]
- HVS 2 — (SDSS J093320.86+441705.4) или (US 708),
- HVS 3 — (HE 0437-5439) возможно, происходит из Большого Магелланова Облака,[14]
- HVS 4 — (SDSS J091301.00+305120.0),
- HVS 5 — (SDSS J091759.42+672238.7),
- HVS 6 — (SDSS J110557.45+093439.5),
- HVS 7 — (SDSS J113312.12+010824.9),
- HVS 8 — (SDSS J094214.04+200322.1),
- HVS 9 — (SDSS J102137.08-005234.8),
- HVS 10 — (SDSS J120337.85+180250.4),
- TYC 8840-1782-1.
Кинематические группы[править | править код]
Группа звёзд, обладающих сходным движением в пространстве и возрастом, называется кинематической группой.[22] Данные звёзды могут иметь общее происхождение, такое как испарение рассеянного скопления, остатки области звездообразования или объединение областей вспышек звездообразования, происходивших в разное время.[23] Большее число звёзд рождалось внутри молекулярных облаков. Образующиеся внутри такого облака звёзды составляют гравитационно связанные рассеянные скопления, содержащие от десятков до тысяч звёзд с похожим химическим составом и возрастом. Со временем такие скопления разрушаются. Группы молодых звёзд при этом покидают скопление или перестают быть связанными друг с другом, формируя звёздные ассоциации. По мере старения таких звёзд ассоциация перестаёт быть различимой, оставляя отдельные движущиеся группы звёзд.
Астрономы имеют возможность определить, принадлежат ли звёзды одной кинематической группе, поскольку для этого звёзды должны обладать одним возрастом, металличностью и собственным движением. Поскольку звёзды в движущейся группе образуются близко друг к другу и примерно в одно время, то обладают похожими характеристиками.[24]
Звёздные ассоциации[править | править код]
Звёздная ассоциация представляет собой слабо связанное скопление звёзд, имеющих одинаковое происхождение, но ставших гравитационно не связанными, хотя и движущимися совместно в пространстве. Ассоциации выделяют по общим векторам движения объектов и возрастам. Также используется анализ химического состава.
Впервые звёздные ассоциации были открыты В. А. Амбарцумяном в 1947 году.[25] Принято называть ассоциации по названию созвездия (или созвездий), в котором находится ассоциация, указывать тип ассоциации и, иногда, номер.
Типы[править | править код]

Область звездообразования в созвездии Единорога, изображение телескопа VISTA.
В. А. Амбарцумян разделил звёздные ассоциации на две группы, OB и T, на основе характеристик звёзд.[25] Третью категорию, R, позднее предложил Сидни ван ден Берг для тех ассоциаций, которые подсвечивают отражательные туманности.[26] OB-, T- и R-ассоциации образуют непрерывный спектр молодых звёздных групп. Пока не ясно, представляют ли эти категории эволюционную последовательность.[27] Некоторые группы проявляют свойства как OB-, так и T-ассоциаций, поэтому классификацию не всегда можно провести однозначно.
OB-ассоциации[править | править код]

Молодые ассоциации, содержащие 10-100 массивных звёзд спектральных классов O и B, называют OB-ассоциациями. Такие ассоциации содержат сотни или тысячи звёзд малых и промежуточных масс. Объекты ассоциации считаются сформировавшимися в одном и том же объёме внутри гигантского молекулярного облака. После того как из системы будет выметен газ и пыль, оставшиеся звёзды окажутся не связанными гравитационно и начнут разлетаться.[28] Считается, что большинство звёзд Млечного Пути образовалось внутри OB-ассоциаций.[28] Звёзды спектрального класса O живут малое время и взрываются как сверхновые примерно спустя миллион лет после образования. В результате, OB-ассоциации существуют всего несколько миллионов лет или меньше. O-B звёзды ассоциации исчерпают запасы вещества для ядерных реакций в течение 10 миллионов лет.
Спутник Hipparcos позволил провести измерения, определившие расположение десятка OB-ассоциаций в пределах 650 пк от Солнца.[29] Ближайшая OB-ассоциация — OB-ассоциация Скорпиона — Центавра, находящаяся на расстоянии 400 световых лет от Солнца.[30]
OB-ассоциации были обнаружены в Большом Магеллановом Облаке и Туманности Андромеды. Такие ассоциации могут быть довольно разреженными и достигать 1500 световых лет в диаметре.[31]
T-ассоциации[править | править код]
Молодые звёздные группы могут содержать ряд молодых звёзд типа T Тельца, находящихся в процессе перехода на главную последовательность. Группы звёзд численностью до тысячи звёзд типа T Тельца называются T-ассоциациями. Ближайшим к Солнцу примером такой ассоциации является ассоциация Тельца — Возничего, расположенная на расстоянии 140 пк от Солнца.[32] Другими примерами T-ассоциаций являются T-ассоциация R Южной Короны, T-ассоциация Волка, T-ассоциация Хамелеона, T-ассоциация Парусов. T-ассоциации часто обнаруживают в окрестности молекулярных облаков, из которых они образовались. Некоторые, хотя и не все включают O-B-звёзды. Представители ассоциации обладают близкими возрастами и химическим составом, а также направлением вектора скорости.
R-ассоциации[править | править код]
Ассоциации звёзд, подсвечивающих отражательные туманности, называют R-ассоциациями.[26] Эти молодые группы звёзд содержат звёзды главной последовательности, недостаточно массивные для разгона молекулярных облаков, в которых эти звёзды образовались.[27] Этот факт позволяет исследовать свойства окружающего звёзды облака. Поскольку R-ассоциации более многочисленны, чем OB-ассоциации, то их можно использовать для выявления структуры спиральных рукавов галактик.[33] Примером R-ассоциации является Единорог R2, находящийся на расстоянии 830 ± 50 пк от Солнца.[27]
Движущиеся группы[править | править код]
Если остатки звёздной ассоциации движутся в Млечном Пути когерентно, то они называются движущейся группой или кинематической группой. Движущиеся группы могут быть старыми, как HR 1614 возрастом 2 миллиарда лет, или молодыми, как группа AB Золотой Рыбы возрастом около 120 миллионов лет.
Движущиеся группы подробно исследовал Олин Эгген в 1960-е годы.[34] Список ближайших молодых движущихся групп составил López-Santiago и др.[35] Ближайшей группой является группа Большой Медведицы, включающая все звёзды астеризма Большой Ковш за исключением Дубхе и Бенетнаш. Солнце находится у внешних границ группы, но не входит в неё. Большая часть представителей группы расположена в области склонений +60°, но из-за близости группы к Солнцу некоторые её звёзды находятся даже в созвездии Южного Треугольника со склонениями около −70°.
Звёздные потоки[править | править код]
Звёздный поток представляет собой ассоциацию звёзд, обращающихся вокруг галактики и являвшихся когда-то шаровым скоплением или карликовой галактикой, которая была разорвана приливным влиянием и вытянута вдоль орбиты.
Примечания[править | править код]
- ↑ Stellar Motions (Extension). Australia Telescope Outreach and Education. Commonwealth Scientific and Industrial Research Organisation (18 августа 2005). Дата обращения: 19 ноября 2008. Архивировано из оригинала 25 декабря 2008 года.
- ↑ Fich, Michel; Tremaine, Scott. The mass of the Galaxy (англ.) // Annual Review of Astronomy and Astrophysics (англ.) (рус. : journal. — 1991. — Vol. 29, no. 1. — P. 409—445. — doi:10.1146/annurev.aa.29.090191.002205. — Bibcode: 1991ARA&A..29..409F.
- ↑ Johnson, Dean R. H.; Soderblom, David R. Calculating galactic space velocities and their uncertainties, with an application to the Ursa Major group (англ.) // Astronomical Journal : journal. — 1987. — Vol. 93, no. 2. — P. 864—867. — doi:10.1086/114370. — Bibcode: 1987AJ…..93..864J.
- ↑ Schönrich, Ralph; Binney, James. Local kinematics and the local standard of rest (англ.) // Monthly Notices of the Royal Astronomical Society : journal. — Oxford University Press, 2010. — Vol. 403, no. 4. — P. 1829—1833. — doi:10.1111/j.1365-2966.2010.16253.x. — Bibcode: 2010MNRAS.403.1829S. — arXiv:0912.3693.
- ↑ Dehnen, Walter; Binney, James J. Local stellar kinematics from HIPPARCOS data (англ.) // Monthly Notices of the Royal Astronomical Society : journal. — Oxford University Press, 1999. — Vol. 298, no. 2. — P. 387—394. — doi:10.1046/j.1365-8711.1998.01600.x. — Bibcode: 1998MNRAS.298..387D. — arXiv:astro-ph/9710077.
- ↑ Johnson, Hugh M. The Kinematics and Evolution of Population I Stars (англ.) // Publications of the Astronomical Society of the Pacific : journal. — 1957. — Vol. 69, no. 406. — P. 54. — doi:10.1086/127012. — Bibcode: 1957PASP…69…54J.
- ↑ Elmegreen, B.; Efremov, Y. N. The Formation of Star Clusters (англ.) // American Scientist (англ.) (рус. : magazine. — 1999. — Vol. 86, no. 3. — P. 264. — doi:10.1511/1998.3.264. — Bibcode: 1998AmSci..86..264E.
- ↑ Carollo, Daniela et al. Two stellar components in the halo of the Milky Way (англ.) // Nature : journal. — 2007. — 13 December (vol. 450, no. 7172). — P. 1020—1025. — doi:10.1038/nature06460. — Bibcode: 2007Natur.450.1020C. — arXiv:0706.3005. — PMID 18075581.
- ↑ Blaauw (1961), «On the origin of the O- and B-type stars with high velocities (the run-away stars), and some related problems» BAN 15, 265
- ↑ Tauris & Takens (1998), «Runaway velocities of stellar components originating from disrupted binaries via asymmetric supernova explosions» A&A 330, 1047
- ↑ Two Exiled Stars Are Leaving Our Galaxy Forever. Space Daily (27 января 2006). Дата обращения: 24 сентября 2009. Архивировано 8 июля 2006 года.
- ↑ Hills, J. G. Hyper-velocity and tidal stars from binaries disrupted by a massive Galactic black hole (англ.) // Nature : journal. — 1988. — Vol. 331, no. 6158. — P. 687—689. — doi:10.1038/331687a0. — Bibcode: 1988Natur.331..687H.
- ↑ 1 2 Brown, Warren R.; Geller, Margaret J.; Kenyon, Scott J.; Kurtz, Michael J. Discovery of an Unbound Hypervelocity Star in the Milky Way Halo (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2005. — Vol. 622, no. 1. — P. L33—L36. — doi:10.1086/429378. — Bibcode: 2005ApJ…622L..33B. — arXiv:astro-ph/0501177.
- ↑ 1 2 Edelmann, H.; Napiwotzki, R.; Heber, U.; Christlieb, N.; Reimers, D. HE 0437-5439: An Unbound Hypervelocity Main-Sequence B-Type Star (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2005. — Vol. 634, no. 2. — P. L181—L184. — doi:10.1086/498940. — Bibcode: 2005ApJ…634L.181E. — arXiv:astro-ph/0511321.
- ↑ Brown, Warren R.; Anderson, Jay; Gnedin, Oleg Y.; Bond, Howard E.; Geller, Margaret J.; Kenyon, Scott J.; Livio, Mario. A Galactic Origin For HE 0437–5439, The Hypervelocity Star Near The Large Magellanic Cloud (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2010. — 19 July (vol. 719). — P. L23. — doi:10.1088/2041-8205/719/1/L23. — Bibcode: 2010ApJ…719L..23B. — arXiv:1007.3493.
- ↑ Brown, Warren R.; Geller, Margaret J.; Kenyon, Scott J. & Kurtz, Michael J. (December 2007), Hypervelocity Stars. III. The Space Density and Ejection History of Main-Sequence Stars from the Galactic Center, The Astrophysical Journal Т. 671 (2): 1708–1716, DOI 10.1086/523642
- ↑ Tauris (2015), «Maximum speed of hypervelocity stars ejected from binaries» MNRAS Letters, in press
- ↑ Maggie McKee. Milky Way’s fastest stars may be immigrants, New Scientist (4 октября 2008). Архивировано 31 мая 2015 года. Дата обращения: 4 октября 2017.
- ↑ Watzke, Megan. Chandra discovers cosmic cannonball, Newswise (28 ноября 2007). Архивировано 25 августа 2017 года. Дата обращения: 19 июня 2017.
- ↑ Zheng Zheng. Nearest Bright ‘Hypervelocity Star’ Found, News Center, University of Utah (7 мая 2014). Архивировано 1 ноября 2014 года. Дата обращения: 19 июня 2017.
- ↑ Warren R. Brown; Margaret J. Geller; Scott J. Kenyon; Michael J. Kurtz; Benjamin C. Bromley. Hypervelocity Stars III. The Space Density and Ejection History of Main Sequence Stars from the Galactic Center (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2007. — 10 September (vol. 671, no. 2). — P. 1708—1716. — doi:10.1086/523642. — Bibcode: 2007ApJ…671.1708B. — arXiv:0709.1471.
- ↑ López-Santiago, J.; Montes, D.; Crespo-Chacón, I.; Fernández-Figueroa, M. J. The Nearest Young Moving Groups (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2006. — June (vol. 643, no. 2). — P. 1160—1165. — doi:10.1086/503183. — Bibcode: 2006ApJ…643.1160L. — arXiv:astro-ph/0601573.
- ↑ Montes, D. et al. Late-type members of young stellar kinematic groups – I. Single stars (англ.) // Monthly Notices of the Royal Astronomical Society : journal. — Oxford University Press, 2001. — November (vol. 328, no. 1). — P. 45—63. — doi:10.1046/j.1365-8711.2001.04781.x. — Bibcode: 2001MNRAS.328…45M. — arXiv:astro-ph/0106537.
- ↑ Johnston, Kathryn V. Fossil Signatures of Ancient Accretion Events in the Halo (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1995. — Vol. 465. — P. 278. — doi:10.1086/177418. — Bibcode: 1996ApJ…465..278J. — arXiv:astro-ph/9602060.
- ↑ 1 2 Israelian, Garik. Obituary: Victor Amazaspovich Ambartsumian, 1912 [i.e. 1908] –1996 (англ.) // Bulletin of the American Astronomical Society (англ.) (рус. : journal. — 1997. — Vol. 29, no. 4. — P. 1466—1467. — Bibcode: 1997BAAS…29.1466I.
- ↑ 1 2 Herbst, W. R associations. I – UBV photometry and MK spectroscopy of stars in southern reflection nebulae (англ.) // Astronomical Journal : journal. — 1976. — Vol. 80. — P. 212—226. — doi:10.1086/111734. — Bibcode: 1975AJ…..80..212H.
- ↑ 1 2 3 Herbst, W.; Racine, R. R associations. V. MON R2 (англ.) // Astronomical Journal : journal. — 1976. — Vol. 81. — P. 840. — doi:10.1086/111963. — Bibcode: 1976AJ…..81..840H.
- ↑ 1 2 OB Associations. GAIA: Composition, Formation and Evolution of the Galaxy (6 апреля 2000). Дата обращения: 14 ноября 2013. Архивировано 3 марта 2016 года.
- ↑ de Zeeuw, P. T.; Hoogerwerf, R.; de Bruijne, J. H. J.; Brown, A. G. A.; Blaauw, A. A HIPPARCOS Census of the Nearby OB Associations (англ.) // The Astronomical Journal : journal. — IOP Publishing, 1999. — Vol. 117, no. 1. — P. 354—399. — doi:10.1086/300682. — Bibcode: 1999AJ….117..354D. — arXiv:astro-ph/9809227.
- ↑ Maíz-Apellániz, Jesús. The Origin of the Local Bubble (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2001. — Vol. 560, no. 1. — P. L83—L86. — doi:10.1086/324016. — Bibcode: 2001ApJ…560L..83M. — arXiv:astro-ph/0108472.
- ↑ Elmegreen, B.; Efremov, Y. N. The Formation of Star Clusters (англ.) // American Scientist (англ.) (рус. : magazine. — 1999. — Vol. 86, no. 3. — P. 264. — doi:10.1511/1998.3.264. — Bibcode: 1998AmSci..86..264E. Архивировано 1 июля 2016 года.
- ↑ Frink, S.; Roeser, S.; Neuhaeuser, R.; Sterzik, M. K. New proper motions of pre-main-sequence stars in Taurus-Auriga (англ.) // Astronomy and Astrophysics : journal. — 1999. — Vol. 325. — P. 613—622. — Bibcode: 1997A&A…325..613F. — arXiv:astro-ph/9704281. Архивировано 7 августа 2010 года.
- ↑ Herbst, W. R-associations III. Local optical spiral structure (англ.) // Astronomical Journal : journal. — 1975. — Vol. 80. — P. 503. — doi:10.1086/111771. — Bibcode: 1975AJ…..80..503H.
- ↑ Eggen, O.J. Moving Groups of Stars. Galactic structure, ed. Adriaan Blaauw and Maarten Schmidt. University of Chicago Press, Chicago, p. 111 (1965). Bibcode: 1965gast.conf..111E
- ↑ López-Santiago, J; Montes, D; Crespo-Chacón, I; Fernández-Figueroa, M.J. The Nearest Young Moving Groups (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2006. — Vol. 643, no. 2. — P. 1160—1165. — doi:10.1086/503183. — Bibcode: 2006ApJ…643.1160L. — arXiv:astro-ph/0601573.
Литература[править | править код]
- Brown; Geller; Kenyon; Kurtz. A Successful Targeted Search for Hypervelocity Stars (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2006. — Vol. 640. — P. 35—. — doi:10.1086/503279. — Bibcode: 2006ApJ…640L..35B. — arXiv:astro-ph/0601580.
- Edelmann, H.; Napiwotzki, R.; Heber, U.; Christlieb, N.; Reimers, D. HE 0437-5439: An Unbound Hypervelocity Main-Sequence B-Type Star (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2005. — Vol. 634, no. 2. — P. L181—L184. — doi:10.1086/498940. — Bibcode: 2005ApJ…634L.181E. — arXiv:astro-ph/0511321.
Ссылки[править | править код]
- Majewski, Steven R. Stellar Motions. University of Virginia (2006). Дата обращения: 25 февраля 2008. Архивировано 25 января 2012 года.
- The Space Velocity and its Components. University of Tennessee. Дата обращения: 25 февраля 2008. Архивировано 16 февраля 2008 года.
- Blaauw A.; Morgan W.W. (1954). “The Space Motions of AE Aurigae and mu Columbae with Respect to the Orion Nebula”. The Astrophysical Journal. 119: 625. Bibcode:1954ApJ…119..625B. DOI:10.1086/145866.
- Hoogerwerf, R.; de Bruijne, J.H.J.; de Zeeuw, P.T. (2000). “The Origin of Runaway Stars”. The Astrophysical Journal. 544 (2): L133. arXiv:astro-ph/0007436. Bibcode:2000ApJ…544L.133H. DOI:10.1086/317315.