Как найти следы прямой в начертательной геометрии

Следы прямой

Следами прямой называют точки её пересечения с плоскостями проекций. В зависимости от того, какую плоскость проекций пересекает прямая в данной точке, различают горизонтальный, фронтальный и профильный след.

Прямые, занимающие общее положение, пересекают три плоскости проекций, линии уровня – две, а проецирующие прямые – одну.

Алгоритм построения следов на эпюре

Найдем следы прямой a, заданной отрезком AB. Как видно на рисунке ниже, AB занимает общее положение, поэтому для решения задачи необходимо построить проекции трех точек.

1. Горизонтальный след H_a. Продлим фронтальную проекцию прямой a до пересечения с осью X в точке H_a”. Полученная точка – фронтальная проекция горизонтального следа. По линии связи на a’ найдем точку H_a‘. Она является горизонтальной проекцией горизонтального следа и совпадает с т. H_a.
2. Фронтальный след F_a. Продлим горизонтальную проекцию a’ до пересечения с осью X в точке F_a‘. Полученная точка – горизонтальная проекция фронтального следа*. По линии связи на прямой a” найдем точку F_a“. Она является фронтальной проекцией фронтального следа и совпадает с т. F_a.
3. Профильный след W_a строится аналогично. Для нахождения двух его проекций, W_a” и W_a‘, необходимо продлить a” и a’ до пересечения с осью Z.

На следующем рисунке показано построение следов горизонтали b​, заданной отрезком CD. Как и другие линии уровня, горизонталь пересекает только две плоскости проекций.

Несмотря на то, что рассмотренный нами алгоритм универсален, лучше понять смысл геометрических построений позволяет наглядное изображение прямой в пространстве.

Примечание

* Фронтальный след прямой по определению является точкой, которая лежит во фронтальной плоскости. Её координата Y равна нулю. Из этого следует, что горизонтальная проекция F’ фронтального следа находится на оси X.

Построение следов прямой – типовая задача по начертательной геометрии.

В предыдущем уроке было рассмотрено положение прямой в пространстве.

Понятие следов прямой

Что такое след? Следы прямой – точки пересечения линии (прямой) с плоскостями проекций. Так как плоскостей проекций – 3, то и следов будет тоже три, однако на чертеже проекция следа совпадает со следом на соответствующей плоскости проекций.

А теперь понятным языком – горизонтальная проекция следа совпадает с горизонтальным следом, фронтальная проекция фронтального следа с фронтальным следом, а профильная проекция профильного – на профильной проекции.

В начертательной геометрии чаще рассматривают только два следа – горизонтальный и фронтальный.

Алгоритм построения следов прямой

Обратите внимание, что при построении следов первым действием затрагивают вторую проекции, то есть при построении горизонтального следа – фронтальную проекцию прямой, при построении фронтального следа – горизонтальную. Построение начинается с доведения до оси какой-либо проекции до пересечения с осью Ox.

Построение горизонтального следа прямой

Пусть задана прямая общего положения АB (рис. 1.). Определим горизонтальный след прямой.

1. Фронтальную проекцию доводим до пересечения с осью Оx (рис 2).

2. Из полученной точки пересечения, по линии связи опускаем точку на горизонтальную проекцию прямой, то есть проводи к оси перпендикуляр.

3. Полученная точка и будет являться горизонтальной проекцией горизонтального следа прямой – точка M’ (рис. 4). При этом точка М” полученная в первом действии является фронтальной проекцией горизонтального следа.

На рис. 4 точкой M’ обозначена горизонтальная проекция горизонтального следа прямой AB, эта точка совпадает с М горизонтальным следом (M’≡M).

Построение фронтального следа прямой

В целом алгоритм построения фронтального и горизонтального следа схожи:

Однако, в первом случае мы находили горизонтальный след, а точнее его горизонтальную проекцию, значит сейчас необходимо найти фронтальную проекцию фронтального следа

1. Точно также проекцию прямой AB, но горизонтальную, продляем до пересечения с осью Оx.

2. Проводим линию связи. Не забываем, что линия связи – вертикальная линия (для горизонтальной и фронтальной проекций), соединяющая две проекции одной точки.

3. Полученная точка на фронтальной проекции прямой и будет являться фронтальной проекцией фронтального следа прямой.

На рис. 5 точкой N” обозначена фронтальная проекция фронтального следа прямой AB, при этом эта точка совпадает с N фронтальным следом (N”≡N). А точка N’ – горизонтальная проекция фронтального следа.

Оба следа можно было найти на одном чертеже, разделение было необходимо для наглядности. На рис. 6 найдены оба следа прямой AB.

Построение следов прямых частного положения

Прямую общего положения, как и профильную прямую, характеризует наличие обоих следов на плоскостях проекций (П’ и П”).

Горизонтальная прямая имеет только фронтальный след и не имеет горизонтального следа, так как фронтальная проекция прямой не пересекается с осью Ox (рис. 7).

Фронтальная прямая имеет только один горизонтальный след и не имеет фронтального потому что горизонтальная проекция прямой не может пересечь ось Ox.

Горизонтально-проецирующая прямая не имеет фронтального следа, а горизонтальный след совпадает с ее выродившейся горизонтальной проекцией (рис. 8, слева).

Фронтально-проецирующая прямая не имеет горизонтального следа, а фронтальный след совпадает с ее фронтальной проекцией (рис. 8, справа).

Профильно-проецирующая прямая не имеет следов ни на одной из двух плоскостей проекций (П’ и П”) (рис 9).

Итак, в этом уроке были рассмотрен алгоритм построения следов прямых общего и частного положения.

В следующем уроке изучим взаимное положение точки и прямой.

Следы прямой

Следом
прямой называют точку пересечения
прямой с плоскостью проекций. Прямая
общего положения пересекается со всеми
тремя плоскостями проекций и имеет три
следа. Прямая, параллельная одной
плоскости проекций, имеет два следа.
Прямая, параллельная двум плоскостям
проекций (проецирующая), имеет один
след. М
– горизонтальный след, N
–фронтальный след. Там, где отрезок АВ
пересекается с горизонтальной плоскостью
проекций, получаем горизонтальный след
М.
Фронтальный след N
получаем
при пересечении отрезка АВ
с фронтальной плоскостью проекции.
Профильный след рассматривать в задачах
не будем (рис. 29).

Рис.29

След
прямой
– это точка, лежащая на плоскости проекций
и самой прямой одновременно. Если точка
лежит на плоскости, то одна ее проекция
совпадает с самой точкой, а вторая
обязательно лежит на оси х.

Для
построения следов прямой АВ
на эпюре поступают следующим образом:
продолжают А”В”
до пересечения с осью х
и отмечают фронтальную проекцию М”,
из М”
восстанавливают перпендикуляр до
пересечения с А’В’
или ее продолжением. Получаем горизонтальный
след М’
и сам след М.

При
продолжении А’В’
до пересечения с осью х
получаем горизонтальную проекцию N’
фронтального следа. Из N’
восстанавливаем _┴
до пересечения с А”В”
или ее продолжением для получения
фронтального следа N”.
N”
совпадает с фронтальным следом N
(рис.30). В наших примерах мы рассматриваем
только горизонтальные и фронтальные
следы прямых.

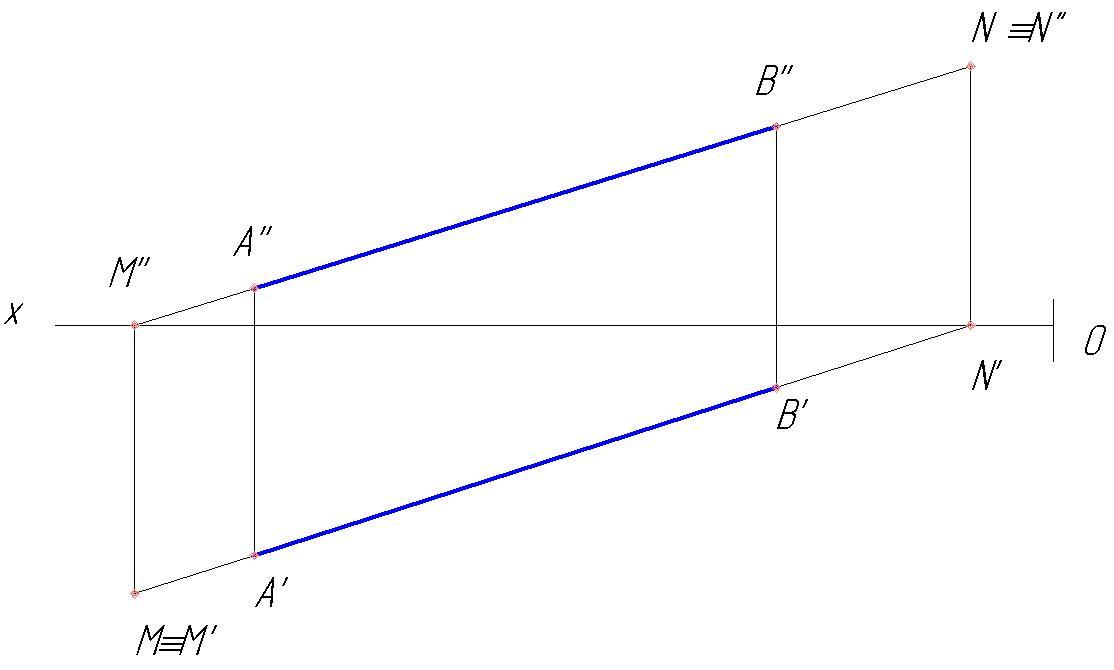Рис.30

Два
следа прямой вполне определяют положение
прямой в пространстве. По следам прямой
можно определить через какие четверти
пространства она проходит, если отрезок
прямой продолжить в обе стороны. До
следа N
прямая проходит через I четверть, между
следами М
и N
– II четверть, за следом М
– III четверть. Можно записать: прямая,
заданная отрезком АВ,
проходит через I-II-III
четверти (рис.31)

Рис.31

Взаимное положение прямых

Две
прямые могут быть: пересекающимися,
параллельными, скрещивающимися.

Две
пересекающиеся прямые
имеют общую точку. На эпюре, при пересечении
одноименных проекций, есть общая точка
(рис.32).

У
параллельных
прямых
а
и b
одноименные проекции параллельны между
собой (рис.33).

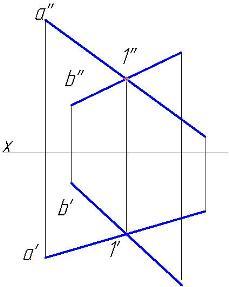
Рис.32

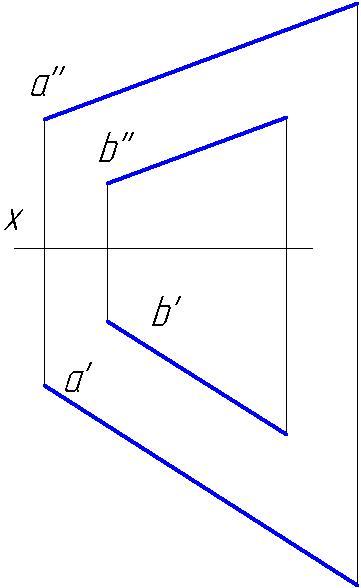Рис.33

Скрещивающиеся
прямые
не имеют общей точки. На эпюре точки
пересечения их одноименных проекций
не лежат на одной линии проекционной
связи (рис.34).

Рис.34

Две
точки скрещивающихся прямых, лежащие
на одном перпендикуляре к плоскостям
проекций, называются конкурирующими.
Конкурирующими точками в нашем примере
являются 1, 2, 3, 4. Точки 1 и 3 принадлежат
прямой а,
а 2, 4 – прямой b.
Точка 2 находится дальше от плоскости
π₂.
На фронтальной проекции l” не увидим –
она закрыта проекцией 2″. На горизонтальной
проекции не будет видна проекция 3′, она
ближе к плоскости π₁
и закрывается проекцией 4″. Определение
взаимного положения конкурирующих
точек необходимо для установления
видимости элементов изображаемого
объекта.

Плоскость Способы задания плоскости

Плоскость
на эпюре можно задавать:

1. тремя
точками, не лежащими на одной прямой;

2. прямой
и точкой, не лежащей не прямой;

3. плоской
фигурой;

4. двумя
параллельными прямыми;

5. двумя
пересекающимися прямыми;

6. следами
(рис. 35).

Следы
плоскости

Соседние файлы в папке Kompyuternaya_grafika

• #
• #

  15.03.20153.99 Mб12Геометрическое черчение учебно-методическое пособие.wbk

• #

2.1. Задание прямой на эпюре

Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.

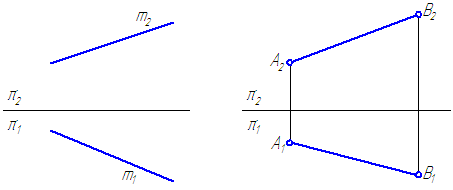
а                                                                  б
Рисунок 2.1 – Проекции прямой

Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.

Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.

Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.

2.2. Прямые частного положения

Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения.

Прямые, параллельные плоскостям проекций, называются прямыми уровня.

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).

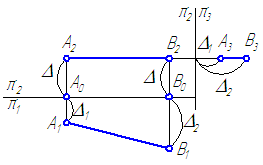
Рисунок 2.2 – Эпюр горизонтали

Если отрезок параллелен плоскости проекций π₁, то его фронтальная проекция А₂В₂ параллельна оси проекций π₁/π₂, а горизонтальная проекция отрезка А₁В₁ определяет истинную величину АВ:

А₂А₀=В₂В₀
А₂В₂ || π₂/π₁

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).

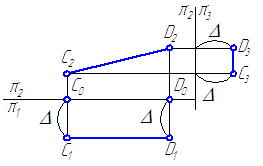
Рисунок 2.3 – Эпюр фронтали

Если отрезок параллелен плоскости проекций π₂, то его горизонтальная проекция параллельна оси проекций π₂/π₁, а фронтальная проекция отрезка C₂D₂ определяет истинную величину CD.

С₁А₀=D₁D₀

C₁D₁ || π₂/π₁

Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).

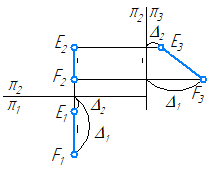
Рисунок 2.4 – Эпюр профильной прямой

Прямые, перпендикулярные плоскостям проекций, называются проецирующими.

Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).

Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).

Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).

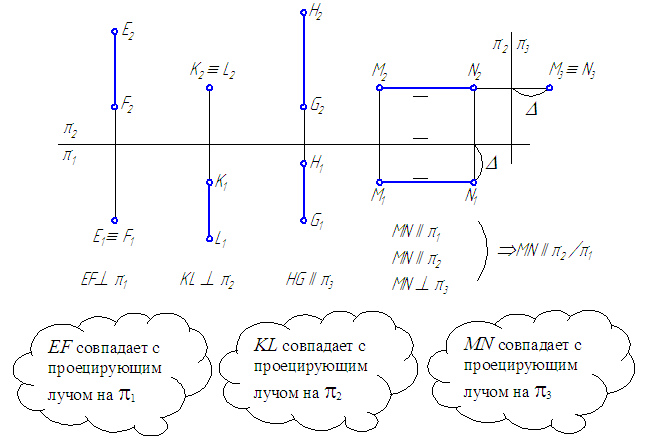
Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH

2.3. Метод прямоугольного треугольника

Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.

Рассмотрим положение отрезка  АВ относительно горизонтальной плоскости проекций π₁ (Рисунок 2.5).

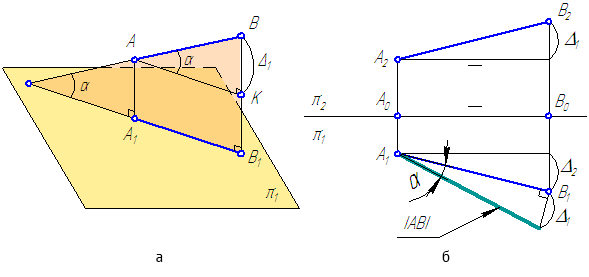
Рисунок 2.5 – Определение истинной величины отрезка общего положения

На рисунке 2.5, а:

АА₁ – расстояние от точки А до плоскости проекций π₁;

ВВ₁ – расстояние от точки В до плоскости проекций π₁;

А₁В₁ – проекция отрезка АВ на π₁;

∠(AB; AK)=∠(AB; A₁B₁)=α – угол наклона прямой АВ к плоскости проекций π₁.

ΔАКВ – прямоугольный треугольник, в котором:

АК=А₁В₁ – катет, равный горизонтальной проекции отрезка АВ;

ВК=ВВ₁–АА₁=Δ₁ – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π₁ (то есть, разности координат Z точек А и В);

АВ – гипотенуза ΔАКВ – истинная величина.

При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.

Истинная величина отрезка может быть найдена как гипотенуза прямоугольного треугольника, одним катетом которого является проекция этого отрезка на плоскость проекций (А₂В₂), а другим – разность координат концов этого отрезка до плоскости (Δ₂), в которой ведется построение. Угол между истинной величиной (АВ) и проекцией (А₂В₂) определяет угол наклона (β) прямой к той плоскости проекций, в которой ведётся построение (Рисунок 2.6).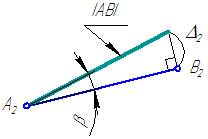

Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π₂

2.4. Точка и прямая

Если точка принадлежит прямой, то её проекции:

1. Принадлежат одноимённым проекциям данной прямой;
2. Лежат на одной линии связи.

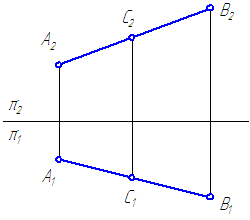
Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:

• С₁∈А₁В₁;
• С₂∈А₂В₂;
• С₁С₂⊥π₂/π₁;

Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:

{frac{A_2C_2}{C_2B_2}=frac{A_1C_1}{C_1B_1}=frac{AC}{CB}}
Справедливо и обратное утверждение.

Упражнение

Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)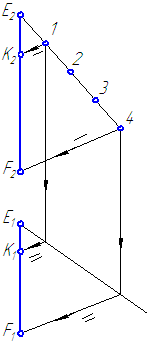

Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:

• 1. Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е₂.
  2. Отложим  на этой прямой от точки Е₂ равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
  3. Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F₂.
  4. Из точки 1 проведём прямую, параллельную прямой (4—F₂) до пересечения с проекцией E₂F₂, таким образом будет найдена фронтальная проекция искомой точки К₂.
  5. Горизонтальную проекцию точки К₁ получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.

  Упражнение

  Определить принадлежность  точки С отрезку прямой АВ (Рисунок 2.9).
  
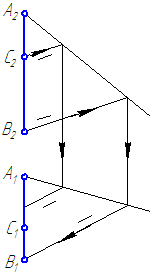
  Рисунок 2.9а – Решение упражнения 2. Способ 1.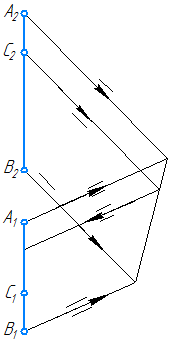

  
  Рисунок 2.9б – Решение упражнения 2. Способ 2.

  Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.

  2.5. Следы прямой

  След прямой – точка пересечения прямой с плоскостью проекций.

  Прямая общего положения в общем случае может быть три следа:

  • горизонтальный след M₁– точка пересечения прямой с горизонтальной плоскостью проекций π₁;
  • фронтальный след N₂– точка пересечения прямой с фронтальной плоскостью проекций π₂;
  • профильный  след L₃ – точка пересечения прямой с профильной плоскостью проекций π₃.

  След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

  • горизонтальный след совпадает со своей горизонтальной проекцией M≡M₁,
  • фронтальный – с фронтальной проекцией N≡N₂,
  • профильный – с профильной проекцией L≡L₃ (Рисунок 2.10).

  

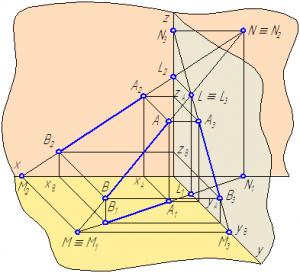
  Рисунок 2.10 – Построение следов отрезка прямой АВ

  Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

  Для построения горизонтального следа прямой АB необходимо:

  1. Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М₂ является фронтальной проекцией горизонтального следа;
  2. Из точки М₂ провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М₁ и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.

  Чтобы построить фронтальный след отрезка АB прямой, необходимо:

  1. Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N₁ является горизонтальной проекцией фронтального следа;
  2. Из точки N₁ провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB  или ее продолжением. Точка пересечения N₂ и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.

  Ниже приводим алгоритм построения следов отрезка прямой АВ:

  A₁B₁ ∩ xO =N₁;       Y_N=0;                   N ∈ xOz (π₂)      ⇒      AB ∩ xOz=N

  A₂B₂ ∩ xO =M₂;       Z_M=0;                  M ∈ xOy (π₁)     ⇒      AB ∩ xOy=M

  A₁B₁ ∩ yO =L₁;        X_L=0;                   L ∈ yOz (π₃)     ⇒      AB ∩ yOz=L

  A₂B₂ ∩ zO =L₂;

  
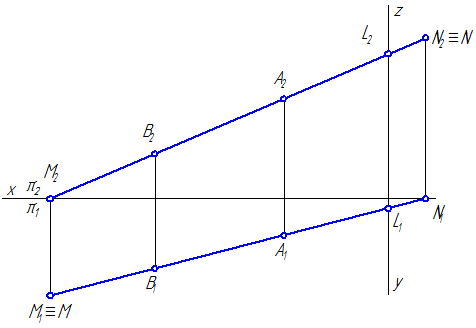
  Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

  Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

  2.6. Взаимное расположение прямых

  Две прямые в пространстве могут быть:

  • параллельными;
  • пересекающимися;
  • скрещивающимися.

  Параллельные прямые – прямые, пересекающиеся в несобственной точке.

  Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).

  
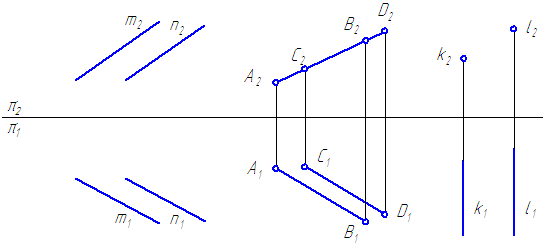
  Рисунок 2.12 – Параллельные прямые
  Пересекающиеся прямые – прямые, имеющие одну общую точку.

  Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).

  {{A_2B_2}cap{C_2D_2}=K_2}

   {{A_1B_1}cap{C_1D_1}=K_1}

   {frac{A_2K_2}{K_2B_2}=frac{A_1K_1}{K_1B_1}}

   {frac{C_2K_2}{K_2D_2}=frac{C_1K_1}{K_1D_1}}

   
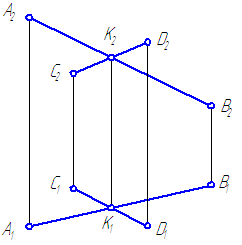
  Рисунок 2.13 – Пересекающиеся прямые

  Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок  2.14).

  
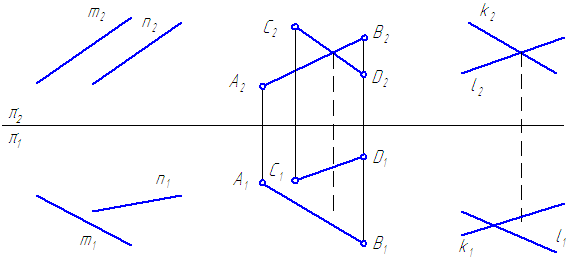
  Рисунок 2.14 — Скрещивающиеся прямые

  2.7. Проекции плоских углов

  Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.

  
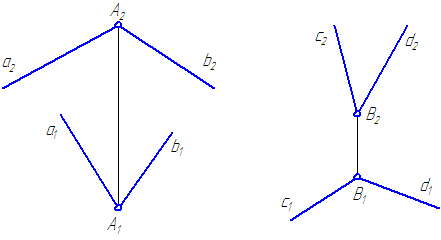
  Рисунок 2.15

  По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.

  Теорема о проецировании прямого угла в частном случае

  Теорема. Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).

  Обратная теорема. Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.

  

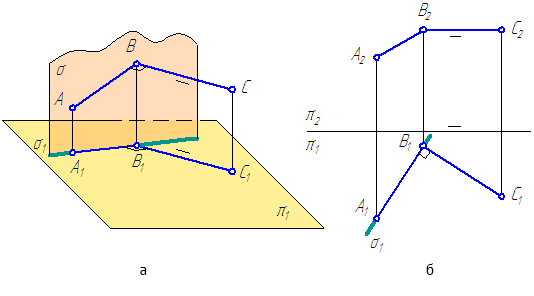
  Рисунок 2.16 – Проецирование прямого угла

  Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,

  причём ВС // π₁ (Рисунок 2.16,б).

  Доказательство:

  1. Проведём через отрезок АВ проецирующую плоскость – σ, σ⊥π₁;
  2. Прямые АВ и ВВ₁ лежат в плоскости σ;
  3. ВС⊥ВВ₁ так как ВС//π₁, а ВВ₁⊥π₁;
  4. Следовательно, ВС⊥σ, а значит ВС перпендикулярна и любой прямой, лежащей в плоскости σ, в частности А₁В₁;
  5. Следовательно В₁С₁⊥σ;
  6. Так как В₁С₁//ВС, то В₁С₁⊥А₁В₁.

  2.8. Задачи для самостоятельного решения

  1. Построить отрезок прямой  АВ // π₁,  равный 35 мм и наклонённый к π₂ под углом 25° (Рисунок 2.17).

  
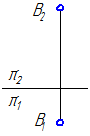
  Рисунок 2.17

  2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π₂ и π₁.

  3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π₁ и 45° — к плоскости проекций π₂.

  4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π₂/π₁ (Рисунок 2.18).

  

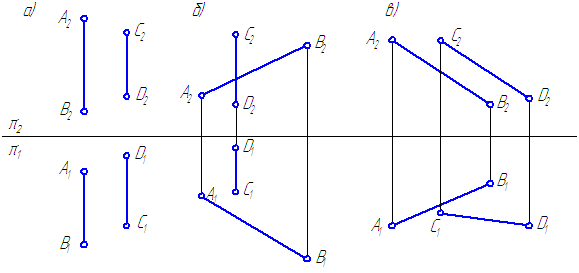
  Рисунок 2.18

2.4. Следы прямой линии

Следом прямой линии называется точка пересечения прямой с плоскостью проекций.

В системе двух плоскостей проекций p₁ и p₂ прямая в общем случае имеет два следа:

• 1. Горизонтальный Н (Н₁, Н₂);
• 2. Фронтальный F (F₁, F₂).

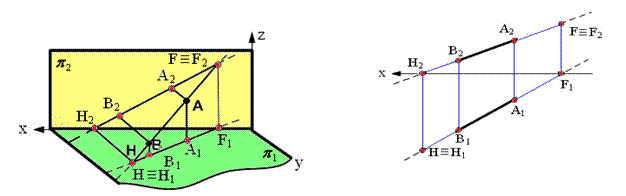
Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.11, а).

Установим правило нахождения следов прямой.

Для нахождения горизонтального следа прямой необходимо:

1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку Н_Х º Н₂)

2) восстановить перпендикуляр в точке Н_Х к оси Х (провести линию связи перпендикулярную к оси Х);

3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром;

4) полученная точка пересечения и будет горизонтальным следом прямой а Н º Н₁ (рис. 2.11, б).

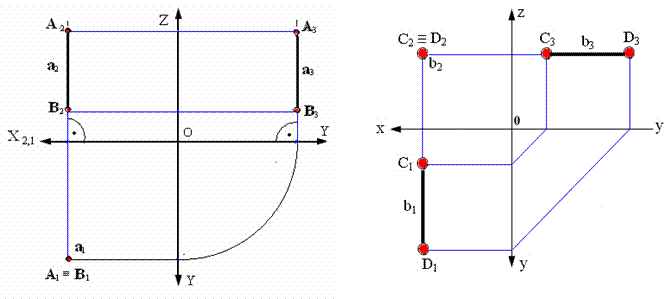
Рис. 2.8. Прямая, перпендикулярная     Рис. 2.9. Прямая, перпендикулярная

горизонтальной плоскости проекций         фронтальной плоскости проекций

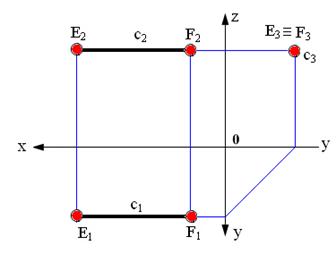
Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций

а                                                                б

Рис. 2.11. Изображение следов прямой линии:

а – в пространстве; б – на эпюре

Для нахождения фронтального следа прямой необходимо:

1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка F_Xº F₁);

2) восстановить перпендикуляр в точке F_X к оси Х;

3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром;

4) полученная точка пересечения Fº F₂ будет фронтальным следом прямой а (рис. 2.11, б).

В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом октанте.

Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.