
{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу

mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона

mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 августа 2022 года; проверки требует 1 правка.

Изображения сил, действующих на скользящее тело.
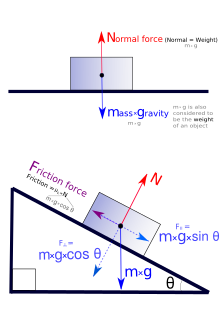
Изображения сил, действующих на тело, находящееся на ровной и наклонной плоскости.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения, от площади соприкосновения[1].
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения и обозначается обычно латинской буквой 





Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда в большей или меньшей степени происходит преобразование механического движения в другие формы движения материи — чаще всего в тепловую форму движения, и происходит нагревание взаимодействующих тел.
Независимость от площади[править | править код]
Так как никакое тело не является абсолютно ровным, сила трения не зависит от площади соприкосновения, и истинная площадь соприкосновения гораздо меньше наблюдаемой. На самом деле, площадь соприкосновения, казалось бы, ровных поверхностей может находиться в пределах 
Обычно это демонстрируется примером:
Два цилиндра из мягких металлов соединяют плоскими частями, а затем с легкостью отрывают. После этого два цилиндра соединяют и немного двигают относительно друг друга. При этом все неровности поверхности притираются друг к другу, образуя максимальную площадь соприкосновения: появляются силы межмолекулярного притяжения. А после разъединить эти два цилиндра становится очень сложно.
Типы трения скольжения[править | править код]
Если между телами отсутствует жидкая или газообразная прослойка (смазочный материал), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
По физике взаимодействия трение скольжения принято разделять на:
- Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазочными материалами — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя;
- Сухое с сухой смазкой (графитовым порошком);
- Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазочного материала) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
- Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
- Граничное, когда в области контакта могут содержаться слои и участки различной природы (оксидные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения;
Также можно классифицировать трение по его области. Силы трения, возникающие при относительном перемещении различных тел, называются силами внешнего трения. Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
Измерение[править | править код]
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики. Поэтому нет точной формулы для коэффициента трения. Его оценка производится на основе эмпирических данных: так как по первому закону Ньютона тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения, то для измерения действующей на тело силы трения достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Таблица коэффициентов трения скольжения[править | править код]
Значения таблицы взяты из справочника по физике[3]
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,99 | 0,20 |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лёд по льду | 0,028 | |
| Металл по асботекстолиту | 0,35-0,50 | |
| Металл по дереву (в среднем) | 0,60 | 0,40 |
| Металл по камню (в среднем) | 0,42-0,50 | |
| Металл по металлу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь (коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примечания[править | править код]
- ↑ 1 2 Билимович Б. Ф. Законы механики в технике. – М., Просвещение, 1975. – Тираж 80000 экз. – с. 58
- ↑ Сила трения. ЗФТШ, МФТИ. Дата обращения: 14 февраля 2019. Архивировано 13 февраля 2019 года.
- ↑ Енохович А. С. Справочник по физике. — Просвещение, 1978. — С. 85. — 416 с.
Калькулятор коэффициента трения
Рассчитайте коэффициент трения по углу наклона или через массу силу трения.
Что известно
Сила трения
Н
Масса
Угол
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
📐 Что считает калькулятор
Калькулятор коэффициента трения — это инструмент, который используется для расчета онлайн коэффициента трения между двумя поверхностями. Коэффициент трения — это величина, которая характеризует силу трения между двумя поверхностями, которые находятся в контакте.
👩🏻💻 Как использовать калькулятор
Для использования калькулятора коэффициента трения необходимо ввести данные о материалах и поверхностях, между которыми идет контакт, а также данные о внешних условиях, таких как давление, скорость и температура. На основе этих данных калькулятор рассчитывает коэффициент трения между двумя поверхностями.
🤔 Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора коэффициента трения зависит от нескольких факторов:
- Качество введенных данных. Чем точнее и полнее введены данные, тем более точными будут результаты. Например, если введены неточные значения для коэффициента трения или других параметров, то это может привести к неточным результатам.
- Условия эксперимента. Коэффициент трения зависит от многих факторов, таких как тип поверхности, скорость, температура и давление. Поэтому, если условия эксперимента изменятся, то это может привести к изменению коэффициента трения.
- Ошибки округления. Когда происходят вычисления с большим количеством знаков после запятой, возможны ошибки округления, которые могут привести к неточным результатам.
- Точность используемых констант. Если в расчетах используются константы, которые имеют низкую точность, то это может привести к неточным результатам.
- Наличие систематических ошибок. Иногда в процессе эксперимента возникают систематические ошибки, которые могут приводить к смещению результатов. Такие ошибки могут быть связаны с некорректной калибровкой приборов, неточным измерением параметров и т.д.
🏗️ Где можно применить калькулятор
Калькулятор коэффициента трения может быть использован в различных областях, включая машиностроение, строительство, физику, материаловедение и т.д. Он может использоваться для определения коэффициента трения между различными материалами и поверхностями, для определения эффективности смазочных материалов, а также для определения влияния различных факторов, таких как давление, скорость и температура, на коэффициент трения.
Калькулятор коэффициента трения может быть полезным инструментом для инженеров, научных работников и студентов, которые занимаются исследованиями в области физики, материаловедения, машиностроения и т.д.
Как вычислить коэффициент трения самостоятельно
Для того чтобы вычислить коэффициент трения, необходимо выполнить определенный эксперимент. Один из самых простых способов – использовать наклонную плоскость.
- Подготовьте наклонную плоскость, установите ее под углом относительно горизонта.
- Положите на плоскость тело, для которого вы хотите определить коэффициент трения.
- Начните наклонять плоскость, пока тело не начнет двигаться. Запишите угол наклона плоскости, при котором тело начинает двигаться.
- Измерьте угол наклона плоскости и определите силу, которая необходима для того, чтобы тело начало двигаться.
- По формуле F = mg sinθ вычислите силу трения F. Здесь m – масса тела, g – ускорение свободного падения, θ – угол наклона плоскости.
- По формуле с = F/N определите коэффициент трения с. Здесь N – нормальная сила, которая действует на тело со стороны плоскости и равна mgcosθ.
Важно отметить, что результаты эксперимента могут быть неточными из-за различных факторов, таких как неровности поверхности плоскости и присутствие внешних сил. Чтобы получить более точный результат, необходимо проводить несколько измерений и усреднять результаты. Также можно использовать более точные приборы для измерения угла наклона и силы.
🤓 Полезные советы
Несколько советов, которые могут помочь при расчете средней скорости:
- Убедитесь, что вы понимаете, как определяется коэффициент трения. Он определяется как отношение силы трения к силе нормального давления между двумя поверхностями.
- Изучите характеристики материалов, которые находятся в контакте. Коэффициент трения зависит от характеристик поверхностей, таких как шероховатость, твердость, состояние поверхности и т. д.
- Учитывайте влияние окружающей среды на коэффициент трения. Например, сухая и чистая поверхность имеет другой коэффициент трения, чем поверхность, покрытая маслом или водой.
- Используйте правильную формулу для расчета коэффициента трения, в зависимости от конкретной задачи. Например, для расчета коэффициента трения скольжения используется формула Ff/Fn, где Ff – сила трения, Fn – сила нормального давления.
- Используйте приближенные значения коэффициента трения для первоначальных расчетов. Для более точных результатов нужно использовать данные, полученные из экспериментов или измерений.
- Проверьте свои расчеты несколько раз, чтобы убедиться в правильности результатов. Небольшие ошибки в расчетах могут привести к существенным изменениям в результатах.
- Используйте единицы измерения, соответствующие конкретной задаче. Например, для расчета коэффициента трения в системах СИ используются Н (ньютон) и м (метры), в то время как в системах английских единиц измерения используются фунты и дюймы.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемые вопросы про вычисление коэффициента трения.
Что такое коэффициент трения?
Коэффициент трения — это физическая величина, которая определяет силу трения между двумя поверхностями. Эта величина обычно обозначается как µ и может быть различной для разных материалов и условий.
Как рассчитать коэффициент трения между двумя поверхностями?
Для расчета коэффициента трения между двумя поверхностями необходимо определить отношение силы трения к нормальной силе, действующей между поверхностями. Это можно сделать путем измерения силы трения и нормальной силы с помощью динамометра и делением первой на вторую.
Как изменить коэффициент трения?
Коэффициент трения может быть изменен путем изменения условий между поверхностями. Например, использование смазки между двумя поверхностями может снизить коэффициент трения. Также можно изменить материалы, из которых изготовлены поверхности, чтобы получить другой коэффициент трения.
Какие еще факторы могут влиять на коэффициент трения?
Кроме материалов поверхностей, на коэффициент трения может влиять их состояние (например, состояние поверхности), скорость движения, температура и влажность.
Каково значение коэффициента трения для различных материалов?
Значение коэффициента трения для различных материалов может значительно различаться и зависит от многих факторов, включая состояние поверхностей, условия окружающей среды и т. д. Например, коэффициент трения между сталью и сталью может быть около 0,6, а между льдом и льдом – около 0,1.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор закона Ома. Рассчитайте сопротивление, силу тока и напряжение в зависимости от известных параметров.
- Калькулятор средней скорости. Рассчитайте онлайн среднюю скорость автомобиля или бегуна по времени и расстоянию.
- Калькулятор мощности тока. Рассчитайте онлайн мощность электрического тока в ваттах (Вт) в зависимости от силы тока, напряжения и сопротивления.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор перевода в тонны. Иногда может потребовать перевести одну единицу веса в другую, например, в тонны. И для этой цели очень пригодится специальный калькулятор.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Коэффициент трения скольжения


4
Средняя оценка: 4
Всего получено оценок: 100.
4
Средняя оценка: 4
Всего получено оценок: 100.
Физическая величина, характеризующая трущиеся поверхности, называется коэффициентом трения скольжения. Величина обозначается буквой μ. Коэффициент трения определяют опытным путём.
Сила трения скольжения
На покоящиеся и движущиеся тела всегда действуют силы трения. Они возникают при соприкосновении твердых тел, твердых тел и жидкостей или газов и подчиняются законам Ньютона. Направление сил трения противоположно движению тела и силам, стремящимся изменить его положение.
В случае, когда тело движется относительно другого, говоря о трении скольжения. Она зависит от:
- Силы нормальной реакции опоры $vec N$,
- От скорости движения (но в вычислениях этой зависимостью пренебрегают),
- От безразмерного коэффициента трения скольжения $mu$, который характеризует свойства и состояние поверхностей соприкосновения.

Коэффициент зависит от свойств материала. Чем больше шероховатость поверхности, тем больше значение коэффициента и, соответственно, больше сила трения. Коэффициент трения смазанных поверхностей будет меньше, чем у несмазанных для одной и той же пары материалов. Также коэффициент трения зависит от скорости. Однако эта зависимость минимальна и ей пренебрегают, если не требуется точность измерения. Поэтому коэффициент трения считается постоянным.
Расчет коэффициента трения скольжения
С достаточно большой точностью силу трения скольжения рассчитывают как предельную силу трения покоя по формуле:
$F_{тр} = mu cdot N$.
Тогда формула коэффициента трения скольжения:
$mu ={{F_{тр}} over {N}}$
Значение N рассчитывается как произведение массы тела на ускорение свободного падения и на косинус угла к поверхности приложения:
$N = m cdot g cdot cos alpha$
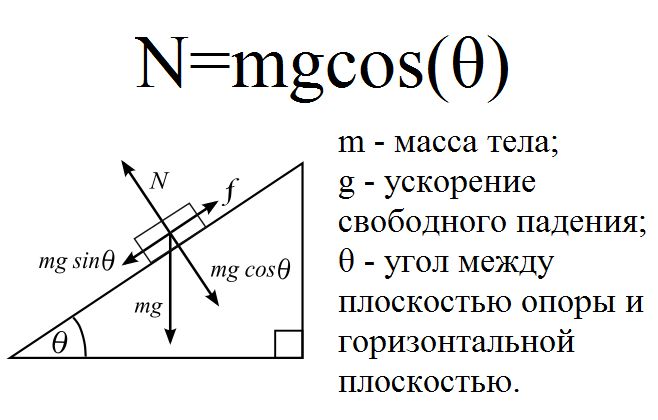
Для большинства пар материалов коэффициент рассчитан опытным путём. Значения находятся в пределах 0,1…0,5. Некоторые значения представлены в таблице.
|
Трущиеся материалы |
Коэффициенты трения |
|
|
Покоя |
При движении |
|
|
Алюминий по алюминию |
0,94 |
|
|
Бронза по бронзе |
0,20 |
|
|
Бронза по чугуну |
0,21 |
|
|
Дерево по дереву |
0,65 |
0,33 |
|
Дерево по камню |
0,46-0,60 |
|
|
Дуб по дубу (вдоль волокон) |
0,62 |
0,48 |
|
Дуб по дубу (перпендикулярно волокнам) |
0,54 |
0,34 |
|
Железо по бронзе |
0,19 |
0,18 |
|
Железо по железу |
0,15 |
0,14 |
|
Железо по чугуну |
0,19 |
0,18 |
|
Каучук по дереву |
0,80 |
0,55 |
|
Каучук по металлу |
0,80 |
0,55 |
|
Кирпич по кирпичу (гладко отшлифованные) |
0,5-0,7 |
|
|
Лёд по льду |
0,028 |
|
|
Медь по чугуну |
0,27 |
|
|
Металл по дереву |
0,60 |
0,40 |
|
Металл по камню |
0,42-0,50 |
|
|
Металл по металлу |
0,18-0,20 |
|
|
Олово по свинцу |
2,25 |
|
|
Полозья деревянные по льду |
0,035 |
|
|
Обитые железом полозья по льду |
0,02 |
|
|
Резина (шина) по твёрдому грунту |
0,40-0,60 |
|
|
Резина (шина) по чугуну |
0,83 |
0,8 |
|
Сталь (коньки) по льду |
0,02-0,03 |
0,015 |
|
Сталь по железу |
0,19 |
|
|
Сталь по стали |
0,15-0,25 |
0,09 при 3 м/с, 0,03 при 27 м/с |
|
Чугун по дубу |
0,65 |
0,30-0,50 |
|
Чугун по стали |
0,33 |
0,13 |
|
Чугун по чугуну |
0,15 |
Коэффициент трения – переменная величина. Поэтому значение коэффициента трения скольжения, приведённые в таблице, являются истинными только при соблюдении определённых условий, в которых были получены.

Что мы узнали?
Коэффициент трения скольжения – физическая величина, характеризующая трущиеся поверхности. Как найти: $mu = {{F_{тр}} over {N}}$. На практике коэффициент рассчитывается исходя из свойств материала эмпирическим путём.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 100.
А какая ваша оценка?
Сила трения. Коэффициент трения
- Причины возникновения трения
- Трение покоя
- Трение скольжения
- Трение качения
- Задачи
- Лабораторная работа №8. Измерение коэффициента трения скольжения
п.1. Причины возникновения трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Сила трения – это сумма межмолекулярных сил, возникающих при деформациях и изломах контактирующих поверхностей за счет разрыва межмолекулярных связей.
Сила трения направлена вдоль поверхностей контактирующих тел.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Сила трения, возникающая при относительной скорости двух контактирующих тел равной нулю, называется силой трения покоя.
Сила трения покоя равна по модулю приложенной силе и направлена в сторону, противоположную возможному движению тела, параллельно контактирующим поверхностям.
Если параллельно поверхности контакта на тело не действует сила, сила трения покоя равна нулю. Максимальное значение силы трения, при котором тело все ещё неподвижно, называется максимальной силой трения покоя.
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | – |
| 200 | Нет | 200 | – |
| 300 | Есть, равномерное | – | 300 |
п.3. Трение скольжения
Силу трения, возникающую в результате движения одного тела по поверхности другого, называют силой трения скольжения.
Сила трения скольжения всегда направлена в сторону, противоположную перемещению тела («тормозит» движение).
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Сила трения скольжения прямо пропорциональна силе реакции опоры: $$ F_{text{тр}}=mu N $$ Коэффициент (mu) называют коэффициентом трения скольжения; величина (mu) зависит от материала трущихся тел и состояния их поверхностей.
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения, возникающая при качении одного тела по поверхности другого, называется силой трения качения.
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Дано:
(m=6 text{т}=6cdot 10^3 text{кг})
(F_{text{тяги}}=30 text{кН}=3cdot 10^4 text{Н})
(gapprox 10 text{м/с}^2)
__________________
(mu-?)

Коэффициент трения $$ mu=frac{F_{text{тр}}}{N}. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow{a}=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow{F_{text{тр}}}+ overrightarrow{F_{text{тяги}}}=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_{text{тр}}=F_{text{тяги}}. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac{F_{text{тр}}}{N}= frac{F_{text{тяги}}}{mg}, mu=frac{3cdot 10^4}{6cdot 10^3cdot 10}=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Дано:
(m=3 text{кг})
(k=3frac{text{Н}}{text{см}}=frac{3 text{Н}}{0,01 text{м}}=300frac{text{Н}}{text{м}})
(mu=0,3)
(gapprox 10 text{м/с}^2)
__________________
(Delta l-?)
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin{gather*} F_{text{упр}}=kDelta l=F_{text{тр}}=mu N=mu mgRightarrow kDelta l=mu mg end{gather*} Получаем: $$ Delta l=frac{mu mg}{k}, Delta l=frac{0,3cdot 3cdot 10}{300}=0,03 (text{м})=3 (text{см}) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Дано:
(v_1=72frac{text{км}}{text{ч}}=20frac{text{м}}{text{с}})
(mu=0,4)
(v_2=0)
(gapprox 10 text{м/с}^2)
__________________
(t, s-?)
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin{gather*} F_{text{тр}}=ma. end{gather*} С другой стороны на горизонтальной дороге $$ F_{text{тр}}=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac{v_2-v_1}{t}. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac{v_1}{t}=mu gRightarrow t=frac{v_1}{mu g} $$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac{20}{0,4cdot 10}=5 (text{с}) $$ Найдем тормозной путь $$ s=v_1t+frac{at^2}{2}=v_1t+ left(frac{overbrace{v_2}^{=0}-v_1}{t}right)frac{t^2}{2}=v_1t -frac{v_1t}{2}=frac{v_1t}{2}=frac{v_1t}{2}cdot frac{v_1}{mu g}=frac{v_1^2}{2mu g} $$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac{20^2}{2cdot 0,4cdot 10}=50 (text{м}) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow{g}=-overrightarrow{N}). Модули этих сил равны По горизонтали (overrightarrow{F_{text{тр}}}=-overrightarrow{F_{text{тяги}}}). Модули этих сил равны $$ F_{text{тяги}}=F_{text{тр}}=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac{F_{text{тяги}}}{mg} $$
Для расчетов используем стандартное значение (g=9,80665 text{м/с}^2).
Погрешность для прямых измерений (F_{text{тяги}}) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text{г}) для (m=100 text{г}), т.е. (delta_m=2text{%}).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text{Н}).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | – | – | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,660}{5}=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,065}{5}=0,013 $$ Относительная погрешность begin{gather*} delta=frac{0,013}{0,332}cdot 100text{%}approx 3,9text{%}\[7pt] mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | – | – | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{2,862}{5}approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,090}{5}=0,018 $$ Относительная погрешность begin{gather*} delta=frac{0,018}{0,572}cdot 100text{%}approx 3,1text{%}\[7pt] mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%} end{gather*}
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text{кг}) | (F_{text{тяги}}, text{Н}) | (mu=frac{F_{text{тяги}}}{mg}) | (Delta=|mu-mu_{text{ср}}|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | – | – | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_{text{ср}}=frac{1,732}{5}approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac{0,043}{5}approx 0,009 $$ Относительная погрешность begin{gather*} delta=frac{0,009}{0,346}cdot 100text{%}approx 2,5text{%}\[7pt] mu ‘_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin{gather*} mu_{text{дд}}=(0,332pm 0,013), delta_mu=3,9text{%} end{gather*}
Для скольжения дерева об наждак был получен коэффициент begin{gather*} mu_{text{дн}}=(0,572pm 0,018), delta_mu=3,1text{%}\[7px] mu_{text{дн}}gt mu_{text{дд}} end{gather*}
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin{gather*} mu’_{text{дд}}=(0,346pm 0,009), delta_mu=2,5text{%} end{gather*} Поскольку begin{gather*} 0,319le mu_{text{дд}}le 0,345 0,337le mu’_{text{дд}}le 0,355 end{gather*} Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
