Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Объём куба через ребро
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
Объём куба через диагональ
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
Объём куба через площадь поверхности
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
См. также
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
![]()
Калькулятор объема куба
Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧊 Что считает калькулятор
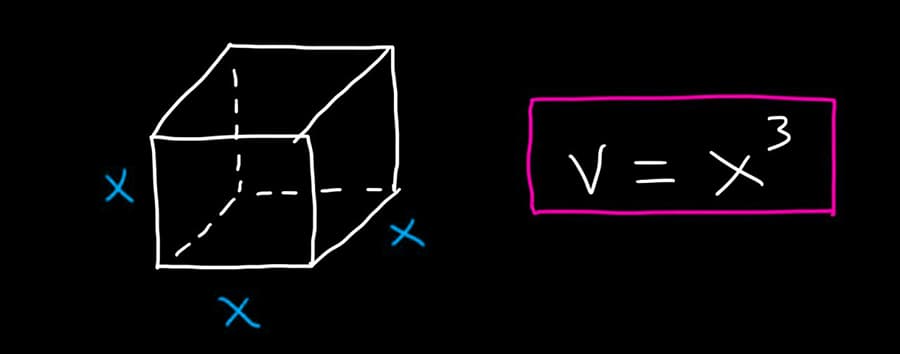
Калькулятор объема куба — это инструмент, который позволяет вычислять объем любого куба и выводить результат в разных единицах измерения.
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы.
Как использовать калькулятор
Укажите значение стороны куба, после этого калькулятор произведет расчёт и выдаст его в указанных единицах измерения. Кроме того, можно указать диагональ куба или диагональ любой его стороны.
Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора объема куба зависит от нескольких факторов:
- Корректность ввода данных. Если вводимые значения длины, ширины и высоты куба некорректны, то расчет объема будет неправильным. Поэтому, важно убедиться в правильности вводимых значений перед выполнением расчета.
- Точность математических операций. Расчет объема куба требует выполнения математических операций, таких как умножение. Если калькулятор не выполняет математические операции точно, то результаты расчетов будут неточными.
- Точность округления. В некоторых случаях, результаты расчетов могут быть округлены. Если калькулятор округляет результаты до неправильного числа знаков, то результаты будут неточными.
- Алгоритм расчета. Различные калькуляторы могут использовать разные алгоритмы расчета. Если алгоритм расчета неправильный, то результаты могут быть неточными.
- Ошибки программирования. Если в программе калькулятора есть ошибки, то результаты расчетов могут быть неправильными. Поэтому, важно использовать калькуляторы, которые были разработаны и протестированы надежными разработчиками.
Где можно применить калькулятор
Калькулятор объема куба может быть использован во многих областях, где требуется расчет объема кубической формы. Некоторые из таких областей включают:
- 🧱 Строительство. Калькулятор объема куба может использоваться строителями при расчете объема кубических блоков, бетонных кубов, кирпичей и других материалов, используемых в строительстве.
- 🏭 Производство. Калькулятор объема куба может использоваться в производственных процессах для расчета объема материалов, таких как металл, пластик, стекло и другие, используемые в производстве кубических изделий.
- 📦 Логистика. Калькулятор объема куба может использоваться при планировании грузоперевозок, чтобы определить, сколько грузовых мест может вместить транспортное средство.
- 🎓 Образование. Калькулятор объема куба может использоваться учителями математики в школах и университетах для обучения геометрии и расчета объема кубических форм.
- 🎨 Интерьер и дизайн. Калькулятор объема куба может использоваться в дизайне интерьера для расчета объема кубических элементов, таких как шкафы, полки, столы и другие.
- 🛠️ Ремонт и обслуживание. Калькулятор объема куба может использоваться в ремонте и обслуживании, чтобы определить количество материалов, необходимых для замены кубических элементов, таких как плитка, обои и другие.
📐 Как посчитать объем куба
Объем куба можно вычислить самостоятельно, используя формулу
V = a³
где V – объем куба, a – длина ребра.
Для того, чтобы вычислить объем куба, нужно измерить длину одного из его ребер с помощью линейки или другого инструмента измерения длины. После этого возведите полученное значение в куб, используя калькулятор или ручной расчет.
Например, если длина ребра куба равна 5 см, то объем куба будет равен V = 5³ = 125 кубических сантиметров.
Важно помнить, что все единицы измерения должны быть одинаковыми – если длина ребра измеряется в сантиметрах, то и объем будет выражен в кубических сантиметрах.
🤔 Полезные советы
Несколько советов, которые могут помочь при вычислении объема куба:
- Определите длину одной из сторон куба. Обычно все стороны куба одинаковые, поэтому вы можете выбрать любую.
- Возведите длину стороны куба в квадрат. Это даст вам площадь одной грани куба.
- Умножьте площадь одной грани куба на 6. Это даст вам общую площадь поверхности куба.
- Определите длину любой из диагоналей куба. Вы можете использовать формулу теоремы Пифагора для нахождения длины диагонали, если известна длина стороны.
- Возвести длину диагонали куба в куб. Это даст вам объем куба.
- Если известна масса куба, можно использовать плотность материала для расчета его объема. Для этого нужно разделить массу на плотность.
- Убедитесь, что вы используете одни и те же единицы измерения при расчете. Например, если длина стороны куба измеряется в сантиметрах, то и объем должен быть выражен в кубических сантиметрах.
❓ Вопросы и ответы
Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.
Что такое объем куба и как его рассчитать?
Объем куба — это мера его вместимости, то есть объем пространства, которое он занимает. Он рассчитывается по формуле V = a³, где a – длина ребра куба.
Как найти длину ребра куба, если известен его объем?
Для этого нужно извлечь кубический корень из объема: a = V^(1/3). Это позволит определить длину ребра куба, зная его объем.
Что произойдет с объемом куба, если увеличить длину его ребра вдвое?
Объем куба увеличится в 8 раз. Это происходит потому, что объем куба пропорционален кубу его длины: V ~ a³. Если длина ребра увеличивается вдвое, то объем увеличивается в 222=8 раз.
Какие единицы измерения используются для объема куба?
Объем куба измеряется в кубических единицах длины, таких как кубические метры (м³), кубические сантиметры (см³), кубические дюймы (дюйм³) и т.д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
|
Как правильно рассчитать объем куба?
Чтобы рассчитать объём куба, надо длину его ребра (а у куба они все одинаковые) взять в куб. Например, длина ребра (Н) 2 см, объём будет рассчитываться так: V = Н х Н х Н, 2 х 2 х 2 = 8. То есть, объём куба с длиной ребра 2 см будет составлять 8 см кубических. автор вопроса выбрал этот ответ лучшим chela 10 лет назад Чтобы найти объем куба, нужно длину умножить на ширину и на высоту. Так как в кубе это все одинаково, достаточно иметь только один размер. Если эти размеры неизвестны, а известна любая диагональ любой грани, то можно найти объем куба за диагональю грани: V=(d*корень двух)все в кубе где d – длина диагонали грани
Проповедник 10 лет назад .чтобы правильно рассчитать объем квадратного куба, нужно сначала найти длину одной из его сторон. Поскольку стороны его все равны, а он квадратный, то объем куба будет рассчитываться по формуле V=a^3, где V- это объем, а- это длина стороны
Андрей0817 9 лет назад Объём вычисляется путём умножения длины, высоты и ширины. Длина – 5 см, ширина – 5 см, высота 5 см = 5*5*5=125 см.
.Здесь легко вычислить объём. А вот если вам привезли машину дров и говорят, что там 7 кубов, то это легко проверить самому. Также , надо умножить длину и ширину кузова машины и эту сумму умножить на высоту уложенных дров. Потом эту сумму ещё и умножить на коэффициент плотности. Он может быть – 0,8 – если дрова сложены плотно друг к другу, а если не плотно, то от 0,7 и до 0,5. Чем плотнее лежат дрова, тем больше коэффициент.
Nikolai Sosiura 9 лет назад Для того, чтобы найти объём куба, нам понадобится произвести умножение некоторых величин. Сначала надо узнать площадь основания куба. Нам придётся умножить высоту на ширину (hxW = A), где: А- площадь, h- высота, W- ширина. Далее множим высоту на уже известную нам площадь основания куба (LxA = V), где V- объём, L- длинна, A- площадь.
Lilka-g 9 лет назад Если мы умножим Длину куба на ширину куба, а затем эту цифру умножим на высоту куба, то получим объем куба. Например если у куба 3 мм ширина, 2 мм длина и 5 мм высота будет так. 3*2=6*5=30. В итоге в этом случаи объем куба будет 30 миллиметров.
Edvard 9 лет назад Это вопрос мне задавали, если не ошибаюсь, еще в шестом классе. Найти объем куба очень легко. Нужно только умножить длину, ширину и высоту куба. Другими словами- возвести одну грань куба в третью степень. Как я уже говорил, нчего сложного.
Roxrite 9 лет назад Если неизвестна длина стороны ребра куба, то необходимо её просто измерить. Допустим, она равна 3 см. Далее возводим в куб (третью степень) это число. Получается 3 в кубе – это 27 см3. Ответ: 27 кубических сантиметров.
Solnce lychik 9 лет назад Объем куба пишется буквой V. А формула достаточно проста: где a это длина грани куба d это диагональ его квадратной грани. у куба двенадцать граней и все они равны. Вот такими формулами можно вычеслить объем куба. Знаете ответ? |
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
Формула объёма куба через ребро
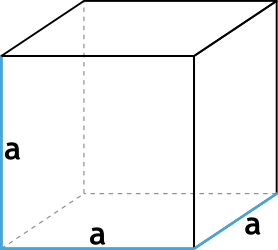
Формула объёма куба через диагональ грани
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
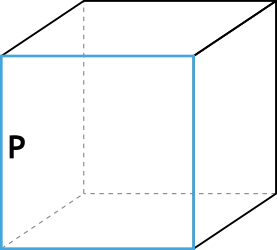
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
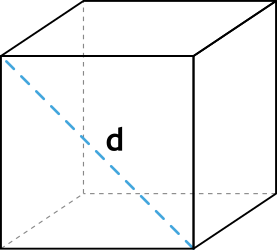
Формула объёма куба через диагональ куба
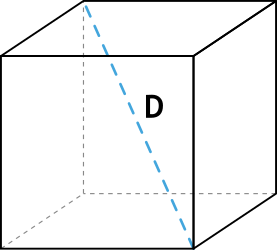
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.


