Как найти кинетическую энергию пули

Убойная
и пробивная способность снаряда
характеризуется его кинетической
энергией (энергией движения), называемой
также живой силой, которая сообщается
снаряду пороховыми газами в момент
вылета из канала ствола.

Кинетическая
энергия движущегося тела вычисляется
по известной из

физики формуле:

Кинетическая
энергия снаряда является важной
характеристикой, показателем его
пробивной способности. Установлено,
например, что пуля стрелкового оружия
обладает достаточной убойной силой для
вывода из строя человека, если ее
кинетическая энергия не менее 8 кгм. Для
поражения же самолета, имеющего легкие
броневые покрытия, пуля крупнокалиберного
пулемета должна иметь энергию около
100—120 кгм. Результат ударного действия
снаряда (пули) зависит от его энергии
при встрече преградой.

От
чего зависит величина кинетической
энергии снаряда?

Пример.
Определить начальную энергию пули Б-32,
если ее вес 64 г и начальная скорость 945
м/с.

Решение.
Выразим вес пули в килограммах q=0,064
кг и, подставив данные в формулу, получим:

.

Как видим, 14,5-мм
пуля обладает очень большим запасом
работы и

поэтому
обладает высокой пробивной способностью.

С
потерей скорости снаряд резко теряет
запас энергии, так как кинетическая
энергия пропорциональна квадрату
скорости снаряда.

Для
определения энергии снаряда у цели надо
в приведенную формулу подставить
скорость снаряда у цели. Определим,
какой кинетической энергией будет
обладать пуля Б-32 у цели, если скорость
пули в этот момент будет 100 м/с.

.

Полученный
ответ можно было предугадать: скорость
пули у цели в 10 раз меньше начальной,
следовательно, энергия пули у цели
меньше начальной в 100 раз.

В
таблицах стрельбы из стрелкового оружия
даются величины энергии пули у цели на
различные дальности стрельбы. Например,
при стрельбе из ручного пулемета РПК
на дальность 500 м кинетическая энергия
пули у цели Ес=38
кгм на дальность 700 Ес=20
кгм и т. д.[11] .

Анализ
данных из таблиц стрельбы показывает,
что пули стрелкового оружия обладают
достаточной убойной силой на дальности
стрельбы до 1000 м пулей обр. 1943 г. и на
дальности до 3000 м пулями обр. 1908 г., и до
1350м пулей обр. 1974 г. [1, 4, 11].

Хорошие
баллистические качества пуль обеспечивают
и достаточную пробивную способность.
Так, 9-мм пистолетная пуля при стрельбе
из пистолета Стечкина пробивает сосновую
доску толщиной 2,5 см на расстоянии до
350 м; 7,62-мм пуля обр. 1943 г. пробивает
армейскую каску на расстоянии 650 м
(80—90% пробитий); 14,5-мм пуля пробивает
20-мм броню на расстоянии до 800 м (при угле
встречи около 90°) [5, 8, 10].

Особое
значение величина кинетической энергии
имеет для боеприпасов при стрельбе по
бронецелям. Большой запас кинетической
энергии бронебойных снарядов обеспечивает
высокую бронепробиваемость. Например,
пуля ПС для АК74 на дальности 700 метров
обладает кинетической энергией, равной
20 кгм, и пробивает стальной шлем
(каску)[11].

3.7 Явление отдачи

Рассматривая
явление выстрела как движение системы
пороховые газы – снаряд – оружие, мы
должны выяснить сущность явления отдачи
оружия.

Пороховые
газы, образующиеся во время выстрела,
давят во все стороны с одинаковой силой*.

Давление
на дно снаряда и на дно гильзы приводит
к поступательному движению снаряда и
ствола.

Движение
ствола и связанных с ним деталей в
сторону, противоположную движению
снаряда во время выстрела под действием
давления пороховых газов, называется
отдачей.

Скорость
отдачи. Из
механики известно, что если на два тела,
находящихся в покое, действует одинаковая
по величине сила, то скорость движения
этих тел обратно пропорциональна их
массам (весам):

Q:q=V₀
: V_отд.,

где:
Q
– вес оружия;
V_отд.
– скорость отдачи.

Отсюда
скорость отдачи равна:

*В
действительности давление на дно снаряда
и дно гильзы различно: давление на дно
гильзы несколько больше чем на дно
снаряда. Однако для наших расчетов этой
разницей можно пренебречь.

Но эта формула не учитывает влияния на
скорость отдачи последействия газов и
поэтому не дает величины наибольшей
(максимальной) скорости отдачи. Формула
наибольшей скорости отдачи может быть
решена следующим образом. Составим
уравнение количеств движения при
выстреле (количеством движения называется
произведение массы тела на его скорость).
Сумма количеств движения системы,
вызываемых действием лишь внутренних
сил, равна нулю:

-М·V_m+m₁·V₀+m₂u=О,

где
-М·V_m
— количество движения оружия назад
(взято со знаком минус); m₁·V₀
– количество
движения снаряда;
m₂·u
– количество движения порохового заряда;

u
– средняя скорость истечения газов.

Найдем
из составленного уравнения наибольшую
(максимальную) скорость отдачи, которая
обозначается V_m
, заменив предварительно массы через
вес, так как веса пропорциональны массам:

–Q·V_m+(q+0,5ω)·V₀+ω·u=0;
Q·V_m=q·V₀+ω·u;

,

где
ω
– вес заряда.

В
числителе правой части вынесем V₀
за скобку:

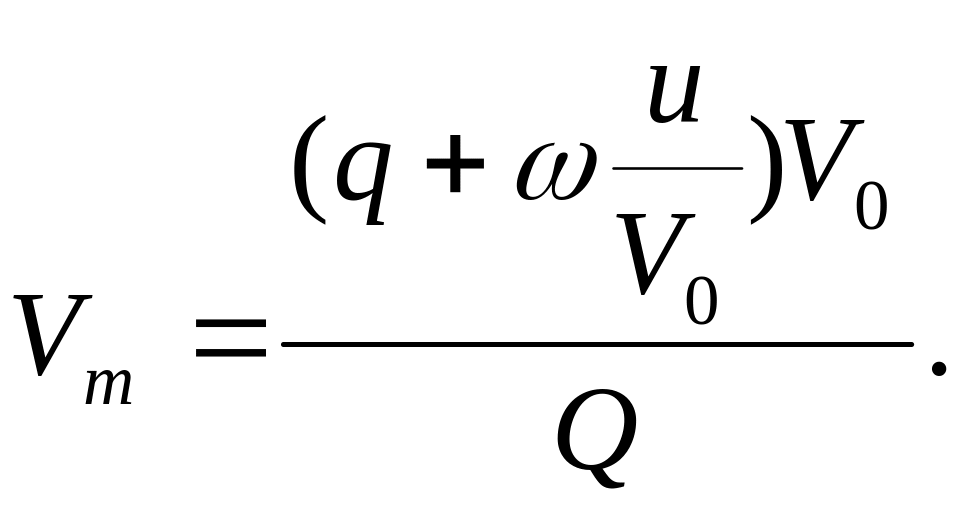
Среднюю
скорость истечения газов из канала
ствола «u»
для стрелкового оружия обычно принимают
равной 1275 м/с.

Отношение
u/V₀
называется коэффициентом
последействия газов
и обозначается через β.
Тогда для стрелкового оружия β=
1275/V₀.
Этот
коэффициент в среднем равен 1,6.

Для
начальных скоростей боеприпасов более
700 м/с значение коэффициента последействия
газов точнее следует определять по
формуле:

β=0,15+(1400:V₀).

С
учетом коэффициента β
формула
выражает наибольшую скорость отдачи
оружия и имеет вид:

Эту
формулу сравним с формулой, выражающей
скорость отдачи без учета веса заряда
и истечения газов:

Они
отличаются лишь тем, что в полной формуле
вместо сомножителя q
имеют скобку (q
+ βω),
причем (q
+ βω
) всегда
больше q.
Значит, скорость отдачи при решении
задач по полной формуле будет всегда
больше, чем скорость, найденная по
приближенной формуле.

Найдем
скорость отдачи ствола 30-мм автоматической
пушки 2А42, если её вес 115 кг, вес снаряда
0,4 кг, вес заряда 0,128кг и начальная
скорость снаряда 990 м/с.

;

;

β=0,15+(1400:990)≈1,4;
V_m=(0,4+1,4x0,128)990:115)≈4,97
м/с.

Это
скорость свободного не торможенного
отката. В действительности же, при
действии противооткатных устройств
орудия скорость отката в момент вылета
снаряда составляет 2,4 – 2,7 м/с.

Решим пример для
стрелкового оружия.

Определить
наибольшую скорость отдачи 7,62-мм
снайперской винтовки при стрельбе пулей
обр. 1908 г. Вес пули q=0,0096
кг; вес заряда ω=0,0031
кг; начальная скорость V₀
=830 м/с. Вес винтовки (заряженной) Q=4,4
кг.

Определим
коэффициент последействия: β=1275:830≈1.5.

П

одставим
данные в формулу:

Такая
скорость отдачи (2 – 3 м/с) воспринимается
стрелком совершенно безболезненно.

Подсчитаем
теперь скорость отдачи винтовки без
учета последействия газов:
V_отд.=(0,0096∙830):4,4=1,81м/с.

По
сравнению с действительной наибольшей
скоростью отдачи (2,85 м/с) результат
решения на 31% меньше. Следовательно, для
верной характеристики явления отдачи
надо рассчитать скорость отдачи с учетом
последействия газов.

Существует
ещё одна формула для определения скорости
отдачи с учетом веса заряда, но без учета
истечения газов в период последействия.

Напишем
вновь уравнение количеств движения
системы при выстреле и заменим массы
через веса:

–Q·V_m
+q·V₀
+ω·u₁=0‚
где u₁
—средняя скорость движения газов
порохового заряда внутри канала ствола.

Так
как скорость движения газов порохового
заряда изменяется от нуля в начале
явления выстрела до V₀
к моменту вылета пули (считают, что газы
к моменту вылета обладают такой же
скоростью, какой обладает пуля), то
средняя скорость движения газов может
быть принята как среднее арифметическое:
u₁=(0+V₀):2=V₀:2.

Подставим
полученное выражение в общее уравнение
количеств движения системы и найдем из
него

V_m=(q∙V₀+ω(V₀:2)):Q.

Вынесем
V₀
за скобку
и получим:

V_m=((q+ω:2)·V₀):Q.

Эта
формула показывает скорость отдачи без
учета реакции истечения газов в период
последействия и в таком виде приведена
в книге Н.М. Филатова «Краткие сведения
об основаниях стрельбы из винтовок и
пулеметов».

Энергия
отдачи. Вес
оружия обозначается через Q,
через V_m
максимальную
скорость отдачи, найденную выше. Тогда
для определения энергии (живой силы)
отдачи общая формула, выражающая величину
кинетической энергии, примет такой вид:

Зная,
что

, подставим значение V_m
в формулу Е_m.

Сократим
числитель и знаменатель на Q
и получим:

Анализируя
формулу, легко установить, что энергия
отдачи прямо пропорциональна весу
снаряда и заряда, и квадрату начальной
скорости сна-

ряда,
но обратно пропорциональна весу оружия.

Определим наибольшую
энергию отдачи в условиях предыдущего
примера, где нами была рассчитана
наибольшая скорость отдачи винтовки в
2,6 м/с:

(вес
винтовки =4,4 кгм);

E_m=(4,4·2,6²):(2·9,81)=1,5кгм.

Следует
заметить, что по выведенным формулам
энергия отдачи определяется только для
неавтоматического оружия. Приведенные
зависимости дают приблизительные
значения для определения энергии отдачи
и для автоматического оружия, действующего
по принципу отвода части газов.

Определение
энергии отдачи для автоматического
оружия, действующего по принципу
использования энергии отдачи, более
сложно, так как необходимо учитывать
целый ряд дополнительных факторов. В
этих образцах оружия часть энергии
отдачи используется полезно, а в
неавтоматическом оружии отдача оказывает
вредное действие.

Способы
уменьшения отдачи.
При стрельбе из автоматов, винтовок,

ручных
пулеметов отдача воспринимается плечом
стрелка. Поэтому должно быть вполне
понятным стремление по возможности
уменьшить энергию отдачи и установить
для каждого вида оружия пределы, выше
которых энергия отдачи не должна быть.

Из
приведенной выше формулы видно, что
уменьшить энергию отдачи можно следующими
путями:

–
уменьшить начальную скорость снаряда,
но это нецелесообразно, так как требуемая
начальная скорость задается при
проектировании оружия, уменьшение же
ее может привести к ухудшению баллистики
снаряда;

–
уменьшить вес заряда за счет применения
порохов, обладающих большей силой, но
так, чтобы это не приводило к уменьшению
начальной скорости;

–
увеличить вес оружия, но это также
нежелательно, ибо ухудшает маневренные
свойства оружия.

Следовательно,
при проектировании оружия необходимо
учесть все условия и выбрать такую
комбинацию величин, чтобы, не ухудшая
свойств оружия, иметь по возможности
наименьшую энергию отдачи. Установлено,
что для ручного оружия энергия отдачи
не должна превышать 2 кгм.

Рассмотренное
явление отдачи, в целом вредно сказывающееся
при стрельбе из стрелкового оружия,
используется в некоторых видах
автоматического оружия для приведения
в действие подвижных частей. К этим
образцам относится оружие, автоматика
которых работает по принципу использования
энергии отдачи. Из современных образцов
Российского стрелкового оружия к этому
классу относятся пистолеты ТТ, Макарова,
Глок и т.д.[15].

У
некоторых видов огнестрельного оружия
применяются для уменьшения отдачи
особые приспособления—дульные
тормоза[15].

Дульный
тормоз представляет собой специальное
приспособление на дульной части ствола,
действуя на которое, пороховые газы
после вылета снаряда уменьшают скорость
отдачи оружия.

Идея
использования дульного тормоза, как
поглотителя энергии отдачи, зародилась
еще в середине ХIХ в. В русской артиллерии
дульный тормоз впервые был применен в
1862 году для трехпудовой бомбовой пушки
обр. 1838 г. Устройство его было простое:
в стенке ствола вблизи дульного среза
было восемь окон, наклоненных к оси
ствола под углом 45˚.

В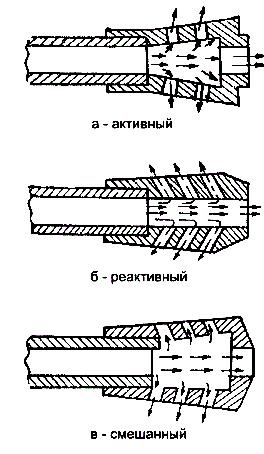

конце ХIХ
века был использован более эффективный
дульный тормоз, предложенный русским
артиллеристом, профессором Артиллерийской
академии Дурляховым. Эти тормозы были
применены для орудий с жестким лафетом.
Создание в начале ХХ века противооткатных
устройств позволило избежать применения
дульных тормозов. В настоящее время, в
связи с повышением могущества орудий,
для сохранения их максимальной подвижности
дульные тормозы вновь получили широкое
распространение.

Рис. 18. Типы дульных
тормозов.

Принцип
действия дульного тормоза легко
объясняется на примере устройства
ствола пулемета ДШК (рис. 18 а). Истекающие
вслед за пулей пороховые газы ударяются
в стенки дульного тормоза, уменьшая
этим действие отдачи. Такой тип тормоза
называется активным.
Кроме этого, существуют тормозы
реактивного
и комбинированного типа.
Их действие понятно из рис. 18 б, в.

В
заключение можно указать, что современные
конструкции дульных тормозов для
артиллерийских систем поглощают до 30%
и выше энергии отдачи. Для орудий малого
калибра и стреляющих с большой начальной
скоростью коэффициент действия дульных
тормозов может доходить до 50 – 70% и выше.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2022 года; проверки требуют 2 правки.

Дульная энергия — начальная кинетическая энергия пули, измеренная на дистанции не более 1 метра от дульного среза ствола.

Рассчитывается по формуле:

где  — масса пули, а  — начальная скорость пули.

С расстоянием скорость, а следовательно и кинетическая энергия пули уменьшается под воздействием сопротивления воздуха. Степень этого уменьшения определяется баллистическим коэффициентом пули.

В системе СИ масса берётся в килограммах, а скорость — в метрах в секунду, в результате получим энергию в джоулях.

В других системах единиц следует преобразовывать величины соответственно — например,

E — энергия (в фут-фунтах)

v — скорость (футов в секунду)

m — масса (в фунтах)

Обычные величины энергии для различных видов оружия[править | править код]

Оружие	Калибр	Кинетическая энергия
ft·lbf (фут-фунты)	Дж (Джоули)
Пневматическое оружие	.177	15	20
Малокалиберный патрон	.22LR	120	160
Пистолетный патрон	9×19 мм Парабеллум	390	520
Промежуточный патрон	5,56×45 мм	1350	1800
Промежуточный патрон	7,62×39 мм	1550	2100
Пуля Бреннеке	12	2000	2700

Характеристики патрона 7,62×54 мм R[править | править код]

Огонь по воздушным целям ведётся на расстояния до 500 м. Дульная энергия пули — 329 кГм (1 кГм = 9,80665 Дж. Длина ствола: 605 мм). Пуля сохраняет своё убойное действие на всей дальности полёта (до 3800 м).
Показатели суммарного рассеивания пуль со стальным сердечником при стрельбе очередями из приведённых к нормальному бою СГ-43 и СГМ^[1]:

Дальность стрельбы, м	Срединные отклонения по высоте, см	Срединные отклонения по ширине, см	Энергия пули, кГм
100	6	5	296
200	12	10	243
300	18	15	198
400	23	20	159
500	29	25	127
600	35	29	101
700	41	34	80
800	47	39	64
900	54	44	53
1000	62	49	46
1100	70	54	41
1200	80	59	37
1300	90	64	34
1400	102	69	31
1500	115	75	28
1600	130	82	25
1700	149	88	21
1800	179	94	17
1900	202	102	14
2000	234	109	10

Где срединное отклонение — половина ширины центральной полосы рассеивания, вмещающей 50 % всех попаданий^[2].

В законодательстве[править | править код]

Россия[править | править код]

Понятие встречается в Федеральном законе «Об оружии».

Оружие с дульной энергией до 3 Дж по законодательству РФ не требует регистрации и не считается собственно оружием^[3][4].

Примечания[править | править код]

См. также[править | править код]

• Начальная скорость пули
• Баллистика — наука о движении тел, брошенных в пространстве, основанная на математике и физике. Она занимается, главным образом, исследованием движения снарядов, выпущенных из огнестрельного оружия, ракетных снарядов и баллистических ракет.

Bullet Kinetic energy is the muzzle energy that is expelled when the bullet leaves the barrel of the firearm. The kinetic energy of the bullet is the energy that is transferred to the target when hit. It is based on the weight of the bullet. Higher the Kinetic energy, higher is the damage. Using this simple online Bullet energy calculator, you can calculate bullet kinetic energy based on the known values of the velocity and weight of the bullet.

Bullet Kinetic energy is the muzzle energy that is expelled when the bullet leaves the barrel of the firearm. The kinetic energy of the bullet is the energy that is transferred to the target when hit. It is based on the weight of the bullet. Higher the Kinetic energy, higher is the damage. Using this simple online Bullet energy calculator, you can calculate bullet kinetic energy based on the known values of the velocity and weight of the bullet.

Определите, какой кинетической энергией будет обладать пуля, вылетевшая из ружья. Скорость её при вылете из ружья равна 600 м/с, а масса — 7,5 г.