План темы
6.1. Понятие
о доверительном интервале
6.2. Алгоритм
нахождения полуширины доверительного
интервала
-
Понятие о доверительном
интервале
Если
бы имелись сведения по всей генеральной
совокупности, то модно было бы довольно
точно найти статистические характеристики,
например,
![]() .
.
Но, как правило, имеется выборка, в
которой порядка десятка точек. По
выборке рассчитывают выборочное среднее![]() .
.
Истинное
значение
![]() может быть как больше, так и меньше
может быть как больше, так и меньше
выборочного![]() ,
,
то есть точное значение![]() попадает в некоторый интервал, центром
попадает в некоторый интервал, центром
которого является выборочное значение![]() .
.
Если
задаться вероятностью
(например, 0,9; 0,99; 0,95) попадания
![]() в интервал, то чем больше будет задана
в интервал, то чем больше будет задана
вероятность, тем шире будет получаться
интервал. Если начать уменьшать,
то интервал будет сужаться.
Описанный
интервал называется доверительным
интервалом, а
– коэффициентом доверия. Чаще всего на
практике берут
![]() .
.
Это означает, что в 95% случаев точное
значение параметра попадает в интервал.
Доверительный
интервал –
это интервал, в который с заданной
вероятностью попадает истинное значение
неизвестного параметра.
Коэффициент
доверия –
это вероятность, с которой доверительный
интервал накроет неизвестный параметр.
-
Алгоритм нахождения полуширины доверительного интервала
По
генеральной совокупности для конкретного
x
можно было бы довольно точно найти
прогноз
![]() .
.
По выборке строится линейная регрессия![]() и за
и за![]() принимают
принимают![]() ,
,
снятое с прямой регрессии.
Доверительный
интервал, в который попадает неизвестное
![]() с некоторым коэффициентом доверия,
с некоторым коэффициентом доверия,
в случае линейной регрессии оказывается
симметричным относительно
![]() .
.
Поэтому достаточно найти полуширину
доверительного интервала.
При
нахождении
используется специально сконструированная
статистика (случайная величина),
распределенная по закону Стьюдента.
Распределение
Стьюдента
![]() возникает каждый раз, когда сравниваются
возникает каждый раз, когда сравниваются
два математических ожидания (два
средних). Распределение Стьюдента
симметрично относительно начала
координат. Число степеней свободы для
критерия Стьюдента![]() .
.
Полуширина
доверительного интервала в точке
прогноза
![]() вычисляется по формуле:
вычисляется по формуле: ,
,
где
![]() – среднеквадратичное отклонение
– среднеквадратичное отклонение
выборочных точек от линии регрессии![]() ,
,
здесь![]() ;
;
![]() –
–
критическая точка распределения
Стьюдента;
![]() –
–
объем выборки;
![]() –
–
точка из области прогнозов.
Прогнозируемый
доверительный интервал для любого x
из области прогнозов записывается:
![]() .
.
Совокупность
доверительных интервалов для всех х
из области прогнозов образует доверительную
область. Для линейной однофакторной
регрессии она симметрична относительно
линии регрессии. Наиболее узкое место
доверительной области в точке
![]() .
.
Прогноз
для произвольного х
дает интервал, в который с вероятностью
попадает неизвестное
![]() .
.
То есть прогноз при заданномх
составит от
![]() до
до![]() с надежностью
с надежностью![]() .
.
Это прогноз с учетом доверительного
интервала.
Тема 7. Нелинейная однофакторная модель
План темы
7.1. Линеаризация
нелинейных зависимостей
7.2. Алгоритм
построения нелинейных эконометрических
моделей
-
Линеаризация
нелинейных зависимостей
Многие экономические процессы не могут
быть адекватно описаны линейной
зависимостью. Примером таких экономических
процессов могут служить: жизненный
цикл товаров, процесс накопления
капитала, маркетинговые усилия фирм и
др.
Наиболее часто
используется пять нелинейных зависимостей,
которые предпочтительнее других
зависимостей тем, что их удается
линеаризовать (свести к линейным):
1.
Степенная зависимость:
![]() .
.
Для
линеаризации прологарифмируем это
уравнение:
![]() .
.
Обозначим![]() .
.
Получим линейную модель от новых
переменных:![]() .
.
Обратное преобразование:![]() .
.
Значит,![]() .
.
2.
Экспоненциальная зависимость:
![]() .
.
Чтобы
ее линеаризовать, прологарифмируем это
уравнение:
![]() .
.
Обозначим:![]() .
.
Получим:![]() .
.
Обратное преобразование:![]() .
.
Значит,![]() .
.
3.
Логарифмическая зависимость:
![]() .
.
Сделаем замену:![]() .
.
Получили:![]() .
.
4.
Обратная зависимость:
![]() .
.
Сделаем замену:![]() .
.
Получили:![]() .
.
5.
Логистическая кривая:
![]() .
.
Сделаем замену:![]() .
.
Получили:![]() .
.
Соседние файлы в папке 3 курс
- #
- #
- #
- #
- #
- #
- #
- #
Определение доверительного интервала косвенного измерения
Пусть искомая
величина y
является известной функцией величин
х1,х2,
…, xn,
каждую из которых находят в результате
прямых измерений:
(1.12)
Ставится задача:
зная доверительные интервалы для
величин, входящих в эту формулу, рассчитать
доверительный интервал для величины
y.
Для того, чтобы
найти среднее значение
результата косвенных измерений, следует
в формулу (1.12) подставить средние значения
величинх1, х2, …,
xn:
.
(1.13)
Полуширину
доверительного интервала Δу
находят по формуле:
(1.14)
где Δхi
– полуширина доверительного интервала
(абсолютная погрешность) величины х
i,,
а значения
частных производных
вычисляются при подстановке средних
значений величин…,.
Если
является степенной функцией вида:
(1.15)
где k,l,…,m
– целые или дробные числа, то формулу
(1.13) можно привести к виду:
(1.16)
Расчет погрешности при измерении плотности
В данной работе
плотность древесины, из которой изготовлен
брусок в форме прямоугольного
параллелепипеда, измеряется косвенно,
то есть вычисляется по формуле, следующей
из формул (1.3) и (1.4):
. (1.17)
Вначале производятся
прямые измерения массы, длины, ширины
и высоты бруска и рассчитываются
соответствующие доверительные интервалы
при одинаковых значениях доверительной
вероятности:
.
Остается рассчитать
доверительный интервал, в котором с
заданной доверительной вероятностью
лежит истинное значение плотности
.
Среднее значение
плотности, как следует из формулы (1.13),
таково
.
(1.18)
Абсолютная
погрешность плотности, как следует из
формул (1.14) и (1.17),
(1.19)
где
;
;
аналогично
Используя эти
выражения для частных производных в
формуле (1.19), и подставляя в них средние
значения величин, получаем:
,
(1.20)
где
– относительные погрешности прямых
измерений массы и линейных размеров
(рассчитанные по формулам (1.2)).
Единица измерения
плотности в СИ 1 кг/м
3.
Широко используются также производные
единицы 1 г/см3,
1 т/м3
и другие.
Порядок выполнения работы
1. Ознакомиться с
устройством штангенциркуля и способом
измерения линейных размеров с его
помощью (Приложение). Определить и
Определить и
записать приборную погрешность для
штангенциркуля – половину цены деления
нониуса.
2. Измерить каждый
из линейных размеров тела в пяти точках
образца, данные занести в таблицу,
образец которой (таблица 1.2) дан для
измерений длины a.
Таблицы для b
и c
аналогичны.
Таблица 1.2
– Результаты
измерения длины
|
№ |
а i, |
, |
Δаi, |
(Δаi)2, |
Δа, |
δa |
|
1. |
||||||
|
… |
||||||
|
5. |
3. С помощью
преподавателя выполнить однократное
взвешивание тела на технических весах.
Определить приборную погрешность весов
Δ
m,
равную половине массы наименьшего
разновеса в комплекте разновесов.
Результат взвешивания записать в виде
г.
4. Измерения линейных
размеров тела являются прямыми, поэтому
для их обработки применить алгоритм,
описанный в пункте «Порядок обработки
результатов многократных прямых
измерений» теоретического введения.
Доверительную вероятность
принять равной 0,95. Результаты представить
в виде:мм,мм,мм.
5. По формуле (1.18)
рассчитать среднее значение плотности
. Так
Так
как измерение плотности является
косвенным, то для расчета погрешности
измерения плотности, то есть полуширины
доверительного интерваланужно использовать формулу (1.20).
6. Результат записать
в виде
г/см3
, а также выразить его в единицах СИ.
Определить, из какой древесины изготовлено
тело, используя таблицу 1.3.
Таблица 1.3 –
Плотность различных пород дерева
|
Древесная порода |
, |
Древесная |
, |
|
Бакаут(«железное |
1100-1400 |
Тополь |
480 |
|
Дуб |
760 |
Осина |
465 |
|
Клен |
750 |
Ель |
450 |
|
Ясень |
750 |
Липа |
450 |
|
Береза |
650 |
Бамбук |
400 |
|
Сосна |
520 |
Бальза |
100-120 |
Погрешность и доверительный интервал: в чем разница?
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84
5.4.5 — Расчет размера выборки
Расчет размера выборки для среднего доверительного интервала генеральной совокупности
Раздел
Напомним, что ((1-alpha))100% доверительный интервал для (mu) равен (bar{x}pm t_{alpha/2}dfrac{s}{ sqrt{n}}), где множитель (t) имеет t-распределение с (df = n — 1). Таким образом, погрешность E равна:
(E=t_{alpha/2}dfrac{s}{sqrt{n}}) 92) Затем округлить до следующего целого числа.
Пример 5-8: Весенние каникулы
Раздел
Маркетинговая исследовательская фирма хочет оценить среднюю сумму, которую студент тратит во время весенних каникул. 2). Мы знаем, что (z_{alpha/2}=1,645) (для 92=31,99)
2). Мы знаем, что (z_{alpha/2}=1,645) (для 92=31,99)
Если мы используем (n = 32), результат будет таким же. Таким образом, более точным ответом на пример будет выборка из 32 учащихся.
S.2 Доверительные интервалы | СТАТ ОНЛАЙН
Давайте рассмотрим основную концепцию доверительного интервала.
Предположим, мы хотим оценить фактическое среднее значение генеральной совокупности (mu). Как вы знаете, мы можем получить только (bar{x}), среднее значение выборки, случайно выбранной из интересующей совокупности. Мы можем использовать (bar{x}) для поиска диапазона значений:
[text{Нижнее значение} < text{среднее значение};; mu < text{Верхнее значение}]
, в котором мы можем быть уверены, содержится среднее значение генеральной совокупности (mu). Диапазон значений называется « доверительный интервал ».
Должно ли использование сотового телефона в руке во время вождения быть незаконным?
Раздел
Нет никаких сомнений в том, что на протяжении многих лет вы видели многочисленные доверительные интервалы для долей населения, о которых сообщалось в газетах.
Например, в газетном сообщении (опрос ABC News, 16-20 мая 2001 г.) был вопрос о том, считают ли взрослые США использование портативного мобильного телефона за рулем незаконным. Из 1027 взрослых американцев, случайно выбранных для участия в опросе, 69% считали, что это должно быть незаконным. Репортер заявил, что «погрешность » опроса составила 3%. Следовательно, доверительный интервал для (неизвестной) доли населения p составляет 69% ± 3%. То есть мы можем быть уверены, что от 66% до 72% всех взрослых американцев считают, что использование мобильного телефона во время вождения автомобиля должно быть незаконным.
Общая форма (наиболее) доверительных интервалов
Раздел
Предыдущий пример иллюстрирует общий вид большинства доверительных интервалов, а именно:
$text{Выборочная оценка} pm text{погрешность}$
Нижний предел получается по формуле:
$text{ нижний предел L интервала} = text{оценка} — text{погрешность}$
Верхний предел получается:
$text{верхний предел U интервала} = text{ оценка} + text{погрешность}$
Как только мы получили интервал, мы можем утверждать, что мы действительно уверены, что значение параметра совокупности находится где-то между значением L и значением U .
До сих пор мы обсуждали расчет и интерпретацию доверительных интервалов в общих чертах. Чтобы быть более конкретным в отношении их использования, давайте рассмотрим конкретный интервал, а именно « t — интервал для среднего значения генеральной совокупности µ ».
(1-α)100%
t -интервал для среднего значения совокупности (mu)
Если нас интересует оценка среднего значения совокупности (mu), весьма вероятно, что мы используйте t -интервал для среднего значения совокупности (mu).
- t -Интервал для среднего значения совокупности
- Формула доверительного интервала для слов:
$text{Выборочное среднее} pm (text{t-множитель} times text{стандартная ошибка})$
- , и вы, возможно, помните, что формула для доверительного интервала в записи:
- $bar{x}pm t_{alpha/2, n-1}left(dfrac{s}{sqrt{n}}right)$
Обратите внимание, что:
- « t -множитель «, который мы обозначаем как (t_{alpha/2, n-1}), зависит от размера выборки через n — 1 (называется « степеней свободы «) и уровень достоверности ((1-alpha)times100%) через (frac{alpha}{2}).
- «стандартная ошибка », которая равна (frac{s}{sqrt{n}}), количественно определяет, насколько значение выборки (bar{x}) варьируется от выборки к выборке.
 То есть стандартная ошибка — это просто другое название предполагаемого стандартного отклонения всех возможных выборочных средних.
То есть стандартная ошибка — это просто другое название предполагаемого стандартного отклонения всех возможных выборочных средних. - количество справа от знака ±, т. е. , « t — множитель × стандартная ошибка «, — это просто более конкретная форма погрешности. То есть предел погрешности оценки среднего значения генеральной совокупности µ вычисляется путем умножения множителя t на стандартную ошибку выборочного среднего.
- формула подходит только в том случае, если выполняется определенное допущение, а именно, что данные нормально распределены.
Очевидно, что выборочное среднее (bar{x}) , выборочное стандартное отклонение s и размер выборки n легко получить из выборочных данных. Теперь нам просто нужно просмотреть, как получить значение множителя t , и все будет готово.
Как определяется множитель t?
Как показано на следующем графике, мы поместили доверительный уровень $1-alpha$ в центр распределения t . Затем, поскольку вся вероятность, представленная кривой, должна равняться 1, вероятность α должна быть поровну разделена между двумя «хвостами» распределения. То есть вероятность левого хвоста равна $frac{alpha}{2}$, а вероятность правого хвоста равна $frac{alpha}{2}$. Если мы сложим вероятности различных частей $(frac{alpha}{2} + 1-alpha + frac{alpha}{2})$, мы получим 1. t -множитель, обозначаемый (t_{alpha/2}), представляет собой t -значение такое, что вероятность «справа от него» равна $frac{alpha}{2}$:
Затем, поскольку вся вероятность, представленная кривой, должна равняться 1, вероятность α должна быть поровну разделена между двумя «хвостами» распределения. То есть вероятность левого хвоста равна $frac{alpha}{2}$, а вероятность правого хвоста равна $frac{alpha}{2}$. Если мы сложим вероятности различных частей $(frac{alpha}{2} + 1-alpha + frac{alpha}{2})$, мы получим 1. t -множитель, обозначаемый (t_{alpha/2}), представляет собой t -значение такое, что вероятность «справа от него» равна $frac{alpha}{2}$:
Неудивительно, что мы хотим быть максимально уверенными, когда оцениваем параметр генеральной совокупности. Вот почему уровни доверия обычно очень высоки. Наиболее распространенными уровнями достоверности являются 90%, 95% и 99%. Следующая таблица содержит сводку значений (frac{alpha}{2}), соответствующих этим общим уровням достоверности. (Обратите внимание, что « коэффициент достоверности «это просто уровень достоверности, представленный в виде доли, а не в процентах. )
)
| Коэффициент доверия $(1-alpha)$ | Уровень достоверности $(1-alpha) times 100$ | $(1-dfrac{alpha}{2})$ | $dfrac{alpha}{2}$ |
|---|---|---|---|
| 0,90 | 90% | 0,95 | 0,05 |
| 0,95 | 95% | 0,975 | 0,025 |
| 0,99 | 99% | 0,995 | 0,005 |
Хорошая новость заключается в том, что статистическое программное обеспечение, такое как Minitab, рассчитает для нас большинство доверительных интервалов.
Давайте возьмем в качестве примера исследователей, которые интересуются средней частотой сердечных сокращений студентов мужского пола. Предположим, что для исследования была выбрана случайная выборка из 130 студентов мужского пола.
Ниже приведены выходные данные Minitab для одновыборочного t -интервального вывода с использованием этих данных.
Одновыборочный T: ЧСС
Описательная статистика
| N | Среднее значение | СтДев | SE Среднее значение | 95% ДИ для $mu$ |
|---|---|---|---|---|
| 130 | 73,762 | 7.062 | 0,619 | (72.536, 74.987) |
$mu$: среднее значение ЧСС
В этом примере исследователей интересовала оценка (mu), частоты сердечных сокращений. Выходные данные показывают, что среднее значение для выборки из n = 130 учащихся мужского пола равно 73,762. Стандартное отклонение выборки (StDev) составляет 7,062, а расчетная стандартная ошибка среднего значения (SE Mean) составляет 0,619. 95% доверительный интервал для среднего $mu$ населения составляет (72,536, 74,987). Мы можем быть на 95% уверены, что средняя частота сердечных сокращений всех студентов мужского пола составляет от 72,536 до 74,9. 87 ударов в минуту.
87 ударов в минуту.
Факторы, влияющие на ширину t-интервала для среднего $mu$
Раздел
Подумайте о ширине интервала в предыдущем примере. В целом, как вы думаете, нам нужны узкие доверительные интервалы или широкие доверительные интервалы? Если вы не уверены, рассмотрите следующие два интервала:
- Мы на 95% уверены, что средний средний балл всех студентов колледжа находится между 1,0 и 4,0.
- Мы на 95% уверены, что средний средний балл всех студентов колледжей составляет от 2,7 до 2,9.
Какой из этих двух интервалов более информативен? Конечно, более узкий дает нам лучшее представление о величине истинного неизвестного среднего среднего балла. В целом, чем уже доверительный интервал, тем больше информации мы имеем о значении параметра совокупности. Поэтому мы хотим, чтобы все наши доверительные интервалы были как можно более узкими. Итак, давайте исследуем, какие факторы влияют на ширину t -интервал для среднего (mu).
Итак, давайте исследуем, какие факторы влияют на ширину t -интервал для среднего (mu).
Конечно, чтобы найти ширину доверительного интервала, мы просто берем разницу в двух пределах:
Ширина = Верхний предел — Нижний предел
Какие факторы влияют на ширину доверительного интервала? Мы можем исследовать этот вопрос, используя формулу для доверительного интервала и наблюдая, что произойдет, если допустить изменение одного из элементов формулы.
[bar{x}pm t_{alpha/2, n-1}left(dfrac{s}{sqrt{n}}right)]
Какова ширина t -интервала для среднего? Если вычесть нижний предел из верхнего предела, вы получите:
[text{Ширина}=2 times t_{alpha/2, n-1}left(dfrac{s}{sqrt{ n}}right)]
Теперь давайте исследуем факторы, влияющие на длину этого интервала. Убедитесь, что каждое из следующих утверждений верно:
- По мере увеличения среднего значения выборки длина остается неизменной.
 То есть выборочное среднее не влияет на ширину интервала.
То есть выборочное среднее не влияет на ширину интервала. - По мере уменьшения стандартного отклонения выборки с ширина интервала уменьшается. Поскольку s является оценкой того, насколько данные изменяются естественным образом, у нас мало контроля над s , кроме как убедиться, что мы делаем наши измерения как можно тщательнее.
- По мере уменьшения доверительного уровня множитель t уменьшается, и, следовательно, ширина интервала уменьшается. На практике мы не хотели бы устанавливать уровень уверенности ниже 9.0%.
- По мере увеличения размера выборки ширина интервала уменьшается. Это фактор, который мы можем изменить с наибольшей гибкостью, единственным ограничением являются наши временные и финансовые ограничения.
При закрытии
В нашем обзоре доверительных интервалов мы сосредоточились только на одном доверительном интервале. Важно понимать, что темы, обсуждаемые здесь — общая форма интервалов, определение множителей t и факторы, влияющие на ширину интервала, — обычно распространяются на все доверительные интервалы, с которыми мы столкнемся в этом курсе.
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
![]()
Тогда случайная величина
![]()
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
![]()
где
![]()
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
![]()
и
![]()
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
![]()
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
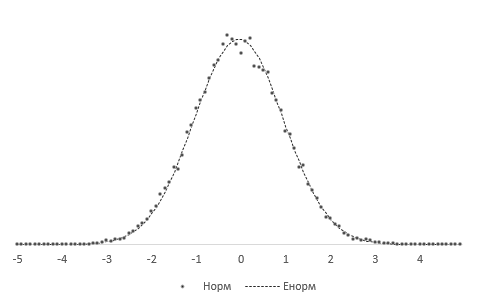
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
![]()
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
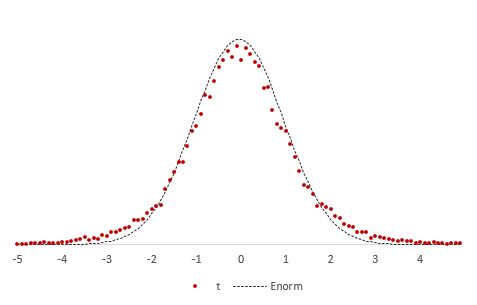
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
![]()
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
![]()
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
![]()
на σX̅. Получим
![]()
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
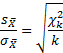
Тогда исходное выражение примет вид
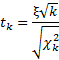
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
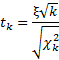
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
![]()
есть частный случай стьюдентова отношения
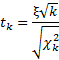
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
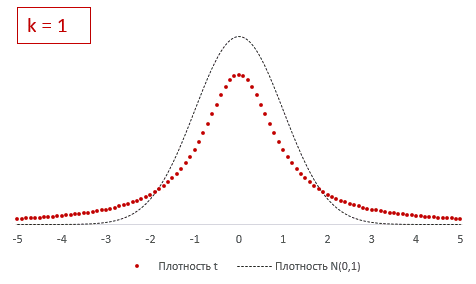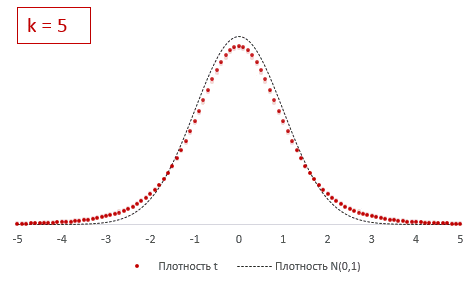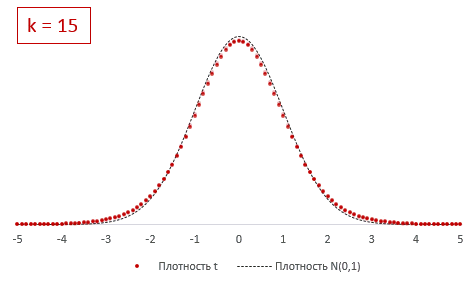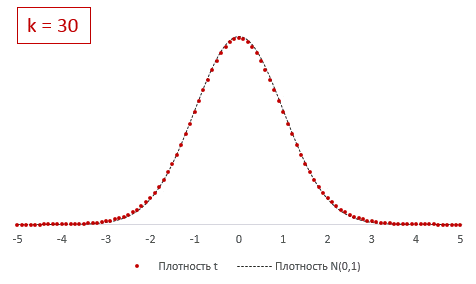
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
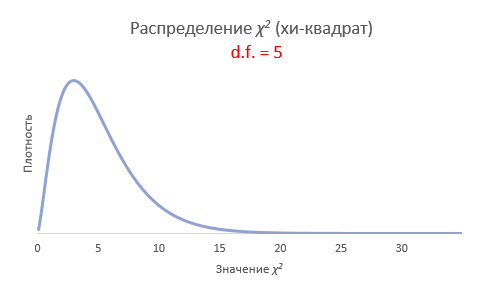
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
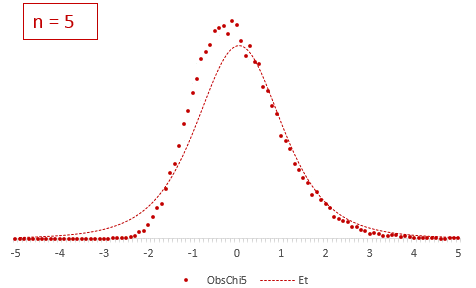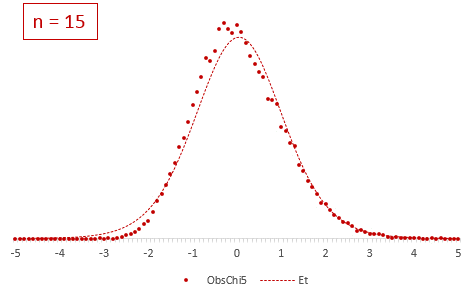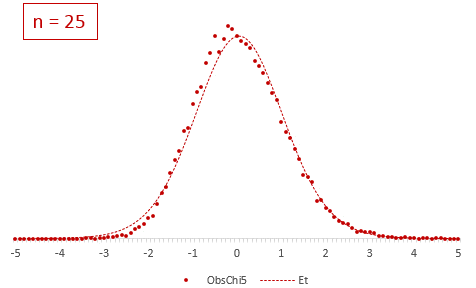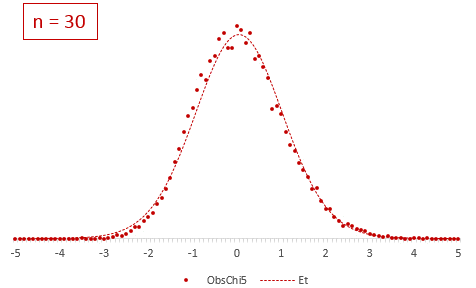
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
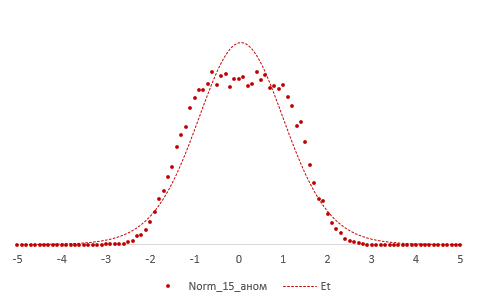
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
![]()
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
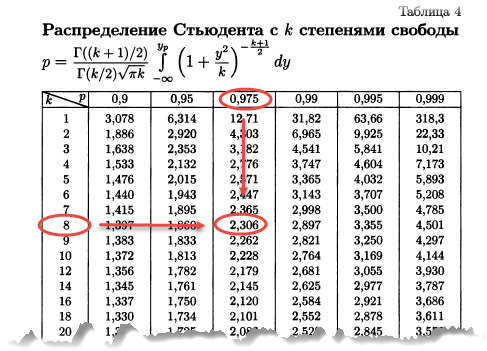
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
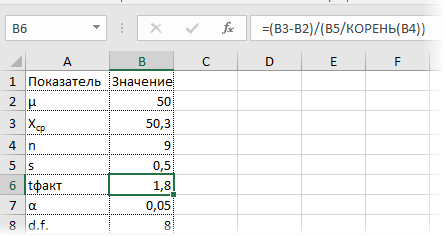
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
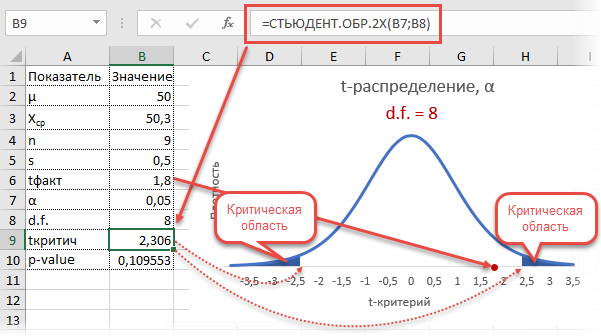
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
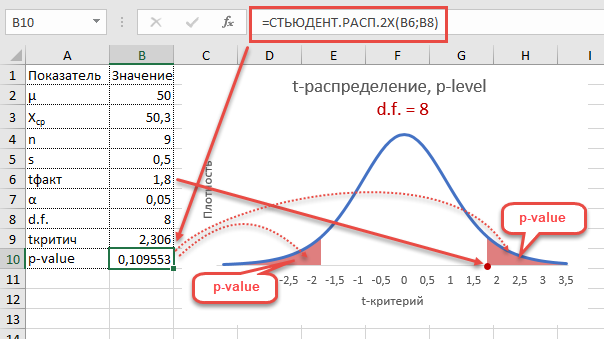
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
![]()
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
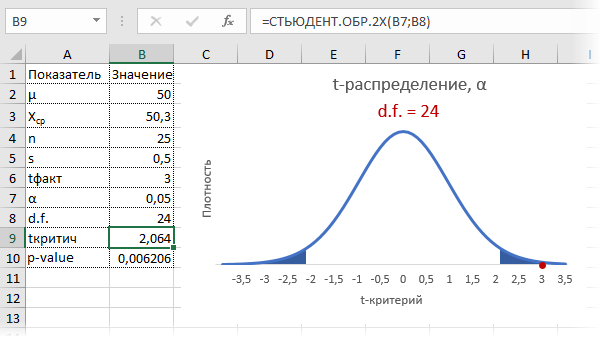
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
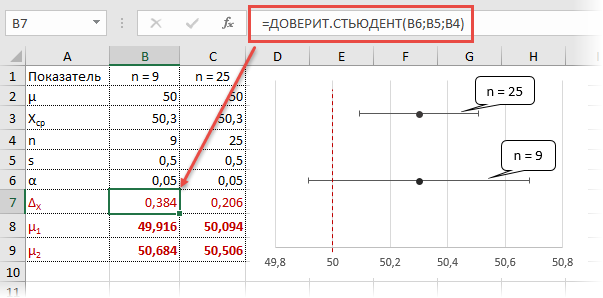
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:

