Как найти окружную силу зубчатого колеса

Усилия в зубчатых цилиндрических передачах

При передаче крутящих моментов в
прямозубой передаче между зубьями
шестерни и колеса возникают силы
взаимодействия. При этом полное давление
на зуб
принято раскладывать на две взаимно
перпендикулярные составляющие: окружное
усилие,
направленное по касательной к основной
окружности, и радиальное усилие,
которое направлено перпендикулярно к
оси вращения (рис.1.15):;(1.47);(1.48)

.
(1.49)

Для определения направления усилий
следует учитывать следующее правило:
окружное усилие и полное (нормальное)
давление на зуб ведомого колеса всегда
совпадают с направлением окружной
скорости; окружное усилие и полное
давление на зуб ведущего колеса (шестерни)
всегда направлено в сторону, противоположную
окружной скорости шестерни; радиальные
усилия направлены к центрам вращения
колес.

В косозубых колесах полное усилие
на зуб принято раскладывать на три
взаимно перпендикулярные составляющие.
Первая составляющая – окружное усилие,
– направленная по касательной к начальной
окружности; вторая – радиальное усилие─ направлена к центру вращения колеса
и третья составляющая – осевое усилие─ направлена параллельно оси вращения
(рис.1.16). Направления
окружного и радиального усилий
определяются как в прямозубых колесах.
Направление осевого усилия зависит от
направления вращения колеса и направления
винтовой линии зуба (левое или правое).
Окружное усилие, как и в любом виде
передач, определяем по формуле

.

Радиальное усилие определяем, используя
значение окружного усилия

. (1.50)

Осевое усилие . (1.51)

Определение величин, входящих
в формулы для расчета зубч. зацеплений
К_Н
и K_F.

Это коэфф. влияния неравномерности
распределения нагрузки на контактную,
изгибную прочность.

K_H
= K_Hα
K_Hβ
K_HV

K_Hα
– коэфф. неравномерности распределения
нагрузки между зубьями зависит от
погрешности окружного шага и
прирабатываемости материала. При НВ>
350 приработка более интенсивна.

K_Hβ– коэфф., учитывающий неравномерности
распределения нагрузки по длине зуба.

K_HV– динамический коэфф., зависит от
окружной скорости и степени точности
зацепления.

Допускаемые напряжения

σ_HPi
= σ_{H lim i} ∙K_HL
i / S_H
I ; σ_FPi
= σ_{F lim i} ∙K_FL
i ∙
K_{FC i} /
S_{F I}
.

Прямозубые σ_HP
=
σ_{HPi min}
; Косозубые
σ_HP =
0,45 (σ_HP1
+ σ_HP2).

Окружной и нормальный модули в косозубой передаче

p_t
–окружной шаг;p_n–нормальный шаг.p_t=p_n/cosβ

m_n=p_n/π – нормальный модуль (стандартный).

m_t=m_n/cosβ– окружной
модуль.

d = m_n∙z
/ cosβ –диаметр
делительной окружности.

Расчеты на прочность цилиндрических косозубых и шевронных передач. Эквивалентное прямозубое колесо

Прочность зуба определяют
его размеры и форма в нормальном сечении.
Форму косого зуба в этом сечении принято
определять через параметры эквивалентного
прямозубого колеса. Профиль зуба
эквивалентного колеса соответствует
профилю зуба косозубого колеса в его
нормальном сечении.

Радиус кривизны эллипса в
точке k
: .

Полуоси эллипса:

;;

Найдем диаметр делительной окружности
эквивалентного колеса

.

Итак, диаметры делительных
окружностей эквивалентных колес равны

;.

Межосевое расстояние a_wv
эквивалентного зацепления, ширина
эквивалентного колеса b_wv
и передаточное число u_v

;;u_v=
u
,

где b_w
– ширина косозубого колеса.

Найдем число зубьев, которое
может разместиться на делительной
окружности эквивалентного колеса

Поскольку диаметр делительной
окружности косозубого колеса равен
,

а диаметр делительной
окружности эквивалентного
колеса –

,

то приведенное
число зубьев эквивалентного колеса
равно

.

Минимальное число зубьев
цилиндрической косозубой передачи

,
откуда

.

Или
.

Силы в цилиндрических
косозубых передачах

Окружная сила:
F_t
= 2000T₁
/d₁.

Осевая сила:
F_а
= F_t
tg
β .

F’_n
= F_t
/ sin
β.

Радиальная сила
направлена к оси вращения соответствующего
зубчатого колеса
F_r
= F’_n
∙tg
α_w
= F_t
∙tg
α_w
/ sin
β.

Полная нагрузка
F_n=
F’_n
/cos
α_w=
F_t
/ (sinβ
∙ cos
α_w).

F_n=
2000∙T₁
∙K_H
/[d₁
∙sinβ
∙ cos
α_w].

Основные предпосылки при
выводе формул расчета косозубой передачи
на контактную прочность

1. Используем формулы для прямозубого
   колеса

для проверочного расчета

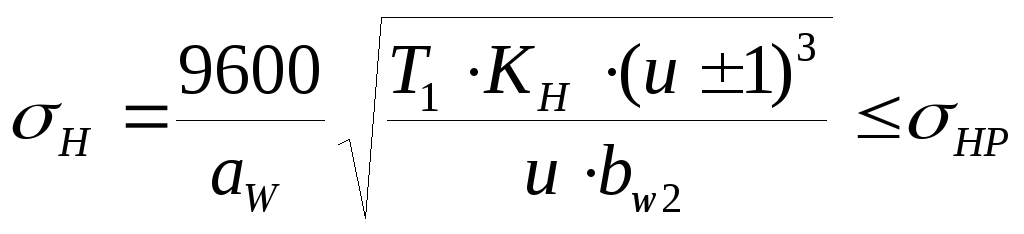. (1)

для
проектного расчета

.
(1,а)

1. Подставим в в (1) и (1,а) значения для
   эквивалентного зацепления

Т_1v
=0,5∙F_n∙d_v1/1000=
[2000∙T₁
∙K_H
∙1,12
/(d₁
∙sinβ
∙ cosα_w)]
∙0,5d₁/1000cos²β.

Т_1v=
T₁
∙K_H
∙1,12
/(sinβ
∙ cosα_w∙cos²β)].

b_wv=
b_w
∙
ε_кос
/cos
β

u_v=
u.

a_wv
= a_wv
/ cos²β.

Принимая β =12^о,
ε =2, α_w=20^о,
получим:

для проектного расчета

для проверочного расчета

.

Для изгибной прочности
косого зуба
поступают аналогично:

;

Здесь Y_F1
– коэффициент формы зуба. Y_F1
определяется для приведенного числа
зубьев эквивалентного колеса

Y_β
─ коэффициент, учитывающий наклон
зубьев (определен экспериментально).

Y_ε
─ коэффициент,
учитывающий перекрытие зубьев:

Y_ε
= 1/ε
.

ε ─
коэффициент перекрытия передачи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчет зубчатой передачи

Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).

Назначение. Зубчатые передачи относятся к механическим передачам зацепления с непосредственным контактом и применяются для изменения скорости или направления вращения ведомого звена с соответствующим изменением крутящего момента, получения точных перемещений, при необходимости точного соответствия скоростей и положений ведущего и ведомого звеньев в произвольный момент времени. Зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой. Вращение ведущего зубчатого колеса преобразуется во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее – колесом. Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными, пересекающимися и перекрещивающимися осями.

а	б	в	г
д	е	ж	з
и	к	л	м

Рис. 81. Виды зубчатых передач: а – внешнего зацепления прямозубая, б – внешнего зацепления косозубая, в – внутреннего зацепления прямозубая, г – внешнего зацепления реечная, д – внешнего зацепления шевронная, е – коническая прямозубая, ж – коническая косозубая, з – коническая круговая, и – коническая круговая – гипоидная, к – внешнего зацепления винтовая, л – передача с круговыми зубьями, м – планетарная.

Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.

Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.

Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают 10, а для закрытой 25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать 0,99.

Геометрический расчет. Передаточное отношение передачи

, (14.1)

где – число зубьев шестерни и колеса соответственно.

Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:

1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.

2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.

При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.

Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:

, (14.2)

где и – начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус – к передаче с внутренним зацеплением.

Стандартизированы номинальные значения межосевых расстояний aw, мм:

1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800

2-й ряд – – 71; 98; 112; 140; 180; 225; 280; 355; 450; 560; 710; 900.

Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:

. (14.3)

Делительные диаметры для зубчатых колес прямозубой передачи

d = zm, (14.4)

для косозубой и шевронной

. (14.5)

где т – модуль зацепления основная характеристика размеров зубчатых и червячных колес. Для обеспечения взаимозаменяемости и унификации инструмента для изготовления модули цилиндрические и конические эвольвентных зубчатых колес стандартизованы: для цилиндрических колес – значения нормальных модулей, для конических – значения окружных делительных модулей в диапазоне 0,05..100мм.

1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;

2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.

Ширина венца цилиндрического зубчатого колеса определяется по одной из формул

, (14.6)

или

, (14.7)

где – коэффициент ширины зубчатого венца по межосевому расстоянию, а – коэффициент ширины зубчатого венца по диаметру шестерни.

Коэффициенты и связаны зависимостью:

. (14.8)

Значения коэффициентов ширины венца зубчатых колес по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.

Рис. 82. Обозначения  элементов зубчатого зацепления.

Для заданного числа зубьев и , коэффициентов смещения исходного контура и , угла наклона зубьев основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:

Параметр	Шестерня	Колесо
Делительный диаметр
Основной диаметр
Начальный диаметр
Диаметр вершин зубьев
Диаметр впадин зубьев
Межосевое расстояние
Делительный угол профиля в торцевом сечении
Коэффициент торцевого перекрытия
Рабочая ширина зубчатого венца
Коэффициент осевого перекрытия (при ширине венца )
Основной угол наклона

Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:

– шестерни ; (14.9)

– колеса ,

где – угловая скорость зубчатого колеса; п – частота вращения зубчатого колеса; – начальный диаметр цилиндрического зубчатого колеса.

Окружная сила цилиндрической зубчатой передачи Ft

, (14.10)

где – крутящий момент на шестерне.

Сила давления между зубьями в цилиндрической прямозубой передаче

. (14.11)

Составляющие этой силы: в цилиндрических прямозубых (рис. 83) и шевронных передачах – окружная сила , и радиальная сила , в конической прямозубой и цилиндрической косозубой передачах – окружная сила , радиальная сила , и осевая сила Fa.

Радиальная сила в цилиндрической передаче

, (14.12)

Осевая сила, действующая на колесо косозубой цилиндрической передачи

, (14.13)

Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности () размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.

Проектные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние

, (14.14)

где – коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430, – момент на зубчатом колесе передачи в , – коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84; – допускаемое контактное напряжение в МПа.

Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий  для расчета на контактную прочность.

Коэффициент ширины венца по межосевому расстоянию для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении = 0,315…0,4; для зубчатых колес из закаленных сталей = 0,25…0,315; при симметричном расположении зубчатых колес относительно опор = 0,4…0,5; для передвижных зубчатых колес коробок скоростей = 0,1…0,2. Принимаются стандартные значения .

Допускаемое контактное напряжение

, (14.15)

где – предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений (табл. 14.1); – коэффициент безопасности; ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Zv – коэффициент, учитывающий окружную скорость передачи; KHL – коэффициент долговечности. Коэффициент безопасности зубчатых колес с однородной структурой материала sH = 1,1; с поверхностным упрочением зубьев sH = 1,2. Коэффициент ZR = 0,9…1; ZR =1,0 при мкм, ZR =0,95 при мкм и ZR =0,9 при мкм. Коэффициент Zv = 1…1.16; чем меньше скорость передачи и тверже зубья, тем меньше Zv. При v << 5м/с Zv = 1. При приближенном расчете можно принимать .

Коэффициент долговечности KHL определяют в зависимости от отношения – базового числа циклов нагружения при котором определяется предел контактной выносливости и – эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. Базовое число циклов напряжений в зубьях принимают в зависимости от твердости НВ рабочей поверхности зубьев либо по формуле

. (14.16)

При эквивалентном числе циклов нагужения зубьев колес больше базового коэффициент долговечности KHL =1. В случае когда эквивалентное число циклов

нагружения зубьев меньше базового то

. (14.17)

Если при расчете колес из нормализованной или улучшенной стали , то принимают .

Таблица 14.1. Предел контактной выносливости при базовом числе циклов

Термическая обработка	Твердость поверхностей зубьев	, Па
Нормализация или улучшение
Объемная закалка
Поверхностная закалка
Цементация или нитроцементация
Азотирование

Эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой

, (14.18)

где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; – частота вращения рассчитываемого зубчатого колеса, ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.

При работе передачи с переменными нагрузками

, (14.19)

где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; – передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения .

Допускаемое контактное напряжение для зубьев прямозубых передач определяют раздельно для шестерни и колеса и в качестве расчетного принимают меньшее из них. При расчете зубьев косозубых передач, в которых зубья шестерни значительно превышают твердость зубьев колеса, расчетное контактное напряжение

, (14.20)

где и – допускаемые контактные напряжения зубьев шестерни и колеса, вычисляемые по формуле (14.15); – минимальное допускаемое напряжение из этих двух допускаемых напряжений.

Полученный по формуле (14.14) межосевое расстояние следует округлить до ближайшего большего стандартного значения. При проектировочном расчете числом зубьев шестерни задаются, а число зубьев колеса . Для зубчатых передач без смещения рекомендуется принимать зубьев для обеспечения отсутствия подрезание зубьев. Для уменьшения габаритных размеров тихоходных зубчатых передач допускается зубьев. В быстроходных передачах в целях уменьшения шума рекомендуется принимать зубьев.

Расчет зубьев на изгибную прочность. Предварительное значение модуля зубчатой передачи определяется из условия проектного расчета зубьев на изгиб.

, (14.21)

Рис. 85. Коэффициент формы зуба.

где – коэффициент для прямозубых передач =14, для косозубых и шевронных =11,2; – коэффициентом формы зуба, который определяется по рис.85; – коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, который определяется по рис.86; – момент на шестерне передачи в , – число зубьев шестерни; а – коэффициент ширины зубчатого венца по диаметру шестерни, который определяется по формуле (14.8), допускаемые напряжения при изгибе зубьев.

Для косых зубьев коэффициент YF определяют не по действительному числу зубьев z, а по эквивалентному по зависимости

. (14.22)

Допускаемое напряжение на изгиб для зубьев

, (14.23)

где – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений (табл.14.2); – коэффициент безопасности зубьев на изгиб; – коэффициент долговечности зубьев на изгиб; – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья; ; коэффициент безопасности =1,7…2,2 (большие значения для литых заготовок).

Рис. 86. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на изгибную прочность. Схемы расположения колес показаны на рис.84.

Таблица 14.2 Пределы выносливости материалов зубчатых колес на изгиб

Вид термообработки и марка стали	Твердость зубьев	, МПа
на поверхности	в сердцевине
Цементация легированных сталей:
содержание Ni более 1% Cr 1% и менее (например, 20ХН2М, 12ХН2, 12ХН3А)	57-63	32-45	950
стали марок 18ХГТ, 30ХГТ, 12Х2Н4А и др.	57-63	32-45	800
Нитроцементация легированных сталей:
25ХГМ	57-63	32-45	1000
25ХГТ, 30ХГТ и др.	57-63	32-45	750
Заделка при нагреве ТВЧ по всему контуру:
стали пониженной прокаливаемости (например, 55ПП)	58-62	28-35	900
стали марок 60ХВ, 60ХН и др.	54-60	25-35	700
стали марок 35ХМА, 40ХН и др.	48-60	25-35	600
Нормализация или улучшение	НВ	180-350	1,35НВ+100
Азотирование легированных сталей	–	24-40	18HRCсерд+50

Коэффициент долговечности определяют в зависимости от отношения – базового числа циклов нагружения при котором определяется предел контактной выносливости и – эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. При эквивалентном числе циклов нагружения зубьев колес больше базового коэффициент долговечности =1.

В случае когда эквивалентное число циклов нагружения зубьев меньше базового, то

. (14.24)

Для зубчатых колес с твердостью поверхности зубьев , а также со шлифованной переходной поверхностью зубьев показатель корня т=6, для зубчатых колес с и нешлифованной переходной поверхностью т=9. Базовое число циклов нагружений зубьев изгибом .

Эквивалентное число циклов перемены напряжений NFE. при работе передачи с постоянной нагрузкой

, (14.25)

где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; – частота вращения рассчитываемого зубчатого колеса, ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.

При работе передачи с переменными нагрузками

, (14.26)

где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; – передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения , показатель степени принимается согласно рекомендациям к формуле (14.24).

Значение коэффициента принимают: при односторонней нагрузке на зубья , а при двусторонней = 0,7…0,8 (большее значение при НВ > 350).

При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости

, (14.27)

где – коэффициент для прямозубой передачи =1400, для косозубой и шевронной =850.

Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния и модуля определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.

Проверочные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

– для прямозубых передач

; (14.28)

– для косозубых передач

, (14.29)

где , – коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления; – коэффициент динамической нагрузки, возникающей в зацеплении.

Таблица 14.3 Значения коэффициента динамических нагрузок

Степень точности	Твердость поверхностей зубьев	υ, м/с
1	2	4	6	8	10
6-я	а
б
7-я	а
б
8-я	а
б
9-я	а
б

Примечания: 1. Твердость поверхности зубьев: а) и или и ; б) и . 2. 3начения в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.

Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а – для расчета на контактную прочность, b – для расчета на изгибную прочность.

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.3.

Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а – для расчета на контактную прочность, b – для расчета на изгибную прочность.

При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

, (14.30)

где – максимальное расчетное напряжение при перегрузке зубьев максимальным моментом ; – допускаемое максимальное контактное напряжение для зубьев; – расчетное контактное напряжение, вызываемое расчетным моментом и определяемое по формуле (14.27) или (14.28). Для зубьев зубчатых колес и термообработкой нормализацией, улучшением или объемной закалкой с отпуском , где – предел текучести материала зубьев при растяжении; для зубьев с термообработкой – цементация, контурная закалка после нагрева ТВЧ – ; для азотированных зубьев . Расчет зубьев по формуле (14.30) производится раздельно для колеса и для шестерни.

Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

, (14.31)

где – коэффициент учитывающий перекрытие зубьев; – коэффициент наклона зубьев; – коэффициент распределения нагрузки между зубьями; – коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи, – коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.

При подстановке окружной силы по зависимости (14.10) формула (14.31) преобразуется к виду

.

Коэффициент, учитывающий перекрытие зубьев

.

При приближенных расчетах для для косозубых передач и прямозубых передач принимают .

Коэффициент наклона зубьев для прямозубых передач , для косозубых определяется по зависимости

, (14.32)

при .

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят , а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.4

Таблица 14.4 Значения коэффициента динамических нагрузок

Степень точности	Твердость поверхностей зубьев	υ, м/с
1	2	4	6	8	10
6-я	а
б
7-я	а
б
8-я	а
б
9-я	а
б

Примечания: 1. Твердость поверхности зубьев: а) и или и ; б) и . 2. 3начения в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.

Если материал зубчатых колес одинаковый, то расчет зубьев на изгиб производят по шестерне, у которой толщина зубьев у основания меньше и соответственно коэффициент формы зубьев YF больше, чем у зубьев колеса. Если материал зубьев шестерни более прочный по сравнению с материалом зубьев колеса, что обычно и принимается, то расчет зубьев на изгиб нужно производить по тому зубчатому колесу, для которого отношение имеет меньшее значение. Рекомендуется материал зубьев шестерни и колеса принимать таким, чтобы отношение для обоих зубчатых колес было примерно одинаковым.

Если известно напряжение изгиба для зуба шестерни, то для зуба колеса условие прочности на изгиб запишется в виде

. (14.33)

При действии кратковременных перегрузок зубья проверяют на пластическую деформацию или хрупкий излом при изгибе от максимальной нагрузки:

, (14.34)

где – максимальное расчетное напряжение на изгиб в зубьях при их перегрузке максимальным моментом ; – допускаемое максимальное напряжение на изгиб для зубьев; – расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом и определяемое по формуле (14.31).

Значение допускаемых максимальных напряжений

на изгиб для зубьев принимают: при твердости поверхности зубьев , где – предел текучести материала зубьев при растяжении; при твердости , где – предел прочности материала зубьев при растяжении. Расчет зубьев по формуле (14.34) производят для менее прочного колеса передачи.

Задача 14.1. Выполнить расчет зубчатой передачи. Выполнить проектный и проверочный расчеты (на контактную и изгибную прочность) косозубой зубчатой передачи быстроходной ступени двухступенчатого цилиндрического редуктора. Параметры циклограммы нагружения шестерни: момент на шестерне , продолжительность работы ; , ; , . Частота вращения шестерни . Передаточное число , передача нереверсивная. Марка стали колес – сталь 40ХН. Способ упрочнения – закалка при нагреве ТВЧ до твердости поверхности зубьев .

Решение. Проектный расчет зубчатой передачи.

Принимаем коэффициент ширины по межосевому расстоянию из стандартного ряда значений .

Коэффициент ширины по диаметру шестерни по формуле (14.8)

.

Ориентировочное значение коэффициента неравномерности распределения нагрузки определяем по рис.84. Твердость зубьев соответствует твердости , согласно зависимостям на рис.88. Для схемы ІІ, при твердости зубьев (рис.84.): .

Предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений определяем по таблице 14.1.

=

Рис.88. Зависимости для определения твердости в единицах

Коэффициент запаса прочности .

Базовое число нагружений для материала шестерни и колеса по формуле (14.16)

Эквивалентное число циклов нагружений зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.19) с учетом того, что частота вращения на всех режимах одинакова и равна . (При постоянном нагружении эквивалентное число циклов определяется по зависимости (14.18))

=

==

= циклов.

Эквивалентное число нагружений зубьев колеса

циклов.

Коэффициенты долговечности для зубьев шестерни и колеса по формуле (14.17)

,

.

Допустимые контактные напряжения по формуле (14.15), с учетом

– для шестерни

;

– для колеса

.

Так как твердость поверхности зубьев шестерни и колеса одинаковы, то в качестве расчетного допускаемого контактного напряжения принимаем меньшее значение

.

Расчетное межосевое расстояние определяем по формуле (14.14) для косозубой передачи

.

Принимаем наибольшее значение из стандартного ряда .

Находим предел усталости зубьев при изгибе по табл. 14.2. для стали 40ХН с упрочнением ТВЧ .

Базовое число циклов нагружений зубьев изгибом .

Эквивалентное число циклов нагружений изгибом зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.26) с учетом (14.24) и того, что частота вращения на всех режимах одинакова и равна :

=

=

= циклов.

Для зубьев колеса эквивалентное число циклов нагружений изгибом

циклов.

Коэффициенты долговечности для зубьев шестерни и колеса на изгиб с учетом того, что и , то .

Допускаемое напряжение на изгиб для зубьев шестерни определим по формуле (14.23) при и

.

Предварительно принимаем коэффициент формы зуба шестерни .

Расчетная ширина венца зубчатого колеса

.

Принимаем стандартный размер ширина венца .

Ширина зубчатого венца шестерни .

Принимаем .

По известному значению межосевого расстояния ориентировочно определяем модуль зацепления по зависимости (14.27) для косозубой передачи

мм.

Принимаем стандартное значение модуля зацепления мм.

Предварительное значение угла наклона зубьев принимаем из диапазона . Принимаем .

Число зубьев шестерни по межосевому расстоянию и модулю определим по зависимости:

.

Принимаем число зубьев шестерни .

Число зубьев колеса

.

Уточнение угла наклона зубьев по межосевому расстоянию и числу зубьев

0,96 и .

Принимаем коэффициент коррекции при изготовлении зубьев .

Расчет геометрических, кинематических и силовых параметров для выполнения проверочных расчетов.

Делительные диаметры колес зацепления:

– шестерни 166,67мм;

– колеса 333,33мм.

Начальные диаметры:

– шестерни 166,67мм;

– колеса 333,33мм.

Диаметр вершин зубьев:

– шестерни 176,67мм,

– колеса 343,33мм.

Диаметр впадин зубьев:

– шестерни 154,17мм,

– колеса 320,83мм.

Делительный угол профиля зуба в торцевом сечении

= 20,760.

Угол зацепления передачи при

.

Коэффициент торцевого перекрытия:

=

=1,66.

Коэффициент осевого перекрытия

=1,12.

Окружная скорость

Принимаем при такой скорости 8-ую степень точности (табл.14.5) с шероховатостью поверхности зубьев мкм.

Таблица 14.5 Степени точности зубчатых передач

Степень точности	Окружная скорость колес, м/с, не более	Область применения
прямозубых	косозубых
6 – я	15	30	Скоростные передачи, делительные механизмы
7 – я	10	15	Передачи при повышенных скоростях и умеренных нагрузках или наоборот
8 – я	6	10	Передачи общего машиностроения, не требующие особой точности
9 – я	2	4	Тихоходные передачи с пониженными требованиями к точности

Проверочные расчеты зубчатого зацепления на контактную прочность зубьев.

Определяем по графику на рис.87. а коэффициент неравномерности распределения нагрузки в зависимости от скорости и 8-ой степени точности изготовления

Определяем по таблице 14.3 коэффициент динамической нагрузки для твердости поверхности зубьев при скорости и 8-ой степени точности изготовления =1,045.

Коэффициент неравномерности

1,26.

Расчет зубьев на контактную прочность выполняем по зависимости (14.29)

Следовательно, условие контактной прочности зубьев выполнено. Допускается превышение над до 5%.

Проверочный расчет на изгибную прочность зубьев. Определяем по графику на рис.87 а коэффициент неравномерности распределения нагрузки на изгиб в зависимости от скорости и 8-ой степени точности изготовления .

Определяем по графику на рис.86 б коэффициент неравномерности распределения по длине контактных линий на изгиб в зависимости от схемы зацепления и твердости зубьев .

Определяем по таблице 14.3 коэффициент динамической нагрузки на изгиб для твердости поверхности зубьев при скорости и 8-ой степени точности изготовления =1,07.

Эквивалентное число зубьев косозубой передачи определяем по формуле (14.22)

– для шестерни ,

– для колеса .

Коэффициент формы зубьев колес принимаем по графику рис.85. в зависимости от эквивалентного числа зубьев:

– для шестерни 3,75,

– для колеса 3,62.

Коэффициент учитывающий угол наклона зубьев определяем по формуле (14.32)

==0,88.

Коэффициент, учитывающий перекрытие зубьев передачи

=0,6.

Окружную силу в зацеплении определим по формуле (14.10)

= 25200Н.

Расчетные напряжения изгиба в зубьях

– для шестерни

,

– для колеса

.

Следовательно, условие прочности зубьев на изгиб обеспечивается.

Задача 14.2. Определить размеры открытой конической зубчатой передачи. Передаваемая мощность N=3,5·103Вт. Передаточное числа i = 4.Частота вращения ведущего вала Передача нереверсивная.

Решение. Углы при вершинах начальных конусов

Выбираем материал зубчатых колес. Материал шестерни – сталь Ст.5, материал колеса – чугун СЧ 21–40 т. к. передача открытая расчет будет производится только из условия прочности зубьев на изгиб.

Допускаемые напряжения изгиба для шестерни

где ;

для колеса

где – предел прочности чугуна СЧ 21-40 на растяжение.

Задаемся числом зубьев шестерни Тогда

Сравнительная прочность зубьев шестерни и колеса на изгиб:

для шестерни

для колеса

Таким образом, расчет следует вести по колесу.

Задаемся:

Расчетный момент на ведущем валу

Здесь принято предварительно K=1,5.

Момент расчетный на ведомом валу (валу колеса) без учета потерь в зацеплении и подшипниках

Максимальный модуль зацепления при коэффициенте износа γ = 1,2

Принимаем из ряда стандартных значений модулей (по ГОСТ 9563-80).

По найденному определяем размеры колес:

Углы конусов выступов

Тогда

.

Длина зуба

Средний модуль

§ 10.3. Силы в зацеплении
В косозубой передаче нормальная сила Fn составляет угол β с торцом колеса (рис. 10.4). Разложив Fn на составляющие, получим:
радиальную силу

Проектировочный расчет. Аналогично расчету прямозубой передачи [см. формулу (9.10)] межосевое расстояние для стальной косозубой пары. Проверочный расчет. Аналогично расчету прямозубой передачи [см. формулу (9.8)] контактные напряжения в поверхностном слое косых зубьев

Так как мы нашли все составляющие формулы межосевого
расстояния то определяем

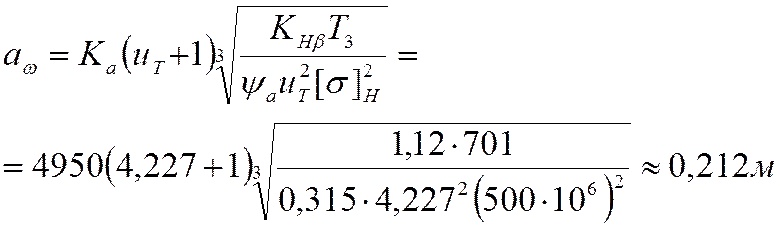
Вычисленное межосевое
расстояние  мм округляем в
большую сторону до стандартного (согласно стандартного ряда см. стр. 33 [1]).  мм.

Стандартный
ряд межосевых расстояний :

Расчётные значения  для
нестандартных редукторов округляют в большую сторону по ряду Ra 40: … 80,
85, 90, 100, 105, 110, 120, 125, 130, дальше через 10 до 250 и через 20 до 420
., мм

7.1.2 Определяем предварительно модуль
зубчатой передачи, мм:

Модуль передачи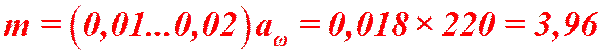

значение модуля передачи округляют в большую сторону
до стандартного значения из ряда чисел (предпочтительно
из первого ряда см. стр. 33 [1])

Стандартный ряд модулей:

ряд 1 – 1,   1,5   2,5   3   
4     5    6     8   10    12     16   20

ряд 2 –  1,25  1,375   1,75   2,25   2,75    3,5    4,5    
5,5     7    9    11  (СТ СЭВ 310-76)

Принимаем модуль

7.1.3   Определяем суммарное  число зубьев:

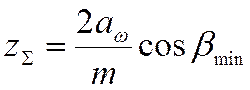, где  – минимальный угол наклона зубьев
(косозубых колес),  для прямозубых колес . 
Тогда суммарное количество зубьев прямозубой зубчатой пары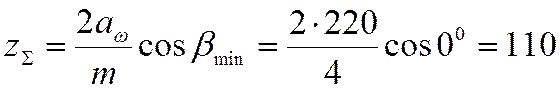 

т.е. .

7.1.4 Определяем число зубьев шестерни и колеса.

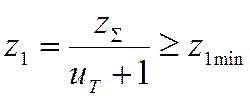, где  – для прямозубой шестерни,  тогда

,

Возьмем в первом приближении число зубьев прямозубой
шестерни на тихоходном валу  .

Число зубьев прямозубого колеса на промежуточном валу зубч.
пары №3 ,           

Находим в первом приближении число зубьев колеса , 

7.1.5 Определяем фактическое передаточное число 
 и его отклонение от заданного

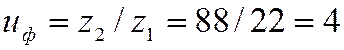, для  отклонение передаточного числа
равно: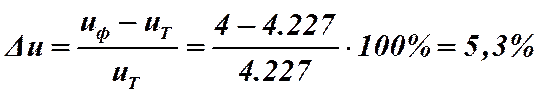    

Так как  5,3%>2,5%  рекомендуемого максимума
отклонений для  и 4%  для  , то в формуле определения количества
зубьев в шестерне округлим дробное число зубьев 21,8 до 21. То
есть, принимаем число зубьев прямозубой шестерни на тихоходном валу  . Тогда  число зубьев колеса , 

Опять выполним проверку :

,

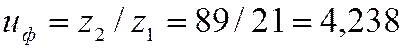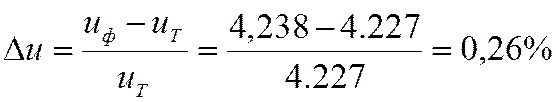
0,26%<2,5%  рекомендуемого максимума отклонений
для  

Поэтому окончательно принимаем   и    .

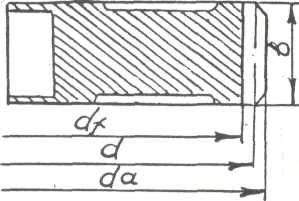7.1.6  Определяем основные геометрические параметры
передачи (прямозубой зубчатой пары шестерня – колесо №3), мм:

– делительный диаметр
шестерни 

– делительный диаметр колеса

проверим этот диаметр по формуле (стр. 33 [1])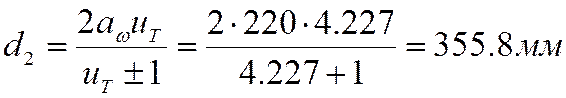

– диаметр впадин зубьев шестерни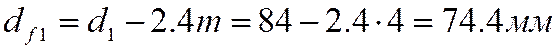

– диаметр впадин зубьев колеса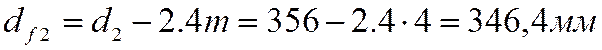

– диаметр вершин зубьев шестерни

– диаметр вершин зубьев колеса

– ширина венца зуба колеса

– ширина венца зуба шестерни  (стр. 33 [1])

7.1.7.  Определение сил в зубчатом зацеплении (пара
зубьев №3 на рис. 2.18)

– определяем окружную силу 
на колесе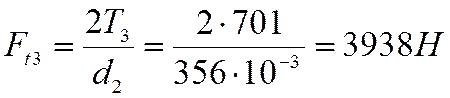

– определяем радиальную силу

где  угол профиля зуба.

7.1.8 Проверка зубьев колеса по контактным напряжениям  (прямозубая
зубч. пара №3)

расчетное контактное 
напряжение в зубьях колеса:

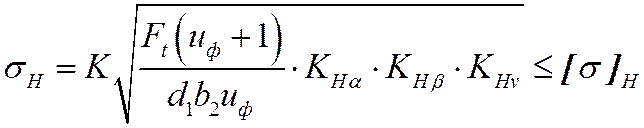, где

 – вспомогательный коэффициент, для прямозубых передач
.

 – коэффициент, учитывающий распределение нагрузки между
зубьями в прямозубой паре (стр. 37 [1]). (для косозубой пары ).

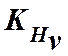 – коэффициент
динамической нагрузки,
который принимают:

– для прямозубых колес:  при твердости НВ < 350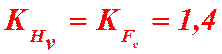     

                                                                              
НВ > 350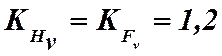       

– 
для косозубых и шевронных колёс:

                                       
при твердости НВ <350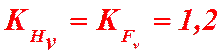       

                                                              
НВ > 350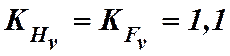        

Примечание: данные взяты
из „Розрахунок і проектування приводів суднових механізмів” ВВ Алексієнко ….,
Миколаїв 2008р.

Окончательно принимаем  –
коэффициент динамической нагрузки
для прямозубых колёс с НВ < 350 для материала шестерни и
колеса.

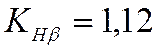 – коэффициент концентрации нагрузки, см.
таблицу 11 в п. 7.1.1 настоящего пособия.

мм – делительный диаметр
прямозубой шестерни.

                       

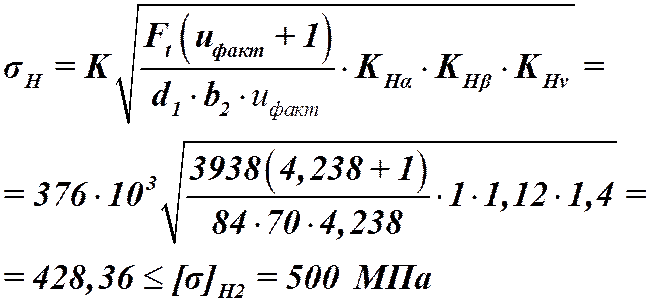
Неравенство выполняется ,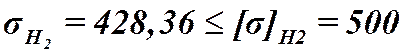
   расчет правильный.

7.1.9 Проверка зубьев колеса по напряжениям изгиба (прямозубая
цилиндрическая зубчатая пара №3)

Расчетное напряжение изгиба в
зубьях колеса

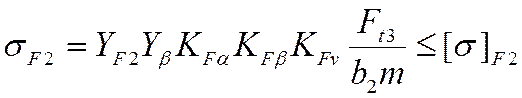, где

– коэффициент, учитывающий распределение нагрузки между
зубьями (стр. 36 [1]).

Допустимые
значения окружных скоростей для передач разной
степени точности.                                                                                                             

Таблица
12.

Степень точности	Допустимая окружная скорость  V, м/с
Прямозубые	Косозубые
цилиндрические	конические	цилиндрические	конические
6	До 15	До 12	До 30	До 20
7	До 10	До 8	До 15	До 10
8	До 6	До 4	До 10	До 7
9	До 2	До 1,5	До 4	До 3

Выбор
коэффициента 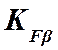                                                                                                           Таблица
13

Размещение колёс относительно опор	Коэффициент
Твёрдость зубъев, НВ	Коэффициент
0,2	0,4	0,6	0,8	1,2
Косольне, опоры – шарикоподшипники	<350	1,16	1,37	1,64	–	–
≥350	1,33	1,7	–	–	–
Косольное, опоры – роликоподшипники	<350	1,1	1,22	1,38	1,57	–
≥350	1,2	1,44	1,71	–	–
Симметричное	<350	1,01	1,03	1,05	1,07	1,14
≥350	1,02	1,04	1,08	1,14	1,3
Несимметричное	<350	1,05	1,1	1,17	1,25	1,42
≥350	1,09	1,18	1,3	1,43	1,73