Алгебра и начала математического анализа, 11 класс
Урок №19. Решение задач с помощью производной.
Перечень вопросов, рассматриваемых в теме
- механический смысл первой производной;
- механический смысл второй производных;
- скорость и ускорение.
Глоссарий по теме
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается f или
или 
Производная от второй производной называется производной третьего порядка и обозначается  или f”’(x). Производную n-го порядка обозначают f(n) (x) или y(n).
или f”’(x). Производную n-го порядка обозначают f(n) (x) или y(n).
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 
Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним механический смысл производной:
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).
Пример 1. Точка движется прямолинейно по закону  (S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
(S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
Решение:
скорость прямолинейного движения равна производной пути по времени, то есть  .
.
Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).
Ответ: 20 м/c.
Пример 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол
 Найдите:
Найдите:
а) угловую скорость вращения маховика в момент t = 6 с;
б) в какой момент времени маховик остановится?
Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t2)=4-0,4t.
Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).
б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.
Ответ: угловая скорость маховика равна (рад/с); t=10 c.
Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t2+2t-5. Найти кинетическую энергию тела  через 3 с после начала движения.
через 3 с после начала движения.
Решение: найдём скорость движения тела в любой момент времени t.
v= S’=(3t2+2t-5)’=6t+2
Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..
Определим кинетическую энергию тела в момент времени t=3.


Ответ: Е=1200 Дж
Производная второго порядка. Производная n-го порядка.
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается  .
.
Производная от второй производной называется производной третьего порядка и обозначается y”’ или f”'(x) Производную n-го порядка обозначают f(n) (x) или y(n).
Примеры. Найдем производные четвёртого порядка для заданных функций:
1) f(x)= sin 2x
f'(x)=cos 2x∙(2x)’= 2cos 2x
f (x)=-2sin2x∙(2x)’=-4sin 2x
(x)=-2sin2x∙(2x)’=-4sin 2x
f”'(x)= -4 cos 2x∙(2x)= -8 cos 2x
f(4)(x)= 8 sin2x∙(2x)’= 16 sin 2x
2) f(x)=23x
f’(x)=3∙ 23x ∙ln2
f (x)= 9∙ 23x ∙ln22
(x)= 9∙ 23x ∙ln22
f”'(x)= 27∙ 23x ∙ln32
f(4)(x)= 81∙ 23x ∙ln42
Механический смысл второй производной.
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 
Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Пример 4. Точка движется прямолинейно по закону S(t)= 3t2-3t+8. Найти скорость и ускорение точки в момент t=4 c.
Решение:
найдём скорость точки в любой момент времени t.
v=S’=(3t2-3t+8)’=6t-3.
Вычислим скорость в момент времени t=4 c.
v(4)=6∙4-3=21(м/с)
Найдём ускорение точки в любой момент времени t.
a= v’= (6t-3)’=6 и a(4)= 6 (м/с2) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=21(м/с); a= v’= 6 (м/с2).
Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t3-3t2+5. Найти силу, действующую на тело в момент времени t=4 c.
Решение: сила, действующая на тело, находится по формуле F=ma.
Найдём скорость движения точки в любой момент времени t.
v=S’=(t3-3t2+5)’=3t2-6t.
Тогда v(4)=3∙42-6∙4=24 (м/с).
Найдём ускорение: a(t)=v’=(3t2-6t)’=6t-6.
Тогда a(4)= 6∙4-6= 18 (м/с2).
F=ma=3∙18= 54 Н
Ответ: F= 54 Н
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Напишите производную третьего порядка для функции:
f(x)= 3cos4x-5x3+3x2-8
_____________________
Решим данную задачу:
f’’’(x)=( 3cos4x-5x3+3x2-8)’’’=(((3cos4x-5x3+3x2-8)’)’)’=((-12sin4x-15x2+6x)’)’=(-48cos4x-30x)’=192sin4x-30.
Ответ: 192sin4x-30
№ 2. Тип задания: выделение цветом
Точка движется прямолинейно по закону S(t)= 3t2+2t-7. Найти скорость и ускорение точки в момент t=6 c.
- v=38 м/с; a=6 м/с2
- v=38 м/с; a=5 м/с2
- v=32 м/с; a=6 м/с2
- v=32 м/с; a=5 м/с2
Решим данную задачу:
Воспользуемся механическим смыслом второй производной:
v= S’(t)=( 3t2+2t-7)’=6t+2.
Вычислим скорость в момент времени t=6 c.
v(6)=6∙6+2=38 (м/с)
Найдём ускорение точки в любой момент времени t.
a= v’= (6t+2)’=6 и a(6)= 6 (м/с2) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=38(м/с); a= v’= 6 (м/с2).
Верный ответ:
- v=38 м/с; a=6 м/с2
- v=38 м/с; a=5 м/с2
- v=32 м/с; a=6 м/с2
- v=32 м/с; a=5 м/с2
На этой странице вы узнаете
- Кто всегда протянет руку помощи в определении производной?
- Что такое сложная функция и зачем тут матрешка?
- Как никогда не ошибаться при решении задач с производными?
Теория теорией, а дифференцировать хочется всегда. Эта статья посвящена практике нахождения производных.
Производные основных функций
Должно быть, вы уже слышали о производной и даже пробовали взять её мозговым штурмом. При отрицательном ответе вам обязательно нужно прокатиться на американских горках в нашей статье «Производная». В ней рассмотрели основные понятия производной.
Главный вопрос этой статьи: как ее находить? Для этого существуют свои формулы и правила, которых необходимо придерживаться для правильного решения заданий.
Ниже приведена таблица с формулами для нахождения производных основных функций. Применяя эти формулы, можно найти производную почти любой функции.
Не пугайтесь, если вам покажется, что их много: это основные формулы, с помощью которых можно решить большинство задач.
| 1 | C’ = 0, C = const |
| 2 | ((x^n)’ = n * x^{n — 1}, x > 0) |
| 3 | ((a^x)’ = a^x * ln(a), a > 0, a neq 1) |
| 4 | ((e^x)’ = e^x) |
| 5 | ((log_{a}x)’ = frac{1}{x * ln(a)}, x > 0, a > 0, a neq 1) |
| 6 | ((ln(x))’ = frac{1}{x}, x > 0) |
| 7 | ((sqrt{x})’ = frac{1}{2sqrt{x}}, x > 0) |
| 8 | (sin(x))’ = cos(x) |
| 9 | (cos(x))’ = -sin(x) |
| 10 | ((tg(x))’ = frac{1}{cos^{2}x}, x neq frac{pi}{2} + pi n, n in Z) |
| 11 | ((ctg(x))’ = -frac{1}{sin^{2}x}, x neq pi n, n in Z) |
Смотреть на формулы и учить их — это круто, прямо ощущаем себя великими учеными. Что может быть круче этого? Только применять их на практике. Рассмотрим несколько примеров нахождения производной.
Пример 1. Найдите производную функции f(x) = 5.
Решение: 5 — это число, то есть константа. Тогда, пользуясь первой формулой в таблице, получаем:
f'(x) = 5′ = 0.
Ответ: 0
Пример 2. Найдите производную функции (f(x) = x^4)
Решение: В этом случае необходимо воспользоваться второй формулой из таблицы.
(f'(x) = (x^4)’ = 4 * x^{4-1} = 4 * x^3)
Ответ: (4x^3)
Пример 3. Найдите производную функции (f(x) = e^x)
Решение: В этом случае необходимо воспользоваться четвертой формулой из таблицы.
(f'(x) = (e^x)’ = e^x)
Ответ: (e^x)
Правила дифференцирования
С полной уверенностью можем сказать, что вам встречались сложные функции. Даже намного сложнее, чем те, которые приведены в таблицах. Там и сумма, и произведение, и формула в формуле. Одним словом: ужас! Как брать производную, если перед функцией стоит коэффициент, или в функцию включено несколько разных выражений? На этот случай существуют правила дифференцирования.
В сложных функциях невозможно пользоваться только формулами для нахождения производной.
Если функция
— усложнена коэффициентом,
— представлена в виде суммы, произведения или частного
— или является сложной функцией,
то для выбора правильной производной необходимо воспользоваться правилами дифференцирования. Они играют роль супергероев от мира производных. Рассмотрим их внимательнее.
1. Коэффициент можно вынести за знак производной.
(k * f(x))’ = k * (f(x))’
Например, необходимо взять производную у функции f(x) = 6sin(x). Тогда, пользуясь правилом дифференцирования и таблицей, получаем ответ 6cos(x).
2. Производная суммы (разности) равняется сумме (разности) производных.
((f(x) pm g(x))’ = f'(x) pm g'(x))
Найдем производную (f(x) = 4x^5 — sqrt{x} + cos(x)).
(f'(x) = (4x^5 — sqrt{x} + cos(x))’ = (4x^5)’ — (sqrt{x})’ + (cos(x))’ = 4 * 5 * x^{5 — 1} — frac{1}{2sqrt{x}} — sin(x))
(f'(x) = 20x^4 — frac{1}{2sqrt{x}} — sin(x). )
3. Производная произведения.
(f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x)
Для примера возьмем производную функции f(x) = x2 * ln(x)
f'(x) = (x2 * ln(x))’ = (x2)’ * ln(x) + x2 * (ln(x))’
(f'(x) = 2x * ln(x) + x^2 * frac{1}{x} = 2x * ln(x) + x)
4. Производная частного.
((frac{f(x)}{g(x)})’ = frac{f'(x) * g(x) — f(x) * g'(x)}{g^{2}(x)})
Возьмем производную функции (f(x) = frac{e^x}{3x})
(f'(x) = frac{(e^x)’ * 3x — ex * (3x)’}{(3x)^2} = frac{e^x * 3x — e^x * 3}{9x^2} = frac{3e^x * (x-1)}{9x^2} = frac{e^x * (x-1)}{3x^2})
5. Производная сложной функции.
Сложная функция — это функция, внутри которой есть другая функция.
Давайте представим матрешку: в одну большую куклу складывается куколка поменьше, а в нее еще меньше и так далее. Точно так же и с функцией: “внутри” одной функции может лежать другая функция.
Например, у нас есть две функции: (sqrt{x}) и cos(x). А теперь попробуем поместить корень в функцию с косинусом, и получим (cos(sqrt{x})). Это и будет сложная функция.

Чтобы найти производную сложной функции, необходимо найти производную “внутренней” функции и умножить ее на производную “внешней” функции.
(f(g(x))’ = g'(x) * f'(g(x))
Найдем производную уже рассмотренной функции (f(x) = cos(sqrt{x})).
(f'(x) = (cos(sqrt{x}))’ = (sqrt{x})’ * (cos(sqrt{x}))’ = frac{1}{2sqrt{x}} * (-sin(sqrt{x})) = -frac{sin(sqrt{x})}{2sqrt{x}})
Исследование функции с помощью производной
В задании нам может быть дана только функция без ее графика. Что делать в таком случае, если нам нужно найти, например, отрезки возрастания, точки экстремума, наибольшее или наименьшее значение функции? Не во всех случаях получится построить график, да и это займет достаточно большое количество времени, которое и без того ограничено на экзамене.
В этом случае мы можем проанализировать поведение функции с помощью производной.
Исследуем функцию f(x) = (x — 4)2(x + 11) + 4.
Cначала возьмем производную от этой функции:
f'(x) = ((x — 4)2(x + 11))‘ + 4′ = ((x — 4)2(x + 11))’ = ((x — 4)2)'(x + 11) + (x — 4)2(x + 11)’
f'(x) = 2(x — 4)(x + 11) + (x — 4)2 * 1 = (x — 4)(2(x + 11) + (x — 4)) = (x — 4)(3x + 18)
Любое исследование функции с помощью производной начинается именно с дифференцирования функции.
Теперь рассмотрим алгоритм нахождения точек минимума и максимума:
2 шаг. Найденную производную необходимо приравнять к 0 и решить полученное уравнение.
3 шаг. Расставить корни полученного уравнения на числовой прямой.
4 шаг. Определяем знаки производной на промежутках. Для этого необходимо подставить любое значение с выбранного промежутка в производную функции.
5 шаг. Определить, какие точки будут точками минимума (в них знак меняется с минуса на плюс), а какие — точками максимума (знак меняется с плюса на минус).
Найдем точки минимума и максимума в нашей функции. Поскольку производную мы уже взяли, можно сразу перейти ко второму шагу:
(x — 4)(3x + 18) = 0
x = 4, x = -6.
Полученные значения х расставляем на числовой прямой:

Теперь определим знаки на промежутках слева направо.
1. Возьмем точку -10 и подставим ее в производную функции:
(-10 — 4)(3 * (-10) + 18) = (-14) * (-12) = 168. Производная на этом промежутке будет положительной.
2. Возьмем точку 0 и подставим ее в производную функции:
(0 — 4)(3 * 0 + 18) = (-4) * 18 = -72. Производная на этом промежутке будет отрицательной.
3. Возьмем точку 5 и подставим ее в производную функции:
(5 — 4)(3 * 5 + 18) = 33. Производная на этом промежутке будет положительной.
Расставим полученные знаки на прямой:
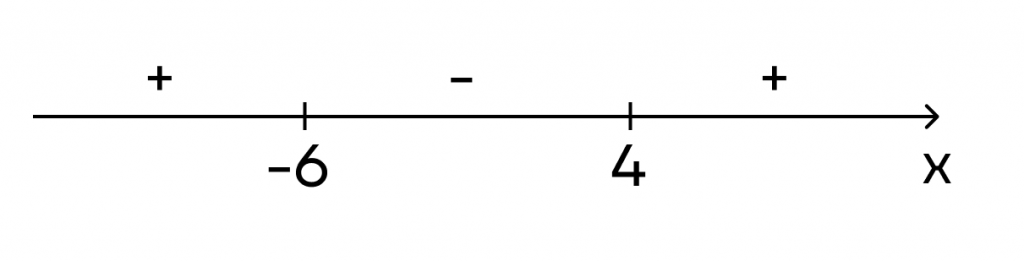
Остался последний пятый шаг. В точке -6 производная меняет знак с плюса на минус, значит, это точка максимума. В точке 4 производная меняет знак с минуса на плюс, значит, это точка минимума.
Важно!
Если в задании встречается формулировка “Найдите точку минимума (максимума) функции”, то необходимо пользоваться именно этим алгоритмом.
Но это не все выводы, которые уже можно сделать о функции. Вспомним, что функция возрастает, когда производная положительна, а убывает, когда производная отрицательна. Поскольку мы уже определили знаки производной, то смело можем сделать вывод, что на промежутках до -6 и после 4 функция будет возрастать, а на промежутке от -6 до 4 — убывать.
Однако могут встретиться задания, в которых необходимо найти наибольшее или наименьшее значение функции на определенном интервале.
Для выполнения таких заданий существует следующий алгоритм нахождения наибольшего и наименьшего значения функции.
Шаг 2. Найти точки минимума и максимума функции.
Шаг 3. Определить, какие из точек минимума и максимума принадлежат заданному интервалу.
Шаг 4. Найти значение функции в отобранных в предыдущем шаге точках, а также в точках, которые являются границами заданного интервала. Для этого необходимо подставить точки в функцию (не в производную от функции).
Для примера найдем наибольшее значение функции f(x) = (x — 4)2(x + 11) + 4 на отрезке [-10; 0].
Первые два шага мы уже выполнили, когда рассматривали алгоритм нахождения точек минимума и максимума. Из них отрезку [-10; 0] принадлежит х = -6 — точка максимума.
Теперь определим значение функции в трех точках:
f(-10) = (-10 — 4)2(-10 + 11) + 4 = 196 + 4 = 200
f(-6) = (-6 — 4)2(-6 + 11) + 4 = 500 + 4 = 504
f(0) = (0 — 4)2(0 + 11) + 4 = 176 + 4 = 180
Наибольшее из полученных значений — это 504. Это и будет ответ.
Может возникнуть вопрос, почему важно проверять значение функции и на границах отрезка? В заданиях ЕГЭ очень часто встречаются случаи, когда нужно найти наибольшее значение, и в интервале лежит точка максимума, или когда нужно найти наименьшее значение функции и в интервале лежит точка минимума. Логично будет проверить только экстремумы, поскольку в них, скорее всего, достигается наибольшее или наименьшее значение.
Однако стоит вспомнить, что мы не видим график функции и не можем с точностью определить, что в экстремуме достигается нужное нам значение. С помощью экстремумов мы можем описать поведение функции: где она возрастает, а где убывает. Но можно столкнуться с графиком, на котором граничная точка будет лежать выше или ниже точки экстремума. Тогда наибольшее или наименьшее значение будет достигаться именно в ней. Пример на картинке (красными линиями обозначены границы отрезка).
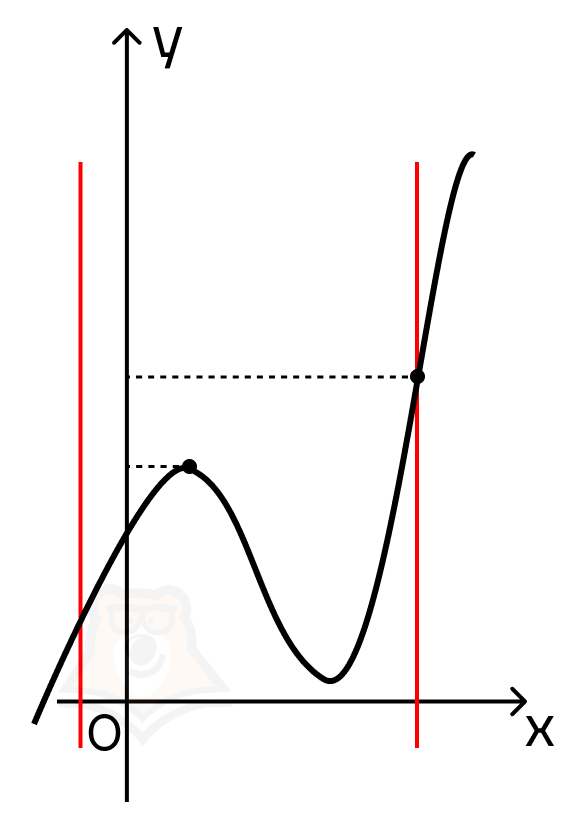
Подведем итог.
Как можно исследовать функцию с помощью производной?
С помощью производной можно с точностью сказать, на каких участках функция будет возрастать и убывать, сколько точек максимума и минимума у нее есть, какое наибольшее или наименьшее значение принимает функция на заданном участке.
Фактчек
- Для нахождения производной необходимо пользоваться специальными формулами для производной. С их помощью можно найти производную любой из основных функций.
- Если функция усложнена коэффициентом, является сложной или представлена в виде суммы, произведения или частного, то необходимо пользоваться правилами дифференцирования. Они помогут правильно найти производную.
- Сложная функция — это функция, внутри которой есть другая функция.
- С помощью производной можно исследовать функцию, а именно найти точки минимума и максимума, определить, на каких участках функция возрастает и убывает, найти наибольшее и наименьшее значение функции на заданном отрезке.
Проверь себя
Задание 1.
Чему будет равна производная f(x) = 3?
- 3;
- 1;
- 0;
- Производную этой функции невозможно найти.
Задание 2.
Чему будет равна производная f(x) = 5x2?
- 10x;
- 10x2;
- 5x2;
- 2x.
Задание 3.
Чему будет равна производная f(x) = 13x + 5 + x3?
- 18 + 3x2;
- 13 + 3x2;
- 18;
- 3x2.
Задание 4.
Чему будет равна производная f(x) = ln(x)?
- x
- (frac{1}{x})
- (frac{1}{2sqrt{x}})
- ex
Задание 5.
Чему будет равна производная f(x) = tg(x)?
- (frac{1}{cos^{2}(x)})
- (-frac{1}{sin^{2}(x)})
- (-frac{1}{cos^{2}(x)})
- (frac{1}{sin^{2}(x)})
Ответы: 1. — 3 2. — 1 3. — 2 4. — 2 5. — 1
Содержание:
Исследование функций с помощью производных
Необходимое условие возрастания и убывания функции
Из определений возрастающей и убывающей функций следует необходимое условие возрастания и убывания функции.
Теорема: Если дифференцируемая функция 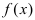
Доказательство: Пусть дифференцируемая функция 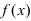 возрастает на сегменте
возрастает на сегменте 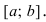 Возьмем произвольную точку
Возьмем произвольную точку 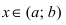 и дадим ей приращение
и дадим ей приращение 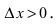 Тогда в силу возрастания функции ее приращение
Тогда в силу возрастания функции ее приращение 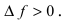 Отсюда следует,что величина
Отсюда следует,что величина 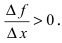 Совершая предельный переход в этом неравенстве при
Совершая предельный переход в этом неравенстве при 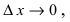 получим
получим 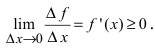 Аналогично теорема доказывается в случае, когда функция
Аналогично теорема доказывается в случае, когда функция 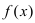 убывает на сегменте
убывает на сегменте 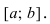
Замечание: С геометрической точки зрения возрастающая на сегменте 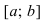 функция
функция 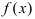 в каждой точке своего графика характеризуется касательной, которая образует с положительным направлением оси абсцисс острый угол. Если функция
в каждой точке своего графика характеризуется касательной, которая образует с положительным направлением оси абсцисс острый угол. Если функция 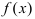 убывает на сегменте
убывает на сегменте 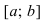 , то касательная образует с положительным направлением оси абсцисс тупой угол.
, то касательная образует с положительным направлением оси абсцисс тупой угол.
Пример:
Найти интервалы возрастания и убывания функции 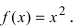
Решение:
Из графика этой функции видно, что 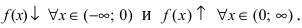 Согласно необходимому признаку возрастания и убывания функции
Согласно необходимому признаку возрастания и убывания функции 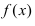 вычислим ее первую производную:
вычислим ее первую производную: 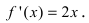 Эта производная будет отрицательной
Эта производная будет отрицательной 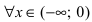 положительной
положительной 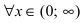 величиной. Следовательно, в полном соответствии с графиком функции
величиной. Следовательно, в полном соответствии с графиком функции 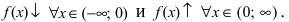
Достаточное условие возрастания и убывания функции
Теорема: Пусть функция 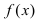 непрерывна на сегменте
непрерывна на сегменте 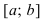 и дифференцируема на интервале
и дифференцируема на интервале 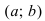 . Если ее первая производная
. Если ее первая производная 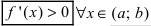 то функция возрастает на сегменте
то функция возрастает на сегменте 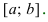 Если ее первая производная
Если ее первая производная 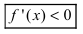
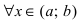 , то функция убывает на сегменте
, то функция убывает на сегменте 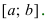
Доказательство: Пусть первая производная функции 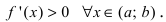 Возьмем из этого интервала две любые точки
Возьмем из этого интервала две любые точки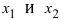 (для определенности примем, что
(для определенности примем, что 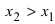 ). Тогда по теореме Лагранжа (см. Лекцию № 19) на интервале
). Тогда по теореме Лагранжа (см. Лекцию № 19) на интервале 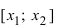 найдется хотя бы одна точка х такая, что
найдется хотя бы одна точка х такая, что 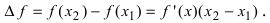 Так как на интервале
Так как на интервале 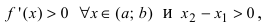 следовательно,
следовательно, 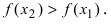
Таким образом, функция 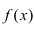 возрастает на сегменте
возрастает на сегменте 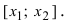 В силу произвольности выбранных точек
В силу произвольности выбранных точек 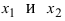 полученное утверждение справедливо для всего сегмента
полученное утверждение справедливо для всего сегмента 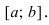 Достаточное условие убывания функции
Достаточное условие убывания функции 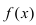 на сегменте
на сегменте 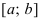 доказать самостоятельно.
доказать самостоятельно.
Условия постоянства функции на сегменте (a; b)
Условия постоянства функции на сегменте 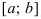 .
.
ТЗ. Пусть функция 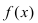 непрерывна на сегменте
непрерывна на сегменте 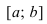 и дифференцируема на интервале
и дифференцируема на интервале 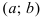 . Если ее первая производная
. Если ее первая производная 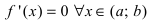 , то функция постоянна на сегменте
, то функция постоянна на сегменте 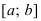 .
.
Доказательство: Пусть первая производная функции 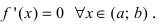 Возьмем произвольную точку
Возьмем произвольную точку 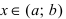 и рассмотрим сегмент
и рассмотрим сегмент 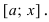 На этом сегменте выполняются все условия теоремы Лагранжа, следовательно,
На этом сегменте выполняются все условия теоремы Лагранжа, следовательно, 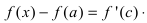
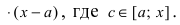 Так как по условию теоремы
Так как по условию теоремы 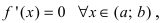 то и в точке с первая производная функции обращается в нуль. Отсюда получаем,что
то и в точке с первая производная функции обращается в нуль. Отсюда получаем,что 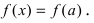 В силу произвольности точки х полученное равенство выполняется
В силу произвольности точки х полученное равенство выполняется 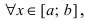 т.е. функция постоянна на сегменте
т.е. функция постоянна на сегменте 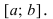
Минимум и максимум (экстремумы) функции
Пусть функция 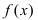 непрерывна в точке
непрерывна в точке 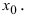
Определение: Функция 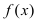 имеет в точке
имеет в точке 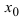 минимум (min), если существует такая
минимум (min), если существует такая 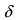 -окрестность точки
-окрестность точки 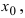 что
что 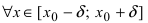 значение функции в любой другой точке
значение функции в любой другой точке 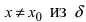 -окрестность точки
-окрестность точки  превышает значение функции в самой точке
превышает значение функции в самой точке 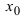 , т.е. выполняется неравенство
, т.е. выполняется неравенство 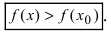
Обозначение 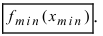
Определение: Функция 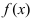 имеет в точке
имеет в точке 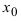 максимум (max), если существует такая
максимум (max), если существует такая 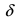 -окрестность точки
-окрестность точки 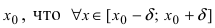 значение функции в любой другой точке
значение функции в любой другой точке 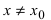 из
из 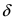 -окрестность точки х0
-окрестность точки х0 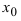 меньше значения функции в самой точке
меньше значения функции в самой точке 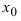 , т.е. выполняется неравенство
, т.е. выполняется неравенство 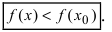
Обозначение 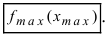
Пример:
Найти на заданном графике точки максимума и минимума (Рис. 77). 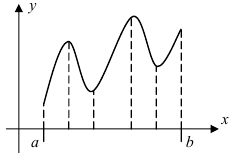
Рис. 77. Максимумы и минимумы заданной функции.
Решение:
Определение: Точки минимума и максимума объединяются под общим названием точки экстремума.
Замечание: Точки экстремума всегда являются внутренними точками области определения функции.
Замечание: Не следует путать минимальное значение функции 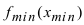 с наименьшим значением функции на сегменте
с наименьшим значением функции на сегменте 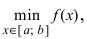 а максимальное значение функции
а максимальное значение функции 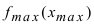 – с наибольшим значением функции на сегмен- те
– с наибольшим значением функции на сегмен- те 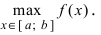
Замечание: Из определения экстремума следует, что в точке минимума выполняется неравенство 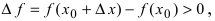 а в точке максимума –
а в точке максимума – 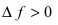 в некоторой малой
в некоторой малой 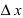 -окрестности точки
-окрестности точки 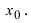
Необходимое условие существования экстремума функции
Теорема: Если дифференцируемая функция 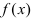 имеет в точке
имеет в точке 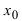 экстремум, то ее первая производная в этой точке равна нулю, т.е.
экстремум, то ее первая производная в этой точке равна нулю, т.е. 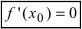
Доказательство: Пусть в точке 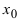 функция
функция 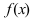 имеет максимум. Так как функция
имеет максимум. Так как функция 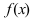 дифференцируема в точке
дифференцируема в точке 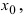 то в этой точке существует ее первая производная
то в этой точке существует ее первая производная 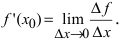 При стремлении
При стремлении 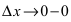 (слева) приращение аргумента
(слева) приращение аргумента 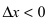 , а приращение функции
, а приращение функции 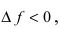 следовательно,
следовательно, 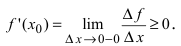 При стремлении
При стремлении 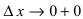 (справа) приращение аргумента
(справа) приращение аргумента 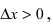 а приращение функции
а приращение функции 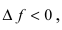 следовательно,
следовательно, 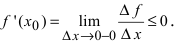 Так как производная в точке
Так как производная в точке 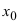 не может одновременно быть и отрицательной и положительной, то в этой точке она равна нулю, т.е.
не может одновременно быть и отрицательной и положительной, то в этой точке она равна нулю, т.е.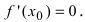 Случай, когда в точке х0
Случай, когда в точке х0 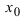 наблюдается минимум, доказать самостоятельно.
наблюдается минимум, доказать самостоятельно.
Замечание: Обращение в нуль первой производной функции в точке х0 я взлетел необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке х0 даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.
Пример:
Доказать, что функция 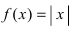 имеет “острый” экстремум в точке
имеет “острый” экстремум в точке 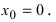
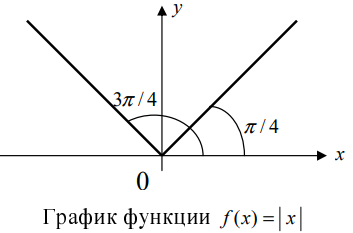
Решение:
Из Рис. 72 видно, что в точке 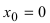 функция определена и непрерывна, одна- ко ее первая производная
функция определена и непрерывна, одна- ко ее первая производная 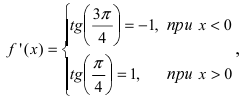 т.е. в точке
т.е. в точке 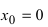 первая производная функции не существует. Однако по графику функции видно, что в точке
первая производная функции не существует. Однако по графику функции видно, что в точке 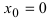 заданная функция имеет “острый” экстремум.
заданная функция имеет “острый” экстремум.
Определение: Точки, в которых первая производная функции обращается в нуль или не существует, называются критическими (стационарными или подозрительными на экстремум).
Замечание: Всякая точка экстремума является критической точкой, однако не любая критическая точка будет экстремумом.
Пример:
Доказать, что функция 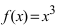 не имеет экстремума в точке
не имеет экстремума в точке 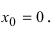
Решение:
В точке 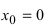 первая производная функции
первая производная функции 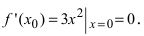 Однако из графика кубической параболы видно (график кубической параболы см. в Лекции № 22), что в точке
Однако из графика кубической параболы видно (график кубической параболы см. в Лекции № 22), что в точке 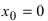 она экстремума не имеет. Следовательно, исследуемая точка является критической точкой, но не точкой экстремума.
она экстремума не имеет. Следовательно, исследуемая точка является критической точкой, но не точкой экстремума.
Исследование функций с помощью производных
Первый и второй достаточные признаки существования экстремума
Первый достаточный признак существования экстремума:
Теорема: Если функция 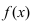 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки
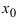 , кроме может быть самой точки
, кроме может быть самой точки 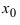 , и при переходе через эту точку слева направо ее первая произвол пая меняет свой знак с “+” на то в точке
, и при переходе через эту точку слева направо ее первая произвол пая меняет свой знак с “+” на то в точке 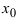 функция
функция 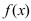 имеет максимум, а если ее первая производная меняет свой знак с на “+”, то в точке
имеет максимум, а если ее первая производная меняет свой знак с на “+”, то в точке 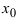 функция
функция 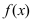 имеет минимум. Если при переходе через точку
имеет минимум. Если при переходе через точку 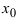 первая производная не меняет свой знак, то в этой точке экстремума нет.
первая производная не меняет свой знак, то в этой точке экстремума нет.
Второй достаточный признак существования экстремума:
Теорема: Если в точке 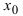 первая производная функции
первая производная функции 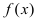 обращается в нуль(
обращается в нуль(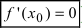 ), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (
), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (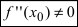 ), то в точке
), то в точке 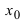 наблюдается экстремум. Если при этом
наблюдается экстремум. Если при этом 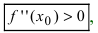 то точка
то точка 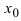 является точкой минимума, а при
является точкой минимума, а при 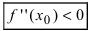 – точкой максимума.
– точкой максимума.
Пример:
Найти и определить тип экстремумов функции 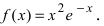
Решение:
Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: 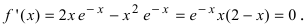 Так как показательная функция
Так как показательная функция 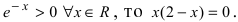 Отсюда находим критические точки
Отсюда находим критические точки 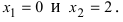 Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:
Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:

При переходе слева направо через точку 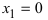 первая производная функция меняет свой знак с “-” на “+,” следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку
первая производная функция меняет свой знак с “-” на “+,” следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку 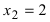 первая производная функция меняет свой знак с “+” на “-” следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции:
первая производная функция меняет свой знак с “+” на “-” следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции: 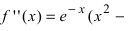
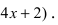 Вычислим значение второй производной функции в точке
Вычислим значение второй производной функции в точке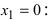
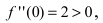 следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке
следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке 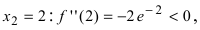 следовательно, в этой точке функция имеет максимум.
следовательно, в этой точке функция имеет максимум.
Наименьшее и наибольшее значения функции на сегменте (a; b)
Наименьшее и наибольшее значения функции на сегменте 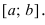
Пусть функция 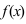 непрерывна на сегменте
непрерывна на сегменте 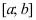 и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри сегмента, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного сегмента. Поэтому для отыскания этих значений применяют следующую схему:
и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри сегмента, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного сегмента. Поэтому для отыскания этих значений применяют следующую схему:
- Находят область определения функции и убеждаются в том, что заданный сегмент входит в эту область.
- Находят критические точки, для чего решают уравнение
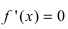 и точки, в которых первая производная функции не существует.
и точки, в которых первая производная функции не существует. - Вычисляют значения функции в критических точках, принадлежащих заданному сегменту, в точках, в которых первая производная функции не существует и на концах заданного сегмента.
- Из полученных чисел выбирают наименьшее
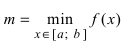 и наибольшее
и наибольшее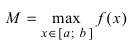 .
.
Пример:
Найти наименьшее и наибольшее значения функции 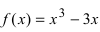 на сегменте
на сегменте 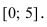
Решение:
Действуя согласно вышеприведенной схеме, находим:
1. 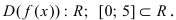 Следовательно, функция определена и непрерывна на заданном сегменте.
Следовательно, функция определена и непрерывна на заданном сегменте.
2. Вычислим первую производную 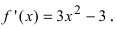 Производная существует на всей числовой оси, поэтому найдем критические точки
Производная существует на всей числовой оси, поэтому найдем критические точки 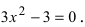 Отсюда на- ходим, что
Отсюда на- ходим, что 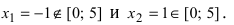
3. Вычислим значение функции в критических точках и на концах заданного сегмента: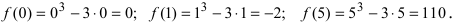
4. Из полученных чисел выбираем наименьшее 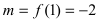 и наибольшее
и наибольшее 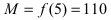 числа, которые определяют наименьшее и наибольшее значения функции
числа, которые определяют наименьшее и наибольшее значения функции 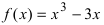 на сегменте
на сегменте 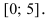
Выпуклость и вогнутость графика функции. Точки перегиба
Определение: График функции 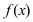 называется выпуклым на интервале
называется выпуклым на интервале 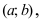 если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 78).
если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 78). 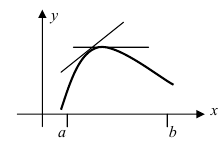
Рис. 78. Выпуклый график функции 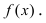
Определение: График функции 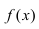 называется вогнутым на интервале
называется вогнутым на интервале 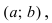 если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 79).
если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 79). 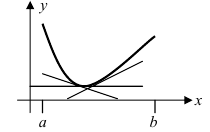
Рис. 79. Вогнутый график функции 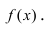
Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:
ТЗ. Если вторая производная функции 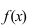 на интервале
на интервале 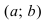 существует и положительна, то на этом интервале график функции
существует и положительна, то на этом интервале график функции 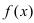 будет вогнутым. Если вторая производная функции
будет вогнутым. Если вторая производная функции 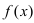 на интервале
на интервале 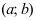 существует и отрицательна, то на этом интервале график функции
существует и отрицательна, то на этом интервале график функции 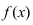 будет выпуклым.
будет выпуклым.
Пример:
Определить интервалы вогнутости и выпуклости графика функции 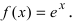
Решение:
Найдем вторую производную от заданной функции 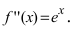 В силу того, что
В силу того, что 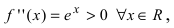 то график функции
то график функции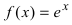 будет вогнутым на всей числовой оси.
будет вогнутым на всей числовой оси.
Пример:
Определить интервалы вогнутости и выпуклости графика функции 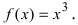
Решение:
Найдем вторую производную от заданной функции 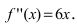 В силу того, что
В силу того, что
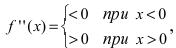 то график функции
то график функции 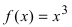 будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.
будет выпуклым при отрицательных значениях аргумента и вогнутым при положительных значениях аргумента.
Определение: Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.
Необходимое и достаточное условия существования точки перегиба
Рассмотрим необходимое условие существования точки перегиба.
Теорема: Если функция 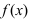 дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба
дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба 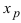 , то в точке перегиба вторая производная равна нулю, т.е.
, то в точке перегиба вторая производная равна нулю, т.е.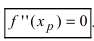
Замечание: Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования такой точки на графике функции.
Пример:
Доказать, что точка 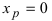 не является точкой перегиба графика функции
не является точкой перегиба графика функции 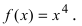
Решение:
Если вычислить вторую производную от заданной функции, то она будет равна 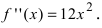 Если приравнять это выражение к нулю, то получим, что точка
Если приравнять это выражение к нулю, то получим, что точка 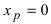 должна быть точкой перегиба графика функции
должна быть точкой перегиба графика функции 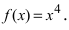 Однако график этой функции (см. Лекцию № 22) на всей числовой оси является вогнутым, т.е. точка
Однако график этой функции (см. Лекцию № 22) на всей числовой оси является вогнутым, т.е. точка 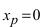 не является точкой перегиба графика функции
не является точкой перегиба графика функции 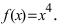
Теорема: Пусть функция 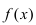 дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке
дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке 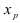 , принадлежащей этому интервалу, обращается в нуль (
, принадлежащей этому интервалу, обращается в нуль (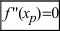 ) или не существует. Если при переходе через точку
) или не существует. Если при переходе через точку 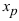 вторая производная функции меняет свой знак, то точка
вторая производная функции меняет свой знак, то точка 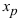 определяет точку перегиба графика функции
определяет точку перегиба графика функции 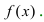
Пример:
Найти точки перегиба и интервалы выпуклости и вогнутости графика функции 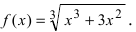
Решение:
Найдем вторую производную заданной функции 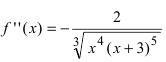 (найти самостоятельно). Найдем точки подозрительные на перегиб: а)
(найти самостоятельно). Найдем точки подозрительные на перегиб: а)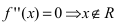 б)
б)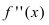 – не существует
– не существует  знаменатель дроби обращается в нуль при
знаменатель дроби обращается в нуль при 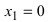 и
и 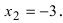 Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:
Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:

Из рисунка видно, что точка 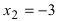 является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка
является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка 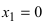 не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
Асимптоты графика функции f (x)
Асимптоты графика функции 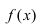
В большинстве практических случаев необходимо знать поведение функции при неограниченном росте (убыли) аргумента. Одним из наиболее интересных случаев, которые возникают при таком исследовании, является случай, когда график функции неограниченно приближается к некоторой прямой.
Определение: Прямая (l): 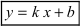 называется асимптотой графика функции
называется асимптотой графика функции 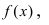 если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента
если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента 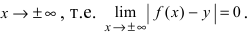
Замечание: График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой (Рис. 80). 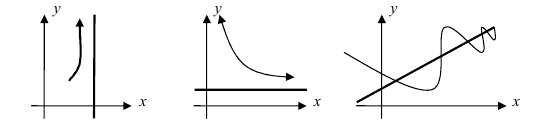
Рис. 80. Различные случаи приближения графика функции к асимптотам.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Определение: Вертикальная прямая 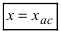 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если 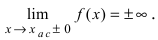 Горизонтальная прямая
Горизонтальная прямая 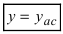 называется горизонтальной асимптотой, если
называется горизонтальной асимптотой, если 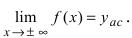 Прямая
Прямая 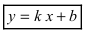 называется наклонной асимптотой (параметр
называется наклонной асимптотой (параметр 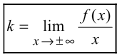 и параметр
и параметр 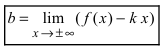 отличаются от
отличаются от 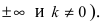
Горизонтальная асимптота является частным случаем наклонной асимптоты: если 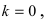 то наклонная асимптота вырождается в горизонтальную
то наклонная асимптота вырождается в горизонтальную 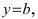 при условии, что
при условии, что 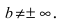 Если параметр
Если параметр 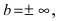 то горизонтальной асимптоты нет.
то горизонтальной асимптоты нет.
Полная схема исследования функции с помощью производных
Из изложенного в Лекциях № 20 и №21 материала следует следующая схема исследования функции с помощью производных:
- Находят область определения функции. При наличии точек разрыва II рода изучают поведение функции в их малой окрестности, т.е. вычисляют лево- и правосторонние пределы. При задании функции словесным образом также вычисляют лево- и правосторонние пределы для граничных точек интервалов, на которых функция описывается разными формулами.
- Находят точки пересечения с координатными осями.
- Определяют четная, нечетная или общего вида заданная функция.
- Определяют периодическая или непериодическая заданная функция.
- Находят критические точки, решая уравнение
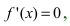 и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (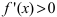 ) и убывания(
) и убывания( 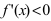 ) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках. - Находят точки подозрительные на перегиб, решая уравнение
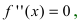 и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (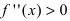 ) и выпуклости (
) и выпуклости (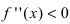 ) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках. - Находят асимптоты графика функции.
- Результаты исследования заносят в сводную таблицу
- Поданным таблицы строят схематичный график функции.
Замечание: При нахождении области определения функции надо помнить о действиях, запрещенных в области действительного переменного:
- нельзя делить на нуль, поэтому выражение, стоящее в знаменателе дроби, не должно равняться нулю;
- нельзя извлекать корень четной степени из отрицательного числа, поэтому выражение, стоящее под корнем четной степени, должно быть неотрицательным (
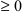 );
); - основание логарифмической функции должно быть строго положительным и не равным единице;
- выражение, стоящее под логарифмом, должно быть строго положительным;
- выражение, стоящее под знаком arcsin или arccos, по модулю не должно превышать единицу (
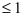 ).
).
Пример:
Исследовать и построить схематичный график функции 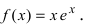
Решение:
Используя схему исследования графика функции с помощью производных, найдем:
1. 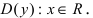
2. Найдем точки пересечения графика функции с координатными осями
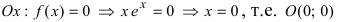 – точка пересечения с осью абсцисс;
– точка пересечения с осью абсцисс;
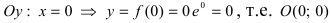 – точка пересечения с осью ординат.
– точка пересечения с осью ординат.
3. Вычислим 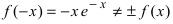 – функция общего вида.
– функция общего вида.
4. Функция непериодическая (периодическими среди элементарных функций являются функции: sinx, cosx, tgx и ctgx).
5. Найдем первую производную функции 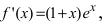 которая существует на всей числовой оси, следовательно, найдем критические точки, решая уравнение
которая существует на всей числовой оси, следовательно, найдем критические точки, решая уравнение 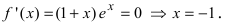 Отложим найденную точку на числовой оси и определим знак первой производной на каждом интервале
Отложим найденную точку на числовой оси и определим знак первой производной на каждом интервале
 Из рисунка видно, что
Из рисунка видно, что 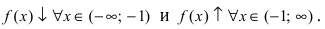 Так как при переходе слева направо через точку х = -1 первая производная меняет свой знак с “-” на “+”, то в точке наблюдается минимум. Вычислим значение функции в минимуме
Так как при переходе слева направо через точку х = -1 первая производная меняет свой знак с “-” на “+”, то в точке наблюдается минимум. Вычислим значение функции в минимуме 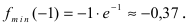
6. Найдем вторую производную функции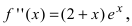 которая существует на всей числовой оси, следовательно, найдем точки, подозрительные на перегиб, решая уравнение
которая существует на всей числовой оси, следовательно, найдем точки, подозрительные на перегиб, решая уравнение 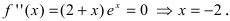 Отложим найденную точку на числовой оси и определим знак второй производной на каждом интервале
Отложим найденную точку на числовой оси и определим знак второй производной на каждом интервале  Из рисунка видно, что
Из рисунка видно, что 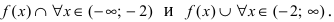 Так как при переходе слева направо через точку х = -2 вторая производная меняет свой знак, то в этой точке наблюдается точка перегиба. Вычислим значение функции в точке перегиба
Так как при переходе слева направо через точку х = -2 вторая производная меняет свой знак, то в этой точке наблюдается точка перегиба. Вычислим значение функции в точке перегиба 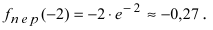
7. Найдем асимптоты графика функции, для чего вычислим угловой коэффициент прямой 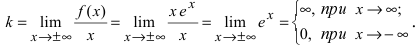 Таким образом, при
Таким образом, при 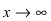 асимптот нет, а при
асимптот нет, а при 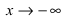 возможна горизонтальная асимптота. Вычислим параметр
возможна горизонтальная асимптота. Вычислим параметр 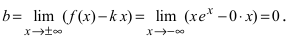 Следовательно, график заданной функции имеет горизонтальную асимптоту у = 0.
Следовательно, график заданной функции имеет горизонтальную асимптоту у = 0.
8. Построим сводную таблицу
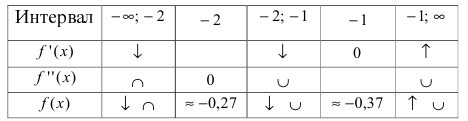
О(0; 0) – точка пересечения с координатными осями.
у = 0 – горизонтальная асимптота.
9. Построим схематичный график функции, выбрав по координатным осям разные масштабы измерения:
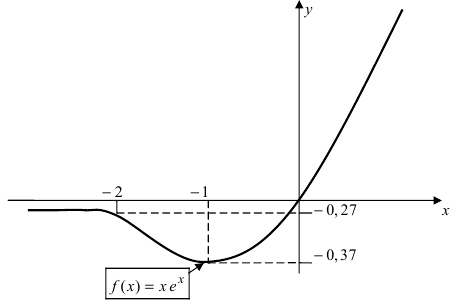
——–
Исследование функций с помощью производных
Определение 1. Функция y=f(x) называется возрастающей (убывающей) на интервале ( a,b ), если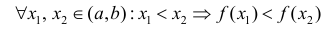
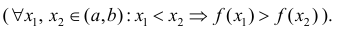
Функция y=f(x) называется неубывающей (невозрастающей) на
интервале ( a,b ), если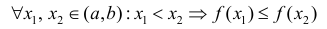
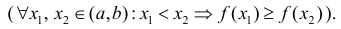
Возрастает:
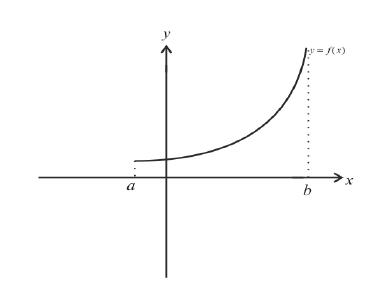
Убывает:
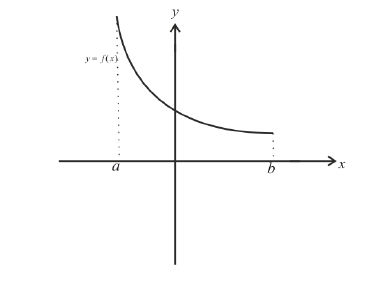
Неубывает:
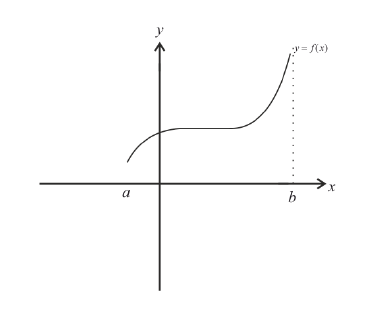
Невозрастает:
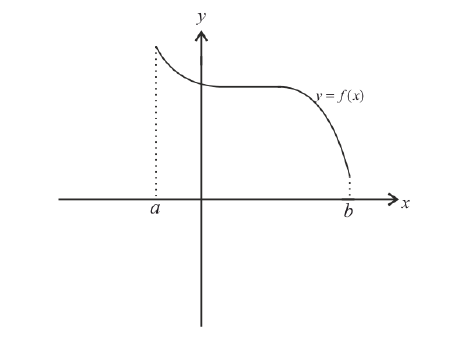
Функции из определения 1 называются монотонными.
Теорема 1. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) не убывала (не возрастала) на этом интервале необходимо и достаточно,
чтобы 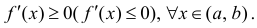
Доказательство. Необходимость. Рассмотрим случай, когда f(x) не
убывает и докажем, что производная 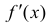 необходимо ≥ 0.
необходимо ≥ 0.
Пусть 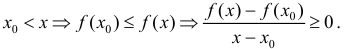
Пусть 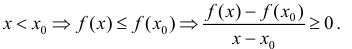
Таким образом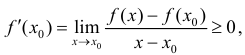 что и требовалось доказать.
что и требовалось доказать.
Достаточность. Рассмотрим случай, когда 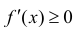 и докажем, что этого достаточно для того, чтобы функция не убывала. Пусть
и докажем, что этого достаточно для того, чтобы функция не убывала. Пусть 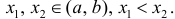
Тогда по теореме Лагранжа (теорема 4 § 12) ∃ точка 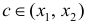 такая, что
такая, что
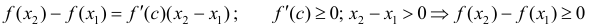 что и требовалось доказать.
что и требовалось доказать.
Теорема 2. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) возрастала (убывала) на этом интервале достаточно, чтобы
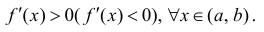 .
.
Доказательство теоремы аналогично доказательству достаточности в теореме 1. Нужно заметить, что условие 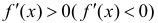 не является необходимым для возрастания (убывания) функции.
не является необходимым для возрастания (убывания) функции.
Пример 1.
Рассмотрим функцию 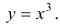 Она возрастает на промежутке ( -1;1). Но условие
Она возрастает на промежутке ( -1;1). Но условие 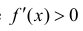 не выполнено в точке
не выполнено в точке 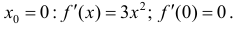
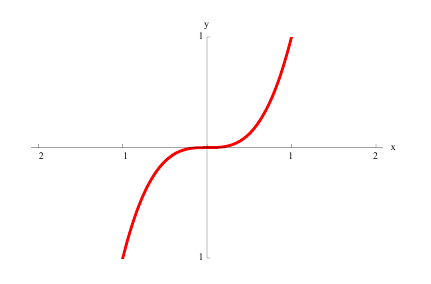
Теорема 3. (необходимое условие экстремума).
Пусть функция y=f(x) определена в некоторой окрестности точки  и имеет в этой точке локальный экстремум (см. определение 1 §12). Тогда ее производная в этой точке равна 0 или не существует.
и имеет в этой точке локальный экстремум (см. определение 1 §12). Тогда ее производная в этой точке равна 0 или не существует.
Доказательство.
Если производная 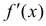 в точке
в точке  не существует, то все доказано. Предположим, что
не существует, то все доказано. Предположим, что 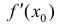 – существует. Тогда по теореме Фермa (теорема 1 §12)
– существует. Тогда по теореме Фермa (теорема 1 §12) 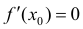 , что и требовалось доказать.
, что и требовалось доказать.
Определение 2. Пусть функция y=f(x) непрерывна в точке  и производная равна 0 или не существует. Тогда точка
и производная равна 0 или не существует. Тогда точка  называется критической точкой для функции y=f(x) или точкой возможного экстремума.
называется критической точкой для функции y=f(x) или точкой возможного экстремума.
Замечание. Для непрерывной функции любая точка локального экстремума
будет критической. Наоборот – не верно.
Пример 2.
Для функции 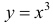 , точка
, точка 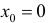 – критическая, но не является точкой локального экстремума.
– критическая, но не является точкой локального экстремума.
Для функции
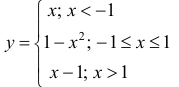
(см. пример 9 §5) 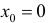 – критическая и локальный максимум;
– критическая и локальный максимум;  =1 критическая и локальный минимум.
=1 критическая и локальный минимум.
Для функции
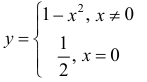
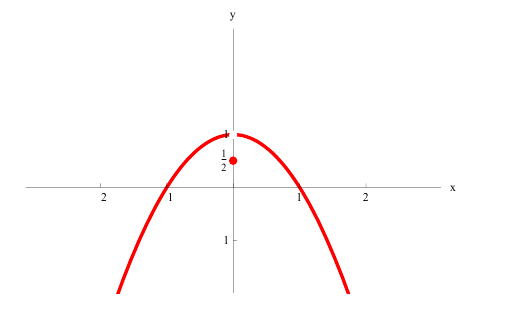
точка 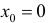 – локального минимума, производная y′ в точке
– локального минимума, производная y′ в точке  не существует. Точка
не существует. Точка  не является критической( в точке
не является критической( в точке  – разрыв 1-ого рода).
– разрыв 1-ого рода).
Для функции
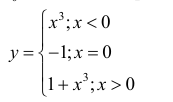
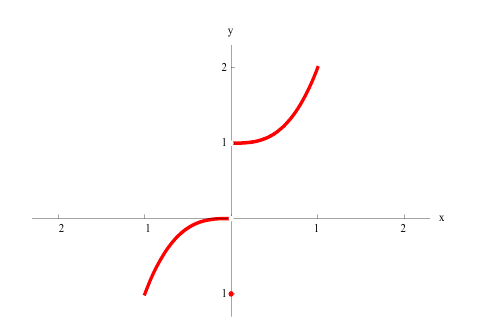
точка  = 0 – точка локального минимума. Точка
= 0 – точка локального минимума. Точка  не является критической( в точке
не является критической( в точке  – разрыв 1-ого рода).
– разрыв 1-ого рода).
Теорема 4. (достаточное условие экстремума функции). Пусть функция y=f(x)
дифференцируема в некоторой окрестности 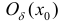 своей критической точки
своей критической точки
 за исключением может быть самой точки
за исключением может быть самой точки  .
.
а) Пусть при переходе через точку  производная
производная 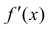 меняет знак с « − »
меняет знак с « − »
на «+» :
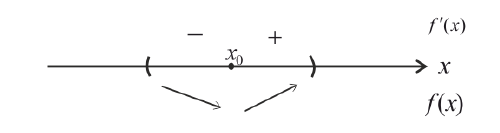
Тогда  – точка локального минимума.
– точка локального минимума.
Пусть при переходе через точку  производная
производная 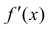 меняет знак с «+» на « − »:
меняет знак с «+» на « − »:
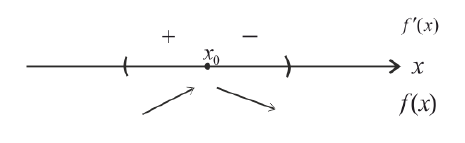
Тогда  – точка локального максимума.
– точка локального максимума.
б) Пусть при переходе через точку  производная
производная 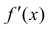 не меняет знака.
не меняет знака.
Тогда  не является точкой локального экстремума.
не является точкой локального экстремума.
Доказательство следует из теоремы 2. При этом важно, чтобы функция y=f(x) была непрерывна в точке  (см. пример 2), а также то, что
(см. пример 2), а также то, что  изолированная критическая точка.
изолированная критическая точка.
Теорема 5. (второе достаточное условие экстремума функции).
Пусть  – стационарная точка для функции y=f(x), то есть
– стационарная точка для функции y=f(x), то есть 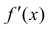 =0.
=0.
Пусть 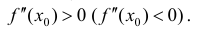 Тогда
Тогда  – точка локального минимума (локального
– точка локального минимума (локального
максимума).
Доказательство. Запишем формулу Тейлора 2-ого порядка для функции y=f(x) в окрестности точки  :
:
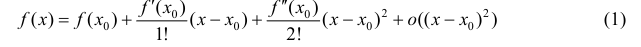
(см. теорему 1 §14).
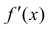 =0, поэтому из (1) следует:
=0, поэтому из (1) следует:
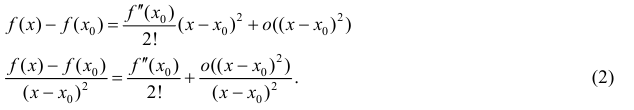
Из (2) следует, что ∃ окрестность точки  , такая что знак
, такая что знак 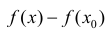 совпадает со знаком
совпадает со знаком 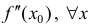 из этой окрестности, что и требовалось доказать.
из этой окрестности, что и требовалось доказать.
Теорема 6. Пусть функция y=f(x) имеет в точке  n производных, причем
n производных, причем
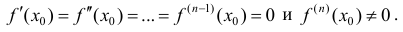 Тогда:
Тогда:
1) если n – четное и 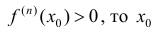 – точка локального минимума;
– точка локального минимума;
2) если n – четное и 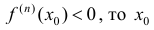 – точка локального максимума;
– точка локального максимума;
3) если n – нечетное, то в точке  локального экстремума нет.
локального экстремума нет.
Доказательство аналогично доказательству теоремы 5.
Пример 3.
Исследовать на экстремум функцию 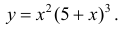
Решение. Функция непрерывна ∀x∈R .
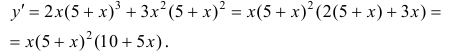
Найдем критические точки: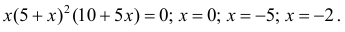
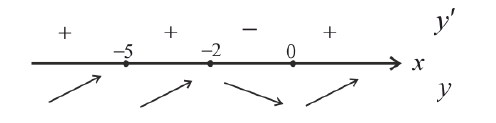
x=-2 – точка локального максимума: y(-2) = 108 y;
x = 0 – точка локального минимума; y(0) = 0.
x = −5 – не является точкой экстремума.
При исследовании функции на экстремум точки разрыва(если они есть)
также наносят на числовую прямую. При переходе через эти точки может
изменятся направление возрастания (убывания) функции.
Замечание. При решении ряда технических и экономических задач приходится находить не локальные, а глобальные экстремумы (наибольшие и наименьшие значения функций на некотором множестве). Из теоремы Вейерштрасса (см. теорему 1 §11) следует, что для непрерывной функции y=f(x) заданной на отрезке [ a,b] глобальные min и max существуют. При этом точки с 1 и с 2 – глобального min и max лежат либо на концах отрезка [ a,b], либо являются критическими для функции f(x).
Пример 4.
Найти наибольшее и наименьшее значение функции 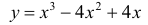 на отрезке [ 0, 3 ].
на отрезке [ 0, 3 ].
Решение. Функция непрерывна ∀x∈R. Найдем критические точки:

Пример 5.
Боковые стороны и меньшее основание трапеции = а . Найти
длину большего основания, при котором площадь трапеции – наибольшая.
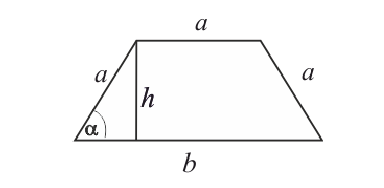
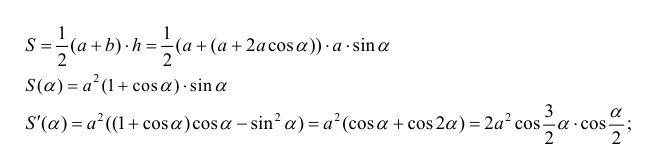
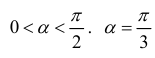 критическая точка для функции S(α).
критическая точка для функции S(α).
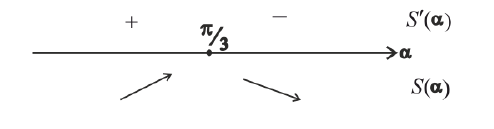
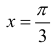 – точка локального максимума.
– точка локального максимума.
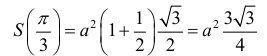 – наибольшее значение площади, при этом
– наибольшее значение площади, при этом
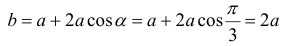 -длина большего основания.
-длина большего основания.
——-
Исследование функций с помощью производных(часть вторая)
Определение 1. Пусть функция y=f(x) дифференцируема на интервале ( a,b) . И пусть 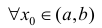 график функции y=f(x) расположен ниже (не выше), чем касательная y=y(x) к нему в точке
график функции y=f(x) расположен ниже (не выше), чем касательная y=y(x) к нему в точке 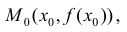 то есть
то есть
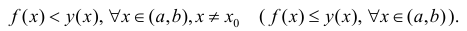 Тогда f( x ) называется выпуклой(нестрого выпуклой вверх).
Тогда f( x ) называется выпуклой(нестрого выпуклой вверх).
Пусть 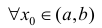 график функции y=f(x) расположен выше (не ниже), чем касательная y=y(x) к нему в точке
график функции y=f(x) расположен выше (не ниже), чем касательная y=y(x) к нему в точке 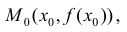 то есть
то есть
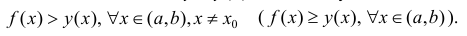 Тогда f(x) называется вогнутой (нестрого вогнутой).
Тогда f(x) называется вогнутой (нестрого вогнутой).
Пример 1.
а) 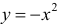 − выпукла на всей оси ( −∞; +∞):
− выпукла на всей оси ( −∞; +∞):
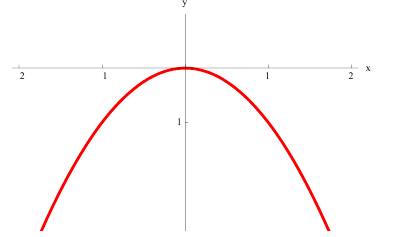
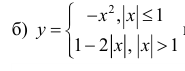 нестрого выпукла вверх на всей оси (−∞; +∞)
нестрого выпукла вверх на всей оси (−∞; +∞)
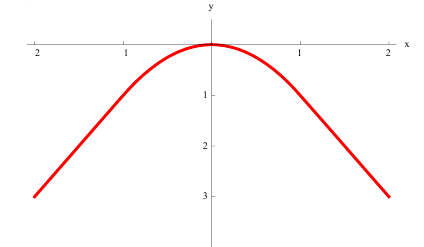
в) 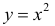 вогнута на всей оси (−∞; +∞):
вогнута на всей оси (−∞; +∞):
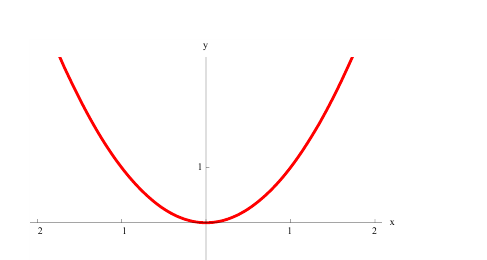
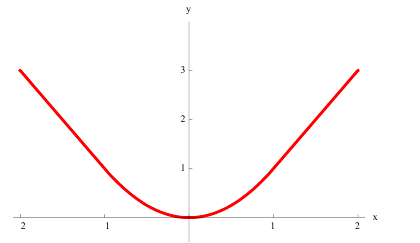
г) 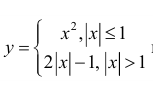 нестрого вогнута на всей оси (−∞; +∞):
нестрого вогнута на всей оси (−∞; +∞):
Теорема 1. Для того, чтобы дифференцируемая функция y=f(x) была вогнутой (выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы ее производная 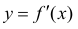 возрастала(убывала) на этом интервале.
возрастала(убывала) на этом интервале.
Докажем для случая, когда y=f(x) – вогнута.
Необходимость. Пусть 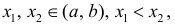
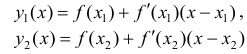 – касательные к графику y=f(x) в точках
– касательные к графику y=f(x) в точках 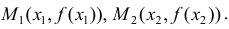 Так как y=f(x) – вогнута, то
Так как y=f(x) – вогнута, то
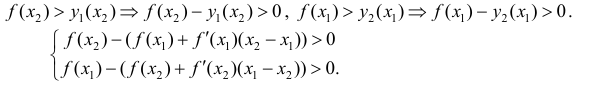
Сложим эти неравенства:
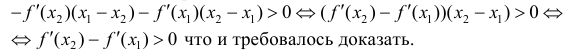
Достаточность. Пусть 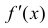 – возрастает. Докажем, что y=f(x) – вогнута.
– возрастает. Докажем, что y=f(x) – вогнута.
Пусть 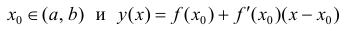 – уравнение касательной в точке
– уравнение касательной в точке 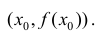
Пусть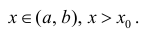 Найдем разность
Найдем разность 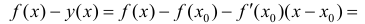 по теореме Лагранжа (терема 4 параграфа 12) =
по теореме Лагранжа (терема 4 параграфа 12) =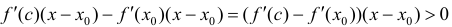 что и требовалось доказать.
что и требовалось доказать.
Теорема 2. Для того, чтобы дифференцируемая функция y=f(x) была нестрого вогнутой (нестрого выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы производная 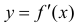 неубывала (невозрастала) на этом интервале.
неубывала (невозрастала) на этом интервале.
Доказательство аналогично доказательству теоремы 1.
Теорема 3. Для того, чтобы дважды дифференцируемая на интервале (a,b) функция y=f(x) была не строго вогнутой (не строго выпуклой) необходимо и
достаточно, чтобы 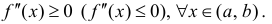
Доказательство следует из теоремы 2 и теоремы 1 §15.
Теорема 4. Для того, чтобы дважды дифференцируемая на интервале (a,b)
функция y=f(x) была вогнутой (выпуклой) на этом интервале достаточно, чтобы 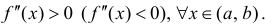
Доказательство следует из теоремы 1 и теоремы 2 §15. Нужно заметить, что
условие 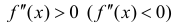 не является необходимым для вогнутости (выпуклости) функции.
не является необходимым для вогнутости (выпуклости) функции.
Пример 2.
Рассмотрим функцию 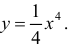 Она вогнута на интервале ( -1;1). Но условие
Она вогнута на интервале ( -1;1). Но условие 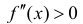 не выполнено в точке
не выполнено в точке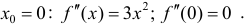
Теорема 6 (достаточное условие перегиба функции). Рассмотрим функцию
y=f(x) дважды дифференцируемую в некоторой окрестности 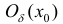 точки
точки
возможного перегиба 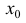 за исключением может быть самой точки
за исключением может быть самой точки 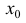
Предположим также, что вторая производная 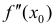 меняет знак при переходе
меняет знак при переходе
через точку 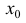 . Тогда
. Тогда 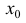 будет точкой перегиба для функции y=f(x).
будет точкой перегиба для функции y=f(x).
Доказательство следует из теоремы 4.
Пример 3.
Найдем точки перегиба и интервалы выпуклости-вогнутости функции
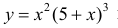 из примера 3 §15.
из примера 3 §15.
Решение.
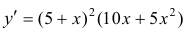 (см. пример 3 §15).
(см. пример 3 §15).
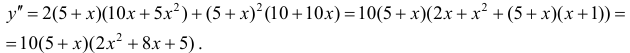
Найдем точки возможного перегиба(точки, где y′′ равна 0 или не существует).
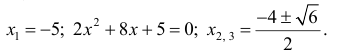
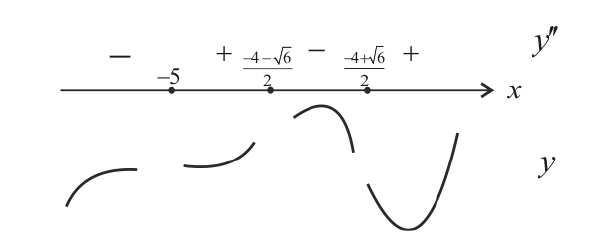
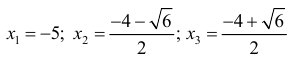 точки перегиба функции.
точки перегиба функции.
При нахождении интервалов выпуклости-вогнутости точки, где функции
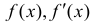 имеют разрывы также наносят на числовую прямую. При переходе
имеют разрывы также наносят на числовую прямую. При переходе
через эти точки может меняться направление выпуклости-вогнутости.
Определение 4. Прямая y= kx +b называется наклонной асимптотой функции y=f(x) при x →+∞ (x→−∞), если 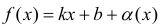 , где a(x) бесконечно-малая функция при x →+∞ (x→−∞) , то есть
, где a(x) бесконечно-малая функция при x →+∞ (x→−∞) , то есть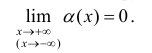
Теорема 7. Для того, чтобы прямая y =kx +b была наклонной асимптотой для функции y=f(x) при x →+∞ (x→−∞) необходимо и достаточно, чтобы существовали пределы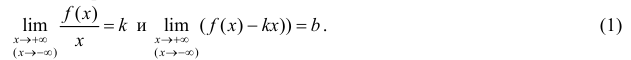
Доказательство. Рассмотрим, например, случай x → +∞ .
Необходимость. Пусть 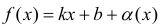 , где a(x) бесконечно-малая функция. Докажем, что выполняются пределы (1).
, где a(x) бесконечно-малая функция. Докажем, что выполняются пределы (1).
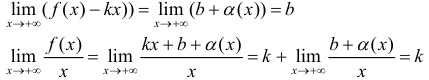 что и требовалось доказать.
что и требовалось доказать.
Достаточность. Пусть выполняется (1). Докажем, что y =kx +b – асимптота для y=f(x).
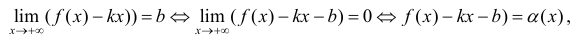 , где a(x) бесконечно-малая функция при x → +∞ , что и требовалось доказать. Таким образом теорема доказана.
, где a(x) бесконечно-малая функция при x → +∞ , что и требовалось доказать. Таким образом теорема доказана.
Замечание. Наличие наклонной асимптоты значит, что при x →+∞ (x→−∞) график функции очень близок к прямой линии y =kx +b.
Пример 4.
Для функции 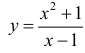 (см. пример 1 §5) y = x+1 – наклонная асимптота при x →±∞ .
(см. пример 1 §5) y = x+1 – наклонная асимптота при x →±∞ .
Для функции 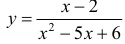 (пример 8 §5) y = 0 – горизонтальная асимптота при x →±∞ (k=0).
(пример 8 §5) y = 0 – горизонтальная асимптота при x →±∞ (k=0).
Для функции 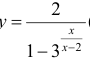 (пример 10 §5) y = −1 – горизонтальная асимптота при x →±∞ .
(пример 10 §5) y = −1 – горизонтальная асимптота при x →±∞ .
Для функции , 1(0 1) 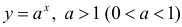 (пример 2 §5) y = 0 – горизонтальная
(пример 2 §5) y = 0 – горизонтальная
асимптота при x →+∞ (x→−∞).
Определение 5. Прямая 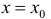 называется вертикальной асимптотой функции y=f(x), если хотя бы один из пределов
называется вертикальной асимптотой функции y=f(x), если хотя бы один из пределов 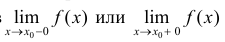 равен ∞.
равен ∞.
Пример 5.
Для функции 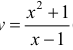 (см. пример 1 §5) прямая x = 1 – вертикальная асимптота, для функции
(см. пример 1 §5) прямая x = 1 – вертикальная асимптота, для функции 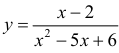 (пример 8 §5) прямая x = 3 – вертикальная асимптота, для функции
(пример 8 §5) прямая x = 3 – вертикальная асимптота, для функции 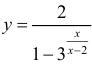 (пример 10 §5) прямая x = 0 – вертикальная асимптота, для функции
(пример 10 §5) прямая x = 0 – вертикальная асимптота, для функции 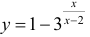 − из упражнения 1 §5 прямая x = 2 – вертикальная асимптота
− из упражнения 1 §5 прямая x = 2 – вертикальная асимптота
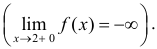
При построении графиков функции используют результаты §15, 16. Это можно проводить по следующей схеме:
1. Найти область определения D(f) функции и исследовать поведение функции в граничных точках D(f) . Определить точки разрыва, вертикальные асимптоты, нули функции, исследовать функцию на периодичность, четность, нечетность.
2. Найти наклонные асимптоты.
3. Найти интервалы монотонности, точки локального экстремума.
4. Найти интервалы выпуклости, вогнутости, точки перегиба.
5. Построить график.
Пример 6.
Провести полное исследование и построить график функции 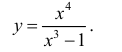
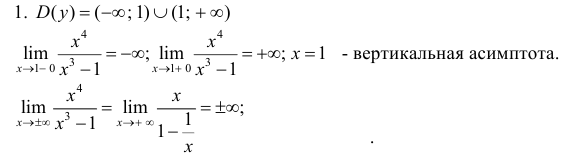
Нули функции 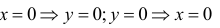
Таким образом график пересекает оси координат в точке О(0; 0). Функция
ни четная, ни нечетная, не периодическая.
2. Наклонные асимптоты. По формулам (1);

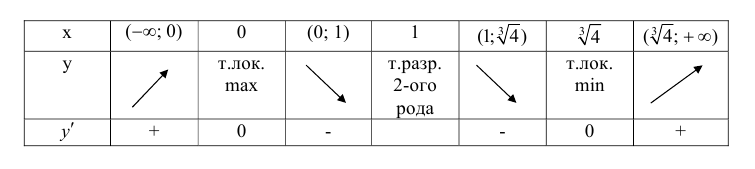
x = 0 – точка локального максимума; 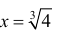 – точка локального минимума;
– точка локального минимума;
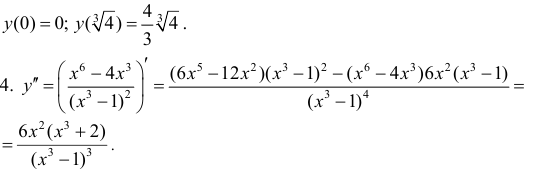
Точки где y′′ равна 0 или не существует: 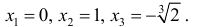
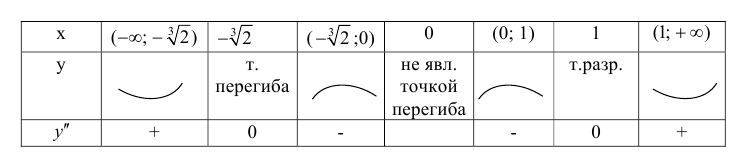
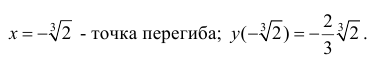
5. График функции.
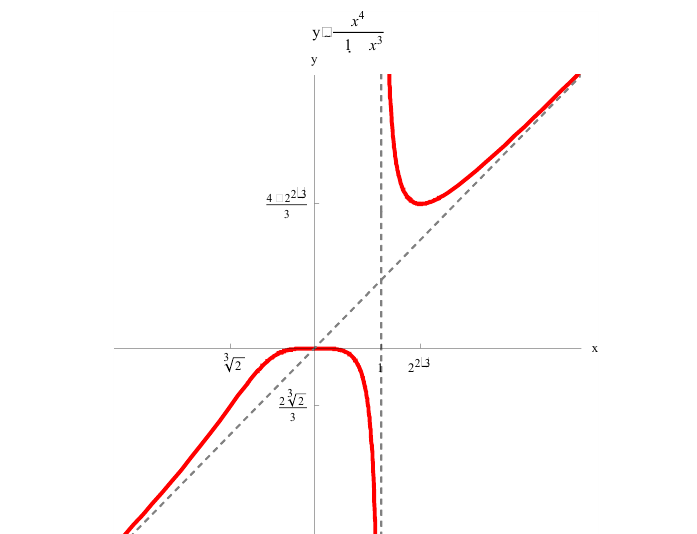
——–
Исследование функции с помощью производных
Монотонность функции
Теорема 9.1. Пусть функция 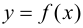 определена на отрезке
определена на отрезке 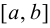 и внутри отрезка имеет конечную производную
и внутри отрезка имеет конечную производную 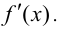 Для того, чтобы функция
Для того, чтобы функция 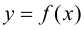 была монотонно возрастающей (убывающей), достаточно, чтобы
была монотонно возрастающей (убывающей), достаточно, чтобы 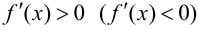 для
для 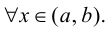
Доказательство.
Возьмем отрезок 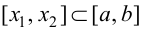 таким образом, чтобы
таким образом, чтобы 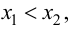 и применим к функции
и применим к функции 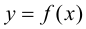 на этом промежутке формулу Лагранжа:
на этом промежутке формулу Лагранжа:
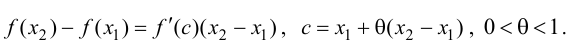
Тогда, если 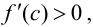 то
то 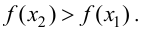 Следовательно, функция
Следовательно, функция 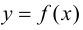 возрастает. Если
возрастает. Если 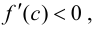 то
то 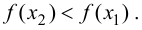 Следовательно, функция
Следовательно, функция 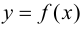 убывает.
убывает.
Замечание 9.1. Утверждение теоремы сохраняет силу и в том случае, если 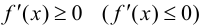 при условии, что производная
при условии, что производная 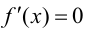 в конечном числе точек внутри отрезка
в конечном числе точек внутри отрезка 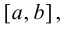 т. е. вышесказанное условие не является необходимым.
т. е. вышесказанное условие не является необходимым.
Пример 9.1. Рассмотрим функцию 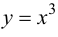 на отрезке
на отрезке 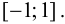 Хотя
Хотя 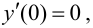 функция возрастает на отрезке
функция возрастает на отрезке 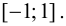
- Заказать решение задач по высшей математике
Достаточные условия экстремума
Теорема 9.2 (первое достаточное условие экстремума). Пусть функция 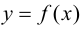 дифференцируема в некоторой проколотой окрестности точки
дифференцируема в некоторой проколотой окрестности точки 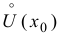 и непрерывна в точке
и непрерывна в точке 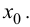 Тогда, если
Тогда, если 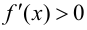 при
при 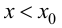 и
и 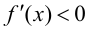 при
при 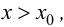 то в точке
то в точке 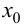 функция имеет локальный максимум; если
функция имеет локальный максимум; если 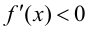 при
при 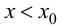 и
и 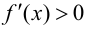 при
при 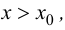 то в точке
то в точке 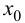 функция имеет локальный минимум.
функция имеет локальный минимум.
Доказательство следует из теоремы 9.1.
Теорема 9.3 (второе достаточное условие экстремума). Если в критической точке 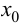 функции
функции 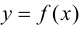 существует
существует 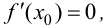 а
а 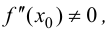 то при
то при 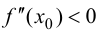 функция имеет локальный максимум, при
функция имеет локальный максимум, при 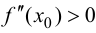 — локальный минимум.
— локальный минимум.
Доказательство.
Если в точке 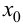 существует вторая производная
существует вторая производная 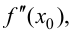 то первая производная
то первая производная 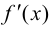 существует в некоторой окрестности этой точки
существует в некоторой окрестности этой точки 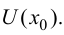 Тогда
Тогда 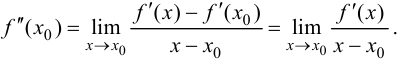
Пусть 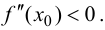 Тогда
Тогда 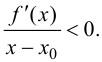
При 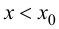 производная
производная 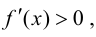 т. е., согласно теореме 9.1, функция
т. е., согласно теореме 9.1, функция 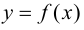 возрастает; при
возрастает; при 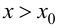 производная
производная 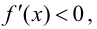 т. е. функция
т. е. функция 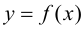 убывает. На основании теоремы 9.2: в точке
убывает. На основании теоремы 9.2: в точке 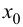 функция имеет локальный максимум.
функция имеет локальный максимум.
Случай 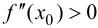 рассматривается аналогично.
рассматривается аналогично.
Замечание 9.2. Так как теорема формулирует только достаточное условие, то при 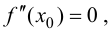 функция может как иметь, так и не иметь экстремум.
функция может как иметь, так и не иметь экстремум.
Пример 9.2. Функция 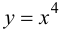 имеет в точке
имеет в точке 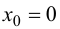 минимум, при этом
минимум, при этом 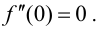 Функция
Функция 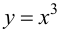 не имеет в точке
не имеет в точке 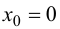 экстремума, при этом также
экстремума, при этом также 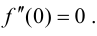
Наибольшее и наименьшее значения функции на отрезке
Пусть функция 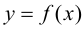 непрерывна на отрезке
непрерывна на отрезке 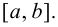 Тогда на этом отрезке функция достигает наибольшего и наименьшего значений, теорема 4.3 Вейерштрасса (раздел 1). Будем предполагать, что на данном отрезке функция
Тогда на этом отрезке функция достигает наибольшего и наименьшего значений, теорема 4.3 Вейерштрасса (раздел 1). Будем предполагать, что на данном отрезке функция 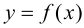 имеет конечное число критических точек. Если наибольшее и наименьшее значения достигаются внутри отрезка
имеет конечное число критических точек. Если наибольшее и наименьшее значения достигаются внутри отрезка 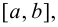 то очевидно, что эти значения будут наибольшим максимумом и наименьшим минимумом функции (если имеется несколько экстремумов). Однако может наблюдаться такая ситуация, что наибольшее или наименьшее значения будут достигаться на одном из концов отрезка (рис. 9.1).
то очевидно, что эти значения будут наибольшим максимумом и наименьшим минимумом функции (если имеется несколько экстремумов). Однако может наблюдаться такая ситуация, что наибольшее или наименьшее значения будут достигаться на одном из концов отрезка (рис. 9.1).
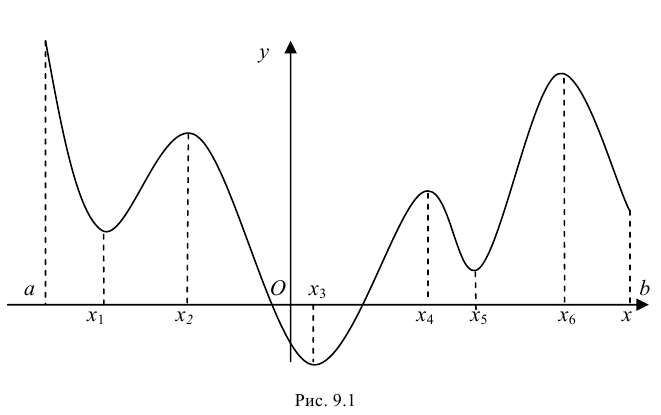
Таким образом, непрерывная функция  на отрезке достигает своего наибольшего и наименьшего значений либо на концах этого отрезка, либо в таких точках этого отрезка, которые являются точками экстремума.
на отрезке достигает своего наибольшего и наименьшего значений либо на концах этого отрезка, либо в таких точках этого отрезка, которые являются точками экстремума.
Исходя из вышесказанного, можно предложить следующий алгоритм поиска наибольшего и наименьшего значений непрерывной функции 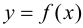 на отрезке
на отрезке 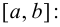
1. Найти все критические точки. Если критическая точка 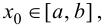 то нужно вычислить в ней значение функции
то нужно вычислить в ней значение функции 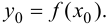 Если критическая точка
Если критическая точка 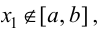 то в дальнейшем решении эта точка во внимание не принимается.
то в дальнейшем решении эта точка во внимание не принимается.
2. Вычислить значения функции на концах отрезка, т. е. найти 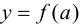 и
и
3. Из всех полученных выше значений функции выбрать наибольшее и наименьшее, они и будут представлять собой наибольшее и наименьшее значения функции 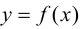 на отрезке
на отрезке 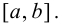
Пример 9.3. Найти наибольшее и наименьшее значения функции 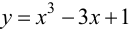 на отрезке [—3; 3].
на отрезке [—3; 3].
Решение.
Так как функция 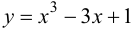 непрерывна на отрезке [-3; 3], то задача имеет решение.
непрерывна на отрезке [-3; 3], то задача имеет решение.
1. Найдем критические точки функции.
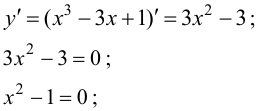
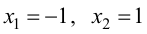 – критические точки.
– критические точки.
Так как 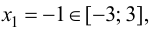 то вычислим
то вычислим 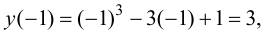
так как 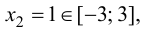 то вычислим
то вычислим 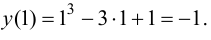
2. Определим значения функции на концах отрезка:
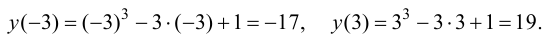
3. Сравним вычисленные значения функции и выберем наибольшее и наименьшее:
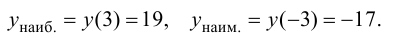
Ответ: 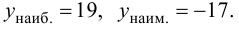
Выпуклость и вогнутость графика функции, точки перегиба
Пусть функция 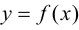 задана на интервале
задана на интервале 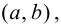 непрерывна на этом интервале и в каждой точке графика этой функции существует единственная касательная.
непрерывна на этом интервале и в каждой точке графика этой функции существует единственная касательная.
Определение 9.1. График функции 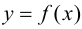 называется выпуклым или выпуклым вверх на интервале
называется выпуклым или выпуклым вверх на интервале 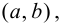 если он расположен ниже любой своей касательной, т. е.
если он расположен ниже любой своей касательной, т. е. 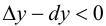 (рис. 9.2); график функции
(рис. 9.2); график функции 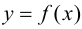 называется вогнутым или выпуклым вниз на интервале
называется вогнутым или выпуклым вниз на интервале 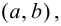 если он расположен выше любой своей касательной, т. е.
если он расположен выше любой своей касательной, т. е. 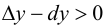 (рис. 9.3).
(рис. 9.3).
Определение 9.2. Точки графика функции, в которых выпуклость сменяется вогнутостью или наоборот, называются точками перегиба графика.
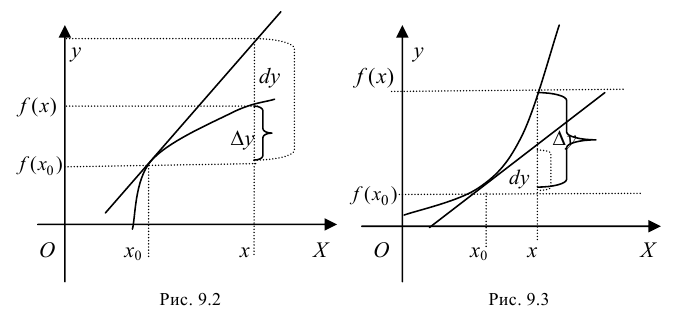
Теорема 9.4. Пусть функция 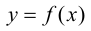 определена и дважды дифференцируема на интервале
определена и дважды дифференцируема на интервале 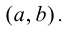 Тогда если
Тогда если 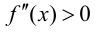 для
для 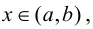 то на этом интервале график функции вогнутый; если
то на этом интервале график функции вогнутый; если 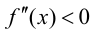 для
для 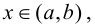 то на этом интервале график функции выпуклый.
то на этом интервале график функции выпуклый.
Доказательство.
Рассмотрим разность 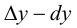 на отрезке
на отрезке 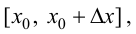 если
если 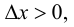 и на отрезке
и на отрезке 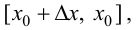 если
если 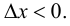 Согласно теореме 7.4 (Лагранжа):
Согласно теореме 7.4 (Лагранжа):
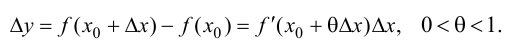
Поэтому 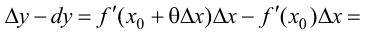
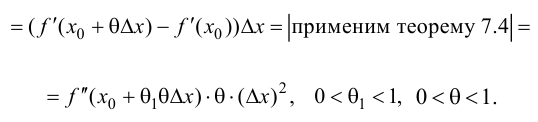
Тогда, при 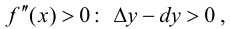 следовательно на этом отрезке график функции будет вогнутый; при
следовательно на этом отрезке график функции будет вогнутый; при 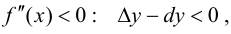 следовательно на этом отрезке график функции будет выпуклый.
следовательно на этом отрезке график функции будет выпуклый.
Теорема 9.5 (необходимое условие точки перегиба). Пусть график функции 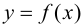 имеет перегиб в точке
имеет перегиб в точке 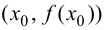 и пусть функция
и пусть функция 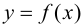 имеет в точке Xq непрерывную вторую производную. Тогда
имеет в точке Xq непрерывную вторую производную. Тогда 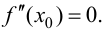
Доказательство.
Пусть 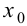 – абсцисса точки перегиба графика функции
– абсцисса точки перегиба графика функции 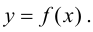 Для определенности будем считать, что выпуклость сменяется вогнутостью, т. е. при
Для определенности будем считать, что выпуклость сменяется вогнутостью, т. е. при 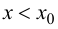 справедливо неравенство
справедливо неравенство 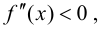 при
при 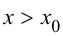 справедливо неравенство
справедливо неравенство 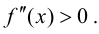 Тогда
Тогда 
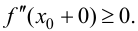 Так как, по условию теоремы, вторая производная в точке
Так как, по условию теоремы, вторая производная в точке 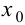 существует, то
существует, то 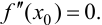
Определение 9.3. Точка 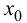 из области определения функции
из области определения функции 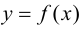 называется критической (стационарной) точкой второго рода, если вторая производная функции в этой точке обращается в нуль
называется критической (стационарной) точкой второго рода, если вторая производная функции в этой точке обращается в нуль 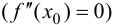 или не существует.
или не существует.
Замечание 9.3. Не всякая точка 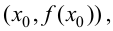 для которой
для которой 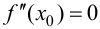 является точкой перегиба.
является точкой перегиба.
Пример 9.4. График функции 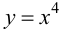 не имеет перегиба в точке (0; 0), хотя
не имеет перегиба в точке (0; 0), хотя 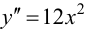 обращается в 0 при
обращается в 0 при 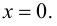
Теорема 9.6 (достаточное условие точки перегиба). Пусть функция 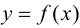 определена и дважды дифференцируема в некоторой окрестности точки
определена и дважды дифференцируема в некоторой окрестности точки 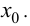 Тогда если в пределах указанной окрестности
Тогда если в пределах указанной окрестности 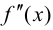 имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки 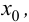 то график функции
то график функции 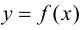 имеет перегиб в точке
имеет перегиб в точке
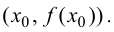
Доказательство.
Из того, что 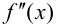 слева и справа от точки
слева и справа от точки 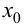 имеет разные знаки, на основании теоремы 9.4 можно сделать заключение, что направление выпуклости графика функции слева и справа от точки
имеет разные знаки, на основании теоремы 9.4 можно сделать заключение, что направление выпуклости графика функции слева и справа от точки 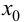 является различным. Это и означает наличие перегиба в точке
является различным. Это и означает наличие перегиба в точке 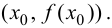
Замечание 9.4. Теорема остается верной, если функция 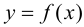 имеет вторую производную в некоторой окрестности точки
имеет вторую производную в некоторой окрестности точки 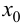 и существует касательная к графику функции в точке
и существует касательная к графику функции в точке 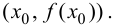 Тогда если в пределах указанной окрестности
Тогда если в пределах указанной окрестности 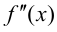 имеет разные знаки справа и слева от точки
имеет разные знаки справа и слева от точки 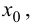 то график функции
то график функции 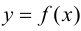 имеет перегиб в точке
имеет перегиб в точке 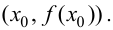
Пример 9.5. Точка (0; 0) является точкой перегиба графика функции 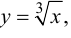 хотя вторая производная функции при
хотя вторая производная функции при 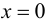 не существует. Касательная к графику функции
не существует. Касательная к графику функции 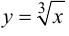 в точке (0; 0) совпадает с осью
в точке (0; 0) совпадает с осью 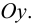
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т. е. при 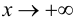 и при
и при 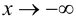 или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к некоторой прямой.
или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к некоторой прямой.
Определение 9.4. Прямая 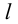 называется асимптотой графика функции
называется асимптотой графика функции 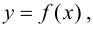 если расстояние
если расстояние 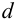 от переменной точки графика функции
от переменной точки графика функции 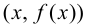 до прямой
до прямой 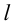 стремится к нулю при удалении точки
стремится к нулю при удалении точки 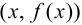 от начала системы координат.
от начала системы координат.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 9.5. Прямая 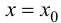 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 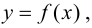 если хотя бы одно из предельных значений
если хотя бы одно из предельных значений 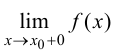 или
или 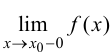 равно
равно 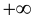 или
или 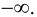
В этом случае расстояние от точки графика функции 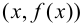 до прямой
до прямой 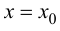 равно
равно 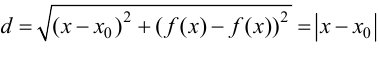 и, следовательно,
и, следовательно, 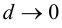 при
при 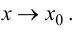
Пример 9.6. График функции 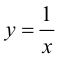 имеет вертикальную асимптоту
имеет вертикальную асимптоту 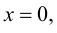 так как
так как 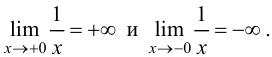
Определение 9.6. Прямая 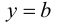 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 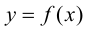 при
при 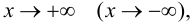 если
если 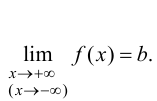
В этом случае расстояние от точки графика функции 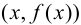 до прямой
до прямой 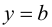 равно
равно 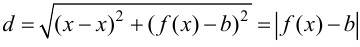 и, следовательно,
и, следовательно, 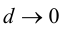 при
при 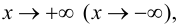 так как
так как 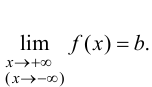
Пример 9.6 (продолжение). График функции 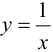 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 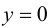 и при
и при 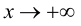 и при
и при 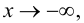 так как
так как 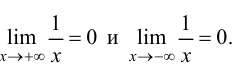
Определение 9.7. Прямая 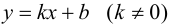 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 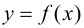 при
при 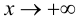
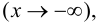 если функцию
если функцию 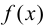 можно представить в виде
можно представить в виде
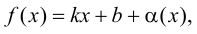 (9.1)
(9.1)
где 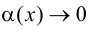 при
при 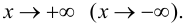
Теорема 9.7. Для того чтобы прямая 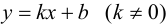 являлась наклонной асимптотой графика функции
являлась наклонной асимптотой графика функции 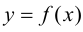 при
при 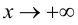
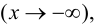 необходимо и достаточно, чтобы существовали конечные пределы:
необходимо и достаточно, чтобы существовали конечные пределы:
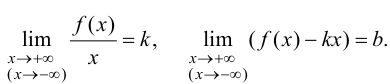 (9.2)
(9.2)
Доказательство. Рассмотрим случай 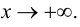
Необходимость.
Если 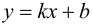 – наклонная асимптота графика функции
– наклонная асимптота графика функции 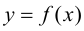 при
при 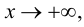 то, используя представление функции по формуле (9.1), получим:
то, используя представление функции по формуле (9.1), получим:
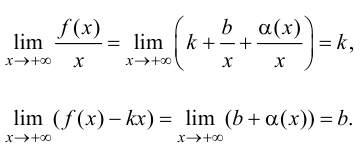
Достаточность.
Пусть существуют пределы (9.2). Тогда из второго равенства следует, что
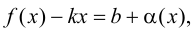 где
где 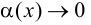 при
при 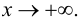
Полученное равенство легко преобразовать к виду (9.1), т. е. прямая 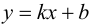 – наклонная асимптота графика функции
– наклонная асимптота графика функции  при
при 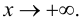
Схема исследования функции и построения ее графика
Рассмотрим примерный план, по которому целесообразно исследовать поведение функции и строить ее график:
1. Найти область определения функции.
2. Проверить выполнение свойств четности или нечетности, периодичности.
3. Указать промежутки непрерывности, точки разрыва и их тип, проверить наличие асимптот.
4. Найти промежутки монотонности и точки экстремума.
5. Найти промежутки выпуклости и вогнутости, точки перегиба.
6. Найти точки пересечения графика функции с осями координат.
7. Построить график функции.
Замечание 9.5. Если исследуемая функция 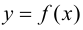 четная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график четной функции симметричен относительно оси ординат.
четная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график четной функции симметричен относительно оси ординат.
Замечание 9.6. Если исследуемая функция 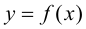 нечетная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график нечетной функции симметричен относительно начала координат.
нечетная, то достаточно исследовать функцию и построить ее график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график нечетной функции симметричен относительно начала координат.
Пример 9.7. Исследовать функцию 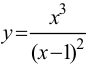 и построить ее график.
и построить ее график.
Решение.
1. 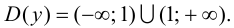
2. Так как область определения функции несимметрична относительно начала координат, то эта функция общего вида, т. е. функция ни четная, ни нечетная, непериодическая.
3. Функция непрерывна на области определения как элементарная. Точкой разрыва является 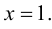 Так как
Так как
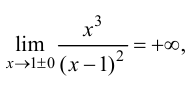
то 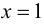 – точка разрыва второго рода. Можно также сделать заключение, что прямая
– точка разрыва второго рода. Можно также сделать заключение, что прямая 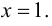 будет являться вертикальной асимптотой графика функции.
будет являться вертикальной асимптотой графика функции.
Проверим наличие горизонтальных асимптот. Так как
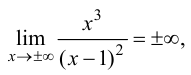
то данная функция не имеет горизонтальных асимптот. Проверим наличие наклонных асимптот. Так как
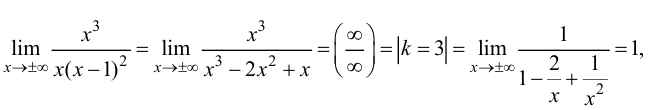
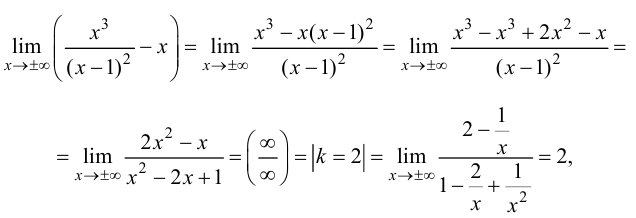
то график функции имеет наклонную асимптоту с угловым коэффициентом 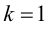 и свободным членом
и свободным членом 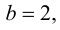 т. е.
т. е. 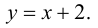
4. Определим промежутки возрастания и убывания функции, точки экстремума. Для этого найдем критические точки первого рода:
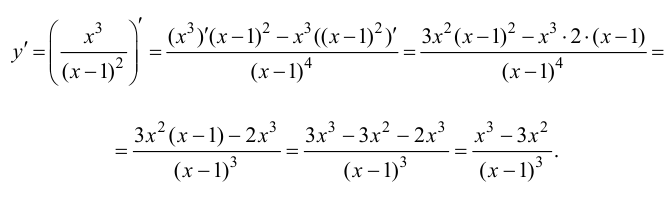
Решим уравнение 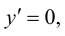 т.е.
т.е. 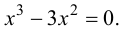 Получаем
Получаем 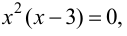
откуда  и
и  – критические точки первого рода. Изменение знака первой производной покажем на числовой оси (рис. 9.4).
– критические точки первого рода. Изменение знака первой производной покажем на числовой оси (рис. 9.4).
Так как 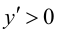 при
при 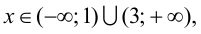 то функция возрастает на указанных промежутках; так как
то функция возрастает на указанных промежутках; так как 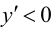 при
при 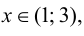 то функция убывает на указанном промежутке. При переходе через точку
то функция убывает на указанном промежутке. При переходе через точку 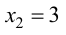 производная
производная 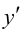 изменяет знак с «-» на «+», следовательно, в этой точке функция имеет минимум, причем
изменяет знак с «-» на «+», следовательно, в этой точке функция имеет минимум, причем 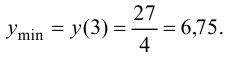
5. Определим промежутки выпуклости и вогнутости графика функции, точки перегиба. Для этого найдем критические точки второго рода:
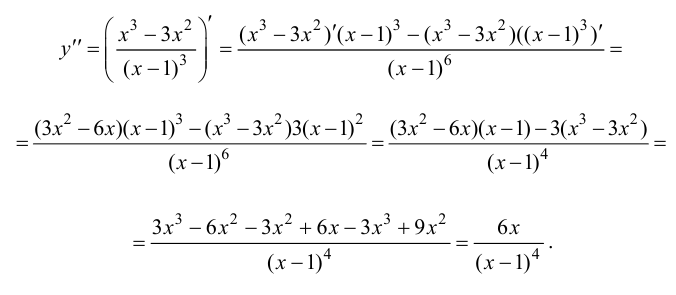
Решим уравнение 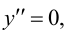 т. е.
т. е. 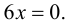 Получаем единственное решение
Получаем единственное решение 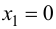 – критическая точка второго рода. Изменение знака второй производной покажем на числовой оси (рис. 9.5).
– критическая точка второго рода. Изменение знака второй производной покажем на числовой оси (рис. 9.5).
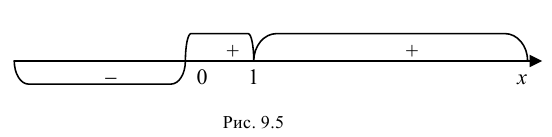
Так как 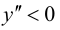 при
при 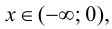 то график функции будет выпуклым на данном промежутке; так как
то график функции будет выпуклым на данном промежутке; так как 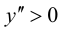 при
при 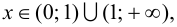 то график функции будет вогнутым на указанных промежутках. При переходе через точку
то график функции будет вогнутым на указанных промежутках. При переходе через точку 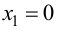 выпуклость графика функции сменяется вогнутостью, следовательно, это абсцисса точки перегиба, тогда ордината
выпуклость графика функции сменяется вогнутостью, следовательно, это абсцисса точки перегиба, тогда ордината 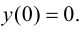 Таким образом, (0; 0) – точка перегиба графика функции.
Таким образом, (0; 0) – точка перегиба графика функции.
6. Найдем точки пересечения графика функции с осями координат.
Для точек оси  всегда
всегда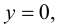 т. е.
т. е. 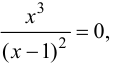 откуда
откуда 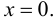
Для точек оси 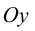 всегда
всегда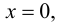 т. е.
т. е. 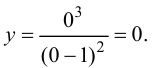
Таким образом, единственной точкой пересечения графика функции с осями координат является начало системы координат 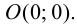
7. Построим график функции на рис. 9.6.
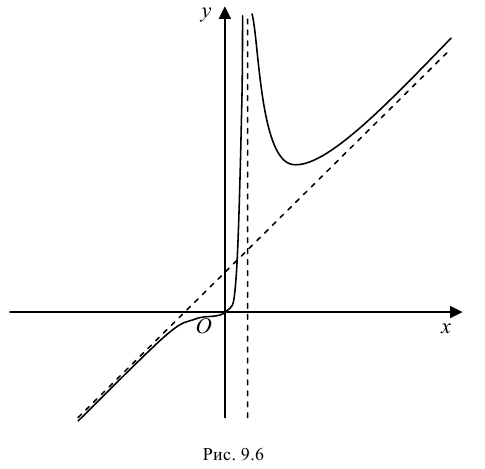
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:

Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:

Решение:

Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:

Пример:

Решение:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Теоремы о дифференцируемых функциях
Рассмотрим функции  и
и  , которые непрерывны на отрезке
, которые непрерывны на отрезке ![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) и дифференцируемы на интервале
и дифференцируемы на интервале  .
.
Теорема Ферма
: если функция  в точке
в точке  имеет локальный экстремум, то
имеет локальный экстремум, то 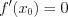 .
.
Геометрический смысл теоремы: касательная к графику функции в точке  параллельна оси абсцисс.
параллельна оси абсцисс.
Теорема Лагранжа: 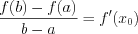 , где
, где  .
.
Геометрический смысл теоремы: касательная к графику функции в точке  параллельна секущей, соединяющей концы графика этой функции.
параллельна секущей, соединяющей концы графика этой функции.
Теорема Ролля: если 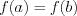 и
и  , то
, то 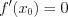 .
.
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.
Теорема Коши: если  , то
, то 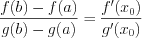 .
.
Исследование функции с помощью первой производной
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке  , то функция возрастает на этом промежутке;
, то функция возрастает на этом промежутке;
б) если  , то функция убывает на этом промежутке.
, то функция убывает на этом промежутке.
Экстремум
функции
Максимумом (минимумом)
функции  называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4).
Максимум и минимум функции называются
экстремумом функции
. Значение аргумента, при котором достигается экстремум, называется
точкой экстремума
. На рисунке 6.4 значения  ,
, ,
,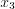 ,
,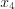 и
и 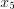 являются точками экстремума рассматриваемой функции.
являются точками экстремума рассматриваемой функции.

Критическими точками
функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение: 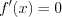 .
.
Алгоритм нахождения точек экстремума функции:
1) находим область определения функции  ;
;
2) находим 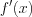 ;
;
3) находим критические точки функции, решая уравнение 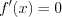 ;
;
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.
Рассмотрим функцию  на отрезке
на отрезке ![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) . Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.
. Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.
Алгоритм нахождения наибольшего и наименьшего
значений
функции  на заданном отрезке:
на заданном отрезке:
1) находим 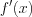 ;
;
2) находим критические точки функции, решая уравнение 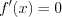 ;
;
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Исследование
функции с помощью второй производной
Критическими точками второго рода
функции  называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.
Критические точки второго рода функции  находят, решая уравнение
находят, решая уравнение 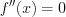 .
.
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба
графика функции.
Если на некотором промежутке выполняется неравенство  , то функция
, то функция  вогнута
вогнута
на этом промежутке, а если 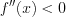 , то функция
, то функция
выпукла
на этом промежутке.
Пример 1.
Найдите промежутки монотонности и точки экстремума функции  .
.
Решение . Используя таблицу производных найдем производную функции:  . Найдем критические точки:
. Найдем критические точки: 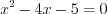 ,
,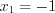 ,
,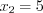 . Нанесем числа
. Нанесем числа  и
и  на координатную прямую и установим знаки производной на полученных промежутках:
на координатную прямую и установим знаки производной на полученных промежутках:
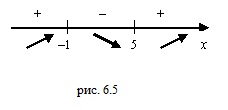
Ответ
: На промежутках  и
и  функция возрастает. На промежутке
функция возрастает. На промежутке 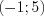 функция убывает. Точки экстремума:
функция убывает. Точки экстремума:  ,
,  .
.
Пример 2.
Найдите точки перегиба и промежутки выпуклости и вогнутости графика функции .
.
Решение
. 1. Используя таблицу производных найдем первую производную функции:  .
.
2. Используя таблицу производных найдем вторую производную функции:  .
.
3. Найдем критические точки второго рода:  ,
, 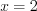 .
.
4. Нанесем точку 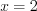 на область определения данной функции и установим знаки ее второй производной на полученных промежутках:
на область определения данной функции и установим знаки ее второй производной на полученных промежутках:
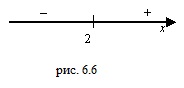
Ответ
: На промежутке  функция выпукла вверх; на промежутке
функция выпукла вверх; на промежутке  функция выпукла вниз;
функция выпукла вниз; 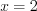 – точка перегиба графика функции.
– точка перегиба графика функции.
Пример 3.
Найдите наибольшее и наименьшее значение функции  на отрезке
на отрезке ![[1;e] LaTeX formula: [1;e]](https://helpy.quali.me/uploads/formulas/eb6e890201c9d8770f7e173603dbc77ae36dc386.1.1.png) .
.
Решение
. 1. По формуле  найдем производную данной функции:
найдем производную данной функции:  .
.
2. Найдем критические точки функции, решая уравнение  , откуда
, откуда  ,
,  .
.
3. Найдем значение функции на концах отрезка ![[1;e] LaTeX formula: [1;e]](https://helpy.quali.me/uploads/formulas/eb6e890201c9d8770f7e173603dbc77ae36dc386.1.1.png) и в критической точке
и в критической точке  , поскольку она принадлежит данному отрезку:
, поскольку она принадлежит данному отрезку:  ,
,  ,
,  .
.
Ответ
: 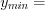
 ,
,  .
.
Приведем схему полного исследования функции  .
.
1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.
