В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
-
3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h

Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
Цилиндр — геометрическое тело, которое можно получить при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор площади поверхности цилиндра
На самом деле, это определение только самого простого, кругового цилиндра. Более общее определение цилиндрического тела следующее:
Цилиндром называют тело, образованное пересечением параллельных друг другу прямых и двух плоских поверхностей.
Такие прямые называются образующими данного цилиндра.
Прямая, перпендикулярная обоим основаниям, является высотой цилиндра.
Плоские поверхности называют основаниями данного цилиндра. Часто, они параллельны друг другу, но не всегда.
Виды цилиндра
Виды цилиндра зависят от того, под каким углом пересекаются образующие и основания нашего тела.
Если угол равен 90 градусам, то получим, так называемый, прямой цилиндр. У него есть ось симметрии – это перпендикуляр, соединяющий центры его оснований.
Если угол другой, то цилиндр называется наклонным.
Если форма основания – гипербола, то цилиндр гиперболический, если парабола — параболический, если эллипс — эллиптический, если круг — круговой.
Если основания цилиндра не параллельны, то он называется косым.
Формула площади поверхности цилиндра
Полная площадь поверхности цилиндра является суммой его боковой площади поверхности и площади оснований.
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь оснований;
SбокS_{text{бок}} — площадь боковой поверхности.
При вычислении площади поверхности цилиндра важным фактором является вид цилиндра. От него зависит и конкретная формула для площади.
Формула площади поверхности кругового цилиндра
Sосн=2⋅π⋅r2S_{text{осн}}=2cdotpicdot r^2
Sбок=2⋅π⋅r⋅hS_{text{бок}}=2cdotpicdot rcdot h
rr — радиус круга (основания кругового цилиндра);
hh — высота этого цилиндра.
Сокращенно, это формулу можно записать так:
S=Sосн+Sбок=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+2cdotpicdot rcdot h=2cdotpicdot rcdot(r+h)
Радиус круга, лежащего в основании прямого кругового цилиндра, имеет длину 6 (см.). Высота цилиндра – 20 (см.). Найдите полную площадь его поверхности.
Решение:
r=6r=6
h=20h=20
По формуле:
S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68S=2cdotpicdot rcdot(r+h)=2cdotpicdot 6cdot(6+20)approx979,68 (см. кв.)
Ответ: 979,68 см. кв.
Формула площади поверхности наклонного кругового цилиндра
Sосн=2⋅π⋅r2S_{text{осн}}=2cdotpicdot r^2
Sбок=p⋅lS_{text{бок}}=pcdot l
rr — радиус круга (основания кругового цилиндра);
pp — периметр сечения наклонного цилиндра перпендикулярно образующей;
ll — длина образующей этого цилиндра.
Найти площадь поверхности наклонного цилиндра, если периметр pp сечения плоскости, составляющей прямой угол с образующей, равен 30 (см.), а сама образующая равна 7 (см.) Радиус окружности, лежащей в основе цилиндра в два раза меньше его образующей.
Решение:
r=l2r=frac{l}{2}
p=30p=30
l=7l=7
Найдем сначала радиус основания:
r=l2=72=3.5r=frac{l}{2}=frac{7}{2}=3.5
Тогда полная площадь:
S=Sосн+Sбок=2⋅π⋅r2+p⋅l=2⋅π⋅3.52+30⋅7≈76,93+210=286,93S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+pcdot l=2cdotpicdot 3.5^2+30cdot 7approx76,93+210=286,93 (см. кв.)
Ответ: 286,93 см. кв.
На сайте Студворк предусмотрено решение контрольных работ на заказ для школьников и студентов.
Тест по теме «Площадь поверхности цилиндра»
Чтобы найти площадь поверхности цилиндра необходимо знать радиус его основания и высоту. Очень важно понимать, что существует две поверхности – боковая и полная. Площадь боковой поверхности включает в себя площадь поверхности цилиндра без учета площади его оснований. Полная же площадь основания цилиндра включает как площадь боковой поверхности, так и обоих оснований цилиндра.
На нашем сайте вы можете рассчитать и объем цилиндра
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые её пересекают.
Содержание:
- калькулятор площади поверхности цилиндра
- формула площади поверхности цилиндра
- формула площади боковой поверхности цилиндра
- примеры задач
Формула площади поверхности цилиндра
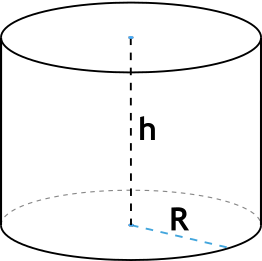
{S_{полн} = 2pi R(h+R)}
R – радиус основания цилиндра
h – высота цилиндра
Формула площади боковой поверхности цилиндра
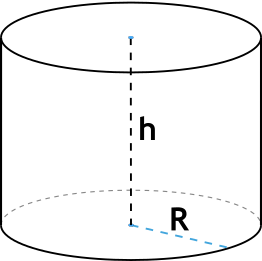
{S_{бок} = 2pi Rh}
R – радиус основания цилиндра
h – высота цилиндра
Примеры задач на нахождение площади поверхности цилиндра
Задача 1
Найдите площадь поверхности цилиндра если его высота равна 5см а радиус 6см.
Решение
Так как необходимо найти площадь полной поверхности цилиндра, воспользуемся первой формулой. Подставим в нее значения из условия и произведем вычисления.
S_{полн} = 2pi R(h+R) = 2pi cdot 6(5+6) = 12pi cdot 11 = 132 pi : см^2 approx 414.69023 : см^2
Ответ: 132 pi : см^2 approx 414.69023 : см^2
Чтобы проверить правильность ответа можно использовать калькулятор .
Задача 2
Найдите площадь боковой поверхности цилиндра, если радиус основания равен 2см а высота 7см.
Решение
Для решения этой задачи нам потребуется вторая формула.
S_{бок} = 2pi Rh = 2pi cdot 2 cdot 7 = 28 pi : см^2 approx 87.96459 : см^2
Ответ: 28 pi : см^2 approx 87.96459 : см^2
Осталось убедиться, что задача решена верно, для этого используем калькулятор .
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Оглавление:
- Площадь поверхности цилиндра – онлайн калькулятор
- Площадь боковой поверхности цилиндра
- Площадь полной поверхности цилиндра
- Площадь цилиндра – формула через диаметр
- Примеры расчета площади цилиндра
- Заключение
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра – онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
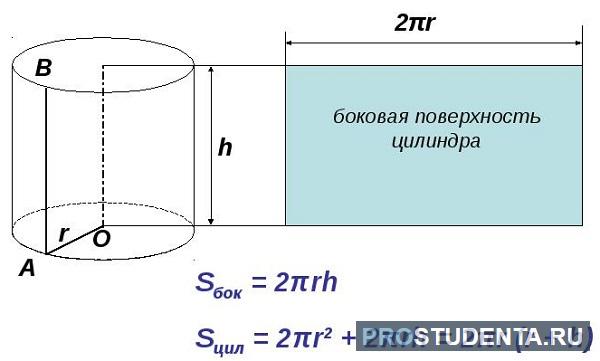
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.
Sбок = 2π * r * h,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.
Конечная формула выглядит следующим образом:
Sпол = 2π * r2 + 2π * r * h.
Площадь цилиндра – формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
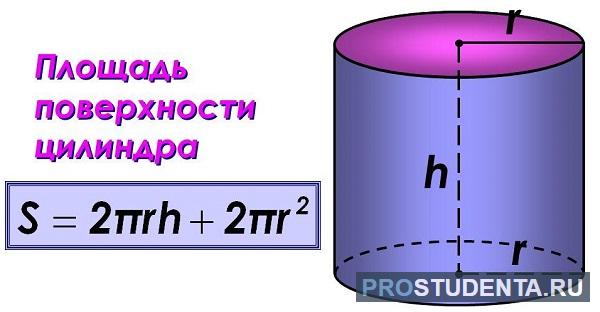
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,
Вместо r в полную формулу нужно вставить значение r = d/2.
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
Sпол = 2 * 3.14 * 242 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм2).
Переводим в привычные м2 и получаем 0,01868928, приблизительно 0.02 м2.
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
Sпол = 3.14 * 0.22/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м2.
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
Sбок = 2 * 3.14 * 1 * 1 = 6.28 м2.
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Площадь поверхности цилиндра
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности цилиндра
Чтобы посчитать площадь поверхности цилиндра воспользуйтесь нашим очень удобным онлайн калькулятором:
Площадь боковой поверхности

Высота цилиндра h =
=
Площадь боковой поверхности цилиндра Sбпц =
0
Округление ответа: Округление числа π:
Площадь полной поверхности

Высота цилиндра h =
=
Площадь полной поверхности цилиндра Sппц =
0
Округление ответа: Округление числа π:
Просто введите данные и получите ответ.
Теория
Площадь боковой поверхности цилиндра
Как вычислить площадь боковой поверхности цилиндра Sбпц, зная высоту цилиндра h и его радиус r (или диаметр d)?
Формулы
Через радиус:
Sбпц = 2⋅π⋅r⋅h
Через диаметр:
Sбпц = π⋅d⋅h
Пример #1
К примеру, посчитаем площадь боковой поверхности цилиндра с высотой 5 см и радиусом 1.5 см:
Sбпц = 2 ⋅ 3.14 ⋅ 1.5 ⋅ 5 = 6.28 ⋅ 7.5 = 47.1 см²
Пример #2
Посчитаем площадь боковой поверхности цилиндра с высотой 10 см и диаметром 4 см:
Sбпц = 3.14 ⋅ 4 ⋅ 10 = 125.6 см²
Площадь полной поверхности цилиндра
Как вычислить площадь полной поверхности цилиндра Sппц, зная высоту цилиндра h и его радиус r (или диаметр d)?
Формулы
Через радиус:
Sппц = 2⋅π⋅r⋅(h+r)
Через диаметр:
Sппц = π⋅d²2 + π⋅d⋅h
Пример #1
К примеру, посчитаем площадь полной поверхности цилиндра с высотой 8 см и радиусом 2 см:
Sппц = 2 ⋅ 3.14 ⋅ 2 ⋅ (8+2) = 6.28 ⋅ 2 ⋅ 10 = 125.6 см²
Пример #2
Посчитаем площадь полной поверхности цилиндра с высотой 2 м и диаметром 0.5 м:
Sппц = 3.14⋅0.5²2 + 3.14⋅0.5⋅2 = 0.3925 + 3.14 = 3.5325 м²
