Как найти максимальную скорость выбиваемых электронов

КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА

Найти максимальную скорость фотоэлектронов, вырываемых с поверхности металла светом с длиной волны λ = 180 нм . Красная граница фотоэффекта λ = 275 нм

Дано:

λ_кр = 275 нм =275·10 -9 м

λ_кр = 180 нм =180·10 -9 м

Решение:

Зная красную границу фотоэффекта, найдем работу выхода

Уравнение Эйнштейна для внешнего фотоэффекта

Откуда максимальная кинетическая энергия

Максимальная скорость фотоэлектронов

Ответ: ;

Определение и уравнение фотоэффекта

Фотоэффект является одним из примеров проявления корпускулярных свойств света. Вылет электронов из освещенных тел, называется внешним фотоэффектом.

Сущность внутреннего фотоэффекта состоит в том, что при освещении полупроводников и диэлектриков от некоторых атомов отрываются электроны, которые, однако, в отличие от внешнего фотоэффекта, не выходят через поверхность тела, а остаются внутри него. В результате внутреннего фотоэффекта возникают электроны в зоне проводимости и сопротивление полупроводников и диэлектриков уменьшается.

При освещении границы раздела между полупроводниками с различным типом проводимости возникает электродвижущая сила. Это явление называется вентильным фотоэффектом.

Уравнение Эйнштейна для внешнего фотоэффекта

Основным уравнением, описывающим внешний фотоэффект, является уравнение Эйнштейна для внешнего фотоэффекта:

где – энергия фотона монохроматической волны света, 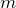— масса электрона, 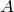— работа выхода электрона из фотокатода.

Уравнение фотоэффекта (1) является следствием закона сохранения энергии. В соответствии с законами сохранения энергии и импульса, поглощение фотона свободными электронами невозможно, и фотоэффект возможен только на электронах, связанных в атомах, молекулах и ионах, а также на электронах твердых и жидких тел.

Из уравнения фотоэффекта существует ряд важных выводов, которые характеризуют это явление:

1. Для данного фотокатода максимальная начальная скорость фотоэлектронов зависит от частоты падающего света и не зависит от его интенсивности.
2. При постоянном спектральном составе падающего света число фотоэлектронов, вырываемых светом из фотокатода за единицу времени, и фототок насыщения пропорциональны энергетической освещенности фотокатода.
3. Для каждого вещества фотокатода существует красная граница фотоэффекта (порог фотоэффекта) – минимальная частота , при которой еще возможен фотоэффект. Длина волны , соответствующая частоте , для большинства металлов находится в ультрафиолетовой части спектра.

Примеры решения задач

Вылет электронов прекратится тогда, когда потенциальная энергия электрона (U) в задерживающем поле станет равной его кинетической энергии (E), то есть:

Запишем уравнение фотоэффекта, в которое входит кинетическая энергия электрона:

Подставим (1.1) в (1.2), получим:

(1.3), откуда:

Полагая, что красная граница фотоэффекта соответствует энергии фотонов, при которой скорость вырываемых с металла электронов равна нулю, получим:

Подставим (1.5) в (1.4), получим:

Ответ
Искомая в задаче частота света может быть рассчитана по формуле:

Задание

Металлическую пластинку (работа выхода A) освещают светом с длинной волны 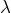. На какое максимальное расстояние от пластинки (d) может удалиться фотоэлектрон, если вне пластинки создано задерживающее однородное электрическое поле с напряженностью E?

Решение
Запишем уравнение фотоэффекта, в которое входит кинетическая энергия электрона:

По закону сохранения энергии, работа которую совершает электрическое поле при движении электрона (, равна максимальному значению кинетической энергии электрона при его максимальной удаленности от поверхности пластинки, следовательно, запишем:

Определить максимальную скорость v_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ ₁ =0,155 мкм; 2) γ-излучением с длиной волны λ ₂ =2,47 пм.

Решение . Максимальную скорость фотоэлектронов определим из уравнения Эйнштейна для фотоэффекта:

Энергия фотона вычисляется по формуле ε = hc / λ , работа выхода А указана в табл. 20 для серебра A =4,7 эВ.

Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена или по классической формуле

или по релятивистской

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона ε много меньше энергии покоя электрона Е , то может быть применена формула (2); если же ε сравнима по размеру с Е , то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3)

1. В формулу энергии фотона ε = hc / λ подставим значения величин h , с и λ и, произведя вычисления, для ультрафиолетового излучения получим

Это значение энергии фотона много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть выражена

по классической формуле (2) ε ₁ = A + ½ m v 2 _max , откуда

(4)

Выпишем величины, входящие в формулу (4): ε ₁ =1,28 × 10 -18 Дж (вычислено выше); A =4,7 эВ = 4,7 × 1,6*10 -19 Дж = 0,75*10 -18 Дж; m =9,11 × 10 -31 кг (см. табл. 24).

Подставив числовые значения в формулу (4), найдем максимальную скорость:

2. Вычислим теперь энергию фотона γ-излучения:

Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией γ-фотона, поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона:

Так как в данном случае кинетическая энергия электрона сравнима с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии,

где E = m c 2 .

Выполнив преобразования, найдем

Сделав вычисления, получим

Следовательно, максимальная скорость фотоэлектронов, вырываемых γ-излучением,

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Фотоэффект. Законы Столетова. Формула Эйнштейна

Изучение закономерностей теплового излучения привело к чрезвычайно важному выводу о существовании квантов энергии, о дискретном характере электромагнитного излучения. Гипотезу о кван­тах излучаемой энергии М. Планк выдвинул в 1900 г. Несколько позже А. Эйнштейн выдвинул гипотезу о том, что свет не только излучается, но и распространяется в пространстве и поглощается также в виде квантов дискретного электромагнитного излучения. Кванты видимого излучения получили название фотонов.

К физическим явлениям, подтверждающим квантовую природу излучения, относится фотоэффект. Фотоэффект – это явление вырывания электронов из атомов и молекул вещества под действием света (электромагнитного из­лучения). Если выбитые электроны вылетают за пределы вещества, то фо­тоэффект называется внешним и наблюдается, главным образом, у ме­таллов. Если же оторванные от своих атомов и молекул электроны ос­таются внутри освещаемого вещества в качестве свободных электро­нов, то фотоэффект называется внутренним. Он наблюдается у некото­рых полупроводников и, в меньшей степени, диэлектриков. Это явление обнаружено Герцем в 1887 г., изучено Столетовым в 1888-89 г.г., т.е. до появления гипотезы Планка. Герц обнаружил, а Столетов изучил и установил, что

испускаемые заряды имеют отрицательный знак;

наибольшее действие на выход электронов оказывают ультрафиолетовые лучи — величина испущенного заряда пропорцио­нальна поглощенной телом энергии.

Схема опытов Столетова по исследованию внешнего фотоэф­фекта изображена на рис. 162. В вакуумной трубке помещают иссле­дуемую пластинку К (катод) и вспомогательный электрод А (анод).

Электроды А и К через потенциометр П подклю­чены к источнику напряжения Е. Напряжение между электродами, на­зываемое анодным, измеряется вольтметром V, а ток в цепи гальвано­метром Г. Если пластинка К не освещается, то ток в цепи отсутст­вует, т.к. вакуумный промежуток между катодом и анодом тока не проводит. Если же исследуемую пластинку осветить светом через окно С, то свет вырвет из пластинки электроны, которые получили название фотоэлектронов. Под действием электрического поля, созданного анодным напряжением, фотоэлектроны будут двигаться к аноду А и далее по замкнутой цепи через гальванометр Г к катоду К. Гальвано­метр покажет наличие тока, который получил название фототока. При помощи потенциометра П можно изменять величину и знак анодного напряжения. Следует иметь в виду, что ток в цепи существует и в том случае, когда анодное напряжение равно нулю, и даже при небольшом отрицательном (задерживающем) напряжении. Объясняется это тем, что вылетевшие из катода фотоэлектроны обладают кинетической энергией, за счет которой совершается работа против сил поля и они достигают анода. На графике на рис. 161 показана типичная зависи­мость силы фототока от анодного напряжения (т.н. вольт-амперная ха­рактеристика) при неизменном световом потоке для двух значений светового потока Ф, когда Ф₁ < Ф₂. Из графика видно, что:

При некотором небольшом напряжении фототок достигает насыщения – все электроны попадают на анод;

При U = 0 фототок не исчезает, значит электроны покидают катод со скоростью, отличной от нуля;

Для того, чтобы фототок стал равным нулю, нужно прило­жить задерживающее напряжение U_з.

Измерив U_з, можно определить максимальную скорость фото­электронов, покидающих катод

.

Исследования Столетова привели к установлению 3-х основных законов фотоэффекта:

Сила фототока насыщения I_н прямо пропорциональна па­дающему световому потоку Ф

где к – коэффициент пропорциональности.

Скорость фотоэлектронов увеличивается с увеличением час­тоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока

Независимо от интенсивности светового потока фотоэффект начинается при определенной для данного вещества минимальной частоте (максимальной длине) световой волны, назы­ваемой красной границей фотоэффекта.

2-й и 3-й законы фотоэффекта противоречат представлениям волновой теории света. Согласно этим представлениям электроны ве­щества должны совершать колебания с амплитудой, пропорциональной амплитуде падающей световой волны. При достаточной амплитуде связь электрона с веществом может быть нарушена и электроны будут вылетать наружу со скоростью, величина которой будет зависеть от амплитуды, т.е. интенсивности падающего света. В действительности такой зависимости нет, скорость электронов зависит только от частоты падающего света.

Для объяснения этого факта Эйнштейн выдвинул гипотезу, что свет не только испускается, но и распространяется и поглощается дис­кретными порциями – квантами. По Эйнштейну квант энергии (света) поглощается полностью одним электроном и энергия кванта hν расходуется на работу по вы­рыванию электрона из вещества А_вых и на сообщение электрону кине­тической энергии

hν = А_вых+

Эта формула получила название формулы Эйнштейна для фотоэффекта.

Работа выхода зависит от рода вещества, состояния и чистоты поверхности и других факторов, экспериментально определена и для некоторых веществ приводится в справочниках. Из формулы Эйнштейна вытекает второй закон фотоэффекта

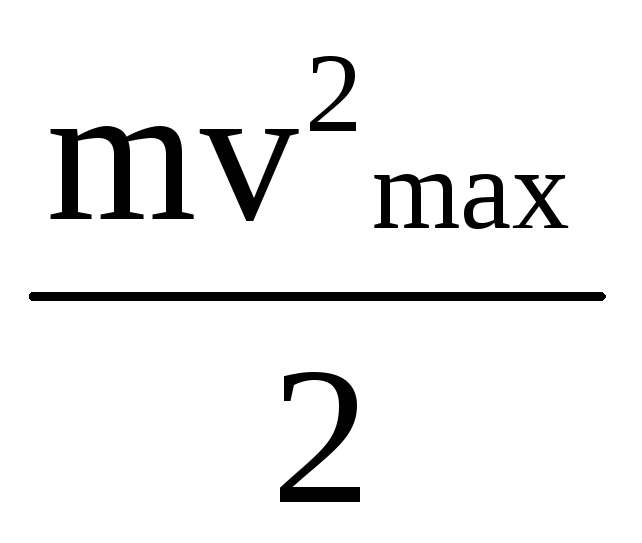= hν — А_вых.

Видно, что максимальная скорость фотоэлектронов, так же как и задерживающий потенциал зависят от частоты света и работы вы­хода электронов из металла, и не зависят от интенсивности светового потока.

Максимальная начальная энергия фотоэлектрона обращается в нуль при значении частоты света

соответствующей крас­ной границе фотоэффекта. Учитывая, что частота и длина волныизлучения связаны отношением, где с – скорость света в вакууме, получаем выражение для длины волныкрасной границы фотоэффекта

.

Фотоэффект безинерционен, т.е. фототок начинается сразу же как на катод попадает свет с частотой ν ≥ ν_кр , тогда как по классическим волновым представлениям требуется довольно значительное время для того, чтобы электромагнитная волна заданной интенсивности могла передать электрону энергию , доста­точную для совершения работы выходы.

При очень больших интенсивностях света, достижимых в на­стоящее время с помощью лазеров, наблюдается многофотонный фото­эффект, когда электрон может одновременно получить энергию не од­ного, а N фотонов. Для этого случая

и красная граница фотоэффекта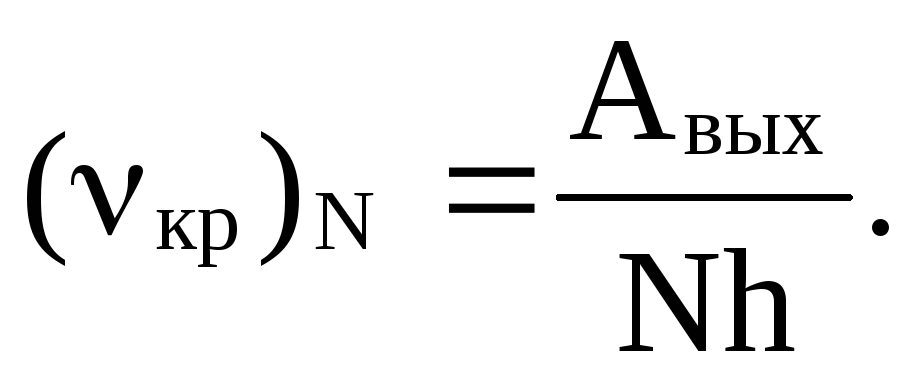

Как найти скорость фотоэлектронов

КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА

Найти максимальную скорость фотоэлектронов, вырываемых с поверхности металла светом с длиной волны λ = 180 нм . Красная граница фотоэффекта λ₀ = 275 нм

Дано:

Решение:

Зная красную границу фотоэффекта, найдем работу выхода

Уравнение Эйнштейна для внешнего фотоэффекта

Откуда максимальная кинетическая энергия

Максимальная скорость фотоэлектронов

Ответ: ;

Фотоэффект в физике и его применение — формулы и определение с примерами

На основе волновой теории света можно предположить, что:

• – свет любой длины волны должен вырывать электроны из металла;
• – на вырывание электрона из металла требуется определенное время;
• – число вырванных электронов и их энергия должны быть пропорциональны интенсивности света.

Александр Григорьевич Столетов (1839–1896) – русский физик. Исследовал внешний фотоэффект, открыл первый закон фотоэффекта. Исследовал газовый разряд, критическое состояние, получил кривую намагничивания железа.

Современная установка для исследования фотоэффекта

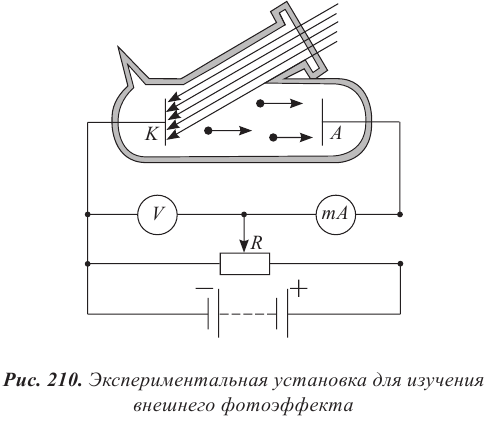
Современная установка для изучения фотоэффекта представляет собой два электрода, помещенных в стеклянный баллон, из которого выкачан воздух (рис. 210). На один из электродов через кварцевое «окошко» падает свет. В отличие от обычного стекла кварц пропускает ультрафиолетовое излучение. На электроды подается напряжение, которое можно менять с помощью потенциометра R и измерять вольтметром V. К освещаемому электроду К − катоду подсоединяют отрицательный полюс батареи. Под действием света катод испускает электроны, которые направляются электрическим полем к аноду, создается электрический ток. Значение силы тока фиксируется миллиамперметром.

Законы фотоэффекта Столетова

Исследования, проведенные русским ученым А.Г. Столетовым и немецким ученым Ф. Ленардом, показали, что законы фотоэффекта не соответствуют классическим представлениям.

На рисунке 211 представлена вольтамперная характеристика, полученная в результате измерений при различных значениях напряжения между электродами.

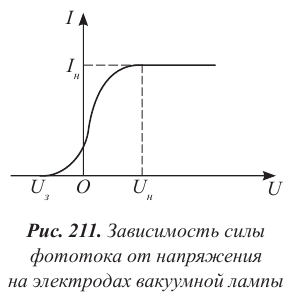
Из графика следует, что:

1. Сила фототока не зависит от напряжения, если оно достигает некоторого значения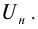

Максимальное значение силы тока 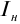называют током насыщения.

Сила тока насыщения − это максимальный заряд, переносимый фотоэлектронами за единицу времени:

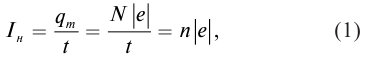
где n − число фотоэлектронов, вылетающих с поверхности освещаемого металла за 1 с, е − заряд электрона.

2. Сила фототока отлична от нуля при нулевом значении напряжения.

3. Если изменить направление электрического поля, соединив катод с положительным полюсом источника тока, а анод − с отрицательным, то скорость фотоэлектронов уменьшится, об этом можно судить по показаниям миллиамперметра: сила тока уменьшается при увеличении отрицательного значения напряжения. При некотором значении напряжения 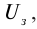который называют задерживающим напряжением, фототок прекращается. Согласно теореме об изменении кинетической энергии, работа задерживающего электрического поля равна изменению кинетической энергии фотоэлектронов:

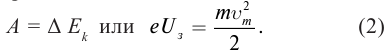
При известном значении 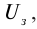можно найти максимальную кинетическую энергию фотоэлектронов.

Исследование фотоэффекта при освещении катода световыми потоками равной частоты, но различной интенсивности дал результат, представленный вольтамперными характеристиками, изображенными на рисунке 212.

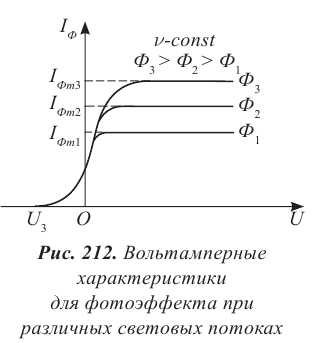
Сила фототока насыщения увеличивается с увеличением интенсивности падающего света.

Вспомните! Фотоэффект – это испускание электронов веществом под действием света или любого другого электромагнитного излучения.

Величина запирающего напряжения от интенсивности света не зависит, для всех потоков она имеет одно и то же значение.

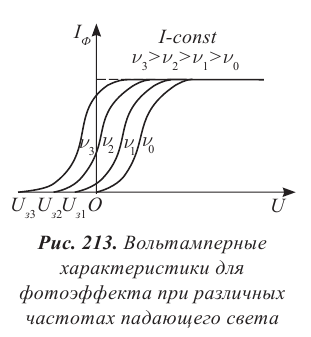
Освещение катода светом одной и той же интенсивности, но разной частоты дало серию вольтамперных характеристик, представленных на рисунке 213. Как следует из графиков, величина задерживающего напряжения 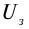увеличивается с увеличением частоты падающего света, при уменьшении частоты падающего света уменьшается, и при некоторой частоте 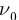задерживающее напряжение равно нулю: 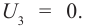При меньших частотах 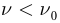фотоэффект не наблюдается.

Минимальную частоту падающего света 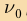, при которой еще возможен фотоэффект, называют красной границей фотоэффекта.

На основании экспериментальных данных Столетовым были сформулированы законы фотоэффекта:

1. Сила фототока прямо пропорциональна интенсивности светового потока.
2. Максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от интенсивности.
3. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света 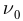(максимальная длина 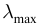), при которой возможен фотоэффект, если 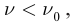то фотоэффект не происходит.

Квантовая теория фотоэффекта

Теоретическое обоснование фотоэффекта было дано в 1905 г. А. Эйнштейном. Он предположил, что свет не только излучается квантами, как утверждал М. Планк, но и распространяется и поглощается порциями, представляет собой поток частиц − фотонов, энергия которых равна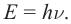

Сам фотоэффект состоит в том, что световые частицы, сталкиваясь с электронами металла, передают им свою энергию и импульс и сами при этом исчезают. Если энергия квантов падающего света больше той работы, которую электрон должен совершить против сил притяжения к положительно заряженным частицам вещества, то электрон вылетает из металла. Становится понятным смысл красной границы фотоэффекта: для вырывания электрона из металла энергия квантов должна быть не меньше, чем 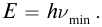Эта энергия и равна работе выхода электрона из данного металла. В случае, когда энергия падающих квантов больше работы выхода, максимальная кинетическая энергия электронов равна разности энергии фотона и работы выхода:

Это и есть формула Эйнштейна для фотоэффекта. Обычно ее пишут в виде:

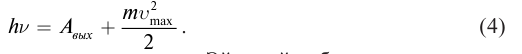
Зависимость силы фототока от интенсивности света Эйнштейн объяснил следующим образом: число вылетающих в единицу времени электронов пропорционально интенсивности света, поскольку интенсивность определяется числом квантов, испускаемых источником в единицу времени. Мощная лампа испускает больше квантов, следовательно, число вырванных электронов светом такой лампы будет больше, чем светом менее мощной лампы.

Энергия вылетающих электронов зависит не от силы света лампы, а от того, какой частоты свет она испускает, от этого зависит энергия фотона и кинетическая энергия фотоэлектрона.

Фотоны, энергия, масса и импульс фотона

Фотон – это частица света. Он не делится на части: испускается, отражается, преломляется и поглощается целым квантом. У него нет массы покоя, неподвижных фотонов не существует.

Энергия фотона

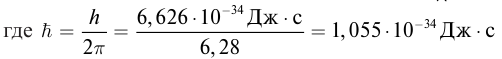− постоянная Планка, 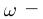циклическая частота.

Масса фотона

Массу фотона определяют, исходя из закона о взаимосвязи массы и энергии:

Измерить массу фотона невозможно, ее следует рассматривать как полевую массу, обусловленную тем, что электромагнитное поле обладает энергией.

Импульс фотона

Фотон – частица света, следовательно, ее импульс равен:

Применение фотоэффекта в технике

Фотоэлементы:

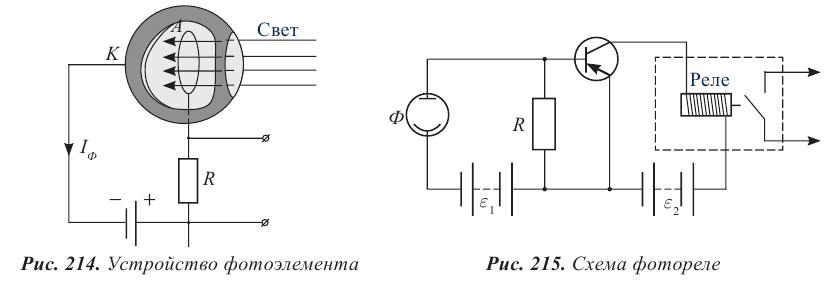
Приборы, принцип действия которых основан на явлении фотоэффекта, называют фотоэлементами. Устройство фотоэлемента изображено на рисунке 214. Внутренняя поверхность К (катод) стеклянного баллона, из которого выкачан воздух, покрыта светочувствительным слоем с небольшим прозрачным для света участком для доступа света внутрь баллона. В центре баллона находится металлическое кольцо А (анод). От электродов сделаны выводы для подключения фотоэлемента к электрической цепи. В качестве светочувствительного слоя обычно используют напыленные покрытия из щелочных металлов, имеющих малую работу выхода, т.е. чувствительных к видимому свету.

Фотоэлементы используют для автоматического управления электрическими цепями с помощью световых пучков.

Фотореле:

Фотоэлектрическое реле срабатывает при прерывании светового потока, падающего на фотоэлемент (рис. 215). Фотореле состоит из фотоэлемента Ф, усилителя фототока, в качестве которого используют полупроводниковый триод, и электромагнитного реле, включенного в цепь коллектора транзистора. Напряжение на фотоэлемент подают от источника тока 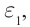а на транзистор − от источника тока 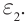Между базой и эмиттером транзистора включен нагрузочный резистор R.

Когда фотоэлемент освещен, в его цепи, содержащей резистор R, идет слабый ток, потенциал базы транзистора выше потенциала эмиттера, и ток в коллекторной цепи транзистора отсутствует.

Если же поток света, падающий на фотоэлемент, прерывается, ток в его цепи сразу прекращается, переход эмиттер – база открывается для основных носителей, и через обмотку реле, включенного в цепь коллектора, пойдет ток. Реле срабатывает, и его контакты замыкают исполнительную цепь. Ее функциями могут быть остановка пресса, в зону действия которого попала рука человека, выдвигание преграды в турникете метро, автоматическое включение освещения на улицах.

Пример решения задачи

Определите постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой 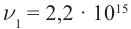Гц, полностью задерживаются разностью потенциалов 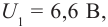а вырываемые светом с частотой 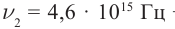− разностью потенциалов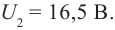

Дано:

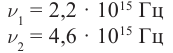
Решение: Запишем уравнение Эйнштейна для электрона, вырванного из металла светом с частотами 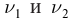соответственно: 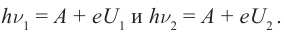Вычитая первое равенство из второго, получим 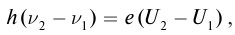откуда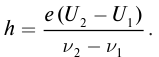

Выполним расчеты: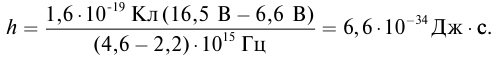

Ответ: h = 6,6 · 10 –34 Дж · с.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Обновлено: 23.05.2023

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Фотоэффект – это вырывание электронов из вещества под действием света.

Ток насыщения – некоторое предельное значение силы фототока.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.

Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.

2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.

3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.

Теоретический материал для самостоятельного изучения

Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.

Коэффициент пропорциональности получил название постоянной Планка, и она равна:

h = 6,63 ∙ 10 -34 Дж∙с.

После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.

В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.

Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.

Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.

Схема установки для изучения законов фотоэффекта

Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения

Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.

Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.

Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.

где А_в – работа выхода электронов;

h – постоянная Планка;

ν_min – частота излучения, соответствующая красной границе фотоэффекта;

с – скорость света;

λкр – длина волны, соответствующая красной границе_.

Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.

Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.

Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:

где – максимальная кинетическая энергия электронов;

Е – заряд электрона;

– задерживающее напряжение.

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:

Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.

Примеры и разбор решения заданий

1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Работа выхода

Запирающее напряжение

Работа выхода – это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.

Запирающее напряжение – это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:

Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.

Работа выхода

Запирающее напряжение

2. Красная граница фотоэффекта для вещества фотокатода λ₀ = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.

Запишем уравнение для фотоэффекта через длину волны:

Условие связи красной границы фотоэффекта и работы выхода:

Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:

Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:

Фотоэффект — это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.
Напомним, что Герц использовал специальный разрядник (вибратор Герца) — разрезанный пополам стержень с парой металлических шариков на концах разреза. На стержень подавалось высокое напряжение, и в промежутке между шариками проскакивала искра. Так вот, Герц обнаружил, что при облучении отрицательно заряженного шарика ультрафиолетовым светом проскакивание искры облегчалось.

Герц, однако, был поглощён исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведённые Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.

Опыты Столетова

В своих знаменитых экспериментах Столетов использовал фотоэлемент собственной конструкции (Фотоэлементом называется любое устройство, позволяющее наблюдать фотоэффект). Его схема изображена на рис. 1 .

Рис. 1. Фотоэлемент Столетова

В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод и анод . На катод и анод подаётся напряжение, величину которого можно менять с помощью потенциометра и измерять вольтметром .

Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны , которые разгоняются напряжением и летят на анод. Включённый в цепь миллиамперметр регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.

В опытах Столетова можно независимо варьировать три величины: анодное напряжение, интенсивность света и его частоту.

Зависимость фототока от напряжения

Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2 .

Рис. 2. Характеристика фотоэлемента

Давайте обсудим ход полученной кривой. Прежде всего заметим, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим .

Здесь кг — масса электрона, Кл — его заряд.

Будем постепенно увеличивать напряжение, т.е. двигаться слева направо вдоль оси из далёких отрицательных значений.

Поначалу тока по-прежнему нет, но точка разворота электронов становится всё ближе к аноду. Наконец, при достижении напряжения , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:

Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.

При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т.е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.

При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под всё большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!

Когда напряжение выходит в область положительных значений, фототок продолжает возрастать. Оно и понятно: электрическое поле теперь разгоняет электроны, поэтому всё большее их число получают шанс оказаться на аноде. Однако достигают анода пока ещё не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т.е. вдоль катода), хоть и развернётся полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.

Наконец, при достаточно больших положительных значениях напряжения ток достигает своей предельной величины , называемой током насыщения, и дальше возрастать перестаёт.

Почему? Дело в том, что напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода — в каком бы направлении и с какими бы скоростями они не начинали движение. Стало быть, дальнейших возможностей увеличиваться у фототока попросту нет — ресурс, так сказать, исчерпан.

Законы фотоэффекта

Величина тока насыщения — это, по существу, количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.

Первый закон фотоэффекта. Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).

Ничего неожиданного в этом нет: чем больше энергии несёт излучение, тем ощутимее наблюдаемый результат. Загадки начинаются дальше.

А именно, будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. Сделать это несложно: ведь в силу формулы (1) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.

Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3 ):

Рис. 3. Зависимость энергии фотоэлектронов от частоты света

Как видим, существует некоторая частота , называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если , то фотоэффекта нет.

Если же nu_0′ alt=’nu > nu_0′ /> , то максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой.

Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом , то фотоэффект не возникает, какова бы ни была интенсивность! Не менее удивительный факт обнаруживается и при nu_0′ alt=’nu > nu_0′ /> : максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.

Все эти факты нашли отражение во втором и третьем законах фотоэффекта.

Второй закон фотоэффекта. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.

Третий закон фотоэффекта. Для каждого вещества существует красная граница фотоэффекта — наименьшая частота света , при которой фотоэффект ещё возможен. При фотоэффект не наблюдается ни при какой интенсивности света.

Трудности классического объяснения фотоэффекта

Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?

Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.

В переменном электрическом поле световой волны электрон начинает совершать колебания.

И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.

Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.

Выглядит опять-таки логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит.

Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.

Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.

Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.

Гипотеза Планка о квантах

Классическая электродинамика отказалась работать не только в области фотоэффекта. Она также дала серьёзный сбой, когда её попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).

Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Как мы прекрасно знаем, ничего подобного не наблюдается.

В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.

Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями — квантами. Энергия кванта пропорциональна частоте излучения:

Cоотношение (2) называется формулой Планка, а коэффициент пропорциональности — постоянной Планка.

Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:

Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.

Уравнение Эйнштейна для фотоэффекта

Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.

Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией .

Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.

Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью .

Каждый фотон монохроматического света, имеющего частоту , несёт энергию .

Фотоны могут обмениваться энергией и импульсом с частицами вещества (об импульсе фотона речь пойдёт в следующем листке); в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.

Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.

Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона ? при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода по извлечению электрона из вещества и на придание электрону кинетической энергии :

Слагаемое оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.

Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода.

Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.

Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта. Давайте посмотрим, какое объяснение получают законы фотоэффекта с точки зрения уравнения Эйнштейна.

1. Число выбиваемых электронов пропорционально числу поглощённых фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает.

Стало быть, пропорционально возрастает число поглощённых фотонов и, соответственно, число выбитых за секунду электронов.

2. Выразим из формулы (4) кинетическую энергию:

Действительно, кинетическая энергия выбитых электронов линейно растёт с частотой и не зависит от интенсивности света.

Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку . Этим полностью объясняется ход графика на рис. 3 .

3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: . Наименьшая частота , определяемая равенством

как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта определяется только работой выхода, т.е. зависит лишь от вещества облучаемой поверхности катода.

Если , то фотоэффекта не будет — сколько бы фотонов за секунду не падало на катод. Следовательно, интенсивность света роли не играет; главное — хватает ли отдельному фотону энергии, чтобы выбить электрон.

Уравнение Эйнштейна (4) даёт возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.

По формуле фотоэффекта
А (вых) + m * v^2 / 2 = h * nu
Здесь А (вых) – работа выхода.
m * v^2 / 2 – кинетическая энергия фотоэлектронов
m – масса электрона, v – его макс. скорость
h * nu – Планковская энергия падающего света
h – постоянная Планка, nu – частота света.

такс) это все онечно круто и подробно) но че-т я после дикого дня не соображаю уже) можно попросить вас решить?) 1) Работа выхода электронов из кадмия равна 4,08 эВ. Какова частота света, если максимальная скорость фотоэлектронов 7,2 • 105 м/с?
2) Каково задерживающее напряжение для электронов, вырванных ультрафиолетовым излучением с длиной волны 0,1 мкм из вольфрамовой пластины?
3) Какова максимальная скорость фотоэлектронов, вылетающих при действии на поверхность цинка ультрафиолетового излучения с длиной волны 150 нм? 4) Падающий на поверхность катода желтый свет вызывает фотоэффект. Обязательно ли возникнет фотоэффект при освещении катода синим светом? оранжевым светом? 5). Какова максимальная скорость фотоэлектронов при действии на катод света длиной волны 450 нм, если красная граница фотоэффекта для данного катода 600 нм? если можно, не только ответы)

а) Скорость фотоэлектронов не зависит от интенсивности падающего света.

б) Число фотоэлектронов пропорционально интенсивности падающего света.

I_ – ток насыщения;

U_ – задерживающее или запирающее напряжение.

Уравнение Эйнштейна для фотоэффекта

E_ – энергия падающего фотона, т.е. частицы света

nu – частота падающего света

nu=frac , где T – период

h – постоянная Планка

A_ – работа выхода электрона из металла, т.е. работа, которую необходимо совершить, чтобы вырвать электрон из вещества

Кинетическая энергия фотоэлектрона:

v_ – скорость фотоэлектрона;

m_ – масса электрона

Красная граница фотоэффекта

Минимальная частота, при которой возможен фотоэффект:

v_ – красная граница по частоте;

lambda – длина волны света

Cвязь между частотой и длиной волны:

c – скорость света в вакууме

lambda_ – красная граница по длине волны

Задерживающее напряжение

Определение: Задерживающее напряжение – это напряжение обратной полярности, при котором все электроны возвращаются назад на тот электрод, с которого были вырваны.

Это происходит, когда работа поля по возращению электронов становится равной кинетической энергии:

Подставим это выражение в уравнение Эйнштейна:

С другой стороны:

q_ – заряд носителя электричества;

v – скорость дрейфа, т.е. направленного движения частиц;

S – площадь поперечного сечения проводника

При увеличении частоты скорость фотоэлектронов растет Rightarrow растет задерживающее напряжение.

При увеличении интенсивности света растет концентрация электронов Rightarrow растет ток насыщения.

Энергия и импульс фотона

Замечание: Фотоны не имеют массы покоя. Рождаясь, они приобретают скорость c.

Корпускулярно-волновой дуализм

Определение: Корпускулярно-волновой дуализм – это двойственность свойств элементарных частиц: они одновременно обладают свойствами частиц и волн.

Читайте также:

  

• Чем отличаются cd r и dvd r диски кратко

  

• Почему второй этап фотосинтеза может осуществляться и в темноте и на свету кратко

  

• Для чего радиоприемнику нужен детектор кратко

  

• Кто такой импотент мужчина простыми словами кратко и ясно

  

• В чем социальная роль и функция воспитателя доу