![]()
Функции с числом е. Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).
Рекомендую вам ещё раз внимательно прочитать статью «Исследование функций. Это нужно знать!» и освежить в памяти изложенную информацию. Не устану повторять, что для того чтобы решать задачи на нахождение наибольшего или наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства производной для исследования функций, знать таблицу производных и правила дифференцирования.
После решения каждой задачи есть разъяснения другого подхода к решению (я обещал вам «хитрости» — они здесь). Рекомендую посмотреть, выглядит график показательной функции.
Рассмотрим задачи:

Найдите наименьшее значение функции у = (х–17)ех–16
на отрезке [15;17].
Мы знаем, что для того, чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо вычислить её значение на границах заданного интервала и в точках, где производная равна нулю. Действуем по алгоритму:
1. Найдём производную заданной функции:
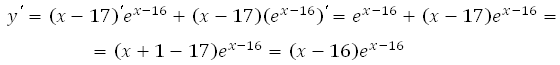
2. Найдем нули производной на заданном отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:
![]()
*Выражение ех-16 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определяем принадлежит ли найденная точка интервалу.
Точка х = 16 принадлежит интервалу [15;17]. Значит значение функции будем вычислять в точках 15, 16 и 17:
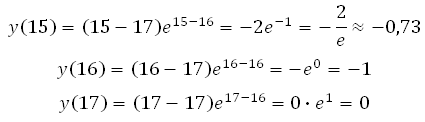
*Учтите, что число е ≈ 2,71. Это нецелое число и неконечная десятичная дробь, поэтому любое выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом, но вы всё равно его проанализируйте. В данной задаче, если мы –2 разделим на число 2,71 то результат будет лежать в пределах от –1 до 0 (можно посчитать столбиком для проверки).
4. Делаем вывод.
Таким образом, наименьшее значение функции равно –1.
Ответ: –1
В этой статье я обещал вам какие-то там «хитрости», которые можно использовать при решении. Если вы поняли теорию производной и знаете, как находить максимальные и минимальные значения, то тогда читайте дальше — представленный приём будет хорошим дополнительным «инструментом» и позволит решать подобные задания мгновенно.
Итак! Мы знаем, что ответом в задачах на ЕГЭ в части В должно быть целое число, либо конечная десятичная дробь.
Посмотрите на данную функцию. Сразу можно сказать, что значение функции будет являться целым числом только при х = 16 или при х = 17, и ни при каких других значениях х. Поэтому достаточно вычислить:
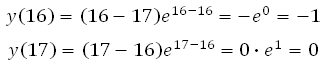
и далее записать ответ.
Ещё один путь решения (без нахождения производной). Сразу подставляем в функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем наименьшее значение:
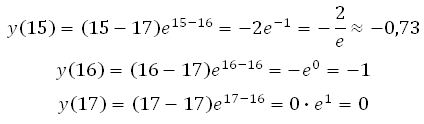
Решите самостоятельно:
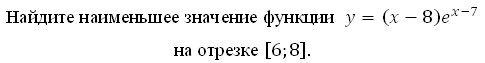
Посмотреть решение

Найдите точку минимума функции у = (х + 18)ех-18
1. Найдём производную заданной функции:
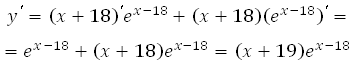
2. Найдем нули производной:
![]()
Получаем, что х = –19.
*Выражение ех-18 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определим знаки производной функции на интервалах (подставляем любые произвольные значения в производную) и изобразим на рисунке поведение функции:
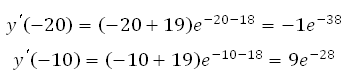
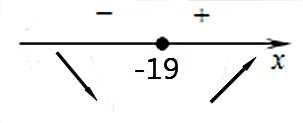
В точке х = –19 функция меняет знак с отрицательного на положительный, значит это искомая точка минимума.
Ответ: –19
Как решать быстрее данный тип задач?
Когда мы получили производную и приравняли её к нулю:
(х + 19)ех–18 = 0
Далее получили, что х=–19. Данное решение и будет являться ответом задачи.
*То есть, в при решении данного типа задач, можно обойтись без определения знаков производной на интервалах. Но будьте осторожны! В других заданиях на нахождение максимума (минимума), где получите несколько нулей производной, её знаки на интервалах нужно определять обязательно.
Решите самостоятельно:
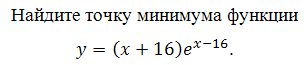
Посмотреть решение

Найдите точку максимума функции у = (3х2 – 15х + 15)е7–х
Найдём производную заданной функции:
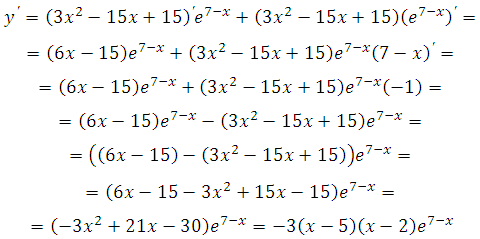
Найдем нули производной:
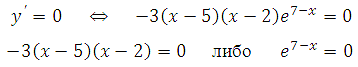
Число е7-х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Решаем – 3 (х–5)(х–2) = 0. Получим х1 = 5 и х2 = 2 .
Определим знаки производной функции (подставляя любые значения из интервалов в найденную производную) и изобразим на рисунке поведение функции:
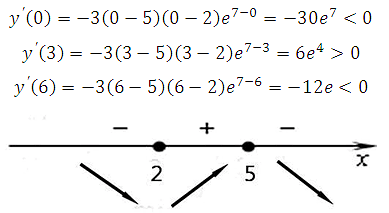
В точке х = 5 функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5
Решите самостоятельно:
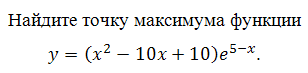
Посмотреть решение

Найдите наибольшее значение функции у = (22 – х)ех–21
на отрезке [16;25].
Найдём производную заданной функции:
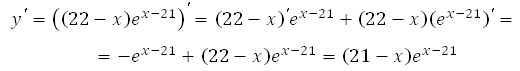
Найдем нули производной:
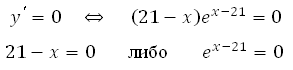
Число ех-21 не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное, значит х = 21.
Полученное значение принадлежит интервалу [16;25].
Вычислим значения данной в условии функции в точках 16, 21 и 25:
*То есть на границах интервала и в точке, где производная обращается в нуль.
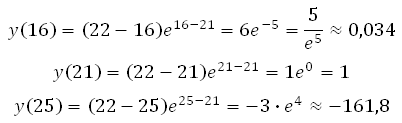
Первый результат меньше единицы (это понятно и без вычислений).
Третий результат так же меньше единицы (отрицательное число).
Значит наибольшее значение функции на заданном интервале равно 1.
*Помните, что ответы с числом е (по требованиеям ЕГЭ) не являются верными.
Ответ: 1
Если у вас всё-таки неразрешимые проблемы с нахождением производной, то подставляйте в исходную функцию все целые значения из интервала и выбирайте наибольшее полученное значение.
*Кроме того, по данной функции сразу видно, что её значение будет целым числом только при х = 21 или при х = 22.
Можете подставить только их в функцию, далее произвести вычисления и выбрать наибольшее значение.
Решите самостоятельно:
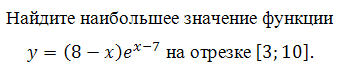
Посмотреть решение

Найдите наибольшее значение функции у = (2х2 – 10х + 10)е х
на отрезке [–4; 3].
Необходимо определить значения на границах интервала, и в точках, где производная обращается в нуль.
Найдём производную заданной функции:
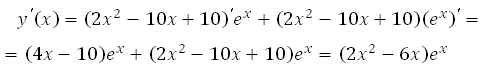
Найдем нули производной:
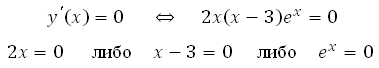
Произведение множителей равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Значит решением являются корни: х1=0 и х2=3
Обе точки принадлежат интервалу [–4;3], х=3 совпадает с границей интервала.
Вычисляем значения функции в точках: – 4, 0 и 3:
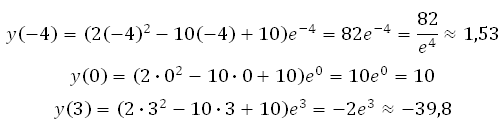
Значит наибольшее значение функции равно 10.
Ответ: 10
*Как вы уже поняли, можно в заданную функцию можно подставить все целые значения х из интервала, и таким образом найти наибольшее значение функции. Но в данном случае придётся перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).
Решите самостоятельно:
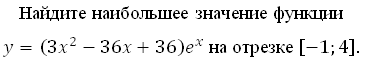
Посмотреть решение

Найдите наименьшее значение функции у = (х + 44)2е–44–х
на отрезке [– 46; –43]
Найдём производную заданной функции:
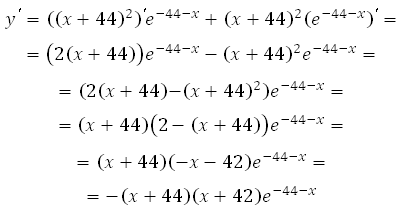
Обратите внимание, что результат мы представили сразу в виде множителей, это будет удобно при вычислении нулей производной.
Найдем нули производной:
![]()
Решением являются корни: х1= – 44 и х2= – 42.
Заданному интервалу [– 46;–43] принадлежит только точка х = – 44.
Вычисляем значения функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке, где производная равна нулю:
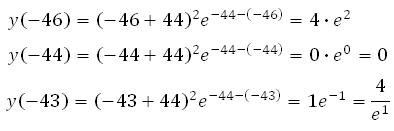
Наименьшее значение функции равно 0.
Ответ: 0
*Как это задание решить быстро?
Учитывая, что ответом должно быть целое число, видно что значение данной функции будет целым только при х= – 44 и х= 44.
указанному в условии интервалу принадлежит х= – 44, вычисляем:
![]()
Решите самостоятельно:
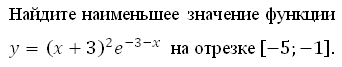
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
На этом закончим. Всем удачи!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Здравствуйте, дорогие
друзья! Экзамен не за горами, мы вышли на финишную прямую, не будем суетиться и
переживать, будем готовиться. И на занятие сегодня я хочу рассмотреть некоторые
аспекты задания № 12 «Исследование функций». Мы поговорим о задачах, в которых
рассматриваются функции и в условии стоят вопросы, связанные с их
исследованием. Рассмотрим основные теоретические моменты, которые необходимо
знать и понимать для их решения.
Это
целая группа задач входящих в ЕГЭ по математике. Обычно ставится вопрос о
нахождении точек максимума (минимума) или определения наибольшего (наименьшего)
значения функции на заданном интервале. Рассматриваются:
— Степенные и
иррациональные функции.
— Рациональные
функции.
— Исследование
произведений и частных.
— Логарифмические
функции.
—
Тригонометрические функции.
Если
вы поняли теорию пределов, понятие производной, свойства производной для
исследования графиков функций и её геометрический смысл, то такие задачи
никакого затруднения у вас не вызовут и вы решите их с
лёгкостью.
Следующая
информация — это теоретические моменты, понимание которых позволит
осознать, как решать подобные задачи. Постараюсь изложить их именно так, чтобы
даже тот, кто эту тему пропустил или изучил слабо, смог без особых затруднений
решать подобные задачи.
В
задачах данной группы, как уже сказано, требуется найти либо точку минимума
(максимума) функции, либо наибольшее (наименьшее) значение функции на
интервале.
Точки
минимума, максимума. Свойства производной.
 Рассмотрим график функции:
Рассмотрим график функции:
Точка
А – это точка максимума, на интервале от О до А функция возрастает, на
интервале от А до В убывает.
Точка
В – это точка минимума, на интервале от А до В функция убывает, на
интервале от В до С возрастает.
В
данных точках (А и В) производная обращается в нуль (равна нулю).
Касательные
в этих точках параллельны оси ox.
 Добавлю,
Добавлю,
что точки, в которых функция меняет своё поведение с возрастания на убывание (и
наоборот, с убывания на возрастание), называются экстремумами.
Важный
момент:
1.
Производная на интервалах возрастания имеет положительный знак (при подстановке
значения из интервала в производную получается положительное число).
Значит,
если производная в определённой точке из некоторого интервала имеет положительное
значение, то график функции на этом интервале возрастает.
2.
На интервалах убывания производная имеет отрицательный знак (при подстановке
значения из интервала в выражение производной получается отрицательное
число).
Значит,
если производная в определённой точке из некоторого интервала имеет
отрицательное значение, то график функции на этом интервале
убывает.
Это
надо чётко уяснить!!!
Таким
образом, вычислив производную и приравняв её к нулю, можно найти точки, которые
разбивают числовую ось на интервалы. На каждом из этих интервалов
можно определить знак производной и далее сделать вывод о её возрастании или
убывании.
*Отдельно
следует сказать о точках, в которых производая не существует. Например, можем
получить производную, знаменатель которой при определённом х обращается в нуль.
Понятно, что при таком х производная не существует. Так вот, данную точку также
необходимо учитывать при определени интервалов возрастания (убывания).
Функция
в точках, где производная равна нулю, меняет свой знак не всегда.
Об этом можно почитать отдельно, но на самом ЕГЭ таких задач не будет.
Вышеизложенные
свойства необходимы для исследования поведения функции на возрастание и
убывание.
Что
ещё необходимо знать для решения оговоренных задач: таблицу производных
и правила дифференцирования. Без этого никак. Это базовые знания, в теме
производной. Производные элементарных функций вы должны знать на отлично.


Исследование
функций
Задачи на нахождение точек максимума и минимума
Алгоритм
нахождения точек максимума (минимума) функции:
1.
Находим производную функции f’(x).
2.
Находим нули производной (приравниванием производную к нулю f’(x)=0 и
решаем полученное уравнение). Также находим точки, в которых производная не
существует (в частности это касается дробно-рациональных функций).
3.
Отмечаем полученные значения на числовой прямой и определяем знаки
производной на этих интервалах путём подстановки значений из интервалов в
выражение производной.
4.
Далее делаем вывод.
Вывод
будет один из двух:
1.
Точка максимума это точка, в которой производная меняет значение с
положительного на отрицательное.
2. Точка
минимума это точка, в которой производная меняет значение с отрицательного
на положительное.
Задачи на нахождение наибольшего или наименьшего
значения функции на интервале.
В
другом типе задач требуется найти наибольшее или наименьшее значение функции на
заданном интервале.
Алгоритм
нахождения наибольшего (наименьшего) значения функции:
1.
Определяем, есть ли точки максимума (минимума). Для этого находим производную f’(x),
затем решаем f’(x)=0 (пункты 1 и 2 из предыдущего алгоритма).
2.
Определяем, принадлежат ли полученные точки заданному интервалу и
записываем лежащие в его пределах.
3.
Подставляем в исходную функцию (не в производную, а в данную в
условии) границы данного интервала и точки (максимума-минимума), лежащие в
пределах интервала (п.2).
4.
Вычисляем значения функции.
5.
Выбираем из полученных наибольшее (наименьше) значение, в зависимости от
того, какой вопрос был поставлен в задаче и далее записываем ответ.
Вопрос:
для чего в задачах на нахождение наибольшего (наименьшего) значения функции
необходимо искать точки максимума (минимума)?
 Ответ
Ответ
лучше всего это проиллюстрировать, посмотрите схематичное изображение
графиков, задаваемых функций:

В
случаях 1 и 2 достаточно подставить границы интервала, чтобы определить
наибольшее или наименьшее значение функции. В случаях 3 и 4 необходимо найти
нули функции (точки максимума-минимума). Если мы подставим границы интервала
(не находя нули функции), то получим неверный ответ, это видно по
графикам.
И
всё дело в том, что мы по заданной функции не можем увидеть как выглядит график
на интервале (имеет ли он максимум или минимум в пределах интервала). Потому
находите нули функции обязательно!!!
Если
уравнение f’(x)=0 не будет иметь решения, это значит, что точек
максимума-минимума нет (рисунок 1,2), и для нахождения поставленной
задачи в данную функцию подставляем только границы интервала.
Ещё
один важный момент. Помните, что ответом должно быть целое число или конечная
десятичная дробь. При вычислении наибольшего и наименьшего значения функции вы
будете получать выражения с числом е и Пи, а также выражения с корнем.
Запомните, что до конца вам их вычислять не нужно, и так понятно, что результат
таких выражений ответом являться не будет. Если возникнет желание
вычислить такое значение, то сделайте это (числа: е ≈ 2,71
Пи ≈ 3,14 ).
Много
наговорила, запутала наверное? По конкретным примерам вы увидите, что всё
просто.
Далее
хочу открыть вам маленький секрет. Дело в том, что многие задания можно решить
без знания свойств производной и даже без правил дифференцирования. Об этих
нюансах я вам обязательно расскажу и покажу как это делается? не пропустите!
Но
тогда зачем же я вообще изложил теорию и ещё сказал, что её нужно знать
обязательно. Всё верно – знать надо. Если её поймёте, тогда никакая
задача в этой теме в тупик вас не поставит.
Те
«хитрости», о которых вы узнаете, помогут вам при решении конкретных
(некоторых) прототипов задач. Как дополнительный инструмент эти приёмы
использовать, конечно, удобно. Задачу можно решить в 2-3 раза быстрее и
сэкономить время на решение части С.
. Но не для всех
примеров применение «стандартного» алгоритма будет рационально. Если следовать
ему в представленных примерах, то процесс решения будет «перегружен»
вычислениями.
Так какие же задания
имеются ввиду?
![]() В условии дана иррациональная, логарифмическая или показательная
В условии дана иррациональная, логарифмическая или показательная
функция:
![]() при чём под корнем, под знаком логарифма или в показателе стоит
при чём под корнем, под знаком логарифма или в показателе стоит
квадратичная функция вида:
Мы рассмотрим подход без
нахождения производной. Вы увидите, что такие задачи можно решать устно.
Что необходимо знать?
Свойство параболы,
напомним его:
![]() Если а > 0, то её
Если а > 0, то её
ветви направлены вверх.
Если а < 0, то её
ветви направлены вниз.
Далее вспомним
координату (абсциссу) вершины параболы:
То есть, это точка
экстремума квадратичной функции (в ней функция меняет своё поведение с
возрастания на убывание или наоборот).
Следующий важный факт
(ключевой для этих задач)!
Если исходная функция
монотонна (непрерывно возрастает или убывает), для нее точка х также будет
точкой экстремума. Таким образом, сформулируем ключевое правило:

И конечно, не теряйте из
виду область допустимых значений заданной функции:
— выражение стоящее под
знаком корня, больше или равно нулю (число неотрицательное).
— выражение стоящее под
знаком логарифма, есть положительное число.
— выражение стоящее в
знаменателе дроби не равно нулю.
В подобных задачах на
нахождение наибольшего и наименьшего значения функции, я бы посоветовала
находить область определения в любом случае (даже не смотря на то, что в
представленных задачах это ничего нам не даёт).
Рассмотрим задачи:
Найдите точку
максимума функции ![]()
Под корнем
квадратичная функция 13 + 6х – х2
Ее график —
парабола, ветви направлены вниз, поскольку а = – 1 < 0
Значит, максимальное
значение функция приобретает в точке:

Проверим, принадлежит ли
полученное значение области определения. То есть будет ли подкоренное выражение
числом неотрицательным:
13 + 6∙3 – 32
= 13 + 18 – 9 = 22 > 0
Почему необходимо это
сделать? Дело в том, что абсцисса соответствующая вершине параболы может не
войти в область определения, это будет означать, что области определения будет
принадлежать только участок ветви параболы (таких заданий на ЕГЭ не будет).
Ответ: 3
Решите самостоятельно: Найдите
точку максимума функции ![]()
Ответ: – 2.
Найдите наименьшее
значение функции ![]()
Под корнем
квадратичная функция х2 + 8х + 185.
Ее график —
парабола, ветви направлены вверх, т.к. а = 1 > 0
Абсцисса вершины
параболы:

Так как ветви
параболы направлены вверх, то в точке х = – 4 функция
х2 + 8х + 185
принимает наименьшее значение.
Функция квадратного
корня монотонно возрастает, значит х = 4 точка минимума всей функции,
вычислим её наименьшее значение:
![]()
Ответ: 13
Решите самостоятельно:
Найдите наименьшее значение функции ![]()
Ответ: 2.
Найдите точку
максимума функции у=log7(–2 – 12х – х2) + 10.
Под знаком логарифма
квадратичная функция –2 – 12х – х2.
График — парабола,
ветви направлены вниз, так как а = – 1 < 0
Абсцисса вершины
параболы:
![]()
Проверим, принадлежит ли
полученное значение х области определения (выражение под знаком логарифма
должно быть число положительное):
– 2 –
12∙(–6) – (–6)2 = – 2 + 72 – 36 = 34 > 0
То есть, в точке х = – 6
функция f (х) = – 2 – 12х – х2
будет иметь максимальное значение.
Значит, и у=log7(–2–12х–х2)+10
в этой точке так же будет иметь максимальное значение.
Ответ: – 6.
Решите самостоятельно: Найдите
точку максимума функции у=log2(2 + 2х – х2) – 2
Ответ: 1.
Найдите наименьшее
значение функции у=log9 (х2 – 10х + 754) + 3
Под корнем
квадратичная функция х2 – 10х + 754.
Ее график — парабола,
ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины
параболы:
![]()
То есть, в точке х
= 5 функция f (x) = х2 – 10х + 754 принимает наименьшее
значение.
Функция log9х
монотонная, значит у =log9 (х2 – 10х + 754) + 3
в точке х = 5 также принимает наименьшее значение, вычислим его:
 Ответ: 6
Ответ: 6
Решите самостоятельно:
Найдите наименьшее значение функции у=log3(х2 –
6х + 10) + 2
Ответ: 2.
Найдите точку максимума функции ![]()
В показателе стоит
квадратичная функция – 30 + 12х – х2.
График — парабола,
ветви направлены вниз, так как а = –1 < 0.
Абсцисса вершины
параболы:

То есть, в точке х = 6
функция f (х) = – 30 + 12х – х2 приобретёт максимальное значение.
Значит и данная функция в этой точке будет иметь также максимальное значение.
Ответ: 6
Решите самостоятельно: Найдите
точку максимума функции: ![]()
Ответ: 3.
Найдите наименьшее
значение функции ![]()
В показателе стоит
квадратичная функция х2 + 16х + 66.
Ее график —
парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины
параболы:

То есть, в точке х
= – 8 функция х2 + 16х + 66 принимает наименьшее значение.
Показательная
функция монотонна, поэтому её наименьшее значение будет также в точке х = – 8,
вычислим его
![]()
Ответ: 36
Решите самостоятельно: Найдите
наименьшее значение функции ![]()
Ответ: 16.
Далее мы поговорим о
задачах на нахождение наибольшего и наименьшего значения логарифмических функций.
Рассмотрим задачи:
Найдите наименьшее значение функции
у=5х–ln (х+5)5 на отрезке [–4,5;0].
Необходимо вычислить значение функции на
концах интервала, и в точках экстремума, если таковые имеются на данном
интервале, и выбрать наименьшее из них.
Вычисляем производную,
приравниваем её к нулю, решаем уравнение.
 Найдем производную заданной функции:
Найдем производную заданной функции:

Найдем нули производной
на заданном отрезке:
*Дробь равна нулю тогда,
когда числитель равен нулю.
 Точка х= – 4 принадлежит заданному интервалу.
Точка х= – 4 принадлежит заданному интервалу.
Таким образом, вычисляем
значение функции в точках: – 4,5; – 4; 0.
Значения с логарифмами,
которые мы получили, вычислить (или проанализировать) можно. И вы убедитесь,
что наименьшим значением функции на данном отрезке является
“– 20”.
Но вычислять их не
обязательно. Почему? Мы знаем, что ответом должно быть либо, целое число, либо
конечная десятичная дробь (это условие ЕГЭ в части с кратким ответом). А
значения с логарифмами: – 22,5 – ln 0,55 и –
ln3125 такого ответа не дадут.
Кроме того, убедится в
том, что в точке х=–4 функция приобретает минимальное значение, можно
определив знаки производной на интервалах от (– 5:– 4) и (– 4;+∞).
Теперь информация для
тех, у кого с производной и пониманием того, как решать подобные задачи, нет
трудностей. Как можно обойтись без вычисления производной и без лишних
расчётов?
Итак, если учесть, что
ответом должно быть целое число, либо конечная десятичная дробь, то такое
значение мы можем получить только тогда, когда х будет являться целым числом,
либо целым с конечной десятичной дробью и при этом под знаком логарифма в
скобках у нас будет единица или число е. В противном случае, мы не сможем
получить оговоренное значение. А это возможно только при х = – 4.
Значит, в этой точке
значение функции будет наименьшим, вычислим его:
![]()
Ответ: – 20
Решить
самостоятельно: Найдите наименьшее значение функции у=3х– ln
(х+3)3 на отрезке [–2,5;0].
Ответ: – 6.
Найдите наибольшее значение функции у=ln
(х+5)5–5х на отрезке [–4,5;0].
Ответ: 20.
Найдите наибольшее значение функции у=х2–13х+11∙lnх+12
на отрезке [13/14; 15/14].
Чтобы найти наименьшее
значение функции на отрезке, необходимо вычислить значение функции на его
концах, и в точках экстремума, если таковые имеются на данном интервале.
Вычислим производную,
приравниваем её к нулю, решим полученное уравнение:

Решив квадратное
уравнение, получим

Точка х = 1,
принадлежит заданному интервалу.
Точка х = 22/4 ему
не принадлежит.
Таким образом, вычисляем
значение функции в точках:

Мы знаем, что ответом
является целое число либо конечная десятичная дробь, значит, наибольшее
значение функции равно 0. В первом и третьем случае такое значение мы не
получим, так как натуральный логарифм данных дробей такого результата не
даст.
Кроме того, убедится в
том, что в точке х = 1 функция приобретает максимальное значение, можно
определив знаки производной на интервалах от (0:1) и (1;+∞).
Как решить такой тип
задач без вычисления производной?
Если учесть, что ответом
должно быть целое число, либо конечная десятичная дробь, то это условие
обеспечивается только тогда, когда х будет являться целым числом, либо целым с
конечной десятичной дробью и при этом под знаком логарифма у нас будет
единица или число е.
Это возможно только при
х = 1.
Значит в точке х = 1 (или 14/14)
значение функции будет наибольшим, вычислим его:
![]()
Ответ: 0
Решите самостоятельно:
Найдите наибольшее значение функции
у = 2х2–13х+9∙lnх+8 на отрезке [13/14; 15/14].
Отмечу, что способ
решения таких заданий без нахождения производных, можно использовать только для
экономии времени при вычислении задания на самом ЕГЭ. И только в том случае,
когда вы отлично понимаете, как решать такие задачи через нахождение
производной (по алгоритму) и хорошо умеете это делать. Бесспорно, что при
решении без производной должен быть некоторый опыт в аналитике.
«Хитрых» приёмов,
которые порой помогают в конкретных заданиях множество, и все их не запомнить.
Важно понимать принципы решения, свойства. Если же вы возложите свои надежды на
какой-то приём, то он может просто не сработать по простой причине: вы его
просто забудете или вам попадёт такой тип задания на ЕГЭ, который видите
впервые.
Ну и, конечно, еще раз
повторю, что для того чтобы решать задачи на нахождение наибольшего или
наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства
производной для исследования функций, знать таблицу производных и правила
дифференцирования.
После решения каждой
задачи есть разъяснения другого подхода к решению («хитрости» — они
здесь). Рассмотрим задачи: связанные с числом е
Найдите наименьшее значение функции
у = (х–17)ех–16 на отрезке [15;17].
Мы знаем, что для того,
чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо
вычислить её значение на границах заданного интервала и в точках, где
производная равна нулю. Действуем по алгоритму:
1. Найдём производную заданной функции:

2. Найдем нули производной на заданном
отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:
![]()
*Выражение ех-16 не
равно нулю ни при каких х, так как известно, что показательная функция имеет
положительные значения на всей области определения.
3. Определяем
принадлежит ли найденная точка интервалу.
Точка х = 16
принадлежит интервалу [15;17]. Значит значение функции будем вычислять в
точках 15, 16 и 17:

*Учтите, что число е ≈
2,71. Это нецелое число и неконечная десятичная дробь, поэтому любое
выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом,
но вы всё равно его проанализируйте. В данной задаче, если мы –2 разделим
на число 2,71 то результат будет лежать в пределах от –1 до 0 (можно
посчитать столбиком для проверки).
4. Делаем вывод.
Таким образом,
наименьшее значение функции равно –1.
Ответ: –1
Далее «хитрости»,
которые можно использовать при решении. Если вы поняли теорию производной и
знаете, как находить максимальные и минимальные значения, то тогда идем
подобные задания мгновенно.
Итак! Мы знаем, что
ответом в задачах на ЕГЭ в части с кратким ответом должно быть целое число,
либо конечная десятичная дробь.
Посмотрите на данную
функцию. Сразу можно сказать, что значение функции будет являться целым
числом только при х = 16 или при х = 17, и ни при каких других
значениях х. Поэтому достаточно вычислить:

и далее записать ответ.
Ещё один путь
решения (без нахождения производной). Сразу подставляем в функцию все
целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем
наименьшее значение:

Решите самостоятельно:

Найдите наибольшее значение функции
у = (22 – х)ех–21 на отрезке [16;25].
Найдём производную
заданной функции:

Найдем нули производной:

Число ех-21 не
может быть равно нулю, так как степень положительного числа всегда даст в
результате число положительное, значит х = 21.
Полученное значение
принадлежит интервалу [16;25].
Вычислим значения данной
в условии функции в точках 16, 21 и 25:
*То есть на границах
интервала и в точке, где производная обращается в нуль.

Первый результат меньше
единицы (это понятно и без вычислений).
Третий результат так же
меньше единицы (отрицательное число).
Значит наибольшее
значение функции на заданном интервале равно 1.
*Помните, что ответы с
числом е (по требованиеям ЕГЭ) не являются верными.
Ответ: 1
Если у вас всё-таки
неразрешимые проблемы с нахождением производной, то подставляйте в исходную
функцию все целые значения из интервала и выбирайте наибольшее полученное
значение.
*Кроме того, по данной
функции сразу видно, что её значение будет целым числом только при х = 21
или при х = 22.
Можете подставить только
их в функцию, далее произвести вычисления и выбрать наибольшее значение.
Решите самостоятельно:

Найдите наибольшее значение функции
у = (2х2 – 10х + 10)е х на отрезке [–4; 3].
Необходимо определить
значения на границах интервала, и в точках, где производная обращается в нуль.
Найдём производную
заданной функции:

Найдем нули производной:

Произведение множителей
равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно
нулю, так как степень положительного числа всегда даст в результате число
положительное.
Значит решением являются корни:
х1=0 и х2=3
Обе точки принадлежат интервалу [–4;3], х=3
совпадает с границей интервала.
Вычисляем значения функции в точках: – 4, 0
и 3:

Значит наибольшее
значение функции равно 10.
Ответ: 10
*Как вы уже поняли,
можно в заданную функцию можно подставить все целые значения х из интервала, и
таким образом найти наибольшее значение функции. Но в данном случае придётся
перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).
Решите самостоятельно:

Найдите наименьшее значение
функции у = (х + 44)2е–44–х на
отрезке [– 46; –43]
Найдём производную заданной функции:

Обратите внимание, что результат мы
представили сразу в виде множителей, это будет удобно при вычислении нулей
производной.
Найдем нули производной:
![]()
Решением являются
корни: х1= – 44 и х2= – 42.
Заданному интервалу [–
46;–43] принадлежит только точка х = – 44.
Вычисляем значения
функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке,
где производная равна нулю:

Наименьшее значение
функции равно 0.
Ответ: 0
*Как это задание решить
быстро?
Учитывая, что ответом
должно быть целое число, видно что значение данной функции будет целым только
при х= – 44 и х= 44.
указанному в условии
интервалу принадлежит х= – 44, вычисляем:
![]()
Решите самостоятельно:

Но в заданиях на нахождение точек минимума
и максимума мы ОБЯЗАТЕЛЬНО должны использовать производную.
Найдите точку
минимума функции у = (х + 18)ех-18
1. Найдём производную
заданной функции:

2. Найдем нули
производной:
![]()
Получаем, что х =
–19.
*Выражение ех-18 не
равно нулю ни при каких х, так как известно, что показательная функция имеет
положительные значения на всей области определения.
 3. Определим знаки производной функции на интервалах (подставляем любые
3. Определим знаки производной функции на интервалах (подставляем любые
произвольные значения в производную) и изобразим на рисунке поведение функции:

В точке х = –19 функция
меняет знак с отрицательного на положительный, значит это искомая точка
минимума.
Ответ: –19
Как решать быстрее
данный тип задач?
Когда мы получили
производную и приравняли её к нулю:
(х + 19)ех–18
= 0
Далее получили, что х=–19. Данное решение и
будет являться ответом задачи.
*То есть, в при решении
данного типа задач, можно обойтись без определения знаков производной на
интервалах. Но будте осторожны! В других заданиях на нахождение максимума
(минимума), где получите несколько нулей производной, её знаки на интервалах
нужно определять обязательно.
Решите самостоятельно:

Найдите точку максимума функции у =
(3х2 – 15х + 15)е7–х
Найдём производную заданной функции:

Найдем нули производной:

Число е7-х не
может быть равно нулю, так как степень положительного числа всегда даст в
результате число положительное.
Решаем – 3
(х–5)(х–2) = 0. Получим х1 = 5 и х2 = 2
.
 Определим знаки производной функции (подставляя любые значения из
Определим знаки производной функции (подставляя любые значения из
интервалов в найденную производную) и изобразим на рисунке поведение функции:

В точке х = 5 функция меняет знак с
положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5
Решите самостоятельно:

Найдите точку
максимума функции у = ln (х–11)–5х+2
Сразу запишем, что х–11>0 (по
определению логарифма), то есть х > 11.
Рассматривать функцию
будем на интервале (11;∞).
Найдём производную
заданной функции:

Найдем нули производной:

Точка х = 11 не входит в
область определения функции и в ней производная не существует. Отмечаем на
числовой оси две точки 11 и 11,2. Определим знаки производной функции,
подставляя произвольные значения из интервалов (11;11,2) и (11,2;+∞) в
найденную производную, и изобразим на рисунке поведение функции:


Таким образом, в точке х=11,2 производная
функции меняет знак с положительного на отрицательный, значит это искомая точка
максимума.
Ответ: 11,2
Решите самостоятельно:
Найдите точку
максимума функции у=ln (х+5)–2х+9.
Найдите точку
минимума функции у=4х– ln (х+5)+8
Сразу запишем, что х+5>0 (по свойству
логарифма), то есть х>–5.
Рассматривать функцию
будем на интервале (– 5;+∞).
Найдём производную
заданной функции:

Найдем нули производной:

Точка х = –5
не входит в область определения функции и в ней производная не существует.
Отмечаем на числовой оси две точки –5 и –4,75. Определим
знаки производной функции, подставляя произвольные значения из интервалов
(–5;–4,75) и (–4,75;+∞) в найденную производную, и изобразим на рисунке
поведение функции:


Таким образом, в точке х= –4,75
производная функции меняет знак с отрицательного на положительный,
значит это искомая точка минимума.
Ответ: – 4,75
Решите самостоятельно:
Найдите точку
минимума функции у=2х–ln (х+3)+7.
Найдите точку
максимума функции у = х2–34х+140lnх–10
По свойству логарифма
выражение, стоящее под его знаком больше нуля, то есть х > 0.
Функцию будем
рассматривать на интервале (0; +∞).
Найдём производную
заданной функции:

Найдем нули производной:

Решая квадратное
уравнение, получим: D = 9 х1 = 10 х2
= 7.
Точка х = 0 не
входит в область определения функции и в ней производная не существует.
Отмечаем на числовой оси три точки 0, 7 и 10.
Ось ох разбивается на
интервалы: (0;7), (7;10), (10; +∞).
 Определим знаки производной функции, подставляя произвольные значения
Определим знаки производной функции, подставляя произвольные значения
из полученных интервалов в найденную производную, и изобразим на рисунке
поведение функции:

Таким образом, в точке х = 7 производная
функции меняет знак с положительного на отрицательный, значит это
искомая точка максимума.
Ответ: 7
Решите самостоятельно:
Найдите точку
максимума функции у = 2х2 –13х+9lnх+8

СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
24 мая
Обновлённая панель инструментов
22 мая
Беседы Решу ЕГЭ по подготовке к ЕГЭ
11 мая
Решение досрочных ЕГЭ по всем предметам
5 мая
Обновленный поиск заданий по ключевым словам
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование тригонометрических функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 26692 

i
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26692: 3401 70043 517179 … Все
Источник: Пробный ЕГЭ по математике Санкт-Петербург 2015. Вариант 2
Решение
·
Видеокурс
·
Помощь
2
Тип 11 № 26693 

i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26693: 70087 3417 3419 … Все
Решение
·
Видеокурс
·
Помощь
3
Тип 11 № 26694 

i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26694: 3437 70133 70137 … Все
Решение
·
Видеокурс
·
Помощь
4
Тип 11 № 26695 

i
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26695: 3457 70187 509500 … Все
Источник: Пробный ЕГЭ по профильной математике Санкт-Петербург 05.04.2016. Вариант 2
Решение
·
Видеокурс
·
Помощь
5
Тип 11 № 26696 

i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26696: 3475 70237 3477 … Все
Решение
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
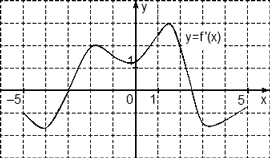
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
15 марта 2011
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
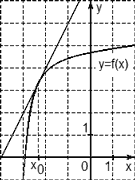
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
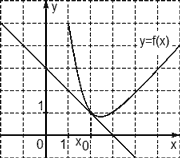
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
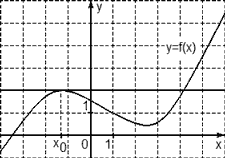
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
![]()
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
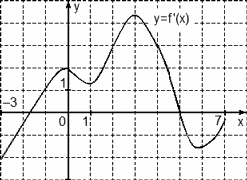
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
![]()
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
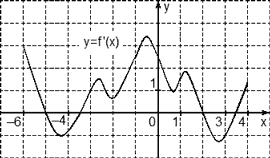
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
![]()
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
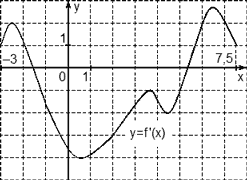
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
![]()
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
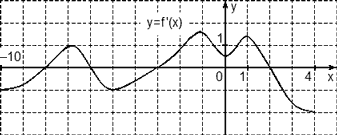
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
![]()
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции

- ЕГЭ 2022, задание 6. Касательная к графику функции

- Схема Бернулли. Примеры решения задач

- Решение задач B6: №362—377

- Четырехугольная пирамида: как найти координаты вершин

- Нестандартная задача B2: студенты, гонорары и налоги