Как найти тип поверхности – Сайт, где вы сможете решить свои вопросы

11.3.1. Классификация поверхностей второго порядка

Алгебраической поверхностью
второго порядка называется
геометрическое место точек пространства,
которое в какой-либо аффинной системе
координат

может быть задано уравнением вида

где старшие коэффициенты

,

,

,

,

,

не равны нулю одновременно. Без ограничения
общности можно считать, что система
координат, в которой задано уравнение
поверхности второго порядка, прямоугольная.
Для каждой поверхности второго порядка
существует прямоугольная система
координат

,
в которой уравнение принимает наиболее
простой (канонический) вид. Она
называется канонической, а
уравнение – каноническим.

Канонические уравнения поверхностей второго порядка

– уравнение эллипсоида;

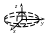
2.

–
уравнение мнимого эллипсоида;

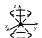
3.

–
уравнение мнимого конуса;

4.

–
уравнение однополостного

гиперболоида;

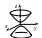
5.

–
уравнение двуполостного

гиперболоида;

6.

–
уравнение конуса;

7.

–
уравнение эллиптического

параболоида;

8.

–
уравнение гиперболического

параболоида;

9.

–
уравнение эллиптического

цилиндра;

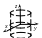
10.

–
уравнение мнимого

эллиптического цилиндра;

11.

– уравнение пары мнимых

пересекающихся плоскостей;

1
2.

– уравнение гиперболического

цилиндра;

13.

– уравнение пары пересекающихся

плоскостей;

14.

– уравнение параболического

цилиндра;

15.

– уравнение пары параллельных

плоскостей;

16.

– уравнение пары мнимых

параллельных плоскостей;

17.

– уравнение пары совпадающих

плоскостей.

В этих уравнениях

,

,

,

,
причем

в уравнениях п.1–3;

в уравнениях п.4–7,9–11.

Поверхности (1),(4)–(9), (12)–(15),(17) называются
вещественными (действительными),
а поверхности (2),(3),(10),(11),(16) – мнимыми.
Вещественные поверхности изображены
в канонических системах координат.
Изображения мнимых поверхностей даются
штриховыми линиями только для иллюстрации.

Поверхность второго порядка называется
центральной, если она имеет
единственный центр (симметрии). В
противном случае, если центр отсутствует
или не является единственным, поверхность
называется нецентральной. К
центральным поверхностям относятся
эллипсоиды (вещественный и мнимый),
гиперболоиды (однополостный и
двуполостный), конусы (вещественный и
мнимый). Остальные поверхности –
нецентральные.

Алгоритм составления канонического уравнения поверхности второго порядка

Пусть в прямоугольной системе координат

поверхность второго порядка описывается
уравнением

Требуется определить ее название и
составить каноническое уравнение. Для
этого нужно выполнить следующие действия:

1. Вычислить ортогональные инварианты

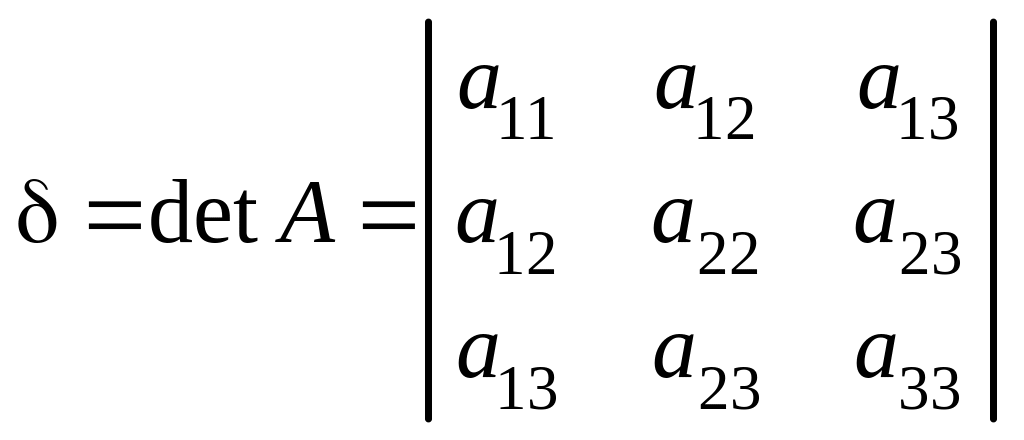
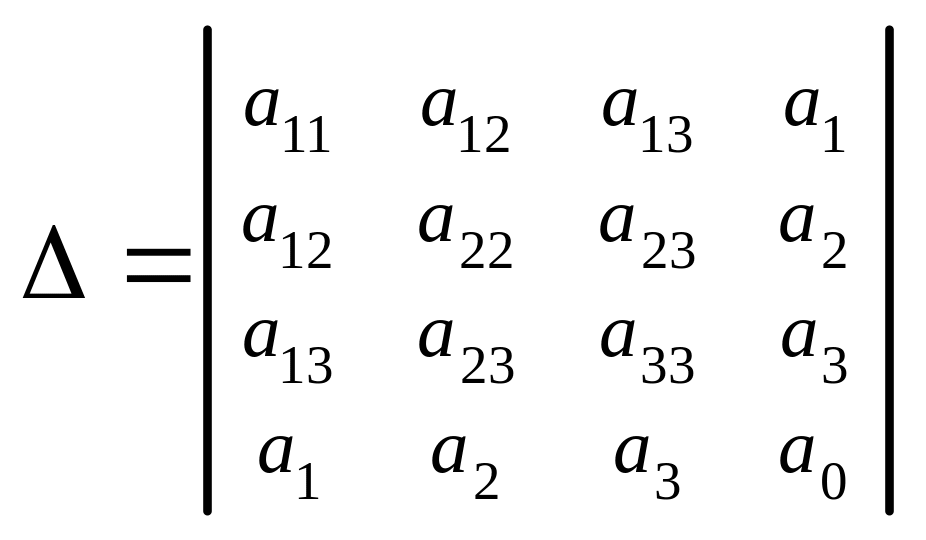
Если

,
то вычислить семиинвариант

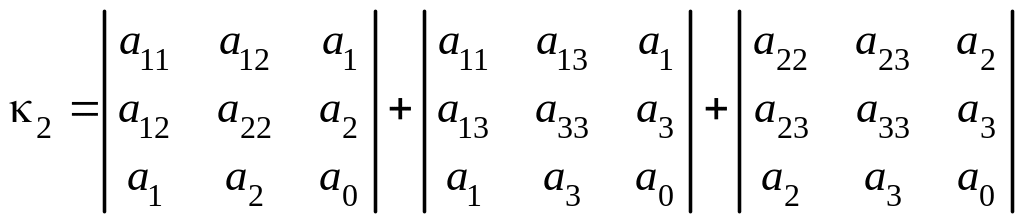
Если

и

,
то вычислить семиинвариант

2. По табл. 11.1 определить название
поверхности, а по названию –каноническое
уравнение поверхности второго порядка.

3. Составить характеристическое уравнение

используя коэффициенты, вычисленные в
п.1, либо разлагая определитель

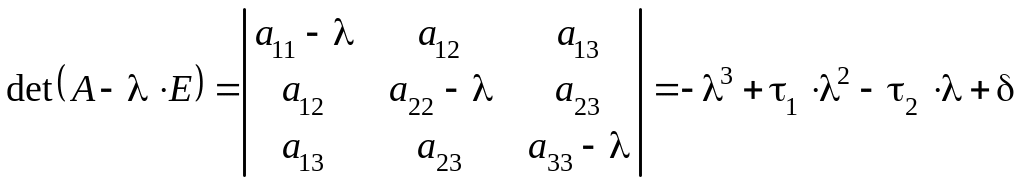
Найти корни

,
,

(с учетом кратности) характеристического
уравнения.

4. Занумеровать корни

,
,

характеристического уравнения в
соответствии с правилами:

а) если поверхность эллиптического
типа, то

;

б) если поверхность гиперболического
типа, то обозначить через

корни одного знака так, чтобы

,
а через

– корень противоположного знака;

в) если поверхность параболического
типа, то

– если нулевой корень двойной, то

и

;

– если нулевой корень простой, а
ненулевые корни одного знака, то

;

– если нулевой корень простой, а
ненулевые корни разных знаков, то

и либо

,
если

или

,
либо

,
если

и

.

5. Вычислить коэффициенты канонического
уравнения и записать его в канонической
системе координат

:

а) для поверхностей эллиптического
типа:

(1) – при

– уравнение эллипсоида

с коэффициентами

,

;

Таблица
11.1. Классификация
поверхностей второго порядка

	Признаки	Название поверхности	№
Центральные поверхности		Эллиптический тип			Эллипсоид	1
	Мнимый эллипсоид	2
	Мнимый конус	3
Гиперболический тип			Однополостный гиперболоид	4
	Двуполостный гиперболоид	5
	Конус	6
Нецентральные поверхности		Параболический тип		Эллиптический параболоид	7
	Гиперболический параболоид	8
			Эллиптический цилиндр	9
	Мнимый эллиптический цилиндр	10
	Пара мнимых пересекающихся плоскостей	11
		Гиперболический цилиндр	12
	Пара пересекающихся плоскостей	13
		Параболический цилиндр	14
		Пара параллельных плоскостей	15
	Пара мнимых параллельных плоскостей	16
	Пара совпадающих плоскостей	17

(2) при

– уравнение мнимого эллипсоида

с коэффициентами

,

;

(3) при

– уравнение мнимого конуса

с коэффициентами

,

;

б) для поверхностей гиперболического
типа:

(4) при

– уравнение однополостного гиперболоида

с коэффициентами

;

(5) при

– уравнение двуполостного гиперболоида

с коэффициентами

,

;

(6) при

– уравнение конуса

с коэффициентами

;

в) для поверхностей параболического
типа:

(7) при

– уравнение эллиптического параболоида

с коэффициентами

,

;

(8) при

– уравнение гиперболического
параболоида

с коэффициентами

;

(9) при

,

,

– уравнение эллиптического цилиндра

с коэффициентами

,

;

(10) при

– уравнение мнимого эллиптического
цилиндра

с коэффициентами

,

;

(11) при

– уравнение пары мнимых пересекающихся
плоскостей

с коэффициентами

;

(12) при

,

,

– уравнение гиперболического цилиндра

с коэффициентами

;

(13) при

– уравнение пары пересекающихся
плоскостей

с коэффициентами

,

;

(14) при

,

,

– уравнение параболического цилиндра

с коэффициентом

;

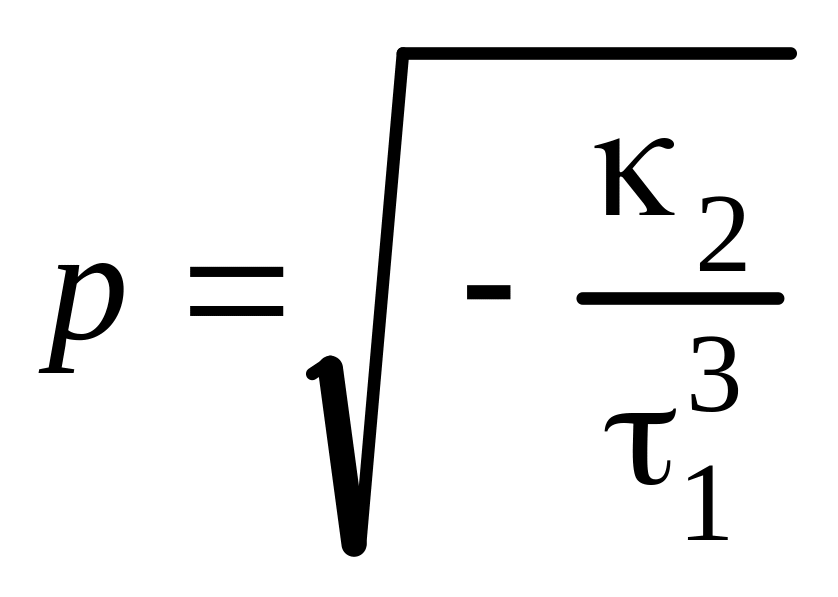
(15) при

– уравнение пары параллельных
плоскостей

с коэффициентом

;

(16) при

– уравнение пары мнимых параллельных
плоскостей

с коэффициентом

;

(17) при

– уравнение пары совпадающих плоскостей

.

Пример 11.10. Определить названия и
составить канонические уравнения
алгебраических поверхностей второго
порядка, заданных в прямоугольной
системе координат

уравнениями:

а)

;

б)

при

,

или

;

в)

;

г)

;

д)

;

е)

при

или

;

ж)

;

з)

;

и)

.

 а)
Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

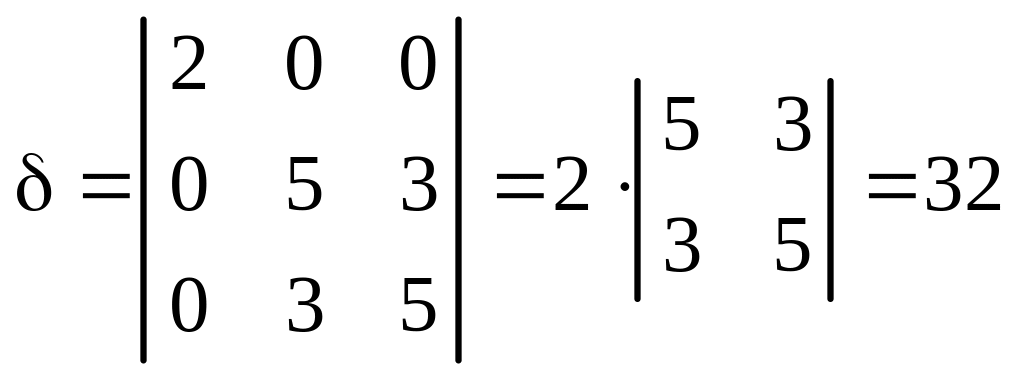
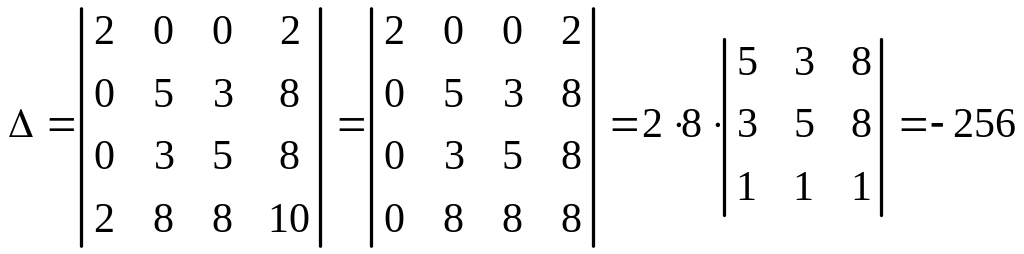
2. По табл. 11.1 определяем, что уравнение
задает эллипсоид, так как

,

,

.

3. Составляем характеристическое
уравнение

и находим его корни:

(двойной корень),

(простой корень).

4. Поскольку поверхность эллиптического
типа, то корни уравнения обозначим

,

,
чтобы выполнялось условие

5. Вычисляем коэффициенты канонического
уравнения эллипсоида:

,

,

.

Таким образом, каноническое уравнение
(1) заданной поверхности имеет вид

б) Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

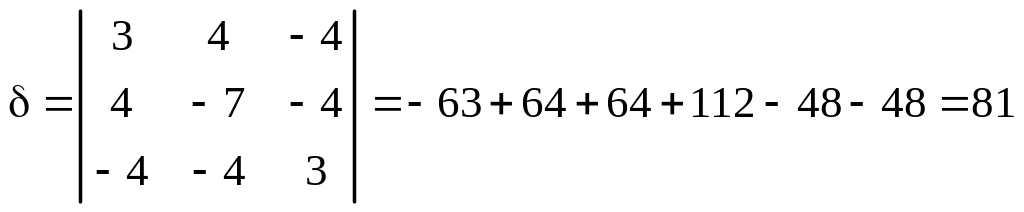
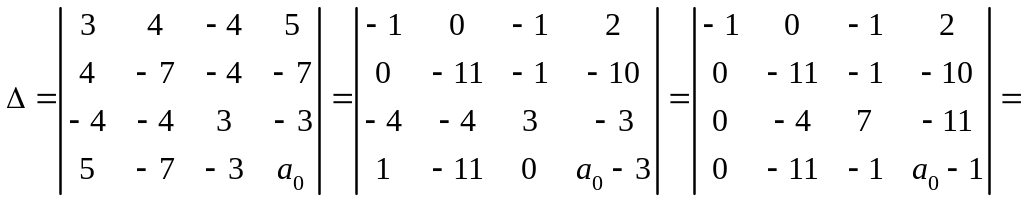
2. По табл. 11.1 определяем, что уравнение
задает поверхность гиперболического
типа, так как

.
При

получаем уравнение однополостного
гиперболоида, так как

,
при

– уравнение конуса, так как

,
при

– уравнение двуполостного гиперболоида,
так как

.

3. Составляем характеристическое
уравнение

и находим его корни:

,

,

(все корни простые).

4. Поскольку поверхность гиперболического
типа, то корни уравнения обозначим

,

,
т.е.

корни одного знака, причем

,
а

– корень противоположного знака.

5. Вычисляем коэффициенты канонического
уравнения:

– однополостного гиперболоида (при

,

,

,

следовательно, каноническое уравнение
(4) имеет вид

;

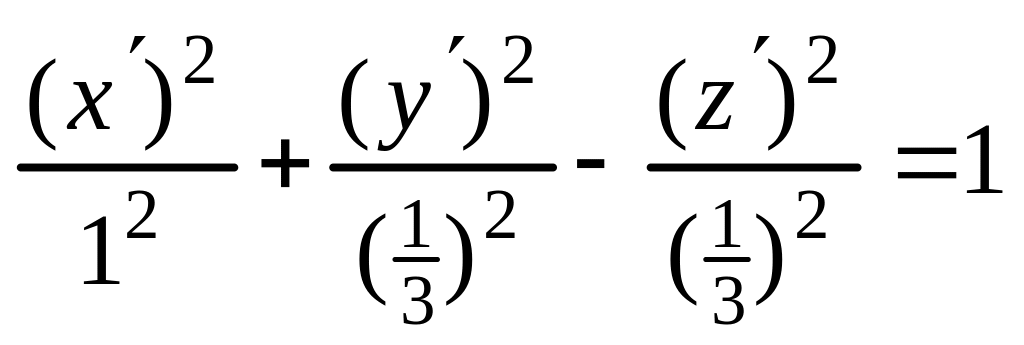
– конуса (при

;

следовательно, каноническое уравнение
(6) имеет вид

;

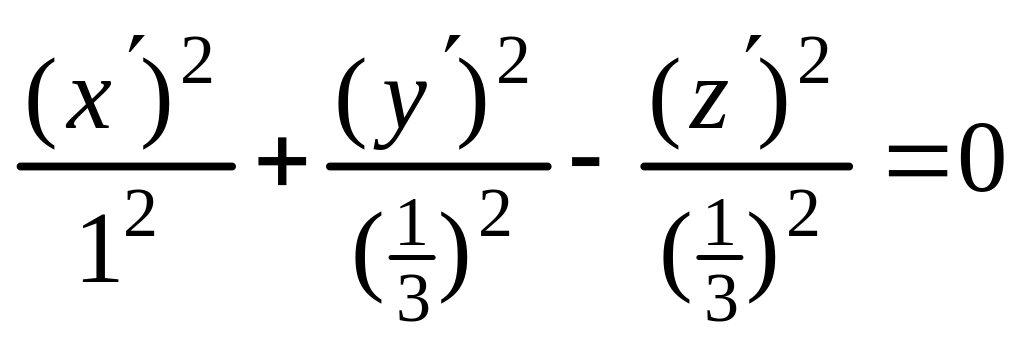
– двуполостного гиперболоида (при

;

следовательно, каноническое уравнение
(5) имеет вид

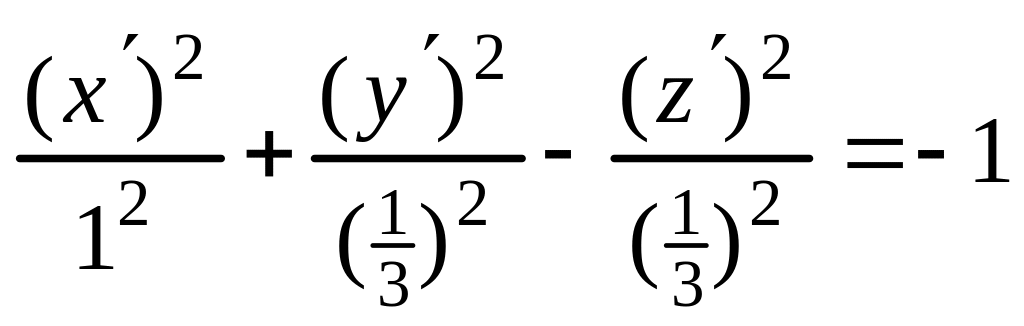
в) Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

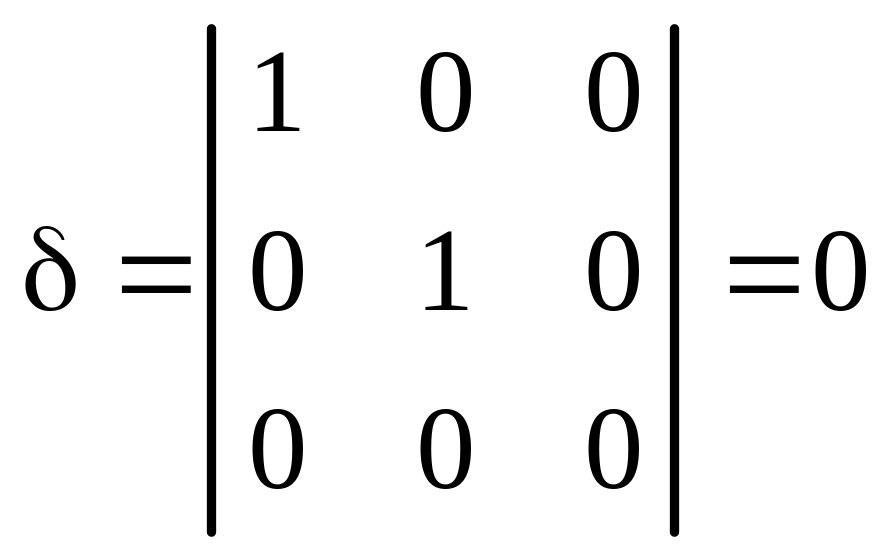
2. По табл. 11.1 определяем, что уравнение
задает эллиптический параболоид,
так как

,

3. Составляем характеристическое
уравнение

и находим его корни:

(двойной корень),

(простой корень).

4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:

– единственный нулевой корень; так как
ненулевые корни одного знака, то

,
чтобы выполнялось условие

5. Вычисляем коэффициенты канонического
уравнения эллиптического параболоида:

Таким образом, каноническое уравнение
(7) заданной поверхности имеет вид

г) Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

2. По табл. 11.1 определяем, что уравнение
задает гиперболический параболоид,
так как

3. Составляем характеристическое
уравнение

и находим его корни:

,

(все корни простые).

4. Поскольку поверхность параболического
типа, то корни характеристического
уравнения обозначим следующим образом:

– единственный нулевой корень; так как
ненулевые корни разных знаков и

,
то

,
тогда

.

5. Вычисляем коэффициенты канонического
уравнения гиперболического параболоида:

,

.

Таким образом, каноническое уравнение
(8) заданной поверхности имеет вид

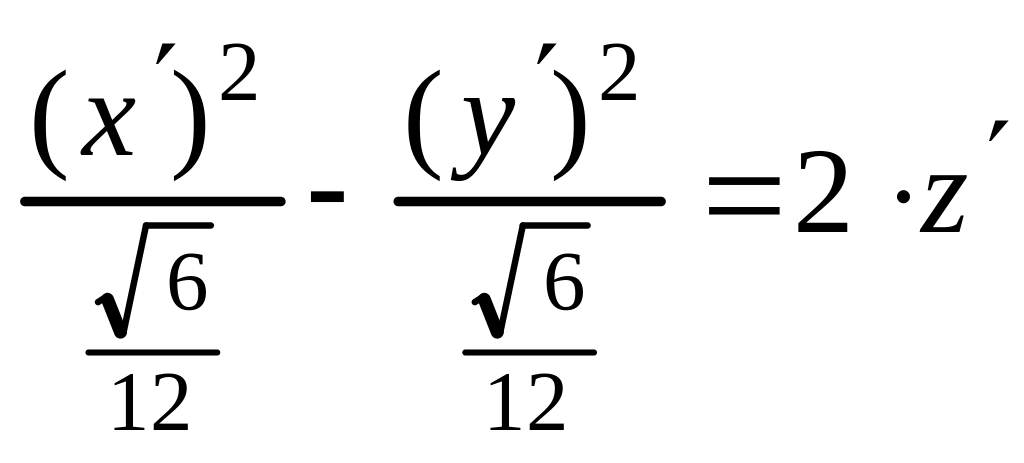
д) Определяем коэффициенты уравнения:

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

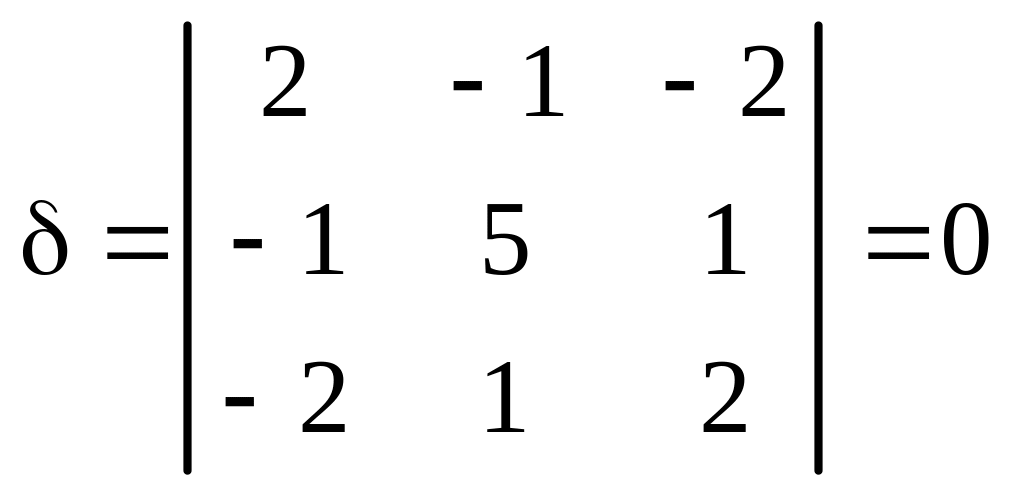
Так как

,
то вычисляем семиинвариант:

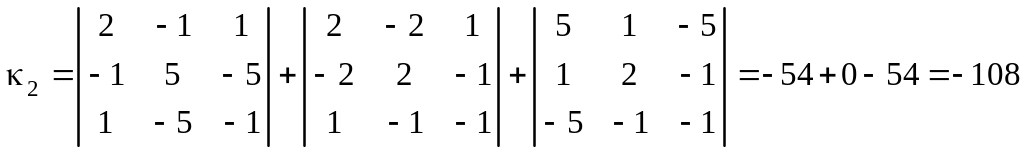
2. По табл. 11.1 определяем, что уравнение
задает эллиптический цилиндр, так
как

3. Составляем характеристическое
уравнение

и находим его корни:

,

,

(все корни простые).

4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:

– единственный нулевой корень; так как
ненулевые корни одного знака, то

,

,
чтобы выполнялось условие

5. Вычисляем коэффициенты канонического
уравнения эллиптического цилиндра:

Таким образом, каноническое уравнение
(9) заданной поверхности имеет вид

е) Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

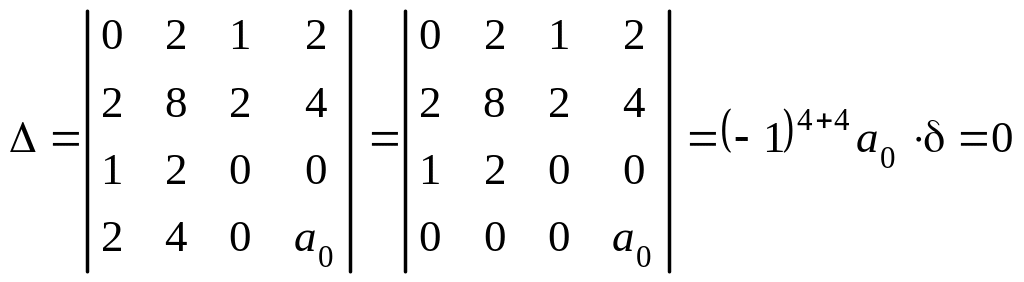
Так как

,
то вычисляем семиинвариант:

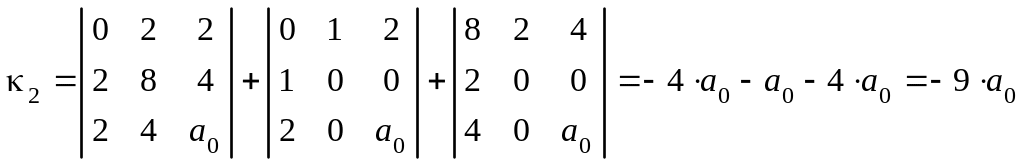
2. По табл. 11.1 определяем, что уравнение
задает поверхность параболического
типа, так как

.
При

получаем уравнение гиперболического
цилиндра, так как

,

,

;
при

– уравнение пары пересекающихся
плоскостей, так как

3. Составляем характеристическое
уравнение

и находим его корни:

,

,

(все корни простые).

– единственный нулевой корень; так как
ненулевые корни разных знаков и

,
то

,
тогда

(при

имеем

и

,
а при

имеем

5. Вычисляем коэффициенты канонического
уравнения:

– гиперболического цилиндра (при

;

следовательно,
каноническое уравнение (12) имеет вид

;

– пары пересекающихся плоскостей (при

;

следовательно, каноническое уравнение
(13) имеет вид

ж) Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

,

,

.

1. Вычисляем инварианты:

,

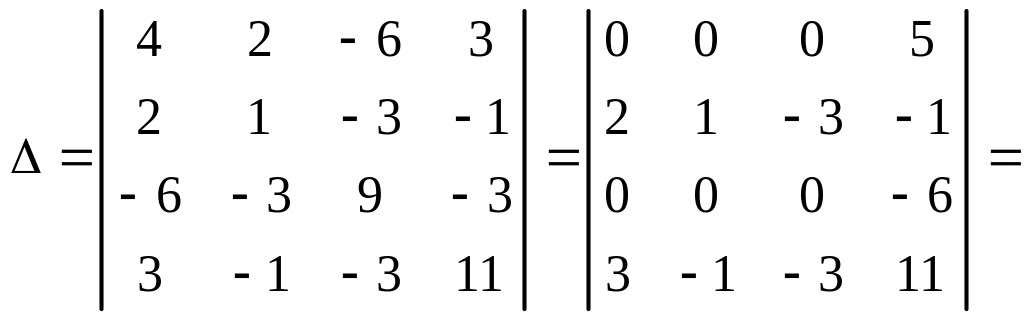
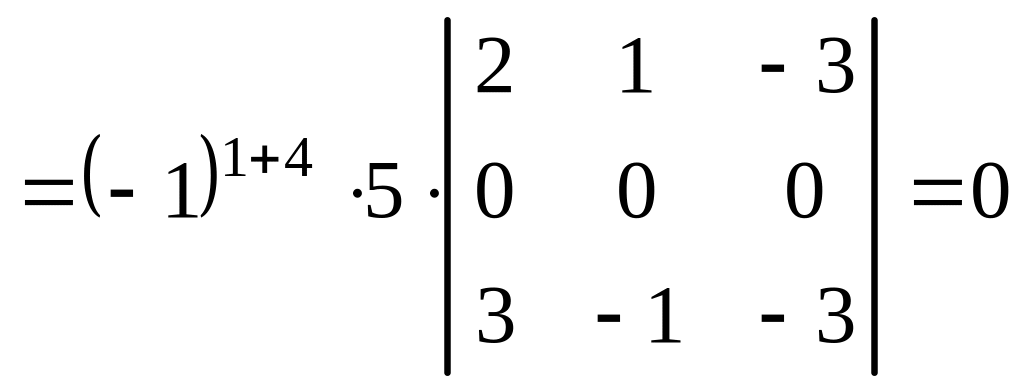
Так как

,
то вычисляем

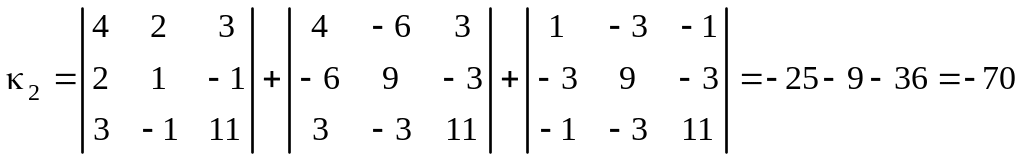
2. По табл. 11.1 определяем, что уравнение
задает параболический цилиндр, так
как

,

,

3. Составляем характеристическое
уравнение

и находим его корни:

(двойной корень),

(простой корень).

4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:

– двойной нулевой корень, а

– ненулевой корень.

5. Вычисляем коэффициент канонического
уравнения параболического цилиндра:

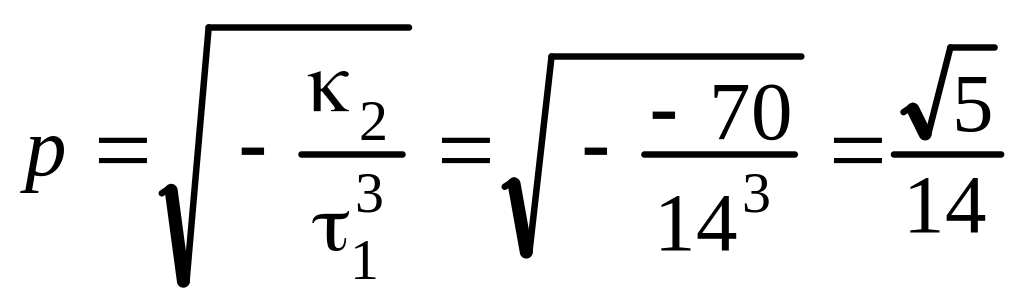
Таким образом, каноническое уравнение
(14) заданной поверхности имеет вид

з) Определяем коэффициенты уравнения:

,

,

,

,

,

,

,

,

1. Вычисляем инварианты:

,

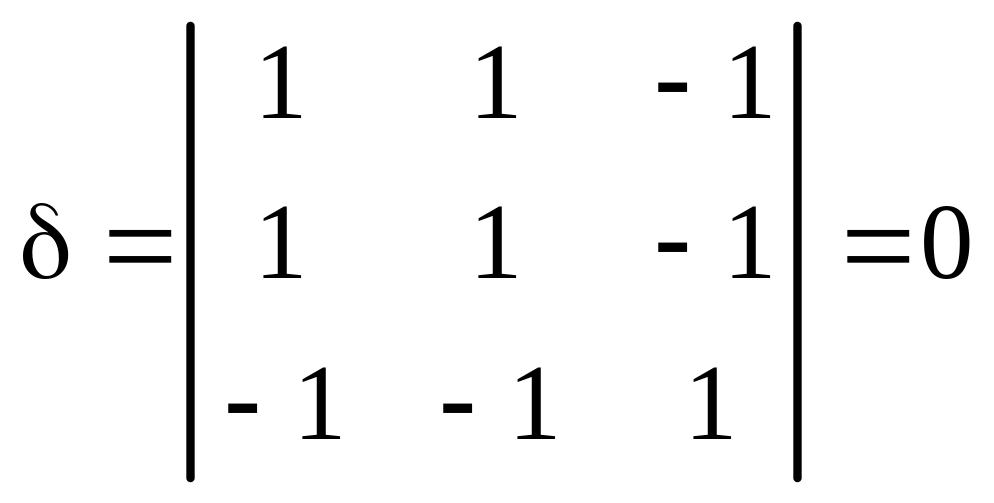
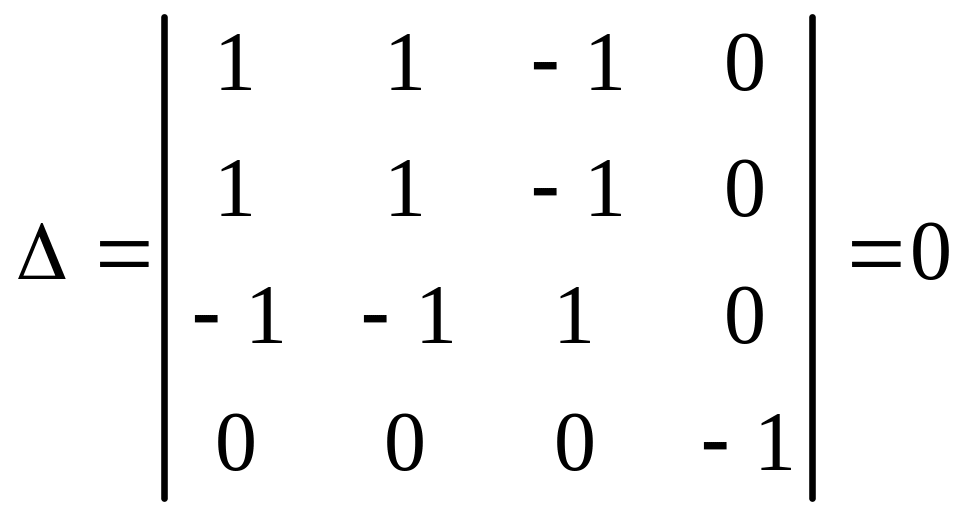
Так как

,
то вычисляем

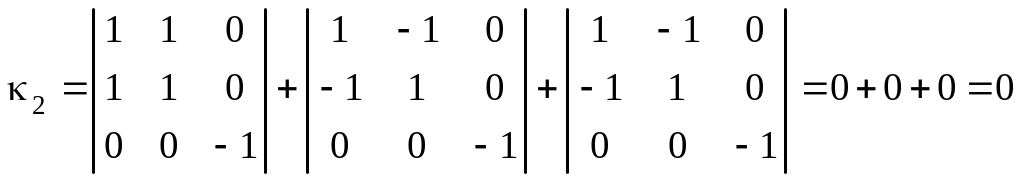
Так как

,
то вычисляем

2. По табл. 11.1 определяем, что уравнение
задает пару параллельных плоскостей,
так как

3. Составляем характеристическое
уравнение

и находим его корни:

(двойной корень),

(простой корень).

4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:

– двойной нулевой корень, а

– ненулевой корень.

5. Вычисляем коэффициент канонического
уравнения пары параллельных плоскостей:

Таким образом, каноническое уравнение
(15) заданной поверхности имеет вид

и) Определяем коэффициенты уравнения:

,

,

1. Вычисляем инварианты:

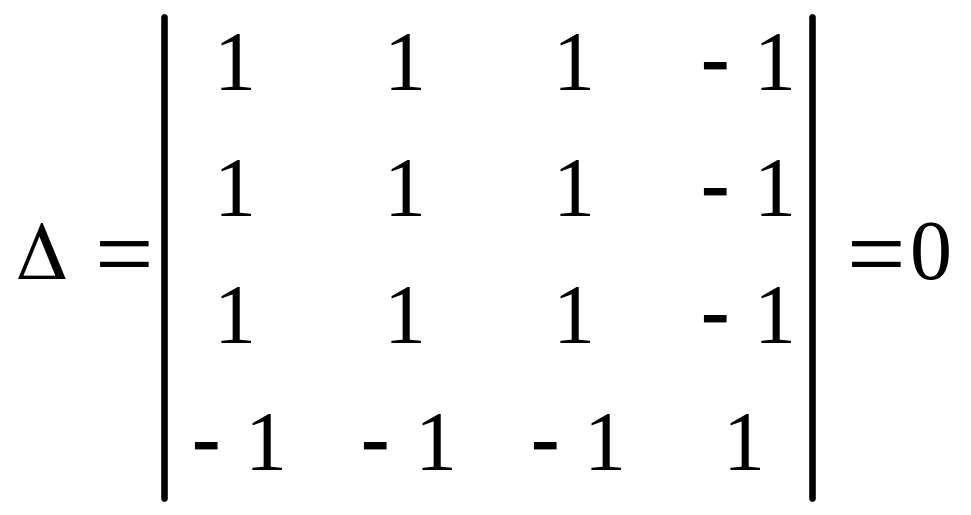
Так как

,
то вычисляем

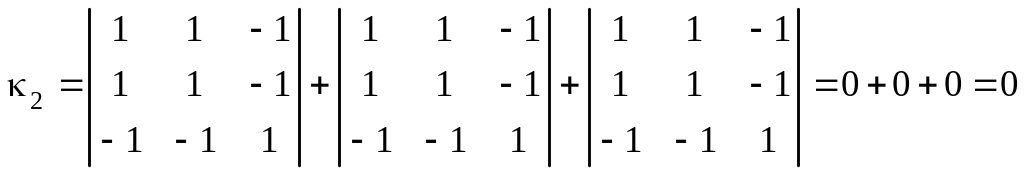
Так как

,
то вычисляем

2. По табл. 11.1 определяем, что уравнение
задает пару совпадающих плоскостей,
так как

3. Составляем характеристическое
уравнение

и находим его корни:

(двойной корень),

(простой корень).

4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:

– двойной нулевой корень, а

– ненулевой корень.

5. Записываем каноническое уравнение
(17) пары совпадающих плоскостей:

.


Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 января 2023 года; проверки требует 1 правка.

Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида

$a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{23}yz+2a_{13}xz+2a_{14}x+2a_{24}y+2a_{34}z+a_{44}=0$

в котором по крайней мере один из коэффициентов $a_{11}$ , $a_{{22}}$ , $a_{{33}}$ , $a_{{12}}$ , $a_{{23}}$ , $a_{{13}}$ отличен от нуля. Является частным случаем квадрики.

Поверхности второго порядка, получающиеся при различных значениях параметров уравнения

Типы поверхностей второго порядка[править | править код]

Цилиндрические поверхности[править | править код]

Поверхность $S$ называется цилиндрической поверхностью с образующей ${vec {l}}$ , если для любой точки $M_{0}$ этой поверхности прямая, проходящая через эту точку параллельно образующей ${vec {l}}$ , целиком принадлежит поверхности $S$ .

Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность $S$ имеет уравнение $f(x,y)=0$ , то $S$ — цилиндрическая поверхность с образующей, параллельной оси $OZ$ .

Кривая, задаваемая уравнением $f(x,y)=0$ в плоскости $z=0$ , называется направляющей цилиндрической поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1$	${displaystyle y^{2}=2px}$	${frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}!=1$

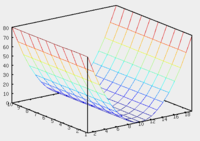
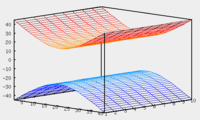
Пара совпавших прямых:	Пара совпавших плоскостей:	Пара пересекающихся плоскостей:
$frac{x^2}{a^2}+frac{y^2}{b^2}=0$	$y^{2}=0$	${frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}!=0$

Конические поверхности[править | править код]

Поверхность $S$ называется конической поверхностью с вершиной в точке $O$ , если для любой точки $M_{0}$ этой поверхности прямая, проходящая через $M_{0}$ и $O$ , целиком принадлежит этой поверхности.

Функция $F(x,y,z)$ называется однородной порядка $m$ , если $forall tin mathbb {R} ;forall x,y,z$ выполняется следующее: ${displaystyle F(tx,ty,tz)=t^{m}F(x,y,z)}$

Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность $S$ задана уравнением $F(x,y,z)=0$ , где $F(x,y,z)$ — однородная функция, то $S$ — коническая поверхность с вершиной в начале координат.

Если поверхность $S$ задана функцией $F(x,y,z)$ , являющейся однородным алгебраическим многочленом второго порядка, то $S$ называется конической поверхностью второго порядка.

Каноническое уравнение конуса второго порядка имеет вид:

${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=0}$

Поверхности вращения[править | править код]

Поверхность $S$ называется поверхностью вращения вокруг оси $OZ$ , если для любой точки $M_{0}(x_{0},y_{0},z_{0})$ этой поверхности окружность, проходящая через эту точку в плоскости $z=z_{0}$ с центром в $(0,0,z_{0})$ и радиусом $r={sqrt {x_{0}^{2}+y_{0}^{2}}}$ , целиком принадлежит этой поверхности.

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность $S$ задана уравнением $F(x^{2}+y^{2},z)=0$ , то $S$ — поверхность вращения вокруг оси $OZ$ .

Эллипсоид:	Однополостной гиперболоид:	Двуполостной гиперболоид:	Эллиптический параболоид:	Гиперболический параболоид:
${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}+{frac {z^{2}}{c^{2}}}=1}$	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=1}$	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=-1}$	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=2z}$	${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=2z}$

В случае, если $a=bneq 0$ , перечисленные выше поверхности являются поверхностями вращения.

Эллиптический параболоид[править | править код]

Уравнение эллиптического параболоида имеет вид

${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=2z.}$

Если $a=b$ , то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой ${displaystyle p=a^{2}=b^{2}}$ , вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.

Пересечение эллиптического параболоида с плоскостью $z=z_{0}>0$ является эллипсом.

Пересечение эллиптического параболоида с плоскостью $x=x_{0}$ или $y=y_{0}$ является параболой.

Гиперболический параболоид[править | править код]

Уравнение гиперболического параболоида имеет вид

${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=2z.}$

Пересечение гиперболического параболоида с плоскостью $z=z_{0}$ является гиперболой.

Пересечение гиперболического параболоида с плоскостью $x=x_{0}$ или $y=y_{0}$ является параболой.

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Центральные поверхности[править | править код]

Если центр поверхности второго порядка существует и единственен, то его координаты $left(x_{0},;y_{0};z_{0}right)$ можно найти, решив систему уравнений:

${begin{cases}a_{11}x_{0}+a_{12}y_{0}+a_{13}z_{0}+a_{14}=0\a_{21}x_{0}+a_{22}y_{0}+a_{23}z_{0}+a_{24}=0\a_{31}x_{0}+a_{32}y_{0}+a_{33}z_{0}+a_{34}=0end{cases}}$

Матричный вид уравнения поверхности второго порядка[править | править код]

Уравнение поверхности второго порядка может быть переписано в матричном виде:

${begin{pmatrix}x&y&z&1end{pmatrix}}{begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\a_{21}&a_{22}&a_{23}&a_{24}\a_{31}&a_{32}&a_{33}&a_{34}\a_{41}&a_{42}&a_{43}&a_{44}end{pmatrix}}{begin{pmatrix}x\y\z\1end{pmatrix}}=0$

Также можно выделить квадратичную и линейную части друг от друга:

${begin{pmatrix}x&y&zend{pmatrix}}{begin{pmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}\end{pmatrix}}{begin{pmatrix}x\y\zend{pmatrix}}+2{begin{pmatrix}a_{14}&a_{24}&a_{34}end{pmatrix}}{begin{pmatrix}x\y\zend{pmatrix}}+a_{44}=0$

Если обозначить
$A={begin{pmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}\end{pmatrix}}quad b={begin{pmatrix}a_{14}&a_{24}&a_{34}end{pmatrix}}quad X={begin{pmatrix}x&y&zend{pmatrix}}^{T}$
, то уравнение приобретает следующий вид:

$X^{T}AX+2bX+a_{44}=0$

Инварианты[править | править код]

Значения следующих величин сохраняются при ортогональных преобразованиях базиса:

Связанных с матрицей $A$ :

Такие инварианты также иногда называют полуинвариантами или семи-инвариантами.

При параллельном переносе системы координат величины $I_{1},I_{2},I_{3},K_{4}$ остаются неизменными. При этом:

Классификация поверхностей второго порядка относительно значений инвариантов[править | править код]

Поверхность	Уравнение	Инварианты
Эллипсоид	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}+{frac {z^{2}}{c^{2}}}=1}$	${displaystyle I_{3}neq 0}$	${displaystyle I_{2}>0,quad I_{1}I_{3}>0}$	${displaystyle K_{4}<0}$
Мнимый эллипсоид	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}+{frac {z^{2}}{c^{2}}}=-1}$	${displaystyle K_{4}>0}$
Точка	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}+z^{2}=0}$	${displaystyle K_{4}=0}$
Однополостный гиперболоид	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=1}$	${displaystyle I_{2}=0}$ или ${displaystyle I_{1}I_{3}leq 0}$	${displaystyle K_{4}>0}$
Двуполостный гиперболоид	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=-1}$	${displaystyle K_{4}<0}$
Конус	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-2z^{2}=0}$	${displaystyle K_{4}=0}$
Эллиптический параболоид	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-2z=0}$	${displaystyle I_{3}=0}$	${displaystyle K_{4}neq 0}$	${displaystyle K_{4}<0}$
Гиперболический параболоид	${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}-2z=0}$	${displaystyle K_{4}>0}$
Эллиптический цилиндр	${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1$	${displaystyle K_{4}=0}$	${displaystyle I_{2}>0}$	${displaystyle I_{1}K_{2}<0}$
Мнимый эллиптический цилиндр	${displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=-1}$	${displaystyle I_{1}K_{2}>0}$
Прямая (пара мнимых пересекающихся плоскостей)	${displaystyle {frac {x^{2}}{a^{2}}}+y^{2}=0}$	${displaystyle K_{2}=0}$
Гиперболический цилиндр	${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1}$	${displaystyle I_{2}<0}$	${displaystyle K_{2}neq 0}$
Пара пересекающихся плоскостей	${displaystyle {frac {x^{2}}{a^{2}}}-y^{2}=0}$	${displaystyle K_{2}=0}$
Параболический цилиндр	${displaystyle y^{2}=2px}$	${displaystyle I_{2}=0}$	${displaystyle K_{2}neq 0}$
Пара параллельных плоскостей	${displaystyle x^{2}-d^{2}=0}$	${displaystyle K_{2}=0}$	$K_{1}<0$
Пара мнимых параллельных плоскостей	${displaystyle x^{2}+d^{2}=0}$	$K_{1}>0$
Плоскость	$x^2=0$	${displaystyle K_{1}=0}$

Примечания[править | править код]

↑ Александров П. С. Глава XIX. Общая теория поверхностей второго порядка. // Лекции по аналитической геометрии. — Наука, 1968. — С. 504-506. — 911 с.

Литература[править | править код]

В. А. Ильин, Г. Д. Ким. Линейная алгебра и аналитическая геометрия. — М.: Проспект, 2012. — 400 с.
В. А. Ильин, Э. Г. Позняк. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
П. С. Александров. Курс аналитической геометрии и линейной алгебры. — М.: ФИЗМАТЛИТ, 1979. — 511 с.
Шаль. Исторический обзор происхождения и развития геометрических методов. Гл. 5, § 46-54. М., 1883.

См. также[править | править код]

Квадрика
Поверхность вращения
Сфера
Цилиндрическая поверхность
Гиперболоид
Параболоид
Эллипсоид
Поверхность Дарбу

Источник

Онлайн-сервис для определение вида кривой или поверхности второго порядка по инваринтам, показывается график кривой. Также находятся ортогональных инварианты и семиинваринты.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Содержание:

Цилиндры
Упражнение
Поверхности второго порядка
Сфера и ее уравнение
Цилиндрические поверхности
Цилиндры второго порядка
Эллипсоид
Гиперболоиды
Параболоиды
Конические поверхности
Поверхность вращения
Понятие о поверхности второго порядка
Общее уравнение поверхности второго порядка, основные определения
Цилиндрические и конические поверхности
Исследование формы поверхностей второго порядка методом сечений

Поверхностью второго порядка в пространстве Поверхности второго порядка называется поверхность, определяемая уравнением второй степени относительно текущих координат

Рассмотрим частные виды поверхностей второго порядка. Сфера с центром в точке Поверхности второго порядка и радиусом имеет уравнение где — заданные числа (рис. 2.18).

Поверхности второго порядка

Раскрыв скобки и перенеся Поверхности второго порядка в левую часть, получим Нетрудно проверить, что уравнение второй степени относительно в котором коэффициенты при равны, а члены с произведениями координат отсутствуют, представляет собой уравнение сферы (кроме случаев, когда это уравнение не определяет никакой поверхности).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Цилиндры

Цилиндрической называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется направляющей цилиндрической поверхности, а сама прямая — образующей. Пусть, например, образующие цилиндрической поверхности параллельны оси Поверхности второго порядка и направляющей служит эллипс (рис. 2.19)

Поверхности второго порядка

в плоскости Поверхности второго порядка с уравнением Эта поверхность называется эллиптическим цилиндром. Пусть — произвольная точка этого цилиндра, а точка — проекция на плоскость Поверхности второго порядка

Ясно, что абсциссы и ординаты точек Поверхности второго порядка и совпадают. Так как точка лежит на эллипсе, то ее координаты х и у удовлетворяют уравнению (2.55). Но тогда этому уравнению удовлетворяют координаты х и у точки Поверхности второго порядка цилиндра. Значит, (2.55) есть уравнение цилиндра.

Итак, уравнение (2.55) на плоскости определяет эллипс, а в пространстве — эллиптический цилиндр с образующей, параллельной направляющей которого является указанный эллипс.

Возможно вам будут полезны данные страницы:

Упражнение

Изобразите самостоятельно:

1) гиперболический цилиндр с уравнением Поверхности второго порядка и образующей, параллельной оси

2) параболический цилиндр с уравнением Поверхности второго порядка и образующей, параллельной оси

Поверхности второго порядка

Определение. Поверхности второго порядка называют геометрическое место точек пространства, декартовые координаты которых удовлетворяют уравнению второй степени.

Сфера и ее уравнение

Сферой называют геометрическое место точек пространства, равноудаленное от заданной точки – центра сферы.

Если центром сферы является точка Поверхности второго порядка а радиус тогда уравнение сферы будет:

Поверхности второго порядка

Если центр сферы находится в начале координат Поверхности второго порядка и радиус тогда уравнение сферы будет:

Цилиндрические поверхности

Поверхность называется цилиндрической, если она образуется прямой (образующая), параллельно к заданной прямой Поверхности второго порядка и которая проходит через заданную линию (направляющая линия). Пример цилиндрической линии изображен на рис. 2.24

Поверхности второго порядка

Если образующая цилиндрической поверхности параллельна оси Поверхности второго порядка а образующая лежит на плоскости и задана уравнением:

Поверхности второго порядка

тогда уравнение цилиндрической поверхности будет:

Поверхности второго порядка

Уравнение Поверхности второго порядка обозначает цилиндрическую поверхность с образующей, что параллельна оси уравнение – цилиндрическая поверхность с образующей, что параллельна оси Поверхности второго порядка

Цилиндры второго порядка

а) Эллиптичным цилиндром называется поверхность (рис. 2.25), каноничное уравнение которой имеет вид:

Поверхности второго порядка

Если Поверхности второго порядка то получим круговой цилиндр:

б) Гиперболичным цилиндром называется поверхность, уравнение которой имеет вид (рис. 2.26):

Поверхности второго порядка

в) Параболическим цилиндром называется поверхность, каноничное уравнение которой имеет вид (рис. 2.27): Поверхности второго порядка

Поверхности второго порядка

Эллипсоид

Эллипсоидом называется поверхность, каноничное уравнение которой имеет вид (рис. 2.28): Поверхности второго порядка

Поверхности второго порядка Отрезки – называются полуосями эллипсоида.

Гиперболоиды

а) однополосный гиперболоид.

Однополосным гиперболоидом (рис. 2.29) называется поверхность, каноническое уравнение которой имеет вид : Поверхности второго порядка

Поверхности второго порядка

Поверхности второго порядка б) Двуполостный гиперболоид. Двуполостным гиперболоидом (рис. 2.30) называется поверхность, каноничное уравнение которой имеет вид: Поверхности второго порядка

Параболоиды

а) Эллиптическим параболоидом (рис. 2.31) называется Поверхности второго порядка поверхность, каноничное уравнение которой имеет вид:

б) Гиперболичным параболоидом (рис. 2.32) называется поверхность, каноничное уравнение которой имеет вид:

Поверхности второго порядка

Конические поверхности

конической поверхностью называется поверхность, которая описана прямой, что проходит через точку – вершину конуса – и что Поверхности второго порядка пересекает заданную линию – направляющую конуса.

Уравнение конуса (рис. 2.33) второго порядка имеет вид: Поверхности второго порядка

Поверхность вращения

Пусть в плоскости Поверхности второго порядка задана линия что имеет уравнение Тогда чтобы получить уравнение поверхности, что образована вращением линии что лежит в плоскости Поверхности второго порядка около оси нужно в уравнение этой линии заменить на Искомое уравнение поверхности вращения будет

Аналогично правила будут иметь место и по отношению к поверхностям, которые образуют обращение плоских линий около других координатных осей.

Примеры: 1) уравнение поверхности, что образуются вращением эллипса Поверхности второго порядка около оси будет (эллипсоид вращения).

2) уравнение поверхности, что образуются вращением гиперболы Поверхности второго порядка около оси будет или (двуполостный гиперболоид).

Примеры решения задач:

Задача 2.126

Обозначить координаты центра сферы и ее радиус:

Поверхности второго порядка

Решение. Предоставим заданное уравнение в виде (2.43), для этого: 1) объединяем в группы члены, которые содержат одноименные координаты;

2) выделим в группах полные квадраты. Получим:

Поверхности второго порядка

Соизмеряя с (2.43), получим Поверхности второго порядка Следует, центр сферы – точка радиус

Задача 2.127

Эллипс с полуосями 5 и 3 вращается около своей большей оси. которая совпадает с началом координат. Сложить уравнение поверхности, что описывает эллипс при вращении.

Решение. Сложим каноническое уравнение эллипса с центром в начале координат, который размещен в плоскости Поверхности второго порядка

Поверхности второго порядка

чтобы получить уравнение поверхности, которая образована вращением в плоскости Поверхности второго порядка около оси необходимо в уравнении эллипса заменить на Получим эллипсоид вращения, который протянул вдоль оси

Поверхности второго порядка или

Задача 2.128

Сложим уравнение конуса с вершиной в начале координат и направляющей:

Поверхности второго порядка

Решение. Канонические уравнения образующих, что проходят через вершину Поверхности второго порядка конуса и точки направляющей, будут:

Поверхности второго порядка

Исключим Поверхности второго порядка в заданных уравнениях. Изменяя через обозначим и из остальных двух уравнений:

подставим полученные значения Поверхности второго порядка и в первое уравнение направляющей, получим:

Поверхности второго порядка или

Задача 2.129

Какие поверхности обозначаются уравнениями:

Поверхности второго порядка

Решение. Каждое из уравнений содержит только две переменные Поверхности второго порядка и и обозначает на плоскости кривые: 1) круг, 2) эллипс, 3) параболу, 4) гиперболу.

В пространстве же каждое из них обозначается цилиндрическую поверхность с образующими, что параллельны оси Поверхности второго порядка так как эти уравнения не содержат переменной . Направляющими этих цилиндрических поверхности являются указанные кривые:

Поверхности второго порядка – уравнение прямого углового цилиндра;

Поверхности второго порядка – уравнение эллиптического цилиндра;

Поверхности второго порядка – уравнение параболического цилиндра;

Поверхности второго порядка – уравнение гиперболичного цилиндра.

Задача 2.130

Гипербола с полуосями 3 и 4 вращается около своей мнимой оси, которая совпадает с осью Поверхности второго порядка Центры гиперболы совпадает с началом координат. Сложить уравнение поверхности, которое получим при вращении гиперболы.

Решение. Сложим каноничное уравнение гиперболы с центром в начале координат, что находятся в плоскости Поверхности второго порядка

Поверхности второго порядка

Чтобы сложить уравнение поверхности, образованной вращением гиперболы, что находится в уравнение гиперболы вместо Поверхности второго порядка подставить

Поверхности второго порядка или

Следует, получим однополосный гиперболоид вращения:

Поверхности второго порядка

Понятие о поверхности второго порядка

Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению.

Общее уравнение поверхности второго порядка, основные определения

Поверхностью второго порядка называется множество точек пространства Поверхности второго порядка , описывается уравнением , левая часть которого является многочленом второй степени относительно переменных :

Поверхности второго порядка

где Поверхности второго порядка коэффициенты уравнения при текущих переменных ; – свободный член; и по крайней мере один из коэффициентов отличается от нуля

Уравнение (10.27) называют общим уравнением поверхности второго порядка. Вид поверхности и ее расположение относительно координатных плоскостей зависит от значений параметров в (10.27).

Если не существует ни одной точки Поверхности второго порядка , которая удовлетворяет общее уравнение, говорится, что оно определяет мнимую поверхность.
Поверхность называется вырожденной, если ее общее уравнение описывает точку, одну или две плоскости. К примеру:

Поверхности второго порядка уравнение точки в

Поверхности второго порядка уравнения двух плоскостей, параллельных

Поверхности второго порядка уравнения двух биссекторных плоскостей.

При изучении поверхностей второго порядка решаются две взаимно обратные основные задачи:
1) по известным геометрическим свойствам точек поверхности составить уравнение соответствующей поверхности;
2) по известным уравнением поверхности установить геометрические свойства ее точек.

Примером решения первой основной задачи является построение уравнения сферы (9.2). Уравнение других важнейших поверхностей рассматриваются ниже.

Цилиндрические и конические поверхности

Цилиндрической поверхностью, или просто цилиндром, называется поверхность, образованная движением прямой, перемещается параллельно самой себе вдоль фиксированной линии (кривой). Подвижную прямую называют образующей, а фиксированную кривую – направляющей цилиндрической поверхности. Направляющей может быть любая сомкнутая или разомкнутая линия.

Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является кривая второго порядка: эллипс (круг), гипербола, парабола. Название цилиндра определяется названием его направляющей. Если образующая параллельна одной из координатных осей, а направляющая лежит в плоскости, перпендикулярной этой оси, то уравнение цилиндра совпадает с уравнением направляющей. При геометрической интерпретации изображается, как правило, часть поверхности между двумя плоскостями, перпендикулярными образующей.
К примеру:

Поверхности второго порядка уравнения эллиптического цилиндра (рис. 10.9 а)

Поверхности второго порядка уравнения гиперболического цилиндра (рис. 10.9 б)

Поверхности второго порядка уравнения параболического цилиндра (рис. 10.9 в).

Поверхности второго порядка

Рис. 10.9

Отсутствие переменной Поверхности второго порядка в приведенных уравнениях означает, что аппликанта точек поверхности может быть любым действительным числом, потому что коэффициент при переменной Поверхности второго порядка в уравнениях следует считать равными нулю. Например, уравнение параболического цилиндра можно записать в виде: . Итак, образующая цилиндра параллельна оси, совпадающей с переменной, которая отсутствует в уравнении поверхности.

Если в уравнениях эллипса и гиперболы положить Поверхности второго порядка , то получим соответственно круговой и равносторонний гиперболический цилиндры.

Конической поверхностью, или конусом, называется поверхность, образованная движением прямой, проходящей через заданную точку, вдоль фиксированной кривой. Подвижную прямую называют образующей, заданную точку – вершиной, а фиксированную кривую – направляющей конуса. Если образующей является кривая второго порядка, то поверхность называется конусом второго порядка.
На рис. 10.10 изображен конус второго порядка, определяется уравнением

Поверхности второго порядка

Рис. 10.10

с вершиной в начале координат, направляющей которого является эллипс

Поверхности второго порядка

в плоскости Поверхности второго порядка

Поверхность симметрична относительно начала координат, а координатные плоскости является ее плоскостями симметрии. Множество точек поверхности с неотъемлемыми (неположительные) аппликатами называется верхней (нижней) полостью конуса.

Если направляющей конуса является круг Поверхности второго порядка , то он называется круговым.

Эллипс, парабола, гипербола – кривые второго порядка – можно получить сечением прямого кругового конуса плоскостями, которые не проходят через его вершину (рис. 10.11). А именно: если плоскость пересекает только одну полость конуса и непараллельных одной из его образующих, то кривой сечения является эллипс; в частном случае – круг;
если секущая плоскость параллельна одной из образующих конуса, то результат сечения – парабола;
если плоскость сечения пересекает обе полости конуса, то кривой сечения является гипербола.

Поверхности второго порядка

Рис. 10.11

Исследование формы поверхностей второго порядка методом сечений

Приведенные выше уравнения поверхностей второго порядка складывались по геометрическим свойствам их точек в соответствии с определений поверхностей. Для решения обратной задачи (по данным уравнением поверхности определить ее вид) применяется метод сечений, суть которого заключается в следующем:

1) анализируют поверхность, устанавливая за ее уравнением линии пересечения (сечения) данной поверхности координатными плоскостями параллельными им;

2) синтезируют определенные на предыдущем шаге геометрические свойства поверхности, что позволяет представить вид поверхности и изобразить ее.

Продемонстрируем применение метода сечений к исследованию уравнения эллиптического параболоида:

Поверхности второго порядка

Исследование предполагает такие шаги:
1) найдем линии пересечения поверхности (10.28) с плоскостью Поверхности второго порядка и плоскостями, параллельными ей :

Если:

а) Поверхности второго порядка , то уравнение (10.29) удовлетворяют лишь координаты точки , то есть плоскость является касательной к данной поверхности;
б) , то получаем воображаемую линию, поскольку плоскости Поверхности второго порядка заданную поверхность не пересекают;
в) , то уравнение (10.29) можно записать в виде:

Поверхности второго порядка

то есть сечением поверхности плоскостями, параллельными Поверхности второго порядка , есть эллипсы, полуоси которых увеличиваются вместе с увеличением (рис. 10.12);

2) установим линию пересечения поверхности с плоскостью Поверхности второго порядка :

Поверхности второго порядка

Это уравнение параболы, расположенной в плоскости Поверхности второго порядка , с осью симметрии .

Поверхности второго порядка

Рис. 10.12

3) определим (аналогичным образом) сечение поверхности плоскостью Поверхности второго порядка : это парабола, которая описывается уравнением , и расположена в плоскости (с осью симметрии ).
4) изображаем согласно рассмотренным выше соответствующие линии (рис. 10.12), что позволяет составить представление о форме исследуемой поверхности. Наконец намечаем обвод – линию, получается как множество точек прикосновения к поверхности прямых, параллельных выбранном направления проектирования.

Аналогично осуществляется построение параболоида Поверхности второго порядка , сечения которого – параболы ветвями вниз, и параболоидов, оси которых совпадают с координатными осями . Уравнение таких поверхностей получаемых из рассмотренного выше с помощью циклической перестановки переменных.

Поверхностью вращения называется поверхность, для которой каждый из ее сечений плоскостью, перпендикулярной одной из координатных осей или произвольной оси Поверхности второго порядка , является кругом. Круговой конус и круговой цилиндр являются примерами таких поверхностей: конус образуется вращением вокруг оси прямой, проходящей через начало координат, а цилиндр – прямой, параллельной оси Поверхности второго порядка , причем прямые не принадлежат плоскости, перпендикулярной оси вращения.

Уравнения поверхностей, симметричные относительно координатных осей или / и координатных плоскостей, называют каноническими, или стандартными.

В заключение отметим, что приведенные сведения используются при изучении интегрирования функций двух переменных и является фундаментом для более глубокого изучения теории поверхностей второго порядка.

Далее в таблице 10.1 приводятся канонические уравнения и изображения важнейших поверхностей второго порядка.

Важнейшие поверхности второго порядка Таблица 10.1

Поверхности второго порядка

Лекции:

Уравнения с одной переменной
Найдите координаты точки пересечения графиков
Геометрический смысл производной в точке
Двойной интеграл: примеры решения
Асимптотическое поведение функций. Сравнение бесконечно малых функций
Координаты вектора
Определение производной
Первый замечательный предел: пример решения
Метод вариации постоянных
Система показательных уравнений

Источник

11.3.1. Классификация поверхностей второго порядка

Канонические уравнения поверхностей второго порядка

Алгоритм составления канонического уравнения поверхности второго порядка

Типы поверхностей второго порядка[править | править код]

Цилиндрические поверхности[править | править код]

Конические поверхности[править | править код]

Поверхности вращения[править | править код]

Эллиптический параболоид[править | править код]

Гиперболический параболоид[править | править код]

Центральные поверхности[править | править код]

Матричный вид уравнения поверхности второго порядка[править | править код]

Инварианты[править | править код]

Классификация поверхностей второго порядка относительно значений инвариантов[править | править код]

Примечания[править | править код]

Литература[править | править код]

См. также[править | править код]

Цилиндры

Упражнение

Поверхности второго порядка

Сфера и ее уравнение

Цилиндрические поверхности

Цилиндры второго порядка

Эллипсоид

Гиперболоиды

Параболоиды

Конические поверхности

Поверхность вращения

Понятие о поверхности второго порядка

Общее уравнение поверхности второго порядка, основные определения

Цилиндрические и конические поверхности

Исследование формы поверхностей второго порядка методом сечений

Вам также может понравиться

Как быстро найти человека в москве

Как вам нашли а теперь продают

Правило как найти целое по его части

Добавить комментарий Отменить ответ