Как найти импеданс цепи – Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.

Формулы

Полное сопротивление Z = R или X_Lили X_C (если присутствует что-то одно)
Полное сопротивление (последовательное соединение) Z = √(R² + X²) (если присутствуют R и один тип X)
Полное сопротивление (последовательное соединение) Z = √(R² + (|X_L – X_C|)²) (если присутствуют R, X_L, X_C)
Полное сопротивление (любое соединение) = R + jX (j — мнимое число √(-1))
Сопротивление R = I / ΔV
Индуктивное сопротивление X_L = 2πƒL = ωL
Емкостное сопротивление X_C = ¹ / _2πƒL = ¹ / _ωL

1
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:^[1]
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
2
Сопротивление — это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R.^[2] Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете измерить сопротивление при помощи мультиметра.
- ΔV — это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I — сила тока, измеряемая в амперах (А).
- R — это сопротивление, измеряемое в омах (Ом).
3
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
- Индуктивным сопротивлением X_C обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.^[3] Чем быстрее меняется направление тока, тем больше индуктивное сопротивление.
- Емкостным сопротивлением X_C обладают конденсаторы, которые накапливают электрический заряд. При изменении направления тока в цепи конденсатор неоднократно обнуляет и накапливает электрический заряд. Чем дольше конденсатор заряжается, тем больше емкостное сопротивление.^[4] Поэтому чем быстрее меняется направление тока, тем меньше емкостное сопротивление.
4
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: X_L = 2πƒL, где L — индуктивность, измеряемая в генри (Гн).^[5]
- Индуктивность L зависит от количества витков в катушке индуктивности.^[6] Также вы можете измерить индуктивность.
- Если вы знакомы с единичной окружностью, то представьте, что один цикл переменного тока равен одному полному вращению этой окружности (на 2π радиан). Если умножить это значение на ƒ, которая измеряется в герцах (единиц в секунду), вы получите результат, измеряемый в радианах в секунду. Это единица измерения угловой скорости, которая обозначается через ω. Вы можете переписать формулу для вычисления индуктивного сопротивления так: X_L=ωL^[7]
5
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: X_C = ¹ / _2πƒC.^[8] С — это емкость конденсатора, измеряемая в фарадах (Ф).
- Вы можете измерить электрическую емкость.
- Эту формулу можно переписать так: X_C = ¹ / _ωL (объяснения см. выше).
Реклама

1
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.^[9]
- Если резисторы соединены последовательно, то полное сопротивление R = R₁ + R₂ + R₃…
- Если резисторы соединены параллельно, то полное сопротивление R = ¹ / _R₁ + ¹ / _R₂ + ¹ / _R₃ …
2
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:^[10]
- Последовательное соединение катушек: X_total = X_L1 + X_L2 + …
- Последовательное соединение конденсаторов: C_total = X_C1 + X_C2 + …
- Параллельное соединение катушек: X_total = 1 / (1/X_L1 + 1/X_L2 …)
- Параллельное соединение конденсаторов: C_total = 1 / (1/X_C1 + 1/X_C2 …)
3
Вычтите индуктивные и емкостные сопротивления, чтобы получить общее реактивное сопротивление. Так как при возрастании одного типа сопротивления другое уменьшается, то они, как правило, компенсируют друг друга. Чтобы найти общее реактивное сопротивление, вычтите меньшее сопротивление из большего.^[11]
- Или воспользуйтесь формулой: X_total = |X_C – X_L|
4
Вычислите импеданс по активному и реактивному сопротивлениям в последовательной цепи. Нельзя просто сложить эти величины, так как они меняются с течением времени, но достигают максимальных значений в разное время.^[12] Поэтому воспользуйтесь формулой:Z = √(R² + X²).^[13]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.^[14]^[15]
5
Вычислите импеданс по активному и реактивному сопротивлениям в параллельной цепи. В этом случае используются комплексные числа (это единственный способ вычислить полное сопротивление в параллельной цепи, в которой есть как активное, так и реактивное сопротивление).
- Z = R + jX, где j — мнимая единица: √(-1). Используйте j вместо i, чтобы не перепутать мнимую единицу (j) с силой тока (I).
- Складывать эти числа нельзя. Например, полное сопротивление может быть представлено так: 60 Ом + j120 Ом.
- Если у вас есть две последовательные цепи, то вы можете отдельно сложить натуральные числа и отдельно — комплексные. Например, если Z₁ = 60 Ом + j120 Ом, а к этой цепи последовательно подключен резистор с Z₂ = 20Ω, то Z_total = 80Ω + j120Ω.
Реклама

Советы

Общее сопротивление (активное и реактивное сопротивления) также может быть выражено через мнимое число.

Об этой статье

Эту страницу просматривали 168 783 раза.

Была ли эта статья полезной?

Источник

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электри́ческий импеда́нс (ко́мплексное электри́ческое сопротивле́ние^[1]^[2]) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.

Понятие и термин ввёл физик и математик О. Хевисайд в 1886 году^[3]^[4].

Аналогия с электрическим сопротивлением проводника на примере резистора[править | править код]

Резистор — пассивный элемент, обладающий исключительно активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения, а также из-за того, что резистор является пассивным элементом (поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение $U$ (подсоединить источник напряжения), то через резистор пойдёт электрический ток $I.$ Если через резистор пропустить электрический ток $I$ (подсоединить источник тока), то между концами резистора возникнет падение напряжения $U.$ Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения $U,$ к току $I$ (см. закон Ома для участка цепи):

${displaystyle R={frac {U}{I}}.}$

Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:

сопротивление идеальной катушки индуктивности стремится к нулю:

если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:

${displaystyle U=0;}$

${displaystyle R={frac {U}{I}}={frac {0}{I}}=0;}$

сопротивление идеального конденсатора стремится к бесконечности:

если приложить к конденсатору некоторое постоянное напряжение $U,$ то при любом значении $U,$ ток через конденсатор будет нулевым:

${displaystyle I=0;}$

${displaystyle R={frac {U}{I}}={frac {U}{0}}=infty .}$

Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:

напряжение между выводами катушки индуктивности не равно нулю;
ток, протекающий через конденсатор, не будет равен нулю.

Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.

Было бы удобно иметь некоторый параметр, аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.

Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитываются и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.

Определение[править | править код]

Импедансом ${hat z}(jomega );$ называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник в установившемся режиме, то есть после завершения переходных процессов. Для линейных пассивных цепей с постоянными параметрами в установившемся режиме импеданс не зависит от времени. Если время $t$ в математическом выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.

${hat z}(jomega );={frac {{hat u}(jomega ,t);}{{hat i}(jomega ,t);}}={frac {U(omega )e^{{j(omega t+phi _{u}(omega ))}}}{I(omega )e^{{j(omega t+phi _{i}(omega ))}}}}={frac {U(omega )e^{{jphi _{u}(omega )}}}{I(omega )e^{{jphi _{i}(omega )}}}}={frac {{hat U}(jomega );}{{hat I}(jomega );}}$

(1)

Здесь:

Исторически сложилось, что в электротехнике обозначение импеданса, комплексных амплитуд и других комплексных функций частоты записывают как ${displaystyle f(jomega ),}$ а не ${displaystyle f(omega ).}$ Такое обозначение подчёркивает, что используются комплексные представления гармонических функций вида ${displaystyle e^{jomega t}.}$ Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: ${displaystyle {dot {U}}(jomega );}$ чтобы отличать от соответствующих действительных величин.

Физический смысл[править | править код]

Алгебраическая форма[править | править код]

Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом ${hat z}(jomega );$ можно рассматривать как последовательно соединенные резистор с сопротивлением $Re ({hat z}(jomega ))$ и чисто реактивный элемент с импедансом ${displaystyle Im ({hat {z}}(jomega )).}$

Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.

Тригонометрическая форма[править | править код]

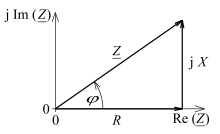
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.

Ограничения[править | править код]

Понятие импеданса в классической форме применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его параметры не менялись со временем и закончились переходные процессы. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени $t,$ поскольку при вычислении импеданса множитель $e^{{jomega t}}$ в (1) не сокращается.

Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).

Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении — для бесконечно малой амплитуды сигнала для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.

Обобщенный импеданс в s-плоскости и преобразование Лапласа[править | править код]

Импедансы, определённые через комплексную частоту ${displaystyle jomega ,}$ позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной ${displaystyle s=sigma +jomega }$ и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал ${displaystyle f_{in}(t)}$ из временного представления должен быть предварительно преобразован в комплексное представление ${displaystyle F_{t}(s)}$ через прямое преобразование Лапласа:

${displaystyle F_{t}(s)=int _{0}^{infty }f_{in}(t)e^{-st},dt.}$

Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы ${displaystyle H(s):}$

${displaystyle F_{t,H}(s)=H(s) F_{t}(s).}$

Двухполюсник	Обобщённый импеданс
Резистор	${displaystyle R,}$
Катушка индуктивности	${displaystyle sL,}$
Конденсатор	${displaystyle {frac {1}{sC}},}$

Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет ${displaystyle R+sL.}$

Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:

${displaystyle f_{F,H}(t)={mathcal {L}}^{-1}[H(s) F_{t}(s)]={frac {1}{2pi j}}int limits _{sigma _{1}-jcdot infty }^{sigma _{1}+jcdot infty }e^{st}H(s) F_{t}(s),ds,}$

где $sigma _{1}$ — некоторое вещественное число, выбираемое из условий сходимости интеграла.

Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение

Пассивный RС-фильтр нижних частот 1-го порядка

Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи ${displaystyle H_{RC}(s)}$ такого делителя:

${displaystyle H_{RC}(s)={frac {1/sC}{R+1/sC}}={frac {1}{sRC+1}}={frac {1}{sT+1}},}$

где обозначено ${displaystyle T=RC}$ — постоянная времени RС-цепи.

Ступенчатый входной сигнал можно выразить через функцию Хевисайда ${displaystyle h(t):}$

${displaystyle U_{in}(t)=U_{0} h(t),}$

где $U_{0}$ — амплитуда ступеньки.

Преобразование Лапласа входного сигнала:

${displaystyle F_{in}(s)={mathcal {L}}[U_{0} h(t)]=int limits _{0}^{infty }e^{-st},U_{0},h(t),dt=U_{0}/s.}$

${displaystyle U_{out}(t)={mathcal {L}}^{-1}[H_{RC}(s) F_{in}(s)]={frac {1}{2pi j}}int limits _{sigma _{1}-jcdot infty }^{sigma _{1}+jcdot infty }e^{st}{frac {1}{sT+1}}cdot {frac {U_{0}}{s}},ds=U_{0}(1-e^{-t/T}).}$

Таким образом, получен отклик цепи при нулевом начальном условии ( ${displaystyle U_{C}=0}$ при $t = 0$ ), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.

Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.

Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.

Вычисление импеданса[править | править код]

Идеальные элементы[править | править код]

Резистор[править | править код]

Для резистора импеданс всегда равен его сопротивлению $R$ и не зависит от частоты:

$z_{R}=R$

(2)

Конденсатор[править | править код]

Ток и напряжение для конденсатора связаны соотношением:

${displaystyle i(t)=C{frac {dU}{dt}}.}$

(3)

Отсюда следует, что при напряжении

${displaystyle {hat {u}}(jomega ,t)=U(omega )e^{j(omega t+phi _{u}(omega ))}}$

(4)

ток, текущий через конденсатор, будет равен:

${displaystyle {hat {i}}(jomega ,t)=C{frac {d}{dt}}left(U(omega )e^{j(omega t+phi _{u}(omega ))}right)=jomega CU(omega )e^{j(omega t+phi _{u}(omega ))}.}$

(5)

После подстановки (4) и (5) в (1) получаем:

${displaystyle {hat {z}}_{C}(jomega )={frac {1}{jomega C}}=-{frac {j}{omega C}}.}$

(6)

Катушка индуктивности[править | править код]

Аналогичное рассмотрение для катушки индуктивности приводит к результату:

${displaystyle {hat {z}}_{L}(jomega );=jomega L.}$

(7)

Общий случай[править | править код]

Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:

${displaystyle {hat {Z}}(jomega ) =R+{frac {1}{jomega C}}+jomega L=R-{frac {j}{omega C}}+jomega L=R+jleft(-{frac {1}{omega C}}+omega Lright).}$

(8)

Экспериментальное измерение импеданса[править | править код]

Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.

Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.

В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.

Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.

Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.

Активная и реактивная составляющие импеданса обычно выражают в омах. Однако, для характеризации антенн, линиях передачи, СВЧ электронных устройств обычно более удобно использовать связанные с ним S-параметры, коэффициент стоячей волны или коэффициент отражения.

Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса^[6].

Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств^[6].

LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.

Применение понятия импеданса[править | править код]

Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого применяется преобразование Лапласа, либо сигнал раскладывается на спектральные компоненты при помощи ряда Фурье (или преобразования Фурье) и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал .

См. также[править | править код]

Внутреннее сопротивление
Адмиттанс
АФЧХ

Примечания[править | править код]

Литература[править | править код]

Бессонов Л. А. Теоретические основы электротехники. — 9-е изд. — М.: Высшая школа, 1996.
Графов Б. М., Укше Е. А. Электрохимические цепи переменного тока. — М.: Наука, 1983.

Источник

Электрический импеданс

Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.

Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.

Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока,
во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора U_R = IR; на выводах конденсатора U_C = IX_C; на выводах катушки U_L = IX_L.

Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах U_X = U_L – U_C .

Пропорционально напряжению, получим общее реактивное сопротивление X = X_L – X_C .

Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , U_R и U_X представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

Тогда получим соотношение, согласно Теореме Пифагора, U ² = U_R² + U_X² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах,
определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.

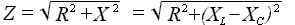
X_L = ωL = 2πfL – реактивное сопротивление индуктивности.

X_C = 1/(ωC) = 1/(2πfC) – реактивное сопротивление ёмкости.

Угол сдвига фаз φ и его дополнение до 90° δ
определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
где действительной его частью является активное сопротивление, а мнимой – реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:

Z = R + jX

Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом – угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:

Z = |Z|e^jargZ = Ze^jφ

Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.

Параллельное соединение

Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений
будем исходить из суммы обратных им величин – проводимостей y = 1/Z, G = 1/R, b = 1/X.

y = 1/Z = √(G² + b²)

Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:

Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:

Y = G – jb

Либо в показательной форме:

Y = |Y|e^-jφ = ye^-jφ

Здесь:

Y – комплексная проводимость.
G – активная проводимость.
b – реактивная проводимость.
y – общая проводимость цепи, равная модулю комплексной проводимости.
e – константа, основание натурального логарифма.
j – мнимая единица.

φ – угол сдвига фаз.

Онлайн-калькулятор расчёта импеданса и угла сдвига фаз

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Последовательное соединение
Z = √(R²+(XL-Xc)²)

Параллельное соединение
Z = 1/√(1/R²+(1/XL-1/Xc)²)

Похожие страницы с расчётами:

Реактивное сопротивление. Расчёт.

Частота резонанса колебательного контура LC. Расчёт.

Реактивная мощность и компенсация. Расчёт.

Источник

Download Article

Impedance is the opposition of a circuit to alternating current. It’s measured in ohms. To calculate impedance, you must know the value of all resistors and the impedance of all inductors and capacitors, which offer varying amounts of opposition to the current depending on how the current is changing in strength, speed, and direction. You can calculate impedance using a simple mathematical formula.

Formula Cheatsheet

Impedance Z = R or X_Lor X_C(if only one is present)
Impedance in series only Z = √(R² + X²) (if both R and one type of X are present)
Impedance in series only Z = √(R² + (|X_L – X_C|)²) (if R, X_L, and X_C are all present)
Impedance in any circuit = R + jX (j is the imaginary number √(-1))
Resistance R = ΔV / I
Inductive reactance X_L = 2πƒL = ωL
Capacative reactance X_C = ¹ / _2πƒC = ¹ / _ωC

1
Define impedance. Impedance is represented with the symbol Z and measured in Ohms (Ω). You can measure the impedance of any electrical circuit or component. The result will tell you how much the circuit resists the flow of electrons (the current). There are two different effects that slow the current, both of which contribute to the impedance:^[1]
- Resistance (R) is the slowing of current due to effects of the material and shape of the component. This effect is largest in resistors, but all components have at least a little resistance.
- Reactance (X) is the slowing of current due to electric and magnetic fields opposing changes in the current or voltage. This is most significant for capacitors and inductors.
2
Review resistance. Resistance is a fundamental concept in the study of electricity. You’ll see it most often in Ohm’s law: ΔV = I * R.^[2] This equation lets you calculate any of these values if you know the other two. For instance, to calculate resistance, write the formula as R = ΔV / I. You can also measure resistance easily, using a multimeter.
- ΔV is the voltage, measured in Volts (V). It is also called the potential difference.
- I is the current, measured in Amperes (A).
- R is the resistance, measured in Ohms (Ω).
Advertisement
3
Know which type of reactance to calculate. Reactance only occurs in AC circuits (alternating current). Like resistance, it is measured in Ohms (Ω). There are two types of reactance, which occur in different electrical components:
- Inductive reactance X_L is produced by inductors, also called coils or reactors. These components create a magnetic field that opposes the directional changes in an AC circuit.^[3] The faster the direction changes, the greater the inductive reactance.
- Capacitive reactance X_C is produced by capacitors, which store an electrical charge. As current flows in an AC circuit changes direction, the capacitor charge and discharges repeatedly. The more time the capacitor has to charge, the more it opposes the current.^[4] Because of this, the faster the direction changes, the lower the capacitive reactance.
4
Calculate inductive reactance. As described above, inductive reactance increases with the rate of change in the current direction, or the frequency of the circuit. This frequency is represented by the symbol ƒ, and is measured in Hertz (Hz). The full formula for calculating inductive reactance is X_L = 2πƒL, where L is the inductance measured in Henries (H).^[5]
- The inductance L depends on the characteristics of the inductor, such as the number of its coils.^[6] It is possible to measure the inductance directly as well.
- If you’re familiar with the unit circle, picture an AC current represented with this circle, with one full rotation of 2π radians representing one cycle. If you multiply this by ƒ measured in Hertz (units per second), you get a result in radians per second. This is the circuit’s angular velocity, and can be written as a lower-case omega ω. You might see the formula for inductive reactance written as X_L=ωL^[7]
5
Calculate capacitive reactance. This formula is similar to the formula for inductive reactance, except capacitive reactance is inversely proportional to the frequency. Capacitive reactance X_C = ¹ / _2πƒC.^[8] C is the capacitance of the capacitor, measured in Farads (F).
- You can measure capacitance using a multimeter and some basic calculations.
- As explained above, this can be written as ¹ / _ωC.

1
Add resistances in the same circuit. Total impedance is simple if the circuit has several resistors, but no inductors or capacitors. First, measure the resistance across each resistor (or any component with resistance), or refer to the circuit diagram for the labeled resistance in ohms (Ω). Combine these according to how the components are connected:^[9]
- Resistors in series (connected end to end along one wire) can be added together. The total resistance R = R₁ + R₂ + R₃…
- Resistors in parallel (each on a different wire that connects to the same circuit) are added as their reciprocals. To find the total resistance R, solve the equation ¹/_R = ¹ / _R₁ + ¹ / _R₂ + ¹ / _R₃ …
2
Add similar reactance values in the same circuit. If there are only inductors in the circuit, or only capacitors, the total impedance is the same as the total reactance. Calculate it as follows:^[10]
- Inductors in series: X_total = X_L1 + X_L2 + …
- Capacitors in series: C_total = X_C1 + X_C2 + …
- Inductors in parallel: X_total = 1 / (1/X_L1 + 1/X_L2 …)
- Capacitors in parallel: C_total = 1 / (1/X_C1 + 1/X_C2 …)
3
Subtract inductive and capacitive reactance to get total reactance. Because one of these effects increases as the other decreases, these tend to cancel each other out. To find the total effect, subtract the smaller one from the larger.^[11]
- You will get the same result from the formula X_total = |X_C – X_L|
4
Calculate impedance from resistance and reactance in series. You can’t just add the two together, because the two values are “out of phase.” This means that both values change over time as part of the AC cycle, but reach their peaks at different times.^[12] Fortunately, if all of the components are in series (i.e. there is only one wire), we can use the simple formula Z = √(R² + X²).^[13]
- The mathematics behind this formula involves “phasors,” but it might seem familiar from geometry as well. It turns out we can represent the two components R and X as the legs of a right triangle, with the impedance Z as the hypotenuse.^[14]^[15]
5
Calculate impedance from resistance and reactance in parallel. This is actually a general way to express impedance, but it requires an understanding of complex numbers. This is the only way to calculate the total impedance of a circuit in parallel that includes both resistance and reactance.
- Z = R + jX, where j is the imaginary component: √(-1). Use j instead of i to avoid confusion with I for current.
- You cannot combine the two numbers. For example, an impedance might be expressed as 60Ω + j120Ω.
- If you have two circuits like this one in series, you can add the real and imaginary components together separately. For example, if Z₁ = 60Ω + j120Ω and is in series with a resistor with Z₂ = 20Ω, then Z_total = 80Ω + j120Ω.

Calculator, Practice Problems, and Answers

Add New Question

Question

What does the j stand for in an impedance calculation?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

The j stands in for the imaginary number √(-1). Normally you would use i for this, but j is used in impedance calculations to avoid confusion with I for current.
Question

How do I calculate line impedance?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

Line impedance is the ratio of complex line voltage to complex line current. You can calculate it with the following equation: Z(z) = V(z)/I(z).
Question

How do I calculate the impedance of the coil connected in series with the capacitor?

If the coil has a resistance, then treat it as an LCR circuit. Z = [(Xc-XL)^2 + R]^0.5, where Z is the impedence, Xc is reactance of the capacitor which is equal to 1/(wC), w being the angular frequency and C being capacitance. XL is reactance of the coil which is equal to wL, L being the inductance of the coil, and R is resistance of the coil. Put R = 0 in case the coil has no resistance.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Total impedance (resistance and reactance) can also be expressed as a complex

References

About This Article

Article SummaryX

To calculate impedance, calculate the resistance and reactance of the circuit, then label resistance as R and reactance as X. Square both R and X, and add the two products together. Take the square root of the sum of the squares of R and X to get impedance. Display the answer in ohms. To learn how to calculate resistance and reactance, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 786,606 times.

Reader Success Stories

Shama Chemicool

Mar 28, 2016

“The article has helped me learn the difference between resistance, reactance, and impedance. I had problems…” more

Did this article help you?

Источник

Что такое комплексное сопротивление или импеданс

Содержание

1 Что такое импеданс и его составляющие
2 Последовательность расчета компонентов импеданса
3 Определение импеданса
4 Видео по теме

Электрический импеданс — это термин, относящийся к цепям переменного тока. Слово происходит от латинского impedіо (сопротивляться). Расчёт комплексного сопротивления или импеданса представляет собой важный этап разработки различных электрических и электронных устройств.

Электронные устройства, требующие определения импеданса

Что такое импеданс и его составляющие

Импеданс электрических цепей — это векторная (двумерная) величина, состоящая из двух независимых скалярных (одномерных) компонентов: активного и реактивного сопротивления. Он обозначается буквой Z и выражает противодействие, которое электронный элемент, схема или система оказывает переменному электротоку. Измеряется в омах.

Виды сопротивлений в электроцепи

Активное сопротивление (R) является мерой интенсивности противодействия движению электронов между атомами. Чем легче атомы отдают/принимают электроны, тем ниже этот параметр, выражающийся в положительных действительных числах. Реактивное сопротивление, обозначаемое буквой Х, представляет собой выражение степени, с которой электронный компонент, схема или система накапливает или высвобождает энергию при колебаниях тока и напряжения за каждый единичный цикл переменного тока. Импедансом часто называют модуль комплексного сопротивления, поэтому реактивное сопротивление выражается в так называемых «мнимых» омах. Оно характерно только для линий переменного тока.

Когда переменный электроток проходит через катушку индуктивности, накапливаемая энергия высвобождается в виде магнитного поля. В этом случае реактивная составляющая импеданса является индуктивной (обозначается +jX_L). Чем быстрее меняется направление тока, тем Х_L больше.

Однако энергия может запасаться и высвобождаться в виде электрического поля, тогда данный параметр будет емкостным (обозначается –jX_C ). Когда ток меняет направление, конденсатор многократно заряжается и разряжается. Чем больше времени конденсатор заряжается, тем сильнее он противодействует электротоку. Поэтому чем быстрее меняется направление электротока, тем ниже емкостное сопротивление.

Реактивное сопротивление обычно умножается на положительный квадратный корень из –1, который представляет собой единичное мнимое число j. Тогда комплексное сопротивление Z выражается как R + jX_L или R – jX_C. Следовательно, активное сопротивление R — это действительная часть комплексного импеданса, а реактивное Х — мнимая.

Графическая интерпретация составляющих импеданса

Левая половина координатной плоскости, представленной на рисунке выше, обычно не используется, поскольку на практике отрицательные сопротивления не встречаются. Индуктивное сопротивление указывается на положительной части линии мнимой оси, а ёмкостное — на отрицательной части линии.

Комплексное электрическое сопротивление фаз может быть определено как отношение электронапряжения к амплитуде электротока, что идентично закону Ома. Фаза импеданса является фазовым сдвигом, соответствующим отставанию электротока от электронапряжения.

Последовательность расчета компонентов импеданса

Найти импеданс или полное сопротивление последовательной цепи довольно просто, если в ней присутствует только какой-то один вид элементов. Импеданс идеального резистора соответствует его активному сопротивлению R, которое называется еще резистивным. Импеданс для катушки индуктивности — это мнимое реактивное сопротивление X_L, а для конденсатора —Х_С.

Если имеется активное сопротивление и один тип реактивного, тогда вычисления выполняются по формуле:

Формула импеданса при наличии активного и одного вида реактивного сопротивления

При наличии всех составляющих полное сопротивление или импеданс находим с помощью такого выражения:

Формула импеданса при наличии всех видов сопротивления в электроцепи

Таким образом, комплексное входное сопротивление цепи выражается как R + jX, где j — мнимое число √(–1).

Векторная диаграмма импеданса

Для расчетов всех составляющих импеданса используются формулы:

Формулы для расчета составляющих импеданса

Комплексное сопротивление и проводимости участков характеризуют замедление тока, которое связано с влиянием материала и формой резистора. Реактивное сопротивление X — это замедление тока из-за электрических и магнитных полей, противодействующих изменениям тока или напряжения. Этот параметр важен для конденсаторов и катушек индуктивности.

Импеданс в цепи переменного электротока

Определение импеданса

Рассчитать импеданс проще всего, если в цепи есть n резисторов, но нет катушек индуктивности или конденсаторов. Сначала измеряется сопротивление на каждом резисторе (или любом аналогичном компоненте). Найденные значения суммируются, если элементы соединены последовательно: R = R₁ + R₂ + … + R_n.

Результирующая величина для n резисторов, включённых параллельно, определяется следующим образом: 1/R = 1/R₁ + 1/R₂+ … +1/R_n.

Если в цепи есть только индуктивная нагрузка или емкостная, импеданс будет соответствовать реактивному сопротивлению:

Для последовательно соединенных катушек индуктивности X = X_L1+ X_L2 + …
Для последовательно соединенных конденсаторов C =X_C1 + X_C2 + …
Для катушек индуктивности, соединенных параллельно X = 1/(1/X_L1+ 1/X_L2 …)
Для конденсаторов, соединенных параллельно: C = 1/(1/X_C1+ 1/X_C2 …)

С ростом частоты электротока сопротивление индуктивностей увеличивается, а конденсаторов уменьшается. Поэтому при их совместном использовании в электрической линии они уравновешивают друг друга. Чтобы найти общее реактивное сопротивление, надо вычесть одно значение из другого: X = |X_C – X_L|.

Величину импеданса можно вычислить для любой электроцепи переменного тока, состоящей из таких линейных пассивных элементов, как резисторы, индуктивности и конденсаторы. Для электроцепи с постоянным током не существует различия между импедансом и сопротивлением. Последний параметр можно рассматривать как импеданс, фазовый угол которого равняется нулю.

Видео по теме

Источник

Формулы

Советы

Об этой статье

Была ли эта статья полезной?

Аналогия с электрическим сопротивлением проводника на примере резистора[править | править код]

Определение[править | править код]

Физический смысл[править | править код]

Алгебраическая форма[править | править код]

Тригонометрическая форма[править | править код]

Ограничения[править | править код]

Обобщенный импеданс в s-плоскости и преобразование Лапласа[править | править код]

Вычисление импеданса[править | править код]

Идеальные элементы[править | править код]

Резистор[править | править код]

Конденсатор[править | править код]

Катушка индуктивности[править | править код]

Общий случай[править | править код]

Экспериментальное измерение импеданса[править | править код]

Применение понятия импеданса[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Электрический импеданс

Последовательное соединение

Параллельное соединение

Онлайн-калькулятор расчёта импеданса и угла сдвига фаз

Formula Cheatsheet

Calculator, Practice Problems, and Answers

Video

References

About This Article

Reader Success Stories

Did this article help you?

Что такое комплексное сопротивление или импеданс

Что такое импеданс и его составляющие

Последовательность расчета компонентов импеданса

Определение импеданса

Видео по теме

Вам также может понравиться

Как составить коэффициент подобия треугольников

Как найти радиус по окружности онлайн калькулятор

Как найти кухню по фото

Добавить комментарий Отменить ответ