Самоиндукция
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.
Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.
Ситуация 1 .Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).

Рис. 1. Вихревое поле препятствует увеличению тока
Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.
Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.
Ситуация 2 . Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).

Рис. 2. Вихревое поле поддерживает убывающий ток
Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.
Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.
Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре.
При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.
При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).
Индуктивность
Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока:
. Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока:
.
Коэффициент пропорциональности обозначается и называется индуктивностью контура:
(1)
Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).
Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея
приобретает вид:
(2)
Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.
Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.

Рис. 3. Самоиндукция при замыкании цепи
В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).
Ключ вначале разомкнут.
При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.
Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.
Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.

Рис. 4. Самоиндукция при размыкании цепи
Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.
При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).
Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.
Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.
Электромеханическая аналогия
Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой
в механике.
1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.
Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.
2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.
При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.
На самом деле эти электромеханические аналогии простираются довольно далеко; они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.
Энергия магнитного поля
Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?
Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.
Чтобы разогнать тело массы из состояния покоя до скорости
, внешняя сила должна совершить работу
. Тело приобретает кинетическую энергию, которая равна затраченной работе:
.
Чтобы после замыкания цепи ток в катушке индуктивности достиг величины
, источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).
Индуктивность служит аналогом массы
; сила тока
является очевидным аналогом скорости
. Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:
(3)
(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).
Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.
Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени
. В течение этого промежутка приращение силы тока равно
; величина
считается настолько малой, что
много меньше, чем
.
За время по цепи проходит заряд
. Вихревое электрическое поле совершает при этом отрицательную работу:
Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):
Интегрируя это от нуля до , найдем работу источника
, которая затрачивается на создание тока
:
Эта работа превращается в энергию магнитного поля созданного тока, и мы приходим к формуле (3).
Разберем задачи ЕГЭ по физике по темам: “Самоиндукция”, “Магнитный поток”, “Индуктивность”, “Электромагнитная индукция”.
Задача 1. На катушке сопротивлением 8,2 Ом и индуктивностью 25 мГн поддерживается постоянное напряжение 55 В. Сколько энергии выделится при размыкании цепи? Какая средняя ЭДС самоиндукции появится при этом в катушке, если энергия будет выделяться в течение 12 мс?
Дано:
R = 8,2 Ом;
L= 25 мГн = Гн;
t = 12 мс = 12;
Найти:
Wм – ? Eis – ?
Решение:
Решение любой задачи по физике должно начинаться с создания модели, которая поясняет ситуацию, описанную в данной задачи. В качестве модели может выступать чертеж, пояснительный рисунок, электрическая схема.
Для этой задачи необходимо начертить электрическую схему.

На схеме изображены катушка индуктивности, источник тока, поддерживающий на ней постоянное напряжение, ключ.
При замкнутом ключе через катушку протекает постоянный электрический ток, величину которого можно рассчитать, используя закон Ома для участка цепи. Катушка аналогична резистору, подключенному в эту цепь.
Энергия магнитного поля рассчитывается по формуле:
(Дж).
Стоит обратить внимание, что эта формула аналогична формуле кинетической энергии в механике:
При размыкании ключа, через катушку начинает протекать уже переменный ток. Поэтому магнитный поток, пронизывающий катушку, меняется. В самой катушке возникает ЭДС индукции, так как в ней течёт переменный ток. Тем самым, возникает явление самоиндукции.
Используя закон электромагнитной индукции в виде приходим к расчету второй неизвестной величины этой задачи:
(B).
В этих расчетах мы не учитывали знак (-), который указан в законе электромагнитной индукции. Смысл этого знака заключен в учёте правила Ленца, определяющего направление индукционного тока. Но так как о направлении индукционного тока речь в задаче не идет, то в расчетах именно получено значение модуля ЭДС самоиндукции.
Ответ: 0,56 Дж, 14 В.
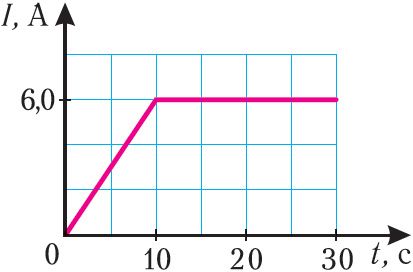
Задача 2. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 15 с. Ответ выразите в мкВ.

Решение
Решение любых графических задач необходимо начинать с «чтения» самого графика. В этой задаче рассматривается зависимость силы тока от времени в цепи, содержащей катушку индуктивности. Необходимо обратить внимание на те интервалы времени, в течение которых происходит изменение силы тока. С изменением этой величины связано изменение магнитного потока и, как следствие, возникновение ЭДС самоиндукции. Сила тока меняется в интервале от 0 до 5 с, от 5 до 10 с и от 15 до 20 с. В интервале от 10 до 15 с сила тока постоянна, изменение магнитного потока не происходит, поэтому . Для участка от 5 до 10 с надо применить закон электромагнитной индукции
.
Для модуля ЭДС самоиндукции, т.е. без учета направления индукционного тока, этот закон будет иметь вид:
.
Данные для расчета необходимо взять из графической зависимости, учитывая при этом перевод в систему «СИ».
(мкВ).
Ответ: 2 мкВ.
Задача 3. Катушка, обладающая индуктивностью , соединена с источником питания с ЭДС
и двумя одинаковыми резисторами
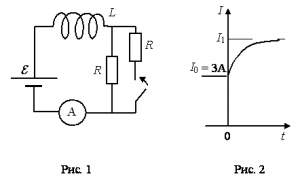
. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.

В момент времени ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения –
Определите значение силы тока
Внутренним сопротивлением источника тока пренебречь.
Решение
В данной задаче необходимо рассмотреть две ситуации, которые происходят до и после замыкания ключа.
- До замыкания ключа в цепи устанавливается постоянная сила тока, которая определяется законом Ома для полной цепи
. Так как по условию внутренним сопротивлением источника можно пренебречь, то
(A).
- После замыкания ключа параллельно к первому резистору подключается второй, имеющий такое же сопротивление. Тогда общее сопротивление цепи можно рассчитать, как
Таким образом, внешнее сопротивление цепи уменьшается в 2 раза.
Наличие в цепи катушки индуктивности, в которой возникает ЭДС самоиндукции, препятствует мгновенному нарастанию силы тока (по аналогии с механикой – тело большой массы не может быстро изменить свою скорость). Поэтому сила тока плавно увеличивается до некоторого значения - Так как ЭДС самоиндукции с течением времени уменьшается до нулевого значения, то ток в цепи будет возрастать в 2 раза, так как общее сопротивление уменьшается также в 2 раза.
(A).
Ответ: 6 А.
Задача 4. Катушка Проволочная рамка площадью 60 см2 помещена в однородное магнитное поле так, что плоскость рамки перпендикулярна вектору индукции . Проекция
индукции магнитного поля на нормаль к плоскости рамки изменяется во времени t согласно графику на рисунке.

Из приведенного ниже списка выберите все верные утверждения о процессах, происходящих в рамке.
- Модуль ЭДС электромагнитной индукции, возникающий в рамке, максимален в интервале от 0 до 1мс.
Ответ. Согласно закону электромагнитной индукции
Т.е. максимальное значение ЭДС индукции будет наблюдаться на интервале максимального измененияс течением времени. В интервале от 0 до 1 мс скорость изменения проекции
наибольшая.
Утверждение верное. - Магнитный поток через рамку в интервале от 2 до 4 мс равен 12 мВб.
Ответ. Формула для расчета магнитного потока имеет вид
В данном временном интервале проекцияпостоянна и равна 2 Тл.
(Вб) = 12 (мВб).
Утверждение верное. - Модуль ЭДС электромагнитной индукции, возникающей в рамке, в интервале от 4 до 6 мс равен 6 В.
Ответ. Согласно закону электромагнитной индукции
(B).
Утверждение неверное. - Модуль скорости изменения магнитного потока через рамку минимален в интервале от 0 до 1 мс.
Ответ. В той задаче изменение магнитного потока связано с изменением проекциииндукции магнитного поля. В интервале от 0 до 1 мс проекция
меняется быстрее всего, потому и изменение магнитного потока максимальное.
Утверждение неверное. - Модуль ЭДС электромагнитной индукции, возникающей в рамке, равен нулю в интервале времени от 2 до 4 мс.
Ответ. Согласно закону электромагнитной индукции
В интервале от 2 до 4 мс проекцияне изменяется, потому
и
.
Тогда в проволочной рамке ЭДС индукции не возникает.
Утверждение верное.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самоиндукция» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Если по катушке идет переменный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет переменный ток. Это явление называют самоиндукцией.
При самоиндукции проводящий контур выполняет двойную роль. С одной стороны, переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, появляется ЭДС индукции εis. По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
Явление самоиндукции можно наблюдать в простых опытах. На рисунке представлена схема параллельного соединения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L, снабженной железным сердечником.
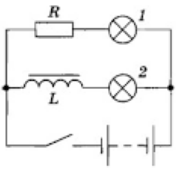
При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (см. график ниже).
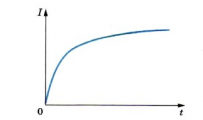
Появление ЭДС самоиндукции при размыкании можно наблюдать в опыте с цепью, схематически показанной на следующем рисунке. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальванометр идет ток (цветная стрелка), направленный против начального тока до размыкания (черная стрелка). Сила тока при размыкании цепи может превышать силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции εis больше ЭДС ε батареи элементов.
Самоиндукция и инерция
Явление самоиндукции проще понять, проведя аналогию с инерцией в механике. Инерция приводит к тому, что под действием силы тело не мгновенно приобретает скорость, а постепенно. Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.
Чтобы увеличить скорость тела, согласно законам механики нужно совершить работу. При торможении тело само совершает работу. Точно так же для создания тока нужно совершить работу против вихревого электрического поля, а при исчезновении тока это поле совершает положительную работу.
Индуктивность
Модуль вектора индукции В магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф ~ В~ I. Это дает право утверждать, что:
Φ=LI
L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком, пронизывающим этот контур. Эту величину также называют индуктивностью контура, или его коэффициентом самоиндукции.
Применив закон электромагнитной индукции, а также считая, что форма контура остается неизменной, и поток меняется только за счет изменения силы тока, получим:
εis=−ΔΦΔt=−LΔIΔt
Эта формула позволяет дать такую формулировку L, которая точно отражает суть этой величины.
Определение
Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Единица измерения индуктивности — генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции в 1 В.
Индуктивность подобна электроемкости. Она зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Пример №1. При равномерном изменении силы тока в катушке на 10 А за 0,02 с в ней возникает ЭДС самоиндукции, равная 200 В. Чему равна индуктивность катушки?
Выразим индуктивность из формулы для ЭДС самоиндукции:
L=−ΔtεisΔI=0,02·20010=−0,4 (Гн)
Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Поэтому само значение индуктивности мы можем принять за модуль полученного результата — 0,4 Гн.
Задание EF17686
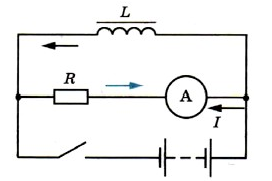
Катушка, обладающая индуктивностью L, соединена с источником питания с ЭДС ε и двумя одинаковыми резисторами R. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.
В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните, почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения – I1. Определите значение силы тока I1. Внутренним сопротивлением источника тока пренебречь.
Алгоритм решения
1.Установить, какими физическими законами можно описать эксперимент.
2.Описать, что происходит до замыкания ключа.
3.Определить, что произойдет после замыкания ключа.
4.Вычислить силу тока в катушке.
Решение
На рисунке 1 изображена схема, в которой катушка индуктивности подключена последовательно к двум параллельно соединенным резистором и источнику тока. Амперметр тоже соединен с катушкой последовательно, следовательно, он определяет силу тока, проходящую через нее.
Для описания процесса можно подходит закон Ома для полной цепи и формула ЭДС самоиндукции, которая будет возникать при изменении силы тока в цепи:
IRобщ=ε+εis
εis=−LΔIΔt
До замыкания ключа общее сопротивление цепи равно сопротивлению одного резистора — R. Так как ток в этом случае постоянный, ЭДС самоиндукции отсутствует. Тогда закон Ома принимает вид:
I0=εR
Когда ключ замыкается, сопротивление в цепи уменьшается вдвое, так как подключается второй резистор:
1Rобщ=1R+1R=2R
Rобщ=0,5R
Изменение сопротивления в цепи вызывает изменение силы тока. В результате возникает ЭДС самоиндукции. Она препятствует изменению силы тока через катушку в соответствии с правилом Ленца. Поэтому сила тока через катушку при замыкании ключа не претерпевает скачка.
Постепенно ЭДС самоиндукции уменьшается до нуля, а сила тока через катушку плавно возрастает до значения:
I1=ε0,5R=2I0
На рисунке 2 начальная сила тока равна 3 А. Следовательно:
I1=3·2=6 (А)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17724
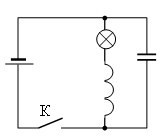 В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление источника тока соответственно равны 12 В и 1 Ом, ёмкость конденсатора 2 мФ, индуктивность катушки 36 мГн и сопротивление лампы 5 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Сопротивлением катушки и проводов пренебречь. Ответ записать в мДж.
В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление источника тока соответственно равны 12 В и 1 Ом, ёмкость конденсатора 2 мФ, индуктивность катушки 36 мГн и сопротивление лампы 5 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Сопротивлением катушки и проводов пренебречь. Ответ записать в мДж.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Установить величину электромагнитного поля катушки и электрического поля конденсатора.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: r = 1 Ом.
• Емкость конденсатора: C = 2 мФ.
• Индуктивность катушки: L = 36 мГн.
• Сопротивление лампы: R = 5 Ом.
2 мФ = 2∙10–3 Ф
36 мГн = 36∙10–3 Гн
Пока ключ замкнут, через катушку L течёт ток определяемый внутренним сопротивлением источника и сопротивлением лампочки. Его можно вычислить, используя закон Ома для полной цепи:
I=εR+r
При этом конденсатор будет заряжен до напряжения U, которое определяется законом Ома для участка цепи:
U=IR
Подставив в это выражение закон Ома для полной цепи, получим:
U=εRR+r
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22=C2(εRR+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR+r)2
После размыкания ключа начинаются затухающие электромагнитные колебания, и вся энергия, запасённая в конденсаторе и катушке, выделится на лампе:
E=Wкон+Wкат=C2(εRR+r)2+L2(εR+r)2
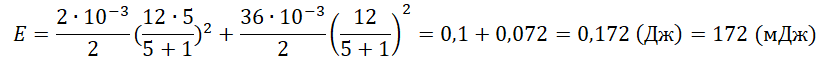 Ответ: 172
Ответ: 172
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18478
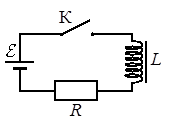 Катушка индуктивности подключена к источнику тока с пренебрежимо малым внутренним сопротивлением через резистор Ом (см. рисунок). В момент ключ К замыкают. Значения силы тока в цепи, измеренные в последовательные моменты времени
Катушка индуктивности подключена к источнику тока с пренебрежимо малым внутренним сопротивлением через резистор Ом (см. рисунок). В момент ключ К замыкают. Значения силы тока в цепи, измеренные в последовательные моменты времени
с точностью 0,01 А, представлены в таблице.

Выберите два верных утверждения о процессах, происходящих в цепи.
Ответ:
- Напряжение на резисторе в момент времени t= 1,0 c равно 1,9 В.
- Энергия катушки максимальна в момент времени t= 0 c.
- ЭДС источника тока равна 18 В.
- Напряжение на катушке максимально в момент времени t= 6,0 c.
- Модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В.
Алгоритм решения
1.Проверить истинность каждого утверждения.
2.Выбрать 2 верных утверждения.
Решение
Согласно утверждению 1, напряжение на резисторе в момент времени t = 1,0 c равно 1,9 В. Так как сила тока еще не установилась, а сопротивление источника тока пренебрежимо мало, вычислить напряжение на резисторе можно с помощью закона Ома для полной цепи:
I=ε−εisR
U=ε−εis=IR=0,19·60=11,4 (В)
Следовательно, утверждение 1 — неверно.
Согласно утверждению 2, энергия катушки максимальна в момент времени t = 0 c. Энергия катушки определяется формулой:
Wкат=LI22
Так как сила тока в начальный момент времени равна нулю, то энергия катушки в это время тоже нулевая.
Следовательно, утверждение 2 — неверно.
Согласно утверждению 3, ЭДС источника тока равна 18 В. Вычислить ЭДС источника тока можно, используя закон Ома для полной цепи в момент, когда сила тока в цепи достигнет максимального значения. В этом случае ЭДС самоиндукции будет равна 0. Тогда:
I=εR
ε=IR=0,3·60=18 (В).
Это действительно так. Следовательно, утверждение 3 — верно.
Согласно утверждению 4, напряжение на катушке максимально в момент времени t = 6,0 c. Напряжение на катушке равно разности напряжения ЭДС источника тока и напряжения на резисторе (так как они соединены последовательно):
U=ε−IR
Так как значение силы тока в момент времени t = 6,0 с максимально, то напряжение на катушке. Следовательно, утверждение 4 — неверно.
Согласно утверждению 5, модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В. Проверяя истинность утверждения 3, мы выяснили, что ЭДС источника тока равна 18 В. Следовательно, ЭДС самоиндукции равна:
εis=ε−IR
Для вычислений используем значения из таблицы для момента времени t = 2,0 с:
εis=18−0,26·60=2,4 (В)
Следовательно, утверждение 5 — верно.
Ответ: 35
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.2k
Физика, 11 класс
Урок 6. Самоиндукция. Индуктивность
Перечень вопросов, рассматриваемых на уроке:
1) индуктивность, самоиндукция, ЭДС самоиндукции;
2) использование явления электромагнитной индукции, принцип действия электрогенератора и электродинамического микрофона;
3) аналогия между самоиндукцией и инертностью;
4) закон самоиндукции, границы его применимости;
5) ЭДС индукции в движущихся проводниках.
Глоссарий по теме
Самоиндукцией называют явление возникновения ЭДС индукции в самом проводнике, по которому идет переменный ток. Эта ЭДС называется ЭДС самоиндукции  .
.
Величину L называют индуктивностью контура или его коэффициентом самоиндукции.
Индуктивность проводника равна 1 Гн, если в нём при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В.
Энергия магнитного поля, созданного током, проходящим по участку цепи с индуктивностью L равна произведения индуктивности и квадрата силы тока деленная на два.
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Основная и дополнительная литература по теме урока:
Обязательная литература:
Мякишев Г.Я.,Буховцев Б.Б.,Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 47 – 52.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа, 2009. – С. 121 – 125.
Целых Д. Об измерении энергии магнитного поля //Квант. – 1998. – № 1. – С. 43-44.
Основное содержание урока
Самоиндукция – это явление возникновения электромагнитной индукции в проводнике при изменении силы тока, протекающего через проводник  .
.
При самоиндукции проводящий контур выполняет двойную роль: переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, то появляется ЭДС индукции  .
.
По правилу Ленца, в момент нарастания тока напряженность вихревого электрического поля направлена против тока, препятствуя нарастанию тока. В момент уменьшения тока вихревое поле наоборот поддерживает его.
ЭДС самоиндукции E_si может быть больше ЭДС источника тока .
.
Генератор – это устройство, преобразующее энергию того или иного вида в электрическую энергию.
Генератор состоит из подвижной части – ротора, и неподвижной части – статора.
Все генераторы состоят из магнита или электромагнита, создающего магнитное поле, и рамки (обмотки) в которой индуцируется ЭДС.
По закону электромагнитной индукции Фарадея, в условиях, когда проводник движется внутри магнитного поля, образуется эффект пересечения магнитных силовых линий. На заряды со стороны магнитного поля действует сила Лоренца и внутри проводника свободные заряды приходят в направленное движение, то есть индуцируется ЭДС (электродвижущая сила), которая имеет магнитное происхождение. Величина индуцированной электродвижущей силы проводника напрямую зависит от скорости изменения магнитного потока (от скорости вращения рамки), пронизывающий проводник. Генераторы вырабатывают переменный электрический ток.
Микрофон осуществляет превращение звуковых колебаний воздуха в колебания электрического тока. Его действие основано на явлении электромагнитной индукции.
В электродинамическом микрофоне мембрана механически жёстко соединена с катушкой, который находится в кольцевом зазоре постоянного магнита (аналогично динамикам). Линии магнитной индукции перпендикулярны виткам катушки.
Звуковая волна вызывает колебание мембраны и, соответственно, колебание звуковой катушки. Катушка движется в магнитном поле, в её витках индуцируется ток, и на концах катушки возникает переменная ЭДС индукции.
Это переменное напряжение вызывает колебание тока в цепи микрофона.
Самоиндукция является частным случаем электромагнитной индукции.
Самоиндукцию можно представить как своеобразный маховик или точнее – силу инерции. При действии на маховик внешней силы сначала сопротивляется этой силе, а при резком прекращении ее действия, когда уже маховик раскручен – еще какое-то время движется по инерции.
Явление самоиндукции используют в системах плавного включения электрических устройств, например, в осветительных приборах, цепях, содержащих трансформаторы, генераторы, электродвигатели, выключение тока проводят медленно, чтобы ЭДС самоиндукции не превысила ЭДС источника, и прибор не вышел из строя, выполняет очень важную роль в: электротехнике и радиотехнике. Индуктивность цепи оказывает существенное влияние на прохождение по цепи переменного электрического тока.
Магнитный поток  пропорционален силе тока I:
пропорционален силе тока I:

где – индуктивность контура, или его коэффициентом самоиндукции. Единицу индуктивности в СИ называют генри (обозначается 1 Гн). Индуктивность зависит от геометрических размеров проводника, его формы, и непосредственно не зависит от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
– индуктивность контура, или его коэффициентом самоиндукции. Единицу индуктивности в СИ называют генри (обозначается 1 Гн). Индуктивность зависит от геометрических размеров проводника, его формы, и непосредственно не зависит от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Индуктивность одного проволочного витка меньше, чем у катушки (соленоида), состоящей из N таких же витков, так как магнитный поток катушки увеличивается в N раз.

если геометрические параметры проводника остаются неизменными и поток меняется только за счет изменения силы тока.
Электродвижущая сила самоиндукции  прямо пропорциональна скорости изменения силы тока, протекающего сквозь проводник, взятого со знаком минус.
прямо пропорциональна скорости изменения силы тока, протекающего сквозь проводник, взятого со знаком минус.
Источник тока, включенный в электрическую цепь, обладает запасом энергии. Источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, идет на образование магнитного поля.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока

Энергию магнитного поля можно выразить и через характеристики поля. Плотность энергии магнитного поля (то есть энергия единицы объёма) пропорциональна квадрату магнитной индукции:  , подобно плотности энергии электрического поля пропорциональной квадрату напряженности электрического поля:
, подобно плотности энергии электрического поля пропорциональной квадрату напряженности электрического поля: 
Запас энергии магнитного поля катушки равен энергии, израсходованной источником тока на преодоление э. д. с. самоиндукции за весь тот промежуток времени, пока сила тока при замыкании цепи возрастала от нуля до некоторого значения. Часть работы ЭДС источника в катушке идет на нагревание ее проводов, а часть, равная э. д. с. самоиндукции, совершает работу против ЭДС самоиндукции.
При движении проводника длиной l в однородном магнитном поле на электроны проводника действует сила Лоренца  .
.

Если концы проводника будут соединены через нагрузку друг с другом, то через проводник потечёт ток.
Сила Лоренца, совершает работу по перемещению зарядов по всей длине проводника l.
Возникающая за счет действия на заряды силы Лоренца ЭДС индукции имеет магнитное происхождение.
Электродвижущая сила индукции в проводнике равна отношению работы по перемещению заряда к этому заряду:

Эта формула справедлива для любого проводника длиной l, движущегося со скоростью v в однородном магнитном поле
Разбор тренировочных заданий
1. Катушка индуктивностью 2 Гн подключена к источнику тока так, как показано на рисунке. Сопротивление лампы равно 70 Ом, ЭДС источника 210 В.
Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите два верных утверждения о процессах, наблюдаемых в опыте.
1) Сила тока в цепи равна 3 А;
2) Энергия магнитного поля равна 18 Дж;
3) Ток через лампу сначала увеличивается, затем достигнув максимального значения не меняется;
4). Магнитный поток пронизывающий катушку сначала уменьшается, потом увеличивается.

Дано:
L=2 Гн
R=70 Ом
Ԑ=210В
r=0
Решение:
1) Согласно закону Ома для полной цепи

Утверждение 1 верно.
2) Энергия магнитного поля:

Утверждение 2 неверно.
3) Согласно явлению самоиндукции, ток в проводнике нарастает постепенно и не меняется, если в проводнике установится постоянный ток.
Утверждение 3 верно.
4) При увеличении тока магнитный поток пронизывающий катушку увеличивается, потом не изменяется.
Утверждение 4 неверно.
Правильные варианты: 1); 3).
2. На рисунке представлен график зависимости силы тока в катушке от времени. Индуктивность катушки равна 2,5 Гн. Найдите два правильных ответа:
1) модуль магнитного потока через катушку в интервале времени от 0 до 1 с равна 1,25 Вб;
2) модуль ЭДС самоиндукции в интервале времени от 1 до 5 с равна 0,625 В;
3) максимальное значение модуля ЭДС самоиндукции для данного графика равна 2,5 В;
4) энергия магнитного поля катушки за 2 секунды, начиная с момента времени t = 6 c равна 0,15625 Дж.

Дано:
L=2,5 Гн
Решение:
1) Модуль магнитного потока через катушку равен:

Утверждение 1 верно.
2) ЭДС самоиндукции согласно формуле равна:

Утверждение 2 неверно.
3) Согласно графику максимальное ЭДС самоиндукции будет на интервале от 5с до 6с.

Утверждение 3 верно.
4) Энергия магнитного поля катушки:

Утверждение 4 неверно.
Правильные варианты: 1); 3).
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током |
| Напечатано:: | Гость |
| Дата: | Четверг, 25 Май 2023, 00:08 |
Оглавление
- Самоиндукция
- Наблюдение самоиндукции
- Энергия магнитного поля
- Примеры решения задач
- Упражнение 24
Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797–1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?
Самоиндукция. Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока I в контуре, то
Коэффициенту пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил название «коэффициент самоиндукции»:
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.
Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,
Если индуктивность контура не изменяется во времени, т. е. L = const, то
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома где R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.
От теории к практике
Какой должна быть скорость изменения силы тока, чтобы в катушке с индуктивностью L = 0,20 Гн возникла ЭДС самоиндукции = 4,0 В?
![]()
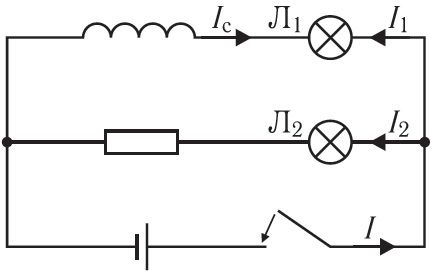
Наблюдение самоиндукции. Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка Л2 начинает светиться практически сразу, а лампочка Л1 — с заметным запаздыванием. При возрастании силы тока I1, созданного источником на участке, образованном катушкой и лампочкой Л1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции Iс направлен навстречу току источника. В результате рост силы тока I1 источника замедляется, и сила тока I1 — |Iс| не сразу достигает своего максимального значения.
![]()
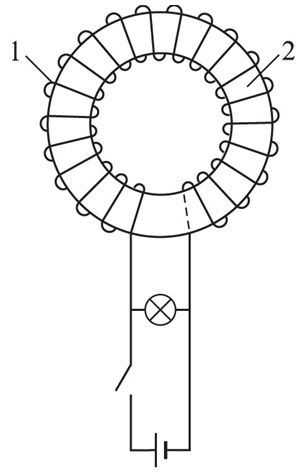
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки с большим количеством витков 1, намотанных на железный сердечник 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 185.1). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.
Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений . Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.
![]()
Энергия магнитного поля. Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
При замыкании цепи, состоящей из источника тока с ЭДС , катушки с индуктивностью L и резистора, сопротивление которого R, сила тока в цепи начнёт возрастать и появится ЭДС самоиндукции
.
Тогда в соответствии с законом Ома сила тока в цепи .
Значит, .
Умножив полученное равенство на IΔt, где Δt — достаточно малый промежуток времени, в течение которого сила тока I остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: .
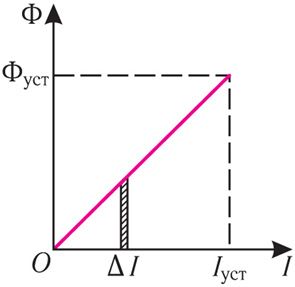
В процессе установления тока, когда сила тока I и магнитный поток Ф = LI возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся в резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени Δt при преодолении ЭДС самоиндукции в процессе установления тока (рис. 185.2):
δAдоп = ФΔI.
Полная дополнительная работа Адоп, равная сумме элементарных дополнительных работ δAдоп в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(I) (см. рис. 185.2).
Эта работа превращается в энергию магнитного поля катушки, поэтому:
где L — индуктивность контура; I — сила тока.
От теории к практике
Какова индуктивность катушки, если при силе тока I = 2,0 А энергия магнитного поля катушки Wм = 1,2 Дж?

![]()
1. Что называют самоиндукцией?
2. В каких опытах можно наблюдать явление самоиндукции?
3. От чего зависит ЭДС самоиндукции?
4. Что называют индуктивностью? В каких единицах в СИ её измеряют?
5. Как вычислить энергию магнитного поля катушки с током?
![]()
6. Почему для создания электрического тока в цепи с катушкой индуктивности источник тока должен затратить энергию?
Примеры решения задач
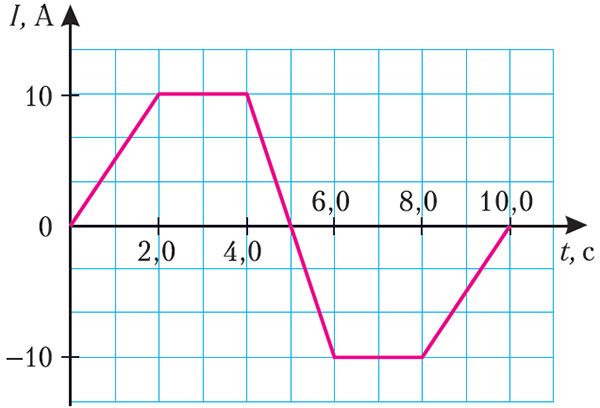
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
Дано:
L = 40 мГн = 4,0 · 10–2 Гн
— ?
Решение: ЭДС самоиндукции . Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
Таким образом,
Ответ: = 0,40 В.
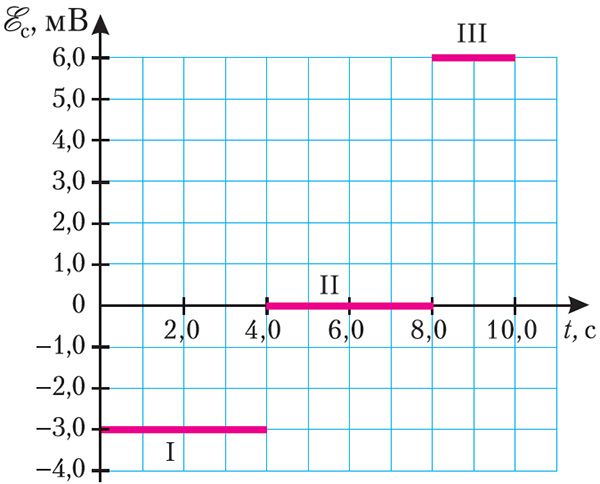
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
Дано:
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔII — ? ΔIII — ?
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции = –3,0 мВ, на участке III —
= 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
;
.
;
.
На участке II графика = 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки .
Следовательно,
.
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
![]()
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Дано:
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
= ‒14,0 В
Фс — ?
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: . Следовательно,
. Тогда
.
Приращение энергии магнитного поля катушки
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.
Упражнение 24
1. Сила тока, проходящего по замкнутому проводящему контуру, I = 1,2 А. Магнитное поле этого тока создаёт магнитный поток Ф = 3,0 мВб через поверхность, ограниченную контуром. Определите индуктивность контура.
2. При равномерном изменении силы тока в катушке на ΔI = –4,0 А за промежуток времени Δt = 0,10 с в ней возникает ЭДС самоиндукции = 20 В. Определите индуктивность катушки.
3. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 1,2 Гн, при равномерном изменении силы тока от I1 = 2,0 А до I2 = 6,0 А за промежуток времени Δt = 0,60 с. Определите приращение энергии магнитного поля при заданном изменении силы тока.
4. На рисунке 188 представлен график зависимости силы тока в катушке, индуктивность которой L = 10 мГн, от времени. Определите ЭДС самоиндукции через промежутки времени t1 = 10 с и t2 = 20 с от момента начала отсчёта времени.
5. Сила тока в катушке равномерно уменьшилась от I1 = 10 А до I2 = 5,0 А. При этом энергия магнитного поля изменилась на ΔWм = –3,0 Дж. Определите индуктивность катушки и первоначальное значение энергии магнитного поля.
6. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 0,12 Гн, при равномерном уменьшении силы тока от I1 = 8,0 А, если за промежуток времени t1 = 0,20 с энергия магнитного поля уменьшилась в α = 2,0 раза.
![]()
7. Энергия магнитного поля катушки с индуктивностью L1 = 0,5 Гн больше энергии магнитного поля катушки с индуктивностью L2 в α = 1,5 раза. Определите индуктивность второй катушки, если отношение собственного магнитного потока через поверхности, ограниченные витками второй катушки, к собственному магнитному потоку через поверхности, ограниченные витками первой катушки, .

Задания
Версия для печати и копирования в MS Word
Тип 13 № 8009 

i
На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.
Спрятать решение
Решение.
За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен
Ответ: 4.
Аналоги к заданию № 8009: 25369 Все
Источник: Демонстрационная версия ЕГЭ−2017 по физике
Раздел кодификатора ФИПИ/Решу ЕГЭ: 3.4.6 Индуктивность. Самоиндукция. ЭДС самоиндукции
Спрятать решение
·
Помощь
