2017-12-15 ![]()
Из проволоки спаяли четырехугольную пирамиду. Все ребра основания имеют сопротивление $r$, боковые ребра – $2r$. К серединам двух соседних ребер основания подводят электрическое напряжение. Найти сопротивление пирамиды.

Решение:

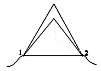
Очевидно, что данная цепь симметрична относительно вертикальной плоскости, проходящей посередине между клеммами цепи (АВС, см. левый рисунок). Поэтому по проводам, лежащим в этой плоскости (ВС и АВ), ток течь не может. Поэтому эти провода можно удалить из цепи без перераспределения тока в других проводах (и, следовательно, без изменения сопротивления цепи).
После удаления этих проводов (см. рисунок посередине) цепь становится эквивалентной цепи, изображенной на правом рисунке (здесь $r$ – сопротивление ребра основания). Находя его, получим
$R = frac{7r}{10}$.
Из проволоки спаяли четырехугольную пирамиду. Все ребра основания имеют сопротивление r, боковые ребра — 2r. К серединам двух соседних ребер основания подводят электрическое напряжение. Найти сопротивление пирамиды.
Спрятать решение
Решение.
Очевидно, что данная цепь симметрична относительно вертикальной плоскости, проходящей посередине между клеммами цепи (ABC, см. левый рисунок). Поэтому по проводам, лежащим в этой плоскости (BC и AB) ток течь не может. Поэтому эти провода можно удалить из цепи без перераспределения тока в других проводах (и, следовательно, без изменения ее сопротивления).
После удаления этих проводов (см. рисунок посередине) цепь становится эквивалентной цепи, изображенной на правом рисунке (здесь r — сопротивление ребра основания). Находя его, получим
Ответ:
————-
Дублирует задание № 655.
Спрятать критерии
Классификатор: Электродинамика. Расчет электрических цепей
Цели: обучающая: систематизировать
знания и умения учащихся решать задачи ан расчет
эквивалентных сопротивлений с помощью моделей,
каркасов и т.д.
Развивающая: развитие навыков логического
мышления абстрактного мышления, умений заменять
схемы эквивалентности, упрощать расчет схем.
Воспитательная: воспитание чувства
ответственности, самостоятельности ,
необходимости навыков приобретенных на уроке в
будущем
Оборудование: проволочный каркас куба,
тетраэдера, сетки бесконечной цепочки
сопротивлений.
ХОД УРОКА
Актуализация:
1. Учитель: “Вспомним последовательное
соединение сопротивлений”.
Учащиеся на доске зарисовывают схему.
и записывают
Rэк=n*R
Uоб=U1+U2
Yоб=Y1=Y2
Учитель: вспомним параллельное соединение
сопротивлений.
Учащийся на доске зарисовывает элементарную
схему:
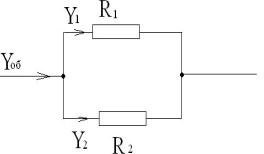
Uоб=U1+U2
Yоб=Y1=Y2
; для
для n равных
Учитель: А теперь будем решать задачи на расчет
эквивалентного сопротивления участок цепи
представлен в виде геометрической фигуры, либо
металлической сетки.
Задача № 1
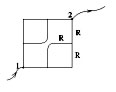
Проволочный каркас в виде куба, рёбра которого
представляют равные сопротивления R. Рассчитать
эквивалентное сопротивление между точками А и В.
Чтобы рассчитать эквивалентное сопротивление
данного каркаса необходимо заменить
эквивалентной схемой. Точки 1, 2, 3 имеют
одинаковый потенциал, их можно соединить в один
узел. А точки (вершины) куба 4, 5, 6 можно соединить в
другой узел по той же причине. Учащиеся имеют на
каждой парте такую модель. После выполнения
описанных действий зарисовывают эквивалентную
схему.

На участке АС эквивалентное сопротивление ![]() ; на СD
; на СD ![]() ; на DB
; на DB ![]() ; и окончательно
; и окончательно
для последовательного соединения сопротивлений
имеем: ![]()
Задача № 2
Рассчитать RЭКВ. этого же куба, если куб
включён в цепь в точках 2 и 4.
По тому же принципу потенциалы точек А и 6 равны,
В и 3 равны. Учащиеся совмещают эти точки на своей
модели и получают эквивалентную схему:
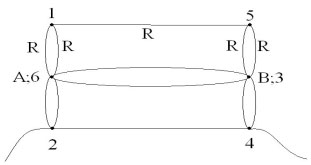
Расчёт эквивалентного сопротивления такой
цепи прост![]()
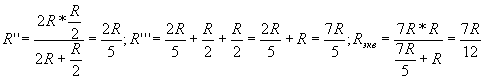
Задача № 3
Эта же модель куба, с включением в цепь между
точками 2 и В. Учащиеся соединяют точки с равными
потенциалами 1 и 3; 6 и 4. Тогда схема будет
выглядеть так:
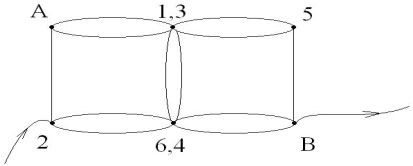
Точки 1,3 и 6,4 имеют равные потенциалы, и ток по
сопротивлениям между этими точками не потечёт и
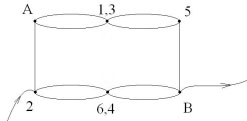
схема упрощается до вида; эквивалентное
сопротивление которой рассчитывается так:
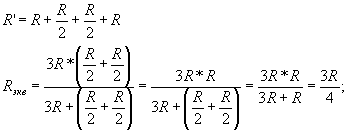
Задача № 4
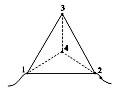
Равносторонняя треугольная пирамида, ребро
которой имеет сопротивление R. Рассчитать
эквивалентное сопротивление при включении в
цепь.
Точки 3 и 4 имеют равный потенциал, поэтому по
ребру 3,4 ток не потечёт. Учащиеся убирают его.
Тогда схема будет выглядеть так:
либо
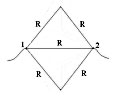
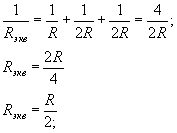
Эквивалентное сопротивление рассчитывается
так:
Задача № 5
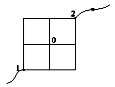
Металлическая сетка с сопротивлением звена
равном R. Рассчитать эквивалентное сопротивление
между точками 1 и 2.
В точке 0 можно звенья отделить, тогда схема
будет иметь вид:
![]() –
–
сопротивление одной половины симметричной по 1-2
точкам. Параллельно ей такая же ветвь, поэтому ![]()
Задача № 6
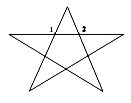
Рассчитать эквивалентное сопротивление
проволочной звезды с сопротивлением каждого
звена R, включённой в цепь между точками 1 и 2.
Звезда состоит из 5-и равносторонних
треугольников, сопротивление каждого![]() .
.
Между точками 1 и 2 один треугольник параллелен
четырём, последовательно соединенным между
собой
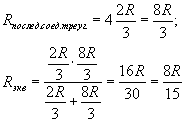
Имея опыт расчёта эквивалентного
сопротивления проволочных каркасов можно
приступить к расчету сопротивлений цепи,
содержащий бесконечное число сопротивлений.
Например:
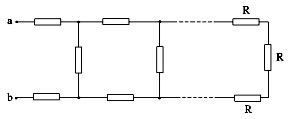
Если отделить звено
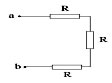
от общей схемы, то схема не изменится, тогда
можно представить ввиде
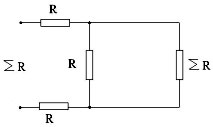
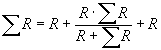 или
или ![]() ,
,
решаем данное уравнение относительно Rэкв.
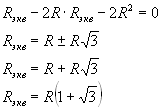
Итог урока: мы научились абстрактно
представлять схемы участков цепи, заменять их
эквивалентными схемами, которые позволяют легко
рассчитать эквивалентное сопротивление.
На дом:
Рассчитать эквивалентное сопротивление
проволочного каркаса из двух окружностей с
радиусами r1 и r2, r2=2r1 между
точками А и В. Сопротивление единицы длинны
проволоки?
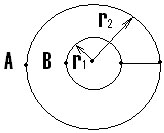
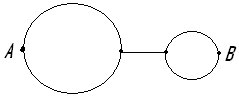
Указание: Эту модель представить в виде:
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
из проволки
Алена
Ученик
(69),
закрыт
5 лет назад
Из проволоки сделали правильную пирамиду,
все ребра которой имею одинаковую длину и одинаковое
сопротивление R . К серединам двух противоположных сторон
подключают источник электрического напряжения
Чему равно сопротивление пирамиды?
Михаил Ермилов
Просветленный
(42561)
10 лет назад
Пусть ток равен i. В первом ребре он разветвлялся пополам: i/2 в каждую сторону.
В каждом конце первого ребра ток делится ещё раз пополам: i/4 в каждое ребро.
И наконец, в последнем ребре они снова складываются: i/2.
Напряжение между точками подключения будет равно:
U=(i/2)*R/2+(i/4)*R+(i/2)*R/2=(3/4)iR.
След-но, полное сопротивление r=U/i=3R/4.