Ирина Алексеевна Антоненко
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Предварительные сведения
Для начала введем сведения и обозначения, которые будут необходимы нам в дальнейшем.
Будем рассматривать треугольник $ABC$ с острыми углами $A$ и $C$. Проведем в нем высоту $BH$. Введем следующие обозначения: $AB=c, BC=a, $$AC=b, AH=x, BH=h $(рис. 1).
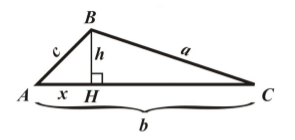
Рисунок 1.
Введем без доказательств теорему о площади треугольника.
Теорема 1
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней, то есть
[S=frac{1}{2}bh]

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Формула Герона
Введем и докажем теорему о нахождении площади треугольника по трем известным сторонам. Эта формула носит название формулы Герона.
Теорема 2
Пусть нам даны три стороны треугольника $a, b и c$. Тогда площадь этого треугольника выражается следующим образом
[S=sqrt{pleft(p-aright)left(p-bright)(p-c)}]
где $p$ – полупериметр данного треугольника.
Доказательство.
Будем пользоваться обозначениями, введенными на рисунке 1.
Рассмотрим треугольник $ABH$. По теореме Пифагора, получим
[h^2=c^2-x^2]
Очевидно, что $HC=AC-AH=b-x$
Рассмотрим треугольник $ CBH$. По теореме Пифагора, получим
[h^2=a^2-{HC}^2] [h^2=a^2-{(b-x)}^2] [h^2=a^2-b^2+2bx-x^2]
Приравняем значения квадрата высоты из двух полученных соотношений
[c^2-x^2=a^2-b^2+2bx-x^2] [2bx=c^2-a^2+b^2] [x=frac{c^2-a^2+b^2}{2b}]
Из первого равенства найдем высоту
[h^2=c^2-{left(frac{c^2-a^2+b^2}{2b}right)}^2] [h^2=frac{{4b^2c}^2-{left(c^2-a^2+b^2right)}^2}{4b^2}] [h^2=frac{left(2bc-c^2+a^2-b^2right)({2bc+c}^2-a^2+b^2)}{4b^2}] [h^2=frac{left(a^2-{left(c-bright)}^2right)({left(c+bright)}^2-a^2)}{4b^2}] [h^2=frac{left(a-c+bright)left(a+c-bright)left(c+b-aright)(c+b+a)}{4b^2}] [h^2=frac{(a+b+c)left(a+b+c-2cright)left(a+b+c-2bright)left(a+b+c-2aright)}{4b^2}]
Так как полупериметр равен $p=frac{a+b+c}{2}$, то есть $a+b+c=2p$, то
[h^2=frac{2pleft(2p-2cright)left(2p-2bright)left(2p-2aright)}{4b^2}] [h^2=frac{4pleft(p-aright)left(p-bright)left(p-cright)}{b^2}] [h=sqrt{frac{4pleft(p-aright)left(p-bright)left(p-cright)}{b^2}}] [h=frac{2}{b}sqrt{pleft(p-aright)left(p-bright)left(p-cright)}]
По теореме 1, получим
[S=frac{1}{2}bh=frac{b}{2}cdot frac{2}{b}sqrt{pleft(p-aright)left(p-bright)left(p-cright)}=sqrt{pleft(p-aright)left(p-bright)left(p-cright)}]
Теорема доказана.
«Формула Герона» 👇
Примеры задач на использование формулы Герона
Пример 1
Найти площадь треугольника, если его стороны равняются $3$ см, $6$ см и $7$ см.
Решение.
Найдем вначале полупериметр этого треугольника
[p=frac{3+6+7}{2}=frac{16}{2}=8 см]
По теореме 2, получим
[S=sqrt{8left(8-3right)left(8-6right)left(8-7right)}=sqrt{8cdot 5cdot 2cdot 1}=4sqrt{5}]
Ответ: $4sqrt{5}$.
Пример 2
Найти площадь параллелепипеда, со сторонами $8$ см и $5$ см и меньшей диагональю, равной $5$ см.
Решение.
Пусть нам дан параллелограмм $ABCD$, где $AD=8 см, AB=5 см и BD=5 см$ (рис. 2).
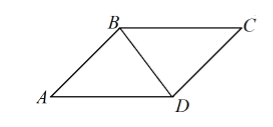
Рисунок 2.
Так как диагональ параллелограмма является его осью симметрии, то треугольники $ABD$ и $BDC$ равны между собой. Следовательно
[S=S_{ABD}+S_{BDC}=2S_{ABD}]
Полупериметр треугольника $ABD$ равен
[p=frac{5+5+8}{2}=frac{18}{2}=9 см]
По теореме 2
[S_{ABD}=sqrt{9left(9-5right)left(9-5right)left(9-8right)}=sqrt{9cdot 4cdot 4cdot 1}=12]
Следовательно
[S=2cdot 12=24]
Ответ: $24$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите площадь треугольника со сторонами 13, 14, 15.
2
Найдите радиус окружности, описанной вокруг треугольника со сторонами 13, 14 и 15.
3
Найдите третью сторону треугольника, если известно, что две другие равны 6 и 7, а площадь равна
4
Две стороны треугольника равны соответственно 5 и 8, а его площадь равна 12. Определите длину третьей стороны.
5
Найдите площадь ромба со стороной 5 и большей диагональю 8.
Пройти тестирование по этим заданиям
В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.
- Формула площади
- Примеры задач
Формула площади
Площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c).
S = √p(p-a)(p-b)(p-c)

Полупериметр (p) вычисляется таким образом:
![]()
Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.
Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.

Примеры задач
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.
Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.
Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
S = √12(12 – 6)(12 – 8)(12 – 10) = √12 ⋅ 6 ⋅ 4 ⋅ 2 = 24 см2.
Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.
Решение
Пусть гипотенуза – это c, известный катет – a, а неизвестный – b.
Применим Теорему Пифагора, чтобы найти длину катета b:
b2 = c2 – a2 = 152 – 92 = 144 см2, следовательно, b = 12 cм.
Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.
Остается только использовать формулу для нахождения площади:
S = √18(18 – 9)(18 – 12)(18 – 15) = √18 ⋅ 9 ⋅ 6 ⋅ 3 = 54 см2.
Формула Герона
Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.
Формулировка теоремы Герона
Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.
Формула и доказательство
Формула Герона выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(S;=;sqrt{pleft(p-aright)left(p-bright)left(p-cright)})
где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.
Чтобы вычислять полупериметр, нужно пользоваться формулой:
(p;=;frac{a+b+c}2)
Приведем доказательство.
Для этого рассмотрим треугольник ABC.
(left|ABright|=c,;left|BCright|=a,;left|ACright|=b)
CH – высота треугольника.
(left|CHright|=h,;left|AHright|=x,;left|BHright|=y)
Тогда (c=x+y).
По теореме Пифагора из треугольников ACH и BCH получаем:
(h^2=b^2-x^2=a^2-y^2)
Из этого:
(y^2-x^2=a^2-b^2)
((y-x)(y+x)=a^2-b^2)
(x+y=c)
Соответственно:
((y-x)c=a^2-b^2) и (y-x=frac1c (a^2-b^2))
Если сложить последнее равенство с (y+x=c), то получается
(y;=;frac{c^2+a^2-b^2}{2c})
Найдем высоту треугольника.
(h^2;=;a^2-y^2=left(a-yright)left(a+yright)=left(a-frac{c^2+a^2-b^2}{2c}right)left(a+frac{c^2+a^2-b^2}{2c}right)=frac{2ac-c^2-a^2+b^2}{2c}timesfrac{2ac+c^2+a^2-b^2}{2c}=frac{b^2-left(a-cright)^2}{2c}timesfrac{left(a+cright)^2-b^2}{2c}=frac{left(b-a+cright)timesleft(b+a-cright)}{2c}timesfrac{left(a+c-bright)timesleft(a+c+bright)}{2c})
Так как (p=frac12left(a+b+cright)), то ( b+c=2p-a),( a+b=2p-c), (a+c=2p-b), (a+b+c=2p).
С помощью этих равенств найдем высоту.
(h^2=frac{left(2p-2aright)left(2p-2cright)left(2p-2bright)2p}{4c^2}=frac{4pleft(p-aright)left(p-cright)left(p-bright)}{c^2})
А так как (S=frac12ch), то теорема доказана.
Для каких треугольников действует теорема
Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.
Примеры решения задач
Задача 1
Рассчитать площадь треугольника, если a=6, b=8, c=6.
Решение
(p=frac{6+8+6}2=10)
Тогда площадь треугольника равна:
(S=10sqrt{left(10-6right)left(10-8right)left(10-6right)}=320)
Ответ: 320 см2.
Задача 2
Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.
Решение
Диагонали AC и BD пересекаются в точке O.
Если AD = 51, AC = 40 и BD = 74, то AO = 20, OD = 37.
По формуле Герона:
(S_{ABCD} = 4S_{AOD} = sqrt{54left(54-51right)left(54-37right)left(54-20right)}=1224)
Ответ: 1224 см2.
Задача 3
В треугольнике ABC три стороны: AB = 26, BC = 30 и AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.
Решение
BP и BQ – высота и биссектриса треугольника.
По формуле Герона:
(S=sqrt{42left(42-30right)left(42-28right)left(42-26right)}=336)
(S = ½ AC·BP)
Поэтому (BP =frac{2S}{AC}=frac{2times336}{28}=24).
По свойству биссектрисы треугольника:
(frac{AQ}{QC}=frac{AB}{BC}=frac{26}{30}=frac{13}{15})
Соответственно (AQ=frac{13}{28}AC = 13).
По теореме Пифагора из треугольника APB получаем:
(AP=sqrt{AP^2-BP^2}=sqrt{26^2-24^2}=sqrt{2times50}=10)
Следовательно, (PQ = AQ – AP = 13 – 10 = 3)
(S_{BPQ} = ½ PQ·BP = frac{3times24}2=36)
Ответ: 36 см2.
Содержание:
- Формулировка теоремы Герона
- Примеры решения задач
Формулировка теоремы Герона
Теорема
Площадь треугольника равна корню из произведения разностей полупериметра
$p$ треугольника (рис 1) и каждой из его сторон $a$, $b$ и $c$ на полупериметр:
$S=sqrt{p(p-a)(p-b)(p-c)}$
где полупериметр
$$p=frac{a+b+c}{2}$$
Треугольник со сторонами $a$, $b$ и $c$.
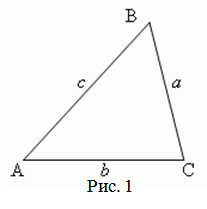
Формула Герона позволяет вычислить площадь треугольника по известным длинам его сторон.
Эта формула содержится в “Метрике” греческого математика и механика Герона Александрийского и названа в его честь.
Герон интересовался треугольниками с целочисленными сторонами. Такие треугольники носят название героновых треугольников.
Простейшим героновым треугольником является египетский треугольник – прямоугольный треугольник со соотношениями сторон
$3 : 4 : 5$ .
Примеры решения задач
Пример
Задание. Вычислите площадь треугольника, зная, что его стороны равны 6 см; 5 см и 2,2 см.
Решение. Полупериметр
$$p=frac{6+5+2,2}{2}=6,6 (mathrm{см})$$
Тогда площадь треугольника, согласно формуле Герона, равна:
$$S=sqrt{6,6 cdot(6,6-6) cdot(6,6-5) cdot(6,6-2,2)}=$$
$$=sqrt{6,6 cdot 0,6 cdot 1,6 cdot 4,4}=sqrt{27,8784}=5,28left(mathrm{см}^{2}right)$$
Ответ. $S=5.28left(mathrm{см}^{2}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
