Содержание
- Геодезические линии
- Решение задач по топографическим планам
- Изменить язык:
- Мобильная версия: Начать изучение
- Масштабы: численный, линейный и поперечный
- Масштабом
- горизонтальным проложением линии
- численный, линейный и поперечный.
- Численным масштабом
- Линейный масштаб
- Поперечный масштаб
- Чтение топографических планов
- Скачать условные знаки для топографических планов:
- Задачи, решаемые по топографическим планам
- Определение прямоугольных координат точек
- Измерение длин линий
- Определение дирекционного угла
- Определение отметок точек и крутизны ската линии местности
Геодезические линии
Из геометрии Евклида мы знаем, что в плоском пространстве кратчайшее расстояние между двумя точками — это прямая линия. Основным признаком прямой линии служит то, что ее длина является минимальной по сравнению с любой кривой, соединяющей те же точки. Оказалось, что в любых метрических пространствах существуют линии, обладающие минимальной длинной. Их принято называть геодезическими линиями.
ОПРЕДЕЛЕНИЕ 11.3. Линия, соединяющая две точки пространства 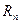 и имеющая наименьшую длину по сравнению с любой другой, проходящей через эти же точки, называется геодезической.
и имеющая наименьшую длину по сравнению с любой другой, проходящей через эти же точки, называется геодезической.
Вывод дифференциального уравнения, основанного на определении 11.3, требует знаний
вариационного исчисления. Поэтому мы воспользуемся другим свойством геодезической линии: при параллельном переносе единичного касательного вектора вдоль геодезической он остается постоянным, т.е. ковариантная производная от его компонент равна нулю. Правда, откровенно следует сказать, что сам процесс параллельного переноса вектора в пространстве Римана теряет свою наглядность и становится неоднозначным. К сожалению, у нас нет иного выхода, как ограничится этим замечанием в надежде на любознательность читателя.
Рассмотрим в 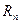 линию, задаваемую параметрическими уравнениями
линию, задаваемую параметрическими уравнениями 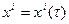 , где
, где 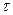 — произвольный параметр. Из математического анализа известно, что
— произвольный параметр. Из математического анализа известно, что 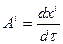 — вектор касательный к данной линии. Нормируем этот вектор на единицу, вводя новый параметр
— вектор касательный к данной линии. Нормируем этот вектор на единицу, вводя новый параметр 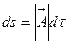 .
.
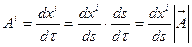 .
.
Отсюда 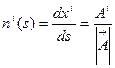 . Вычислим ковариантную производную от
. Вычислим ковариантную производную от 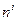 и приравняем ее нулю.
и приравняем ее нулю.
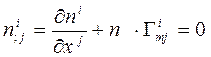
Умножим это равенство на 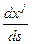 и просуммируем по
и просуммируем по 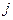 .
.
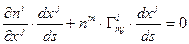
Учитывая зависимость 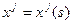 и формулу вычисления сложной производной,
и формулу вычисления сложной производной,
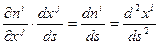
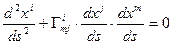 (11.5)
(11.5)
Формула (11.5) задает дифференциальное уравнение геодезической линии в римановых пространствах. Если пространство Евклида рассматривать как частный случай риманового с кривизной равной нулю, то в нем всегда можно ввести ДСК, где все 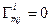 и уравнение (11.5) принимает вид:
и уравнение (11.5) принимает вид: 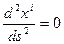 . Решением этого уравнения является прямая линия, задаваемая системой параметрических уравнений:
. Решением этого уравнения является прямая линия, задаваемая системой параметрических уравнений: 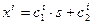 .
.
Упражнение 11
1. Вывести уравнение геодезической линии, пользуясь определением геодезической как кривой экстремальной длины.
2. Найти символы Кристоффеля и компоненты тензора кривизны в 2-мерном пространстве вида:
a) 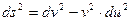 ,
,
b) 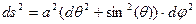
3. Вычислить в ортонормированном базисе тензор кривизны для метрики:
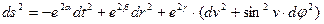 ,
,
где 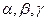 — функции от
— функции от 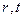 .
.
Найти для этой метрики тензор Риччи, скалярную кривизну и тензор Эйнштейна.
1. Пчелин Б. К. Векторный анализ. — М., 1969.
2. Краснов М. Л. и др. Векторный анализ. — М., 1978.
3. Фомин А. В., Будак В. Г. Кратные интегралы и ряды. — М., 1967.
4. Кухлинг Х. Справочник по физике . — М., 1982.
5. Кочин К. Е. Векторное исчисление и начала тензорного исчисления.— М., 1957.
6. Рашевский П. К. Тензорный анализ и риманова геометрия. — М., 1967
7. Дубровин Б. А. Современная геометрия — М., 1979.
8. Мак — Конелл Дж. Введение в тензорный анализ. — М., 1969.
Дата добавления: 2016-10-17 ; просмотров: 1043 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Решение задач по топографическим планам
Изменить язык: 

Мобильная версия:  Начать изучение
Начать изучение
Масштабы: численный, линейный и поперечный
Масштабом
горизонтальным проложением линии
С помощью масштаба решаются две задачи: 1 — определение длины линии на топографическом плане (карте); 2 — построение заданной линии на топографическом плане (карте).
Применяется три типа масштаба:
численный, линейный и поперечный.
Численным масштабом
Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.
Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности. Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е. 50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.
При работе с планом в ряде случаев пользуются линейным масштабом.
Линейный масштаб

Рис.1
Основанием линейного масштаба называется отрезок АВ линейного масштаба (основная доля масштаба), равный обычно 2 см. Он переводится в соответствующую длину на местности и подписывается. Крайнее левое основание масштаба делят на 10 равных частей.
Наименьшее деление основания линейного масштаба равно 1/10 основания масштаба.
Пример: для линейного масштаба (использующегося при работе на топографическом плане масштаба 1:2000), показанного на рисунке 1, основание масштаба АВ равно 2 см (т.е. 40 метрам на местности), а наименьшее деление основания равно 2 мм, что в масштабе 1:2000 соответствует 4 м на местности.
Отрезок cd (рис. 1), взятый с топографического плана масштаба 1:2000, состоит из двух оснований масштаба и двух наименьших делений основания, что, в итоге, соответствует на местности 2х40м+2х2м = 88 м.
Более точное графическое определение и построение длин линий можно сделать с помощью другого графического построения — поперечного масштаба (рис. 2).
Поперечный масштаб
Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм. Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).
Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.
Пример: отрезок ав (рис. 2), взятый с плана масштаба 1:2000, соответствует на местности 137,6 м (3 основания поперечного масштаба (3х40=120 м), 4 наименьших деления основания (4х4=16 м) и 4 наименьших деления масштаба (0.4х4=1.6 м), т.е. 120+16+1.6=137.6 м) .
Остановимся на одной из важнейших характеристик понятия «масштаб».
Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба. Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм. На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Рис.2
Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.
Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.
Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.

Рис.3
Чтение
топографических планов
Для пользования топографическими планами необходимо изучить условные знаки, принятые для данного масштаба. Условные знаки – графические обозначения, которые показывают местоположение предметов и явлений, а также их количественные и качественные характеристики. Они издаются в виде отдельных таблиц или таблиц на учебных планах. Условные знаки делятся на масштабные (контурные), и внемасштабные.
Масштабными называются условные знаки, которыми местные предметы изображаются в масштабе данного плана, т.е. крупные объекты, например, пашни, луга, леса, моря, озера и т.п.
Внемасштабные условные знаки – знаки, показывающие предметы, которые вследствие своей малости не могут быть изображены в масштабе плана (ширина дорог, колодцы, родники, мосты, опоры ЛЭП, столбы электросети и т.д.). Величина этих знаков не соответствует истинным размерам изображаемых предметов.
Линейные знаки — картографические условные знаки, применяемые для изображения объектов линейного характера, длина которых выражается в масштабе карты, но ширина значительно превышает их фактическую ширину.
Площадные условные знаки — картографические условные знаки, применяемые для заполнения площадей объектов, выражающихся в масштабе карты.
Внемасштабные линейные знаки — картографические условные знаки, применяемые для изображения объектов линейного характера, длина которых не выражается в масштабе карты.
Внемасштабные площадные условные знаки — картографические условные знаки, применяемые для изображения объектов, площади которых не выражаются в масштабе карты (плана).
Пояснительные подписи — подписи, поясняющие вид или род изображенных на карте объектов, а также их количественные и качественные характеристики.
Штриховые элементы карты (плана) — элементы карты (плана), выполненные линиями, штрихами или точками.
Фоновые элементы карты (плана) — элементы карты (плана), выполненные каким-либо цветовым фоном.
Скачать условные знаки для топографических планов:

Задачи, решаемые
по топографическим планам
По топографическому плану можно решить ряд задач, в том числе определить: прямоугольные координаты точки; длину линии; дирекционный угол и румб линии; отметку точки; уклон, крутизну ската и др. Порядок решения этих задач показан на примере учебного плана масштаба 1:2000.
Определение прямоугольных
координат точек
На топографических планах наносится координатная сетка, образующая квадраты со сторонами 10 см. Вертикальные линии сетки параллельны оси абсцисс, а горизонтальные — оси ординат. Координаты вершин квадратов координатной сетки подписываются. Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
Пример : запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.
Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.
Пример: пользуясь координатной сеткой, циркулем и поперечным масштабом, по топографическому плану можно определить прямоугольные координаты точки А (рис. 4), находящейся в квадрате 79,2 – 66,2. Необходимо помнить, что абсциссы возрастают к северу, а ординаты — к востоку.
Сначала записывают в метрах абсциссу Х (южной) линии квадрата, в котором находится точка А, т.е. Х(южной линии сетки) =79200,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба. Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.

Рис.4
Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата У(западной линии сетки) =66200,0 м прибавляют длину отрезка Δy =y(A)-y(b), равную 141,6 м, и получают Y(А) = 66200,0 + 141,6 = 66341,6 м.
Измерение длин линий
Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба.
Определение
дирекционного угла
Дирекционным углом α называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана, по ходу часовой стрелки, до направления данной линии.
Дирекционный угол α линии АВ можно измерить с помощью транспортира. На рис. 5 представлены дирекционные углы α1, α2, α3, и α4 четырех линий М-1, М-2, М-3, М-4.

Рис.5
Дирекционный угол заданного направления α пр называется прямым , а противоположного – обратным α обр (рис. 6).

Рис.6
Связь между прямым и обратным дирекционными углами выглядит так:

Румбом (r) называется острый горизонтальный угол между северным или южным направлением оси ОХ координатной сетки и направлением данной линии. Румбы могут иметь значения от 0 до 90 градусов и сопровождаются названием четверти, в которой находится линия. На рис. 7 показаны румбы четырех линий М-1, М-2, М-3, М-4. Румбы этих линий записывают: СВ: r1; ЮВ: r2; ЮЗ: r3; и СЗ: r4, где, например, СВ — наименование румба, а r1 — значение румба. Например, так выглядит записанный румб: ЮВ: 30º15′

Рис.7
Румб заданного направления r пр. называется прямым , а противоположного – обратным r обр. Прямой и обратный румбы равны по величине и отличаются только наименованием (рис. 8).
Например, если прямой румб равен r пр = СВ: 350º, то обратный румб равен r обр= ЮЗ: 350º.

Рис.8
Таблица перехода от дирекционных углов α к румбам r приведена ниже.
Формулы перехода от дирекционных углов к румбам

Определение отметок точек
и крутизны ската линии местности
Высотой Н точки местности называется расстояние по направлению отвесной линии от точки до уровенной поверхности.
Например, Н(А) = A(a) – высота точки А над уровенной по-верхностью PQ, Н(В) = B(b) — высота точки B над уровенной по-верхностью PQ (рис. 9).
Отметкой точки местности называется численное значение высоты точки. Например, Н(А) = 150 м, Н(В) =149 м.
На топографическом плане рельеф изображается надписями отметок отдельных характерных точек, условными знаками (промоина, обрыв и т. п.) и горизонта-лями.
Горизонталями называются замкнутые кривые линии, со-единяющие точки местности с одинаковыми отметками. Горизонтали образуются путём пересечения поверхности местности секущими горизонтальными плоскостями, проведенными через заданное расстояние, которое называется высотой сечения рельефа h.
Заложением называется расстояние d на плане между двумя соседними горизонталями (рис. 9 – 11).

Рис.9
По отметкам двух смежных (соседних) горизонталей можно определить отметку точки, лежащей между ними. Например: отметка первой точки В на нижней (рис. 10) горизонтали H1 = 161 м, отметка второй точки А на верхней (рис. 10) горизонтали H2 = 162 м (т.е. высота сечения рельефа h = 1 м), заложение d = 16,8 м, расстояние от первой горизонтали до точки С равно с = 7,6 м (рис. 10). Тогда (с требуемой точностью до 0,1 м) вычисляем отметку НС точки С по формуле


Крутизна ската — это угол, образуемый направлением ската с горизонтальной плоскостью в данной точке А. Уклон u линии местности – это тангенс угла наклона ν линии местности (тангенс крутизны ската) к горизонтальной плоскости (рис. 11).

Рис.11

Чем больше угол наклона, тем скат круче.
Для нашего примера уклон линии местности между горизонталями равен
Источник
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
Страница 1 из 2
-

- Регистрация:
- 22 май 2013
- Сообщения:
- 3
- Симпатии:
- 0
Здравствуйте, уважаемые, форумчане.
Убедительно прошу помочь определить длину линий между точками А-В, А-Д и Д-С, имеющих координаты (участок в пригороде Челябинска):
А (Х=602075.06; У=2315870.38)
В (Х=602068.24; У=2315889.28)
С (Х=602059.37; У=2315889.40)
Д (Х=602069.34; У=2315867.81)
Спасибо!#1
-

Форумчанин
- Регистрация:
- 2 май 2010
- Сообщения:
- 703
- Симпатии:
- 133
-

- Регистрация:
- 22 май 2013
- Сообщения:
- 3
- Симпатии:
- 0
Перерегистрация личного садового участка
#3
-

Команда форума
ФорумчанинAB = √ ((Xb-Xa)²+(Yb-Ya)²).
#4
-

Форумчанин
- Регистрация:
- 2 ноя 2012
- Сообщения:
- 356
- Симпатии:
- 45
АВ-20.09 м., ВС-8.87 м., СД-23.78 м., ДА-6.27 м.
#5
-

- Регистрация:
- 22 май 2013
- Сообщения:
- 3
- Симпатии:
- 0
Уважаемый, Маркс.
Спасибо Вам Огромное за ответ.
Желаю Вам Удачи!#6
-

Форумчанин
- Регистрация:
- 2 ноя 2012
- Сообщения:
- 356
- Симпатии:
- 45
-

Команда форума
Форумчаниндо чего народ ленивый пошел, даже при помощи обычного калькулятора посчитать не хотят, все на подносе ждут.
#8
-

Форумчанин
да лано если человек с геодезией не знаком, то ему формула как темный лес…
#9
-

Форумчанин
- Регистрация:
- 28 сен 2013
- Сообщения:
- 465
- Симпатии:
- 77
Это не геодезия, это теорема Пифагора…
#10
-

Форумчанин
Анука объясните мне эту формулу с точки зрения теоремы Пифагора, примем, что геодезию я незнаю, с точки зрения обычного обывателя.
#11
-

Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.923
- Симпатии:
- 4.779
А что тут, собственно, странного даже для ученика, изучающего прямоугольный треугольник?
#12
-

Форумчанин
Анука объясните мне эту формулу с точки зрения теоремы Пифагора, примем, что геодезию я незнаю, с точки зрения обычного обывателя.
#13
-

Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.923
- Симпатии:
- 4.779
На листочке в клеточку и осями координат, как в математике, нанесите эти 2 точки. Не только самый умный ученик догадается, как найти расстояние между точками.
#14
-

Форумчанин
- Регистрация:
- 2 май 2010
- Сообщения:
- 703
- Симпатии:
- 133
Андрей Р., как можно объяснить теорему Пифагора с точки зрения теоремы Пифагора? Да и зачем? Или вы обывателей совсем за дураков держите?
#15
-

Форумчанин
Андрей, а ваш обычный обыватель геометрию в школе проходил? 11 класс, нахождение длины вектора АБ, если известны координаты А и Б.
#16
ЮС, dverovoz и stout нравится это.
-

Форумчанин
Прождал ночь, прикольно, никто так и не обьяснил связь вот этой формулы AB = √ ((Xb-Xa)²+(Yb-Ya)²) с теоремой пифагора, славо богу Geo_major, скинул видео урок, в нем можно отследить связь.
geoscreen, схренали, я прошу объяснить формулу, что в ней есть катеты, а что гипотенуза, и откуда они взялись…
Все умные, вот только обьясните мне почему обычный человек которым является ТС, не смог по этой такой простой и понятной формуле посчитать расстояния, а сказал:Для меня было интересно смогут или нет люди считающие себя специалистами объяснить решение простой задачи, человеку который в простой жизни с координатами не сталкивается, и для которого теорема Пифагора, осталась в дальнем детстве, или скатится на стандартное да ты че совсем дурак этож теорема Пифагора, UnknownUser, В.Шуфотинский, geoscreen, спасибо я вижу вы настоящие специалисты, и знаете как правильно все объяснить…

Я очередной раз все понял, всем спасибо.
#17
-

Команда форума
Форумчанини чё там объяснять? Подставляй числа из 1 поста и все дела. Даже буковки я специально написал те же

#18
-

Форумчанин
Коллеги, давайте жить дружно. ТС уже и думать забыл об этом, а мы тут начинаем уходить в дебри формул.

Единственный момент, что ТС сумел найти в интернете наш форум, чтобы создать тему и задать вопрос, но не сумел найти в том же самом яндексе ответ.
И если на самом деле эти данные ему нужны для перерегистрации участка, то меня терзают смутные сомнения….То тут либо ещё один фоксал появился, либо некоторые кадастровые инженерА не знают геодезию. Ведь перерегистрация земельного участка в себя включает
Раскрыть Спойлер
Свернуть Спойлер
Землеустроительные работы при перерегистрации права на земельный участок включают в себя три этапа:
1. Подготовительный этап – включает в себя согласование сроков и стоимости работ, анализ правоустанавливающих и правоудостоверяющих документов на участок, оформление заказа и заключение договора, проведение необходимых заказчику консультаций по земельным вопросам.2. Полевой этап – это проведение на местности геодезической съемки Вашего участка, выявление сохраненных межевых знаков и подписание Акта согласования границ со смежными землепользователями.
3. Камеральный этап – обработка результатов геодезической съемки, формирование проекта границ земельного участка, с последующим формированием межевого дела.
Перерегистрация земельного участка проводиться по ряду причин. Это может быть и уточнение площади участка, перерегистрация права на участок в связи с оформлением наследства, для совершения сделки или просто Ваше желание иметь на руках свидетельство нового образца.
В некоторых случаях при перерегистрации участка Вам потребуется согласовать с местной администрацией (сельской, поселковой или городской) его конфигурацию, т.к. в большинстве случаев при производстве землеустроительных работ обнаруживается расхождение площади участка по свидетельству и фактической площади. После проведения геодезической съемки участка и согласований конфигурации и площади, наши специалисты сформируют землеустроительное дело на Ваш участок и передадут его на освидетельствование в местный отдел Роснедвижимости.
#19
-

Форумчанин
- Регистрация:
- 28 сен 2013
- Сообщения:
- 465
- Симпатии:
- 77
Андрей! Длина одного катета – то же самое, что разница координат X. Длина второго катета – разница координат Y. Гипотенуза – это другое название нашей линии. В общем, самая классическая теорема Пифагора.
#20
Страница 1 из 2
Поделиться этой страницей
При вычислении
длин линий в результат измерения вводят
поправки, которые исключают влияние
систематических погрешностей.
Поправка
∆Dк
за
компарирование мерного прибора.
При измерении линий фактическая длина
мерного прибора отличается от номинала
на величину поправки за компарирование
l
= l0
+ ∆lк.
Оцифровка мерного прибора соответствует
номиналу, поэтому результат измерения
остатка обозначим через r0.
В этом случае фактическая длина
остатка r
за счет
поправки за компарирование изменится
на величину, пропорциональную длине
остатка, т. е.
r
= r0
+ (∆к/l0)r0
(26.1)
Аналогичное
равенства можно записать для отрезка,
чья длина кратна номинальной длине
ленты l0
D
= n(l0
+ ∆lк),
(26.2)
где n
– число целых мерных лент, отложенных
в процессе измерения отрезка.
Полная длина линии
запишется как сумма (24.1) и (24.2)
D
= n(l0
+ ∆lк)
+ (r0
+
![]()
r0).
(26.3)
Раскроем скобки
и перепишем формулу (24.3) в несколько
ином виде
D
= (nl0
+ r0)
+
![]()
к.
(26.4)
Величина (nl0
+ r0)
– эта длина линии, вычисленная с
номинальным значением длины мерного
прибора. Обозначив ее через D0,
запишем
D
= D0
+ (D0/l0)∆lк
.
Величину
∆Dк
= D
– D0
= (D0/l0)∆lк
называют поправкой
в длину мерного прибора за компарирование.
Поправка
∆D
t за
температуру
мерного
прибора.
При измерении линий температура мерного
прибора t
обычно
отличается от температуры компарирования
t0.
В этом случае длина мерного прибора
равна
l
= l0
+ α(t
– t0)l0
где α
–
коэффициент
линейного расширения материала мерного
прибора (для стали α
= 12,5.10-6).
Соответственно
изменится длина остатка
r
= r0
+ α(t –
t0)r0.
С учетом предыдущего
соотношения получим уравнение, учитывающее
поправку за температурное расширение
прибора.
D
= (nl0
+ r0)
+ α (t –
t0)
(nl0
+ r0),
но nl0
+ r0
=D0,
тогда
D
= D0
+ α (t
– t0)
D0.
Величину
∆Dt
= D
– D0
= α(t
– t0)D0.
называют поправкой
в длину линии за температуру мерного
прибора.
Если при измерении
линий для создания топографических
планов разность температур по абсолютной
величине не превышает 8º, то поправку
за температуру не учитывают. При
учете поправок обычно измеряют температуру
воздуха, а не мерного прибора. Возникающая
при этом погрешность мала и не влияет
на точность измерений.
При измерении длин
линий на конструкциях зданий и сооружений
дополнительно учитывают температурные
расширения конструкций. Если температуру
конструкций при эксплуатации обозначить
через tэ,
то поправку за температуру можно
вычислить по формуле
∆Dt
= ∆α(tср–
tэ)D0
+ ∆tαсрD0,
(26.5)
где αср,
tср
– средние
значения соответственно коэффициентов
линейного расширения и температур
конструкций и мерного прибора; ∆α,
∆t
– разности
коэффициентов линейного расширения и
температур конструкций мерного прибора.
Поправку по формуле
(26.5) учитывают при выполнении высокоточных
линейных измерений на конструкциях
уникальных сооружений.
На объектах массовой
застройки из сборных железобетонных
конструкций разность коэффициентов
линейного расширения ∆α.
близка к
нулю (0,5.10-6),
поэтому первый член правой части
равенства (26.5) мал. Тогда
∆Dt
= ∆tαсрD0.
Наибольшие
затруднения при измерениях вызывает
определение температуры конструкций,
так как для этого приходится в них делать
лунки. Поэтому поправки по формуле
(26.5) учитывают только при возведении
зданий повышенной этажности и промышленных
сооружений с пролетами между опорами
более 6м.
На типовых зданиях
массовой застройки для упрощения
вычислений и измерений значения поправок
метровых делений прибора приводят
к значениям температуры эксплуатации
здания, что позволяет обойтись без учета
температуры.
Поправка
∆Dν,h
за приведение линии к горизонту.
Горизонтальное положение d
наклонной
линии D
находят по углу наклона v
или по превышению h
(рис. 31).
Если известен угол
наклона, то из прямоугольного треугольника
АВС имеем
d
= D
cos ν.
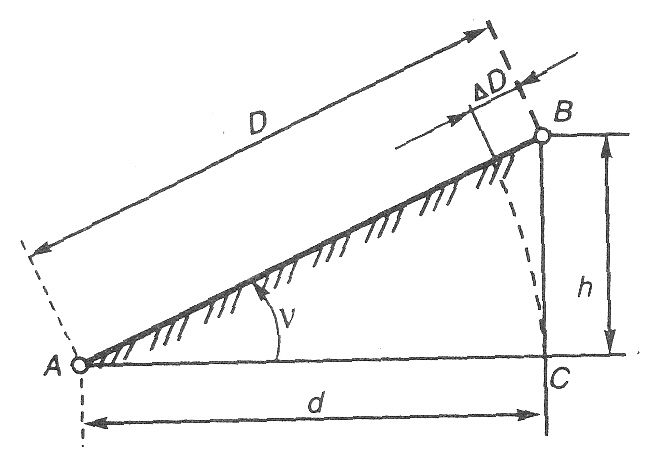
Рис.
31. Поправка за приведение линии к
горизонту
При вычислениях
горизонтальных проложений используют
микрокалькуляторы. При отсутствии
микрокалькулятора для упрощения
вычислений в результаты измерений
вводят поправку
∆ Dν
= d
– D
= – D(1
– cosν)
= –2D
sin(ν/2)
Поправка за
приведение линий к горизонту всегда
отрицательна,, так как горизонтальное
проложение всегда меньше длины наклонной
линии.
При углах наклона
менее 10º синус изменяется пропорционально
значениям угла. Поэтому sin (v/2)≈
0,5 sin
v.
Тогда
∆Dν
= –0,5sin2ν
Если известно
превышение концов измеряемой линии, то
по теореме Пифагора (рис. 31)
имеем
D2
= d2
+h2;
h2
= D2
– d2
=
(D
– d)
(D
+ d).
При вычислениях
поправки обычно удерживают две–три
значащие цифры, поэтому можно принять
d≈D.
Если учесть, что ∆Dh
= d
– D,
то
∆Dh
= – h2/2D
(24.6)
Если линия имеет
перегибы ската, то поправки за приведение
к горизонту вычисляют по частям. При
этом линию разбивают на отрезки с
равномерными скатами, а поправку для
каждого отрезка вычисляют раздельно
по формуле (24.6).
Окончательно
горизонтальное проложение линии с
учетом всех поправок вычисляют по
формуле
d
= D0
+ ∆Dк
+ ∆Dt
+ ∆Dν,h.
При измерении
линий могут быть допущены промахи и
грубые погрешности. Один вид промахов
(оцифровку делений) был отмечен выше.
Существует еще целый ряд погрешностей,
влияние которых на суммарный результат
измерений можно существенно уменьшить.
Эти погрешности носят систематический
характер по влиянию на результат, но
случайны по величине. Чтобы уменьшить
их величины, необходимо учитывать
следующее.
1. Отклонение концов
рулетки от створа измерений всегда
увеличивает измеряемую длину. Чем меньше
отклоняются концы от створа, тем меньше
погрешность измерения. При измерениях
для многих целей укладку мерных приборов
в створ производят с использованием
оптических труб. К такому приему прибегают
в тех случаях, когда хотят получить
результат с относительной погрешностью
менее 1:3000 от измеряемой длины. Отклонения
от створа концов 30 и 50-метровых рулеток
более чем на 0,15м
недопустимы.
2. Большую погрешность
в измеряемую длину может внести разное
натяжение прибора при эталонировании
и практической работе. Следует избегать
избыточного натяжения, так как тонкое
полотно рулеток растягивается, при этом
часто не восстанавливая начальную
длину. Достаточно точно (до ± 100 Н) можно
выдержать натяжение, используя для
этого ручные приборы – динамометры
типа ПН-2 или пружинные бытовые весы.
3. Недопустимо
ослаблять внимание при отсчитывании
по концам мерного прибора или его
фиксации. Достигнутая точность может
быть утрачена при неодновременном
снятии отсчетов, подвижке мерного
прибора во время фиксации его концов.
Поэтому не следует пренебрегать
возможностью дважды или даже трижды
взять отсчеты по концам мерного прибора
и сравнить разности отсчетов по
переднему и заднему концам (П – 3).
Разность отсчетов (для одного пролета
измерений) при работе рулетками не
должна превышать 2мм, а при измерении
мерными лентами – 1см.
4. Необходимо
следить не только за превышением концов
мерного прибора, но и за его изгибом
в вертикальной плоскости. Точность
определения поправки за наклон зависит
от точности определения превышений:
чем короче линия, тем точнее надо знать
превышение. Как правило, достаточно его
знать с погрешностью до 1,0…1,5 см на 100м
длины.
5. При введении
поправок за отличие температуры, данной
в уравнении рулетки (+20Сº),
и температуры измерений следует помнить,
что измеряют температуру воздуха, а
поправку вводят за изменение температуры
металлического полотна мерного прибора.
Поэтому при прямом солнечном облучении
мерного прибора термометр подкладывают
под его полотно и держат 3…5 мин. с тем,
чтобы точнее определить температуру
мерного полотна. Разность температуры
воздуха и мерного прибора измеряют
с погрешностью не грубее 5 Сº.
6. Существенно
исказить результат измерения может
плохое закрепление точек, между
которыми ведется измерение. Вязкая
почва, зыбко забитые кол, штырь или
шпилька, изменяющие свое положение от
случайных ударов, приводят к появлению
недопустимых погрешностей в измеряемой
длине. Назад
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
12.03.20156.3 Mб35Краткий курс аналитической геометрии.pdf
- #
- #
- #
- #
- #
- #
8.1. Измерение длин линий мерными лентами и рулетками
Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.
Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.
Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.
Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.
Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.
Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.
Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:
l = l0 + Dl + a l0 (t– t0). (8.1)
Здесь l – длина ленты при температуре t; l0 – номинальная длина; Dl – поправка к номинальной длине при температуре компарирования t0 ; a – температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.
Вешение линии. Перед измерением длины линии на её концах устанавливают вехи. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то в их створе ставят дополнительные вехи (створом двух точек называют проходящую через них вертикальную плоскость). Вешение обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи A (рис. 8.1, а), а рабочий по его указаниям ставит веху 1 так, чтобы она закрыла собой веху B. Таким же образом последовательно устанавливают вехи 2, 3 и т. д. Установка вех в обратном порядке, то есть «от себя», является менее точной, так как ранее выставленные вехи закрывают видимость на последующие.
|
|
Рис. 8.1. Вешение линии: а – “на себя”; б – через препятствие; в – то же (вид в плане). |
Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D – вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D1, то есть в створ точек C и B. Затем из точки С веху переносят в точку С1 и так далее до тех пор, когда обе вехи окажутся в створе AB.
Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n – число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).
Длину измеряют дважды – в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях – 1/1000). За окончательное значение принимают среднее.
Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.
Поправка за компарирование определяется по формуле
Dk = n Dl ,
где Dl – отличие длины ленты от 20 м и n – число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.
Поправка за температуру определяется по формуле
Dt = aD(t–t0)
где a – термический коэффициент расширения (для стали a = 0,0000125); t и t0 – температура ленты во время измерений и при компарировании. Поправку Dt учитывают, если ½t–t0½>10°.
Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D
d = D cosn , (8.2)
где n – угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где
Dn = d – D = D (cosn – 1) = -2D sin2 ![]() . (8.3)
. (8.3)
По формуле (8.3) составляют таблицы, облегчающие вычисления.
Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.
Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.
Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.
Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами – глазным 1 и предметным 4.
|
|
|
Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона
Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 – 30¢.
Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.
Точность измерений лентой в разных условиях различна и зависит от многих причин – неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.
Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.
Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта di определяют по формуле
di = П – З,
где П и З – передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).
Если линия имеет наклон, необходимо учесть поправку
![]() ,
,
где h – превышение между концами пролёта, измеряемое нивелиром.
Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 – 1:10000.
ГЕОДЕЗИЧЕСКОЕ РАССТОЯНИЕ
- ГЕОДЕЗИЧЕСКОЕ РАССТОЯНИЕ
-
длина кратчайшей геодезической линии, соединяющей две точки (или два множества). В вариационном исчислении Г. р.- значение исследуемого функционала на экстремали, соединяющей две рассматриваемые точки.
ГЕОКРИОЛОГИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ – математич. задачи, возникающие при изучении процессов и явлений, происходящих в мерзлых почвах и горных породах, географич. распространения и условий формирования сезонномерзлых и многолетнемерзлых горных пород (вечной мерзлоты). Интересные Г. м. з. возникают при изучении проблемы взаимодействия температурных и влажностных полей в зонах с подвижными границами раздела фаз. Характерной особенностью Г. м. з. является то, что процессы тепло- и массообмена, происходящие при промерзании и оттаивании пород, тесно связаны между собой. Задача сводится к системе квазилинейных уравнений параболич. типа, поскольку тепло- и влагообменные характеристики среды существенно зависят от искомых функций. Типичными примерами подобных задач являются исследование промерзания влагонасыщенных тонкодисперсных пород, к-рое сопровождается миграцией влаги к фронту промерзания н пучением, а также исследование оттаивания грубодисперсных пород, сопряженное с инфильтрацией и фильтрацией влаги. Особое значение для инженерной геологии имеет решение многомерной Стефана задачи, для областей со сложной конфигурацией, в частности о чаше протанвання при гражданском и промышленном строительстве. Решение вопросов истории, геокриологпи приводит к необходимости исследования многофронтовой задачи Стефана с учетом образования зон и вырождения их в точку. Важное значение при этом имеет увязка процессов промерзания и оттаивания в верхних слоях литосферы с радиационно-тепло-вым балансом. В. <И. Дмитриев. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ – последовательность чисел, каждое из к-рых равно предыдущему, умноженному на нек-рое постоянное для данной прогрессии число
 (знаменатель прогрессии). Г. п. наз. возрастающей, если
(знаменатель прогрессии). Г. п. наз. возрастающей, если  , убывающей, если
, убывающей, если  ; если
; если  , то Г. п.- знакочередующаяся. Любой член Г. п.
, то Г. п.- знакочередующаяся. Любой член Г. п. 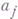 выражается через ее первый член
выражается через ее первый член 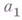 и знаменатель
и знаменатель  формулой
формулой
а сумма первых пчленов Г. п. (знаменатель к-рой не равен 1) – формулой

Если
 , то при неограниченном возрастании числа псумма
, то при неограниченном возрастании числа псумма  стремится к пределу
стремится к пределу 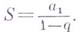 Это число
Это число 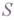 наз. суммой бесконечно убывающей геометрической прогрессии. Выражение
наз. суммой бесконечно убывающей геометрической прогрессии. Выражение 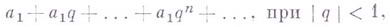
– простейший пример сходящегося ряда -геометрический ряд, число
 является суммой геометрии, ряда.
является суммой геометрии, ряда. Термин “Г. п.” связан со свойством любого члена Г. п. с положительными членами:
 т. е. любой член есть геометрическое среднее между предыдущим и последующим ее членами, о. А. Иванова.
т. е. любой член есть геометрическое среднее между предыдущим и последующим ее членами, о. А. Иванова.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Полезное
Смотреть что такое “ГЕОДЕЗИЧЕСКОЕ РАССТОЯНИЕ” в других словарях:
-
геодезическое зенитное расстояние — Угол между направлениями на геодезический зенит данной точки и на другую точку. [ГОСТ 22268 76] Тематики геодезия Обобщающие термины системы координат EN geodetic zenith distance DE geodätische Zenitdistanz FR distance zénithale géodésiques … Справочник технического переводчика
-
Геодезическое зенитное расстояние — 54. Геодезическое зенитное расстояние D. Geodätische Zenitdistanz E. Geodetic zenith distance F. Distance zénithale géodésiques Угол между направлениями на геодезический зенит данной точки и на другую точку Источник: ГОСТ 22268 76: Геодезия.… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации
-
Геодезические инструменты — геодезические приборы, механические, оптико механические, электрооптические и радиоэлектронные устройства для измерения длин линий, углов, превышений при построении астрономо геодезической сети (См. Астрономо геодезическая сеть) и… … Большая советская энциклопедия
-
Корпус военных топографов — Основание Указ императора Александра I 28 января 1822 года Ликвидация Постановление СНК СССР 1918 год Корпус военных топографов (КВТ) (до 1866 Корпус топографов) был организован в 1822 году для централизов … Википедия
-
Астрономия — (от греческих слов άστρον, светило, и νόμος, закон) наука о небесных светилах. В обширном значении этого слова А. включает в себе исследование всего того, что можно знать о небесных светилах: солнце, луне, планетах, кометах, падающих звездах,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
СП 47.13330.2012: Инженерные изыскания для строительства. Основные положения — Терминология СП 47.13330.2012: Инженерные изыскания для строительства. Основные положения: 8.4.9 Биологические (флористические геоботанические, фаунистические) исследования выполняют для определения видового состава флоры и основных растительных… … Словарь-справочник терминов нормативно-технической документации
-
Электрооптический дальномер — светодальномер, прибор для измерения расстояний по времени прохождения измеряемого расстояния электромагнитными волнами оптического или инфракрасного диапазонов. Э. д. делятся на импульсные и фазовые (в зависимости от того, каким способом … Большая советская энциклопедия
-
Струве, Василий Яковлевич — (Friedrich Georg Wilhelm) знаменитый астроном, устроитель и первый директор Пулковской обсерватории; родился 15 (4) апреля 1793 г. в Альтоне, где отец его, видный филолог и математик, был в это время директором местной гимназии Христианеум. В… … Большая биографическая энциклопедия
-
Исландия — 1) остров на С. Атлантического океана. Открыт норманнами в IX в. и был назван по имени первого обследовавшего остров мореплавателя Гардарсхольм остров Гардара (holm остров ). Но закрепилось название Исланд, русск. Исландия ледяная страна (Island) … Географическая энциклопедия
![inj_geo_1-245.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-245.jpg)
![inj_geo_1-247.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-247.jpg)
![inj_geo_1-248.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-248.jpg)
