Mod числа как найти формула

Mod числа как найти формула

Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть a и b — целые числа, причём bneq 0. Деление с остатком a («делимого») на b («делитель») означает нахождение таких целых чисел q и r, что выполняется равенство:

a=bcdot q+r

Таким образом, результатами деления с остатком являются два целых числа: q называется неполным частным от деления, а r — остатком от деления. На остаток налагается дополнительное условие: {displaystyle 0leqslant r<|b|,} то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения a=bcdot q+r при заданных выше условиях. Если остаток равен нулю, говорят, что a нацело делится на b.

Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).

Примеры
Проверка: 78=33cdot 2+12.
Проверка: -78=33cdot (-3)+21.
Проверка: {displaystyle -9=1cdot (-13)+4.}
Проверка: {displaystyle 9=90cdot 0+9.}

Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.

Определение[править | править код]

Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше[1].

Для вычисления неполного частного от деления a на положительное число b следует разделить (в обычном смысле) a на b и округлить результат до ближайшего целого в меньшую сторону:

{displaystyle q=leftlfloor {frac {a}{b}}rightrfloor ,} когда b>0.

где полускобки {displaystyle leftlfloor cdot rightrfloor } обозначают взятие целой части. Значение неполного частного q позволяет вычислить значение остатка r по формуле:

{displaystyle r=a-bcdot q.}

Для отрицательного делителя нужно округлять частное в большую сторону:

{displaystyle q=leftlceil {frac {a}{b}}rightrceil ,} когда b<0.

Операция «mod» и связь со сравнениями[править | править код]


Величина остатка может быть получена бинарной операцией «взятия остатка» от деления a на b, обозначаемой mod:

{displaystyle r=a{bmod {b}}.}

Не следует путать это обозначение с обозначением сравнения по модулю b. Формула для r влечёт выполнение сравнения:

{displaystyle requiv a{pmod {b}},}

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства 0leqslant r<|b|, необходимого для того, чтобы r было остатком.

В программировании[править | править код]

Операция вычисления неполного частного и остатка в различных языках программирования

Язык Неполное
частное		 Остаток Знак остатка
ActionScript % Делимое
Ada mod Делитель
rem Делимое
Бейсик MOD Не определено
Си (ISO 1990) / % Не определено
Си (ISO 1999) / % Делимое[3]
C++ (ISO 2003) / % Не определено[4]
C++ (ISO 2011) / % Делимое[5]
C# / % Делимое
ColdFusion MOD Делимое
Common Lisp mod Делитель
rem Делимое
D / % Делимое[6]
Delphi div mod Делимое
Eiffel // \ Делимое
Erlang div rem Делимое
Euphoria remainder Делимое
Microsoft Excel (англ.) QUOTIENT() MOD() Делитель
Microsoft Excel (рус.) ЧАСТНОЕ() ОСТАТ()
FileMaker Div() Mod() Делитель
Fortran mod Делимое
modulo Делитель
GML (Game Maker) div mod Делимое
Go / % Делимое
Haskell div mod Делитель
quot rem Делимое
J |~ Делитель
Java / % Делимое[7]
Math.floorDiv Math.floorMod Делитель (1.8+)
JavaScript .toFixed(0) % Делимое
Lua % Делитель
Mathematica Quotient Mod Делитель
MATLAB idivide(?, ?, 'floor') mod Делитель
idivide rem Делимое
MySQL DIV MOD
%		 Делимое
Oberon DIV MOD +
Objective Caml mod Не определено
Pascal div mod Делимое[8]
Perl Нет % Делитель
PHP Нет[9] % Делимое
PL/I mod Делитель (ANSI PL/I)
Prolog (ISO 1995) mod Делитель
PureBasic / Mod
%		 Делимое
Python // % Делитель
QBasic MOD Делимое
R %/% %% Делитель
RPG %REM Делимое
Ruby / % Делитель
Scheme modulo Делитель
SenseTalk modulo Делитель
rem Делимое
Tcl % Делитель
Verilog (2001) % Делимое
VHDL mod Делитель
rem Делимое
Visual Basic Mod Делимое

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается: 

78 mod 33 = 12
78 div 33 = 2

Знак остатка[править | править код]

Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

  • Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
  • Знак остатка совпадает со знаком делителя: неполное частное округляет к -infty .

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.

Как запрограммировать, если такой операции нет?[править | править код]

Неполное частное можно вычислить через деление и взятие целой части: q=left[{frac {a}{b}}right], где [x], в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды mod остаток программируется как a-qb.

Если b положительно, а знак r совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой r'=(b+(aoperatorname {mod}b))operatorname {mod}b.

Неполное частное и неотрицательный остаток от деления на степень двойки 2^{n} — это битовый сдвиг {displaystyle agg n} (для чисел со знаком — арифметический) и {displaystyle aoperatorname {&} (2^{n}-1)}.

Обобщения[править | править код]

Вещественные числа[править | править код]

Если два числа a и b (отличное от нуля) относятся к множеству вещественных чисел, a может быть поделено на b без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.

Формально:

если a,bin {mathbb {R}},bneq 0, то {displaystyle a=bq+r}, где 0leqslant r<|b|.
Пример

Деление 7,9 на 2,1 с остатком даёт:

{displaystyle leftlfloor {frac {7{,}9}{2{,}1}}rightrfloor =3} (неполное частное);
{displaystyle 7{,}9-3cdot 2{,}1=1{,}6} (остаток).

Гауссовы целые числа[править | править код]

Гауссово число — это комплексное число вида a+bi, где a,b — целые числа. Для них можно определить деление с остатком: любое гауссово число u можно разделить с остатком на любое ненулевое гауссово число v, то есть представить в виде:

u=vq+r,

где частное q и остаток r — гауссовы числа, причём |r|<|v|.
Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, {displaystyle 7+2i} можно разделить на {displaystyle 3-i} тремя способами:

{displaystyle 7+2i=(3-i)(2+i)+i=(3-i)(1+i)+3=(3-i)(2+2i)+(-1-2i).}

Многочлены[править | править код]

При делении с остатком двух многочленов f(x) и g(x) для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:

{displaystyle f(x)=q(x)g(x)+r(x)}, причём {displaystyle deg(r)<deg(g)}.
Пример
{frac {2x^{2}+4x+5}{x+1}}=2x+2 (остаток 3), так как: {displaystyle 2x^{2}+4x+5=(x+1)(2x+2)+3}.

См. также[править | править код]

  • Алгоритм Евклида
  • Делимость
  • Наибольший общий делитель
  • Непрерывная дробь
  • Сравнение по модулю

Примечания[править | править код]

  1. ↑ 1 2 Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
  2. ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
  3. ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the / operator is the algebraic quotient with any fractional part discarded. [This is often called «truncation toward zero».]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится.
  4. ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
  5. ↑ N3242=11-0012 (Working draft), текст совпадает с C99
  6. ↑ D language specification (англ.). dlang.org. Дата обращения: 29 октября 2017. Архивировано из оригинала 3 октября 2017 года.
  7. ↑ Арнолд, Кен, Гослинг, Дж., Холмс, Д. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
  8. ↑ Стандарт 1973 года: div — division with truncation.
  9. ↑ PHP: Arithmetic Operators — Manual. Дата обращения: 27 ноября 2014. Архивировано 19 ноября 2014 года.
  10. ↑ DIV — Unsigned Divide
Источник

Скачать пример рабочей книги

Загрузите образец книги

Это руководство по Excel демонстрирует, как использовать Функция Excel MOD чтобы вычислить остаток после деления.

Функция MOD возвращает остаток или модуль числа после выполнения деления. Однако функция MOD предназначена не только для того, чтобы помочь нам с проблемами разделения. Он становится еще более мощным, когда мы хотим искать каждый N-й элемент в списке или когда нам нужно сгенерировать повторяющийся шаблон.

Чтобы использовать функцию таблицы MOD Excel, выберите ячейку и введите:

Синтаксис и входные данные функции MOD:

1 = МОД (число; делитель)

количество – Число.

делитель – Число, на которое нужно разделить.

Что такое функция MOD?

Функция MOD возвращает остаток или модуль числа после выполнения деления. Однако функция MOD предназначена не только для того, чтобы помочь нам с проблемами разделения. Он становится еще более мощным, когда мы хотим искать каждый N-й элемент в списке или когда нам нужно сгенерировать повторяющийся шаблон.

MOD Базовая математика

Когда вы пытаетесь разделить 13 на 4, вы можете сказать, что ответ – 3 остатка 1. «1» в этом случае называется модулем (отсюда и название функции MOD). Тогда в формуле мы могли бы написать

И на выходе будет 1.

Эта таблица дает еще несколько иллюстраций того, как будет работать ввод / вывод MOD.

Обратите внимание, что когда на входе было 3, не было остатка, и, следовательно, на выходе формулы было 0. Кроме того, в нашей таблице мы использовали функцию СТРОКА для генерации наших значений. Большая часть возможностей MOD будет заключаться в использовании функции ROW (или COLUMN), как мы увидим в следующих примерах.

MOD Суммируйте каждую вторую строку

Рассмотрим эту таблицу:

Для наглядности второй столбец имеет формулу

Чтобы добавить все четные строки, вы можете написать формулу СУММЕСЛИ, и критерии будут искать 0 значений в столбце B. Или, чтобы добавить все нечетные строки, задайте критерий поиска 1 значения.

Однако нам вообще не нужно создавать вспомогательный столбец. Вы можете объединить возможности MOD в SUMPRODUCT, чтобы сделать все за один шаг. Наша формула для этого была бы

1 = СУММПРОИЗВ (A2: A5; – (MOD (B2: B2; 2) = 0)

Поскольку он находится в СУММПРОИЗВЕ, функция МОД сможет обрабатывать ввод нашего массива. Мы уже видели результат в вспомогательном столбце, но массив из нашего MOD в этой формуле будет {0, 1, 0, 1}. После проверки значений, равных 0, с применением двойного унарного массива, массив будет {1, 0, 1, 0}. Затем СУММПРОИЗВ выполняет свое волшебство или умножает массивы для получения {2, 0, 4, 0}, а затем суммирует, чтобы получить желаемый результат, равный 6.

MOD Суммировать каждую N-ю строку

Поскольку формула MOD (x, N) будет выводить 0 для каждого N-го значения, мы можем использовать это, чтобы помочь формулам выбирать, какие значения использовать в других функциях. Посмотри на эту таблицу.

Наша цель – получить значения из каждой строки с пометкой «Итого». Обратите внимание, что Итого появляется каждые 3rd строки, но начиная со строки 4. Наша функция MOD, таким образом, будет использовать 3 как 2nd аргумент, и нам нужно вычесть 1 из первого аргумента (поскольку 4 -1 = 3). Таким образом, нужные нам строки (4, 7, 10) будут кратны 3 (3, 6, 9). Наша формула для суммирования желаемых значений будет

1 = СУММПРОИЗВ (C2: C10; – (МОД (СТРОКА (A2: A10) +2; 3) = 0))

Созданный массив преобразуется следующим образом:

12345 {2, 3, 4, 5, 6, 7, 8, 9, 10}{1, 2, 3, 4, 5, 6, 7, 8, 9}{1, 2, 0, 1, 2, 0, 1, 2, 0}{Ложь, Ложь, Истина, Ложь, Ложь, Истина, Ложь, Ложь, Истина}{0, 0, 1, 0, 0, 1, 0, 0, 1}

В нашем массиве критериев SUMPRODUCT теперь настроено, как нам нужно получать каждые 3rd значение, и мы получим желаемый результат в размере 90 долларов.

Сумма MOD по столбцам

До сих пор мы использовали примеры, которые идут вертикально и используют СТРОКУ, но вы также можете двигаться горизонтально с помощью функции СТОЛБЕЦ. Рассмотрим этот макет:

Мы хотим подвести итоги по всем пунктам. Наша формула для этого могла бы быть

1 = СУММПРОИЗВ (B2: E2 * (MOD (COLUMN (B2: E2); 2) = 0)

В этом случае мы настроены на получение каждые 2nd столбец в пределах нашего диапазона, поэтому СУММПРОИЗВ сохранит только ненулевые значения для столбцов B и D. Для справки, вот таблица, показывающая номера столбцов и их соответствующие значения после выбора MOD 2.

Выделите каждую N-ю строку

Еще одно распространенное место использования функции MOD – это когда вы хотите, чтобы выделенная строка отображалась в каждой N-й строке. Общая форма для этого будет

1 = MOD (СТРОКА () ± Смещение, N) = 0

Где N это количество строк между каждой выделенной строкой (т.е., чтобы выделить каждые 3rd ряд, N = 3), и Компенсировать – это необязательно число, которое нам нужно добавить или вычесть, чтобы наша первая выделенная строка выровнялась с N (то есть, чтобы выделить каждые 3rd ряду, но начинаем со строки 5, нам нужно вычесть 2, так как 5-2 = 3). Обратите внимание, что при использовании функции СТРОКА, опуская любые аргументы, она вернет номер строки из ячейки, в которой находится формула.

Давайте воспользуемся нашей таблицей ранее:

Чтобы выделить все строки итогов, мы создадим новое правило условного форматирования с формулой

1 = МОД (СТРОКА () – 1, 3) = 0

Когда условное форматирование применяет эту формулу, в строке 2 будет отображаться

1234 = МОД (2-1; 3) = 0= МОД (1, 3) = 0= 1 = 0= Ложь

Строка 3 получит аналогичный результат, но затем строка 4 увидит

1234 = МОД (4-1; 3) = 0= МОД (3, 3) = 0= 0 = 0= Верно

Таким образом, наше правило работает правильно, как показано здесь:

Выделите целые или четные числа

Вместо того, чтобы выделять определенные строки, вы также можете проверить фактические значения в ячейках. Это может быть полезно, когда вы хотите найти числа, кратные N. Например, чтобы найти числа, кратные 3, ваша формула условного формата будет выглядеть так:

До этого момента мы имели дело с целыми числами. Однако вы можете ввести десятичную дробь (например, 1,234), а затем разделить ее на 1, чтобы получить только десятичную часть (например, 0,234). Эта формула выглядит как

Зная это, чтобы выделить только целые числа, формула условного формата будет

Объедините каждые N ячеек

Ранее мы использовали MOD, чтобы сообщать компьютеру, когда нужно брать значение за каждый N-й элемент. Вы также можете использовать его для запуска более крупной формулы. Рассмотрим этот макет:

Мы хотим объединить имена вместе, но только через каждые 3rd строка, начинающаяся со строки 2. Для этого используется формула

1 = ЕСЛИ (МОД (СТРОКА () + 1, 3) = 0, СЦЕПИТЬ (A2, “”, A3, “”, A4), “”)

Наша функция MOD – это то, что действует как критерий для общей функции IF. В этом примере нам нужно добавить 1 к нашей СТРОКЕ, потому что мы начинаем со строки 2 (2 + 1 = 3). Когда выход MOD равен 0, формула выполняет конкатенацию. В противном случае он просто возвращается пустым.

Подсчет четных / нечетных значений

Если вам когда-либо приходилось подсчитывать, сколько четных или нечетных значений находится в диапазоне, вы знаете, что COUNTIF не может этого сделать. Однако мы можем сделать это с помощью MOD и SUMPRODUCT. Давайте посмотрим на эту таблицу:

Формула, которую мы будем использовать для нахождения нечетных значений, будет

1 = СУММПРОИЗВ (1 * (МОД (A2: A7; 2) = 1))

Вместо того, чтобы загружать некоторые номера строк, наш MOD будет загружать фактические значения ячеек в массив. Общее преобразование будет происходить следующим образом:

1234 {5, 5, 3, 3, 2, 1}{1, 1, 1, 1, 0, 1} <- Взял мод 2{True, True, True, True, False, True} <- Проверено, было ли значение 0{1, 1, 1, 1, 0, 1} <- умножить на 1 для преобразования из True / False в 1/0

Затем СУММПРОИЗВ складывает значения в нашем массиве, давая желаемый ответ: 5.

Повторяющийся узор

Все предыдущие примеры проверяли вывод MOD на предмет значения. Вы также можете использовать MOD для создания повторяющегося шаблона чисел, что, в свою очередь, может быть очень полезно.

Во-первых, предположим, что у нас есть список элементов, которые мы хотим повторить.

Вы можете попробовать скопировать и вставить вручную сколько угодно раз, но это будет утомительно. Вместо этого мы захотим использовать функцию ИНДЕКС для получения наших значений. Чтобы ИНДЕКС работал, нам нужно, чтобы аргумент строки был последовательностью чисел, которая идет {1, 2, 3, 1, 2, 3, 1 и т. Д.}. Мы можем сделать это с помощью MOD.

Во-первых, мы начнем с функции СТРОКА. Если вы начнете с

А затем скопируйте это вниз, вы получите базовую числовую последовательность {1, 2, 3, 4, 5, 6,…}. Если мы применили функцию MOD с 3 в качестве делителя,

мы получим {1, 2, 0, 1, 2, 0,…}. Мы видим, что у нас есть повторяющийся шаблон «0, 1, 2», но в первой серии отсутствует начальный 0. Чтобы исправить это, сделайте резервную копию шага и вычтите 1 из номера строки. Это изменит нашу начальную последовательность на {0, 1, 2, 3, 4, 5,…}

1 = МОД (СТРОКА (A1) -1; 3)

А после выхода из MOD у нас есть {0, 1, 2, 0, 1, 2,…}. Это приближается к тому, что нам нужно. Последний шаг – добавить 1 в массив.

1 = МОД (СТРОКА (A1) -1; 3) +1

Что теперь дает числовую последовательность {1, 2, 3, 1, 2, 3,…}. Это наша желаемая последовательность! Подключив его к функции ИНДЕКС, мы получим нашу формулу

1 = ИНДЕКС (MyList; МОД (СТРОКА (A1) -1; 3) +1)

Теперь результат будет выглядеть так:

Примеры модов в VBA

Вы также можете использовать функцию ЛИНЕЙН в VBA.

В VBA MOD – это оператор (точно так же, как операторы плюс, минус, умножение и деление). Итак, выполнение следующих операторов VBA

123456 Диапазон (“C2”) = Диапазон (“A2”) Диапазон мод. (“B2”)Диапазон (“C3”) = Диапазон (“A3”) Диапазон мод. (“B3”)Диапазон (“C4”) = Диапазон (“A4”) Диапазон мод. (“B4”)Диапазон (“C5”) = Диапазон (“A5”) Диапазон мод (“B5”)Диапазон (“C6”) = Диапазон (“A6”) Диапазон мод. (“B6”)Range (“C7”) = Range (“A7”) Mod Range (“B7”)

даст следующие результаты

Для аргументов функции (известные_y и т. Д.) Вы можете либо ввести их непосредственно в функцию, либо определить переменные, которые будут использоваться вместо них.

Вернуться к списку всех функций в Excel

Google Таблицы MOD Функция

Функция MOD работает в Google Таблицах точно так же, как и в Excel:

Источник


Загрузить PDF


Загрузить PDF

В статистике модой во множестве чисел называется число, которое встречается в этом множестве наиболее часто. Мод может быть несколько: если в наборе данных одинаково часто встречаются два или больше разных числа, его называют соответственно бимодальным или мультимодальным — иными словами, все значения, встречающиеся максимальное число раз, образуют моды данного множества. В данной статье описано, как найти моду (моды) множества.

  1. Изображение с названием Find the Mode of a Set of Numbers Step 1

    1

    Запишите числа множества. Моду обычно определяют на наборе статистических данных или множестве численных значений. Таким образом, для нахождения моды вам понадобится набор чисел. Моду сложно определить в уме, если чисел достаточно много, поэтому в большинстве случаев лучше записать все числа или набрать их на компьютере. Если у вас есть карандаш и бумага, достаточно записать все числа. Если же вы работаете за компьютером, удобнее использовать Excel.

    • Метод определения моды легче понять на примере. Рассмотрим в данном разделе следующий набор чисел: {18, 21, 11, 21, 15, 19, 17, 21, 17}. В приведенных ниже шагах мы найдем моду этого множества.

  2. Изображение с названием Find the Mode of a Set of Numbers Step 2

    2

    Расположите числа в порядке возрастания. После того как вы выпишете все числа, полезно переписать их в порядке возрастания. Хотя можно обойтись и без этого, так найти моду будет проще, поскольку одинаковые числа расположатся рядом. Для больших наборов данных это просто необходимо, так как попытка просмотреть неупорядоченный список и подсчитать, сколько раз каждое число появляется в нем, довольно трудоемка и может привести к ошибкам.

    • Если вы используете карандаш и бумагу, переписывание поможет вам сэкономить время в дальнейшем. Просмотрите числа, найдите наименьшее значение, вычеркните его из первоначального множества и занесите в новый список. Повторите то же самое для второго, затем для третьего наименьшего числа и так далее, при этом записывайте каждое число столько раз, сколько оно встречается в исходном наборе данных.
    • Компьютер предоставляет больше возможностей — например, в большинстве программ для работы с электронными таблицами можно упорядочить список значений от наименьшего к наибольшему всего лишь несколькими щелчками мыши.
    • В нашем примере после упорядочения получаем следующую последовательность чисел: {11, 15, 17, 17, 18, 19, 21, 21, 21}.

  3. Изображение с названием Find the Mode of a Set of Numbers Step 3

    3

    Подсчитайте, сколько раз повторяется каждое число. После того как вы перепишете значения в порядке возрастания, подсчитайте, сколько раз встречается каждое число. Поищите число, которое чаще всего попадается в списке. Если чисел сравнительно немного и они расположены в порядке возрастания, это довольно просто: найдите самую большую группу одинаковых значений и подсчитайте, сколько раз они повторяются.

    • Если вы используете карандаш и бумагу, попробуйте записать над каждой группой одинаковых чисел, сколько раз они повторяются. Если вы пользуетесь компьютерной программой для работы с электронными таблицами, можно поступить подобным образом: запишите результаты подсчетов в соседние ячейки или используйте одну из опций для анализа данных.
    • В нашем списке ({11, 15, 17, 17, 18, 19, 21, 21, 21}) 11 и 15 встречаются по одному разу, 17 попадается дважды, 18 и 19 встречаются по одному разу, а 21 встречается три раза. Таким образом, в данном наборе значений чаще всего встречается число 21.

  4. Изображение с названием Find the Mode of a Set of Numbers Step 4

    4

    Определите значение (или значения), которые встречаются наиболее часто. После того как вы подсчитаете, сколько раз встречается каждое число, найдите значения, которые повторяются наибольшее количество раз. Это и есть мода данного множества. Помните, что набор чисел может иметь не одну, а несколько мод. Если в множестве наиболее часто встречаются два числа (то есть они повторяются одинаковое количество раз), такое множество называют бимодальным, если три числа — тримодальным и так далее.

    • В нашем множестве ({11, 15, 17, 17, 18, 19, 21, 21, 21}) наиболее часто встречается значение 21, поэтому 21 является модой.
    • Если бы кроме 21 нашлось еще одно число, которое также встречается три раза, (например, если бы множество включало еще одно число 17), то оно наряду с 21 было бы модой.

  5. Изображение с названием Find the Mode of a Set of Numbers Step 5

    5

    Не путайте моду множества чисел с его средним значением и медианой. При статистическом анализе часто рассматривают вместе такие понятия, как среднее значение, медиана и мода. Их легко спутать, так как они имеют схожие названия и иногда их значения совпадают. Однако независимо от того, совпадает или нет мода множества с его медианой или средним значением, следует помнить, что это три абсолютно разных понятия (смотрите ниже).

    • Чтобы найти среднее значение множества, следует сложить все числа и поделить на их количество. Для нашего примера ({11, 15, 17, 17, 18, 19, 21, 21, 21}) среднее значение составляет 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160/9 = 17,78. Мы поделили сумму значений на 9, поскольку данное множество состоит из 9 чисел.

      Изображение с названием Find the Mode of a Set of Numbers Step 5Bullet1

    • Медиана представляет собой «среднее число», которое разделяет меньшие и бо́льшие значения множества на две равные половины. Например, для нашего набора значений ({11, 15, 17, 17, 18, 19, 21, 21, 21}) медианой является число 18, так как слева и справа от него стоит по четыре числа. Учтите, что если множество содержит четное количество чисел, оно не имеет единственной медианы. В этом случае медианой обычно считают среднее значение тех двух чисел, которые расположены посередине.

      Изображение с названием Find the Mode of a Set of Numbers Step 5Bullet2

    Реклама

  1. Изображение с названием Find the Mode of a Set of Numbers Step 6

    1

    Множество не имеет моды, если каждое значение встречается в нем одинаковое число раз. Если все значения в данном наборе чисел попадаются одинаковое количество раз, то у этого множества нет моды, поскольку ни одно число не встречается чаще, чем любое другое. Например, моды не имеют те множества, в которые каждое число входит по одному разу. Это же касается тех множеств, в которых каждое число встречается дважды, трижды и так далее.

    • Если мы изменим набор чисел в нашем примере на {11, 15, 17, 18, 19, 21}, так чтобы каждое значение встречалось лишь один раз, то он не будет иметь моды. То же верно и для множества, в котором все числа встречаются дважды, например {11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21}.

  2. Изображение с названием Find the Mode of a Set of Numbers Step 7

    2

    Помните, что моду нечислового набора данных можно определить точно так же, как для числовых множеств. Как правило, большинство наборов данных являются «количественными», то есть содержат данные в виде чисел. Тем не менее встречаются и такие множества, члены которых выражены не в виде чисел. В таких случаях можно сказать, что «мода» — это то значение, которое встречается чаще всего в наборе данных (как и для числовых множеств).[1]
     При этом определить моду будет возможно, в то время как медиану или среднее значение — нельзя.

    • Предположим, при осмотре небольшого участка земли определили вид каждого растущего на нем дерева. Получился следующий список: {кедр, ольха, кедр, сосна, кедр, кедр, ольха, ольха, сосна, кедр}. Такой набор данных называют номинальным, поскольку входящие в него члены представляют собой названия. В этом случае модой является кедр, так как данное слово встречается чаще других (пять раз), в то время как ольха и сосна встречаются соответственно три и два раза.
    • В рассмотренном выше примере невозможно найти среднее значение и медиану, так как набор данных содержит не числа, а названия.

  3. Изображение с названием Find the Mode of a Set of Numbers Step 8

    3

    При одномодальном симметричном распределении мода, среднее значение и медиана совпадают. Как отмечалось выше, в некоторых случаях мода, медиана и/или среднее значение могут совпадать. В частности, если плотность распределения того или иного набора данных образует идеально симметричную кривую с одной модой (например, гауссиану или колоколообразную кривую), мода, среднее значение и медиана равны друг другу. Плотность распределения отображает относительную частоту определенных значений, поэтому мода будет находиться точно посередине симметричной кривой распределения, так как эта самая высокая точка на графике соответствует наиболее распространенному значению. Поскольку набор данных симметричен, эта точка на графике будет соответствовать также медиане (центральной точке в наборе данных) и среднему значению.

    • В качестве примера рассмотрим набор чисел {1, 2, 2, 3, 3, 3, 4, 4, 5}. Если мы отложим эти значения на графике, то получим симметричную кривую, которая достигает максимальной высоты 3 при x = 3 и опускается до 1 при x = 1 и x = 5. Значение 3 встречается чаще всего, поэтому оно является модой. Так как 3 расположено в центре и по обе стороны от него находится четыре числа, оно является также медианой. И наконец, среднее значение данного множества составляет 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3, то есть число 3 является также средним значением.
    • Исключение из этого правила составляют симметричные множества с более чем одной модой — они имеют по одной медиане и среднему значению, с которыми не совпадают несколько мод.

    Реклама

Советы

  • Набор данных может иметь несколько мод.
  • Если все числа встречаются лишь по одному разу, множество не имеет моды.

Реклама

Что вам понадобится

  • Бумага, карандаш и ластик

Об этой статье

Эту страницу просматривали 47 353 раза.

Была ли эта статья полезной?

Источник

Improve Article

Save Article

Like Article

  • Read
  • Discuss

    • Improve Article

    Save Article

    Like Article

    Given a big number ‘num’ represented as string and an integer x, find value of “num % a” or “num mod a”. Output is expected as an integer.

    Examples : 

    Input:  num = "12316767678678",  a = 10
Output: num (mod a) ≡ 8

    The idea is to process all digits one by one and use the property that 

    xy (mod a) ≡ ((x (mod a) * 10) + (y (mod a))) mod a

    where, x : left-most digit

    y: rest of the digits except x.

    for example: 

    625 % 5 = (((6 % 5)*10) + (25 % 5)) % 5 = 0

    Below is the implementation.

    Thanks to utkarsh111 for suggesting the below solution.

    C++

    #include <iostream>

    using namespace std;

    int mod(string num, int a)

    {

        int res = 0;

        for (int i = 0; i < num.length(); i++)

            res = (res * 10 + num[i] - '0') % a;

        return res;

    }

    int main()

    {

        string num = "12316767678678";

        cout << mod(num, 10);

        return 0;

    }

    Java

    import java.io.*;

    class GFG {

        static int mod(String num, int a)

        {

            int res = 0;

            for (int i = 0; i < num.length(); i++)

                res = (res * 10 + num.charAt(i) - '0') % a;

            return res;

        }

        public static void main(String[] args)

        {

            String num = "12316767678678";

            System.out.println(mod(num, 10));

        }

    }

    Python3

    def mod(num, a):

        res = 0

        for i in range(0, len(num)):

            res = (res * 10 + int(num[i])) % a

        return res

    num = "12316767678678"

    print(mod(num, 10))

    C#

    using System;

    public class GFG {

        static int mod(String num, int a)

        {

            int res = 0;

            for (int i = 0; i < num.Length; i++)

                res = (res * 10 + num[i] - '0') % a;

            return res;

        }

        public static void Main()

        {

            String num = "12316767678678";

            Console.WriteLine(mod(num, 10));

        }

    }

    PHP

    <?php

    function mod($num, $a)

    {

        $res = 0;

        for ($i = 0; $i < $r = strlen($num); $i++)

            $res = ($res * 10 +

                    $num[$i] - '0') % $a;

        return $res;

    }

    $num = "12316767678678";

    echo mod($num, 10);

    ?>

    Javascript

    <script>

    function mod(num, a)

    {

        let res = 0;

        for(let i = 0; i < num.length; i++)

            res = (res * 10 +

                parseInt(num[i])) % a;

        return res;

    }

    let num = "12316767678678";

    document.write(mod(num, 10));

    </script>

    Time Complexity : O(|num|)

    • Time complexity will become size of num string as we are traversing once in num.

    Auxiliary Space: O(1)

    Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
     

    Last Updated :
    10 Apr, 2023

    Like Article

    Save Article

    Источник

    Время на прочтение
    4 мин

    Количество просмотров 230K

    Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!

    Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.

    Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.

    В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»

    Позовите ребят из секты «mod не остаток»! Это для вас.

    Что такое mod?

    Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.

    Термин mod означает операцию modulo, с модулем 2 в данном случае. Большинство языков программирования используют % для обозначения такой операции: 5 % 2 = 1.

    Вот где мы попадаем в странную серую область.

    Математика циферблата

    Помню, как учил это в школе, а потом забыл. Существует тип математики, называемый «модульной арифметикой», которая имеет дело с циклическими структурами. Самый простой способ представить это — циферблат с циклом 12. Для математика циферблат — это mod 12. Если хотите понять, можно ли равномерно разделить 253 часа на дни, то можете применить операцию 253 mod 24, результатом будет 13, поэтому ответ «нет»! Мы можем ответить «да» только если результат 0.

    Другой вопрос, который вы можете задать: «Если я выеду в 6 вечера, сколько времени будет по приезду через 16 часов?». Это будет 6 + 16 mod 12, то есть 10.

    Криптографы любят mod, потому что при использовании с действительно большими числами можно создать нечто, известное как «односторонние функции». Это специальные функции, которые позволяют легко вычислить что-то в одном направлении, но не в обратном.

    Если я скажу вам, что 9 является результатом возведения в квадрат, вы можете легко определить, что на входе было 3. Перед вами весь процесс от начала до конца. Если я скажу, что 9 является результатом mod 29, то будет сложнее понять, что на входе.

    Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.

    Впрочем, не будем отклоняться от темы.

    Остатки и математика циферблата

    Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.

    Рассмотрим такую задачу: 

    const x = 19 % 12;
console.log(x);

    Каково значение x? Делим числа и получаем 7 как остаток от 12. Это верный ответ. Как насчет такого:

    const y = 19 % -12;
console.log(y);

    Используя обычную математику, мы можем умножить -12 на -1, что даёт 12, и у нас по-прежнему остаётся 7, поэтому наш ответ снова 7.

    JavaScript с этим согласен:

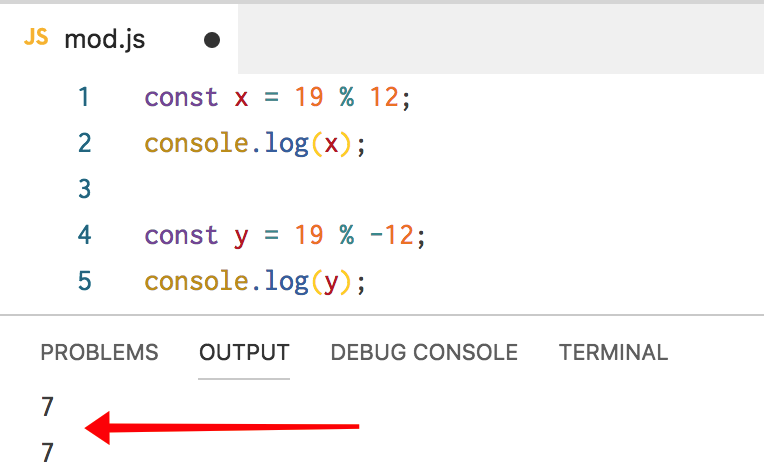
    C# тоже согласен:

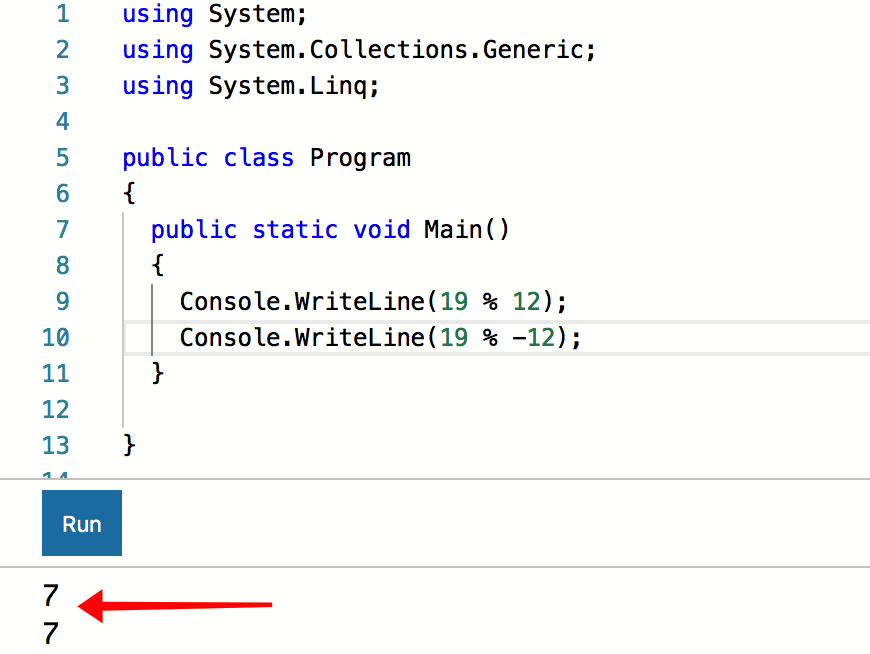
    Google согласен с первым утверждением, но не согласен со вторым:

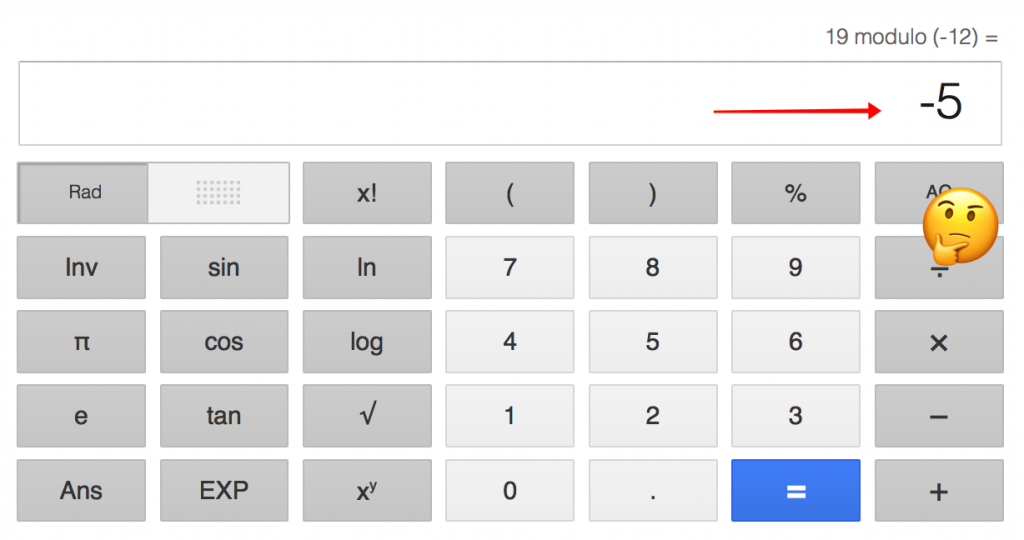
    Ruby согласен с Google:

    Во имя Дейкстры, что здесь происходит?

    Вращение часов назад

    Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.

    Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:

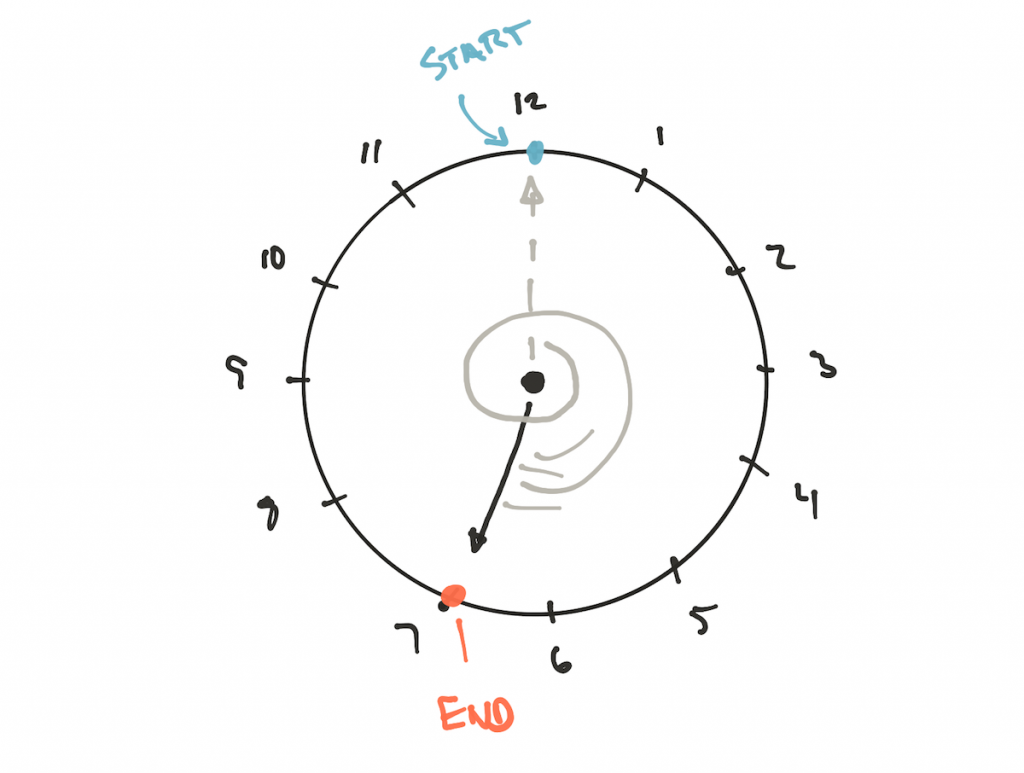
    Конечный результат 7. Мы это знаем и мы можем доказать математически. Но что насчёт 19 mod -12? Здесь нужно использовать другие часы:

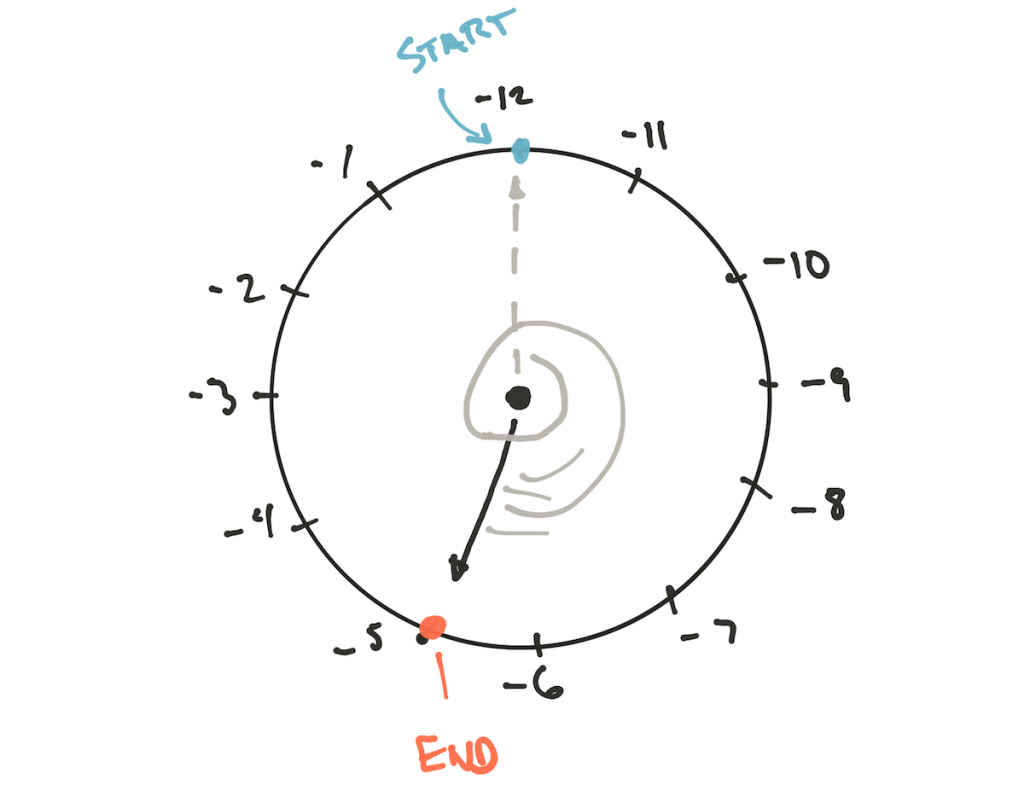
    Модуль равен -12, и мы не можем игнорировать или изменить его, умножив на -1, поскольку модульная арифметика так не работает. Единственный способ правильно рассчитать результат — переставить метки на часах так, чтобы мы двигались от -12 или вращали часы против часовой стрелки, что даёт тот же результат.

    Почему не начать метки с -1, двигаясь к -2, и т.д.? Потому что в таком случае мы будем двигаться назад и постоянно уменьшать результат, пока не достигнем -12, и в этот момент сделаем прыжок +12, а modulo так не работает.

    Это известная вещь

    Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:

    Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.

    Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:

    Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.

    А как на вашем языке?

    Ну и что?

    Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:

    1. Я представляю, как этот вопрос займёт меня врасплох на собеседовании.
    2. Я представляю, как этот попадёт в продакшн, а разработчики будут несколько часов выяснять, почему математика не работает.

    Это также забавный факт на случай, если рядом появится ваш педантичный друг-программист.

    Источник

    Добавить комментарий