
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Сумма тангенсов
Примеры решения задач
ПРИМЕР 1
| Задание | Проверить, что |
| Доказательство |
Применим формулу суммы тангенсов
Представим т.е. Что и требовалось доказать. |

| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.
Формулы тангенса суммы и разности углов устанавливают соотношение между тангенсом общей суммы или разности аргументов и тангенсами отдельных аргументов — слагаемых.
При всех допустимых значениях аргументов справедливы формулы:
тангенса суммы аргументов:
tg(α+β)=tgα+tgβ1−tgα⋅tgβ
; (1)
тангенса разности аргументов:
tg(α−β)=tgα−tgβ1+tgα⋅tgβ
. (2)
Оговорка о допустимых значениях аргументов означает, что все тангенсы имеют смысл, т. е. выполняются условия:
, для формулы (1),
α−β≠π2+πm,m∈ℤ
, для формулы (2).
Эти формулы очень важны и широко применяются не только в математике, но и в физике — особенно в радиотехнике.
Вывод формул естественным образом получается из определения функции тангенса и использования уже известных формул синуса и косинуса суммы и разности аргументов.
Докажем формулу тангенса суммы аргументов. Имеем:
.
Разделим каждое из слагаемых числителя и знаменателя на
cosα⋅cosβ
,
учитывая, что значение дроби от этого не изменится и что
cosα⋅cosβ≠0
из принятых выше условий
для допустимых значений аргументов, т. е.
α≠π2+πk,β≠π2+πnk,n∈ℤ
. Тогда:
tg(α+β)=sin(α+β)cos(α+β)=sinα⋅cosβ+cosα⋅sinβcosα⋅cosβ−sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ+cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ−sinα⋅sinβcosα⋅cosβ=tgα+tgβ1−tgα⋅tgβ
— что и требовалось доказать.
Аналогично доказывается формула тангенса разности аргументов:
tg(α−β)=sin(α−β)cos(α−β)=sinα⋅cosβ−cosα⋅sinβcosα⋅cosβ+sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ−cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ+sinα⋅sinβcosα⋅cosβ=tgα−tgβ1+tgα⋅tgβ.
Сумма тангенсов
ОПРЕДЕЛЕНИЕ
Сумма тангенсов двух углов (
alpha
) и (
beta
) равна отношению синуса суммы (
alpha+beta
) к произведению косинусов этих углов:
(
operatorname{tg} alpha+operatorname{tg} beta=frac{sin (alpha+beta)}{cos alpha cdot cos beta}
)
Примеры решения задач
ПРИМЕР 1
Проверить, что (
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)
Применим формулу суммы тангенсов
(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=frac{sin left(15^{circ}+60^{circ}right)}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}
)
Представим (
cos 15^{circ}
) в (
cos 15^{circ}=cos left(90^{circ}-75^{circ}right)=sin 75^{circ}
) и подставим в предыдущее равенство: (
frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{sin 75^{circ} cos 60^{circ}}=frac{1}{cos 60^{circ}}=2
)
т.е.
(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)
ПРИМЕР 2
Найти значение выражения (
operatorname{tg}^{3 pi}+operatorname{tg} frac{pi}{8}
)
Представим сумму разность в виде
(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=frac{sin left(frac{3 pi}{8}+frac{pi}{8}right)}{cos frac{3 pi}{8} cdot cos frac{pi}{8}}=frac{sin frac{pi}{2}}{frac{1}{2}left(cos frac{pi}{4}+cos frac{pi}{2}right)}=frac{1}{frac{1}{2}left(frac{sqrt{2}}{2}+0right)}=frac{4}{sqrt{2}}=2 sqrt{2}
)
(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=2 sqrt{2}
)
Содержание:
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен 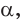
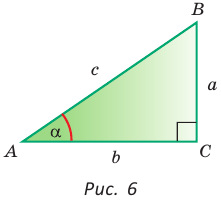
Определения синуса, косинуса, тангенса и котангенса острого угла
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
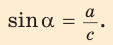
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
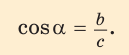
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
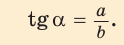
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
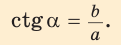
Пример:
Угол К в 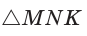 равен 90° (рис. 7).
равен 90° (рис. 7).
Тогда:
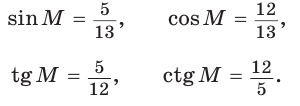
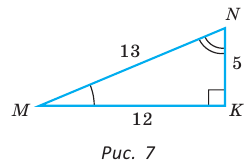
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
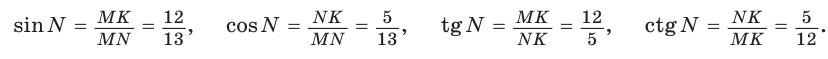
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 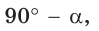 равны, т. е.
равны, т. е. 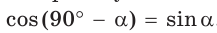 . Так же
. Так же 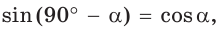
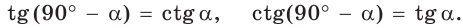 Например,
Например, 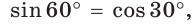
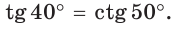
А теперь выполните Тест 1 и Тест 2.
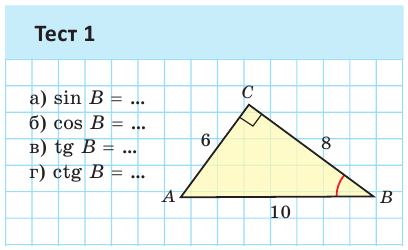
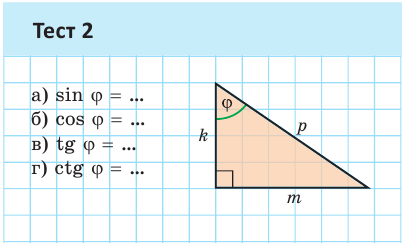
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
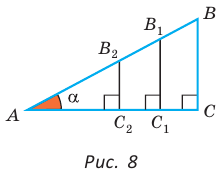
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в  (рис. 8)
(рис. 8) 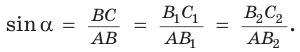
Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
Рассмотрим прямоугольный треугольник АВС, у которого 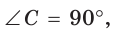
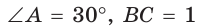 (рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
(рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
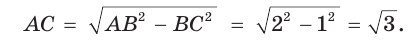 Тогда:
Тогда:
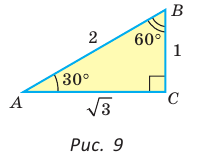
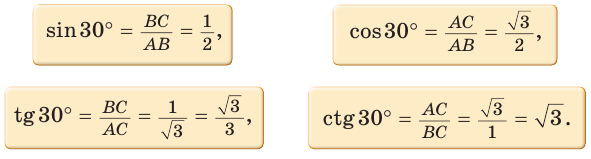
Так как 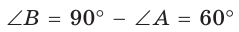 (см. рис. 9), то
(см. рис. 9), то

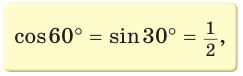
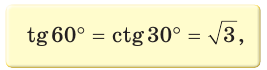
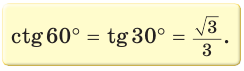
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 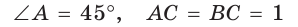 (рис. 10). По теореме Пифагора
(рис. 10). По теореме Пифагора
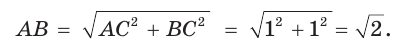
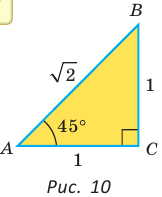
Тогда:
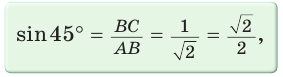
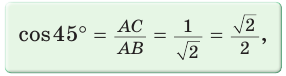
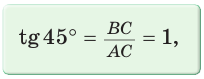
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
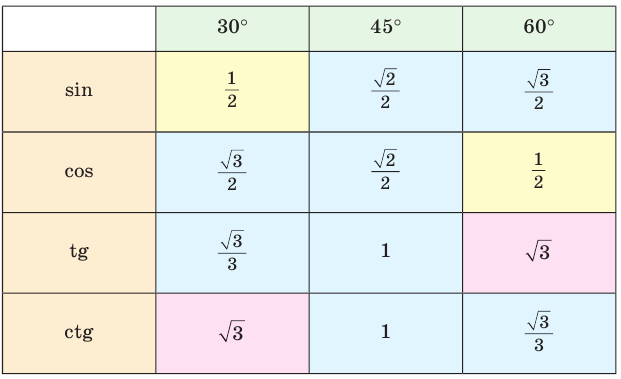
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 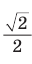 . а приближенное — 0,7071.
. а приближенное — 0,7071.
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно  . На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
. На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
А теперь выполните Тест 3.

Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 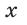 соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так:
соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так: 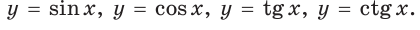
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 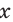 справедливо:
справедливо: 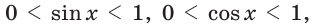 следовательно синус и косинус острого угла положительны и меньше 1.
следовательно синус и косинус острого угла положительны и меньше 1.
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
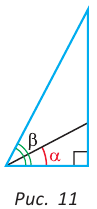
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 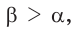 то
то
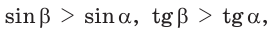 но
но 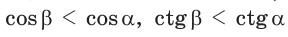 (cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
(cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
Пример №1
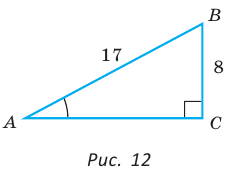
В прямоугольном треугольнике АВС, где 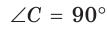 , катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
, катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
Решение:
По теореме Пифагора найдем катет 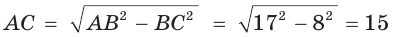 (см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда
(см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда 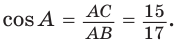
Ответ: 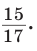
Пример №2
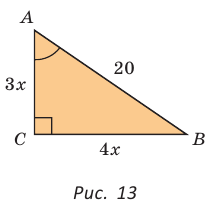
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 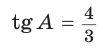 (рис. 13). Найти площадь треугольника.
(рис. 13). Найти площадь треугольника.
Решение:
Так как 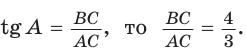 Обозначим
Обозначим 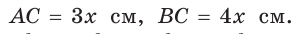 По теореме Пифагора
По теореме Пифагора 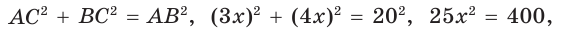
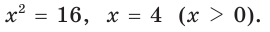 Тогда
Тогда 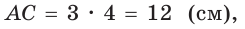 ВС = 4 • 4 = 16(см),
ВС = 4 • 4 = 16(см), 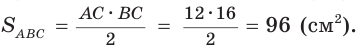
Ответ: 96 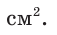
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен 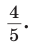
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен 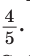
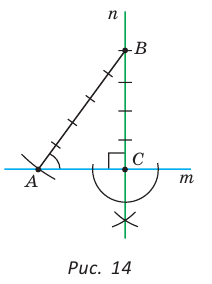
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую 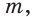 отмечаем на ней точку С и строим прямую
отмечаем на ней точку С и строим прямую 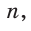 проходящую через точку С перпендикулярно прямой
проходящую через точку С перпендикулярно прямой 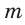 (вспомните по рисунку алгоритм построения). 2) На прямой
(вспомните по рисунку алгоритм построения). 2) На прямой 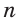 от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой
от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой 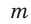 получаем точку А.
получаем точку А.
Угол ВАС — искомый.
Доказательство:
Из 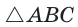 находим
находим 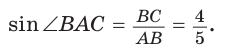
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
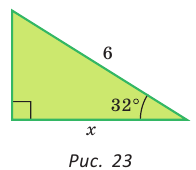
Решение:
Примем длину искомого катета за 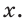
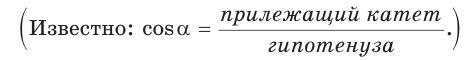
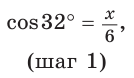


Ответ: 5,1.
Пример №5
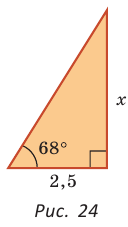
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за 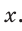
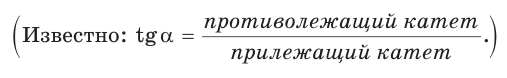
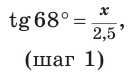
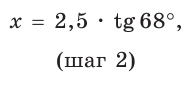

Ответ: 6,2.
Пример №6
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за 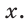
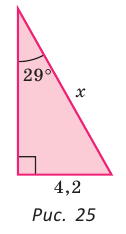
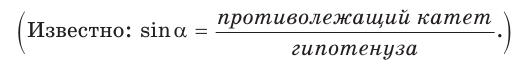
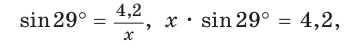
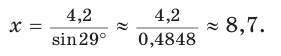
Ответ: 8,7.
Правила решения прямоугольного треугольника
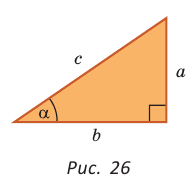
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
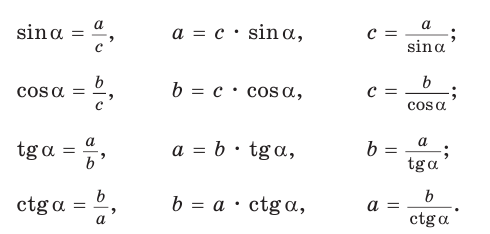
Удобно пользоваться следующими правилами:
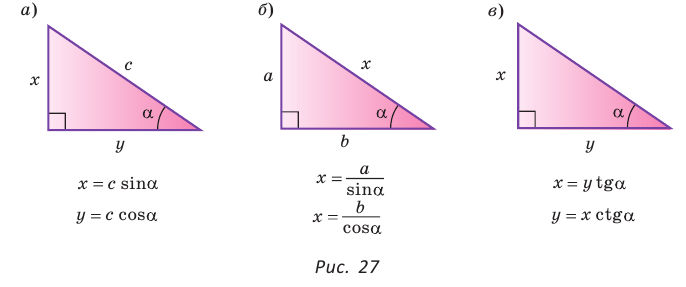
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 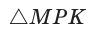 известно:
известно: 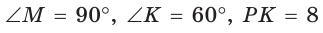 (рис. 28).
(рис. 28).
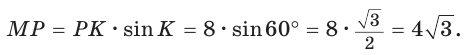
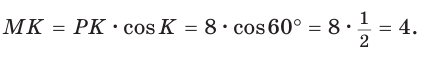
Полезно запомнить!
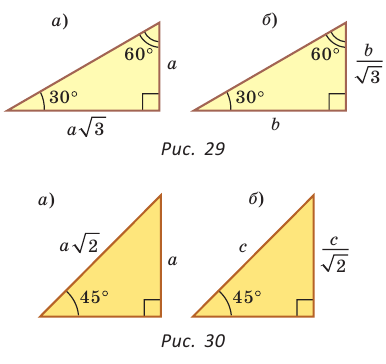
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 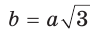 (рис. 29, а). А если дан больший катет
(рис. 29, а). А если дан больший катет 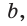 то меньший катет
то меньший катет 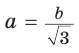 (рис. 29, б).
(рис. 29, б).
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 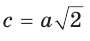 (рис. 30, а), а если дана гипотенуза с, то катет
(рис. 30, а), а если дана гипотенуза с, то катет 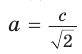 (рис. 30, б).
(рис. 30, б).
Пример №8
В прямоугольном треугольнике АВС известно: 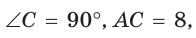
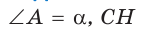 — высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
— высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
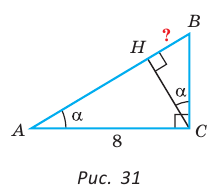
Решение:
Заметим, что 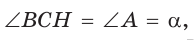 так как эти углы дополняют
так как эти углы дополняют 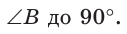 Из
Из 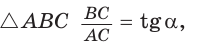
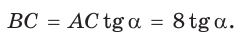 Из
Из 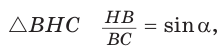
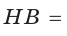
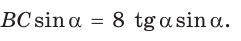
Ответ: 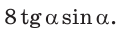
Пример №9
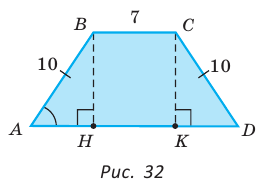
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 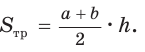 Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим:
Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим: 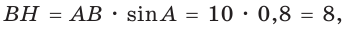 откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда
откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда 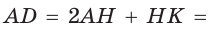
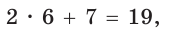
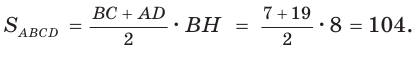
Ответ: 104.
Тригонометрические формулы
Используя формулы 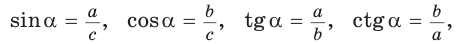 где
где 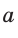 и
и 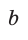 — катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
— катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
1. Основное тригонометрическое тождество
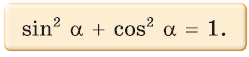
Доказательство:
По теореме Пифагора 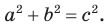
Тогда 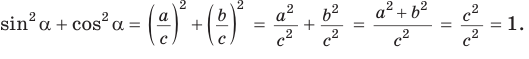
Следствие:
Так как синус и косинус острого угла а положительны, то
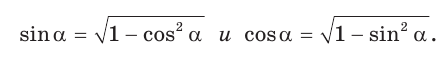
2. Выражение тангенса и котангенса через синус и косинус
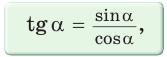
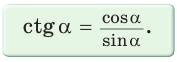
Доказательство:
a)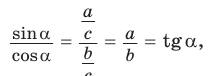 б)
б)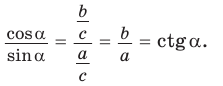
Следствие:
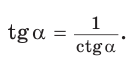
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 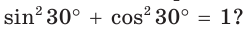 Да, это верно, так как
Да, это верно, так как 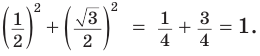
3. Основная задача
Дано: 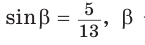 — острый угол.
— острый угол.
Найти: 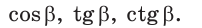
Решение:
Способ 1. Используем основное тригонометрическое тождество: 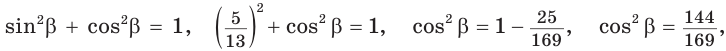
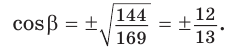 Так как косинус острого угла больше нуля, то
Так как косинус острого угла больше нуля, то 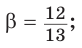 откуда
откуда 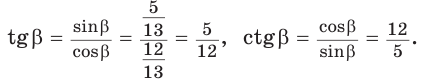
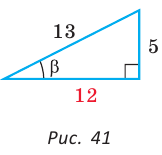
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 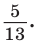 Поэтому этот угол равен
Поэтому этот угол равен 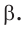 По теореме Пифагора другой катет равен
По теореме Пифагора другой катет равен 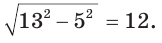 Тогда
Тогда 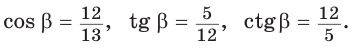
Способ 3. Пусть катет, противолежащий углу 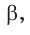 равен 5х, тогда гипотенуза равна
равен 5х, тогда гипотенуза равна 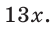 По теореме Пифагора прилежащий катет равен
По теореме Пифагора прилежащий катет равен 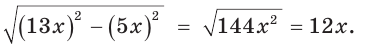 Отсюда
Отсюда 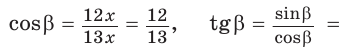
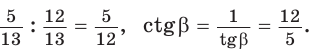
Ответ: 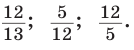
Пример №10
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 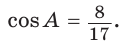 . Найти периметр параллелограмма.
. Найти периметр параллелограмма.
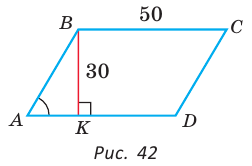
Решение:
Из треугольника АВК находим: 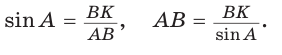 Из основного тригонометрического тождества следует:
Из основного тригонометрического тождества следует: 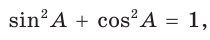
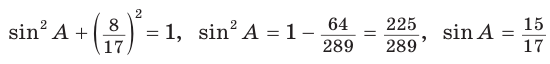 (так как угол А — острый, то sinA > 0). Тогда
(так как угол А — острый, то sinA > 0). Тогда 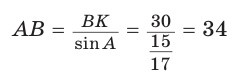 (см )
(см ) 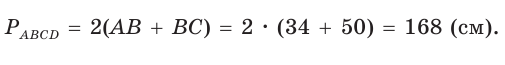
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
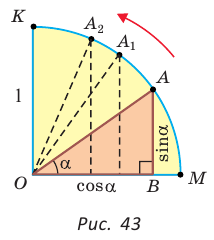
Решение:
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 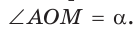 Опустим из точки А перпендикуляр АВ на ОМ. Тогда
Опустим из точки А перпендикуляр АВ на ОМ. Тогда 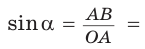
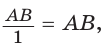
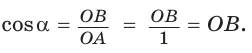 При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол
При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол 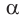 будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы:
будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы: 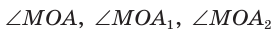 и т. д.). Величина катета АВ, противолежащего углу
и т. д.). Величина катета АВ, противолежащего углу 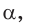 будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
Из формулы 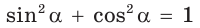 также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
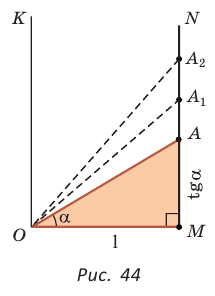
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 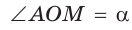 (рис. 44). По определению
(рис. 44). По определению 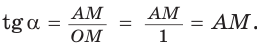 Угол
Угол 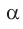 станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки
станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки 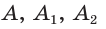 и т. д. При этом угол
и т. д. При этом угол 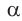 и его тангенс начнут возрастать. Таким образом, когда угол
и его тангенс начнут возрастать. Таким образом, когда угол 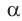 при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
К такому же выводу можно прийти, рассматривая формулу 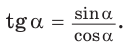 При увеличении угла
При увеличении угла 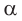 от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
Пример №12
В основании прямоугольного параллелепипеда 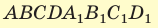 лежит квадрат, диагональ которого
лежит квадрат, диагональ которого 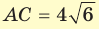 см. Диагональ
см. Диагональ 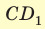 боковой грани составляет с ребром основания
боковой грани составляет с ребром основания 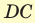 угол
угол  (рис. 46). Найдите объем параллелепипеда.
(рис. 46). Найдите объем параллелепипеда.
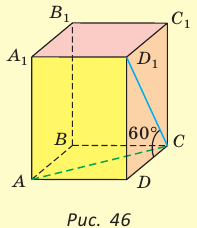
Решение:
Объем прямоугольного параллелепипеда находится по формуле 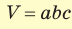 , где а, b и с — его измерения. Так как ABCD — квадрат, то
, где а, b и с — его измерения. Так как ABCD — квадрат, то 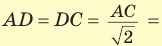
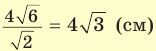 . Из прямоугольного треугольника
. Из прямоугольного треугольника 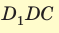 находим
находим 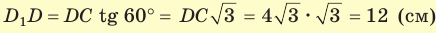 . Искомый объем
. Искомый объем 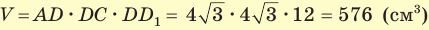 .
.
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 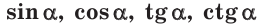 для любого угла а от 0° до 180°
для любого угла а от 0° до 180°
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси 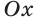 против часовой стрелки отложим острый угол
против часовой стрелки отложим острый угол 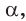 сторона которого пересекает полуокружность в точке
сторона которого пересекает полуокружность в точке 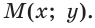 . Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем:
. Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем: 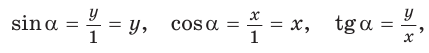
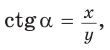 то есть синус, косинус,
то есть синус, косинус,
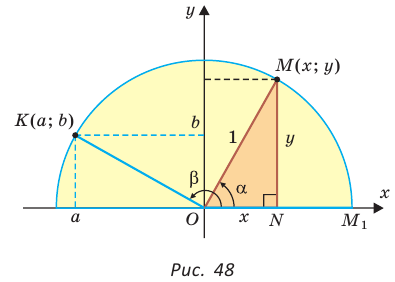
тангенс и котангенс острого угла а выражаются через координаты 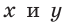 точки
точки 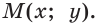 Точно так же определяются значения
Точно так же определяются значения 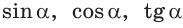 и
и 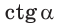 для любого угла а из промежутка
для любого угла а из промежутка 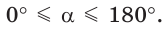 Таким образом, синусом угла а называется ордината
Таким образом, синусом угла а называется ордината 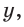 косинусом — абсцисса
косинусом — абсцисса 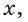 тангенсом — отношение ординаты к абсциссе
тангенсом — отношение ординаты к абсциссе 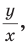 а котангенсом — отношение абсциссы к ординате
а котангенсом — отношение абсциссы к ординате 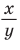 точки М единичной полуокружности.
точки М единичной полуокружности.
Например, для тупого 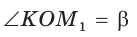 (рис. 48), где
(рис. 48), где 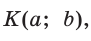 получим:
получим:
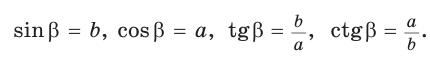
Для любого положения точки 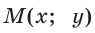 на единичной полуокружности верно равенство
на единичной полуокружности верно равенство 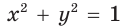 (докажите самостоятельно). Поэтому для углов
(докажите самостоятельно). Поэтому для углов 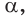 где
где  верно основное тригонометрическое тождество
верно основное тригонометрическое тождество 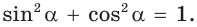
Также верны тождества: 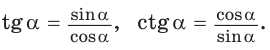
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
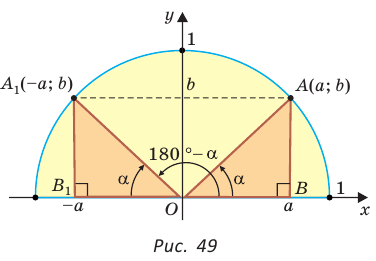
Пусть 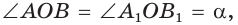 откуда
откуда 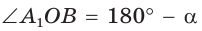 (рис. 49). Так как
(рис. 49). Так как 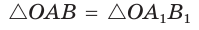 по гипотенузе и острому углу, то
по гипотенузе и острому углу, то 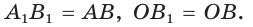 Точки
Точки 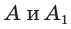 имеют координаты:
имеют координаты: 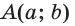 и
и 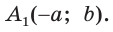 Тогда
Тогда 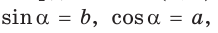
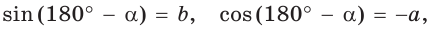 то есть для углов от 0° до 180° справедливы равенства:
то есть для углов от 0° до 180° справедливы равенства:
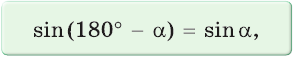
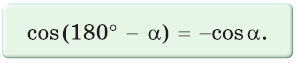
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1. 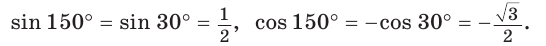
Разделив почленно равенство 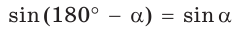 на равенство
на равенство 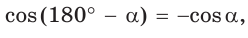 а затем наоборот, получим равенства:
а затем наоборот, получим равенства:
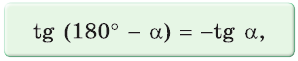
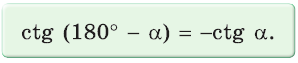
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2. 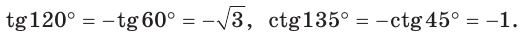
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
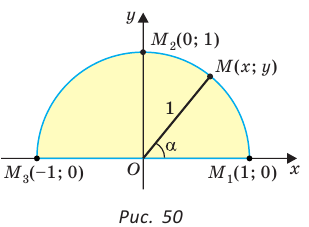
Если луч ОМ совпадет с лучом 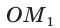 (рис. 50), то будем считать, что
(рис. 50), то будем считать, что 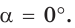 Тогда:
Тогда:
а) 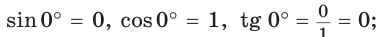 значение
значение 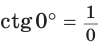 не определено, так как деление на нуль невозможно;
не определено, так как деление на нуль невозможно;
б) 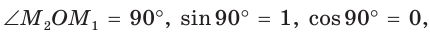
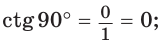 значение
значение 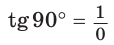 не определено, так как деление на нуль невозможно; в)
не определено, так как деление на нуль невозможно; в) 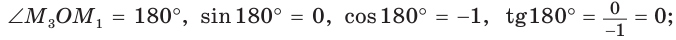 значение
значение 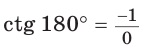 не определено, так как деление на нуль невозможно.
не определено, так как деление на нуль невозможно.
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 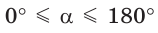 справедливы неравенства:
справедливы неравенства: 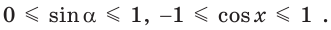
Пример №13
Найти 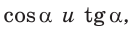 если
если 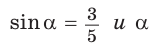 – тупой угол.
– тупой угол.
Решение:
Способ 1. Так как 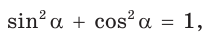 то
то 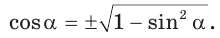 Поскольку угол
Поскольку угол 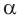 — тупой, то его косинус отрицательный. Поэтому
— тупой, то его косинус отрицательный. Поэтому 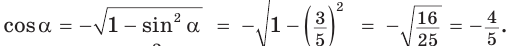 Тогда
Тогда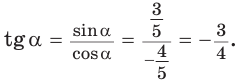
Способ 2. Синус острого угла 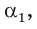 смежного с данным тупым углом
смежного с данным тупым углом 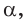 равен также
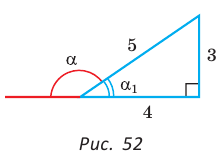
равен также 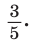 Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем
Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем 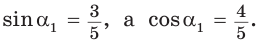 Так как косинусы смежных углов противоположны, то
Так как косинусы смежных углов противоположны, то 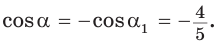 . Аналогично,
. Аналогично, 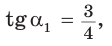
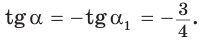
Ответ: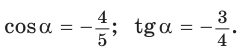
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е. 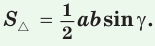
Доказательство:
Пусть в треугольнике 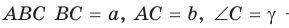 — острый,
— острый, 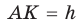 — высота (рис. 56, а).
— высота (рис. 56, а).
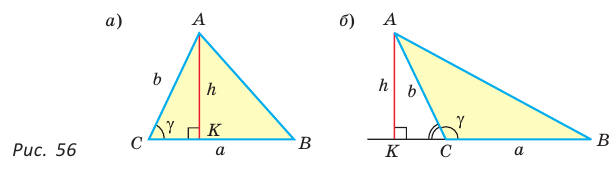
Из прямоугольного треугольника 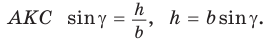 Тогда
Тогда 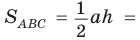
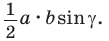
Если угол 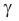 тупой (рис. 56,
тупой (рис. 56, 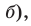 то
то 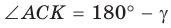 — острый. Из прямоугольного треугольника АКС следует, что
— острый. Из прямоугольного треугольника АКС следует, что 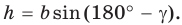 Так как
Так как 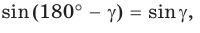 то
то 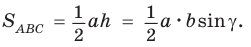
Если 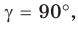 то
то 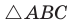 — прямоугольный с катетами
— прямоугольный с катетами 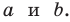 Учитывая, что
Учитывая, что  получим:
получим: 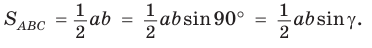
Теорема доказана.
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е. 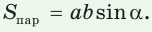
Используя рисунок 57, докажите эту теорему самостоятельно.
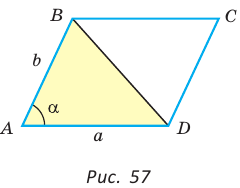
Замечание. Если 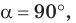 то параллелограмм является прямоугольником. Его площадь
то параллелограмм является прямоугольником. Его площадь 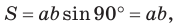 так как
так как  Таким образом, формула площади прямоугольника
Таким образом, формула площади прямоугольника 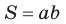 — частный случай формулы площади параллелограмма
— частный случай формулы площади параллелограмма 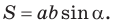

Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
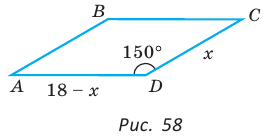
Решение:
Полупериметр параллелограмма равен 18 см. Если 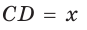 см, то
см, то 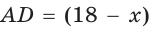 см.
см.
Тогда
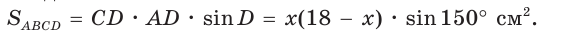
Так как 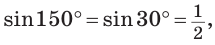 то
то 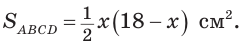
По условию 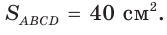 Составим и решим уравнение:
Составим и решим уравнение: 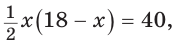
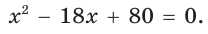 По теореме Виета (обратной)
По теореме Виета (обратной) 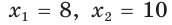 — корни.
— корни.
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е. 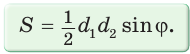
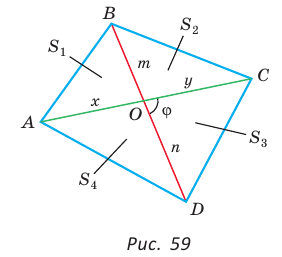
Доказательство:
Пусть диагонали 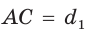 и
и 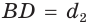 четырехугольника ABCD (рис. 59) пересекаются в точке О,
четырехугольника ABCD (рис. 59) пересекаются в точке О, 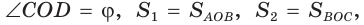
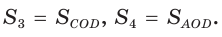 Докажем, что
Докажем, что 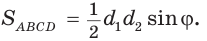
Обозначим 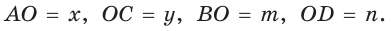 Заметим, что
Заметим, что 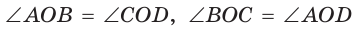 как вертикальные,
как вертикальные, 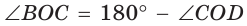 по свойству смежных углов. Поэтому
по свойству смежных углов. Поэтому 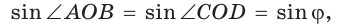
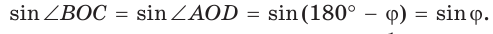 По формуле площади треугольника
По формуле площади треугольника 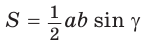 у получим:
у получим:
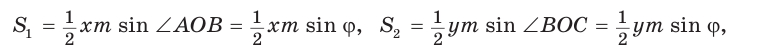
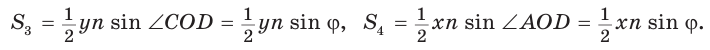
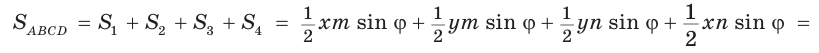
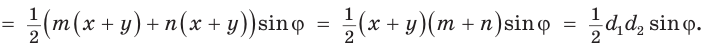
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 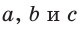 выполняется пропорция
выполняется пропорция 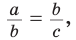 то число
то число 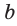 называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции
называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции 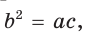 откуда
откуда 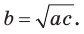 В такой форме записи число
В такой форме записи число 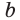 еще называют средним геометрическим чисел а и с.
еще называют средним геометрическим чисел а и с.
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 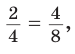 или
или 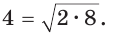
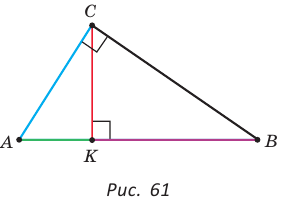
В прямоугольном треугольнике АВС, где 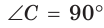 , проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
, проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 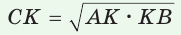 (см. рис. 61).
(см. рис. 61).
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е. 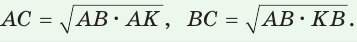
Доказательство:
а)3аметим, что если 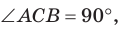
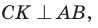 то
то 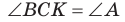 (эти углы дополняют
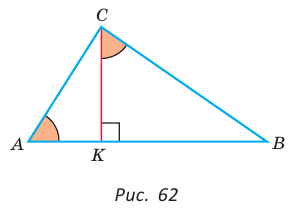
(эти углы дополняют 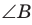 до 90°) (рис. 62). Из
до 90°) (рис. 62). Из 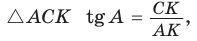 из
из 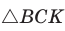
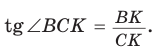 Отсюда
Отсюда 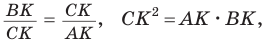
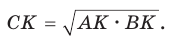
б) Из 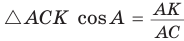 , из
, из 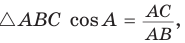 откуда
откуда 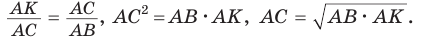
Аналогично доказывается, что 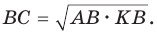 Теорема доказана.
Теорема доказана.
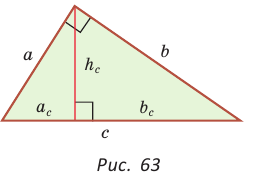
Обозначив катеты 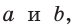 гипотенузу с, высоту
гипотенузу с, высоту 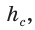 проекции катетов на гипотенузу
проекции катетов на гипотенузу 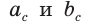 (рис. 63), получим следующие формулы:
(рис. 63), получим следующие формулы:
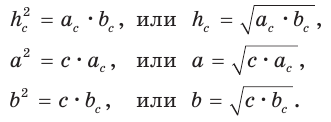
Пример №17
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
Пусть СН — высота прямоугольного треугольника АВС 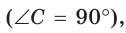 АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то 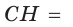
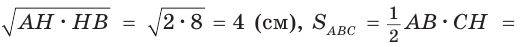
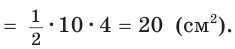
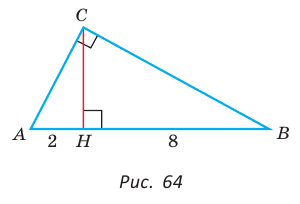
Ответ: 20 см2.
Пример №18
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 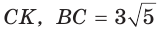 см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
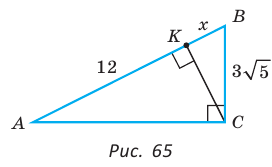
Решение:
Пусть 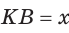 см, тогда
см, тогда 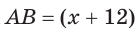 см.
см.
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 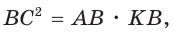 т. е.
т. е. 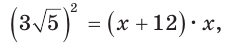
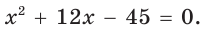 По теореме Виета (обратной)
По теореме Виета (обратной) 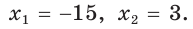 По смыслу задачи
По смыслу задачи 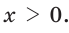 Значит, КВ = 3 см, АВ = 15 см.
Значит, КВ = 3 см, АВ = 15 см.
Ответ: 15 см.
Пример №19
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок 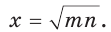
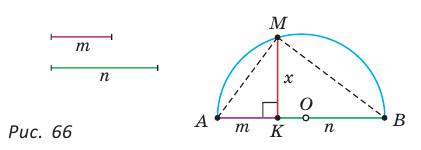
Построение.
1) На произвольной прямой откладываем данные отрезки: 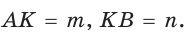
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 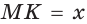 — среднее пропорциональное отрезков
— среднее пропорциональное отрезков 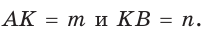
Доказательство:
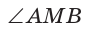 — прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу
— прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу 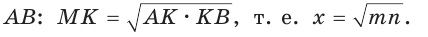
Повторение*
В 8-м классе мы доказали следующую теорему:
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 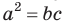 (рис. 70).
(рис. 70).
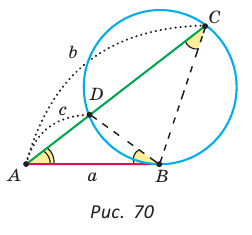
Как видим, отрезок 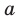 является средним пропорциональным между отрезками
является средним пропорциональным между отрезками 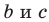 секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
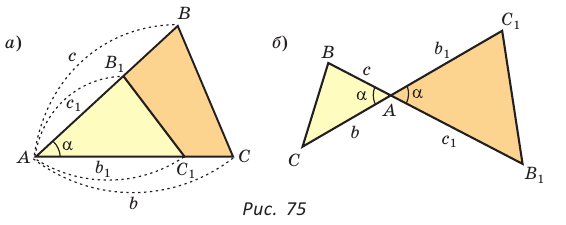
Теорема о площадях треугольников с общим (равным) углом
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е. 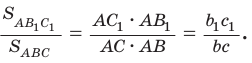
Доказательство:
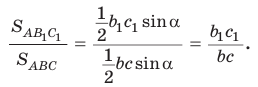
Следствие: Верно:
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти 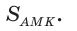
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
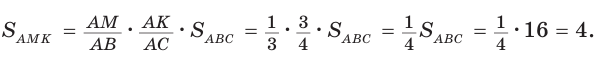
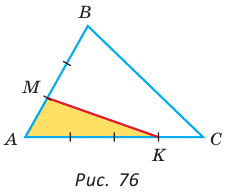
Способ 2. 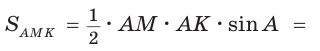
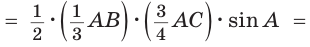
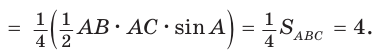
Ответ: 4.
Теорема Менелая
Если дан треугольник АВС и прямая 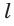 пересекает стороны ВС, АВ и продолжение стороны АС в точках
пересекает стороны ВС, АВ и продолжение стороны АС в точках 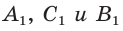 соответственно (рис. 79), то
соответственно (рис. 79), то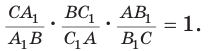
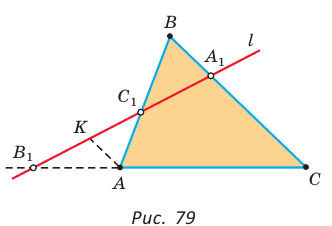
Доказательство:
Проведем отрезок 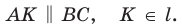 Так как
Так как 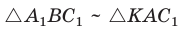 и
и  (по двум углам), то
(по двум углам), то 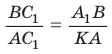 и
и 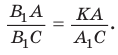 Перемножив почленно указанные пропорции, получим
Перемножив почленно указанные пропорции, получим
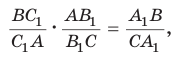 откуда
откуда 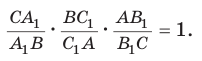
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой 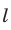 с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
Пример №21
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
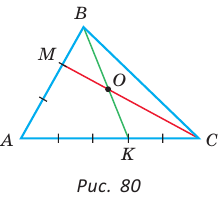
Решение:
Способ 1 (теорема Менелая). Рассмотрим 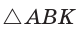 (рис. 80). Прямая
(рис. 80). Прямая 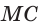 пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая
пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая 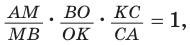 откуда
откуда 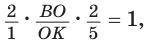
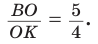
Способ 2 (теорема Фалеса обобщенная). Проведем 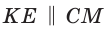 (рис. 81). По теореме Фалеса
(рис. 81). По теореме Фалеса 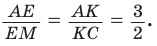 Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда
Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда 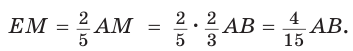
Но 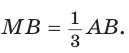 Отсюда
Отсюда 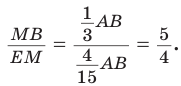 Для
Для 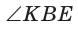
по теореме Фалеса 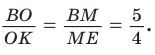
Ответ: 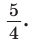
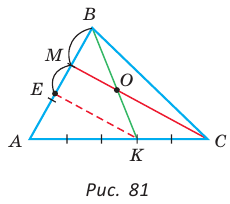
Пример №22
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
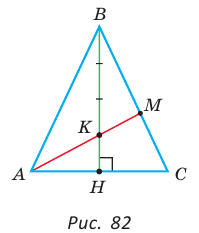
Решение:
1) 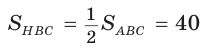 (ВН — высота и медиана треугольника АВС).
(ВН — высота и медиана треугольника АВС).
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке 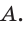 Тогда
Тогда 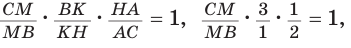
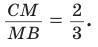 Откуда
Откуда 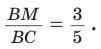
3) 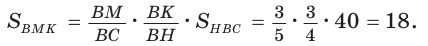
4) 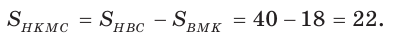
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
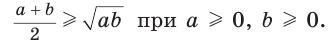
Например, 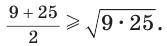 Действительно,
Действительно, 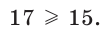
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 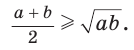 Получим:
Получим: 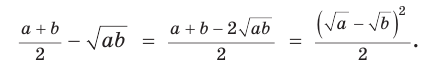 Так как
Так как 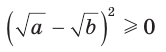 при всех допустимых
при всех допустимых 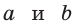 , то
, то 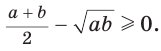 Следовательно, неравенство
Следовательно, неравенство 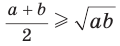 верно.
верно.
Неравенство 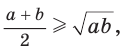 где
где 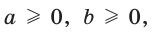 называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
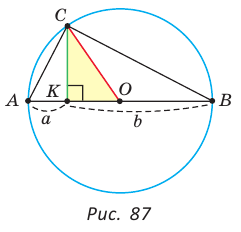
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 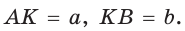 Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то
Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то  прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике
прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике 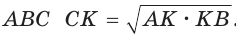 . Но радиус ОС равен половине диаметра АВ, т. е.
. Но радиус ОС равен половине диаметра АВ, т. е. 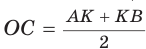 . В
. В 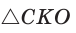 катет меньше гипотенузы, т. е.
катет меньше гипотенузы, т. е. 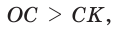 так как катет меньше гипотенузы. Отсюда
так как катет меньше гипотенузы. Отсюда 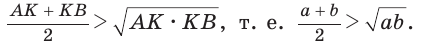
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и  становится равнобедренным и прямоугольным. Поэтому справедливо неравенство
становится равнобедренным и прямоугольным. Поэтому справедливо неравенство 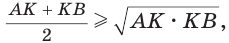 т. е
т. е 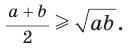
ЗАПОМИНАЕМ
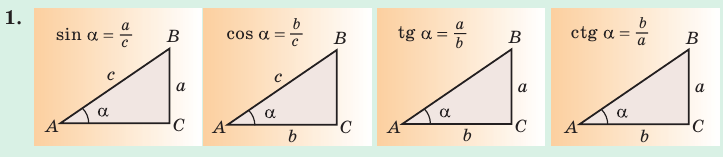
2. Значения тригонометрических функций углов 30 45°, 60°:
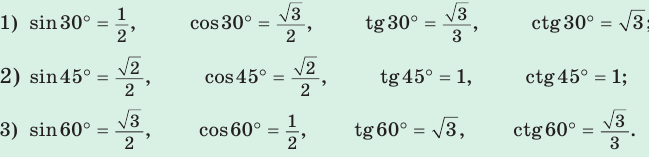
3. Тригонометрические формулы (тождества):
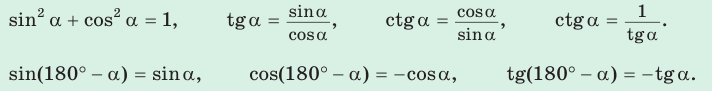
Примеры: 
4. Формулы площади треугольника и параллелограмма:

5. Среднее пропорциональное в прямоугольном треугольнике:
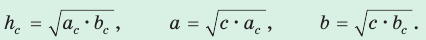
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол – определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
Тригонометрические формулы
Тригонометрические формулы — часто встречающиеся математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента.
- тригонометрические функции
- основные тригонометрические формулы
- тригонометрические функции суммы и разности углов
- тригонометрические функции двойного угла
- формулы тройного угла
- формулы понижения степени
- формулы преобразования суммы и разности тригонометрических функций в произведение
- формулы преобразования произведений функций
- универсальная тригонометрическая подстановка
Тригонометрические функции
Синус
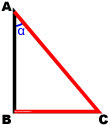
Синусом острого угла α в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
sin α
Косинус
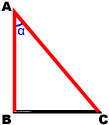
Косинусом острого угла α в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
cos α
Тангенс
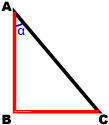
Тангенсом острого угла α в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.
tg α =sin αcos α
,
α ≠π2 + πn
,
n є Z
Котангенс

Котангенсом острого угла α в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему катету.
ctg α =cos αsin α
,
α ≠ π + πn
,
n є Z
Секанс
Секанс — это тригонометрическая функция обратная косинусу.
sec α =1cos α
,
α ≠π2 + πn
,
n є Z
Косеканс
Косеканс — это тригонометрическая функция обратная синусу.
cosec α =1sin α
,
α ≠ π + πn
,
n є Z
Основные тригонометрические формулы
Тригонометрические функции суммы и разности углов
Синус суммы двух углов
sinα + β = sin α · cos β + cos α · sin β
Синус разности двух углов
sinα – β = sin α · cos β – cos α · sin β
Косинус суммы двух углов
cosα + β = cos α · cos β – sin α · sin β
Косинус разности двух углов
cosα – β = cos α · cos β + sin α · sin β
Тангенс суммы двух углов
tgα + β =tg α + tg β1 – tg α · tg β
Тангенс разности двух углов
tgα – β =tg α – tg β1 + tg α · tg β
Котангенс суммы двух углов
ctgα + β =ctg α · ctg β – 1ctg β + ctg α
Котангенс разности двух углов
ctgα – β =ctg α · ctg β + 1ctg β – ctg α
Тригонометрические функции двойного угла
Синус двойного угла
sin 2α = 2 sin α · cos α
Косинус двойного угла
cos 2α = cos2 α – sin2 α
Тангенс двойного угла
tg 2α =2 tg α1 – tg2 α
Котангенс двойного угла
ctg 2α =ctg2 α – 12 ctg α
Формулы тройного угла
Синус тройного угла
sin 3α = 3 sin α – 4 sin3 α
Косинус тройного угла
cos 3α = 4 cos3 α – 3 cos α
Тангенс тройного угла
tg 3α =3 tg α – tg3 α1 – 3 tg2 α
Котангенс тройного угла
ctg 3α =3 ctg α – ctg3 α1 – 3 ctg2 α
Формулы понижения степени
Формулы преобразования суммы и разности тригонометрических функций в произведение
,
где
r2 = a2 + b2
,
sin φ =br
,
tg φ =ba
Формулы преобразования произведений функций
Универсальная тригонометрическая подстановка
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
