Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2023 года; проверки требуют 2 правки.
Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица[1], которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в двумерном пространстве[править | править код]
В двумерном пространстве поворот можно описать одним углом 
- или
.
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:
Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).
Матрица поворота в трёхмерном пространстве[править | править код]
Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол 
- Вращение вокруг оси
:
- Вращение вокруг оси
:
- Вращение вокруг оси
:
- Матрица поворота последовательности поворотов в некотором оговорённом порядке:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси[2]. Например, при повороте на угол 






Матрица поворота в n-мерном пространстве[править | править код]
Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.
Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости[3]. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.
Итак, аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.
Например:
— матрица поворота в 5-мерном пространстве в плоскости 
— матрица поворота в 7-мерном пространстве в плоскости 
Изменение оси поворота[править | править код]
Пусть 




где 

где 

Перестановочность поворотов[править | править код]
Если 





то 


При этом последовательность поворотов можно поменять, видоизменив поворот 
где матрица 



поскольку 

Выражение матрицы поворота через углы Эйлера[править | править код]
Последовательные повороты около осей 



Ось 







.
В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:
- 1) Поворот около осей:
- 2) Соответственно:
- 3)
- 4)
- 5)
- 6)
- 7)
- 8)
- 9)
- 10)
- 11)
- 12)
Матрица поворота вокруг произвольной оси[править | править код]
Пусть ось вращения задана единичным вектором 

Тогда матрица поворота в декартовых координатах имеет вид:
Выражение матрицы поворота через кватернион[править | править код]
Если задан кватернион 
Свойства матрицы поворота[править | править код]
Если 


Примечания[править | править код]
См. также[править | править код]
- Матрица перехода
- Поворот
Литература[править | править код]
- Лурье А. И. Аналитическая механика. — М.:Физматлит. — 1961. — 824 с.
Ссылки[править | править код]
- Поворот плоскости. Матрица поворота
Кватернионы, матрицы поворота и перепроецирование векторов между системами координат
Пришлось это мне в последнее время поработать с задачами, где нужно было оперировать кватернионами и заниматься перепроецированием векторов в разные системы координат (это еще называется заменой базиса). Сначала по чужим формулам — причем с опечатками и даже, как выяснилось, с фактическими ошибками — а потом делать свои, по аналогии. И всё даже работало! Но сохранялся какой-то туман в понимании происходящего. А всё, как оказалось, из-за этих ошибок: их комбинация давала систему, в целом сохраняющую корректность, неверным путем таки достигался верный результат. Зато такая удача сильно мешала осознанию проблемы и прояснению природы феномена «верный итог при подозрительных формулах». При этом разбираться досконально времени все не было — работает же, числа выдает правильные, чего тебе еще надо, собака? Вперед, нужно больше золота кода! А вот сейчас пришел момент, когда я, похоже, окончательно всё понял, и хочу поделиться получившейся картинкой с окружающими. Вдруг кому пригодится, и себе памятка.
Заранее оговорюсь, что материал не претендует на академичность изложения, а скорее просто описывает удобный для запоминания способ интерпретации того, что происходит при перепроецировании векторов.
Стало быть, речь у нас пойдет в особенности о проекциях и поворотах.

Исходные посылки
Описание кватернионов и матриц поворота как таковых опущу, предполагаю, что читатели знакомы с ними. Вектор здесь будет пониматься в его интуитивном представлении, как отрезок прямой в трехмерном пространстве, имеющий длину и направление. Исходное положение вектора будет иметь индекс «–», конечное — индекс «+».
Кватернионы и матрицы поворота могут быть использованы как для выполнения пространственного поворота векторов, так и для описания взаимной ориентации систем координат. В частности, для описания положения целевой системы координат относительно исходной: как нужно повернуть исходную, чтобы ее оси совпали с одноименными осями целевой. Матрица поворота (она же матрица ориентации, для случая описания взаимной ориентации систем координат) может быть получена из нормированного кватерниона ориентации по известным из литературы формулам. Обратное тоже верно: можно получить кватернион ориентации из матрицы.
Вектор , подлежащий повороту, задается величинами его проекций (длинами проекций) на оси исходной системы координат: три числа – проекции на три ортогональных оси . Получается матрица-столбец размерности 3х1, которая также называется вектором. Чтобы не смешивать в тексте подобную запись проекций вектора с интуитивным представлением о нем, я буду и дальше называть эту запись «матрицей-столбцом».
Поворот вектора
Поворачивать вектор можно, как уже сказано, и с помощью матрицы, и с помощью кватерниона.
Поворот с использованием матрицы: матрица поворота умножается на исходную матрицу-столбец. На выходе имеем другую, результирующую матрицу-столбец:
Поворот с использованием кватерниона ориентации выполняется в два шага:
- Из исходной матрицы-столбца и кватерниона вычисляется промежуточная матрица-столбец , где – операция векторного произведения векторов;
- Вычисляется значение результирующей матрицы-столбца по формуле
Числа в результирующей матрице-столбце, полученной любым из этих способов — это проекции вектора в его новом, повернутом положении, на оси все той же исходной системы координат.
С поворотом вектора дело ясное, вопросов нет.
Перепроецирование вектора
А вот задача перепроецирования вектора из одной системы координат в другую несколько контринтуитивна. Формулировка задачи: необходимо узнать, как некоторый вектор, заданный в исходной системе координат, выглядит в целевой системе. Иначе говоря, по проекциям вектора на оси исходной системы узнать проекции вектора на оси целевой. При этом задан кватернион или матрица ориентации целевой системы относительно исходной.
Может показаться, что для решения этой задачи нужно просто повернуть вектор из исходной системы координат в целевую, пользуясь кватернионом или матрицей ориентации второй относительно первой. Однако это не так! Выполнив подобную операцию, мы узнаем только, как новый, повернутый вектор выглядит в осях все той же исходной системы, а это не то, что нас интересует .
Важно, однако, обратить внимание на то, что после проведения подобного поворота сам вектор окажется ориентирован относительно целевой системы координат так же, как он был до операции ориентирован относительно исходной. В этом кроется ключ к правильному ходу действий. Для получения проекций интересующего нас вектора на целевую систему координат нужно выполнить операцию «в обратную сторону»:
- Задать в целевой системе координат «временный» вектор с теми же величинами проекций на оси этой целевой системы, какие есть у интересующего нас («заданного») вектора на оси исходной системы. Таким образом, «временный» вектор будет ориентирован относительно целевой системы так же, как заданный вектор ориентирован относительно исходной;
- Определить ориентацию исходной системы относительно целевой. Здесь легко: нужная ориентация описывается либо кватернионом, сопряженным к имеющемуся (), либо матрицей , обратной по отношению к имеющейся; причем для матрицы ориентации, чей определитель всегда равен 1, обратная матрица совпадает с транспонированной , поэтому достаточно транспонировать имеющуюся матрицу ориентации;
- Повернуть «временный» вектор с использованием полученного кватерниона/матрицы. Вектор повернется относительно целевой системы координат так же, как относительно нее повернута исходная система. При этом, в силу всего сказанного ранее, а) «временный» вектор станет ориентирован уже относительно исходной системы так, как был ранее ориентирован относительно целевой, и, следовательно, точно совпадет с заданным вектором, и б) результатом операции будет матрица-столбец, описывающая, как теперь «временный» (а значит, и заданный) вектор выглядит в осях целевой системы координат.
Ура, это именно то, что нам нужно!
Кроме того, быстро становится очевидно, что с точки зрения реализации никакой «временный» вектор (в смысле «матрица-столбец») на самом деле не нужен: в ходе операции он никак не модифицируется, и при этом численно является копией исходного вектора. Так что, разумеется, можно спокойно брать сам исходный вектор и проводить операции с ним. Описание выше лишь подробнее иллюстрирует смысл происходящего.
Матрицы поворота, углы Эйлера и кватернионы (Rotation matrices, Euler angles and quaternions)
Объект обычно определяется в удобной для его описания локальной системе координат (ЛСК), а его положение в пространстве — в глобальной системе координат (ГСК).
В трёхмерном пространстве переход из одной СК в другую описывается в общем случае системой линейных уравнений:

Уравнения могут быть записаны через матрицы аффинных преобразований в однородных координатах одним из 2-х способов:

В ортогональных СК оси X, Y и Z взаимно перпендикулярны и расположены по правилу правой руки:
На рисунке справа большой палец определяет направление оси, остальные пальцы — положительное направление вращения относительно этой оси.
Все три вектора направлений есть единичными.

Ниже приводится единичная матрица для 2-х способов записи уравнений геометрических преобразований. Такая матрица не описывает ни перемещения, ни вращения. Оси ЛСК и ГСК совпадают.
Далее рассматривается матрица для второго способа матричной записи уравнений (матрица справа). Этот способ встречается в статьях значительно чаще.
При использовании матрицы вы можете игнорировать нижнюю строку. В ней всегда хранятся одни и те же значения 0, 0, 0, 1. Она добавлена для того, чтобы мы могли перемножать матрицы (напомню правило перемножения матриц и отмечу, что всегда можно перемножать квадратные матрицы). Подробнее см. Композиция матриц. Однородные координаты.
Остальные 12 значений определяют координатную систему. Первый столбец описывает компоненты направления оси X(1,0,0). Второй столбец задает направление оси Y(0,1,0), третий – оси Z (0,0,1). Последний столбец определяет положение начала системы координат (0,0,0).
Как будет выглядеть матрица Евклидового преобразования (преобразование движения) для задания ЛСК , с началом в точке (10,5,0) и повёрнутой на 45° вокруг оси Z глобальной СК, показано на рисунке.

Рассмотрим сначала ось X. Если новая система координат повернута на 45° вокруг оси z, значит и ось x повернута относительно базовой оси X на 45° в положительном направлении отсчета углов. Таким образом, ось X направлена вдоль вектора (1, 1, 0), но поскольку вектор системы координат должен быть единичным, то результат должен выглядеть так (0.707, 0.707, 0). Соответственно, ось Y имеет отрицательную компоненту по X и положительную по Y и будет выглядеть следующим образом (-0.707, 0.707, 0). Ось Z направления не меняет (0, 0, 1). Наконец, в четвертом столбце вписываются координаты точки начала системы координат (10, 5, 0).
Частным случаем матриц геометрических преобразований есть матрицы поворота ЛСК относительно базовых осей ГСК. Вектора осей ЛСК здесь выражены через синусы и косинусы углов вращения относительно оси, перпендикулярной к плоскости вращения.
От матрицы преобразований размером 4*4 можно перейти непосредственно к матрице поворота 3*3, убрав нижний ряд и правый столбец. При этом, система линейных уравнений записывается без свободных элементов (лямда, мю, ню), которые определяют перемещение вдоль осей координат.
Путем перемножения базовых матриц можно получать комбинированные вращения. Ниже рассмотрены возможности комбинировать вращениями через матрицы поворота на примерах работы с углами Эйлера.
Матрицы поворота и углы Эйлера
От выбора осей и последовательности вращения зависит конечный результат. На рисунках отображена следующая последовательность вращения относительно осей ЛСК:
- оси Z (угол alpha);
- оси X (угол beta);
- оси Z (угол gamma).
Получил от читателя этой статьи вопрос: «Как понять, из каких углов поворота вокруг осей X,Y,Z можно получить текущее положение объекта, когда в качестве задания мы уже имеем повернутый объект, а нужно вывести его в это положение, последовательно повернув его из какого-то начального положения до полного совмещения с заданным?»
Мой ответ: «Если я правильно понял вопрос, то Вас интересует, как от начального положения перейти к заданному положению объекта, используя для этого элементарные базовые аффинные преобразования.
Начну с аналогии. Это как в шахматах. Мы знаем как ходит конь. Необходимо переместить его в результате многоходовки в нужную клетку на доске — при условии, что это возможно.
Подробно эта проблематика рассмотрена в статье Преобразование координат при калибровке роботов.
Умение правильно выбирать последовательность элементарных геометрических преобразований помогает в решении множества других задач (см. Примеры геометрических преобразований).»
Можно получить результирующую матрицу, которая определяет положение ГСК относительно ЛСК. Для этого необходимо перемножить матрицы с отрицательными углами в последовательности выполнения поворотов:
Почему знак угла поворота меняется на противоположный? Объяснение этому простое. Движение относительно. Абстрагируемся и представим, что ГСК меняет положение относительно неподвижной ЛСК. При этом направление вращения меняется на противоположное.
Перемножение матриц даст следующий результат:
Результирующую матрицу можно использовать для пересчета координат из ГСК в ЛСК:
Для пересчета координат из ЛСК в ГСК используется результирующая обратная матрица.
В обратной матрице последовательность поворота и знаки углов меняются на противоположные (в рассматриваемом примере снова на положительные) по сравнению с матрицей определения положения ГСК относительно ЛСК.
Перемножение матриц даст следующий результат:
Выше был рассмотрен случай определения углов Эйлера через вращение относительно осей ЛСК. То же взаимное положение СК можно получить, выполняя вращение относительно осей ГСК:
- оси z (угол (gamma+pi/2));
- оси y (угол угол beta);
- оси z (угол (-alpha)).
Определение углов Эйлера через вращение относительно осей ГСК позволяет также просто получить зависимости для пересчета координат из ЛСК в ГСК через перемножение матриц поворота.
В рамках рассматриваемой задачи вместо угла gamma в матрицe Az используем угол gamma+pi/2.
Также легко можно перейти к зависимостям для пересчета координат из ГСК в ЛСК.
Обратная матрица получается перемножением обратных матриц в обратном порядке по сравнению с прямым преобразованием. При этом каждая из обратных матриц вращения может быть получена заменой знака угла на противоположный.
Детально с теоретическими основами аффинных преобразований (включая и вращение) можно ознакомиться в статье Геометрические преобразования в графических приложениях
Примеры преобразований рассмотрены в статьях:
Axis Angle представление вращения
Выбрав подходящую ось (англ. rotation axis) и угол (англ. rotation angle) можно задать любую ориентацию объекта.
Обычно хранят ось вращения в виде единичного вектора и угол поворота вокруг этой оси в радианах или градусах.
q = [ x, y, z, w ] = [ v, w ]
В некоторых случаях удобно хранить угол вращения и ось в одном векторе. Направление вектора при этом совпадает с направлением оси вращения, а его длина равна углу поворота:
q = [ x, y, z]; w=sqrt (x*x +y*y +z*z)
В физике, таким образом хранят угловую скорость. Направление вектора совпадает с направлением оси вращения, а длина вектора равна скорости (в радианах в секунду).
Можно описать рассмотренные выше углы Эйлера через Axis Angle представление в 3 этапа:
q1 = [ 0, 0, 1, alpha]; q2 = [ 1, 0, 0, beta]; q3 = [ 0, 0, 1, gamma ]
Здесь каждое вращение выполняется относительно осей текущего положения ЛСК. Такое преобразование равнозначно рассмотренному выше преобразованию через матрицы поворота:
Возникает вопрос, а можно ли 3 этапа Axis Angle представления объединить в одно, подобно матрицам поворота? Попробуем решить геометрическую задачу по определению координат последнего вектора вращения в последовательности преобразований через Axis Angle представления:
q = [ x, y, z, gamma ]
Есть ли представление q= [x, y, z, gamma] композицией последовательности из 3-х этапов преобразований? Нет! Координаты x, y, z определяют всего лишь положение оси Z ЛСК после первого и второго этапов преобразований:
При этом ось Z, отнюдь, не есть вектор вращения для Axis Angle представления, которое могло бы заменить рассмотренные 3-х этапа преобразований.
Еще раз сформулирую задачу, которая математически пока не решена: «Необходимо найти значение угла (rotation angle) и положение оси (rotation axis), вращением относительно которой на этот угол можно заменить комбинацию из 3-х поворотов Эйлера вокруг осей координат».
К сожалению, никакие операции (типа объединения нескольких преобразований в одно) с Axis Angle представлениями нельзя выполнить. Не будем расстраиваться. Это можно сделать через кватернионы, которые также определяют вращение через параметры оси и угол.
Кватернионы
Кватернион (как это и видно по названию) представляет собой набор из четырёх параметров, которые определяют вектор и угол вращения вокруг этого вектора. По сути такое определение ничем не отличается от Axis Angle представления вращения. Отличия лишь в способе представления. Как же хранят вращение в кватернионе?
q = [ V*sin(alpha/2), cos(alpha/2) ]
В кватернионе параметры единичного вектора умножается на синус половины угла поворота. Четвертый компонент — косинус половины угла поворота.
Таблица с примерами значений кватернионов:
Представление вращения кватернионом кажется необычным по сравнению с Axis Angle представлением. Почему параметры вектора умножаются на синус половины угла вращения, четвертый параметр — косинус половины угла вращения, а не просто угол?
Откуда получено такое необычное представление кватерниона детально можно ознакомиться в статье Доступно о кватернионах и их преимуществах. Хотя программисту не обязательно знать эти детали, точно также как и знать, каким образом получены матрицы преобразования пространства. Достаточно лишь знать основные операции с кватернионами, их смысл и правила применения.
Основные операции над кватернионами
Кватернион удобно рассматривать как 4d вектор, и некоторые операции с ним выполняются как над векторами.
Сложение, вычитание и умножение на скаляр.
Смысл операции сложения можно описать как «смесь» вращений, т.е. мы получим вращение, которое находится между q и q’.
Что-то подобное сложению кватернионов выполнялось при неудачной попытке объединить 3 этапа Axis Angle представления.
Умножение на скаляр на вращении не отражается. Кватернион, умноженный на скаляр, представляет то же самое вращение, кроме случая умножения на 0. При умножении на 0 мы получим «неопределенное» вращение.
Пример сложения 2-х кватернионов:
Норма и модуль
Следует различать (а путают их часто) эти две операции:
Модуль (magnitude), или как иногда говорят «длина» кватерниона:
Через модуль кватернион можно нормализовать. Нормализация кватерниона — это приведение к длине = 1 (так же как и в векторах):
Обратный кватернион или сопряжение ( conjugate )
Обратный кватернион задает вращение, обратное данному. Чтобы получить обратный кватернион достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион.
Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0).
Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 кватернион представляется как (w=1; x = 0; y = 0; z=0), то есть, у него длина вектора оси = 0.
Фрагмент программной реализации:
Инверсный (inverse) кватернион
Существует такой кватернион, при умножении на который произведение дает нулевое вращение и соответствующее тождественному кватерниону (identity quaternion), и определяется как:
Тождественный кватернион
Записывается как q[0, 0, 0, 1]. Он описывает нулевой поворот (по аналогии с единичной матрицей), и не изменяет другой кватернион при умножении.
Скалярное произведение
Скалярное произведение полезно тем, что дает косинус половины угла между двумя кватернионами, умноженный на их длину. Соответственно, скалярное произведение двух единичных кватернионов даст косинус половины угла между двумя ориентациями. Угол между кватернионами — это угол поворота из q в q’ (по кратчайшей дуге).
Вращение 3d вектора
Вращение 3d вектора v кватернионом q определяется как
причем вектор конвертируется в кватернион как
и кватернион обратно в вектор как
Умножение кватернионов
Одна из самых полезных операций, она аналогична умножению двух матриц поворота. Итоговый кватернион представляет собой комбинацию вращений — сначала объект повернули на q, а затем на q’ (если смотреть из глобальной системы координат).
Примеры векторного и скалярного перемножения 2-х векторов векторное произведение — вектор: Скалярное произведение — число:
Пример умножения 2-х кватернионов:
Конвертирование между кватернионом и Axis Angle представлением
В разделе Axis Angle представление вращения была сделана неудачная попытка объединить 3 Axis Angle представления в одно . Это можно сделать опосредовано. Сначала Axis Angle представления конвертируются в кватернионы, затем кватернионы перемножаются и результат конвертируется в Axis Angle представление.
Пример конвертирования произведения 2-х кватернионов в Axis Angle представление:
Фрагмент программы на C:
Конвертирование кватерниона в матрицу поворота
Матрица поворота выражается через компоненты кватерниона следующим способом:
где
Проверим формулы конвертирования на примере конвертирования произведения 2-х кватернионов в матрицу поворотов:
Определяем элемент матрицы m[0][0] через параметры кватерниона:
Соответствующее произведению кватернионов (q1 и q2) произведение матриц поворотов было получено ранее (см. Матрицы поворота и углы Эйлера):
Как видим, результат m[0][0], полученный через конвертирование, совпал с значением в матрице поворота.
Фрагмент программного кода на С для конвертирования кватерниона в матрицу поворота:
При конвертировании используется только умножения и сложения, что является несомненным преимуществом на современных процессорах.
Часто для задания вращений используют только кватернионы единичной длины, но это не обязательно и иногда даже не эффективно. Разница между конвертированием единичного и неединичного кватернионов составляет около 6-ти умножений и 3-х сложений, зато избавит во многих случаях от необходимости нормировать (приводить длину к 1) кватернион. Если кусок кода критичен по скорости и вы пользуетесь только кватернионами единичной длины тогда можно воспользоваться фактом что норма его равна 1.
Конвертирование матрицы поворота в кватернион
Конвертирование матрицы в кватернион выполняется не менее эффективно, чем кватерниона в матрицу, но в итоге мы получим кватернион неединичной длины. Его можно нормализовать.
Фрагмент программного кода конвертирования матрицы поворота в кватернион:
Вращение фигуры в 3-х мерном пространстве
Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в трёхмерном пространстве
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
Вращение вокруг оси y:
Вращение вокруг оси z:
После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;
По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);
По оси Z
x’=x*cos(L)-y*sin(L);
y’=-x*sin(L)+y*cos(L);
z’=z;
Все три поворота делаются независимо друг от друга, т.е. если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).
[spoiler title=”источники:”]
http://api-2d3d-cad.com/euler_angles_quaternions/
http://grafika.me/node/82
[/spoiler]
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора:
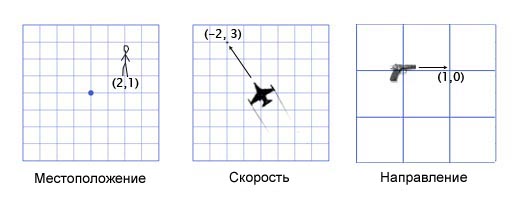
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
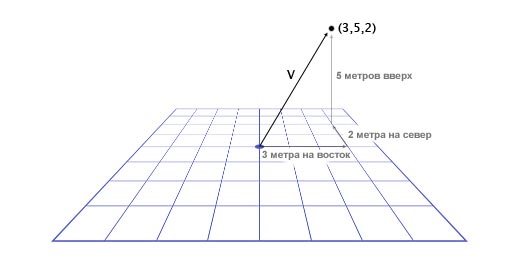
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
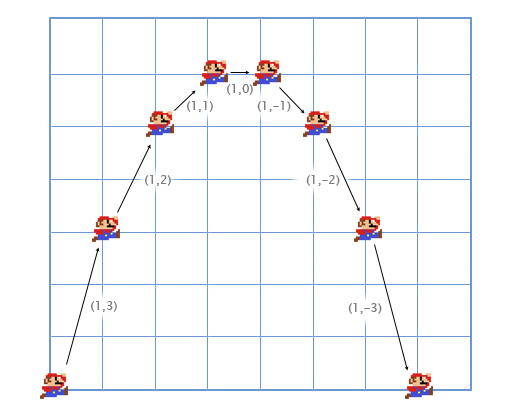
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
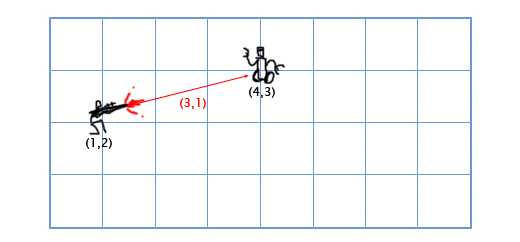
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x2 + y2 = h2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x2 + y2).
Итак, скорость нашего корабля равна:
|V| = sqrt(42 + 32) = sqrt(25) = 5
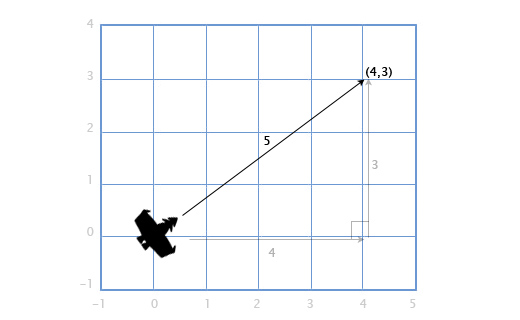
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x2 + y2 + z2)
Расстояние
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(22+12) = sqrt(5) = 2.23
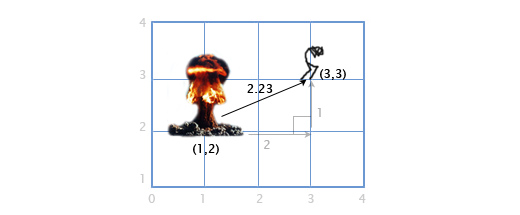
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5)2 + (4/5)2 = 9/25 + 16/25 = 25/25 = 1
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
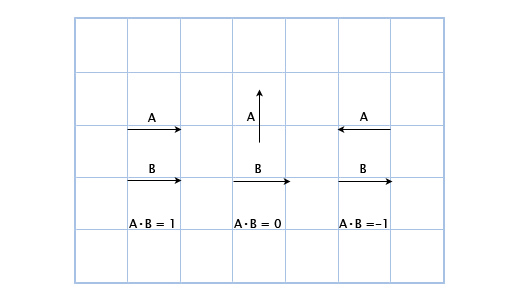
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
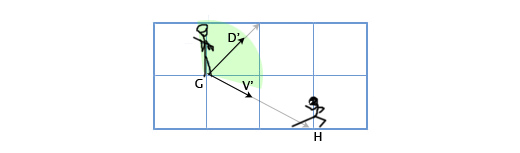
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
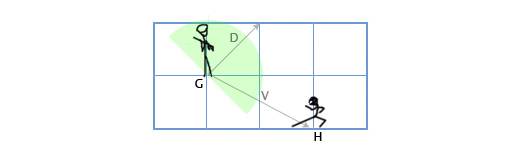
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
A•B = |A||B|cosΘ
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Θ = acos([AB] / [|A||B|])
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
Θ = acos(AB)
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(12 + 12) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(22 + (-1)2) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
//Инициализируем вектора
vec2 guard_pos = vec2(1,3);
vec2 guard_facing = vec2(1,1);
vec2 hero_pos = vec2(3,2);
//Рассчитываем нормализованные вектора
vec2 guard_facing_n = normalize(guard_facing);
vec2 guard_to_hero = normalize(hero_pos - guard_pos);
//Рассчитываем угол
float angle = acos(dot(guard_facing_n, guard_to_hero));
Векторное произведение
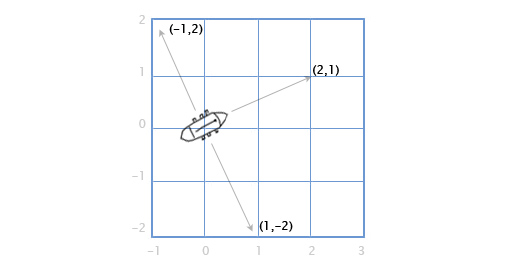
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.

Векторное произведение A(a1,a2,a3) и B(b1,b2,b3) будет равно:
(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1)
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
vec3 cross(vec3 a, vec3 b) {
vec3 result;
result[0] = a[1] * b[2] - a[2] * b[1];
result[1] = a[2] * b[0] - a[0] * b[2];
result[2] = a[0] * b[1] - a[1] * b[0];
return result;
}
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
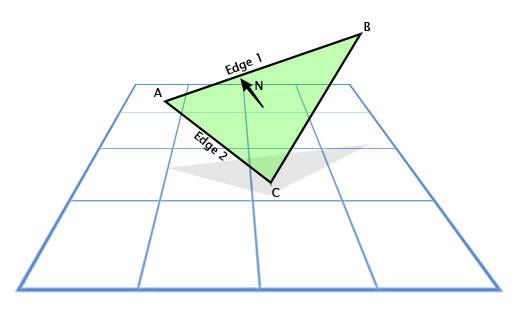
Вот так это выглядит в коде:
vec3 GetTriangleNormal(vec3 a, vec3 b, vec3 c) {
vec3 edge1 = b-a;
vec3 edge2 = c-a;
vec3 normal = cross(edge1,edge2);
return normal;
}
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
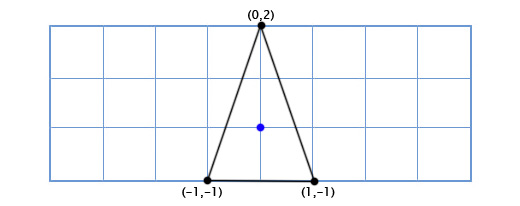
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
vec2 rotate(vec2 point, float angle){
vec2 rotated_point;
rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
return rotated_point;
}
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:

Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
Пусть теперь наш корабль выглядит вот так:
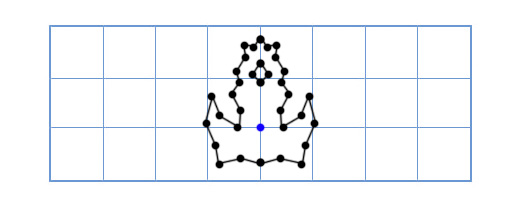
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
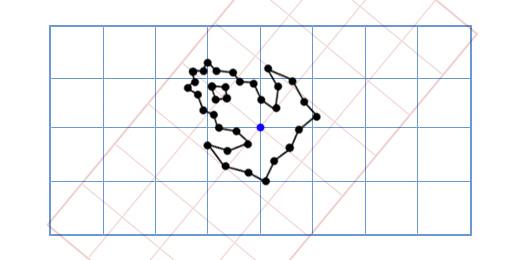
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
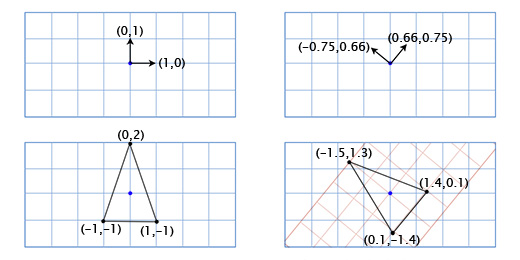
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
x(a,b) + y(c,d)
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
[a c
b d]
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
(a,c)•(x,y) + (b,d)•(x,y)
Будучи записанным по-другому, это выражение выглядит так:
x(a,b) + y(c,d)
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
[1 0 0 1]
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
[0.66 -0.75 0.75 0.66]
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
void RotateShip(float degrees){
Matrix2x2 R = GetRotationMatrix(degrees);
for(int i=0; i<num_points; ++i){
rotated_point[i] = R * point[i];
}
}
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
[a c e b d f 0 0 1]
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
[x y 1]
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
[a d g b e h c f i]
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
[a d g j b e h k c f i l 0 0 0 1]
И добавляем единицу [1] в вектор, как здесь:
[x y z 1]
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
vec2 rotate(vec2 point, float angle){
vec2 rotated_point;
rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
return rotated_point;
}
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
[cos(Θ) -sin(Θ) sin(Θ) cos(Θ)]
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
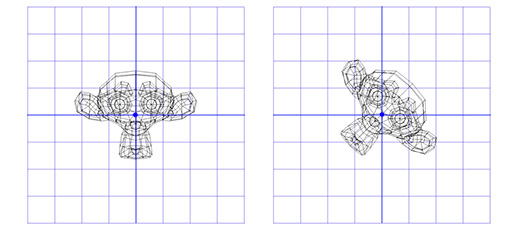
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
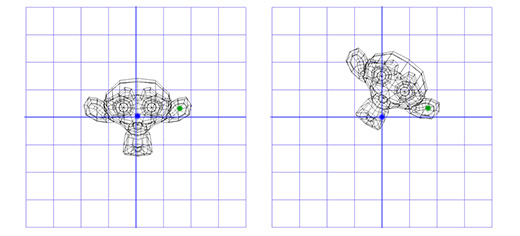
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T-1. Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
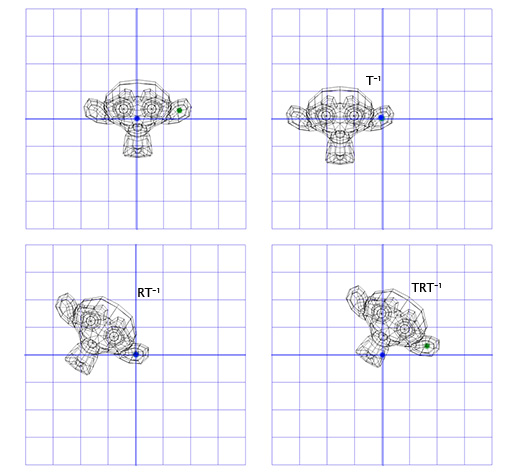
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
[cos(Θ) -sin(Θ) 0 sin(Θ) cos(Θ) 0 0 0 1]
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
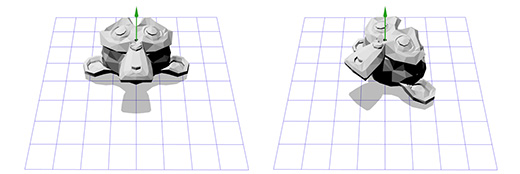
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
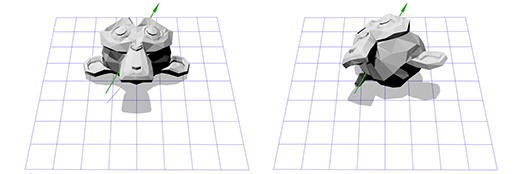
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
B = (0,0,1);
C = cross(A,B);
B = cross(C,A);
Тут показана иллюстрация для каждого шага:
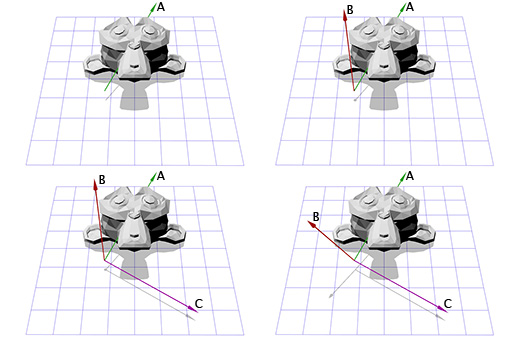
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
[B0 C0 A0 B1 C1 A1 B2 C2 A2]
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
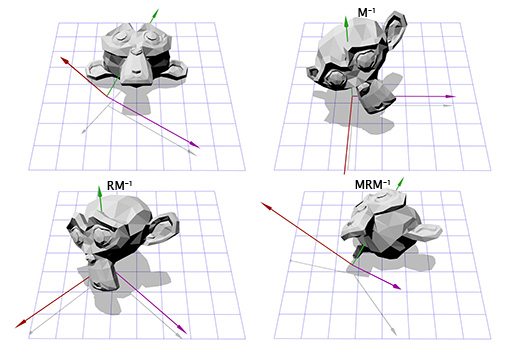
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M-1RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
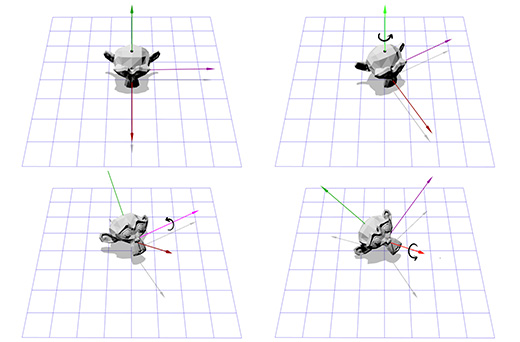
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.

Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
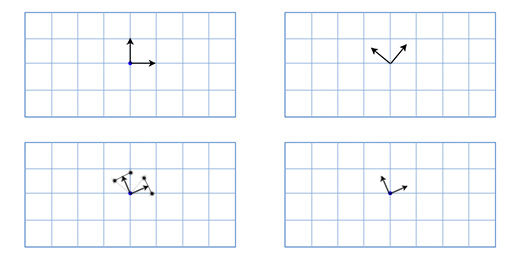
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).

Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
Если
каждая точка P(x, y, z)
отображается на точку P’
(x’, y’, z’)
в соответствии с уравнениями
![]()
где а1,
а2,
а3 – константы,
то этот процесс называется переносом
в трехмерном пространстве. Такой перенос
может быть записан в матричной форме
[x’
y’
z’
1] = [x
y
z
1] T
T=
Поворот вокруг
координатных осей может быть описан
матрицей без использования однородных
координат. Будем использовать правую
координатную систему, считая вращение
вокруг оси положительным, если оно
соответствует положительному направлению
этой оси по правилу винта с правой
резьбой, как это показано на рисунке.
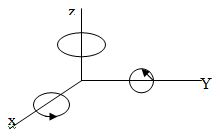
Рассмотрим поворот
вокруг оси z на
угол α и для сокращения
обозначим cos α
= c и sin α
=s.
Тогда можно записать
[x’y’
z’]=[x
y
z]
Rz
Rz = ![]()
Матрицу Rz можно
использовать для получения матриц Rx и Ry,
определяющих поворот вокруг соответствующих
осей, чисто формальным образом, то есть
без применения картинки. Это делается
путем циклических перестановок,
получаемых заменой каждой из
букв x, y, z на
последующую, считая, что за буквой z следует
буква х.
Матрица Rz превращается
в матрицу Rx циклическим
переносом каждой строки на одну позицию
и затем выполнением аналогичной операции
для столбцов:
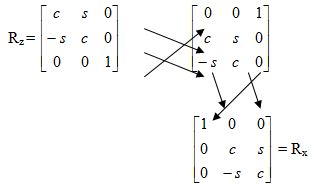
Так же
матрица Rx преобразуется
в «последующую» матрицу Ry
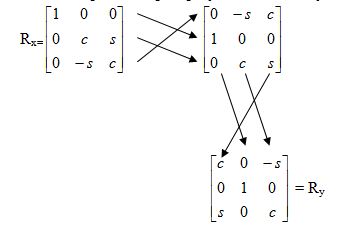
Суммируя сказанное,
получим следующие матрицы
Rx= ![]()
Ry= ![]()
Rz = ![]()
Для поворота точки
вокруг оси х на
угол α матрица Rx используется
следующим образом:
[x’ y’
z’] = [x y z] Rx
Матрицы Ry и Rz применяются
аналогично.
Как известно,
уравнения для преобразований могут
интерпретироваться как изменения
координат. Перенос точки на определенное
расстояние вправо описывает теми
же уравнениями перенос системы координат
на такое же расстояние влево. На практике
удобнее перемещать координатную систему
вместо точки, но для этого требуется
инвертирование матрицы. Запишем для
наших матриц соответствующие им
инвертированные матрицы.
Т-1 =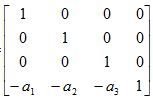
Rx-1=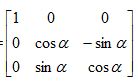
Ry-1=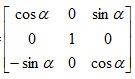
Rz-1 =![]()
Теперь можно найти
матрицу R для
поворота вокруг любой прямой линии,
проходящей через точку начала координат
О. Для определенности будем полагать,
что поворот осуществляется вокруг
вектора v,
начало которого расположено в точке
О. Тогда положительное направление
вращения соответствует направлению
вектора по правилу винта с правой
резьбой. Как и ранее поворот будем
осуществлять на угол α.
Если
концевая точка вектора v задана
в ортогональных координатах, то сначала
вычислим его сферические координаты ![]()
.
![]()
Если ![]()
=
0, то будем считать, что ![]()
.
В противном случае
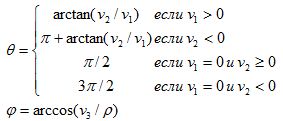
Возможно, Вы помните
обратное вычисление
![]()
Теперь стратегия
заключается в таком изменении системы
координат, чтобы вектор v (ось
вращения) совпадал с новым
направлением положительной
полуоси z..
[x’ y’
z’] = [x y z] Rz-1
Rz-1 =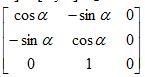
Ось x’
определяет положительное направление
вектора (v1, v2,
0).
Теперь повернем
оси x’
и z’
вокруг оси y’
на угол ![]()
до
совпадения оси z’
с вектором v.
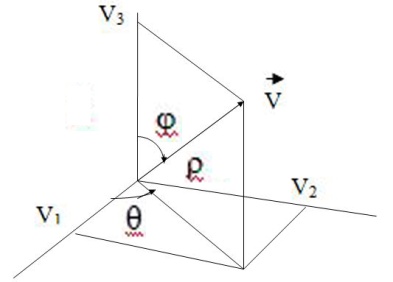
Перепишем это
условие как
[x’’ y’’ z’’]=[x’ y’ z’] Ry-1
Ry-1=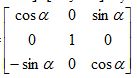
Фактический поворот
вокруг вектора v на
угол α теперь можно выполнить как
поворот вокруг осиz’’
.То есть
[x’’’ y’’’ z’’’]
=[x’’ y’’ z’’] Rv
Rv =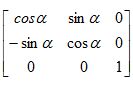
К этому моменту
достигнуто выполнение соотношения
[x’’’ y’’’ z’’’]
=[x y z] Rz-1 Ry-1 Rv
Координаты
[x’’’ y’’’ z’’’] относятся
к самой последней системе координат,
тогда как их необходимо выразить в
исходной системе. Обозначим эти
координаты в исходной системе
черезx*, y*, z*.
Переход к исходной системе инвертированных
матриц Rz-1 и Ry-1 ,(которые
будут совпадать с матрицами Rz и Ry)
в обратном порядке для преобразования
точки x’’’, y’’’, z’’’:
[x*
y*
z*]
=[x’’’
y’’’
z’’’]
Ry Rz
Это означает, что
полный поворот вокруг вектора v на
угол α вычисляется по формуле
[x* y* z*]
=[x’’’ y’’’ z’’’] Rz-1 Ry-1 Rv Ry Rz
где
Rz-1 =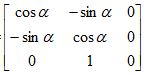
Ry-1 = 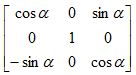
Rv = ![]()
Ry= 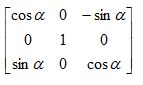
Rz = ![]()
Для последующего
применения запишем
Rz-1 Ry-1 Rv Ry Rz =R
=![]()
До сих пор мы
говорили о повороте относительно
вектора, привязанного к точке начала
координат – точке О. Теперь поставим
задачу определения поворота относительно
вектора, начало которого расположено
в любой произвольной точке А (а1,
а2,
а3).
Для этого будем использовать вектор v для
вычисления матрицы R таким
же образом, как и ранее. Затем нужно
выполнить три следующих шага.
1. Выполним
перенос из заданной точки в точку начала
координат О, используя однородные
координаты и следующую матрицу:
Т-1=
2. Осуществим
поворот относительно оси, проходящей
через точку О, как и ранее, но
матрицу R обходимо
тривиальным образом расширить, чтобы
можно было использовать однородные
координаты
R*
=
3. Применим
преобразование, обратное шагу 1, используя
матрицу
T=
После этого матрица
обобщенного поворота вычисляется как
RGEN =
T-1 R*
T
И ее можно
использовать следующим образом
[x*
y*
z*
1] = [x
y
z
1] RG
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тут всё просто. Для начала рассмотрим более простую задачу: какие координаты будут у единичного вектора, который повёрнут относительно оси абсцисс на угол α? Ответ: (cos α, sin α). Это чуть ли не определение косинуса и синуса.
Что такое координаты? Это коэффициенты в разложении вектора по базису:
r = i cos α + j sin α
Здесь r – искомый вектор, i и j – базисные вектора.

Таким образом, поворачивать базисный вектор в ортонормированном базисе очень просто.
Теперь вспомним, что нам надо повернуть не базисный вектор, а указанный. Обозначим его буквой v. Так вот, повернуть его очень просто: надо сделать его базисным! Точнее, надо построить ортонормированный базис с его участием. В конце концов, ортонормированный базис на плоскости – это всего лишь два перпендикулярных вектора одинаковой длины, и один из них у нас уже есть.
Чтобы найти второй вектор, надо повернуть вектор v на 90 градусов. Это делается куда проще, чем поворот на произвольный угол:

Как видно, если у вектора v координаты были (x, y) – то у перпендикулярного вектора u координаты будут (-y, x). Можете проверить сами – это верно для любого квадранта. И обратите ещё раз внимание на разные знаки у координат: именно отсюда в дальнейшем возникнет интересующее вас несоответствие.
И так, у нас есть ортонормированный базис, у нас если формула поворота базисного вектора, и нам надо его повернуть:

Кажется, всё готово для получения ответа. Получаем формулу в векторном виде:
r = v cos α + u sin α
Теперь подставим в формулу координаты обоих векторов и…
rx = x cos α – y sin α
ry = y cos α + x sin α































