Как найти угол восьмиугольника вписанного в окружность

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Решение:

Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.

Величина угла в восьмиугольнике равна:
n=8

∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:

Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Восьмиугольник вписанный в окружность найти угол

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Решение:

Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.

Величина угла в восьмиугольнике равна:
n=8

∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:

Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Нахождение угла восьмиугольника, вписанного в окружность

Условие задачи для наглядности изображается схематически на рисунке. Для начала определяется величина внутреннего угла равностороннего восьмиугольника, применяя формулу нахождения суммы всех углов n-угольника. Величина искомого угла АВС вычисляется как разность между величиной внутреннего угла восьмиугольника и величинами углов СВА и DBC. В ходе дальнейшего решения доказывается равенство углов CBA=DBC. Вычислив величину угла CBA, определяется величина искомого угла.

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/vosmiugolnik-vpisannyy-v-okruzhnost-nayti-ugol

http://www.virtualacademy.ru/lesson/1220/

[/spoiler]

Skip to content

Задания

Версия для печати и копирования в MS Word

Восьмиугольник, виды, свойства и формулы.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник, выпуклый и невыпуклый восьмиугольник

Правильный восьмиугольник (понятие и определение)

Свойства правильного восьмиугольника

Формулы правильного восьмиугольника

Правильный восьмиугольник в природе, технике и культуре

Шестиугольник

Восьмиугольник, выпуклый и невыпуклый восьмиугольник:

Восьмиугольник – это многоугольник с восемью углами.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый восьмиугольник

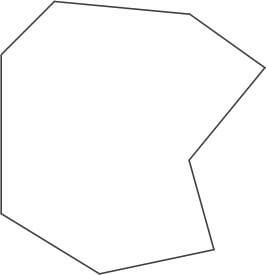
Рис. 2. Невыпуклый восьмиугольник

Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

Свойства правильного восьмиугольника:

1. Все стороны правильного восьмиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇ = a₈. 

2. Все углы равны между собой и составляют 135°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = α₈ = 135°.

Рис. 4. Правильный восьмиугольник

3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.

Рис. 5. Правильный восьмиугольник

5. Количество диагоналей правильного восьмиугольника равно 20.

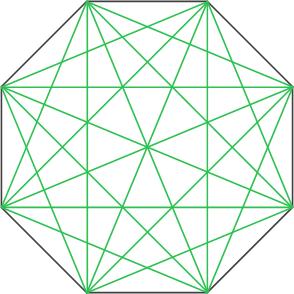
Рис. 6. Правильный восьмиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

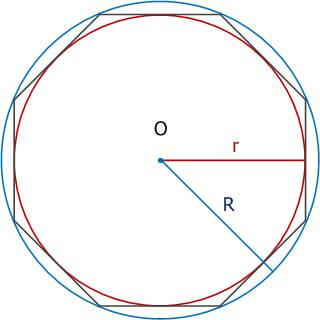
Рис. 7. Правильный восьмиугольник

Формулы правильного восьмиугольника:

Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.

Формула константы правильного восьмиугольника:

Формула периметра правильного восьмиугольника:

Формулы площади правильного восьмиугольника:

Формулы радиуса окружности, вписанной в правильный восьмиугольник:

Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:

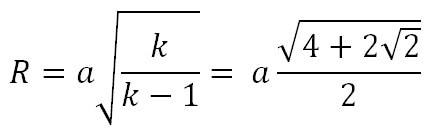
Формулы стороны правильного восьмиугольника:

Правильный восьмиугольник в природе, технике и культуре:

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.

Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
7 154