5″А” класс
Математика
Тема урока
Деление с остатком.
Введение в тему урока
Ребята, сегодня новая тема «Деление с остатком»
Не всегда натуральные числа делятся нацело. Когда мы сталкиваемся с таким видом деления, то обычно говорят, что числа делятся с остатком. Сегодня мы с вами узнаем, как правильно находить остаток и проверять, верно ли мы выполнили все действия.
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Если при делении натуральных чисел остаток равен нулю, то договорились считать, что делимое делится на делитель без остатка, или делится нацело.
Данный вид примеров вам встречался в начальной школе.
Прочитайте очень внимательно материал в учебнике на стр. 99
Запишите эту формулу к себе в тетрадь и выучите.
a : b = c(r)
а – делимое,
b – делитель,
c – неполное частное,
r – остаток.
Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток. С помощью букв оно записывается так:
a = bc + r
Запишите эту формулу к себе в тетрадь и выучите.
-Как вы думаете, чем мы будем сегодня заниматься на уроке?
Работа по учебнику
№533 (1 столбик) письменно в тетради
Посмотрите внимательно на картинку, как правильно вычислять.
Решение задач на деление с остатком.
Решите задачи письменно в тетради
1) В пачке 57 тетрадей. В классе 26 учеников. Учитель раздал тетради поровну. Сколько тетрадей достанется каждому, сколько тетрадей останется?
2) Мама сварила 17 л варенья. Сколько двухлитровых банок ей необходимо взять, чтобы разлить все варенье? Сколько литров варенья останется?
Задача 529 стр. 100 (письменно в тетради)
Сначала узнайте массу 10 болванок.
После того, как узнаете массу 10 болванок, сможете узнать, сколько деталей по 18кг можно отлить и сколько чугуна останется.
Решение уравнений (письменно в тетради)
а) (38 + в) * 12 = 840
б) 14 * (р – 30) = 630
в) (43 – х) * 17 = 289
Решите уравнения и сделайте проверку.
Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть 






Таким образом, результатами деления с остатком являются два целых числа: 





Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).
- Примеры
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Определение[править | править код]
Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше[1].
Для вычисления неполного частного от деления 



когда
.
где полускобки 


Для отрицательного делителя нужно округлять частное в большую сторону:
когда
.
Операция «mod» и связь со сравнениями[править | править код]
Величина остатка может быть получена бинарной операцией «взятия остатка» от деления 

Не следует путать это обозначение с обозначением сравнения по модулю 

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства 

В программировании[править | править код]
| Язык | Неполное частное |
Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % |
Делимое | |
| Ada | mod |
Делитель | |
rem |
Делимое | ||
| Бейсик | |
MOD |
Не определено |
| Си (ISO 1990) | / |
% |
Не определено |
| Си (ISO 1999) | / |
% |
Делимое[3] |
| C++ (ISO 2003) | / |
% |
Не определено[4] |
| C++ (ISO 2011) | / |
% |
Делимое[5] |
| C# | / |
% |
Делимое |
| ColdFusion | MOD |
Делимое | |
| Common Lisp | mod |
Делитель | |
rem |
Делимое | ||
| D | / |
% |
Делимое[6] |
| Delphi | div |
mod |
Делимое |
| Eiffel | // |
\ |
Делимое |
| Erlang | div |
rem |
Делимое |
| Euphoria | remainder |
Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() |
MOD()
|
Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() |
ОСТАТ()
|
|
| FileMaker | Div() |
Mod() |
Делитель |
| Fortran | mod |
Делимое | |
modulo |
Делитель | ||
| GML (Game Maker) | div |
mod |
Делимое |
| Go | / |
% |
Делимое |
| Haskell | div
|
mod |
Делитель |
quot
|
rem |
Делимое | |
| J | |~ |
Делитель | |
| Java | /
|
%
|
Делимое[7] |
Math.floorDiv
|
Math.floorMod
|
Делитель (1.8+) | |
| JavaScript | .toFixed(0) | % |
Делимое |
| Lua | % |
Делитель | |
| Mathematica | Quotient
|
Mod |
Делитель |
| MATLAB | idivide(?, ?, 'floor') |
mod |
Делитель |
idivide |
rem |
Делимое | |
| MySQL | DIV |
MOD% |
Делимое |
| Oberon | DIV |
MOD |
+ |
| Objective Caml | mod |
Не определено | |
| Pascal | div |
mod |
Делимое[8] |
| Perl | Нет | % |
Делитель |
| PHP | Нет[9] | % |
Делимое |
| PL/I | mod |
Делитель (ANSI PL/I) | |
| Prolog (ISO 1995) | mod |
Делитель | |
| PureBasic | / |
Mod% |
Делимое |
| Python | // |
% |
Делитель |
| QBasic | |
MOD |
Делимое |
| R | %/% | %% |
Делитель |
| RPG | %REM |
Делимое | |
| Ruby | /
|
% |
Делитель |
| Scheme | modulo |
Делитель | |
| SenseTalk | modulo |
Делитель | |
rem |
Делимое | ||
| Tcl | % |
Делитель | |
| Verilog (2001) | % |
Делимое | |
| VHDL | mod |
Делитель | |
rem |
Делимое | ||
| Visual Basic | |
Mod |
Делимое |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
78 mod 33 = 12 78 div 33 = 2
Знак остатка[править | править код]
Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
- Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
- Знак остатка совпадает со знаком делителя: неполное частное округляет к
.
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.
Как запрограммировать, если такой операции нет?[править | править код]
Неполное частное можно вычислить через деление и взятие целой части: ![q=left[{frac {a}{b}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a5108d8efbb2b9259f9487fc6f9f7bb61aa7337)
![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
При отсутствии команды mod остаток программируется как 
Если 


Неполное частное и неотрицательный остаток от деления на степень двойки 


Обобщения[править | править код]
Вещественные числа[править | править код]
Если два числа 



Формально:
- если
, то
, где
.
- Пример
Деление 7,9 на 2,1 с остатком даёт:
(неполное частное);
(остаток).
Гауссовы целые числа[править | править код]
Гауссово число — это комплексное число вида 



,
где частное 

Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, 

Многочлены[править | править код]
При делении с остатком двух многочленов 

, причём
.
- Пример
(остаток 3), так как:
.
См. также[править | править код]
- Алгоритм Евклида
- Делимость
- Наибольший общий делитель
- Непрерывная дробь
- Сравнение по модулю
Примечания[править | править код]
- ↑ 1 2 Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
- ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
- ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the
/operator is the algebraic quotient with any fractional part discarded. [This is often called «truncation toward zero».]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится. - ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
- ↑ N3242=11-0012 (Working draft), текст совпадает с C99
- ↑ D language specification (англ.). dlang.org. Дата обращения: 29 октября 2017. Архивировано из оригинала 3 октября 2017 года.
- ↑ Арнолд, Кен, Гослинг, Дж., Холмс, Д. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
- ↑ Стандарт 1973 года: div — division with truncation.
- ↑ PHP: Arithmetic Operators — Manual. Дата обращения: 27 ноября 2014. Архивировано 19 ноября 2014 года.
- ↑ DIV — Unsigned Divide
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
8 : 2 = 4 (к.)
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как это записать?
8 : 3 = 2 (ост. 2)

Как сделать проверку?
2 • 3 + 2 = 8
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
16 : 7 = 2 (ост. 2)
23 : 8 = 2 (ост. 7)
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
43 : 8 = 5 (ост. 3)
остаток 3 < делимого 5
34 : 4 = 8 (ост. 2)
остаток 2 < делимого 4
Правило 3
Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
7 : 10 = 0 (ост. 7)
6 : 9 = 0 (ост. 6)
Порядок решения
14 : 5 = 2 (ост. 4)
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
10 : 5 = 2
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
4 < 5
Решение верно.
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
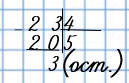
, где 23 – делимое, 4 – делитель, 5 – неполное частное, а 3 – остаток.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 76. Урок 29,
Петерсон, Учебник, часть 3
Страница 77. Урок 29,
Петерсон, Учебник, часть 3
Страница 79. Урок 30,
Петерсон, Учебник, часть 3
Страница 80. Урок 30,
Петерсон, Учебник, часть 3
Страница 81. Урок 31,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 32,
Петерсон, Учебник, часть 3
Страница 87. Урок 33,
Петерсон, Учебник, часть 3
Страница 108. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 60. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 35,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 17. Урок 6,
Петерсон, Учебник, часть 1
Страница 59. Урок 24,
Петерсон, Учебник, часть 2
Страница 91. Урок 40,
Петерсон, Учебник, часть 2
Страница 5. Урок 2,
Петерсон, Учебник, часть 3
4 класс
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 51. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 62. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 531,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 537,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 552,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1024,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1074,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1109,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 552,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 794,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Номер 437,
Мерзляк, Полонский, Якир, Учебник
Номер 499,
Мерзляк, Полонский, Якир, Учебник
Номер 516,
Мерзляк, Полонский, Якир, Учебник
Номер 727,
Мерзляк, Полонский, Якир, Учебник
Номер 1171,
Мерзляк, Полонский, Якир, Учебник
Задание 470,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 476,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 635,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 113,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 423,
Мерзляк, Полонский, Якир, Учебник
Номер 530,
Мерзляк, Полонский, Якир, Учебник
Номер 574,
Мерзляк, Полонский, Якир, Учебник
Номер 582,
Мерзляк, Полонский, Якир, Учебник
Номер 583,
Мерзляк, Полонский, Якир, Учебник
Номер 602,
Мерзляк, Полонский, Якир, Учебник
Номер 797,
Мерзляк, Полонский, Якир, Учебник
Номер 856,
Мерзляк, Полонский, Якир, Учебник
Номер 871,
Мерзляк, Полонский, Якир, Учебник
Номер 1123,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 139,
Мерзляк, Полонский, Якир, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 207,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 302,
Мерзляк, Полонский, Якир, Учебник
Номер 304,
Мерзляк, Полонский, Якир, Учебник
Номер 305,
Мерзляк, Полонский, Якир, Учебник
Номер 306,
Мерзляк, Полонский, Якир, Учебник
Как найти делимое при делении с остатком? заранее спасибо
Ирина Карагулова
Знаток
(317),
на голосовании
7 лет назад
Голосование за лучший ответ
Лолита Ивановна
Гуру
(3404)
7 лет назад
надо неполное частное умножить на делитель и прибавить остаток получишь делимое
Ирина КарагуловаЗнаток (317)
7 лет назад
спасибо
Лолита ИвановнаГуру (3404)
7 лет назад
рада помочь
Денис Гаран
Просветленный
(27862)
7 лет назад
A div B = C
A mod B = D
следовательно
B * C + D = A
Похожие вопросы
План урока
- Понятие деления с остатком.
- Сравнение остатка и делителя.
- Правило нахождения делимого.
Цели урока
- Знать понятия «неполное частное», «остаток».
- Уметь делить с остатком.
- Уметь решать задачи с помощью деления с остатком.
Разминка
- Какие компоненты деления вы знаете?
- Как найти делимое?
- Как найти делитель?
- Можно ли разделить число 8 на 3?
Как разделить число 15 на 4? Давайте решим задачу — разделите 15 орехов между 4 белками так, чтобы им досталось поровну орехов.
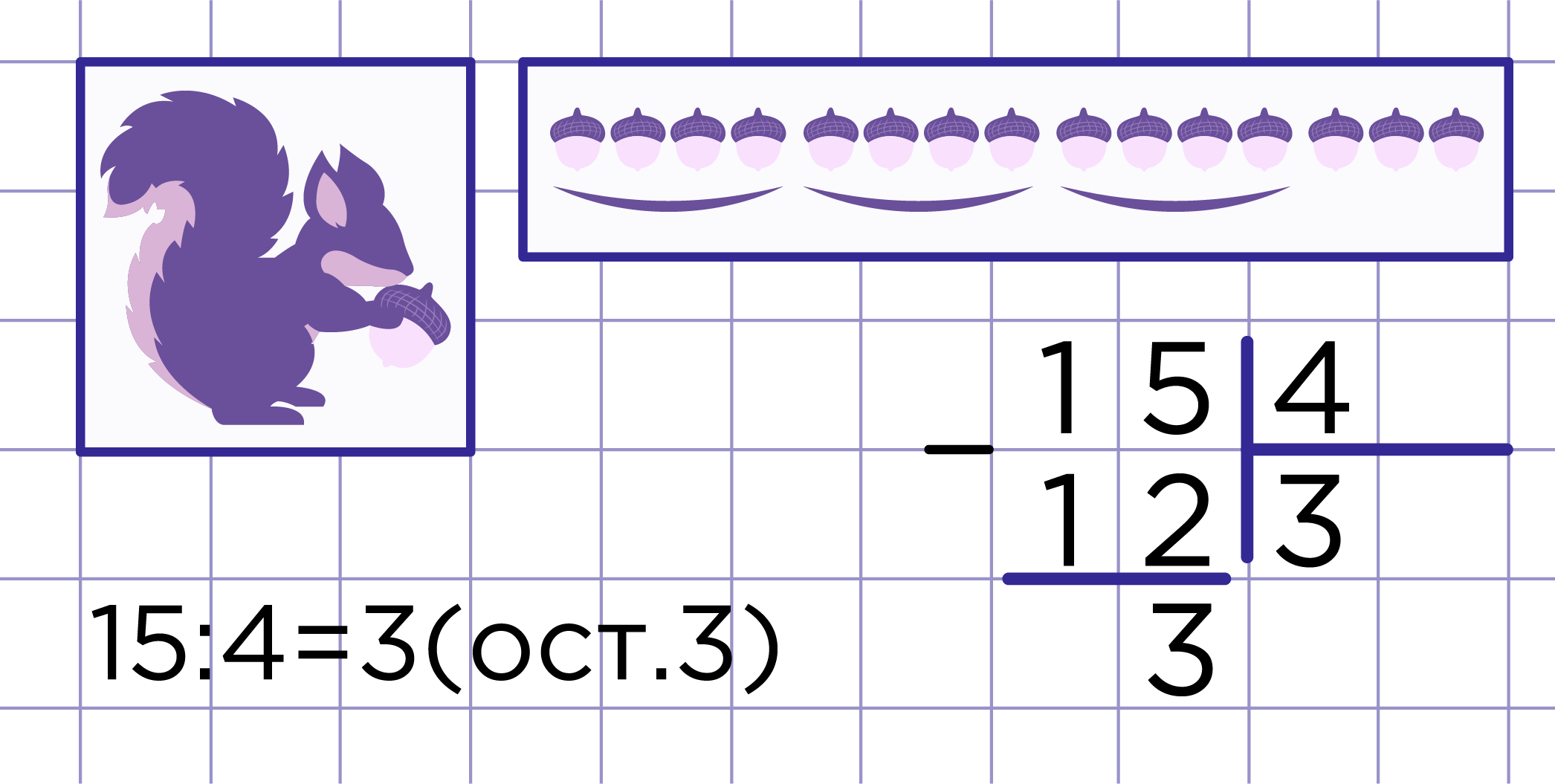
Рис. 1
На рис.1 показано, что каждой белке достанется по 3 ореха, но при этом еще 3 ореха останется. Можно записать следующее равенство:
15 = 4 · 3 + 3;
Рассмотрим еще один пример: 708 : 19 = 37 (ост. 5)
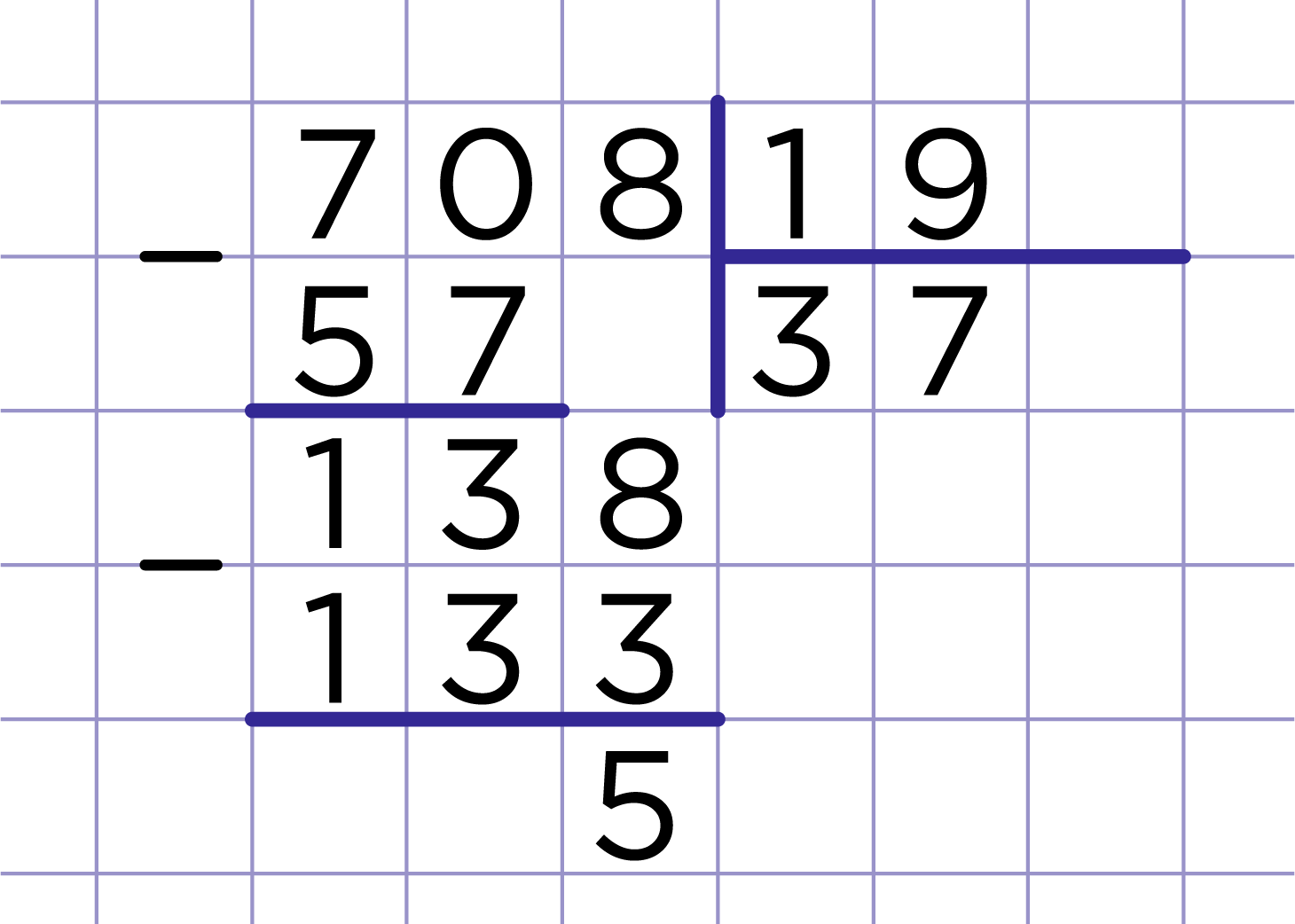
Рис. 2
Заметим, что 37 — это наибольшее число, произведение которого на 19 меньше делимого 708. Число 37 — неполное частное; число 5 — остаток.
Остаток всегда меньше делителя: 5 < 19.
Чтобы найти делимое, нужно делитель умножить на неполное частное и прибавить остаток.
a = bq + r, где a — делимое, b — делитель, q — неполное частное, r — остаток.
Может ли остаток быть равен нулю? Рассмотрим равенство: 34 = 17 · 2.
Можно равенство написать по-другому: 34 = 17 · 2 + 0. В таком случае говорят, что остаток равен нулю и число 34 делится нацело на число 17.
Оля разделила число 84 на некоторое число и получила остаток 4. Какое число делила Оля?
Решение
Найдем произведение неполного частного и делителя:
84 – 4 = 80.
Методом подбора найдем возможные делители числа 80.
80 = 80 · 1 = 40 · 2 = 20 · 4 = 16 · 5 = 10 · 8.
Так как остаток 4 должен быть меньше делителя, то делителем может быть любое из чисел 80, 40, 20, 16, 5, 10, 8.
Ответ: 80; 40; 20; 16; 5; 10; 8.
Выполните деление с остатком: 1) 48 : 5; 2) 678 : 24; 3) 882 : 40.
Найдите делимое, если делитель равен 12, неполное частное — 6, а остаток — 8.
Тетрадь стоит 16 р. Какое наибольшее количество тетрадей можно купить, имея 100 р.?
Петя разделил число 108 на некоторое число и получил остаток 10. На какое число делил Петя?
Контрольные вопросы
1. Как найти делимое (при делении с остатком)?
2. Может ли остаток быть больше делителя?
3. Что означает фраза «делится нацело»?
Итоги:
В случаях, когда одно число не делится нацело на другое, говорят о делении с остатком. Чтобы найти делимое, нужно неполное частное умножить на делитель и к произведению прибавить остаток.
Ответы
Упражнение 1
1) 9 (ост. 3); 2) 28 (ост. 6); 3) 22 (ост. 2).
Упражнение 2
80.
Упражнение 3
6 тетрадей.
Упражнение 4
49, 14 или 98.









