Оценка погрешности определения момента инерции
1. Найти и сравнить систематическую и
случайную ошибки определе-
ния
t.Случайную ошибку![]()
вычислить по формуле

Для доверительной вероятности P=0,95
и N=5,
=2,8.
Систематическая ошибка определяется
классом точности прибора и ошибкой,
связанной с конечной скоростью реакции
человека, которую можно принять равной
0,1с. В нашем случае приборной ошибкой
можно пренебречь по сравнению с этой
величиной и считать систематическую
ошибку равной 0,1с, а ошибку рассчитать
по формуле
![]()
2. Рассчитать и занести в таблицу 4
относительные ошибки определения
величин t, m и
d.
Таблица 4
|
Положение оси вращения |
|
|
|
|
J кгм2 (метод приведенной длины) |
|
Призма |
|||||
|
Призма |
3. Рассчитать максимальную абсолютную
ошибку определения момента инерции по
формуле

Результат определения момента инерции
с указанием абсолютной ошибки занести
в таблицу 4.
Примечание. Значения величин
gиизвестны с большой точностью, и
следовательно относительные ошибки,
вносимые округлением этих величин,
могут быть сделаны как угодно малыми,
т. е. заведомо меньшими, чем ошибки
измерения остальных величинm,
d, t .Практически
это означает, что при вычислениях
значенияgи
достаточно принять равными 9,81 м/с2и 3,14 соответственно.
Контрольные вопросы
1. Дайте определение гармонических
колебаний.
2. Что называется математическим
маятником, физическим маятником?
3. Что называется приведенной длиной
физического маятника?
4. Как выводится формула периода колебаний
физического маят-
ника ?
5. Найдите момент инерции физического
маятника, используемого в данной работе,
относительно оси, проходящей через
центр масс.
6. Почему при выполнении лабораторной
работы следует брать очень малые
амплитуды колебаний?
7. Как изменится частота колебаний
маятника, если его поднять на большую
высоту?
Cписок литературы
1. Детлаф А. А., Яворский Б. М. Курс
физики.М.: Высш. шк.,
1989.
2. Савельев И. В. Курс физики.М.:
Наука, 1989.Т. 2.
3. Методические указания к вводному
занятию по физическому практикуму.М.:
МИИТ, 1988.
4. Большова К.М., Пустовалов Г.Е., Краткий
курс общей физики, ч.I(2).М.:
Изд. МГУ, 1982.
Работа 5а определение ускорения свободного падения
Цель работы. Определение ускорения
свободного падения методом, основанным
на свойстве взаимной обратимости центра
качания и точки подвеса физического
маятника.
Введение
Период
колебаний физического маятника (см.
рисунок 5)
определяется по формуле
![]() (1)
(1)
где J
— момент инерции относительно
оси подвеса;
m
— масса маятника;
d
— расстояние
между осью вращения и центром тяжести
маятника.
Длина математического маятника с
периодом колебаний, равным периоду
колебаний данного физического маятника,
называется приведенной длиной физического
маятника. Эта величина определяется
соотношением
![]() (2)
(2)
Вывод формул (1) и (2) приведен во введении
к работе 5.
Точка, находящаяся на расстоянии
![]() от оси вращения по линии, проходящей
от оси вращения по линии, проходящей
через центр тяжести, называется центром
качания физического маятника. Можно
показать, что если ось вращения
поместить в центр качания, то маятник
будет совершать колебания с тем же
периодом. Для этого подставим в формулу
(2) момент инерции в соответствии с
теоремой Гюйгенса — Штейнера:
![]() .
.
Получим
![]() (3)
(3)
где![]() момент инерции
момент инерции
тела относительно оси, проходящей через
центр тяжести тела параллельно оси,
проходящей через точку подвеса.
Заметим, что из выражения (3) следует
![]() (4)
(4)
Если подвесить маятник так, чтобы ось
вращения проходила через центр качания,
то она будет находиться от центра тяжести
на расстоянии![]() Приведенную длину перевернутого маятника
Приведенную длину перевернутого маятника
можно найти по формуле (3), учитывая, что
расстояние от оси вращения до центра
тяжести![]() ,аmи
,аmи![]() остались прежними. Центр качания
остались прежними. Центр качания
перевернутого маятника по формуле (3)
будет находиться от оси вращения на
расстоянии
![]() .
.
Учитывая выражение (4), находим, что
![]() .
.
Таким образом, во всяком физическом
маятнике на прямой, проходящей через
центр тяжести (центр инерции), можно
указать пары точек, лежащих по разные
стороны от центра тяжести и являющихся
взаимно обратимыми, т. е. через них
проходят оси вращения, относительно
которых период колебаний маятника
одинаков.
УДК 531.535
С.Е. Пилипосян
ПОГРЕШНОСТИ ИЗМЕРЕНИЯ МОМЕНТА ИНЕРЦИИ ПРОИЗВОЛЬНОГО ТВЕРДОГО ТЕЛА
Нижегородский государственный технический университет им. Р.Е. Алексеева
Приведена оценка погрешностей измерений момента инерции неоднородного твердого тела, проведенных по методу регистрации периодов колебаний.
В измерениях применяются двойной жесткий подвес, секундомер, линейка и угломер. Выявлены условия эксперимента, в которых погрешности измерений минимальны и не превышают 0,5%.
Ключевые слова: момент инерции неоднородного твердого тела, физический маятник, двойной жесткий подвес, погрешность измерения коррелированных случайных величин, функция Н.Е. Жуковского.
Введение
Сложность геометрических форм и неоднородность выпускаемых изделий и механизмов затрудняют теоретический расчет важных характеристик этих тел – момента инерции и положения центра масс. В настоящее время успешно применяются различные методы, позволяющие измерить момент инерции и находить точку центра масс как для гигантских гидротурбин, самолетов, вагонов скоростных поездов, автомобилей так и для миниатюрных элементов часового механизма. Для каждого изделия (или его макета) применяется определенная методика и создается специальная установка, учитывающая его массу, размеры, форму и обеспечивающая минимальные погрешности в измерениях момента инерции.
В работе [1] показано, что метод регистрации периода колебаний для изделий или их макетов, обладающих радиусом инерции Я < 0,50 м (относительно центральной оси выбранного направления), обеспечивает большую точность, чем метод измерения приведенной длины. В приложении приведено описание методики и схема экспериментальной установки (подробнее см. [1]), позволяющих измерить момент инерции неоднородного тела с точностью не ниже 0,5 % и находить точку его центра масс с погрешностью не более чем 1 мм.
Такие измерения позволяют еще в стадии проектирования изделий (автомобилей, летательных аппаратов, вагонов, кораблей и т. д.) решить вопросы их маневренности (момент инерции) и устойчивости (положение центра масс). Высокая точность измерений требует всесторонней и точной оценки статистических и систематических погрешностей измерений, что позволяет уточнить соответствующие оценки, приведенные в работе [2].
1. Производные периода колебаний и чувствительность метода
Если центральная ось инерции твердого тела массы т фиксирована, то его центральный момент инерции 3 и радиус инерции Я относительно выбранной оси являются константами: 3 = тЯ. Период малых колебаний такого физического маятника вокруг оси, параллельной к выбранной центральной оси и находящейся от нее на расстоянии а, имеет вид
О, а)=^/4ЯЯ (аIЯ + Я /а)/* 4*Я (X + X1)/£ =7Ф+Х) =0′ Х) ,0)
где X=а IЯ – безразмерный параметр, удобный для дальнейшего рассмотрения.
В этом случае между переменными а и X устанавливается взаимно однозначная связь и для описания движения физического маятника они являются равносильными:
а=ЯX, Са=Я(Х, Да=ЯДХ, (I(а)Аа=(/(X)ДХ.
В теории функций комплексного переменного выражение 0,5 ( z+117 ), где 7=х + у -комплексное число, называют функцией Н.Е. Жуковского [3], ввиду того, что он весьма
© Пилипосян С.Е., 2012.
успешно применил эту функцию для решения многих важных практических задач. Из формулы (1) видно, что при Я = 0,125 м, когда Г.л =1 с, период колебаний можно представить в виде
или Т = w .
То (Я, X)=^(4ПЯI Я)(X + X1) 0,5(X + Х-1) ,
Если 0 < X <1 или 1< X <да, то связь Т и X является взаимно однозначной [3]. По-
видимому, обсуждаемую здесь задачу можно считать еще одним приложением функции Жуковского для действительного переменного X.
Постоянство Я означает, что если для расстояния а период колебаний равен Т, то для расстояния а получим такое значение периода Т , которое удовлетворяет равенству
Я2=агТо1% I ()- а2 = а2То2%1 (4П) – а2.
или аХ2 -ОС=(а22 -а12)4П1=(а -а1)(а2+а1)4П1.
Для отношения приращений величин Т и а , с учетом (1) получим
= (X – X-1)
Да ёа Т^3″
(2)
8
43
4,00
2,00
0,00
-2,00
-4,00
-6,00
,00
-10,00
-12,00
-14,00
-16,00
1 Лямбда
00 п, 00 2, )0 3, 00 4, 00 5, 00 6,0
‘ <
00
Рис. 1. Зависимость йТй I ёа от X
Если а > Яс, то ёТ01 ёа >0, а когда а < Яс, то ёТ01 ёа <0 (рис. 1). Кроме того,
-да, если а ^ 0 ( X ^ 0 )
с1Т
—= <¡0, если а = Я (X = 1) . (3)
ёа с
0, если а ^да (X ^да)
Из рис. 1 видно, что когда X существенно меньше единицы, нахождение расстояния а путем измерения периода колебаний Т (с заданной погрешностью ДТ ), позволяет более точно определить а, поскольку небольшое изменение а приводит к значительному изменению Т •
Момент инерции тела с массой т относительно оси вращения, параллельной к заданной центральной оси тела и находящейся от нее на расстоянии а представляется выражением
/ = таТ^/(4п2) =/ + та = тЯ2 + та = т(а ), где Т – период гармонических колебаний твердого тела. Следовательно,
/ = таТ^к / (4п2 ) —та = тЯ. (4)
Момент инерции тела можно представить в виде функции
У = У (т, а, Т) или У = У (т, а, Я ).
Центральный момент инерции / в этом случае оказывается функцией двух переменных т, Я. Величина Т в этих условиях является однозначной функцией расстояния а.
Следовательно, Т и а не являются независимыми переменными.
Погрешность измерения У необходимо оценить с учетом этой связи.
Дифференцируя выражение (4) для / по а, найдем зависимость приращения / от
изменения расстояния а на Да . Если считать, что т, g, п , известные с большой точностью, константы, то получим
а/
Д/ Да =
с аа
Г2таТ£ ёТ , mT02g
Л
— 2та
V
Да.
(5)
У
4п ёа 4п
Относительное изменение значения У , если значение а изменилось на малую величину Да и, вследствие этого, значение Т изменилось на ДТ, будет:
(/).
д/ 1 а/
у / аа
Да =
2таТК ёТ тТV
Л
V
‘тКаТ^ + т^ — 2та2
4п’
Л
ёа 4п
— 2та
Да
У
тЯ
V
2п
ёа
4п
Д а
тЯ а
Щ-
2 ёТ
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
а Т—0 + / — та V2п ёа . у
Да
тЯ^а
С учетом формулы (2), получим
( ^/с )а, Т
тК Л
ёТ
V 2п
аТ—1 + тЯ — та
2лЛ/Я VX
ёа (*—1)
Да
У
тЯ а
V 2п2
кТ-
ёа
– +1 — X2
1 Да
У
Я X
+ 1 — X2
ТК)
^^ ^л/^+ХДТ — ( Х Х ) п^Я Я
с с
Да =_£_а.д. — м)д.=
Я X 2п2 Я ёа Я
(6)
Да=
^+1—X’
Да Я X
= 0.
То есть истинное значение / не зависит от значения а, если расстояние а и соответствующее значение периода колебаний Т измерены без погрешностей. Однако на эксперименте измерение Т и а производится независимо и с ненулевой погрешностью. Следова-
с
с
тельно, несмотря на то, что измеряемые переменные Т и а жестко связаны, тем не менее, измерения их значений с погрешностью ДТ и Да, соответственно, не зависят друг от друга.
Чтобы выяснить, связаны ли знаки их отклонений от соответствующих средних значений ( Т ± ДТ, а ± Да ) или ( Т ± ДТ, а + Да ), необходимо провести множество совместных измерений этих величин в одних и тех же условиях эксперимента и, рассчитав коэффициент корреляции, убедиться, что в обсуждаемой нами задаче для этой пары величин он имеет отрицательное значение [4, 5]
* (Т’ a Ь^ГТТТ1 < 0 • (7)
° ( T0 ) П ( a )
Если предположить, что случайная величина J = J (m, a, T0) распределена по нор-
мальному закону, то на основании выражения (6), получим
Л
( )a, T
Г maaTg dT 2 2
-0–0 + mR – ma
V
2п da
Да X Tog dTo
У
mR’a 2% a da
Да + (l-X2
2Да.
a
^Tg^Ji Wx-1 + X ду. | (X-1 -X)
(8)
2nXR
дт+(1-x2;
П
R
Дa.
При условии независимости погрешностей ДТ и Да, можно считать, что
_ I/ г-
( ^ X. т|
( X-1 – X )
Л2
Дa
R
(9)
Из этой формулы, следует, что когда X=a / R = 1, то есть когда значение a=R = const, относительная погрешность измерения (SJ ) т определяется только погрешностью измерения времени ДТ . Для тела с радиусом инерции R = 0,125м она принимает значение
(SJ ) – ДТ = -1,4 ДТ=1,^78ДТ=3,96-ДТ •
( c Л’ Т V п2 0 л/0,125 0 , 0 , 0
При ДТ = 0,001c, получим
( J )a
=3,96 – ДТ = 0,4% •
(10)
(11)
Относительная погрешность, связанная с измерением массы тела, будет
Т2
Т Т g 2 п2
J = ma—–ma = mR ,
c 4п2 c
( J )
V . /m
1 J
, __c
J dm
Дm= —— R2Дm= . Следовательно, mR c m
( J )m, a, t| = J ^ )2 ^ ^^
Y
WX-1 + XДT
( X-1 – X )
V
Дa
R
(12)
Из (12) видно, что при Х=1, Ц < 0,125м, ДТ = 0,001с и Дт / т = 0,1%, относительная погрешность измерения момента инерции главным образом определяется абсолютной погрешностью измерения периода колебаний. Пусть значения величин п, т, Ц, Т, а нам известны абсолютно точно. Тогда изменение значения а на Да приведет к такому изменению значения Т , что центральный момент инерции останется неизменным. Приравнивая правую часть (12) к нулю, снова приходим к равенству (2)
c
c
c
ДТ^ ёТ0 (я, X) _ п (X — ^)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Да ёа ^[Кя ^ + X3
Это равенство показывает, насколько и в какую сторону (уменьшения или увеличения) сдвинется истинно среднее значение гауссова распределения периода малых колебаний Т твердого тела, обладающего радиусом инерции Яс, если истинно среднее значение гауссова распределения расстояния центральной оси тела от оси его вращения а=Яс X изменится на величину Да=Яс^. График этой зависимости в области определения 0<Xявляется важной характеристикой обсуждаемого метода измерения момента инерции твердого тела (рис. 1).
В этой связи представляют интерес производные более высокого порядка
(Я, X)/ ёа , являющиеся непрерывными функциями, обладающими двумя асимптотами и одним экстремальным значением (см. рис. 2-4).
В табл. 1 для заданного значения Да=0,001м (абсолютная погрешность измерения расстояния от оси вращения), Яс=0,05м, а=Да/Яс =0,02, ДГ=0,001сек (абсолютная погрешность измерения периода колебаний), и текущего значения X, приведены значения величин
ёТ ё2Т ё3Т ёТ
Т, Ь , —,
‘ пп’ ‘
пр ёа ёа
. Величина X по необходимости меняется с небольшим шагом
ёа ёа
ДХ= 0,000001 в интервале значений 0,05 <Х<100,0.
Поставленную в этой работе задачу лучше решить, выполняя два измерения при разных значениях а0. Сначала находим значение ё для расстояния а0, удовлетворяющего условию
X=а / Я =(а + ё)/ Я = 0,5 . Большое значение к обеспечивает высокую точность определения ё (рис. 1). Момент инерции в этих условиях, как следует из (12), определяется с относительной погрешностью ( &/) « 3 %. После нахождения центральной оси проводится ещё одно измерение
при X=а / Я =( а + ё) / Я =1,0, обеспечивающее высокую точность определения
12,00
: ё Т
■ ёа
X
00 1, 00 2, 00 3, 00 4, )0 5, )0 6, 00 7, 00 8,
1 0,00 – –
,00
,00
4,00
2,00
0,00
-2,00
-4,00
00
(5J ) »0,5% (на рис. 5 видно, что при 0,95R <a<1,05R значение AJ / J »0,4%).
^ с ‘ m, a, T с с с с
Рис. 2. Зависимость d2T0 / da2 от X
Согласно равенству (2) при X=a = 1 ^ dT = 0.
R dX
с
dT (Л^
Величина —=R— меняет знак при переходе точки X=a / R = 1. dX с da с
В интервале 0 < X <1 ^ dT < 0, lim dT = -го.
dX dX
В интервале 1< X <+да ^ dT > 0, lim dT = 0.
dX dX
Следовательно, в интервале 1< X <+да величина dT / dX обладает максимумом (рис. 1) и в точке максимума вторая производная равняется нулю (рис. 2).
=R d2T=п irl (-x6+6X4+3X2) (13)
dX2 с da2 2)1 g (X5 + X3)3/2 . ( )
d 2T
Вторая производная равняется нулю, когда —Х6 + 6Х4 + 3Х2 = 0. Ввиду того, что Х > 0, получаем равенство Х4 — 6Х2 — 3=0. Единственным физическим корнем этого уравнения является Х=2.5424. В этой точке d2T / dХ2 меняет знак с положительного на отрицательный (рис. 2). Величина d2T / dХ2 достигает своего минимума при некотором значении Х, после чего с ростом Х —монотонно стремится к нулю d2Т/ d)Х ——0. Чтобы найти значение Х, при котором dT / dХ принимает минимальное значение, вычислим величину (ГТ / d)).
^кз зп Ц Х4 (Х6 —15Х4 — т2—5) dХ3 ~cda3 ” 4)1 % (Х5 + Х3 )5 / 2 .
Когда Х —^+0, то величина dъT / dХ ——да.
т г л d3Т Зп Цс 1 „
Когда Х—+да, то величина-—— —-—+0 .
dХ3 4 % Х5 / 2
Найдём значение Х, при котором = 0 .
dХ3
Для этого нужно решить уравнение Х — 15Х4 — 13Х — 5=0 . После обозначения у = Х2, получим кубическое уравнение у —15у —13у—5=0.
С помощью обозначения у=х+5 приведём его к виду х3 — 88х—320=0. Решив это уравнение методом Кардана [6], получим х=10,84; у=15,84; Х=3,98.
В точке Х = 3,98 величина diT/d)) меняет свой знак с отрицательного на положительный (рис. 3).
Далее, после достижения своего максимума, с ростом Х монотонно стремится к
dХ3
нулю, оставаясь положительным. Чтобы найти значение Х в точке этого максимума, продифференцируем по Х и приравняем к нулю.
^ # = 3п КХ6 +140>6 +154>4 + 1т2 + 35)
ёХ4 с ёа4 8 g ‘ ‘ ,ч7’2
( х5+х3)7
(15)
15,00
10,00
5,00
0,00
-5,00
-10,00
-15,00
-20,00
-25,00
-30,00
X
00 2, 00 4,0 30 6, )0 8, 00 10 00 12
1
00
Рис. 3. Зависимость Ст / ёа от X
Л1СЛ .А ё4Т 105п К 1 Из выражения (15) видно, что когда Х ^+0, то величина-^- —-,
ёХ4 8 У g Х9 / 2
когда Х , то величина-^
ёТ -15л К 1
ёХ4 8 У g X’
С Т
Между этими асимптотическими предельными значениями функция- принимает ну-
ёХ4
левое значение, и при некотором значении X достигает своего минимального значения (рис. 4). Введя обозначение у = Х2, в равенство -5Х8 + 140Х6 + 154Х! +124Х2 + 35 = 0, получим
4 з 154 2 124 _ _
у – 28у–у–у – 7 = 0.
5 5
С 3Т
(16)
Решив (16), найдём значение X, при котором – достигает максимума. На рис. 1-4
ёХ3
приведены графики функций -,
ёт а2т аът с?т
ёа ёа2 ёаа ёа
для испытуемого тела с радиусом инер-
ции К = 0,05 м в зависимости от переменной X. Если привести эти графики для тела с радиусом инерции К =1 м (когда а=Х -1м), то эти же функции для тела с другим значением радиуса инерции Яс можно получить простым умножением на соответствующую степень Яс.
Систематическая относительная погрешность измерения 3 , связанная с немалым значением амплитуды угла отклонения физического маятника, представляется выражением / ч 3 (т, а, Т)-3 (т, а, Т) / 2ч/ 4 , , , ЧЛЧ2
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
(53= * ( ‘ , 7 ) ^ ‘ 0) =(1 + Х)(4(К(™(а))) -1).
3, (т, а, Т) п /
(17)
С поправкой на эту систематическую погрешность для 3 получим
3 (т, а, Т) = 3 (т, а, Т)-Д3 =
с 7 7 0 / с 7 7 / с, ф
= 3с (т, а, Т )-(3с (т, а, Т ) + та2)| 1 -(—К(вт(а))
2 Л
У 2
( 3с ( т, а, Т )+та2)(—К ( вт ( а ))) – та2 = 3 ( т, а, Т )(—К ( вт ( а ))
– та
Таким образом, измеренное значение момента инерции неоднородного твердого тела относительно центральной оси, параллельной выбранному направлению АА1, можно представить в виде
2 / „ т 2 / _ т 2
3 = 3с (m, a, 70)(1 ±(53са, т) = 3 (m, ^ Т)(1^(&/.)т +(&/.)2 +(5.7.) ) =
= 3С ( т, а, Т )
1+
/ Дт
т
2
^ Хл/х1 + ХДТ
о ‘ П
п2Я
‘( Х-1 – Х )
2
Я
Да
(18)
40,00
30,00
20,00
10,00
0,00
-10,00
-20,00
-30,00
-40,00
47 £ 1
00 2, 00 4, )0 1 6, )0 8, 00 10 00 12 00 14 00__д 16
00
3 (т, а, Т)=3(т, а, Т )(— К(вт (а)))
– та
Рис. 4. Зависимость й4Т / йа* от X
В монографии Гернета М.М. и Ротобыльского В.Ф. [2] для расчета погрешности измерений обсуждаемым здесь методом приведены две формулы, требующие уточнения:
&/ =^(&/„)2 +()2 +()2 +(ы.г)2 (ср. с формулой (I8)), где
&7 =1 1-4К
2
сф 2
п
2
I _0_
ч” К ,
(ср. с формулой (17)).
Систематическая погрешность неточно оценена (при Х=1 она равна нулю при любом значении амплитуды угла отклонения маятника) и неправильно использована. Она использована в качестве статистической, когда ее следует использовать как поправку.
В табл. 1 приведены величины Т, £ , СТ , СТ , СТ , СТ в диапазоне 0,05 < Х <100.
пр ёа ёа2 СС1 ёаА
Таблица 1
Яс = 0,05м, а=Да/Я =0,001м/0,05м=0,02=2%, Да/а= а/Х=0,02/ X
X т, с Ьпр , м СТ/Са=к/2 С2Т/Са2 С3Т/Са3 с?Ша4
0,050 2,0080 1,0025 -3,996E+2 2,410E+5 -2,407Е+8 3,37Е+11
0,300 0,8548 0,1817 -2,279E+1 2,823Е+3 -4,614Е+5 1,066Е+8
0,500 0,7090 0,1250 -8,509E+0 8,055Е+2 -7,991Е+4 1,084Е+7
0,800 0,6421 0,1025 -1,762E+0 2,399Е+2 -1,638Е+4 1,387Е+6
0,990 0,6342 0,1000 -6,438E-2 1,307Е+2 -7,882Е+3 5,562Е+5
1,000 0,6342 0,1000 0,000E+0 1,268Е+2 -7,610Е+3 5,327Е+5
1,010 0,6342 0,1000 6,248E-2 1,231Е+2 -7,350Е+3 5,105Е+5
1,050 0,6346 0,1001 2,946E-1 1,094Е+2 -6,410Е+3 4,321Е+5
1,100 0,6356 0,1005 5,49Ш-1 9,461Е+1 -5,431Е+3 3,537Е+5
1,200 0,6395 0,1017 9,609E-1 7,135Е+1 -3,962Е+3 2,426Е+5
1,300 0,6451 0,1035 1,273E+0 5,425Е+1 -2,941Е+3 1,707Е+5
1,400 0,6521 0,1057 1,51Ш+0 4,146Е+1 -2,215Е+3 1,227Е+5
1,500 0,6601 0,1083 1,693E+0 3,177Е+1 -1,689Е+3 8,976Е+4
1,800 0,6883 0,1178 2,020E+0 1,411Е+1 -7,923Е+2 3,812Е+4
1,900 0,6985 0,1213 2,08Ш+0 1,059Е+1 -6,248Е+2 2,929Е+4
2,000 0,7090 0,1250 2,127E+0 7,800Е+0 -4956Е+2 2,271Е+4
2,200 0,7306 0,1327 2,184E+0 3,813Е+0 -3,162Е+2 1,397Е+4
2,540 0,7681 0,1467 2,212E+0 1,854Е-2 -1,511Е+2 6,496Е+3
3,000 0,8187 0,1667 2,183E+0 -2,183Е+0 -5,531Е+1 2,513Е+3
3,800 0,9039 0,2032 2,071E+0 -3,121Е+0 -4,155Е+0 5,448Е+2
3,980025 0,9224 0,2116 2,042E+0 -3,139Е+0 -7,707Е-6 3,871Е+2
4,200 0,9447 0,2219 2,008E+0 -3,119Е+0 3,468Е+0 2,524Е+2
5,300 1,0506 0,2744 1,846E+0 -2,729Е+0 8,564Е+0 6,418Е+0
5,393369 1,0592 0,2789 1,833E+0 -2,689Е+0 8,579Е+0 2,922Е-5
5,393370 1,0592 0,2789 1,833E+0 -2,689Е+0 8,579Е+0 -3,394Е-5
5,500 1,0689 0,2841 1,819E+0 -2,644Е+0 8,562Е+0 -6,126Е+0
7,000 1,1985 0,3571 1,644E+0 -2,059Е+0 6,792Е+0 -2,870Е+1
10,000 1,4252 0,5050 1,397Е+0 -1,313Е+0 3,522Е+0 -1,473Е+1
20,000 2,0080 1,0025 9,990E-1 -4,920Е-1 7,193Е-1 -1,733Е+0
50,000 3,1716 2,5010 6,338E-1 -1,265Е-1 7,557Е-2 -7,515Е-2
100,000 4,4846 5,0005 4,484E-1 -4,481Е-2 1,343Е-2 -6,705Е-3
Погрешность измерения центрального момента инерции, согласно формуле (18), будет
( 53,)
т, а, Т
1
( Дт
х^Х-1+ХДт
о * П
Л2
( Х-1 – Х )
Да
(20)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
т’ У I Я У
На рис. 5 приведен график функции (20) для трех значений радиуса инерции испытуемого тела Я = 0,05 м; Я = 0,125 м; Я = 0,5 м при фиксированных значениях
ДТ = 0,001 сек; Да = 0,001 м; (Дт) / т=0,001.
Как видно из табл. 2 и на рис. 5, момент инерции твердого тела, обладающего радиусом инерции Я = 0,125 м относительно выбранной центральной оси, можно измерить с погрешностью не хуже 0,5 %, если измерения провести в условиях, когда 0,8 < Х < 1,1. Значения периода колебаний приведенные в табл. 2 соответствуют колебаниям тела с радиусом инерции Я = 0,125 м.
Таблица 2
2
X Т(сек) 5J;0,05 5J;0,125 5J; 0,5 Лd;0,05 Лd;0,125 Лd; 0,5
0,100 2,253 0,198 0,07921 0,0198 0,00716 0,01132 0,02264
0,200 1,617 0,096 0,03843 0,0097 0,02119 0,0335 0,067
0,300 1,352 0,0607 0,02434 0,0062 0,04204 0,06647 0,13294
0,400 1,207 0,0421 0,01694 0,0044 0,07233 0,11437 0,22874
0,500 1,121 0,0302 0,01225 0,0034 0,11753 0,18583 0,37166
0,600 1,068 0,0217 0,00896 0,0027 0,18885 0,29859 0,59719
0,700 1,034 0,0153 0,00658 0,0023 0,31258 0,49424 0,98847
0,800 1,015 0,0104 0,00495 0,0021 0,56761 0,89747 1,79493
0,900 1,006 0,0072 0,00411 0,0021 1,34817 2,13164 4,26328
1,000 1,003 0,0064 0,00412 0,0022 #ДЕЛ/0! #ДЕЛ/0! #ДЕЛ/0!
1,100 1,005 0,008 0,00477 0,0025 1,82121 2,87958 5,75917
1,200 1,011 0,0106 0,00575 0,0027 1,04066 1,64542 3,29085
1,300 1,020 0,0136 0,00686 0,003 0,78566 1,24224 2,48448
1,400 1,031 0,0165 0,00802 0,0033 0,662 1,04672 2,09344
1,500 1,044 0,0194 0,00919 0,0037 0,59083 0,93418 1,86837
1,600 1,058 0,0223 0,01036 0,004 0,54585 0,86307 1,72613
1,700 1,073 0,0251 0,01153 0,0044 0,5158 0,81555 1,6311
1,800 1,088 0,0278 0,0127 0,0047 0,49504 0,78272 1,56544
1,900 1,104 0,0305 0,01385 0,0051 0,48043 0,75963 1,51927
2,000 1,121 0,0332 0,015 0,0055 0,47011 0,74331 1,48663
2,100 1,138 0,0358 0,01614 0,0059 0,46288 0,73188 1,46375
2,200 1,155 0,0384 0,01728 0,0062 0,45793 0,72406 1,44812
2,300 1,173 0,041 0,01842 0,0066 0,45473 0,71899 1,43798
2,400 1,190 0,0436 0,01956 0,007 0,45287 0,71606 1,43211
2,500 1,207 0,0461 0,02069 0,0074 0,45208 0,7148 1,4296
2,600 1,225 0,0487 0,02183 0,0078 0,45213 0,71488 1,42976
2,700 1,242 0,0512 0,02297 0,0082 0,45286 0,71604 1,43208
2,800 1,260 0,0537 0,0241 0,0086 0,45415 0,71808 1,43615
2,900 1,277 0,0562 0,02524 0,009 0,4559 0,72084 1,44168
3,000 1,295 0,0587 0,02638 0,0095 0,45802 0,7242 1,44839
Заключение
Используемый метод измерения позволяет с помощью обычного секундомера, линейки, угломера и несложной экспериментальной установки [1] измерить с высокой точностью
центральный момент инерции неоднородных твердых тел, обладающих радиусом инерции Я < 0,50 м.
с 7
Положение точки центра масс определяется с точностью не хуже 1мм, а относительная погрешность измерения момента инерции не превышает 0,5 %.
Зависимость периода от амплитуды колебаний приводит к систематическим погрешностям измерения момента инерции.
Уточнены оценки погрешностей в ранее проведенных аналогичных экспериментах с измерением периода колебаний [2]. В частности, показано, что необходим учет корреляции между периодом колебаний Т и расстоянием а центра масс тела от оси вращения.
Чтобы обеспечить приведенные точности, необходимо провести два измерения: для значений X=а / Я « 0,5 и X=а / Я «1,0.
0,07 0,06 0,05 0,04 0,03 0,02 0,01
0,00
0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50
Рис. 5
Период малых колебаний и приведенная длина физического маятника выражаются функцией Н.Е. Жуковского – w с помощью формул
Т ( R, X) = 2^1 ( 2Rw) / £ = ^^L^, Lv=2Rw, Т = 2TJ2R / g, (L) = 2R ,
mm с о 7 V пр f min c
то есть при R = 0,125 м, Т (R, X)=yfw сек и L^= 25w м .
Удвоенное значение первой производной периода колебаний по параметру a=RX представляет собой чувствительность к используемого метода измерения величины d=a ~ a0 [1]. Поэтому приведены графики зависимости периода колебаний и его производных (до четвертого порядка включительно) от параметра X.
Приведены графики и таблицы погрешностей измерений для тел с радиусом инерции Я = 0,05 м; Я = 0,125 м; Яс = 0,50 м в зависимости от X (рис. 5).
Приложение
Для фиксации ориентации тела относительно оси вращения в этой работе используется жёсткий двойной подвес (рис. 6). На эксперименте точка центра масс С испытуемого тела оказывается на некотором расстоянии ё от выбранного направления АА1 . Поэтому закрепляем тело в точках пересечения заданного направления АА1 с поверхностью тела с помощью винтов, имеющих конусные наконечники, далее чуть-чуть расслабляем крепёжный винт А 1, вследствие чего тело свободно вращается в гравитационном поле притяжения земли вокруг оси АА1. Таким образом, точка С всегда оказывается внизу от прямой АА1 на расстоянии ё от неё в вертикальной плоскости АА1ВВ1.
Рис. 6. Схематический вид жёсткого подвеса с опытным образцом
С помощью двух пар дополнительных крепёжных винтов, имеющих конусные заострения и симметрично расположенных по отношению к точкам А и А1, фиксируем это положение (положение 1) образца. Регистрируем расстояние а0 оси АА1 от оси вращения ВВ1. Далее выводим из равновесия систему (образец + жёсткий подвес) на определенный угол
Фтах 20° и измеряем суммарное время N »1 колебаний, регистрируя амплитудное значение угла отклонения фтахЛГ после N колебаний. Находим период её колебаний Т . Поворачивая образец на угол 180° вокруг оси АА1, закрепляем его в новом положении (положение 2) и аналогичным образом измеряем период колебаний Т .
Далее образец поворачиваем на угол 90о вокруг оси АА1 по часовой стрелке или против часовой стрелки, закрепляем его в этом положении (положение 3) и снова измеряем период колебаний Т физического маятника. Поскольку на эксперименте обычно хорошо выполняется неравенство ё<<а , то в положении 3 обычно хорошо выполняется равенство % « а. Поэтому результаты измерения в этом положении могут служить приближенной оценкой для величины Jc.
Во всех трёх положениях стараемся измерять совокупное время как можно большего числа N колебаний при соблюдении условии, что угол ф поддается наблюдению невооруженным глазом. В каждом положении измерение повторяем три раза и определяем среднее значение периода (т). Периоды Т1 и Т2 соответствуют расстояниям % = % + ё, % = % ~ё от выбранной центральной оси тела до оси вращения ВВ1. В данном случае известна сумма расстояний параллельных осей от выбранной центральной оси твердого тела % + % = 2% и
необходимо найти ё= (% — % ) / 2 .
Конструкция подвеса позволяет изменять значение величины % дискретно с шагом, равным 15 мм. Равенство АВ=А1В1 выполняется с точностью 0,5 мм. Силы трения в точках В и В1 незначительны (качание на цилиндрических шипах со смазкой).
Величина ё определяется формулой (см. равенство (13) в работе [1])
ти)_. („.о
1Ч*2—(?+Т2:) (Т+т:)—1Чп21«
В зависимости от конкретных значений величин Я, %, ё во время измерений возможны три варианта: 1) X2 < <1; 2) X2 < 1 < ; 3) 1 < X2 < .
С учетом (П.1) и того, что % > % = % — 2ё, получим
Если 0<ё<а <%+ё<Я ^ X <X <1, то
0 0 с 2 1 3
Т >Т1 >тт1„ ^ Т — Т <(Т+Т22)—^ / я.
Следовательно, критерием первого варианта будет
% < 0,125- 0,99456- Т=0,12432- Т м.
Если же Я < а — ё < %+ё ^ 1< X < X , то
с 0 0 2 1 3
Т- < Т < Т ^ 16%0^2 / я—(Т+?22) > 0.
Следовательно, критерием третьего варианта будет
% >0,12432(Т2+Т2)/2 м .
Наконец, если % — ё <Я <%+ё ^ X2 <1<X, то
0,12432 (Т +Т2) / 2 м < % < 0,12432 Т 2м.
Это двойное неравенство является критерием второго варианта.
Вычисление значения ё по формуле (П.1) позволяет определить положение центральной оси, параллельной к заданному направлению АА1. Далее определяется момент инерции относительно найденной центральной оси при X«1,0 (второй вариант). Аналогично находится центральная ось в перпендикулярном к АА1 направлении. Таким же путём определяется направление третей центральной оси инерции, перпендикулярной к первым двум, и положение точки центра масс. Использованный метод и конструкция подвеса позволяют также определить центробежные моменты инерции испытуемого неоднородного тела для найденной тройки центральных ортогональных осей [7].
Учет массы и момента инерции жесткого подвеса приведен в работе [1].
Библиографический список
1. Пилипосян, С.Е. Измерение момента инерции произвольного твердого тела // Труды НГТУ. – Н.Новгород, 2010. № 4(83). С. 100-110.
2. Гернет, М.М. Определение моментов инерции / М.М. Гернет, В.Ф. Ратобыльский. – М.: Машиностроение, 1969. – 315 с.
3. Лаврентьев, М.А. Методы теории функции комплексного переменного / М.А. Лаврентьев, Б.В. Шабат. – М.: Наука, 1973. – 736 с.
4. Худсон, Д. Статистика для физиков: [пер. с англ.] /Д. Худсон; под ред. Е.М. Лейкина. – 2-е изд. – М.: Мир, 1970. – 292 с.
5. Яноши, Л. Теория и практика обработки результатов измерений: [пер. с англ.] /Л. Яноши; под ред. Н.П. Клепикова. – 2-е изд. – М.: Мир, 1968. – 462 с.
6. Смирнов, В.И. Курс высшей математики. В 2-х т. Т 1. / В.И. Смирнов. – М.: Наука, 1967. -480 с.
7. Стороженко, В.А. Синхронизация вращения в задаче определения главной центральной оси инерции неоднородного твёрдого тела. Проблемы механики / В.А. Стороженко. – М.: Физма-тлит, 2003.
Дата поступления в редакцию 13.04.2012
S.E. Piliposian
MEASUREMENT ERROR OF RANDOM SOLID BODY MOMENT OF INERTIA
Nizhny Novgorod State Technical University n.a. R.Y. Alekseev
The article contains the estimation of random solid body moment of inertia measurement error. The measurements were performed based on the method of vibration period recording.
A dual hard suspension, a ruler, an angle gage and a time-interval recorder were used in measurements. The work identifies experiment conditions, which provide minimum (not exceeding 0.5%) measurement error.
Key words: heterogeneous solid body moment of inertia, physical pendulum, dual hard suspension, measurement error of correlated varieties, Joukowski function.
Томский межвузовский центр дистанционного образования
Томский государственный университет систем управления и радиоэлектроники (ТУСУР)
Кафедра промышленной электроники (ПрЭ)
Лабораторная работа по курсу «Общая физика»
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЁРДЫХ ТЕЛ
Целью настоящей работы является определение момента инерции твердых тел и экспериментальная проверка справедливости теоремы Штейнера на примере физического маятника.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на Миллисекундомер 9. Физический Миллисекундомер выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средняя величина периода колебаний маятника:
Формула для экспериментального расчета момента инерции прямого тонкого стержня:
 , (3.2)
, (3.2)
s сис (t) – систематическая абсолютная погрешность.
Мерой точности результатов измерений является относительная погрешность. Формула для расчета погрешности косвенных измерений:
Класс точности прибора не указан, выбираем значение абсолютной погрешности ∆ l как половину цены деления (0,005 м).
Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину:
Выражение теоремы Штейнера:
где, I0 –момент инерции относительно оси, проходящий через центр масс;
l – расстояние между осями.
Доверительный интервал для l 2 :
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Результаты прямых и косвенных измерений представлены в таблице.
| 2 | 15 | 18,567 | 1,237 | 0,0625 | 0,0340 |
| 3 | 15 | 18,166 | 1,211 | 0,0441 | 0,0274 |
| 4 | 15 | 18,086 | 1,206 | 0,0289 | 0,0220 |
| 5 | 15 | 18,527 | 1,235 | 0,0169 | 0,0176 |
| 6 | 15 | 20,129 | 1,342 | 0,0081 | 0,0144 |
| 7 | 15 | 25,056 | 1,670 | 0,0025 | 0,0124 |
На основании полученных опытных данных рассчитаем среднюю величину периода колебаний маятника по формуле (3.1) и результаты занесём в таблицу 1.
Рассчитаем относительную погрешность момента инерции по формуле (3.4)
Рассчитаем доверительный интервал σ( I ) для каждого значения момента инерции I по формуле (3.9) и результаты занесем в таблицу 2.
Определим t , l 2 , I с учетом доверительных интервалов и результаты занесем в таблицу 2 для каждого значения.
Таблица доверительных интервалов.
| № измерения | l 2 — σ( l 2 ) | l 2 + σ( l 2 ) | σ( I ) | I — σ( I ) | I + σ( I ) |
| 1. | 0,0812 | 0,0870 | 0,0011 | 0,0406 | 0,0428 |
| 2. | 0,0600 | 0,0650 | 0,0009 | 0,0331 | 0,0349 |
| 3. | 0,0420 | 0,0462 | 0,0008 | 0,0267 | 0,0282 |
| 4. | 0,0273 | 0,0305 | 0,0008 | 0,0212 | 0,0228 |
| 5. | 0,0156 | 0,0182 | 0,0007 | 0,0169 | 0,0183 |
| 6. | 0,0072 | 0,0090 | 0,0008 | 0,0136 | 0,0152 |
| 7. | 0,0020 | 0,0030 | 0,0012 | 0,0112 | 0,0136 |
Рассчитаем коэффициенты a и b линеаризованного графика
методом наименьших квадратов:
| N | X | y | xy | x^2 | Y^2 |
| 1 | 0,0841 | 0,0417 | 0,003507 | 0,00707 | 0,00174 |
| 2 | 0,0625 | 0,0340 | 0,002125 | 0,00391 | 0,00116 |
| 3 | 0,0441 | 0,0274 | 0,001208 | 0,00194 | 0,00075 |
| 4 | 0,0289 | 0,0220 | 0,000636 | 0,00084 | 0,00048 |
| 5 | 0,0169 | 0,0176 | 0,0003 | 0,00029 | 0,00031 |
| 6 | 0,0081 | 0,0144 | 0,000116 | 0,00007 | 0,00021 |
| 7 | 0,0025 | 0,0124 | 3,1E-05 | 0,00001 | 0,00015 |
 |
0,2471 | 0,1695 | 0,007923 | 0,01412 | 0,0048 |
S1 =  ; S1 =0.2471
; S1 =0.2471
S2 =  ; S2 = 0,1695
; S2 = 0,1695
S3 =  ; S3 = 0,007923;
; S3 = 0,007923;
S4 =  ; S4 = 0,01412;
; S4 = 0,01412;
S5  ; S5 = 0.037757;
; S5 = 0.037757;
S6 =  ; S6 =0,0048;
; S6 =0,0048;
Используя график линеаризованной зависимости I = f (l 2 ), изображённой на рис.4.1 определим собственный момент инерции I 0 относительно оси проходящей через его центр масс, что составило:
Произведём расчёт момента инерции прямого тонкого стержня длиной d относительно оси перпендикулярной стержню и проходящей через его середину по формуле (3.11):
Экспериментальное значение массы стержня определяем по коэффициенту наклона прямой, m=(0,0340 кг×м 2 – 0,0144 кг×м 2 )/(0,0625 м 2 – 0,0081м 2 )=0,0196 кг×м 2 /0,0544 м 2 =0,360 кг.
Анализ графика на рис.4.1. показывает, что через экспериментальные точки и доверительные интервалы можно провести прямую линию. Следовательно, зависимость I = f (l 2 ) является линейной, значит, зависимость момента инерции твёрдого тела от квадрата расстояния от оси вращения до центра масс подтверждена экспериментально.
Найденное значение момента инерции I 0 прямого тонкого стержня длиной d на графике и рассчитанное по формуле (3.11) совпадают.
В результате проделанной лабораторной работы мы определили момент инерции I 0 физического маятника относительно оси, проходящей через центр масс, и момент инерции относительно оси, не проходящий через центр его масс и проверили справедливость теоремы Штейнера на примере физического маятника.
6. Контрольные вопросы.
6.1 Как формулируется понятия инерции материальной точки и твёрдого тела?
Внутреннее свойство тел сохранять состояние своего движения в отсутствии сил и реагировать на их действия изменением состояния движения, сопротивляясь этим изменениям, называют, в общем случае, инерционностью.
6.2 В каких ситуациях применима теорема Штейнера?
Если известен момент инерции тела относительно любой оси, проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера. Суть, которой состоит в применении формулы:
где l – расстояние между осью симметрии тела и осью вращения,
I 0 – момент инерции тела относительно оси симметрии.
Момент инерции I относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
6.4 Под действием какой силы совершается колебательное движение маятника?
Колебательные движения физического маятника совершаются под действием силы тяжести около неподвижной горизонтальной оси, не проходящей через его центр тяжести. Силу тяжести P = mg можно разложить на две составляющие, одна из которых P 2 уравновешивается реакцией подвеса. Под действием другой P1 маятник приходит в движение. На основании второго закона Ньютона для динамики вращательного движения запишем:
где M – момент вращающей силы;
ε – угловое ускорение.
6.5 Является ли момент инерции аддитивной величиной?
Момент импульса твёрдого тела складывается из моментов импульса составляющих его материальных точек, т.е. момент импульса – аддитивная величина. Момент импульса материальной точки относительно произвольной точки пространства называют векторное произведение радиус-вектора материальной точки в системе отсчёта выбранной точки:
6.6 Объяснить метод определения момента инерции с помощью физического маятника.
Используя график линеаризованной зависимости I = f ( l 2 ) можно вычислить массу стержня и собственный момент инерции, а также сравнить результаты расчёта и опыта.
Для этого сравним наше уравнение с уравнением прямой
где а – угловой коэффициент,
Угловой коэффициент определяется как
где ∆ x – приращение аргумента,
∆ y – соответствующее приращение функции.
6.7 Какой маятник называется физическим?
Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести совершает колебания около неподвижной горизонтальной оси, не проходящей через центр масс.
Период Т малых колебаний физического маятника равен:
6.8 При каких формальных допущениях справедлива формула периода колебаний маятника (3.7)?
6.9 Как записывается основной закон динамики вращательного движения?
Основное уравнение (закон) динамики вращательного движения: при воздействии момента внешних сил твёрдое тело вращается вокруг неподвижной оси с угловым ускорением, прямо пропорциональным моменту сил и обратно пропорциональным моменту инерции тела относительно данной оси:
где М – результирующий момент внешних сил, действующих на тело,
ß – угловое ускорение,
I – момент инерции тела относительно оси вращения.
Источник
Лабораторная работа: Определение момента инерции твердых тел
Федеральное Агентство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Лабораторная работа по курсу «Общая физика»
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
Выполнил: студент группы
Целью настоящей работы является изучение основных законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока и сравнение его с расчетным значением.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Схема экспериментальной установки на основе машины Атвуда приведена на рис. 2.1.
Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Опоры 9 используют для регулировки положения установки на лабораторном столе.
Принцип работы машины Атвуда заключается в следующем. Когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если же на один из грузов (обычно на правый) положить перегрузок, то система выйдет из равновесия, и грузы начнут двигаться с ускорением.
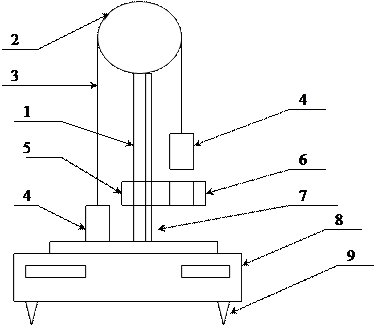
5 – средний кронштейн;
9 – регулировочная опора.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средние значение времени и средние значение квадрата времени 2 > прохождения грузом с перегрузкомпутиh :
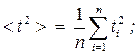
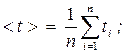
Абсолютная суммарная погрешность измерения времени прохождения пути h :
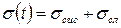
Абсолютная случайная погрешность измерения времени прохождения пути h :
стандартная абсолютная погрешность измерения времени:
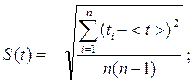
n – число измерений;
– среднее значение времени прохождения пути.
Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения путиh :
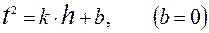 (3.7)
(3.7)
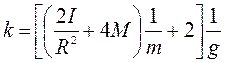 установки:
установки:
где I − его момент инерции блока ;
g – ускорение свободного падения.
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Результаты измерений времени прохождения груза
| Название: Определение момента инерции твердых тел Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 22:14:53 05 июня 2011 Похожие работы Просмотров: 1201 Комментариев: 15 Оценило: 4 человек Средний балл: 3.8 Оценка: неизвестно Скачать |
| Номер измерения | h1 =28,0 см | h2 =22,0 см | h3 =18,0 см | h4 =12,0 см | h5 =8,0 см |
| 1 | 3,617 | 3,281 | 3,092 | 2,348 | 1,986 |
| 2 | 3,73 | 3,23 | 2,891 | 2,346 | 1,921 |
| 3 | 3,797 | 3,414 | 3,133 | 2,521 | 2,099 |
| 4 | 3,597 | 3,414 | 3,061 | 2,323 | 2,058 |
| 5 | 3,837 | 3,238 | 2,882 | 2,412 | 2,096 |
 |
3,716 | 3,315 | 3,012 | 2,39 | 2,032 |
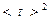 |
13,815 | 10,999 | 9,082 | 5,717 | 4,134 |
Из таблицы методического указания к лабораторному практикуму по физике А.Г. Риппа определим коэффициент Стьюдента.
Расчет погрешностей для построения графиков при коэффициенте
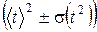 , с 2
, с 2
| Номер серии опытов |
Среднеквадра-тичное отклонение 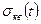 , с , с |
Случайная погрешность 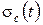 , с , с |
Абсолютная погрешность 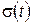 , с , с |
|
| 1 | 0,05 | 0,11 | 0,11 | 13,815 ± 0,8 |
| 2 | 0,04 | 0,08 | 0,08 | 10,999 ± 0,5 |
| 3 | 0,05 | 0,11 | 0,11 | 9,082 ± 0,7 |
| 4 | 0,04 | 0,08 | 0,08 | 5,717 ± 0,4 |
| 5 | 0,04 | 0,08 | 0,08 | 4,134 ± 0,3 |
Определяем абсолютную систематическую приборную погрешность измерения времени согласно методическому указанию к лабораторному практикуму по физике А.Г. Риппа
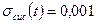 с.
с.
Метод наименьших квадратов для построения прямых по экспериментальным точкам :
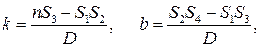
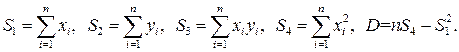
k= 0,49 с 2 /м угловой коэффициент прямой
b= 0,06 с 2 отрезок, отсекаемый прямой от оси OY
Искомая зависимость имеет вид: t 2 = 0,49∙ h , с 2 (4.1)
Вычислим значения ординат прямой линии для двух контрольных точек при произвольных значениях h по выражению 4.1:
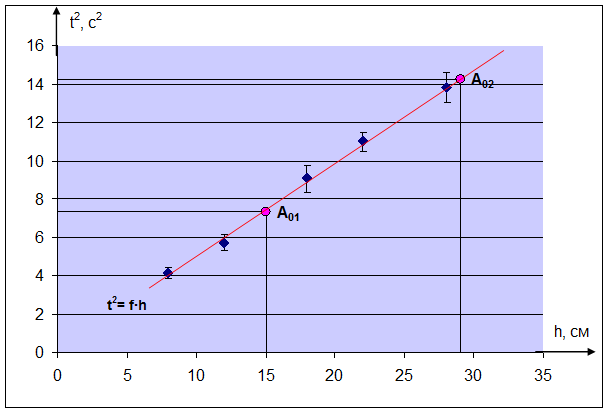
Рисунок 4.1. Зависимость квадрата времени t 2 от пройденного пути h
Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:
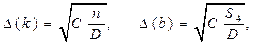

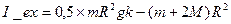 I_ex = 16986 г∙см 2
I_ex = 16986 г∙см 2
Абсолютная погрешности косвенного определения момента инерции блока I э в ходе эксперимента, по формуле:
 ∆(I_ex) = 552 г∙см 2
∆(I_ex) = 552 г∙см 2
Экспериментальное значение момента инерции блока:
Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок (латунь, r = 8400 кг/м 3 ), рассчитать его момент инерции.
Объём сплошного диска V_CD= π∙d∙R 2
Масса сплошного диска m_CD= p∙ V_CD
m_CD = 890 г = 0,89 кг
Момент инерции сплошного диска I_CD= 1/2∙ m_CD∙r2 2
Так как оси, проходящие через центры масс вырезанных дисков, не совпадают с осью вращения всего блока, то момент инерции I_can каждого диска находится по теореме Штейнера.
Объём каждого выреза V_can= π∙d∙ r2 2
Масса каждого вырезанного диска m_can= p∙V_can
m_can=142 г = 0,142 кг
Момент инерции каждого вырезанного диска относительно его центра масс:
Ic=1/2∙m_can∙ r2 2 Ic = 639 г∙см 2
вырезанного диска в метрах
Момент инерции каждого вырезанного диска относительно оси вращения блока:
I_can=Ic+ m_can∙ r1 2 I_can = 639 г∙см 2
Момент инерции цилиндрического отверстияI отв относительно оси, проходящей через центр масс блока, определяем по формуле:
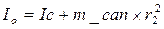 = 2911 г∙см 2
= 2911 г∙см 2
Момент инерции блока с тремя вырезами в виде малых дисков
I_an= I_CD-3∙ I_can I_an = 16298 г∙см 2
Полученные экспериментальным и аналитическим способами моменты инерции можно сравнить, получив отличие между ними в процентах, при помощи нижеследующего соотношения:
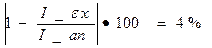
Значение собственного момента инерции,полученное в ходе эксперимента равно:
Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок, рассчитан его момент инерции:
Значение собственного момента инерции,полученное в ходе эксперимента, больше расчетного
Несовпадение экспериментального результата с расчетным можно объяснить тем, что не учитывался момент сил трения. Это и привело к завышенному значению собственного момента инерции блока в эксперименте.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое момент сил и момент инерции?
Моментом силы относительно оси называется физическая величина, численно равная произведению величины составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на плечо этой составляющей, т.е. на кратчайшее расстояниеr от оси вращения до линии действия
Момент силы относительно оси есть вектор, направленный вдоль этой оси и связан с направлением вращения правилом правого винта.
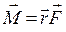
Момент инерции характеризует инерционные свойства вращающихся тел. Чем больше момент инерции тела, тем труднее изменить его угловую скорость. Момент инерции во вращательном движении аналогичен массе тела в поступательном движении. Момент инерции тела относительно некоторой оси зависит от распределения его массы относительно оси вращения.
где r – расстояние от элемента dm до оси вращения.
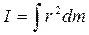 Момент инерции всего тела запишется в виде интеграла
Момент инерции всего тела запишется в виде интеграла
где интегрирование осуществляется по всему телу.
2. Моменты каких сил действуют на блок?
 Т1 и Т2 – силы натяжения нитей.
Т1 и Т2 – силы натяжения нитей.
На блок действуют моменты сил натяжения нитей:
Вращательное движение блока описывается уравнением:
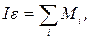 Рис. 6.1
Рис. 6.1
— сумма моментов сил, приложенных к блоку.
Согласно рис.6.1 вращательное движение блока описывается уравнением
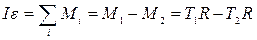
3. Как рассчитать момент инерции блока?
Сформулировать теорему Штейнера.
Момент инерции блока рассчитывается как:
где I диск – момент инерции сплошного диска;
I отв – момент инерции цилиндрического отверстия (“дырки”).
Момент инерции цилиндрического отверстияI отв относительно оси, проходящей через центр масс блока, определяем согласно теоремы Штейнера.
Момент инерции I относительно произвольной оси, равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин; точность вычислений.
Источник
Adblock
detector
