Содержание:
- Пример с решением
- Приближенные вычисления с помощью степенных рядов
- Вычисление интеграла
ПОСТАНОВКА ЗАДАЧИ: Вычислить приближенно с помощью дифференциала значение функции  в точке
в точке 
План решения:
Если приращение  аргумента х мало по абсолютной величине, то
аргумента х мало по абсолютной величине, то
 1. Выбираем точку а, ближайшую к
1. Выбираем точку а, ближайшую к  и такую, чтобы легко вычислялись значения
и такую, чтобы легко вычислялись значения 
2. Вычисляем 
3. По формуле (1) вычисляем  .
.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример с решением
Вычислить приближенно с помощью дифференциала значение функции  в точке
в точке 
Решение:
1. Ближайшая к 1,97 точка, в которой легко вычислить значения  — это точка
— это точка 
2. Вычисляем:
 3. По формуле (1) имеем
3. По формуле (1) имеем
 Ответ.
Ответ. 
Возможно вам будут полезны данные страницы:
Пример: Приближенные вычисления с помощью степенных рядов
Вычислить интеграл
 с точностью
с точностью  разложима в степенной ряд, имеющий радиус сходимости
разложима в степенной ряд, имеющий радиус сходимости  Решение:
Решение:
Практические вычисления обычно сводятся к суммированию того или иного числового ряда. В данном случае такой ряд получается, если разложить подынтегральное выражение в степенной ряд и проинтегрировать его почленно.
1. Разлагаем подынтегральную функцию в степенной ряд по степеням 
и определяем его область сходимости.
2. Степенной ряд можно интегрировать почленно по любому отрезку, принадлежащему интервалу сходимости. Поэтому, интегрируя почленно полученный ряд и используя формулу Ньютона-Лейбница, получаем
 3. Вычисляем сумму числового ряда с заданной точностью (оценивая остаток ряда).
3. Вычисляем сумму числового ряда с заданной точностью (оценивая остаток ряда).
ЗАМЕЧАНИЕ. Если разложить подынтегральную функцию в ряд не по степеням  , а по степеням
, а по степеням  , то ряд будет сходится быстрее, т.е. для обеспечения заданной точности может потребоваться меньше слагаемых, однако в итоге вычисления оказываются более сложными.
, то ряд будет сходится быстрее, т.е. для обеспечения заданной точности может потребоваться меньше слагаемых, однако в итоге вычисления оказываются более сложными.
Пример: Вычислить интеграл
 с точностью
с точностью  .
.
Решение:
1. Разлагаем подынтегральную функцию в ряд Тейлора по степеням  :
:
 Разложение справедливо при всех
Разложение справедливо при всех  .
.
2. Интегрируем почленно полученный ряд:
 3. Оценим остаток ряда. Так как ряд знакочередующийся,
3. Оценим остаток ряда. Так как ряд знакочередующийся,
 и
и  то справедливо неравенство
то справедливо неравенство
 Для вычисления интеграла с заданной точностью достаточно взять два члена ряда, так как
Для вычисления интеграла с заданной точностью достаточно взять два члена ряда, так как
 4. Производя вычисления, получаем
4. Производя вычисления, получаем
 Ответ.
Ответ. 
Пример: Пользуясь разложением в ряд , вычислить с точностью до 0,0001.
Решение:
Чтобы можно было пользоваться формулой (2), необходимо выразить значение аргумента в радианной мере. , = ^ = £,0.3491
Получаем  Подставляя это значение в формулу, получаем
Подставляя это значение в формулу, получаем

Полученный ряд является знакочередующимся и удовлетворяет условиям Лейбница. Так как  , то этот
, то этот
и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом,

Пример: Вычислить с точностью до 0,01.
Решение:
Воспользуемся разложением  , где 2 (см. пример 5 в предыдущей теме):
, где 2 (см. пример 5 в предыдущей теме):
 Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
 Таким образом, мы можем отбросить этот остаток и получаем
Таким образом, мы можем отбросить этот остаток и получаем

Пример Вычислить с точностью до 0,0001.
Решение:
Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.
 так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
 поэтому его и следующие за ним члены можно отбросить.
поэтому его и следующие за ним члены можно отбросить.


Лекции:
- Умножение матриц
- Линейные дифференциальные уравнения второго порядка
- Взаимное расположение плоскостей
- Уравнения касательной и нормали
- Наименьшее значение функции
- Декартова система координат: примеры решения
- Реляционная модель данных
- Арифметические n-мерные векторные пространства
- Операции над множествами
- Фундаментальная система решений
Разложение функции в ряд Маклорена.
1.
f
(x)
= ex.

Ряд

сходится к функции ех
на всей числовой оси.
2.
f
(x)
= cos
x.
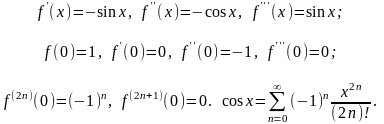
Аналогично

.
Ряд
Маклорена для sin
x
и cos
x
сходится к ним на всей числовой оси, т.
е. R
= ¥.
3.

Согласно
формуле суммы членов геометрической
прогрессии со знаменателем х,
|x|<1,
имеем

Интегрируя
левую и правую части равенства от 0 до
х,
при |x|<1
получаем
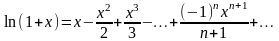
,
Очевидно,
область сходимости полученного ряда
х
( ̶ 1; 1].
4.
f
(x)
= (1+ x)α,
где х > 1, α – любое действительное
число.




Полученный
ряд называется биномиальным.


При
любом α данный степенной ряд сходится
к функции (1+ x)α
на (–1;
1).
5.
f
(x)
= arctg
x.
Используем сумму геометрической
прогрессии со знаменателем –t2
( |t|
< 1).

Интегрируя
левую и правую части по t
от 0 до х
( |x|
< 1) получаем

Этот
ряд сходится на интервале [ ̶ 1; 1].
6.
f
(x)
= arcsin x.
Рассмотрим
функцию

Разложим
её в ряд, используя разложение ряда (1+
х)α
при α = –
½

Это
разложение справедливо при R
= 1. Интегрируя левую и правую части от
0 до х
находим
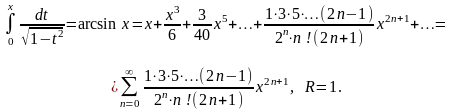
Замечание.
Можно показать во всех полученных
разложениях, что Rn(x)→0
при п
→ ¥.
Вычисление определенных интегралов с помощью рядов
Степенные
ряды имеют разнообразные приложения.
С их помощью с любой заданной точностью
вычисляют значения функций (в частности
значения π и e).
Значительную роль играют степенные
ряды в приближенных методах решений
дифференциальных уравнений. Определенные
интегралы от различных типов функций
за малым исключением не вычисляются по
формуле Ньютона – Лейбница, например,





и
др.
С
помощью рядов находят приближенные
значения таких определенных интегралов,
которые или не выражаются через
элементарные функции или сложны для
вычислений. Среди них часто встречающиеся
в практических приложениях математики.
Рассмотрим
несколько
примеров.
-
Пусть
требуется вычислить интеграл

.
Здесь
первообразная от

не
является элементарной функцией. Для
вычисления
этого интеграла разложим подынтегральную
функцию в ряд

заменяя
в разложении

,тогда

.
Интегрируя
обе части этого равенства в пределах
от 0 до a,
получим

С
помощью этого равенства мы можем при
любом a
вычислить данный интеграл с любой
степенью точности.
2.
Пусть требуется вычислить интеграл

Этот интеграл не берется в элементарных
функциях, поскольку первообразная
функции
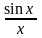
не является элементарной. В то же время
эта первообразная легко выражается в
виде степенного ряда.
Из
равенства

получаем

,
последний
ряд сходится при всех значениях x.
Интегрируя
почленно, получим

.
Сумма
ряда вычисляется с любой заданной
степенью точности при всех a.
Сводная
таблица основных формул по теме
«Функциональные ряды»
|
Понятие |
Определение, |
|
Функциональный ряд |
Ряд вида где |
|
Степенной ряд |
х0 х0 |
|
Радиус ходимости |
По признаку По |
|
Ряд Тейлора |
f + …+ + … |
|
Ряд Маклорена |
f + …+ + … |
|
Разложение |
|
ПРИМЕРЫ
РЕШЕНИЯПРАКТИЧЕСКИХ ЗАДАЧ
Пример
1.Найти
область сходимости степенного ряда

.
Решение.

.
Найдем радиус сходимости ряда по
формуле (4):

.
Интервал
сходимости ряда (–5; 5). Исследуем
сходимость ряда на концах интервала
сходимости. При

получим ряд

,
который сходится по признаку Лейбница.
При

получим ряд

,
который сходится (это ряд Дирихле).
Область сходимости данного ряда

.
Пример
2.
Определить интервал сходимости ряда

.
Решение.
Применяя признак сходимости Даламбера,
получим

Так
как предел не зависит от x
и меньше единицы, то значит ряд сходится
при всех значениях x.

.
Пример
3.
Определить интервал сходимости ряда

.
Решение.
Этот ряд расходится при всех значениях
x,
кроме

,
так как

при
,
каково бы ни было x,
отличное от 0.

Пример
4.
Определить интервал сходимости ряда

.
Решение.
Здесь


.
Поэтому
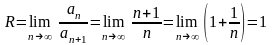
.
Следовательно,
данный ряд сходится на интервале (–1;
1).
Исследуем
поведение ряда на концах интервала
сходимости, то есть в точках

.
При
x
= 1 получаем гармонический ряд

(он расходится).
При
x
= –1 получаем ряд

.
Он сходится в силу признака
Лейбница .
Данный ряд сходится в любой точке
полуинтервала

и расходится вне его.
Пример
5. Разложить
в ряд по степеням х функцию

.
Воспользуемся
разложением

Полагаем

и получим
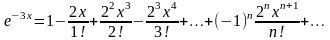
.
Отсюда

.
Пример
6. Разложить
в ряд по степеням х функцию
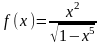
.
Запишем

и воспользуемся разложением

Положим

,

.
Тогда


или

Пример
7. Разложить
функцию
в ряд по степеням
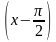
Воспользуемся
разложением функции f
(x) в ряд Тейлора
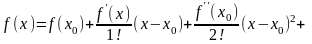
В последней формуле
примем х0 = π / 2. Последовательно
Дифференцируя,
найдём:
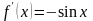
;

;

;

;

;

;

;

;

;

;
и т.д., таким образом

Пример
8 Вычислить
определенный интеграл
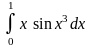
с точностью
до 0,001
Решение.
Разложим
подынтегральную функцию в степенной
ряд. Воспользуемся
уже известным рядом:

.
Заменив в нем x
на
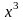
,
получим

.
Умножим обе части равенства на

:
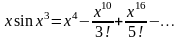
,
отсюда
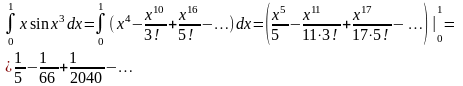
Замечаем, что
третий член ряда по абсолютной величине
меньше 0,001. Следовательно, для решения
данной задачи, согласно признаку
Лейбница, надо взять сумму первых двух
членов, что обеспечит требуемую точность:

.
ЗАДАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найти
область сходимости степенных рядов:
1.
;
2.

;
3.
;
4.
.
Ответы:1).
[ ̶ 1,5; 0,5] ; 2). ( ̶∞;+∞); 3). [ ̶

/3;
/3 ]; 4). [ ̶ 2; 2)
Разложить
в ряд по степеням
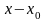
функции:
6.
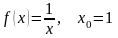
7.

8
10.

18
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приближённые вычисления определённых интегралов с помощью рядов. Первая часть.
Пусть требуется вычислить определенный интеграл $intlimits_{a}^{b}f(x)dx$ с некоторой наперёд заданной точностью $varepsilon$. Если непосредственное нахождение первообразной подынтегральной функции $f(x)$ чересчур громоздко, или же интеграл $int f(x)dx$ вообще не берётся, то в этих случаях можно использовать функциональные ряды. В частности, применяются ряды Маклорена, с помощью которых получают разложение в степенной ряд подынтегральной функции $f(x)$. Именно поэтому в работе нам будет нужен документ с рядами Маклорена.
Степенные ряды, которые мы и станем использовать, сходятся равномерно, поэтому их можно почленно интегрировать по любому отрезку, лежащему внутри интервала сходимости. Схема решения подобных задач на вычисление интегралов с помощью рядов проста:
- Разложить подынтегральную функцию в функциональный ряд (обычно в ряд Маклорена).
- Произвести почленное интегрирование членов записанного в первом пункте функционального ряда.
- Вычислить сумму полученного во втором пункте числового ряда с заданной точностью $varepsilon$.
Задачи на вычисление интегралов с помощью рядов популярны у составителей типовых расчётов по высшей математике. Поэтому в данной теме мы разберём пять примеров, в каждом из которых требуется вычислить определенный интеграл с точностью $varepsilon$.
Пример №1
Вычислить $intlimits_{0}^{frac{1}{2}}e^{-x^2}dx$ с точностью до $varepsilon=10^{-3}$.
Решение
Сразу отметим, что интеграл $int e^{-x^2}dx$ не берётся, т.е. первообразная подынтегральной функции не выражается через конечную комбинацию элементарных функций. Иными словами, стандартными способами (подстановка, интегрирование по частям и т.д.) первообразную функции $e^{-x^2}$ найти не удастся.
Для таких задач есть два варианта оформления, поэтому рассмотрим их отдельно. Условно их можно назвать “развёрнутый” и “сокращённый” варианты.
Развёрнутый вариант оформления
Запишем разложение функции $e^x$ в ряд Маклорена:
$$e^x=1+x+frac{x^2}{2}+frac{x^3}{6}+ldots$$
Данное разложение верно при всех $xin{R}$. Подставим $-x^2$ вместо $x$:
$$e^{-x^2}=1-x^2+frac{left(-x^2right)^2}{2}+frac{left(-x^2right)^3}{6}+ldots=1-x^2+frac{x^4}{2}-frac{x^6}{6}+ldots$$
Интегрируем полученное разложение на отрезке $left[0;frac{1}{2}right]$:
$$intlimits_{0}^{frac{1}{2}}e^{-x^2}dx=intlimits_{0}^{frac{1}{2}}left(1-x^2+frac{x^4}{2}-frac{x^6}{6}+ldotsright)dx=\
=left.left(x-frac{x^3}{3}+frac{x^5}{10}-frac{x^7}{42}+ldotsright)right|_{0}^{1/2}=
frac{1}{2}-frac{1}{3cdot{2^3}}+frac{1}{10cdot{2^5}}-frac{1}{42cdot{2^7}}+ldots$$
Получили сходящийся знакочередующийся ряд. Это значит, что если для вычисления приближенного значения заданного интеграла взять $k$ членов полученного ряда, то погрешность не превысит модуля $(k+1)$-го члена ряда.
Согласно условию, точность $varepsilon=10^{-3}$. Так как $frac{1}{42cdot{2^7}}=frac{1}{5376}<10^{-3}$, то для достижения требуемой точности достаточно ограничиться первыми тремя членами знакочередующегося ряда:
$$intlimits_{0}^{frac{1}{2}}e^{-x^2}dxapproxfrac{1}{2}-frac{1}{3cdot{2^3}}+frac{1}{10cdot{2^5}}=frac{443}{960}.$$
Погрешность полученного равенства не превышает $frac{1}{5376}$.
Однако суммировать обычные дроби – дело утомительное, поэтому чаще всего расчёты ведут в десятичных дробях:
$$intlimits_{0}^{frac{1}{2}}e^{-x^2}dxapproxfrac{1}{2}-frac{1}{3cdot{2^3}}+frac{1}{10cdot{2^5}}approx{0{,}5}-0{,}0417+0{,}0031approx{0{,}461}.$$
Разумеется, в этом случае нужно учитывать погрешность округления. Первое слагаемое (т.е. $0{,}5$) было рассчитано точно, поэтому никакой погрешности округления там нет. Второе и третье слагаемые брались с округлением до четвёртого знака после запятой, посему погрешность округления для каждого из них не превысит $0,0001$. Итоговая погрешность округления не превысит $0+0{,}0001+0{,}0001=0{,}0002$.
Следовательно, суммарная погрешность равенства $intlimits_{0}^{frac{1}{2}}e^{-x^2}dxapprox{0{,}461}$ не превысит $0{,}0002+frac{1}{5376}<10^{-3}$, т.е. значение интеграла вычислено с требуемой точностью.
Отмечу, что большинство авторов методичек и учебных пособий не учитывают погрешность округления, хоть это и не совсем корректно. В дальнейших примерах данной темы я буду упоминать про эту погрешность, если она возникнет.
Сокращённый вариант оформления
Запишем разложение функции $e^x$ в ряд Маклорена:
$$e^x=sumlimits_{n=0}^{infty}frac{x^n}{n!}$$
Данное разложение верно при всех $xin{R}$. Подставим $-x^2$ вместо $x$:
$$e^{-x^2}=sumlimits_{n=0}^{infty}frac{left(-x^2right)^n}{n!}=sumlimits_{n=0}^{infty}frac{(-1)^ncdot{x}^{2n}}{n!}$$
Интегрируем полученный ряд на отрезке $left[0;frac{1}{2}right]$:
$$intlimits_{0}^{frac{1}{2}}e^{-x^2}dx=intlimits_{0}^{frac{1}{2}}sumlimits_{n=0}^{infty}frac{(-1)^ncdot{x}^{2n}}{n!}dx=
sumlimits_{n=0}^{infty}frac{(-1)^n}{n!}intlimits_{0}^{frac{1}{2}}x^{2n}dx=\
=sumlimits_{n=0}^{infty}frac{(-1)^n}{n!}left.frac{x^{2n+1}}{2n+1}right|_{0}^{1/2}=
sumlimits_{n=0}^{infty}frac{(-1)^ncdotleft(frac{1}{2}right)^{2n+1}}{n!cdot(2n+1)}=
sumlimits_{n=0}^{infty}frac{(-1)^n}{n!cdot(2n+1)cdot{2^{2n+1}}}$$
Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $varepsilon$):
$$sumlimits_{n=0}^{infty}frac{(-1)^n}{n!cdot(2n+1)cdot{2^{2n+1}}}=frac{1}{2}-frac{1}{24}+frac{1}{320}-frac{1}{5376}+ldots$$
Все рассуждения, что были сделаны относительно погрешностей в развёрнутом варианте оформления остаются в силе, т.е.
$$intlimits_{0}^{frac{1}{2}}e^{-x^2}dxapproxfrac{1}{2}-frac{1}{3cdot{2^3}}+frac{1}{10cdot{2^5}}approx{0{,}461}.$$
Чем сокращённый вариант записи лучше развёрнутого?
Во-первых, нам не нужно угадывать, сколько членов ряда взять в изначальном разложении, чтобы вычислить определенный интеграл с заданной точностью. Например, мы записали в самом начале решения:
$$e^{-x^2}=1-x^2+frac{x^4}{2}-frac{x^6}{6}+ldots$$
Однако почему мы решили, что нужно взять именно четыре члена ряда? А вдруг нужно взять два члена ряда или пять, или сто? Если бы только шестой член ряда оказался меньше чем $varepsilon$, – что тогда? А тогда пришлось бы возвращаться в самое начало решения, добавлять ещё пару членов ряда и интегрировать их. А если и этого не хватит, то проделать эту процедуру ещё раз.
Сокращённый вид записи таким недостатком не страдает. Мы получаем числовой ряд, записанный в общем виде, поэтому можем брать столько его членов, сколько потребуется.
Далее, при интегрировании в развёрнутом способе записи мы находили первообразную четыре раза. При интегрировании в сокращённом способе записи, по сути, мы нашли лишь первообразную для $x^{2n}$.
Исходя из вышеперечисленных причин, я предпочитаю именно сокращённый способ записи. В дальнейнем все решения в этой теме будут оформлены в сокращённой форме.
Ответ: $intlimits_{0}^{frac{1}{2}}e^{-x^2}dxapprox{0{,}461}$.
Пример №2
Вычислить определённый интеграл $intlimits_{0}^{0{,}2}frac{1-cosfrac{5x}{3}}{x}dx$ с точностью до $varepsilon=10^{-3}$, разложив подынтегральную функцию в ряд Маклорена и проинтегрировав почленно.
Решение
Начнём с разложения подынтегральной функции $frac{1-cosfrac{5x}{3}}{x}$ в ряд Маклорена. Запишем разложение функции $cos{x}$ в ряд Маклорена:
$$cos{x}=sumlimits_{n=0}^{infty}frac{(-1)^ncdot{x}^{2n}}{(2n)!}$$
Данное разложение верно при всех $xin{R}$. Подставим вместо $x$ дробь $frac{5x}{3}$:
$$cos{frac{5x}{3}}=sumlimits_{n=0}^{infty}frac{(-1)^ncdot{left(frac{5x}{3}right)}^{2n}}{(2n)!}=
sumlimits_{n=0}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}.$$
Теперь разложим $1-cosfrac{5x}{3}$:
$$
1-cosfrac{5x}{3}=1-sumlimits_{n=0}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}
$$
Забирая из суммы $sumlimits_{n=0}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}$ первый член, получим:
$$sumlimits_{n=0}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}=1+sumlimits_{n=1}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}$$
Следовательно:
$$
1-sumlimits_{n=0}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}=1-left(1+sumlimits_{n=1}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}right)=\
=-sumlimits_{n=1}^{infty}frac{(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}
=sumlimits_{n=1}^{infty}frac{-(-1)^ncdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}=sumlimits_{n=1}^{infty}frac{(-1)^{n+1}cdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}.
$$
Последнее, что остаётся – это разделить на $x$:
$$
frac{1-cosfrac{5x}{3}}{x}=frac{1}{x}cdotsumlimits_{n=1}^{infty}frac{(-1)^{n+1}cdot{5^{2n}}cdot{x}^{2n}}{3^{2n}cdot{(2n)!}}=
sumlimits_{n=1}^{infty}frac{(-1)^{n+1}cdot{5^{2n}}cdot{x}^{2n-1}}{3^{2n}cdot{(2n)!}}.
$$
Интегрируем данное разложение на отрезке $left[0;frac{1}{5}right]$:
$$
intlimits_{0}^{0{,}2}frac{1-cosfrac{5x}{3}}{x}dx=intlimits_{0}^{frac{1}{5}}sumlimits_{n=1}^{infty}frac{(-1)^{n+1}cdot{5^{2n}}cdot{x}^{2n-1}}{3^{2n}cdot{(2n)!}}dx=
sumlimits_{n=1}^{infty}frac{(-1)^{n+1}cdot{5^{2n}}}{3^{2n}cdot{(2n)!}}intlimits_{0}^{frac{1}{5}}{x}^{2n-1}dx=\
=sumlimits_{n=1}^{infty}frac{(-1)^{n+1}cdot{5^{2n}}}{3^{2n}cdot{(2n)!}}cdotleft.frac{x^{2n}}{2n}right|_{0}^{1/5}=
sumlimits_{n=1}^{infty}frac{(-1)^{n+1}}{{2n}cdot 3^{2n}cdot{(2n)!}}
$$
Получили знакочередующийся ряд. Запишем несколько первых членов этого ряда (до тех пор, пока записанный член не станет меньше $varepsilon$):
$$sumlimits_{n=1}^{infty}frac{(-1)^{n+1}}{{2n}cdot 3^{2n}cdot{(2n)!}}=frac{1}{36}-frac{1}{7776}+ldots$$
Так как $frac{1}{7776}<varepsilon$, то для вычисления интеграла с точностью $varepsilon$ достаточно первого члена полученного числового ряда:
$$intlimits_{0}^{0{,}2}frac{1-cosfrac{5x}{3}}{x}dxapproxfrac{1}{36}approx{0{,}028}.$$
Ответ: $intlimits_{0}^{0{,}2}frac{1-cosfrac{5x}{3}}{x}dxapprox{0{,}028}$.
Продолжение темы вычисления интегралов с помощью рядов Маклорена продолжим во второй части.
Печатать книгу
Численное интегрирование
Численное интегрирование
| Сайт: | Электронные курсы ТПУ |
| Курс: | Информационные технологии 1 |
| Книга: | Численное интегрирование |
| Напечатано:: | Гость |
| Дата: | Четверг, 25 Май 2023, 09:47 |
Оглавление
- Численное интегрирование
- 1. Методы прямоугольников
- 2. Метод трапеций
- 3. Процедура вычисления интеграла
- 4. Вычисление интегралов с заданной точностью и оценка методов интегрирования
- 5. Основная часть программы
Численное интегрирование
Задача вычисления интегралов возникает во многих областях прикладной математики. В большинстве случаев не удается найти аналитической формулы, т. е. выразить неопределенный интеграл в виде алгебраических и трансцендентных функций. Даже если аналитическая формула находится, то она получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем другими способами. Распространенными являются также случаи, когда подынтегральная функция задается графиком или таблицей экспериментально полученных значений. В таких ситуациях используют различные методы численного интегрирования, которые основаны на том, что интеграл представляется в виде предела интегральной суммы (суммы площадей), и позволяют определить эту сумму с приемлемой точностью.
Пусть требуется вычислить определенный интеграл

при условии, что A и B конечны и f(x) является непрерывной функцией x во всем интервале A ≤ x ≤ B. Значение интеграла I представляет собой площадь, ограниченную кривой f(x), осью x и прямыми x = A, x = B. Вычисление I проводится путем разбиения интервала от A до B на множество меньших интервалов, приближенным нахождением площади каждой полоски, получающейся при таком разбиении, и дальнейшем суммировании площадей этих полосок.
Суть методов численного интегрирования состоит в замене подынтегральной функции f(x) вспомогательной, интеграл от которой легко вычисляется в элементарных функциях. Обычно f(x) заменяется некоторым интерполяционным многочленом, что приводит к квадратурным формулам:
 ,
,
где xi – узлы интерполяции;
i – произвольный номер узла;
Ci – коэффициенты;
R – остаточный член, или погрешность метода.
Неучет (отбрасывание) R приводит к погрешности усечения. К этим погрешностям в процессе вычислений добавляются погрешности округления. Геометрическая интерпретация численного интегрирования представлена на рис. 5.1. и 5.2.
1. Методы прямоугольников
Самыми простыми методами численного интегрирования являются методы прямоугольников. При этом непосредственно используется замена определенного интеграла интегральной суммой:
 , hi = xi – xi –1 , xi –1 ≤ zi ≤ xi
, hi = xi – xi –1 , xi –1 ≤ zi ≤ xi
В качестве точек zi могут выбираться левые (z i= xi –1) или правые (zi = xi) границы элементарных отрезков. Обозначая yi = f(xi) , получим формулы:
- метод левых прямоугольников: I = h1 y0 + h2 y1 +…+ hn yn –1 + R;
- метод правых прямоугольников: I = h1 y1 + h2 y2 +…+ hn yn + R;
- более точным является метод средних прямоугольников, использующий значения функции в средних точках элементарных отрезков:
 ;
;
xi -1/2 = 0,5(xi -1 + xi) = xi -1 + 0,5 hi, i = 1, 2, …, n.
Для частного случая hi = h = const формулы примут вид
 ;
;
;
, h = (B – A) / n.
Если координату выразить через начальную точку и принять, что I ≈ S, то получим формулы, готовые для применения в операторе цикла с переменной:
– для метода левых прямоугольников;
– для метода правых прямоугольников;
– для метода средних прямоугольников.
Рис. 5.1. Графическая интерпретация методов прямоугольников
2. Метод трапеций
В данном методе f(x) заменяется на линейный интерполяционный многочлен, т. е. на элементарном отрезке [xi –1, xi] подынтегральная функция представляет собой отрезок прямой линии. Значение I в пределах [xi –1, xi], равное площади криволинейной фигуры, заменяется площадью прямоугольной трапеции с высотой hi и основаниями f(xi –1), f(xi):
Si = 0,5 (yi -1 + yi) hi, i = 1, 2, …, n.
После сложения этих соотношений получим формулу трапеций
.
Если шаг интегрирования постоянный (hi = h = const), то
.
Если координату выразить через начальную точку и принять, что I » S, то получим формулу, готовую для применения в операторе цикла с переменной
.
Рис. 5.2. Графическая интерпретация метода трапеций
3. Процедура вычисления интеграла
Процедура вычисления интеграла при заданном числе разбиений и границами интегрирования должна иметь входные параметры этих величин и выходной параметр результата. Выходной параметр должен содержать перед собой ключевое слово var для передачи параметра по ссылке.
Здесь должен вычисляться шаг в соответствии с числом разбиений.
Сумма может вычисляться при помощи цикла for по числу разбиений или при помощи циклов repeat или while с перемещением текущей точки от начальной до конечной. Например, для метода правых прямоугольников процедура может быть описана так:
procedure integral(a,b:real;n:integer; var s:real);
var i:integer; h:real;
begin
h:=abs(b-a)/n; s:=0;
for i:=1 to n do
s:=s+h*f(a+h*i);
end;
Конечно, перед описанием процедуры необходимо описать подынтегральную функцию f(x). Смотрите описание функций в 3.1.
Замечание! При вычислении интеграла функция должна браться по модулю, т. к. площадь фигуры всегда положительна, независимо от того, что функция может быть и отрицательной. Для упрощения программы модуль можно вставить сразу в описание функции.
4. Вычисление интегралов с заданной точностью и оценка методов интегрирования
Оценка погрешности усечения R в формулах численного интегрирования оказывается трудоемкой и малоэффективной из-за трудностей оценки производных высокого порядка подынтегральных функций. Поэтому в практических расчетах для достижения требуемой точности вычислений или допустимой погрешности E используют правило Рунге.
Согласно этому правилу вычисление заданного интеграла проводят для разных интервалов разбиения отрезка [A,B]. Так, если начальное число интервалов разбиения есть n и соответствующее ему приближенное значение интеграла – In, то для числа интервалов 2n получим значение интеграла I2n. Число интервалов можно увеличивать в 2, 3 и т. д. раз по сравнению с базовым значением n. При двукратном увеличении числа отрезков погрешность D приближенного значения интеграла для методов прямоугольников и трапеций оценивается как
Δ = | In – I2n | / 3.
Если Δ > E, то количество интервалов разбиения [A,B] опять увеличивают вдвое, т. е. значение I вычисляют для 4n. Такое удвоение повторяют до тех пор, пока не выполнится условие Δ < E. Необходимо помнить, что общая погрешность вычислений, равная сумме погрешностей усечения и округления, сначала с ростом интервалов разбиения уменьшается за счет уменьшения ошибки усечения до некоторого «критического» значения nкр, а затем увеличивается из-за увеличения ошибок округления.
Таким образом, не для всякой функции можно получить результат с заданной погрешностью.
- Методы левых и правых прямоугольников практически не применяются из-за их низкой точности.
- В некоторых случаях метод средних дает лучшую точность, чем метод трапеций.
5. Основная часть программы
Основная часть программы должна содержать ввод с клавиатуры начального числа разбиений и погрешности вычислений. Для обеспечения заданной точности интеграла процедура его вычисления должна выполняться в цикле. Причём сначала сохраняется старое значение интеграла, затем увеличивается число разбиений и вычисляется новое значение интеграла. Цикл работает пока разница между старым и новым значениями интеграла не станет меньше заданной точности.
При выводе результата полезно также вывести конечное число разбиений, чтобы знать, на сколько частей нужно разбить отрезок для обеспечения заданной точности вычисления интеграла.
Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.
Численное интегрирование применяется, когда:
- Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.
- Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например,
.
В этих двух случаях невозможно вычисление интеграла по формуле Ньютона — Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.
Одномерный случай[править | править код]

Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида
где 


При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.
Частным случаем является метод построения интегральных квадратурных формул для равномерных сеток, известный как формулы Котеса. Метод назван в честь Роджера Котса. Основной идеей метода является замена подынтегральной функции каким-либо интерполяционным многочленом. После взятия интеграла можно написать
где числа 






Частными случаями формул Котеса являются: формулы прямоугольников (



Метод прямоугольников[править | править код]
Пусть требуется определить значение интеграла функции на отрезке ![left[{a},{b}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a78fe649f1f47c2dbbd33721e77fbdf02813fdfc)


Обозначим через 


Каждая из сумм — интегральная сумма для 
![left[{a},{b}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a78fe649f1f47c2dbbd33721e77fbdf02813fdfc)
Если заданная функция — положительная и возрастающая, то эта формула выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников, также называемая формулой левых прямоугольников, а формула
выражает площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников, также называемая формулой правых прямоугольников.
Чем меньше длина отрезков, на которые делится отрезок ![left[{a},{b}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a78fe649f1f47c2dbbd33721e77fbdf02813fdfc)
Очевидно, стоит рассчитывать на бо́льшую точность, если брать в качестве опорной точки для нахождения высоты точку посередине промежутка. В результате получаем формулу средних прямоугольников:
где 
Учитывая априорно бо́льшую точность последней формулы при том же объёме и характере вычислений её называют формулой прямоугольников
Метод трапеций[править | править код]
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.
Площадь трапеции на каждом отрезке:
Погрешность аппроксимации на каждом отрезке:
где
Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины 
где
Погрешность формулы трапеций:
где
Метод парабол (метод Симпсона)[править | править код]
Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид
.
Если разбить интервал интегрирования на 
где 
Увеличение точности[править | править код]
Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.
Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.
При стремлении количества разбиений к бесконечности оценка интеграла стремится к его истинному значению для аналитических функций для любого численного метода.
Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге.
Метод Гаусса[править | править код]
Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий порядок точности (0 — методы правых и левых прямоугольников, 1 — методы средних прямоугольников и трапеций, 3 — метод парабол (Симпсона)).
Если мы можем выбирать точки, в которых мы вычисляем значения функции 
.
В общем случае, используя 



Значения узлов 


![{displaystyle a_{i}={frac {2}{(1-x_{i}^{2}),[P_{n}'(x_{i})]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8eabbd72084d4b6e951ba8602d8abb1d60c50ae)

Для 


(полином определен на отрезке ![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
Наиболее известен метод Гаусса по пяти точкам.
Метод Гаусса — Кронрода[править | править код]
Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша точности, в отличие от простых методов, где точность увеличивается в несколько раз при каждом новом разбиении.
Кронродом был предложен следующий метод оценки значения интеграла
,
где 






Тогда для оценки погрешности можно использовать эмпирическую формулу:
,
где 

Метод Чебышёва[править | править код]
Метод Чебышева (или как его иногда называют Гаусса — Чебышева) является одним из представителей методов наивысшей алгебраической точности Гаусса. Его отличительной особенностью является наличие у подынтегральной функции множителя 
,
где 


Метод Гаусса-Лагера[править | править код]
Метод Гаусса-Эрмита[править | править код]
Интегрирование при бесконечных пределах[править | править код]
Для интегрирования по бесконечным пределам нужно ввести неравномерную сетку, шаги которой нарастают при стремлении к бесконечности, либо можно сделать такую замену переменных в интеграле, после которой пределы будут конечны.
Аналогичным образом можно поступить, если функция особая на концах отрезка интегрирования.
См. в том числе Метод Самокиша.
Методы Монте-Карло[править | править код]
Рисунок 3. Численное интегрирование функции методом Монте-Карло
Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:
Этот алгоритм требует определения экстремумов функции на интервале и не использует вычисленное точное значение функции 
Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.
Методы Рунге — Кутты[править | править код]
Ме́тоды Ру́нге — Ку́тты — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем — итеративные методы явного и неявного приближённого вычисления, разработанные около 1900 года немецкими математиками К. Рунге и М. В. Куттой.
Метод сплайнов[править | править код]
Многомерный случай[править | править код]

В небольших размерностях можно так же применять квадратурные формулы, основанные на интерполяционных многочленах. Интегрирование производится аналогично одномерному интегрированию.
Для больших размерностей эти методы становятся неприемлемыми из-за быстрого возрастания числа точек сетки и/или сложной границы области. В этом случае применяется метод Монте-Карло. Генерируются случайные точки в нашей области и усредняются значения функции в них. Так же можно использовать смешанный подход — разбить область на несколько частей, в каждой из которых (или только в тех, где интеграл посчитать не удаётся из-за сложной границы) применить метод Монте-Карло.
Примеры реализации[править | править код]
Ниже приведена реализация на Python 3 метода средних прямоугольников, метода средних трапеций, метода Симпсона и метода Монте-Карло.
import math, random from numpy import arange def get_i(): return math.e ** 1 - math.e ** 0 def method_of_rectangles(func, min_lim, max_lim, delta): def integrate(func, min_lim, max_lim, n): integral = 0.0 step = (max_lim - min_lim) / n for x in arange(min_lim, max_lim-step, step): integral += step * func(x + step / 2) return integral d, n = 1, 1 while abs(d) > delta: d = (integrate(func, min_lim, max_lim, n * 2) - integrate(func, min_lim, max_lim, n)) / 3 n *= 2 a = abs(integrate(func, min_lim, max_lim, n)) b = abs(integrate(func, min_lim, max_lim, n)) + d if a > b: a, b = b, a print('Rectangles:') print('t%st%st%s' % (n, a, b)) def trapezium_method(func, min_lim, max_lim, delta): def integrate(func, min_lim, max_lim, n): integral = 0.0 step = (max_lim - min_lim) / n for x in arange(min_lim, max_lim-step, step): integral += step*(func(x) + func(x + step)) / 2 return integral d, n = 1, 1 while abs(d) > delta: d = (integrate(func, min_lim, max_lim, n * 2) - integrate(func, min_lim, max_lim, n)) / 3 n *= 2 a = abs(integrate(func, min_lim, max_lim, n)) b = abs(integrate(func, min_lim, max_lim, n)) + d if a > b: a, b = b, a print('Trapezium:') print('t%st%st%s' % (n, a, b)) def simpson_method(func, min_lim, max_lim, delta): def integrate(func, min_lim, max_lim, n): integral = 0.0 step = (max_lim - min_lim) / n for x in arange(min_lim + step / 2, max_lim - step / 2, step): integral += step / 6 * (func(x - step / 2) + 4 * func(x) + func(x + step / 2)) return integral d, n = 1, 1 while abs(d) > delta: d = (integrate(func, min_lim, max_lim, n * 2) - integrate(func, min_lim, max_lim, n)) / 15 n *= 2 a = abs(integrate(func, min_lim, max_lim, n)) b = abs(integrate(func, min_lim, max_lim, n)) + d if a > b: a, b = b, a print('Simpson:') print('t%st%st%s' % (n, a, b)) def monte_karlo_method(func, n): in_d, out_d = 0., 0. for i in arange(n): x, y = random.uniform(0, 1), random.uniform(0, 3) if y < func(x): in_d += 1 print('M-K:') print('t%st%s' % (n, abs(in_d/n * 3))) method_of_rectangles(lambda x: math.e ** x, 0.0, 1.0, 0.001) trapezium_method(lambda x: math.e ** x, 0.0, 1.0, 0.001) simpson_method(lambda x: math.e ** x, 0.0, 1.0, 0.001) monte_karlo_method(lambda x: math.e ** x, 100) print('True value:nt%s' % get_i())
Литература[править | править код]
- Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение (пер. с англ.).. — Изд. второе, стереотип.. — М.: Мир, 2001. — 575 с. — ISBN 5-03-003392-0.
- Самарский А. А., Гулин А. В. Численные методы: Учеб. пособие для вузов. — М.: Наука. Гл. ред. физ-мат. лит., 1989. — 432 с. — ISBN 5-02-013996-3.
- Пискунов Н. С. Дифференциальное и интегральное исчисления : Учеб. пособие для вузов: В 2 т. — 13-е изд.. — М.: Наука. Гл. ред. физ-мат. лит., 1985. — 432 с.
- Болтачев Г.Ш. Численные методы в теплофизике. Курс лекций Лекция 3: Численное интегрирование
См. также[править | править код]
- Численное дифференцирование
- Вычислительные методы
- Список квадратурных формул
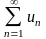











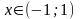








![{displaystyle M_{2,i}=max _{xin [x_{i-1},,x_{i}]}{left|f''(x)right|}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41d5ba8dc72fe3f14153a35ab8b69f8cb6d3fed8)

![{displaystyle M_{2}=max _{xin [a,,b]}{left|f''(x)right|}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc62e9032665193492aad8f3ffa8b77861ba4b43)


