Как составить матрицу гурвица – Сайт, где вы сможете решить свои вопросы

Предыдущие лекции по теории автоматического управления можно посмотреть здесь:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

В теории «Управления техническими системами» общепринято понятие качество управления, состоящее из трех основных составляющих:

устойчивость САР (или запасы устойчивости);
точность САР;
качество переходного процесса.

Необходимо заметить, что если не обеспечена устойчивость замкнутой САР, то говорить о точности и, тем более, о качестве переходного процесса – бессмысленно.

Поэтому понятие «устойчивость» – важнейшее понятие для САР.

Приведем «механическую» аналогию понятия «устойчивость»

Рисунок 6.1.1 а) абсолютно устойчивое положение, б) неустойчивое положение, в) нейтральное (безразличное) положение.

В положении а) при отклонении шарика от нижнего положения он обязательно вернется в свое устойчивое положение (низ «воронки»).

В положении б) малейшее отклонение шара от состояния равновесия приведет к «скатыванию» его вниз; т.е. шар не вернется сам назад на вершине «горки».

В положении в) при воздействии на шар он начнет перемещаться в горизонтальном направлении и, если нет трения, то шар будет двигаться с постоянной скоростью.

Если реальная замкнутая САР имеет свойства, аналогичные а), то она «хорошая», если б) – «совсем плохая». Нужно так проектировать САР, чтобы ее свойства были похожи на а), т.е. если какое-то возмущающее воздействие отклонит систему от равновесия, то система управления обязана вернуть техническую систему в состояние равновесия.

Ранее мы водили передаточную функуию для по возмущающему воздействию для замкнутой САР (см. формулу 5.4 в предыдущей лекции). Уравнения динамики замкнутой САР, описываемую в переменных «вход-выход»:

Решения для такого уравнения будет являтся суммой двух функций: $y(t)=y_{соб}(t)+y_{вын}(t)$ , где $y_{соб}(t)$ – собственное решение, при и вынужденное $y_{вын}(t)$ решение вызванное воздействием.

Решим характеристическое уравнение (подробнее смотри здесь…)

$a_ncdot lambda^n_n+a_{n-1}cdot lambda^{n-1}_{n-1}+...+a_1cdot lambda_1+a_0 =0$

Решая уравнение (6.1.2), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения , тогда собственное решение примет вид:

$y_{соб}(t)=sum_{j=1}^n c_jcdot e^{lambda_jcdot t} mathbf{(6.1.3)}$

В зависимости от значения возможно несколько вариантов вида функуции. На рисунке 6.1.2 представлены варинаты поведения функции вида $c_jcdot e^{lambda_jcdot t}$ в случае когда является реальными числом или комплексным числом .

Рисунок 6.1.2 Возможная вид решения

Анализ вышеприведенных рисунков показывает, что система может вернуться в исходное состояние, если все составляющие $с_jcdot e^{lambda_jcdot t }$ при будут стремиться к нулю. А для этого показатель степени должен быть отрицательным. Поэтому условием устойчивости является отрицательное значение реальной части корней т.е. необходимо чтобы корни характеристического уравнения лежали в левой полуплоскости.

Рисунок 6.1.3 Расположение корней характеристического уравнения

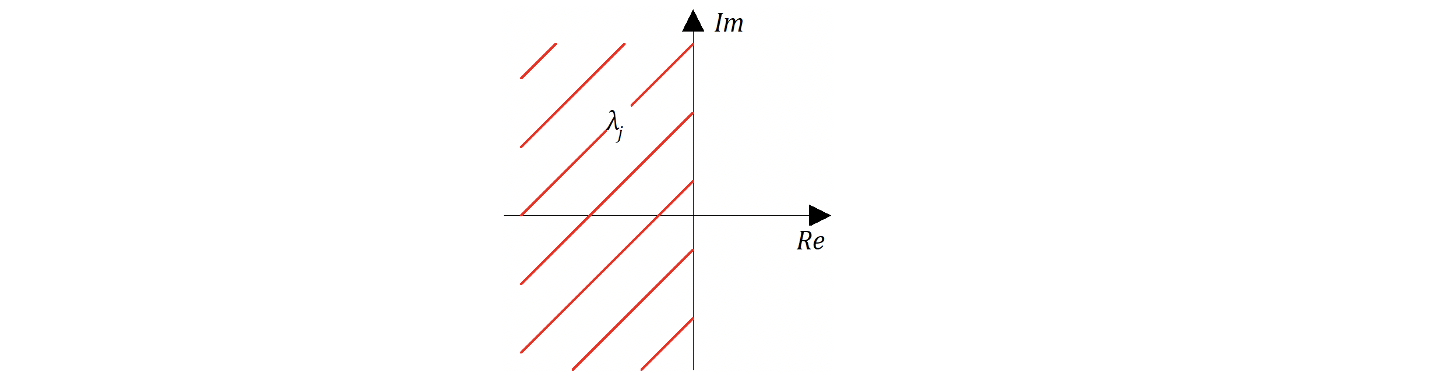
Если корни комплексные, то процесс колебательный, если корни реальные, то процес аперодический (затухающий). Причем ось ординат соответствует границам устойчивости (апериодической или колебательной). Таким образом, вопрос об устойчивости или неустойчивости замкнутой (и разомкнутой) САР определяется по расположению корней соответствующего характеристического уравнения.

Для не замкнутой САР вместо устойчивость определяется корнями характеристического уравнения знаменателя передаточной функции в предыдущей лекции мы выводили формулу рассчета передаточной фунции замкунутой САР, по предаточной функции разомкнутоф САР:

Таким образом, вопрос об устойчивости или неустойчивости замкнутой и разомкнутой САР определяется по расположению корней соответствующего характеристического уравнения.

$left [ begin{align} D(lambda)=0 - для замкнутой САР \L(lambda) =0 - для разомкнутой САР end{align} mathbf{(6.1.3)}right.$

Если все корни характеристического уравнения лежат (расположены) в левой полуплоскости – линейная (или линеаризованная) САР устойчива.

Необходимо заметить, что коэффициенты уравнения совпадают с коэффициентами многочлена (полинома) следовательно полюса замкнутой САР тождественно совпадают с корнями характеристического уравнения , где – корни характеристического уравнения; – полюса перредаточной функции.

Напомним, полюсом передаточной функции называется значение её аргумента, при котором знаменатель функции обращается в ноль.

Используя приблизительно такие же рассуждения сходимости степенных функций Ляпуновым были сформулированы 3 теоремы об устойчивости линейных САР:

Если все корни характеристического уравнения или полюса передаточной функции САР расположены в левой полуплоскости, то линеаризованная САР обязательно вернется в исходное состояние при снятии внешнего воздействия, выведшего эту САР из состояния равновесия. Следовательно САР – устойчива.
Если хотя бы один полюс (или корень характеристического уравнения) передаточной функции САР расположен в правой полуплоскости (при всех остальных в левой полуплоскости), линейная (линеаризованная) САР никогда не вернется в исходное (равновесное) состояние при снятии внешнего воздействия, которое вывело данную САР из исходного состояния равновесия. Следовательно САР – неустойчива.
Если хотя бы один из полюсов передаточной функции САР (корней характеристического уравнения) находится на мнимой оси (при всех остальных в левой полуплоскости) об устойчивости линеаризованной САР ничего сказать нельзя, т.к. учет нелинейных (отброшенных) членов в динамике САР может дать любой результат (устойчива или неустойчива).

Резюмируя вышесказанное, отметим, что:

Наиболее простым способом определения устойчива или неустойчива САР (как замкнутая, так и разомкнутая) является решение уравнения для замкнутой САР (или для разомкнутой САР) или решение характеристического уравнения или– для разомкнутой САР).

Если САР задана в переменных состояния, то вопрос об устойчивости САР определяется матрицей А – собственной матрицей:

$left { begin{align} x'=Acdot x+Bcdot u \ y =C cdot x + D cdot u end{align} mathbf{(6.1.5)}right.$

Если собственные числа матрицы А лежат в левой полуплоскости – САР устойчива; если хотя бы одно собственное число лежит в правой полуплоскости – линейная САР неустойчива.

Собственные числа (согласно разделу «Линейная алгебра») находятся из уравнения:

где: – матрица размера ; – единичная матрица

$E = begin{bmatrix} 1 &0 &cdots & 0 \ 0 & 1 &cdots & 0 \ vdots &vdots &ddots &vdots \ 0 &0 &0 &1 end{bmatrix}$

Это означает, что уравнение принимает:

$left | begin{matrix} a_{11}-lambda_1 &a_{12} &cdots & a_{1n} \ a_{21} & a_{22} - lambda_2 &cdots & a_{2n} \ vdots &vdots &ddots &vdots \ a_{n1} &a_{n2} &cdots &a_{nn}-lambda_n end{matrix} right |=0 mathbf{(6.1.7)}$

решая, находим

Фактически уравнения (6.1.6) и (6.1.7) – характеристические уравнения САР. Поэтому, если САР задана в переменных состояния, то характеристический полином при задании САР в переменных «вход-выход» может быть определен как:

$D(s)=left [ begin{align} det[A -E cdot s] = 0 - если размерность матрицы A четная \det[Ecdot s -A]=0 - если размерность матрицы A нечетная end{align} right.$

Чисто математически задача определения устойчивости сводится к решению степенного уравнения или к проблеме нахождения собственных чисел матрицы А.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

Наиболее просто необходимое условие устойчивости линейных (линеаризованных) САР формулируется для систем, записанных в переменных «вход-выход», причем оно применяется в одинаковой «редакции» как для замкнутых, так и для разомкнутых САР. Это условие доказывается с использованием характеристического полинома D(s) – для замкнутых САР, или L(s) – для разомкнутых САР. Сделаем вывод на основании D(s)

Разложим многочлен D(s) на элементарные линейные сомножители :

$D(s)=a_ncdot s^n+a_{n-1}cdot s^{n-1}+...+a_1cdot s+a_0$ $D(s)=a_ncdot(s-s_1)cdot(s-s_2)cdot ...cdot(s-s_n) mathbf{(6.2.1)}$

где: – полюса передаточной функции замкнутой САР.

Предположим, что и что все полюса расположены в левой полуплоскости:

$left | begin{align} s_1 &= -|alpha_1 | \s_2&=-|alpha_2|+icdotbeta_2; \s_3&=-|alpha_2|-icdot beta_2;\s_4&=-|alpha_3|+icdotbeta_3;\ s_5&=-|alpha_3|-icdotbeta_3;\&............ end{align} right.$

где: – действительный полюс; – – комплексно-сопряженные полюса.

Подставим значения в выражение 6.2.1 заметим, что если перемножать любые две скобки в выражении 6.2.1, которые содержат комплексно сопряженные скобки например мы получим выражение типа: .

В первой скобке мы получим выражение: Таким образом мы получаем только полжительные коэффициенты полинома Таким образом можно сформулировать необходимое условие устойчивости линейных САР:

Необходимым условием устойчивости линейных САР является положительность всех коэффициентов в полиноме – для замкнутых САР, или в – для разомкнутых САР.

Для систем 1-го и 2-го порядка необходимое условие является и достаточным.

Но для систем, имеющих порядок , выполнение необходимого условия невсегда является достаточным.

Тем не менее, необходимое условие «очень удобно», т.е. если хотя бы один коэффициент в D(s) отрицателен, то однозначно – САР неустойчива.

Если необходимое условие выполнено , то если порядок матрицы больше 2 необходимо либо вычислить корни характеристического уравнения (полюса передаточной функции), либо используя какой-либо из критериев устойчивости сделать соответствующий вывод об устойчивости САР.

6.3. Алгебраический критерий устойчивости Гурвица.

Как отмечалось выше, устойчивость любой САР можно определить, вычислив значение всех полюсов (или корней соответствующего характеристического уравнения). Однако далеко не все способны без компьютера (калькулятора) решить степенное уравнение выше квадратного (кубическое и т.д.).

Критерий Гурвица, являющийся частным случаем критерия Раусса, позволяет не решая уравнений типа или сделать вывод об устойчивости САР на основании «несложных» вычислений с использованием коэффициентов характеристического полинома.

Представим полином в измененном виде:

$D(s)=a_0cdot s^n+ a_1cdot s^{n-1}+ ...+ a_{n-1}cdot s +a_n mathbf{(6.3.1)}$

Данное выражение полинома позволяет соcтавить матрицу Гурвица, для этого:

по главной диагонале по главной диагонали слева направо выставляются коэффициенты характеристического уравнения от до ;
от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
на место коэффициентов с индексами меньше нуля или больше ставатся нули:

$Г = begin{bmatrix} a_1 &a_3 &a_5 &cdots & 0 &0 \ a_0 & a_2 &a_4 &cdots &0 &0\0 &a_1 &a_3 &cdots &0 &0\ vdots &vdots &vdots &ddots &vdots &vdots \0 &0 &0 &cdots &a_{n-1} &0 \ 0 &0 &0 &cdots &a_{n-2} &a_n end{bmatrix}$

Составив эту матрицу можно сфомулировать критерий:

Для того, чтобы замкнутая САР (или разомкнутая) была устойчивой, необходимо и достаточно, чтобы были положительны все n главных определителей Гурвицевой матрицы Г.

$left { begin{align} Delta_1 &= a_1>0; \ Delta_2 &= left |begin{matrix} a_1 &a_3\ a_0 &a_2 end{matrix} right |>0; \ Delta_3 &= left | begin{matrix}a_1 &a_3 &a_5 \ a_0 &a_2 &a_2 \ 0 &a_1 &a_3 end{matrix} right |>0; \ cdots \ Delta_{n} &= Delta_{n-2}cdot a_n >0. end{align} right.$

Если все определители больше нуля, то линейная САР устойчива.

Если все определители больше нуля и то САР находится на апереодической границе устойчивости.

Если все определители, кроме $Delta_{n-1}$ больше нуля, а опеределитель $Delta_{n-1} =0$ и Р , то САР находится на колебательного границы устойчивости.

Пример 1

Определить, устойчива или нет следующая система САР:

Рисунок 6.3.1 САР для анализа устойчивости

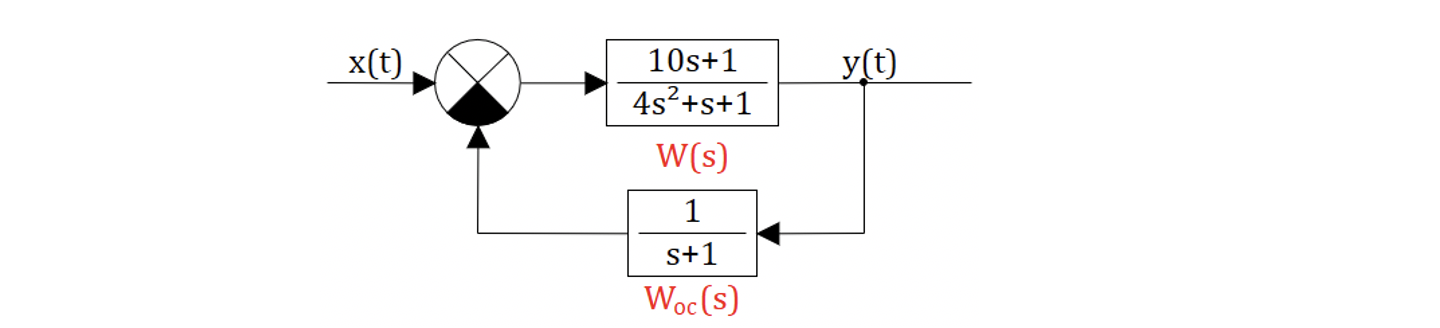
Найдем главную передаточную функцию замкнутой САР:

$Ф(s)=frac{W(s)}{W_{oc}(s)}=frac{10cdot s+1}{(4cdot s^2+s+1)cdot left [1+frac{10cdot s+1}{4cdot s^2+s+1}cdot frac{1}{s+1} right]}=\ =frac{(10cdot s+1)cdot(s+1)}{(s+1)cdot(4cdot s^2+s+1)+(10cdot s+1)}=frac{(10cdot s+1)cdot(s+1)}{underbrace{4cdot s^3+5cdot s^2+12cdot s+2}_{D(s)}}$

Все коэффициенты полинома – положительные:

$D(s)=underbrace{4}_{a_0}cdot s^3+underbrace{5}_{a_1}cdot s^2+underbrace{12}_{a_2}cdot s+underbrace{2}_{a_3}$

А значит САР может быть устойчива. Составим матрицу Гурвица, и найдем ее определители:

$Г=begin{bmatrix} 5 &2 &0\ 4 &12 &0 \ 0 &5 & 2 end{bmatrix}Rightarrow left { begin{align} Delta_1 &=5>0; \ Delta_2 &= left | begin{matrix} 5 &2\ 4&12 end{matrix} right | =5cdot12-4cdot2=52>0 \ Delta_3 &= 52 cdot 2>0; end{align} right.$

Все определители матрицы Гурвица больше нуля, следовательно САР устойчива.

Пример 2

Используя критерий Гурвица, выполнить анализ устойчивости следующей САР:

Рисунок 6.3.2 САР для анализа устойчивости

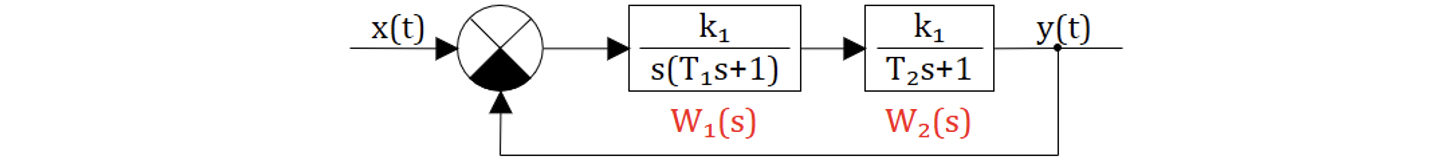
Общая передаточная функция разомкнутой системы САР:

$W(s) =frac{overbrace{k_1cdot k_2}^K}{scdot(T_1cdot s+1)cdot(T_2cdot s+1)}$

Корни знаменателя передаточной функцийй размкнутой САР:

$s_1=-frac{1}{T_1}; s_2 =-frac{1}{T_2}; s_3 =0$

Поскольку разомкнутая САР находится на границе устойчивости.

Передаточная функция замкнутой САР:

$Ф(s)=frac{W_1(s)cdot W_2(s)}{1+W_1(s)cdot W_2(s)}Rightarrow$ $Ф(s)=frac{overbrace{k_1cdot k_2}^K}{scdot(T_1cdot s+1)cdot(T_2cdot s+1)+underbrace{k_1cdot k_2}_K}=underbrace{frac{K}{T_1cdot T_2cdot s^3+(T_1+T_2)cdot s^2+s+k}}_{D_s}$ $D(s)=underbrace{T_1cdot T_2}_{a_0}cdot s^3+underbrace{(T_1+T_2)}_{a_1}cdot s^2+underbrace{1}_{a_2}cdot s+underbrace{k}_{a_3}$

Выражения для матрицы Гурвица:

$Г=begin {bmatrix}(T_1+T_2) & K & 0\ T_1cdot T_2 &1 &0\ 0 &(T_1+T_2)& K end{bmatrix}$

Главные определители матрицы Гурвица:

$left {begin{align} Delta_1&=T_1+T_2 >0\ Delta_2&=T_1+T_2-Kcdot T_1cdot T_2 >0\ Delta_3 &=Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right.$

Очевидно из формулы для определиттеля следует что для устойчивости САР необходимо чтобы

Рисунок 6.3.3. Условие устойчивости по

В случае когда постоянные времени положительны условие устойчивости можно вычислить получить из выражения для второго определителя:

$T_1+T_2 - Kcdot T_1cdot T_2 >0Rightarrow k< frac{1}{T_1}+frac{1}{T_2}$

Рисунок 6.3.4 Полные условия устойчивости

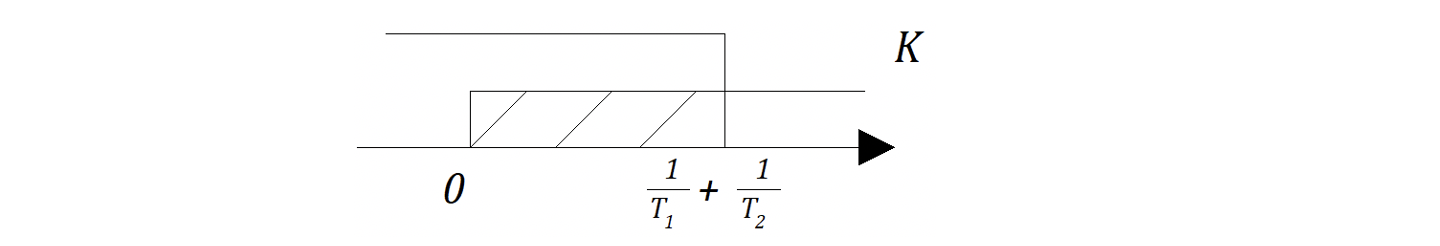
Полученный результат свидетельствует, что если , то для того, чтобы САР была устойчивой, необходимо, чтобы выполнит следующие условия:

$0<K<frac{1}{T_2}+frac{1}{T_1}$

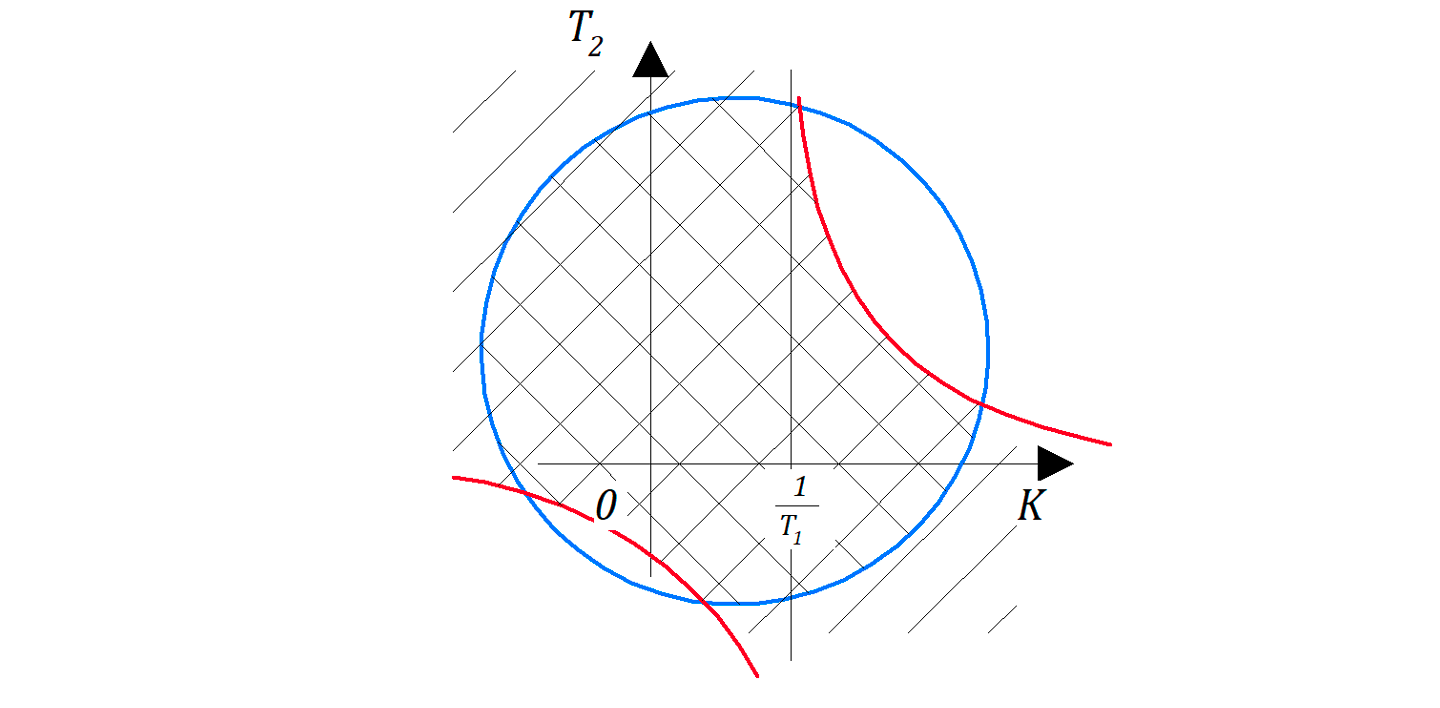
Усложним задачу: предположим, что в системе САР изображенной на рис. 6.3.2 возможно варьировать (изменять) коэффициент усиления и постоянную времени, например, В этом случае область устойчивости может быть отображена в виде фигуры в координатах

Рисунок 6.3.5 Область устойчивости

Система неравенств такая же, что и выше, для определителей матрицы Гурвица:

$left {begin{align} Delta_1&=T_1+T_2 >0\ Delta_2&=T_1+T_2-Kcdot T_1cdot T_2 >0\ Delta_3 &=Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right. Rightarrow$ $left {begin{align} & T_1+T_2 >0\ & T_1+T_2-Kcdot T_1cdot T_2 >0\& Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right. Rightarrow K< left ( frac{1}{T_1}+frac{1}{T_2} right ) Rightarrow frac{1}{T_2}>K-frac{1}{T_1} Rightarrow$ $Rightarrow left { begin{align} T_2<frac{1}{K-frac{1}{T_1}} если K>frac{1}{T_1}\ T_2>frac{1}{frac{1}{T_1}-K} если K<frac{1}{T_1} end{align} right.$

Рисунок 6.3.6. Область устойчивости для САР с переменными T2 и К

Примеры из видео можно взять здесь..

Продолжение темы устойчивости:

6.4 Частотный критерий устойчивости Михайлова.

6.5. Частотный критерий Найквиста

6.6. Понятие об областях устойчивости

Источник

Критерии устойчивости Рауса–Гурвица и Михайлова
(геометрический критерий устойчивости)

Пусть имеем линейное дифференциальное уравнение с постоянными вещественными коэффициентами:

$a_0y^{(n)}+a_1y^{(n-1)}+ldots+a_ny=0quad (a_0,a_1,ldots,a_n=text{const},~a_0>0).$

(1)

Нулевое решение yequiv0 уравнения (1) асимптотически устойчиво, если все корни характеристического уравнения

$f(lambda)equiv a_0lambda^n+a_1lambda^{n-1}+ldots+a_n=0$

(2)

имеют отрицательные вещественные части.

Критерий Рауса—Гурвица. Для того чтобы все корни уравнения (2) имели отрицательные вещественные части, необходимо и достаточно, чтобы были положительными все главные диагональные миноры матрицы Гурвица

$begin{pmatrix}a_1&a_0&0&0&0&0&{}&0\ a_3&a_2&a_1&a_0&0&0&{}&0\ a_5&a_4&a_3&a_2&a_1&a_0&cdots&0\ cdots&cdots &cdots &cdots &cdots &cdots &cdots&cdots\ 0&0&0&0&0&0&{}&a_n end{pmatrix}!.$

(3)

Матрица Гурвица составляется так. По главной диагонали выписываются коэффициенты многочлена (2), начиная с a_1 и оканчивая a_n . Столбцы состоят поочередно из коэффициентов только с нечетными или только с четными индексами, причем в число последних включается коэффициент a_0 . Все остальные элементы матрицы, отвечающие коэффициентам с индексами, большими или меньшими , полагаются равными нулю. Главные диагональные миноры матрицы Гурвица имеют вид

$Delta_1=a_1,quad Delta_2=begin{vmatrix}a_1&a_0\a_3&a_2end{vmatrix},quad Delta_3=begin{vmatrix}a_1&a_0&0\a_3&a_2&a_1\a_5&a_4&a_3end{vmatrix},quad ldots,quad Delta_n=begin{vmatrix}a_1&a_0&0&{}&0\a_3&a_2&a_1&{}&0\a_5&a_4&a_3&{}&0\ cdots&cdots&cdots&cdots&cdots\ 0&0&0&{}&a_nend{vmatrix}.$

Таким образом, условие Гурвица гласит: для устойчивости решения yequiv0 уравнения (1) необходимо и достаточно, чтобы выполнялись соотношения

Delta_1>0,quad Delta_2>0,quad ldots,quad Delta_n>0.

(4)

Так как $Delta_n=a_nDelta_{n-1}$ , то условие Delta_n>0 может быть заменено требованием a_n>0 .

Пример 1. Исследовать на устойчивость нулевое решение уравнения

y''''+5y'''+13y''+19y'+10y=0.

(11)

Решение. Составляем характеристическое уравнение

f(lambda)equiv lambda^4+5lambda^3+13lambda^2+19lambda+10=0

Здесь a_0=1,~a_1=5,~a_2=13,~a_3=19,~a_4=10 . Выписываем диагональные миноры Гурвица

$Delta_1=5>0,~ Delta_2=begin{vmatrix}5&1\19&13end{vmatrix}=46>0,~ Delta_3=begin{vmatrix}5&1&0\19&13&5\0&10&19end{vmatrix}=424>0,~ Delta_4=begin{vmatrix}5&1&0&0\19&13&5&1\0&10&19&13\0&0&0&10end{vmatrix}=4240>0,$

Итак, Delta_1>0,~Delta_2>0,~Delta_3>0,~Delta_4>0 . Следовательно, тривиальное решение yequiv0 уравнения (5) асимптотически устойчиво.

Вычисление можно, например, организовать так. Составляем сначала старший минор Гурвица Delta_n . По нему легко выписываются все младшие миноры $Delta_{n-1},ldots,Delta_1$ . Затем начинаем вычислять последовательно Delta_1,,Delta_2 и т.д. Если встретился отрицательный минор, решение неустойчиво и дальнейший подсчет не нужен.

Геометрический критерий устойчивости (критерий Михайлова)

Рассмотрим линейное дифференциальное уравнение n-го порядка с постоянными вещественными коэффициентами

$a_0y^{(n)}+a_1y^{(n-1)}+ldots+a_ny=0.$

(1)

Его характеристическое уравнение

$f(lambda)equiv a_0lambda^{n}+a_1lambda^{n-1}+ldots+a_n=0.$

(2)

Критерий Михайлова позволяет решить вопрос о расположении корней характеристического уравнения (2) на комплексной плоскости и, следовательно, решить вопрос об устойчивости нулевого решения уравнения (1). Полагая lambda=iomega , получаем

f(iomega)= u(omega)+iv(omega),

где

$u(omega)=a_n-a_{n-2}omega^2+a_{n-4}omega^4-ldots,quad v(omega)=a_{n-1}omega-a_{n-3}omega^3+ldots$

Геометрический критерий устойчивости Михайлова

Величину f(iomega) при заданном значении параметра omega можно изобразить в виде вектора на комплексной плоскости Ouv с началом в начале координат.

При изменении omega в интервале (-infty,+infty) конец этого вектора опишет некоторую кривую — так называемую кривую Михайлова (рис. 45). Так как функция u(omega) четная, то кривая Михайлова симметрична относительно оси и поэтому достаточно строить часть кривой, отвечающую изменению параметра omega от до +infty .

Если многочлен f(lambda) степени имеет корней с положительной вещественной частью и n-m корней с отрицательной, то угол varphi поворота вектора f(iomega) при изменении omega от до +infty равен $varphi=(n-2m)frac{pi}{2}$ .

Ясно, что для устойчивости решения уравнения (1) необходимо и достаточно, чтобы m=0 .

Критерий Михайлова. Для устойчивости нулевого yequiv0 решения уравнения (1) необходимо и достаточно, чтобы

1) вектор f(iomega) при изменении omega от до +infty совершил поворот на угол $varphi=nfrac{pi}{2}$ , т.е. сделал $frac{n}{4}$ оборотов против часовой стрелки;

2) годограф f(iomega) при изменении omega от до +infty не проходил через начало (0;0) .

Отсюда следует, что для устойчивости решения уравнения (1) необходимо, чтобы все корни уравнений u(omega)=0, v(omega)=0 были вещественными и перемежающимися друг с другом, т.е. между любыми двумя корнями одного уравнения должен находиться корень другого уравнения.

Пример 1. Исследовать на устойчивость нулевое решение yequiv0 уравнения

$y^{mathsf{IV}}+y'''+4y''+y'+y=0.$

Решение. Составляем характеристический многочлен

f(lambda)=lambda^4+lambda^3+4lambda^2+lambda+1.

Далее,

f(iomega)=omega^4-iomega^3-4omega^2+iomega+1,quad u(omega)=omega^4-4omega^2+1,quad v(omega)=-omega^3+omega=omega(1-omega)(1+omega).

Построим кривую (рис.46) $begin{cases}u=u(omega),\ v=v(omega),end{cases}0leqslantomega<+infty.$

$begin{array}{|c|c|c|c|c|}hline omega&0&sqrt{2-sqrt{3}}&1&sqrt{2+sqrt{3}}\ hline u&1&0&-2&0\ hline v&0&+&0&-\ hlineend{array}quad lim_{omegato+infty}frac{v}{u}=0.$

Угол поворота радиуса-вектора $varphi=4{cdot}frac{pi}{2}=(n-2m)frac{pi}{2}$ . Отсюда n-2m=4 и так как n=4 , то m=0 , т.е. все корни характеристического уравнения лежат в левой полуплоскости. Значит, тривиальное решение yequiv0 асимптотически устойчиво.

График кривой, заданной параметрически

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Матрица Гурвица или матрица Рауса – Гурвица (в математике) или матрица устойчивости (в инженерном деле) — структурированная квадратная матрица, построенная из коэффициентов вещественного полинома.

Матрица Гурвица и критерий устойчивости Гурвица[править | править код]

Пусть дан полином с вещественными коэффициентами

${displaystyle p(z)=a_{0}z^{n}+a_{1}z^{n-1}+cdots +a_{n-1}z+a_{n}}$

тогда квадратная матрица $ntimes n$

${displaystyle H={begin{pmatrix}a_{1}&a_{3}&a_{5}&dots &dots &dots &0&0&0\a_{0}&a_{2}&a_{4}&&&&vdots &vdots &vdots \0&a_{1}&a_{3}&&&&vdots &vdots &vdots \vdots &a_{0}&a_{2}&ddots &&&0&vdots &vdots \vdots &0&a_{1}&&ddots &&a_{n}&vdots &vdots \vdots &vdots &a_{0}&&&ddots &a_{n-1}&0&vdots \vdots &vdots &0&&&&a_{n-2}&a_{n}&vdots \vdots &vdots &vdots &&&&a_{n-3}&a_{n-1}&0\0&0&0&dots &dots &dots &a_{n-4}&a_{n-2}&a_{n}end{pmatrix}}.}$

называется матрицей Гурвица, соответствующей полиному $p(z)$ . Адольф Гурвиц в 1895 году установил, что этот полином с ${displaystyle a_{0}>0}$ устойчив (то есть все его корни имеют строго отрицательную вещественную часть) тогда и только тогда, когда все ведущие главные миноры матрицы ${displaystyle H(p)}$ положительны:

${displaystyle {begin{aligned}Delta _{1}(p)&={begin{vmatrix}a_{1}end{vmatrix}}&&=a_{1}>0,\[2mm]Delta _{2}(p)&={begin{vmatrix}a_{1}&a_{3}\a_{0}&a_{2}\end{vmatrix}}&&=a_{2}a_{1}-a_{0}a_{3}>0,\[2mm]Delta _{3}(p)&={begin{vmatrix}a_{1}&a_{3}&a_{5}\a_{0}&a_{2}&a_{4}\0&a_{1}&a_{3}\end{vmatrix}}&&=a_{3}Delta _{2}-a_{1}(a_{1}a_{4}-a_{0}a_{5})>0end{aligned}}}$

и так далее. Миноры ${displaystyle Delta _{k}(p)}$ называются определителями Гурвица. Точно так же, если ${displaystyle a_{0}<0}$ тогда многочлен устойчив тогда и только тогда, когда главные миноры имеют чередующиеся знаки, начиная с отрицательного.

Матрицы устойчивости Гурвица[править | править код]

В инженерном деле и теории устойчивости квадратная матрица $A$ называется матрицей Гурвица, если каждое собственное значение $A$ имеет строго отрицательную вещественную часть, то есть

${displaystyle mathop {mathrm {Re} } [lambda _{i}]<0,}$

для каждого собственного значения $lambda _{i}$ . $A$ также называется матрицей устойчивости, потому что тогда дифференциальное уравнение

${displaystyle {dot {x}}=Ax}$

асимптотически устойчиво, то есть ${displaystyle x(t)to 0}$ когда ${displaystyle tto infty .}$

Если ${displaystyle G(s)}$ является (матричной) передаточной функцией, то $G$ называется передаточной функцией Гурвица, если полюса всех элементов $G$ имеют отрицательную реальную часть. Обратите внимание — не обязательно, чтобы ${displaystyle G(s)}$ для конкретного аргумента $s$ была матрицей Гурвица — она даже не должна быть квадратной. Связь состоит в том, что если $A$ — матрица Гурвица, то динамическая система

${displaystyle {dot {x}}(t)=Ax(t)+Bu(t)}$

${displaystyle y(t)=Cx(t)+Du(t),}$

имеет гурвицеву передаточную функцию.

Любая гиперболическая неподвижная точка (или точка равновесия) непрерывной динамической системы локально асимптотически устойчива тогда и только тогда, когда якобиан динамической системы устойчив по Гурвицу в неподвижной точке.

Матрица устойчивости Гурвица играет важную роль в теории управления. Система устойчива, если ее управляющая матрица является матрицей Гурвица. Отрицательные вещественные части собственных значений матрицы представляют собой отрицательную обратную связь. Точно так же система по своей природе неустойчива, если хотя бы одно из собственных значений имеет положительную вещественную часть, представляющую собой положительную обратную связь.

См. также[править | править код]

M-матрица
P-матрица
Теорема Перрона – Фробениуса
Z-матрица

Источники[править | править код]

Asner, Bernard A., Jr. On the Total Nonnegativity of the Hurwitz Matrix (англ.) // SIAM Journal on Applied Mathematics (англ.) (рус. : journal. — 1970. — Vol. 18, no. 2. — P. 407—414. — doi:10.1137/0118035.
Dimitrov, Dimitar K. Almost strict total positivity and a class of Hurwitz polynomials (англ.) // Journal of Approximation Theory (англ.) (рус. : journal. — 2005. — Vol. 132, no. 2. — P. 212—223. — doi:10.1016/j.jat.2004.10.010.
Gantmacher, F. R. Applications of the Theory of Matrices. — 1959.
Hurwitz, A. Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Teilen besitzt (нем.) // Mathematische Annalen : magazin. — 1895. — Bd. 46, Nr. 2. — S. 273—284. — doi:10.1007/BF01446812.
Khalil, Hassan K. Nonlinear Systems. — 2002.
Lehnigk, Siegfried H. On the Hurwitz matrix (англ.) // Zeitschrift für Angewandte Mathematik und Physik (англ.) (рус. : journal. — 1970. — Vol. 21, no. 3. — P. 498—500. — doi:10.1007/BF01627957. — Bibcode: 1970ZaMP…21..498L.

Внешние ссылки[править | править код]

Hurwitz matrix (англ.). PlanetMath.

Источник

Задача
отыскания критерия устойчивости для
систем, описываемых
дифференциальными
уравнениями любого порядка, была
сформулирована
Максвеллом
в 1868 году. Эта задача была впервые решена
в алгебраической
форме
Раусом в 1873 году для уравнений четвертой
и пятой степени
и
в 1877 году – полностью.

Поскольку
критерий Рауса дан в форме алгоритма,
определяющего
последовательность
математических операций, необходимых
для решения
задачи,
использование его в практике является
неудобным. Поэтому большее
распространение
получил алгебраический критерий
устойчивости, сформулированный в 1895
году математиком А. Гурвицем. Этот
критерий был найден Гурвицем по просьбе
словацкого профессора Стодолы,
занимавшегося исследованием процесса
регулирования турбин.

Ниже критерий
Гурвица приводится без доказательства.

Для
характеристического уравнения (5.9)
составим квадратную матрицу (таблицу)
коэффициентов, содержащую п
строк
и п
столбцов:

(5.11)

Эта таблица
составляется следующим образом.

По
диагонали от левого верхнего до правого
нижнего углов выписываются все
коэффициенты по порядку от а₁
до
а_п.
Каждая
строка дополняется коэффициентами с
возрастающими индексами слева направо
так, чтобы чередовались строки с нечетными
и четными индексами. В случае отсутствия
данного коэффициента, а также если
индекс его меньше нуля или больше п,
на
месте его пишется нуль.

Критерий
устойчивости сводится к тому, что при
а₀
>
0 должны быть больше нуля все п
определителей
Гурвица, получаемых из квадратной
матрицы коэффициентов.

Определители
Гурвица составляются по следующему
правилу (см. (5.11)):

(5.12)

(5.13)

(5.14)

Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:

(5.15)

Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию а_п
>
0, т. е. к положительности свободного
члена характеристического уравнения.

Условия
нахождения системы на границе устойчивости
можно получить, приравнивая нулю
последний определитель:
,
при положительности всех остальных
определителей. Как следует из (5.15), это
условие распадается на два условия:а_п
=0
и
.
Первое условие соответствует границе
устойчивости первого типа (апериодическая
граница устойчивости) и второе –
границе устойчивости второго типа
(колебательная граница устойчивости).

Раскрывая
определители, фигурирующие в общей
формулировке критерия устойчивости
Гурвица, можно получить в виде частных
случаев критерии устойчивости для
системы первого, второго, третьего,
четвертого и более них порядков.

1. Уравнение первого
порядка

Для этого уравнения
критерий Гурвица дает

т.
е. коэффициенты характеристического
уравнения должны быть положительными.

2. Уравнение второго
порядка

Для этого уравнения
критерий Гурвица требует

Последний
определитель, как отмечалось выше,
сводится к условию положительности
последнего коэффициента: а₂
>0.

Таким
образом, и для уравнения второго порядка
необходимым и достаточным условием
устойчивости является положительность
всех коэффициентов характеристического
уравнения.

3. Уравнение третьего
порядка

Для этого уравнения
получаем условия

Третий
(последний) определитель Δ₃
дает условие а₃
>
0. Условие Δ₂
>0 , при а₀
>
0, а₁
>
0 и а₃
>
0 может выполняться только при а₂
>.
0.

Следовательно,
для уравнения третьего порядка уже
недостаточно положительности всех
коэффициентов характеристического
уравнения. Требуется еще выполнение
определенного соотношения между
коэффициентами:

4. Уравнение
четвертого порядка

На
основании критерия Гурвица можно
получить, что для уравнения четвертого
порядка, кроме положительности всех
коэффициентов, требуется выполнение
условия

5. Уравнение пятого
порядка

Для
уравнения пятого порядка, кроме
положительности всех коэффициентов,
должны выполняться еще два условия:

Как
видно, уже для уравнения пятой степени
условия устойчивости по критерию Гурвица
получаются достаточно громоздкими.
Поэтому использование этого критерия
практически ограничивается уравнениями
четвертого порядка.

Рис. 5.4

Существенным
недостатком критерия Гурвица является
также то, что для уравнений высоких
порядков в лучшем случае можно получить
ответ о том, устойчива или неустойчива
система автоматического регулирования.
При этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменить параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые были бы более
удобными в инженерной практике.

Для
иллюстрации применения критерия
Гурвица рассмотрим пример на
определение
устойчивости дистанционной следящей
системы. Принципиальная и структурная
схемы изображены на рис. 5.4. В качестве
чувствительного элемента использованы
два сельсина (СД
и
СП),
включенные
по трансформаторной схеме. Передаточная
функция сельсинов равна коэффициенту
передачи схемы:

где
ошибка,
равная разности углов поворота командной
и исполнительной осей.

Передаточная
функция усилителя:

где
k₂
– коэффициент усиления и Т_у
–
постоянная времени усилителя.

Передаточная
функция двигателя (Д):

где
коэффициент
передачи двигателя но скорости, аT_M
– электромеханическая постоянная
времени двигателя совместно с оконечным
каскадом усилителя.

Передаточная
функция редуктора (Р)
равна
его коэффициенту передачи, определяемому
передаточным отношением:

Так
как цепь регулирования состоит из
включенных последовательно звеньев,
то передаточная функция разомкнутой
цепи будет равна произведению передаточных
функций отдельных звеньев:

где

общий коэффициент усиления разомкнутой
цепи.

Характеристическое
уравнение:

После
подстановки

получаем

В
данном случае характеристическое
уравнение имеет третий порядок. Нетрудно
видеть, что условие положительности
всех коэффициентов выполняется
всегда, если выполнено условие К
>0,
что будет при правильном согласовании
направления вращения двигателя со
знаком рассогласования.

Дополнительное
условие
,
накладываемое на коэффициенты
характеристического уравнения, сводится
при подстановке значений коэффициентов
(
и
)
к неравенству

которое и является
условием устойчивости рассматриваемой
системы.

Из
этого неравенства, в частности, можно
заметить, что увеличение каждой постоянной
времени сказывается отрицательно на
устойчивости системы, так как при этом
снижается предельное значение общего
коэффициента усиления К,
при
котором система еще остается устойчивой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В результате получим замкнутую систему, в которой будут наблюдаться незатухающие колебания с постоянной амплитудой, а, как мы знаем, это характерно для систем, находящихся на границе устойчивости (см. рис. 7.2,е в разделе 7.1). Таким образом, прохождение графика АФХ разомкнутой системы через точку (–1, 0i) свидетельствует о нахождении соответствующей замкнутой системы на границе устойчивости.
Теперь рассмотрим второй случай. Предположим, в ходе того же самого опыта на выходе разомкнутой системы установились колебания с тем же сдвигом фазы π, но с меньшей амплитудой:

φ = ±π ; Aвых < Aвх.

Это состояние соответствует точке АФХ разомкнутой системы, лежащей на вещественной оси правее точки (–1, 0i) (Mраз(ω) = Aвых/Aвх < 1, φраз(ω) = ±π).
После отключения генератора колебаний и замыкания отрицательной обратной связи на вход Wраз(iω) поступит сигнал с меньшей амплитудой, чем создавал генератор. Пройдя через регулятор и объект, этот сигнал снова будет несколько ослаблен (так как Mраз(ω) < 1), в следующий момент времени поступит по обратной связи на вход Wраз(iω) с еще меньшей амплитудой, и это будет повторяться снова и снова. Таким образом, в данном случае с течением времени амплитуда колебаний в замкнутой системе будет непрерывно уменьшаться, стремясь к нулю, т.е. будет наблюдаться затухающий процесс, что, как известно, характерно для устойчивых систем (рис. 7.2,г).
В третьем возможном случае на выходе разомкнутой системы установятся колебания со сдвигом фазы π и большей амплитудой, нежели входные колебания:

φ = ±π ; Aвых > Aвх,

что соответствует точке АФХ разомкнутой системы, лежащей на вещественной оси левее точки (–1, 0i) (Mраз(ω) = Aвых/Aвх > 1, φраз(ω) = ±π).
Здесь при прохождении через регулятор и объект сигнал усиливается (Mраз(ω) > 1), и его подача по обратной связи на вход Wраз(iω) приводит к возникновению колебательного процесса с непрерывно нарастающей амплитудой («расходящегося»), как на рис. 7.2,д, т.е. замкнутая система оказывается неустойчивой.
Из сказанного становится ясно, что об устойчивости замкнутой системы можно судить на основании расположения амплитудно-фазовой характеристики разомкнутой системы относительно точки с координатами (–1, 0i) (рис. 7.7).
Критерий Найквиста – Михайлова формулируется следующим образом.
Замкнутая система устойчива, если она устойчива в разомкнутом состоянии, и ее амплитудно-фазовая характеристика (построенная для всех значений ω от 0 до бесконечности) не охватывает точку с координатами (–1, 0i).
Если амплитудно-фазовая характеристика проходит через точку с координатами (–1, 0i), система находится на границе устойчивости. Если АФХ охватывает точку с координатами (–1, 0i), то система неустойчива.

Источник

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

6.3. Алгебраический критерий устойчивости Гурвица.

Пример 1

Пример 2

Критерии устойчивости Рауса–Гурвица и Михайлова(геометрический критерий устойчивости)

Геометрический критерий устойчивости (критерий Михайлова)

Матрица Гурвица и критерий устойчивости Гурвица[править | править код]

Матрицы устойчивости Гурвица[править | править код]

См. также[править | править код]

Источники[править | править код]

Внешние ссылки[править | править код]

Вам также может понравиться

Треснул фундамент дома как исправить

Как найти тел если он выключен

Мультики бен как он нашел часы

Добавить комментарий Отменить ответ

Критерии устойчивости Рауса–Гурвица и Михайлова
(геометрический критерий устойчивости)