Если известно сколько составляет часть от целого, то по известной части можно “восстановить”
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
![]()
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
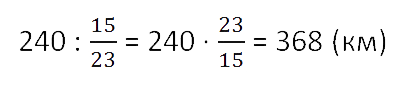
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
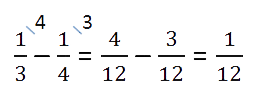
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
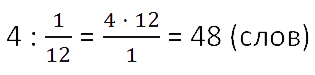
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Мы уже научились находить часть от числа (см. здесь).
А сегодня мы поговорим о том, как найти число по его части (число по его дроби). Эти умения необходимы при решении задач.
Обратимся опять же к пицце.

1. Пиццу разрезали на 8 кусков. Один кусок весит 60 г. Надо узнать вес пиццы. Мы знаем, что пиццу разрезали на 8 частей, т.е. 1 кусок – это 1/8 от целого.
Изобразим это на схеме:
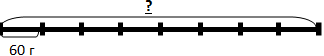
Если 1 кусок весит – 60 г, значит, вся пицца весит в 8 раз больше и надо 60 г умножить на 8.
В дроби 1/8 – знаменатель 8. Итак, чтобы найти целое – надо вес 1 части умножить на знаменатель.
2. Рассмотрим другой пример:
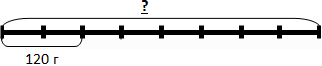
2 куска пиццы весят 120 г. Надо узнать вес целой пиццы.
Как поступим в этом случае?
Вес целой пиццы мы узнавали в предыдущем случае: вес одного куска умножали на число кусков. Значит, надо узнать вес одного куска. Для этого 120 : 2 = 60 (г)
А потом 60 умножим на 8 (как в примере 1).
Итак: 2/8 = 120
данное число 120 разделили на 2 (это числитель дроби), а потом умножили на 8 (это знаменатель дроби):
120 : 2 х 8
Заменим деление на дробь:
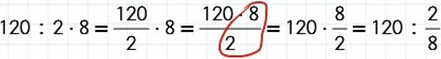
![]()
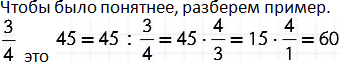
Итак, для того чтобы было легко найти целое по его дроби и дробь от целого, используйте памятку.

Похожие статьи
Эта информация доступна зарегистрированным пользователям
В этом уроке мы научимся, зная дробь от числа, находить все число.
Также мы узнаем, как делать аналогичные действия для процентов, то есть по данному количеству процентов находить все число.
Потом применим полученные навыки для решения задач.
Сформулируем, в чем состоит задача нахождения числа по его дроби.
Имеется дробь; она говорит о том, какая часть от числа нам дана.
Имеется число, равное данной дробной части от искомого числа.
Мы уже умеем находить дробь от числа. Вспомним как это делать.
Эта информация доступна зарегистрированным пользователям
Чтобы найти дробь от числа нам нужно исходное число умножить на эту дробь, тогда получится какое-то значение, обозначающее дробь от числа.
В этой задаче было известно все число и то, какую дробную часть от него необходимо получить. Дробь от числа оставалась неизвестной.
В задаче этого урока дробь от числа нам уже известна, а все число, напротив, только предстоит найти.
Для его нахождения можно составить уравнение, аналогичное тому, которое было на картинке выше. Отличие будет только в том, какие переменные нам известны.
Решая это уравнение, вы переносите известный нам множитель, то есть дробь, в правую часть.
Как делить на дробь мы изучили в прошлом уроке. Напомним, что для этого надо домножить на взаимно обратное число к этой дроби.
Итак, вы получили выражение для неизвестного числа.
Сформулируем правило: чтобы найти дробь от числа необходимо разделить известную часть числа на дробь.
Эта информация доступна зарегистрированным пользователям
Пример 1
(mathbf{frac{3}{4}}) от числа равны 21-му, найдите исходное число.
Для решения необходимо разделить известную часть на дробь, то есть 21 разделить на (mathbf{frac{3}{4}})
(mathbf{21divfrac{3}{4}=21cdotfrac{4}{3}=frac{21cdot4}{3}=frac{7cdot4}{1}=28})
Пример 2
(mathbf{frac{2}{7}}) от числа равны 12, найдите исходное число.
Для решения надо разделить данную часть числа на данную дробь, то есть 12 разделить на (mathbf{frac{2}{7}})
(mathbf{12divfrac{2}{7}=12cdotfrac{7}{2}=frac{12cdot7}{2}=frac{6cdot7}{1}=42})
Пример 3
Далеко не всегда часть числа делится на числитель данной дроби; в таких случаях мы будем получать в ответе не целые числа, а дроби или смешанные числа.
(mathbf{frac{2}{3}}) от числа равны 11, найдите исходное число.
Во всем остальном решение ничем не будет отличаться- также разделим дробь от числа, равную (mathbf{frac{2}{3}}), на величину дроби, равную 11 и получим результат.
(mathbf{11divfrac{2}{3}=11cdotfrac{3}{2}=frac{11cdot3}{2}=frac{33}{2}=16frac{1}{2}})
Для получения ответа нам понадобилось выделить целую часть.
Важен еще один случай.
Никто не гарантирует, что данная нам часть числа сама по себе не будет являться дробью.
Такого случая не стоит пугаться, а стоит придерживаться алгоритма, а именно делить часть числа на то, какой дробью она является.
Пример 4
(mathbf{frac{5}{6}}) от числа равны (mathbf{frac{2}{3}}), найдите все число.
Для решения этого примера разделим (mathbf{frac{2}{3}})- часть числа, на (mathbf{frac{5}{6}})- дробь.
(mathbf{frac{2}{3}divfrac{5}{6}=frac{2}{3}cdotfrac{6}{5}=frac{2cdot6}{3cdot5}=frac{2cdot2}{5}=frac{4}{5}})
Все исходное число равняется (mathbf{frac{4}{5}})
Эта информация доступна зарегистрированным пользователям
Теперь представим, что дан какой-то определенный процент от числа и необходимо найти, от какого числа брали процент.
Вспомним, что процент- это способ записи десятичной дроби.
То есть, чтобы из процента получить десятичную дробь, которую он обозначает, надо величину процента разделить на 100.
Поэтому для решения такого рода задач надо преобразовать процент в десятичную дробь, а дальше сделать все то же самое: разделить число на эту дробь.
Пример 1
Известно, что зарплата работника увеличилась на 2 000 рублей или на 25 процентов. Какая зарплата у работника была изначально?
Решение:
Переведем проценты в дроби: (mathbf{25%=25div100=0.25})
Разделим число на дробь: (mathbf{2000div0.25=8000})
Ответ: изначально зарплата работника была 8000 рублей.
Сформулируем правило.
Чтобы найти число по проценту от него, надо перевести процент в десятичную дробь, а после разделить данную часть числа на полученную дробь.
Пример 2
Сказано, что 9% от числа равны 81. Необходимо найти все число.
Решение:
Первым действием переводим проценты в десятичную дробь.
(mathbf{9%=9div100=0.09})
Вторым действием делим данное число на эту дробь.
(mathbf{81div0.09=900})
Ответ: искомое число 900
Эта информация доступна зарегистрированным пользователям
Задачи, в которых фигурируют дроби от числа часто встречаются не только в школьных учебниках и задачниках, но и в реальной жизни, поэтому стоит уделить им особое внимание.
Сначала разберем некоторые из таких задач вместе, а дальше вы попробуете свои силы в самостоятельном решении задач.
Часть задач тривиальна, иными словами, их решение очевидно, достаточно лишь увидеть в них формулу, подставить в нее данные значения и получить результат.
Пример:
Айсберг возвышается над водой на (mathbf{frac{1}{11}}) своей высоты.
Капитан корабля заметил, что от воды до макушки айсберга по вертикали 16 метров.
Какова общая высота айсберга?
Решение:
В данном случае мы сразу можем сказать, что все число- это общая высота айсберга, дробь от числа- 16 (метров), а величина дроби- (mathbf{frac{1}{11}}).
Соответственно, по правилу, для получения ответа мы делим 16 на (mathbf{frac{1}{11}}) и получаем результат.
(mathbf{16divfrac{1}{11}=16cdot11=176}) (метр)- общая высота айсберга
Ответ: 176 (метров).
Некоторые задачи для своего решения требуют более глубокого анализа.
Пример:
Магазин продал (mathbf{frac{2}{3}}) пар новых кроссовок специальной партии, после чего на складе осталось 56 пар.
Какого размера была специальная партия?
Решение:
В данной задаче, если не вчитываться в условие, интуитивно хочется просто поделить 56 на (mathbf{frac{2}{3}}) и получить ответ, но ответ не будет правильным.
Если посмотреть внимательно, то 56 пар соответствуют оставшейся части партии, в то время как дробь (mathbf{frac{2}{3}}) описывает проданную часть.
Но мы пока не знаем общего количества пар и не можем сказать, какому числу соответствует (mathbf{frac{2}{3}})
Зато мы можем вычислить размер оставшейся части.
Если вся партия – это 1, и продано (mathbf{frac{2}{3}}), значит осталась (mathbf{frac{1}{3}}) товара.
Эта дробь соответствует 56 оставшимся парам.
Дальнейшие действия аналогичны рассмотренным в предыдущей задаче.
Теперь оформим решение:
1) (mathbf{1-frac{2}{3}=frac{1}{3}}) составляет оставшаяся часть от всего размера партии
2) (mathbf{56divfrac{1}{3}=56cdot3=168}) (пар) кроссовок всего было в партии
Ответ: 168 (пар).
Вам могут встретиться задачи и с более сложными условиями, все их разобрать невозможно, но главное:
- не давать себя запутать
- расписать, какой части какая дробь и какое число соответствует
- понять, где данных достаточно, чтобы узнать что- то новое
- и так постепенно продвигаться к ответу
Эта информация доступна зарегистрированным пользователям
Задачи математики часто диктуются другими науками, в том числе экономикой.
Существуют поднауки других наук, связанные с математикой. Примерами таких могут служить математическая физика, изучающая, как следует из названия, физические модели, а также математическая экономика, о которой мы вам сейчас расскажем.
Предметом изучения этой теории является математическое описание экономических объектов, явлений и процессов.
В самом деле, интересно применить мощнейший математический аппарат к таким насущным вопросам, как изменение цен и доходов, изменение предпочтений покупателей и пр.
Истоки математической экономики идут с XVII века. Тогда преподаватели германских университетов начали использовать новый стиль преподавания, который включал в себя статистику. Там, где появляется статистика, то есть множество чисел, появляется и математика, которая выявляет какие-то закономерности.
К примеру, расчет среднего дохода крестьян не является сложной задачей и сводится к вычислению среднего арифметического, но тоже является задачей математики.
В это же время группа английских ученых создала метод «численной аргументации государственной политики», который затрагивал темы налогов, сборов, таможенных пошлин, и прочие экономические процессы, в которых участвует государство.
К XIX веку появляется и развивается классическая школа политической экономики, чьим лицом принято считать Адама Смита.
Эта информация доступна зарегистрированным пользователям
Именно в этот период математика начала активно применяться в экономике.
В дальнейшем все большее количество математических инструментов переходило в экономику, а в наши дни на нее трудятся еще и информационные технологии.
Так что в наши дни великим экономистом может быть не тот, кто изначально учился на экономиста, а успешный математик или программист.
Тема урока:
«Нахождение числа по его дроби»
Цель урока:
научить находить число по его части.
Задачи:
Регулятивные:
– самостоятельно организовывать свое
рабочее место в соответствии с целью выполнения заданий;
– определять правильность выполнения заданий;
– самостоятельно оценивать свою работу на
уроке.
Познавательные:
– актуализировать знания о простых дробях,
значении числителя и знаменателя дроби;
– научить находить число по его дроби,
моделировать решение задач на части с помощью схем;
Коммуникативные:
– участвовать в диалоге, слушать и
понимать других, оформлять свои мысли в устной и письменной речи;
– сотрудничать с учителем и
одноклассниками.
Личностные:
– осмысление личностного смысла учения,
понимать позицию другого.
Форма урока:
ознакомления с новым материалом.
Оборудование:
Ход
урока
Организационный момент
Здравствуйте
дети, откройте свои тетради и запишите число. Сегодня 16 апреля. Посередине
строки пишем «Классная работа». Не забываем про удвоенную букву «с».
Перед
тем как приступить к новой теме проверим домашнюю работу и проведем устный
счет.
Актуализация опорных знаний
Проверка домашнего задания
Устный счет (слайд 2)
1. Найдите сумму чисел 390 и 320. (710)
2. Найдите разность чисел 580 и 410. (130)
3. Найдите произведение чисел 32 и 6.
(192)
4. Загадали число. Его увеличили на 220 и
получили 490. Какое число было загадано? (270)
 5. Загадали число. Его
5. Загадали число. Его
уменьшили на 130 и получили 580. Какое число было загадано? (450)
6. На сколько разность между 560 и 230
меньше чем их сумма? (330)
7. Во сколько раз 600 больше 200? (3)
8. Длина коридора 30 м, ширина его 5 м.
Найти его площадь. (30*5=150)
Самоопределение к деятельности
– Рассмотрите чертеж (слайд 3). Чему равна
одна часть? (12:4=3(см))
12 см
– Найдите длину всего отрезка. (3*6=18
(см))
– Прочитайте тему урока (слайд 4).
Сформулируйте цели. (слайд
5)
Работа по теме урока
Объяснение нового материала
– Решим задачу (слайд 6).
Мама израсходовала ½ ленты для украшения
платья, что составило 135 см. Сколько ленты у мамы было до начала работы?
– Будем рассуждать так: ½ – это одна из 2
– ух равный частей ленты. Значит во всей ленте таких частей – 2, так как ½
длины ленты равна 135 см, то длина всей ленты в 2 раза больше. Умножим 135 см
на 2, получится 270 см, значит первоначальная длина всей ленты 270 см.
– Решим задачу (слайд 7).
Миша загадал число и сообщил, что 2/5
загаданного числа равны 374. Какое число загадал Миша?
Сначала найдем чему равна 1/5 часть
загаданного числа, она в два раза меньше 374. Разделим 374 на 2 получится 187.
В загаданном числе таких частей – 5. Умножим 187 на 5 получится 935. Значит
Миша загадал число 935.
– Послушав объяснение, скажите, как найти
число по его дроби? (Что бы найти число по его дроби, нужно известную часть
числа разделить на числитель этой дроби, а затем умножить на её знаменатель)
Работа по учебнику
Упр. №1 стр. 76
– Сколько
половинок в целом? (2)
– Как найти цену
хлеба? (5 р .60 к. * на 2)
– Запишите
решение.
–
Сколько стоит буханка хлеба? (11 р., 20 к.)
Упр.
№ 2 стр. 76
– Как
будете находить неизвестное число? (219:3*5)
– Запишите
решение.
– Назовите
число (365)
– Как
найти число по его дроби?
Физкультминутка
Деревцо
всё выше, выше. (Дети имитируют дуновение ветра, качая туловище
то
в одну, то в другую сторону. На слова «тише, тише» дети приседают,
на
«выше, выше» — выпрямляются.)
Ветер
веет над полями
Ветер
веет над полями,
И
качается трава. (Дети плавно качают руками над головой.)
Облако
плывет над нами,
Словно
белая гора. (Потягивания — руки вверх.)
Ветер
пыль над полем носит.
Наклоняются
колосья —
Вправо-влево,
взад-вперёд,
А
потом наоборот. (Наклоны вправо-влево, вперёд-назад.)
Мы
взбираемся на холм, (Ходьба на месте.)
Там
немного отдохнём. (Дети садятся.)
Ветер
тихо клен качает
Ветер
тихо клен качает,
Вправо,
влево наклоняет:
Раз
— наклон и два — наклон,
Зашумел
листовою клен. (Ноги на ширине плеч, руки за голову. Наклоны туловища вправо и
влево.)
Закрепление
изученного материала
Работа по учебнику
Упр. № 5 стр. 76
(коллективная работа)
–
Назовите вид задачи. (На встречное движение, но поезда вышли не одновременно)
–
Какой путь прошел первый поезд до отправления второго поезда? (40*4=160)
–
Какое расстояние они прошли одновременно навстречу друг другу? (1060 – 160 =
900 (км))
–
Какая скорость сближения поездов? (40 + 50 = 90 (км/ч))
–
Через сколько часов после отправления второго поезда они встретятся? (900:90 =
10 (ч))
–
На каком расстоянии от города А произошла встреча? (160+40*10= 560 (км) )
Решение:
40
км/ч
50 км/ч
4
часа проехал
А
В
1060 км
1)
4*40=160 (км) – проехал первый поезд до выхода второго;
2)
1060 – 160 = 900 (км) – было между поездами, когда выехал второй поезд;
3)
40 + 50 = 90 (км/ч) – скорость сближения поездов;
4)
900:90 = 10 (ч) – через 10 часов после отправления второго поезда они
встретятся;
5)
160+40*10= 560 (км) – от города А встретятся поезда.
Ответ:
через 10 часов; 560 км.
Рефлексия
–
Сейчас я вам раздам карточки, надо быстрее всех решить задачу. Предлагаю решить
одно задание с карточки, но в этом задании есть подвох, чем сложнее задание,
тем выше оценка, чем легче задание, тем ниже оценка. У вас 5 минут.
Оценивание
работы будет следующим: задание №1 на отметку “3”, задание №2 на отметку “4” и
задание №3 на отметку “5”.
1.
На покупку игрушек девочка потратила 150 р., что составило 3/8 всех её денег.
Сколько всего денег было у девочки?
2.
Масса 2/3 тыквы составляет 5 кг 400 г. Найди массу всей тыквы.
3.
С трех участков собрали 2 115 т пшеницы. С первого участка собрали 2/5
всего урожая, а со второго участка – на 86 т меньше, чем с первого. Сколько
тонн пшеницы собрали с третьего участка?
Подведение
итогов урока (слайд 8)
–
Как найти число по его дроби?
–
Оцените, насколько хорошо вы поняли новую тему.
–
Оцените свою работу на уроке.
Домашнее
задание (слайд 9)
Упр.
№7 стр. 76
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Нахождение числа по его дроби
Замечание 1
Чтобы найти число по данному значению его дроби нужно это значение разделить на дробь.
Пример 1
Антон за неделю учебы заработал три четверти отличных отметок. Сколько всего отметок получил Антон, если отличных отметок было 6.
Решение.
По условию задачи $6$ отметок – это $frac{3}{4}$.
Найдем количество всех отметок:
$6div frac{3}{4}=6 cdot frac{4}{3}=frac{6 cdot 4}{3}=frac{2 cdot 3 cdot 4}{3}=2 cdot 4=8$.
Ответ: всего $8$ отметок.
Пример 2
Выкосили $frac{4}{9}$ пшеницы на поле. Найти площадь поля, если было скошено $36$ га.
Решение.
По условию задачи $36$ га – это $frac{4}{9}$.
Найдем площадь всего поля:
$36div frac{4}{9}=36 cdot frac{9}{4}=frac{36 cdot 9}{4}=frac{4 cdot 9 cdot 9}{4}=81$.
Ответ: площадь всего поля $81$ га.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 3
За один день автобус проехал $frac{2}{3}$ маршрута. Найти продолжительность намеченного маршрута, если за день автобус проехал $350$ км?
Решение.
По условию задачи $350$ км – это $frac{2}{3}$.
Найдем продолжительность всего маршрута автобуса:
$350div frac{2}{3}=350 cdot frac{3}{2}=frac{350 cdot 3}{2}=175 cdot 3=525$.
Ответ: продолжительность намеченного маршрута $525$ км.
Пример 4
Рабочий поднял производительность своего труда на $% $и сделал за такой же срок на $24$ детали больше, чем было запланировано. Найти количество деталей, запланированных для выполнения рабочим.
Решение.
По условию задачи $24$ детали = $8%$, а $8% = 0,08$.
Найдем количество деталей, запланированных для выполнения рабочим:
$24div 0,08=24div frac{8}{100}=24 cdot frac{100}{8}=frac{24 cdot 100}{8}=frac{3 cdot 8 cdot 100}{8}=300$.
Ответ: запланировано $300$ деталей для выполнения рабочим.
«Нахождение числа по его дроби, дробные выражения» 👇
Пример 5
В цехе отремонтировали $9$ станков, что составляет $18%$ всех станков цеха. Сколько станков находится в цехе?
Решение.
По условию задачи $9$ станков = $18%$, а $18% = 0,18.$
Найдем количество станков в цехе:
$9div 0,18=9div frac{18}{100}=9 cdot frac{100}{18}=frac{9 cdot 100}{18}=frac{9 cdot 100}{2 cdot 9}=frac{100}{2}=50$.
Ответ: в цехе $50$ станков.
Дробные выражения
Рассмотрим дробь $frac{a}{b}$, которая равна частному $adiv b$. В таком случае частное от деления одного выражения на другое удобно записывать также с помощью черты.
Пример 6
Например, выражение $(13,5–8,1)div (20,2+29,8)$ можно записать следующим образом:
$frac{13,5-8,1}{20,2+29,8}$.
После выполнение расчетов получим значение данного выражения:
$frac{13,5-8,1}{20,2+29,8}=frac{5,4}{50}=frac{10,8}{100}=0,108$.
Определение 1
Дробным выражением называется частное двух чисел или числовых выражений, в котором знак $«:»$ заменен дробной чертой.
Пример 7
$frac{2,4}{1,3 cdot 7,5}$, $frac{frac{5}{8}+frac{3}{11}}{2,7-1,5}$, $frac{2a-3b}{3a+2b}$, $frac{5,7}{ab}$ – дробные выражения.
Определение 2
Числовое выражение, которое записывается выше дробной черты, называется числителем, а числовое выражение, которое записывается ниже дробной черты, – знаменателем дробного выражения.
В числителе и знаменателе дробного выражения могут стоять числа, числовые или буквенные выражения.
Для дробных выражений могут применяться правила, которые справедливы для обыкновенных дробей.
Пример 8
Найти значение выражения $frac{5 frac{3}{11}}{3 frac{2}{7}}$.
Решение.
Умножим числитель и знаменатель данного дробного выражения на число $77$:
$frac{5 frac{3}{11}}{3 frac{2}{7}}=frac{5 frac{3}{11} cdot 77}{3 frac{2}{7} cdot 77}=frac{406}{253}=1,6047…$
Ответ: $frac{5 frac{3}{11}}{3 frac{2}{7}}=1,6047…$
Пример 9
Найти произведение двух дробных чисел $frac{16,4}{1,4}$ и $1 frac{3}{4}$.
Решение.
$frac{16,4}{1,4} cdot 1 frac{3}{4}=frac{16,4}{1,4} cdot frac{7}{4}=frac{4,1}{0,2}=frac{41}{2}=20,5$.
Ответ: $frac{16,4}{1,4} cdot 1 frac{3}{4}=20,5$.
Пример 10
Найти сумму двух дробей $frac{2}{0,7}+frac{3}{1,4}$.
Решение.
$frac{2}{0,7}+frac{3}{1,4}=frac{4+3}{1,4}=frac{7}{1,4}=frac{70}{14}=5$.
Ответ: $frac{2}{0,7}+frac{3}{1,4}=5$.
Для выполнения сложения дробных выражений удобно сразу их преобразовать к виду обыкновенных дробей, а затем выполнить сложение:
$frac{2}{0,7}+frac{3}{1,4}=frac{20}{7}+frac{30}{14}=frac{20}{7}+frac{15}{7}=frac{35}{7}=5$.
Пример 11
Найти значение выражения: $frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}$.
Решение.
$frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}=frac{frac{7 cdot 33}{11 cdot 21}+1,23}{2,3}=frac{1+1,23}{2,3}=frac{2,23}{2,3}=frac{9,79}{2,3}=0,96956…$
Ответ: $frac{frac{7}{11} cdot frac{33}{21}+1,23}{5,1-2,8}=0,96956…$
Пример 12
Найти значение выражения $frac{2,48+3 frac{5}{9} cdot 1 frac{1}{8}}{6,1-3,7}$.
Решение.
В числителе смешанные числа преобразуем к виду неправильных дробей и выполним вычисления:
$frac{2,48+3 frac{5}{9} cdot 1 frac{1}{8}}{6,1-3,7}=frac{2,48+frac{32}{9} cdot frac{9}{8}}{2,4}=frac{2,48+4}{2,4}=frac{6,48}{2,4}=2,7$.
Ответ: $2,7$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
