Владислава Беляева
Ученик
(110),
на голосовании
10 лет назад
Голосование за лучший ответ
А.К. (лично)
Искусственный Интеллект
(247048)
10 лет назад
ну если радиус 21 мм, то длина L=2 * пи * R
Я и то в 51 год помню как
НатУша
Искусственный Интеллект
(198286)
10 лет назад
Может длину образующей конуса?
Тогда по теореме Пифагора
33^2 + 21^2 =
ояс
Просветленный
(44425)
10 лет назад
Слава открой книжку и прочитай всё, что там написано о конусе. А если Длина образующей конуса, то ответ_ будет такой-корень квадратный из 1530 ;
Длина основания конуса =2*пи*R; пи=3.14
“2*3.14*21=131.88
Похожие вопросы
Зная площадь основания конуса, можно рассчитать радиус, диаметр и периметр основания конуса, преобразовав стандартные формулы.
r=√(S_(осн.)/π)
d=2√(S_(осн.)/π)
P=2πr=2√(πS_(осн.) )
Высота, образующая и радиус конуса соединяются в прямоугольный треугольник, из которого по теореме Пифагора можно найти любое значение, зная остальные два. Угол наклона конуса можно найти из этого же треугольника через отношение тангенса, а уже через него во втором, равнобедренном треугольнике вычислить угол раствора конуса. (рис.40.1,40.2)
l=√(h^2+r^2 )=√(h^2+S_(осн.)/π)
tanβ=h/r
α=180°-2β
Вычислить площадь боковой поверхности конуса через площадь основания и высоту можно, заменив радиус и образующую конуса в формуле на соответствующие выражения. Чтобы найти площадь полной поверхности конуса, следует поступить аналогично.
S_(б.п.)=πrl=√(πS_(осн.) (h^2+S_(осн.)/π) )
S_(п.п.)=S_(осн.)+√(πS_(осн.) (h^2+S_(осн.)/π) )
Объем конуса в стандартном виде представляет собой отношение произведения высоты и площади основания к трем, поэтому его можно вычислить сразу через площадь основания и высоту, заданные в условии.
V=1/3 hS_(осн.)
Чтобы найти радиус сферы, вписанной в конус, нужно умножить высоту на выражение, найденное для радиуса, и разделить это на сумму образующей и радиуса. Радиус сферы, описанной около конуса, будет равен образующей во второй степени, деленной на удвоенную высоту. (рис. 40.3, 40.4)
r_1=hr/(l+r)=(h√(S_(осн.)/π))/(√(h^2+S_(осн.)/π)+√(S_(осн.)/π))
R=(h^2+r^2)/2h=(h^2+S_(осн.)/π)/2h
Основание конуса – это его единственная круглая грань, самый широкий круг в стопке кругов, идущий вверх или вниз по длине конуса. Например, если вы наполнили конус мороженого, основание было бы его вершиной. Основание конуса – это круг, поэтому, если вы знаете радиус конуса, вы можете найти площадь основания, используя формулу площади для круга.
Радиус и Пи
Радиус, обычно обозначаемый как «r» конуса, представляет собой расстояние от центра основания конуса до стороны основания конуса. Pi определяется как окружность круга, деленная на его диаметр. Он всегда имеет одинаковое значение: примерно 3, 14. В зависимости от уровня точности, который вам нужен в ваших вычислениях, число pi может быть расширено до бесконечного числа цифр после десятичной точки. Например, число пи, расширенное до семи цифр, будет равно 3.1415926. Тем не менее, 3.14 считается достаточно хорошим приближением для основных геометрических уравнений.
Нахождение территории базы
Площадь круга, или A, и площадь основания конуса, равна pi, умноженному на его радиус в квадрате: A = pi xr ^ 2. Число в квадрате равно этому числу, умноженному на себя. Если бы ваш конус имел радиус 7 дюймов, вы бы вычислили площадь следующим образом: A = pi x 7 дюймов ^ 2 = 3, 14 x 7 дюймов x 7 дюймов = 153, 86 квадратных дюймов
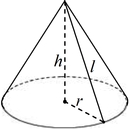
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H
1) Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3∙πR²H. Получите: R²=3V/πH, откуда R=√ (3V/πH)
. 2) Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=πRL. Вы получите R=S/πL.
3) Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L²=R²+H². Выразите из данной формулы R, получите: R²=L²-H² и R=√ (L²-H²).
4) Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол α между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L∙sinα.
5) Если известны образующая конуса L и угол β между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L∙cosβ. Если известны высота конуса H и угол α между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H∙tgα.
6) Пример: образующая конуса L равна 20 см и угол α между образующей и высотой конуса равен 15º. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом α противолежащий этому углу катет R вычисляется по формуле R=L∙sinα. Подставьте соответствующие значения, получите: R=L∙sinα=20∙sin15º. Sin15º находится из формул тригонометрических функций половинного аргумента и равен 0,5√ (2-√3). Отсюда катет R=20∙0,5√ (2-√3) = 10√ (2-√3) см. Соответственно, радиус основания конуса R равен 10√ (2-√3) см.
7) Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30º, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30º, то найдите радиус по формуле: R=1/2L.
