
СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
математика
Математика
Информатика
≡ Русский язык
Письменный экзамен
Устное собеседование
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
сайты – меню – вход – новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
 |
 |
На сайте что-то не так? Отключите адблок
Новости
1 мая
Новый сервис: можно исправить ошибки!
1 мая
Бесплатные курсы подготовки к ЕГЭ и ОГЭ
29 апреля
Разместили актуальные шкалы ОГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
21 апреля
Разместили варианты из заданий открытого банка ФИПИ ОГЭ по русскому языку
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
6 марта
Изменения ВПР 2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 18 № 348586 

i
На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите длину его большей диагонали.
Спрятать решение
Решение.
Из рисунка видно, что длина большей диагонали ромба — 6.
Ответ: 6.
Аналоги к заданию № 348446: 348586 349027 349478 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Прототип задания
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите длину его большей диагонали.
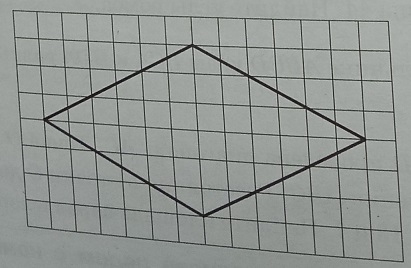
Источник: ОГЭ Ященко 2022 (50 вариантов)
Решение:
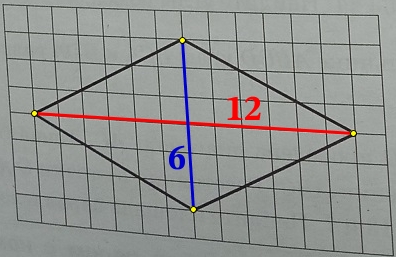
Длина большей диагонали равна 12.
Ответ: 12.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 19
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:04.10.2021
- Рубрика записи18. Фигуры на квадратной решётке
- Автор записи:Andrei Maniakin
На клетчатой бумаге с размером клетки 1Х1 изображен ромб. Найдите длину его большей диагонали
Видео 18 ОГЭ Задача найти большую диагональ ромба канала В Плюсе
Показать
Свойства ромба
1. Противолежащие стороны ромба параллельны и равны.
AB parallel CD,;BC parallel AD
AB = CD,;BC = AD

2. Диагонали ромба перпендикулярны.
ACperp BD

Доказательство
Так как ромб является параллелограммом, то его диагонали делятся пополам.

Значит, triangle BOC = triangle DOC по трем сторонам (BO = OD, OC — совместная, BC = CD). Получаем, что angle BOC = angle COD, и они смежны.
Rightarrow angle BOC = 90^{circ} и angle COD = 90^{circ}.
3. Точка пересечения диагоналей делит их пополам.
AC=2cdot AO=2cdot CO
BD=2cdot BO=2cdot DO

4. Диагонали ромба являются биссектрисами его углов.
angle 1 = angle 2; ; angle 5 = angle 6;
angle 3 = angle 4; ; angle 7 = angle 8.
Доказательство

По причине того, что диагонали разделены точкой пересечения пополам, и все стороны ромба равны друг другу, то вся фигура делится диагоналями на 4 равных треугольника:
triangle BOC, ; triangle BOA, ; triangle AOD, ; triangle COD.
Это значит, что BD, AC — биссектрисы.
5. Диагонали образуют из ромба 4 прямоугольных треугольника.

6. Любой ромб может содержать окружность с центром в точке пересечения его диагоналей.

7. Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
AC^2 + BD^2 = 4cdot AB^2
Признаки ромба
1. Параллелограмм с перпендикулярными диагоналями является ромбом.

begin{cases} AC perp BD ABCD end{cases} — параллелограмм, Rightarrow ABCD — ромб.
Доказательство

ABCD является параллелограммом Rightarrow AO = CO; BO = OD. Также указано, что AC perp BD Rightarrow triangle AOB = triangle BOC = triangle COD = triangle AOD — по 2-м катетам.
Получается, что AB = BC = CD = AD.
Доказано!
2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб.
Доказательство

angle A = angle C, поскольку ABCD — параллелограмм. AC — биссектриса angle A и angle C.
Следовательно, triangle ABC = triangle ADC и оби фигуры — равнобедренные треугольники.

Это означает, что AB = BC = CD = DA, и ABCD — ромб.
На заметку: не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом.
К примеру:

Это уже не ромб, не смотря на перпендикулярность диагоналей.
Для отличия стоит запомнить, что сначала четырехугольник должен быть параллелограммом и иметь признаки параллелограмма 1 и 2
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сумма внутренних углов любого четырехугольника равна (360^circ).
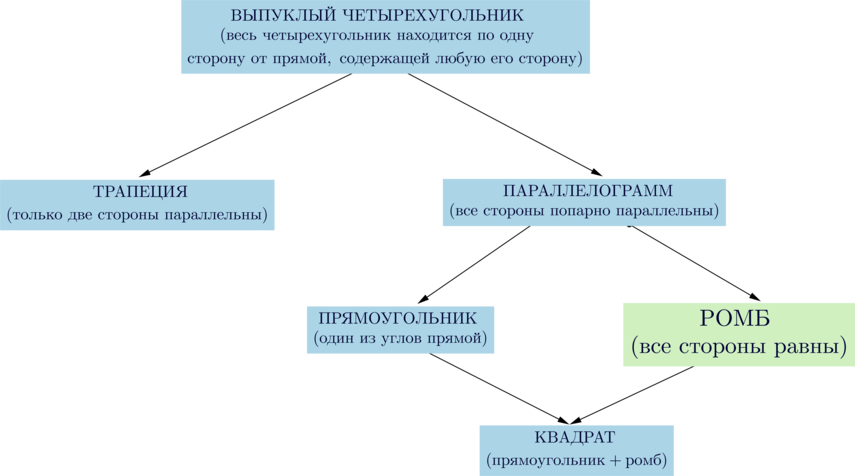
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
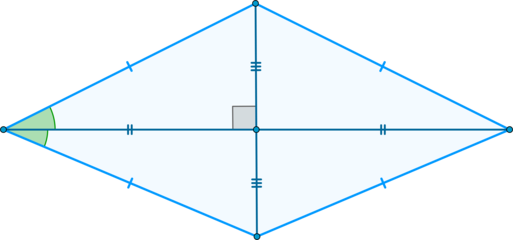
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.

2. Площадь ромба равна половине произведения его диагоналей.

Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} — angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
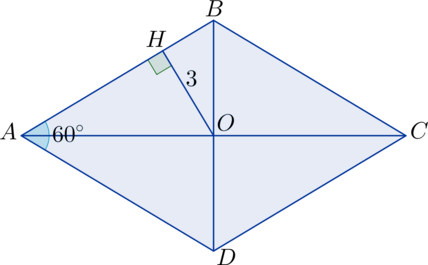
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
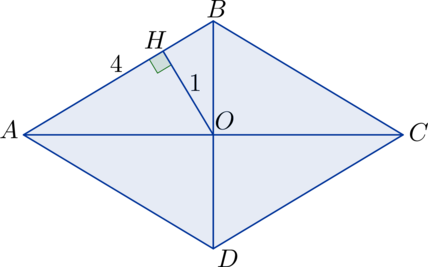
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = .
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
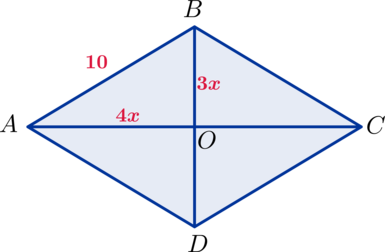
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ

Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
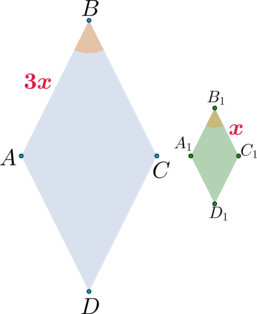
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.

Кайф или жесть? Новая шкала перевода баллов ЕГЭ 2022 по математике
Кайф или жесть? Новая шкала перевода баллов ЕГЭ 2022 по математике
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Фигуры на квадратной решетке
В 19 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания. Давайте на них посмотрим.
Разбор типовых вариантов задания №19 ОГЭ по математике
Первый вариант задания
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.
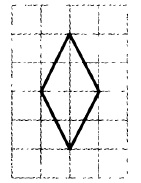
Решение:
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4.
Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Ответ: 4.
Второй вариант задания
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.
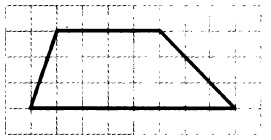
Решение:
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее — 4 клеткам. Полусумма оснований:
( 8 + 4 ) / 2 = 6
Ответ: 6
Третий вариант задания
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
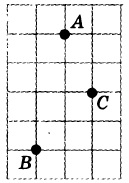
Решение:
Проведем необходимые отрезки:
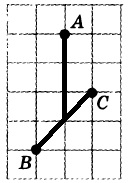
Из рисунка можно вычислить длину — это 3.
Ответ: 3.
Демонстрационный вариант ОГЭ 2019
Найдите тангенс острого угла, изображённого на рисунке.
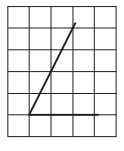
Решение:
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:
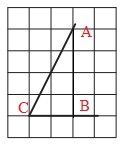
Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.
Согласно определению тангенса, из треугольника ∆АВС можем записать:
tg∠C=AB/BC.
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
АВ=4, ВС=2.
Получаем:
tg∠C=4/2=2.
Ответ: 2
Четвертый вариант задания
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
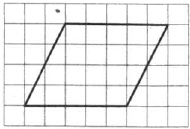
Решение:
Площадь параллелограмма вычисляется так:
S=a·ha
Обозначим a и ha на рисунке:
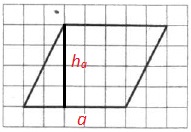
Теперь определим их длины по рисунку:
a=5; ha=4.
Вычисляем искомую площадь:
S=5·4=20.
Ответ: 20
Пятый вариант задания
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
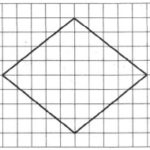
Решение:
Площадь ромба будем искать через его диагонали:
S=d1·d2/2
Линии диагоналей обозначим на рисунке красным:
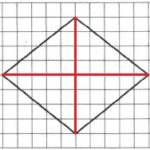
Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:
d1=8; d2=10.
Находим площадь фигуры:
S=8·10/2=40.
Ответ: 40
Введение
В этой
заметке приводится решение задачи под номером №18 варианта № 29. В задании
указаны размеры только квадратиков клетчатой бумаги, на которой изображен ромб,
диагональ которого требуется найти. Задача № 18 из варианта № 34 решается
аналогично.
Условия
задачи
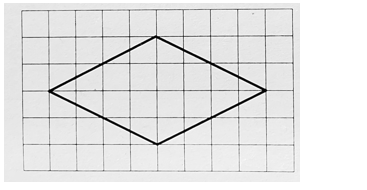
Дано:
ромб на
клетчатой бумаге
Размер каждой клетки 1×1
Найти большую диагональ ромба
База
данных
В решении
будут использованы следующие сведения
- Диагональ
ромба — это отрезок, соединяющий две его противоположные вершины
Решение
Построим диагонали ромба
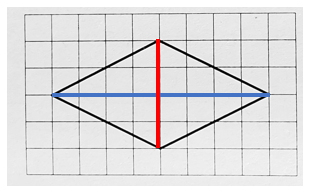
Как видно из чертежа, длина красной диагонали равна длине четырёх клеток, а длина синей – восемь клеток, стало быть, большая диагональ синяя и её длина равна восьми.
Ответ: 8
Основные выводы
Похоже, экзаменаторы проверяют, знаете
ли вы, что такое диагонали ромба, и можете ли на глаз определить, которая из
них больше.
Желаю новых
успехов в подготовке к ОГЭ!
