Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июля 2021 года; проверки требуют 10 правок.
Файл:Скорость небесного тела
Скорость кеплеровского движения небесного тела вокруг Солнца, а также её радиальная и поперечная компоненты (анимация).
Орбитальная скорость тела (обычно планеты, естественного или искусственного спутника, кратной звезды) — скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.
Определение[править | править код]
В полярных координатах выражение для орбитальной скорости 
где:
— гравитационный параметр, равный G(M + m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела;
— фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение
— для эллипса и гиперболы);
— эксцентриситет (
для эллипса,
для параболы,
— для гиперболы);
— истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела.
Орбитальная скорость также может вычисляться по общей формуле
где
— гравитационный параметр,
— расстояние между вращающимся телом и центральным телом,
— удельная орбитальная энергия,
— длина большой полуоси (или вещественной оси).
При этом
Орбиты Земли[править | править код]
| Орбита | Расстояние между центрами масс, км | Высота над поверхностью Земли, км |
Орбитальная скорость, км/с | Орбитальный период | Удельная орбитальная энергия, МДж/кг |
|---|---|---|---|---|---|
| Поверхность Земли, для сравнения | 6 400 | 0 | 7,89 | — | −62,6 |
| Низкая околоземная орбита | 6 600—8 400 | 200—2 000 | круговая: 7,8—6,9 эллиптическая: 6,5—8,2 |
89—128 мин | −29,8 |
| Высокоэллиптическая орбита спутников Молния | 6 900—46 300 | 500—39 900 | 1,5—10,0 | 11 ч 58 мин | −4,7 |
| Геостационарная орбита | 42 000 | 35 786 | 3,1 | 23 ч 56 мин | −4,6 |
| Орбита Луны | 363 000—406 000 | 357 000—399 000 | 0,97—1,08 | 27,3 дня | −0,5 |
Солнечная система[править | править код]
| Планета (другое тело) |
Орбитальная скорость, км/с |
|---|---|
| Меркурий | 47,36 |
| Венера | 35,02 |
| Земля | 29,78 |
| Марс | 24,13 |
| Церера | 17,88 |
| Юпитер | 13,07 |
| Сатурн | 9,69 |
| Уран | 6,81 |
| Нептун | 5,43 |
| Плутон | 4,66 |
| Хаумеа | 4,48 |
| Макемаке | 4,41 |
| Эрида | 3,43 |
| Луна | 1,02 |
Примечания[править | править код]
- ↑ Балк М. Б. Скорость спутника и её компоненты // Элементы динамики космического полета. — М.: Наука, 1965. — С. 61—62. — 340 с. — (Механика космического полета).
Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?
Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.
Оглавление
- 1 Первая космическая скорость
- 1.1 Расчет
- 2 Вторая космическая скорость
- 2.1 Расчет
- 3
- 4 Третья космическая скорость
- 4.1 Расчет
- 5 Четвертая космическая скорость
- 6 Пятая космическая скорость
- 7 Почему спутники не падают на Землю
Первая космическая скорость
Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.
Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.
Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.
Расчет




Вторая космическая скорость
Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.
Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.
Движение тела на второй космической скорости происходит по параболической траектории.
Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.
Расчет


Третья космическая скорость
Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.
Расчет



Для Солнечной системы это величина равна 16,650 км/с.
Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.
КА «Новые горизонты» покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, «Новые горизонты» добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.
Четвертая космическая скорость

Эта та скорость, которая позволит покинуть галактику в данной точке.
Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.
Пятая космическая скорость
Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.
Для Земли эта скорость будет равна 43,6 км/с.
Почему спутники не падают на Землю

Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.
На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.
То есть, спутники падают, но промахиваются и не попадают в Землю.
Еще больше космоса и интересных фактов в телеграмм-канале.
Четверг, 11 февраля, 2016

В космосе гравитация обеспечивает силу, из-за которой спутники (такие, как Луна) вращаются по орбитам вокруг более крупных тел (таких, как Земля). Эти орбиты в общем случае имеют форму эллипса, на чаще всего, этот эллипс не сильно отличается от окружности. Поэтому в первом приближении можно считать орбиты спутников круговыми. Зная массу планеты и высоту орбиты спутника над Землей, можно рассчитать, какой должна быть скорость движения спутника вокруг Земли.
Расчет скорости движения спутника вокруг Земли
Вращаясь по круговой орбите вокруг Земли, спутник в любой точке своей траектории может двигаться только с постоянной по модулю скоростью, хотя направление этой скорости будет постоянно изменяться. Какова же величина этой скорости? Её можно рассчитать с помощью второго закона Ньютона и закона тяготения.
Для поддержания круговой орбиты спутника массы ![]() в соответствии со вторым законом Ньютона потребуется центростремительная сила:
в соответствии со вторым законом Ньютона потребуется центростремительная сила: ![]() , где
, где ![]() — центростремительное ускорение.
— центростремительное ускорение.
Как известно, центростремительное ускорение определяется по формуле:
![]()
где ![]() — скорость движения спутника,
— скорость движения спутника, ![]() — радиус круговой орбиты, по которой движется спутник.
— радиус круговой орбиты, по которой движется спутник.
Центростремительную силу обеспечивает гравитация, поэтому в соответствии с законом тяготения:
![]()
где ![]() кг — масса Земли,
кг — масса Земли, ![]() м3⋅кг-1⋅с-2 — гравитационная постоянная.
м3⋅кг-1⋅с-2 — гравитационная постоянная.
Подставляя все в исходную формулу, получаем:
![]()
Выражая искомую скорость ![]() , получаем, что скорость движения спутника вокруг Земли равна:
, получаем, что скорость движения спутника вокруг Земли равна:
![]()
Это формула скорости, которую должен иметь спутник Земли на заданном радиусе ![]() (т.е. расстоянии от центра планеты) для поддержания круговой орбиты. Скорость не может меняться по модулю, пока спутник сохраняет постоянный орбитальный радиус, то есть пока он продолжает обращаться вокруг планеты по круговой траектории.
(т.е. расстоянии от центра планеты) для поддержания круговой орбиты. Скорость не может меняться по модулю, пока спутник сохраняет постоянный орбитальный радиус, то есть пока он продолжает обращаться вокруг планеты по круговой траектории.
При использовании полученной формулы следует учитывать несколько деталей:
- В качестве радиуса нужно использовать расстояние от центра Земли, а не высоту над поверхностью.
Следовательно, расстояние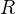 в формуле – это расстояние между центрами двух тел. В том случае, если известна высота спутника над поверхностью Земли, то для нахождения
в формуле – это расстояние между центрами двух тел. В том случае, если известна высота спутника над поверхностью Земли, то для нахождения 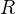 к этой высоте нужно прибавить радиус Земли, который приблизительно равен 6400 км.
к этой высоте нужно прибавить радиус Земли, который приблизительно равен 6400 км. - Данная формула верна для спутников, находящихся за пределами атмосферы.
Однако в случае искусственных спутников это не совсем так. Даже на высоте 600 км от Земли имеет место определённое сопротивление воздуха. Постепенно это сопротивление, т.е. трение о воздух, заставляет спутники снижаться, и в конце концов они сгорают при входе в атмосферу. На высоте менее 160 км орбита спутника существенно понижается при каждом обороте вокруг Земли из-за сопротивления воздуха. - Скорость спутника на круговой орбите не зависит от его массы.
Если представить себе, что сопротивлением воздуха можно пренебречь, и Луна обращается вокруг Земли на расстоянии 640 км, то для сохранения орбиты она должна двигаться с такой же точно скоростью, что и искусственный спутник на той же высоте, хотя масса и размеры Луны намного больше.
Искусственные спутники Земли, как правило, обращаются вокруг планеты на высоте от 500 до 2000 км от поверхности планеты. Рассчитаем, с какой скоростью должен двигаться такой спутник на высоте 1000 км над поверхностью Земли. В этом случае ![]() км. Подставляя числа, получаем:
км. Подставляя числа, получаем:
![]() км/с.
км/с.
Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем
Для решения этой задачи мы принимаем несколько допущений: 1) орбита спутника – окружность (строго говоря, она – эллипс, но с очень малым эксцентрисететом), 2) Земля – шар, радиусом 6400 км (опять же, строго говоря, Земля – не совсем шар, но по сравнению с её радиусом этими отличиями можно пренебречь).
Для того, чтобы спутник оставался на орбите, в соответсвии со вторым законм Ньютона, к нему нужно приложить силу F=ma, где a – ускорение, направленное к центру Земли.
В свою очередь это ускорение вычисляется по формуле a=v*v/(R+h), то есть “скорость спутника в квадрате разделить на расстояние центрами масс двух тел”. Здесь R – радус земли, а h – высота спутника над поверхностью Земли.
Наконец, центростремительная сила, действующая на спутник, возникает из-за притяжения Земли, поэтому используем формулу закона всемирного тяготения F=G(mM/R*R). Здесь G – гравитационная постоянная, равная 6,67*10Е-11 (т.е. 6,67 умножить на 10 в -11 степени), m – масса спутника, M – масса Земли, равная 6*10Е24 кг (6 умножить на 10 в 24 степени), R – радиус земли, равный 6,4*10Е6 м.
Соединим эти формулы и выразим скорость. Получим v=sqrt(G*M/(R+h)) (корень квадратный из произведения G на частное от M на R+h). Видим, что скорость спутника не зависит от его массы. Подставив в это выражение все известные нам данные, получим, что скорость равна почти 7615 метров в секунду или, округляя, 7,6 км/с.
9,8 K
Комментировать ответ…Комментировать…
Первая космическая скорость
Первая космическая скорость – это скорость, с которой спутник движется вокруг планеты по круговой орбите, не удаляясь от планеты и не падая на нее.
То есть, для первой космической скорости орбита — это окружность. Расстояние от центра планеты до спутника равно ( R = left( r + h right) ). Это представлено на рисунке 1.

Рис. 1. Спутник (черная точка), вращается вокруг планеты (центральная окружность) по круговой орбите (пунктир).
Формула для вычисления первой космической скорости
Первую космическую скорость можно посчитать по формуле:
[ large boxed { |v| = sqrt{G cdot frac{M}{r + h}} }]
( v left( frac{text{м}}{text{c}} right) ) (метры в секунду) – первая космическая скорость
( M left( text{кг} right) ) (килограммы) — масса планеты, вокруг которой движется спутник
( r left( text{м} right) ) (метры) – радиус планеты
( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до спутника
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Первая космическая скорость в цифрах для некоторых небесных тел
первая космическая скорость у поверхности Земли ( v = 8000 left( frac{text{м}}{text{c}} right) )
первая космическая скорость у поверхности Солнца ( v = 437000 left( frac{text{м}}{text{c}} right) )
первая космическая скорость у поверхности Луны ( v = 1680 left( frac{text{м}}{text{c}} right) )
первая космическая скорость у поверхности Марса ( v = 3530 left( frac{text{м}}{text{c}} right) )
Как выводится формула первой космической скорости
Рассмотрим движение спутника вокруг Земли.
Земля и спутник притягиваются, запишем закон притяжения между планетой и спутником
[ F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]
При круговом движении на спутник действует центростремительная сила (как и на любое тело при таком движении).
[ F_{text{ц}} = m cdot frac{v^{2} }{left( r + h right)} ]
Мы можем записать эти уравнения в виде системы.
[ begin{cases} displaystyle F = Gcdot frac {m cdot M}{(r+h)^{2}} \ displaystyle F_{text{ц}} = m cdot frac {v^{2}}{(r+h)} \ end{cases} ]
Земля и спутник притягиваются, благодаря этому спутник движется вокруг Земли по круговой орбите. Значит, притяжение между спутником и Землей – это центростремительная сила. Именно она заставляет спутник двигаться вокруг планеты по окружности. На языке математики это запишется так:
[ F = F_{text{ц}} ]
А если равны левые части уравнений, то будут равны и правые:
[ G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot frac{v^{2} }{left( r + h right)} ]
Масса ( m ) спутника и расстояние ( R ) между телами встречается в обеих частях уравнения. Поделим обе части уравнения на массу спутника.
[ G cdot frac{M}{ left( r + h right)^{2}} = frac{v^{2} }{left( r + h right)} ]
Теперь умножим обе части уравнения на расстояние (left( r + h right) ). Получим:
[ G cdot frac{M}{left( r + h right)} = v^{2} ]
Извлечем корень квадратный из обеих частей уравнения, чтобы получить скорость:
[ sqrt{G cdot frac{M}{left( r + h right)}} = |v| ]
Все)
Вам будет интересно почитать:
Закон всемирного тяготения
Движение по окружности, центростремительная сила и центростремительное ускорение
Ускорение свободного падения
Вторая космическая скорость
Оценка статьи:
![]() Загрузка…
Загрузка…



