Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[ 6 frac{2}{13}+4 frac{1}{13}=? ]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]
Теперь можем придать нашему первоначальному выражению следующий вид:
[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
![]()
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]
Со знаменателем дела обстоят куда проще:
[ ln e^{2}=2 ]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Содержание
- Нахождение значения выражения: правила, примеры, решения
- Как найти значение числового выражения?
- Простейшие случаи
- Выражения со скобками
- Выражения с корнями
- Выражения со степенями
- Выражения с дробями
- Выражения с логарифмами
- Выражения с тригонометрическими функциями
- Общий случай числового выражения
- Вычисление значений выражений рациональными способами
- Нахождение значений выражений с переменными
- Опишите возможные способы вычисления значения выражения вида а + b + с?
- (49 + 44) — 39 найди значения выражений всеми возможными способами?
- Найди значение выражения всеми возможными способами (54 + 37) — 35?
- Объясни способ вычисления значения разности 37 — 20 =?
- Найди значения выражений (39 + 45) — 67 всеми возможными способами?
- Расставьте в выражении 2 * 2 — 2 / 2 скобки всеми возможными способами и найдите значения выражений?
- Расставьте в выражении 2х2 — 2 : 2 скобки всеми возможными способами с найдите значение каждого выражения?
- Закончи записи?
- Дайте обоснование способу вычисления 36 + 7 = 36 + (4 + 3) = (36 + 4) + 3 = 40 + 3 = 43?
- Почему для вычисления значения выражения (40 + 8) — (10 + 9) такой же способ применить нельзя?
- Вычисли значение выражения разными способами?
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки » + » , » · » , » — » , » ÷ » , то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14 — 2 · 15 ÷ 6 — 3 .
Выполним сначала умножение и деление. Получаем:
14 — 2 · 15 ÷ 6 — 3 = 14 — 30 ÷ 6 — 3 = 14 — 5 — 3 .
Теперь проводим вычитание и получаем окончательный результат:
14 — 5 — 3 = 9 — 3 = 6 .
Вычислим: 0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 .
Сначала выполняем преобразование дробей, деление и умножение:
0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12
1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 · 4 11 · 11 12 = 1 2 — ( — 14 ) + 2 9 .
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
1 2 — ( — 14 ) + 2 9 = 1 2 + 14 + 2 9 = 14 + 13 18 = 14 13 18 .
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0 , 5 · ( 0 , 76 — 0 , 06 ) .
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0 , 5 · ( 0 , 76 — 0 , 06 ) = 0 , 5 · 0 , 7 = 0 , 35 .
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 .
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 = 1 + 2 · 1 + 2 · 1 + 2 · 3 4
1 + 2 · 1 + 2 · 1 + 2 · 3 4 = 1 + 2 · 1 + 2 · 2 , 5 = 1 + 2 · 6 = 13 .
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями — 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 .
Сначала вычисляем подкоренные выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 = — 6 — 1 + 15 3 = 8 3 = 2
2 , 2 + 0 , 1 · 0 , 5 = 2 , 2 + 0 , 05 = 2 , 25 = 1 , 5 .
Теперь можно вычислить значение всего выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 = 2 + 3 · 1 , 5 = 6 , 5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3 + 1 3 — 1 — 1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3 + 1 3 — 1 = 3 — 1 .
3 + 1 3 — 1 — 1 = 3 — 1 — 1 = 1 .
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 .
Начинаем вычислять по порядку.
2 3 · 4 — 10 = 2 12 — 10 = 2 2 = 4
16 · 1 — 1 2 3 , 5 — 2 · 1 4 = 16 * 0 , 5 3 = 16 · 1 8 = 2 .
Осталось только провести операцию сложение и узнать значение выражения:
2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 = 4 + 2 = 6 .
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2 — 2 5 · 4 5 — 1 + 3 1 3 6 .
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2 — 2 5 · 4 5 — 1 + 3 1 3 6 = 2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6
2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6 = 2 — 2 5 · 2 2 · 5 — 2 + 3 2 = 2 2 · 5 — 2 — 2 5 + 3 2
2 2 · 5 — 2 — 2 5 + 3 2 = 2 — 2 + 3 = 1 4 + 3 = 3 1 4
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3 , 2 2 — 3 · 7 — 2 · 3 6 ÷ 1 + 2 + 3 9 — 6 ÷ 2 .
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3 , 2 2 = 3 , 2 ÷ 2 = 1 , 6
7 — 2 · 3 6 = 7 — 6 6 = 1 6
1 + 2 + 3 9 — 6 ÷ 2 = 1 + 2 + 3 9 — 3 = 6 6 = 1 .
Перепишем наше выражение и вычислим его значение:
1 , 6 — 3 · 1 6 ÷ 1 = 1 , 6 — 0 , 5 ÷ 1 = 1 , 1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 2 5 — 1 — 2 5 — 7 4 — 3 .
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
2 5 — 1 = 2 5 + 1 5 — 1 5 + 1 = 2 5 + 1 5 — 1 = 2 5 + 2 4
Исходное выражение принимает вид:
2 5 — 1 — 2 5 — 7 4 — 3 = 2 5 + 2 4 — 2 5 — 7 4 — 3 .
Вычислим значение этого выражения:
2 5 + 2 4 — 2 5 — 7 4 — 3 = 2 5 + 2 — 2 5 + 7 4 — 3 = 9 4 — 3 = — 3 4 .
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log 2 4 + 2 · 4 можно сразу вместо log 2 4 записать значение этого логарифма, а потом выполнить все действия. Получим: log 2 4 + 2 · 4 = 2 + 2 · 4 = 2 + 8 = 10 .
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log 5 — 6 ÷ 3 5 2 + 2 + 7 . Имеем:
log 5 — 6 ÷ 3 5 2 + 2 + 7 = log 3 27 + 7 = 3 + 7 = 10 .
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 .
log 2 log 2 256 = log 2 8 = 3 .
По свойству логарифмов:
log 6 2 + log 6 3 = log 6 ( 2 · 3 ) = log 6 6 = 1 .
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log 5 729 log 0 , 2 27 = log 5 729 log 1 5 27 = log 5 729 — log 5 27 = — log 27 729 = — log 27 27 2 = — 2 .
Теперь можно переходить к вычислению значения исходного выражения.
log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 = 3 + 1 + — 2 = 2 .
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: t g 2 4 π 3 — sin — 5 π 2 + cosπ .
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
Подставляем значения в выражение и вычисляем его значение:
t g 2 4 π 3 — sin — 5 π 2 + cosπ = 3 2 — ( — 1 ) + ( — 1 ) = 3 + 1 — 1 = 3 .
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 .
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 = cos 2 π 8 cos 5 π 36 + π 9 — 1 = cos π 4 cos π 4 — 1 = 1 — 1 = 0 .
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения — 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 .
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 . Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π
Теперь можно узнать значение синуса:
sin π 6 + 2 · 2 π 5 + 3 π 5 = sin π 6 + 2 π = sin π 6 = 1 2 .
Вычисляем значение подкоренного выражения:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 4 = 2 .
Со знаменателем дроби все проще:
Теперь мы можем записать значение всей дроби:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 = 2 2 = 1 .
С учетом этого, запишем все выражение:
— 1 + 1 + 3 9 = — 1 + 1 + 3 3 = — 1 + 1 + 27 = 27 .
— 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 = 27 .
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56 + 8 — 3 , 789 ln e 2 — 56 + 8 — 3 , 789 ln e 2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 2 3 — 1 5 + 3 · 289 · 3 4 3 · 2 3 — 1 5 + 3 · 289 · 3 4 . Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 1 3 .
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0 , 5 x — y при заданных x = 2 , 4 и y = 5 .
Подставляем значения переменных в выражение и вычисляем:
0 , 5 x — y = 0 , 5 · 2 , 4 — 5 = 1 , 2 — 5 = — 3 , 8 .
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х + 3 — х , очевидно, имеет значение 3 , и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения x x равно единице для всех положительных иксов.
Источник
Опишите возможные способы вычисления значения выражения вида а + b + с?
Математика | 10 — 11 классы
Опишите возможные способы вычисления значения выражения вида а + b + с.
Дайте обоснование этим способам и проиллюстрируйте их на конкретных примерах.

От переменны слагаемых сумма не изменяется.

(49 + 44) — 39 найди значения выражений всеми возможными способами?
(49 + 44) — 39 найди значения выражений всеми возможными способами.

Найди значение выражения всеми возможными способами (54 + 37) — 35?
Найди значение выражения всеми возможными способами (54 + 37) — 35.

Объясни способ вычисления значения разности 37 — 20 =?
Объясни способ вычисления значения разности 37 — 20 =.

Найди значения выражений (39 + 45) — 67 всеми возможными способами?
Найди значения выражений (39 + 45) — 67 всеми возможными способами.

Расставьте в выражении 2 * 2 — 2 / 2 скобки всеми возможными способами и найдите значения выражений?
Расставьте в выражении 2 * 2 — 2 / 2 скобки всеми возможными способами и найдите значения выражений.

Расставьте в выражении 2х2 — 2 : 2 скобки всеми возможными способами с найдите значение каждого выражения?
Расставьте в выражении 2х2 — 2 : 2 скобки всеми возможными способами с найдите значение каждого выражения.

Закончи записи?
Сравни выражение и способы вычисления их значений.

Дайте обоснование способу вычисления 36 + 7 = 36 + (4 + 3) = (36 + 4) + 3 = 40 + 3 = 43?
Дайте обоснование способу вычисления 36 + 7 = 36 + (4 + 3) = (36 + 4) + 3 = 40 + 3 = 43.

Почему для вычисления значения выражения (40 + 8) — (10 + 9) такой же способ применить нельзя?
Почему для вычисления значения выражения (40 + 8) — (10 + 9) такой же способ применить нельзя?
Значение какой разности мы вычислить не можем?

Вычисли значение выражения разными способами?
Вычисли значение выражения разными способами.
Подчеркни самый удобный из этих способов.
На этой странице вы найдете ответ на вопрос Опишите возможные способы вычисления значения выражения вида а + b + с?. Вопрос соответствует категории Математика и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.
Источник
Содержание
- Нахождение значения выражения, примеры, решения.
- Как найти значение числового выражения?
- Простейшие случаи
- Со скобками
- С корнями
- Со степенями
- Находим значение выражения с дробями
- С логарифмами
- Как найти значение тригонометрического выражения?
- Общий случай
- Рациональные способы вычисления значений выражений
- Нахождение значения буквенного выражения и выражения с переменными
Нахождение значения выражения, примеры, решения.
После того, как мы узнали что такое значение выражения, логичным будет разобраться с вопросом как найти значение выражения. Сейчас мы рассмотрим правила нахождения значений выражений. Начнем с числовых выражений, и будем продвигаться от самых простых случаев, когда выражение содержит лишь числа и соединяющие их знаки арифметических действий, и закончим общим случаем, когда в выражении, значение которого нужно найти, содержатся скобки, дроби, корни, степени и другие функции. В конце покажем, как находить значения буквенных выражений и выражений с переменными при выбранных значениях переменных. Всю теорию снабдим примерами с подробным описанием решений.
Навигация по странице.
Как найти значение числового выражения?
Перевод условий задач на математический язык часто дает числовые выражения, то есть, выражения, составленные из чисел и знаков действий. Они могут быть как очень простыми, состоящими из чисел и знаков арифметических действий, так и достаточно сложными и громоздкими, содержащими скобки, степени, дроби, корни и т.п. Но составленное выражение зачастую является лишь промежуточным этапом решения задачи, а ответ заключается в значении составленного выражения. Так мы приходим к задаче — найти значение выражения.
Разберемся с правилами, по которым вычисляются значения выражений.
Простейшие случаи
Знакомство с правилами нахождения значений выражений начнем со случаев, когда числовое выражение не содержит в своей записи ничего другого, кроме чисел и знаков арифметических действий. Эти случаи мы и назвали простейшими.
Чтобы успешно находить значения таких выражений, нужно уметь выполнять действия с различными числами, а также иметь представление о порядке выполнения действий в выражениях без скобок.
Итак, если числовое выражение составлено из чисел и знаков +, −, · и :, то по порядку слева направо нужно сначала выполнить умножение и деление, а затем – сложение и вычитание, что позволит найти искомое значение выражения.
Приведем решение примеров для пояснения.
Вычислите значение выражения 14−2·15:6−3 .
Чтобы найти значение выражения, нужно выполнить все указанные в нем действия в соответствии с принятым порядком выполнения этих действий. Вначале по порядку слева направо выполняем умножение и деление, получаем 14−2·15:6−3=14−30:6−3=14−5−3 . Теперь также по порядку слева направо выполняем оставшиеся действия: 14−5−3=9−3=6 . Так мы нашли значение исходного выражения, оно равно 6 .
Найдите значение выражения  .
.
В данном примере нам сначала нужно выполнить умножение 2·(−7) и деление с умножением в выражении  . Вспомнив, как выполняется умножение чисел с разными знаками, находим 2·(−7)=−14 . А для выполнения действий в выражении
. Вспомнив, как выполняется умножение чисел с разными знаками, находим 2·(−7)=−14 . А для выполнения действий в выражении  сначала заменяем смешанное число обыкновенной дробью
сначала заменяем смешанное число обыкновенной дробью  , после чего переходим от деления на дробь к умножению на обратное число
, после чего переходим от деления на дробь к умножению на обратное число  , и выполняем умножение обыкновенных дробей:
, и выполняем умножение обыкновенных дробей:  .
.
Подставляем полученные значения в исходное выражение:  .
.
Осталось записать десятичную дробь в виде обыкновенной дроби  , вспомнить правило вычитания отрицательных чисел
, вспомнить правило вычитания отрицательных чисел  , сгруппировать и сложить обыкновенные дроби
, сгруппировать и сложить обыкновенные дроби  , и сложить обыкновенную дробь с натуральным числом
, и сложить обыкновенную дробь с натуральным числом  .
.
Так мы нашли искомое значение выражения.
 .
.
Со скобками
Теперь разберемся, как найти значение выражения, содержащего в своей записи скобки, указывающие порядок выполнения действий. При этом сначала следует находить значение выражений в скобках, придерживаясь принятого порядка выполнения действий, а затем выполнять остальные действия, что приведет к искомому значению исходного выражения. Это правило перекликается с порядке выполнения действий в выражениях без скобокпорядком выполнения действий в выражениях со скобками.
Покажем решение примера.
Вычислите значение выражения 0,5·(0,75−0,05) .
В данном примере для нахождения значения выражения нам нужно будет выполнять действия с десятичными дробями. Так как исходное выражение содержит скобки, то сначала нужно найти значение выражения в них, имеем 0,5·(0,75−0,05)=0,5·0,7 . Остается выполнить умножение: 0,5·0,7=0,35 .
Аналогично находятся значения выражений, содержащих скобки в скобках. Удобно нахождение значения начинать со внутренних скобок и продвигаться к внешним.
Найдите значение выражения 1+2·(1+2·(1+2·(1−1/4))) .
Во внутренних скобках находится выражение 1−1/4 , его значение равно 3/4 . Подставив его в исходное выражение, оно примет вид 1+2·(1+2·(1+2·3/4)) . Опять вычисляем значение выражения во внутренних скобках, не забывая, что умножение выполняется перед сложением, 1+2·3/4=1+3/2=5/2 , и подставляем это значение в последнее выражение: 1+2·(1+2·5/2) . Остается найти значение выражения в скобках, после чего можно будет закончить вычисления: 1+2·(1+2·5/2)=1+2·6=13 .
Запишем краткое решение:
1+2·(1+2·(1+2·(1−1/4)))= 1+2·(1+2·(1+2·3/4))= 1+2·(1+2·(1+2·3/4))= =1+2·(1+2·5/2)= 1+2·6=13 .
Итак, в нахождении значений выражений со скобками нет ничего сложного, главное – соблюдать последовательность выполнения действий, и не допускать вычислительных ошибок.
С корнями
Числовые выражения, значения которых требуется найти, могут в своей записи содержать различные знаки, в частности, корни. Как найти значение корня, под которым стоит число, объясняет материал статьи извлечение корней.
А как быть, когда под знаком корня находится числовое выражение? Чтобы получить значение такого корня, нужно сначала найти значение подкоренного выражения, придерживаясь принятого порядка выполнений действий. Например,  .
.
В числовых выражениях корни следует воспринимать как некоторые числа, и корни целесообразно сразу заменить их значениями, после чего находить значение полученного выражения без корней, выполняя действия в принятой последовательности.
Найдите значение выражения с корнями  .
.
Сначала найдем значение корня  . Для этого, во-первых, вычислим значение подкоренного выражения, имеем −2·3−1+60:4=−6−1+15=8 . А во-вторых, находим значение корня
. Для этого, во-первых, вычислим значение подкоренного выражения, имеем −2·3−1+60:4=−6−1+15=8 . А во-вторых, находим значение корня  .
.
Теперь вычислим значение второго корня из исходного выражения:  .
.
Наконец, мы можем найти значение исходного выражения, заменив корни их значениями:  .
.
 .
.
Достаточно часто, чтобы стало возможно найти значение выражения с корнями, предварительно приходится проводить его преобразование. Покажем решение примера.
Каково значение выражения  .
.
Мы не имеем возможности заменить корень из трех его точным значением, что не позволяет нам вычислить значение этого выражения описанным выше способом. Однако мы можем вычислить значение этого выражение, выполнив несложные преобразования. Применим формулу разности квадратов:  . Учитывая свойства корней, получаем
. Учитывая свойства корней, получаем  . Таким образом, значение исходного выражения равно 1 .
. Таким образом, значение исходного выражения равно 1 .
 .
.
Со степенями
Когда в выражении, значение которого мы находим, присутствуют степени, то их значения вычисляются до выполнения остальных действий. Вычислению значений степеней чисел посвящена статья возведение в степень.
Если основание и показатель степени являются числами, то их значение вычисляется по определению степени, например, 3 2 =3·3=9 или 8 −1 =1/8 . Встречаются также записи, когда основание и/или показатель степени являются некоторыми выражениями. В этих случаях нужно найти значение выражения в основании, значение выражения в показателе, после чего вычислить значение самой степени.
Найдите значение выражения со степенями вида 2 3·4−10 +16·(1−1/2) 3,5−2·1/4 .
В исходном выражении две степени 2 3·4−10 и (1−1/2) 3,5−2·1/4 . Их значения нужно вычислить до выполнения остальных действий.
Начнем со степени 2 3·4−10 . В ее показателе находится числовое выражение, вычислим его значение: 3·4−10=12−10=2 . Теперь можно найти значение самой степени: 2 3·4−10 =2 2 =4 .
В основании и показателе степени (1−1/2) 3,5−2·1/4 находятся выражения, вычисляем их значения, чтобы потом найти значение степени. Имеем (1−1/2) 3,5−2·1/4 =(1/2) 3 =1/8 .
Теперь возвращаемся к исходному выражению, заменяем в нем степени их значениями, и находим нужное нам значение выражения: 2 3·4−10 +16·(1−1/2) 3,5−2·1/4 = 4+16·1/8=4+2=6 .
2 3·4−10 +16·(1−1/2) 3,5−2·1/4 =6 .
Стоит заметить, что более распространены случаи, когда целесообразно провести предварительное упрощение выражения со степенями на базе свойств степени.
Найдите значение выражения  .
.
Судя по показателям степеней, находящихся в данном выражении, точные значения степеней получить не удастся. Попробуем упростить исходное выражение, может быть это поможет найти его значение. Имеем

 .
.
Степени в выражениях зачастую идут рука об руку с логарифмами, но о нахождении значений выражений с логарифмами мы поговорим в одном из следующих пунктов.
Находим значение выражения с дробями
Числовые выражения в своей записи могут содержать дроби. Когда требуется найти значение подобного выражения, дроби, отличные от обыкновенных дробей, следует заменить их значениями перед выполнением остальных действий.
В числителе и знаменателе дробей (которые отличны от обыкновенных дробей) могут находиться как некоторые числа, так и выражения. Чтобы вычислить значение такой дроби нужно вычислить значение выражения в числителе, вычислить значение выражения в знаменателе, после чего вычислить значение самой дроби. Такой порядок объясняется тем, что дробь a/b , где a и b – некоторые выражения, по сути представляет собой частное вида (a):(b) , так как черта дроби означает знак деления.
Рассмотрим решение примера.
Найдите значение выражения с дробями  .
.
В исходном числовом выражении три дроби  и
и  . Чтобы найти значение исходного выражения, нам сначала нужно эти дроби, заменить их значениями. Сделаем это.
. Чтобы найти значение исходного выражения, нам сначала нужно эти дроби, заменить их значениями. Сделаем это.
В числителе и знаменателе дроби  находятся числа. Чтобы найти значение такой дроби, заменяем дробную черту знаком деления, и выполняем это действие:
находятся числа. Чтобы найти значение такой дроби, заменяем дробную черту знаком деления, и выполняем это действие:  .
.
В числителе дроби  находится выражение 7−2·3 , его значение найти легко: 7−2·3=7−6=1 . Таким образом,
находится выражение 7−2·3 , его значение найти легко: 7−2·3=7−6=1 . Таким образом,  . Можно переходить к нахождению значения третьей дроби.
. Можно переходить к нахождению значения третьей дроби.
Третья дробь  в числителе и знаменателе содержит числовые выражения, поэтому, сначала нужно вычислить их значения, а это позволит найти значение самой дроби. Имеем
в числителе и знаменателе содержит числовые выражения, поэтому, сначала нужно вычислить их значения, а это позволит найти значение самой дроби. Имеем  .
.
Осталось подставить найденные значения в исходное выражение, и выполнить оставшиеся действия:  .
.
 .
.
Часто при нахождении значений выражений с дробями приходится выполнять упрощение дробных выражений, базирующееся на выполнении действий с дробями и на сокращении дробей.
Найдите значение выражения  .
.
Корень из пяти нацело не извлекается, поэтому для нахождения значения исходного выражения для начала упростим его. Для этого избавимся от иррациональности в знаменателе первой дроби:  . После этого исходное выражение примет вид
. После этого исходное выражение примет вид  . После вычитания дробей пропадут корни, что нам позволит найти значение изначально заданного выражения:
. После вычитания дробей пропадут корни, что нам позволит найти значение изначально заданного выражения:  .
.
 .
.
С логарифмами
Если числовое выражение содержит логарифмы, и если есть возможность избавиться от них, вычислив значение логарифмов, то это делается перед выполнением остальных действий. Например, при нахождении значения выражения log24+2·3 , логарифм log24 заменяется его значением 2 , после чего выполняются остальные действия в обычном порядке, то есть, log24+2·3=2+2·3=2+6=8 .
Когда под знаком логарифма и/или в его основании находятся числовые выражения, то сначала находятся их значения, после чего вычисляется значение логарифма. Для примера рассмотрим выражение с логарифмом вида  . В основании логарифма и под его знаком находятся числовые выражения, находим их значения:
. В основании логарифма и под его знаком находятся числовые выражения, находим их значения:  . Теперь находим логарифм, после чего завершаем вычисления:
. Теперь находим логарифм, после чего завершаем вычисления:  .
.
Если же логарифмы не вычисляются точно, то найти значение исходного выражения может помочь предварительное его упрощение с использованием свойств логарифмов. При этом нужно хорошо владеть материалом статьи преобразование логарифмических выражений.
Найдите значение выражения с логарифмами  .
.
Начнем с вычисления log2(log2256) . Так как 256=2 8 , то log2256=8 , следовательно, log2(log2256)=log28=log22 3 =3 .
Логарифмы log62 и log63 можно сгруппировать. Сумма логарифмов log62+log63 равна логарифму произведения log6(2·3) , таким образом, log62+log63=log6(2·3)=log66=1 .
Теперь разберемся с дробью  . Для начала основание логарифма в знаменателе перепишем в виде обыкновенной дроби как 1/5 , после чего воспользуемся свойствами логарифмов, что позволит нам получить значение дроби:
. Для начала основание логарифма в знаменателе перепишем в виде обыкновенной дроби как 1/5 , после чего воспользуемся свойствами логарифмов, что позволит нам получить значение дроби:  .
.
Осталось лишь подставить полученные результаты в исходное выражение и закончить нахождение его значения:

 .
.
Как найти значение тригонометрического выражения?
Когда числовое выражение содержит синус, косинус, тангенс, котангенс или арксинус, арккосинус, арктангенс, арккотангенс и т.п., то их значения вычисляются перед выполнением остальных действий. Если под знаком тригонометрических функций стоят числовые выражения, то сначала вычисляются их значения, после чего находятся значения тригонометрических функций.
Найдите значение выражения  .
.
Обратившись к статье нахождение значений тригонометрических функций, получаем  и cosπ=−1 . Подставляем эти значения в исходное выражение, оно принимает вид
и cosπ=−1 . Подставляем эти значения в исходное выражение, оно принимает вид  . Чтобы найти его значение, сначала нужно выполнить возведение в степень, после чего закончить вычисления:
. Чтобы найти его значение, сначала нужно выполнить возведение в степень, после чего закончить вычисления:  .
.
 .
.
Стоит отметить, что вычисление значений выражений с синусами, косинусами и т.п. зачастую требует предварительного преобразования тригонометрического выражения.
Чему равно значение тригонометрического выражения  .
.
Преобразуем исходное выражение, используя тригонометрические формулы, в данном случае нам потребуются формула косинуса двойного угла и формула косинуса суммы:

Проделанные преобразования помогли нам найти значение выражения.
 .
.
Общий случай
В общем случае числовое выражение может содержать и корни, и степени, и дроби, и какие-либо функции, и скобки. Нахождение значений таких выражений состоит в выполнении следующих действий:
- сначала корни, степени, дроби и т.п. заменяются их значениями,
- дальше действия в скобках,
- и по порядку слева направо выполняется оставшиеся действия — умножение и деление, а за ними – сложение и вычитание.
Перечисленные действия выполняются до получения конечного результата.
Найдите значение выражения  .
.
Вид данного выражения довольно сложен. В этом выражении мы видим дробь, корни, степени, синус и логарифм. Как же найти его значение?
Продвигаясь по записи слева на право, мы натыкаемся на дробь вида  . Мы знаем, что при работе с дробями сложного вида, нам нужно отдельно вычислить значение числителя, отдельно – знаменателя, и, наконец, найти значение дроби.
. Мы знаем, что при работе с дробями сложного вида, нам нужно отдельно вычислить значение числителя, отдельно – знаменателя, и, наконец, найти значение дроби.
В числителе мы имеем корень вида  . Чтобы определить его значение, сначала надо вычислить значение подкоренного выражения
. Чтобы определить его значение, сначала надо вычислить значение подкоренного выражения  . Здесь есть синус. Найти его значение мы сможем лишь после вычисления значения выражения
. Здесь есть синус. Найти его значение мы сможем лишь после вычисления значения выражения  . Это мы можем сделать:
. Это мы можем сделать:  . Тогда
. Тогда  , откуда
, откуда  и
и  .
.
Со знаменателем все просто:  .
.
Таким образом,  .
.
После подстановки этого результата в исходное выражение, оно примет вид  . В полученном выражении содержится степень
. В полученном выражении содержится степень  . Чтобы найти ее значение, сначала придется найти значение показателя, имеем
. Чтобы найти ее значение, сначала придется найти значение показателя, имеем  .
.
Итак,  .
.
 .
.
Если же нет возможности вычислить точные значения корней, степеней и т.п., то можно попробовать избавиться от них с помощью каких-либо преобразований, после чего вернуться к вычислению значения по указанной схеме.
Рациональные способы вычисления значений выражений
Вычисление значений числовых выражений требует последовательности и аккуратности. Да, необходимо придерживаться последовательности выполнения действий, записанной в предыдущих пунктах, но не нужно это делать слепо и механически. Этим мы хотим сказать, что часто можно рационализировать процесс нахождения значения выражения. Например, значительно ускорить и упростить нахождение значения выражения позволяют некоторые свойства действий с числами.
К примеру, мы знаем такое свойство умножения: если один из множителей в произведении равен нулю, то и значение произведения равно нулю. Используя это свойство, мы можем сразу сказать, что значение выражения 0·(2·3+893−3234:54·65−79·56·2,2)· (45·36−2·4+456:3·43) равно нулю. Если бы мы придерживались стандартного порядка выполнения действий, то сначала нам бы пришлось вычислять значения громоздких выражений в скобках, а это бы заняло массу времени, и в результате все равно получился бы нуль.
Также удобно пользоваться свойством вычитания равных чисел: если от числа отнять равное ему число, то в результате получится нуль. Это свойство можно рассматривать шире: разность двух одинаковых числовых выражений равна нулю. Например, не вычисляя значения выражений в скобках можно найти значение выражения (54·6−12·47362:3)−(54·6−12·47362:3) , оно равно нулю, так как исходное выражение представляет собой разность одинаковых выражений.
Рациональному вычислению значений выражений могут способствовать тождественные преобразования. Например, бывает полезна группировка слагаемых и множителей, не менее часто используется вынесение общего множителя за скобки. Так значение выражения 53·5+53·7−53·11+5 очень легко находится после вынесения множителя 53 за скобки: 53·(5+7−11)+5=53·1+5=53+5=58 . Непосредственное вычисление заняло бы намного больше времени.
В заключение этого пункта обратим внимание на рациональный подход к вычислению значений выражений с дробями – одинаковые множители в числителе и знаменателе дроби сокращаются. Например, сокращение одинаковых выражений в числителе и знаменателе дроби  позволяет сразу найти ее значение, которое равно 1/2 .
позволяет сразу найти ее значение, которое равно 1/2 .
Нахождение значения буквенного выражения и выражения с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных. То есть, речь идет о нахождении значения буквенного выражения для данных значений букв или о нахождении значения выражения с переменными для выбранных значений переменных.
Правило нахождения значения буквенного выражения или выражения с переменными для данных значений букв или выбранных значений переменных таково: в исходное выражение нужно подставить данные значения букв или переменных, и вычислить значение полученного числового выражения, оно и является искомым значением.
Вычислите значение выражения 0,5·x−y при x=2,4 и y=5 .
Источник
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выражения
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.

д. заменяются их значениями. - Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменными
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выражения
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменными
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выражения
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменными
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.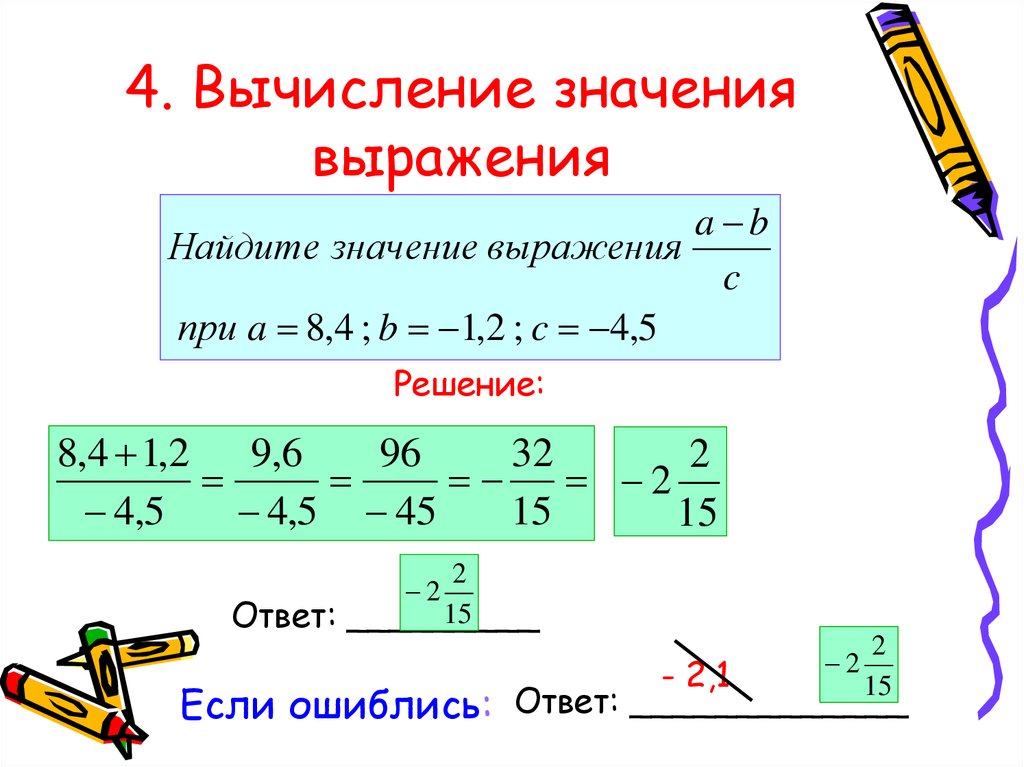
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выражения
Вычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.
 д. заменяются их значениями.
д. заменяются их значениями. - Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменными
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Как находить значение выражения 8 класс
Содержание
- Как найти значение числового выражения?
- Простейшие случаи
- Выражения со скобками
- Выражения с корнями
- Выражения со степенями
- Выражения с дробями
- Выражения с логарифмами
- Выражения с тригонометрическими функциями
- Общий случай числового выражения
- Вычисление значений выражений рациональными способами
- Нахождение значений выражений с переменными
- Информация
- Урок 1.
 Алгебра 8 класс
Алгебра 8 класс - Конспект урока «Рациональные выражения»
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки » + » , » · » , » — » , » ÷ » , то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14 — 2 · 15 ÷ 6 — 3 .
Выполним сначала умножение и деление. Получаем:
14 — 2 · 15 ÷ 6 — 3 = 14 — 30 ÷ 6 — 3 = 14 — 5 — 3 .
Теперь проводим вычитание и получаем окончательный результат:
14 — 5 — 3 = 9 — 3 = 6 .
Вычислим: 0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 .
Сначала выполняем преобразование дробей, деление и умножение:
0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12
1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 · 4 11 · 11 12 = 1 2 — ( — 14 ) + 2 9 .
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
1 2 — ( — 14 ) + 2 9 = 1 2 + 14 + 2 9 = 14 + 13 18 = 14 13 18 .
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0 , 5 · ( 0 , 76 — 0 , 06 ) .
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0 , 5 · ( 0 , 76 — 0 , 06 ) = 0 , 5 · 0 , 7 = 0 , 35 .
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 .
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 = 1 + 2 · 1 + 2 · 1 + 2 · 3 4
1 + 2 · 1 + 2 · 1 + 2 · 3 4 = 1 + 2 · 1 + 2 · 2 , 5 = 1 + 2 · 6 = 13 .
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями — 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 .
Сначала вычисляем подкоренные выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 = — 6 — 1 + 15 3 = 8 3 = 2
2 , 2 + 0 , 1 · 0 , 5 = 2 , 2 + 0 , 05 = 2 , 25 = 1 , 5 .
Теперь можно вычислить значение всего выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 = 2 + 3 · 1 , 5 = 6 , 5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3 + 1 3 — 1 — 1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3 + 1 3 — 1 = 3 — 1 .
3 + 1 3 — 1 — 1 = 3 — 1 — 1 = 1 .
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 .
Начинаем вычислять по порядку.
2 3 · 4 — 10 = 2 12 — 10 = 2 2 = 4
16 · 1 — 1 2 3 , 5 — 2 · 1 4 = 16 * 0 , 5 3 = 16 · 1 8 = 2 .
Осталось только провести операцию сложение и узнать значение выражения:
2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 = 4 + 2 = 6 .
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2 — 2 5 · 4 5 — 1 + 3 1 3 6 .
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2 — 2 5 · 4 5 — 1 + 3 1 3 6 = 2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6
2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6 = 2 — 2 5 · 2 2 · 5 — 2 + 3 2 = 2 2 · 5 — 2 — 2 5 + 3 2
2 2 · 5 — 2 — 2 5 + 3 2 = 2 — 2 + 3 = 1 4 + 3 = 3 1 4
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3 , 2 2 — 3 · 7 — 2 · 3 6 ÷ 1 + 2 + 3 9 — 6 ÷ 2 .
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3 , 2 2 = 3 , 2 ÷ 2 = 1 , 6
7 — 2 · 3 6 = 7 — 6 6 = 1 6
1 + 2 + 3 9 — 6 ÷ 2 = 1 + 2 + 3 9 — 3 = 6 6 = 1 .
Перепишем наше выражение и вычислим его значение:
1 , 6 — 3 · 1 6 ÷ 1 = 1 , 6 — 0 , 5 ÷ 1 = 1 , 1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 2 5 — 1 — 2 5 — 7 4 — 3 .
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
2 5 — 1 = 2 5 + 1 5 — 1 5 + 1 = 2 5 + 1 5 — 1 = 2 5 + 2 4
Исходное выражение принимает вид:
2 5 — 1 — 2 5 — 7 4 — 3 = 2 5 + 2 4 — 2 5 — 7 4 — 3 .
Вычислим значение этого выражения:
2 5 + 2 4 — 2 5 — 7 4 — 3 = 2 5 + 2 — 2 5 + 7 4 — 3 = 9 4 — 3 = — 3 4 .
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log 2 4 + 2 · 4 можно сразу вместо log 2 4 записать значение этого логарифма, а потом выполнить все действия. Получим: log 2 4 + 2 · 4 = 2 + 2 · 4 = 2 + 8 = 10 .
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log 5 — 6 ÷ 3 5 2 + 2 + 7 . Имеем:
log 5 — 6 ÷ 3 5 2 + 2 + 7 = log 3 27 + 7 = 3 + 7 = 10 .
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 .
log 2 log 2 256 = log 2 8 = 3 .
По свойству логарифмов:
log 6 2 + log 6 3 = log 6 ( 2 · 3 ) = log 6 6 = 1 .
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log 5 729 log 0 , 2 27 = log 5 729 log 1 5 27 = log 5 729 — log 5 27 = — log 27 729 = — log 27 27 2 = — 2 .
Теперь можно переходить к вычислению значения исходного выражения.
log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 = 3 + 1 + — 2 = 2 .
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: t g 2 4 π 3 — sin — 5 π 2 + cosπ .
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
Подставляем значения в выражение и вычисляем его значение:
t g 2 4 π 3 — sin — 5 π 2 + cosπ = 3 2 — ( — 1 ) + ( — 1 ) = 3 + 1 — 1 = 3 .
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 .
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 = cos 2 π 8 cos 5 π 36 + π 9 — 1 = cos π 4 cos π 4 — 1 = 1 — 1 = 0 .
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо.
 Сначала — умножение и деление, затем — сложение и вычитание.
Сначала — умножение и деление, затем — сложение и вычитание.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения — 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 .
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 . Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π
Теперь можно узнать значение синуса:
sin π 6 + 2 · 2 π 5 + 3 π 5 = sin π 6 + 2 π = sin π 6 = 1 2 .
Вычисляем значение подкоренного выражения:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 4 = 2 .
Со знаменателем дроби все проще:
Теперь мы можем записать значение всей дроби:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 = 2 2 = 1 .
С учетом этого, запишем все выражение:
— 1 + 1 + 3 9 = — 1 + 1 + 3 3 = — 1 + 1 + 27 = 27 .
— 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 = 27 .
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56 + 8 — 3 , 789 ln e 2 — 56 + 8 — 3 , 789 ln e 2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 2 3 — 1 5 + 3 · 289 · 3 4 3 · 2 3 — 1 5 + 3 · 289 · 3 4 . Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 1 3 .
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0 , 5 x — y при заданных x = 2 , 4 и y = 5 .
Подставляем значения переменных в выражение и вычисляем:
0 , 5 x — y = 0 , 5 · 2 , 4 — 5 = 1 , 2 — 5 = — 3 , 8 .
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х + 3 — х , очевидно, имеет значение 3 , и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения x x равно единице для всех положительных иксов.
Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.
Информация
© adminreshak.ru
Урок 1. Алгебра 8 класс
Конспект урока «Рациональные выражения»
На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.
Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Целые и дробные выражения называют рациональными выражениями.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.
Дробное выражение при некоторых значениях переменных может не иметь смысла.
Чтобы найти значение рационального выражения, надо:
1) подставить числовое значение переменной в данное выражение;
2) выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.
Как вы уже знаете, выражение вида называется дробью.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Найдите значение дроби.
Найдите допустимые значения переменной в выражениях:
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Чтобы найти значение рационального выражения, надо:
1) Подставить числовое значение переменной в данное выражение;
2) Выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Например, запишем следующее выражение:
a + 5
Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
a = 5
Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Значение переменной x подставляется в выражение x + 10
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Вспомните второй урок «Основные операции». Чтобы понять сложение мы привели пример 5 + 2 = 7 и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Решение:
a + b = c
10 + 6 = 16
Ответ: при a = 10 и b = 6, переменная c равна 16.
Значение выражения
Фраза «выполнить действие» означает выполнить одну из операций действия.
В учебниках младших классов часто можно встретить задания следующего содержания: выполнить действия, и далее перечисляются примеры, которые нужно решить. Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Например, дано выражение 10 + 6, и от нас требуют найти значение этого выражения. Это означает, что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:
10 + 6 = 16
Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
- 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
- 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
- 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5
Задания для самостоятельного решения
Задание 1. Найдите значение выражения 5 + x при x = 4
Показать решение
Задание 2. Найдите значение выражения a + 3 при a = 7
Показать решение
Задание 3. Найдите значение выражения a + a + a при a = 10
Показать решение
Задание 4. Найдите значение выражения a + b при a = 10 и b = 20
Показать решение
Задание 5. Найдите значение выражения b + b + b при b = 5
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Опубликовано Автор
переменных выражений | Определение, примеры решений, вопросы
Содержание
| 1. |
Введение в переменные выражения |
| 2. | Определение постоянной переменной, члена и коэффициента |
| 3. | Переменное выражение (алгебраическое выражение) |
| 4. | Типы переменных выражений |
| 5. | Нестандартное мышление! |
| 6. | Упражнение по вычислению переменных выражений |
| 7. | Решенные примеры для переменных выражений |
| 8. | Спорные вопросы по выражениям переменных |
| 9. | Практические вопросы по выражениям переменных |
| 10. | Важные темы |
| 11. | Образцы заданий олимпиады по математике |
| 12. | Часто задаваемые вопросы (FAQ) |
Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на «почему», стоящем за «что». Учащиеся могут изучить огромное количество интерактивных рабочих листов, визуальных материалов, симуляций, практических тестов и многого другого, чтобы глубже понять концепцию.
Запишитесь на БЕСПЛАТНОЕ пробное занятие уже сегодня! и участвуйте в LIVE онлайн-классе Cuemath вместе со своим ребенком.
Введение в переменные выражения
Джеймс и Натали играли со спичками и придумали составлять из них узоры из чисел.
Джеймс взял 4 спички и составил число (4)
Натали добавила еще 3 спички, чтобы сформировать узор из двух (4)s.
Затем Джеймс снова добавил еще 3 спички, чтобы сформировать узор из трех (4)s.
Внезапно Натали засомневалась, сколько нужно спичек, чтобы составить узор из десяти (4) s?
Из существующего шаблона они поняли, что им нужно (4+ 9 (3)) палочек, чтобы сделать это, так как им нужен шаблон с десятью (4)с.
Из этого они сделали вывод, что им нужно (4+(n-1)3) палочек, чтобы составить узор из (n) числа (4) палочек.
Здесь (4+(n-1)3) называется алгебраическим выражением.
Определение переменной, константы, члена и коэффициента
- Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
В приведенном выше примере (n) является переменной, и здесь она может принимать значения (1,2,3,…)
Некоторые примеры переменных в математике: (a,b, х, у, г, м, ) и т. д.
- Символ, имеющий фиксированное числовое значение, называется константой.
Все числа являются константами.
Некоторые примеры констант: (3, 6, dfrac{-1}{2}, sqrt{5}) и т. д.
- Терм представляет собой переменную отдельно (или) отдельно константу (или) он может быть комбинацией переменных и констант посредством операции умножения или деления.
Некоторые примеры терминов: (3x^2, dfrac{-2}{3}y, sqrt{5m},) и т. д.
Здесь числа, умножающие переменные, равны (3, dfrac{-2}{3} ) и (5), которые называются коэффициентами .
CLUEless по математике? Узнайте, как CUEMATH Учителя объяснят вашему ребенку Variable Expressions с помощью интерактивных симуляций и рабочих листов, чтобы им больше никогда не приходилось запоминать что-либо по математике!
Исследуйте живые, интерактивные и персонализированные онлайн-классы Cuemath, чтобы ваш ребенок стал экспертом по математике. Запишитесь на БЕСПЛАТНОЕ пробное занятие сегодня!
Переменное выражение (алгебраическое выражение)
Переменное выражение (или) алгебраическое выражение представляет собой комбинацию терминов с помощью таких операций, как сложение, вычитание, умножение, деление и т. д.
Пример переменного выражения
Пример переменного выражения (или) алгебраическое выражение равно (5x + 7)
92+2(-2)+7 &= 5(4)-4+7 \&= 20-4+7\&= 23end{align}]
Итак, ответ (23 )
Типы переменных выражений
Существует (5) типов переменных выражений (или) алгебраических выражений.
9{-1} +2г+3г)
| Типы | Значение | Примеры |
|---|---|---|
|
Одночлен |
Think Tank
- Всякий ли многочлен является многочленом?
- Является ли каждый многочлен многочленом?
Действия по вычислению переменных выражений
Вот упражнение с переменными выражениями.
Здесь вы можете выбрать одно из заданных выражений переменных и указать значение(я) для его переменной(й).
Затем вы можете оценить и ввести значение решения переменного выражения в соответствии с введенными вами значениями.
Не беспокойтесь, если вы введете неверный ответ на выражение.
Он покажет вам пошаговое объяснение правильного ответа.
Помогите своему ребенку получить более высокие баллы с помощью собственного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Проведите тест сейчас.
Решенные примеры
В мешке (25) апельсинов. Напишите переменное выражение (алгебраическое выражение) для количества апельсинов в (x) количестве мешков.
Решение:
Количество апельсинов в одном мешке = (25)
Количество мешков = (x)
Таким образом, количество апельсинов в (x) мешках = ( 25x)
Требуемое выражение переменной (= 25x )
Вычислите данное выражение переменной для (a = 7; b = -3) и (c = 2)
[6ab + 7bc + 9ca]
Решение
Данное алгебраическое выражение равно (6ab + 7bc + 9ca)
Подставьте следующие значения в приведенное выше выражение:
(a = 7; ;b = -3; ; c = 2)
[begin{align}6ab !+! 7bc !+! 9ca&!=! 6(7)(-3) !+! 7(-3)(2) !+! 9(2)(7)\[0,3см]&!=!!-!126!-!42!+!126\[0,3см]&!=! !-!42end{align}]
[6ab + 7bc + 9ca = — 42 ]
Укажите правильный вариант(ы).
(4x+5) является …
(a) Одночлен
(b) Двучлен
(c) Трехчлен 92-3x+2) в (x=2)
Практические вопросы
Важные темы
Ниже приведены список тем, которые тесно связаны с переменными выражениями. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
- Сложение и вычитание
- Факторизация
Образцы заданий олимпиады по математике
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, ежегодно проводимый для школьников. Это побуждает детей развивать свои навыки решения математических задач с точки зрения конкуренции.
Вы можете БЕСПЛАТНО скачать образцы бумаг по классам ниже:
- Образец бумаги IMO Class 1
- Образец бумаги IMO Class 2
- Образец бумаги IMO, класс 3
- Образец бумаги IMO класса 4
- Образец бумаги IMO Class 5
- Образец бумаги IMO класса 6
- Образец бумаги IMO класса 7
- Образец бумаги IMO Class 8
- Образец бумаги IMO класса 9
- Образец бумаги IMO Class 10
Чтобы узнать больше об олимпиаде по математике, нажмите здесь
Часто задаваемые вопросы (FAQ)
1.
Как написать переменное выражение?
Переменное выражение зависит от условия.
Например, «(3) больше, чем (x)» можно записать как выражение переменной (x+3)
«(7) меньше, чем сумма (a) ) и (b)» можно записать как выражение переменной (a+b-7)
2. Что такое пример переменной?
Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
Некоторые примеры переменных в математике: (a,b,x,y,z,m,) и т.д.
Дополнительную информацию можно найти в разделе «Определение переменной, константы, термина и коэффициента» на этой странице.
3. Какие существуют 3 типа переменных?
3 типа переменных:
- Независимые переменные
- Зависимые переменные
- Контролируемые переменные
4. Всегда ли выражения должны иметь переменную?
Нет, выражение не обязательно должно иметь переменную.
Например, такие константы, как (2, -3, dfrac{-3}{4}), также называются выражениями.
5. Как определить переменную?
Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
Некоторые примеры переменных в математике: (a,b,x,y,z,m,) и т. д.
6. Что такое переменная? Приведите пример.
Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
Некоторые примеры переменных в математике: (a,b,x,y,z,m,) и т.д.
Оценка: вычисление выражений и многочленов
Функции
Purplemath
Что такое «оценка» в математике?
«Оценка» в основном означает «упрощение выражения до одного числового значения». Иногда вам будет дано числовое выражение, которое вам нужно будет только упростить; это скорее вопрос порядка операций. В этом уроке я сконцентрируюсь на аспекте оценки «подключи и пыхти»: подставляя значения для переменных и «пыхтя» мой путь к упрощенному ответу.
Содержимое продолжается ниже
MathHelp.
com
Вычисление выражений
(Кстати, да, «подключи и пыхни» — довольно стандартная терминология. Это не «технический» термин, так что вы, вероятно, не увидите это есть в вашем учебнике, но вы наверняка услышите это от других учеников и, возможно, от своего преподавателя.)
Обычно единственной сложной частью оценивания является отслеживание знаков «минус». Я настоятельно рекомендую вам широко использовать круглые скобки, особенно когда вы только начинаете.
Что является примером оценки?
Чтобы найти ответ, я просто подставляю заданные значения, стараясь использовать круглые скобки, особенно вокруг знаков «минус». Особенно, когда я только начинаю, может быть полезно сначала нарисовать круглые скобки:
a 2 b
( ) 2 ( )
3 (−2) 906
(4)(3)
12
Обратите внимание, как использование круглых скобок помогло мне отслеживать знак «минус» в значении и . Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2 и получить -4, что было бы неправильно.
Кстати, оказалось, что значения переменных c и d нам не нужны. Когда вам дается большой набор выражений для оценки, вы должны ожидать, что часто будет та или иная переменная, которая не будет включена ни в одно конкретное упражнение в наборе.
В этом упражнении мне дали дополнительную информацию. нет b в выражении, которое они хотят, чтобы я оценил, поэтому я могу игнорировать это значение в своей работе:
(−2) − (−4)(4)
−2 − (−16)
−2 + 16
16 − 2
14
Я должен позаботиться о том, чтобы не пытаться «распределить» показатель степени через круглые скобки. Показатели НЕ распределяются по сложению! Я никогда не должен пытаться сказать, что ( b + d ) 2 то же самое, что b 2 + d 2 906:30 . Это НЕ одно и то же! Я должен вычислить выражение в его нынешнем виде:
( (3) + (4) ) 2
( 7 ) 2
49
В этом выражении возведение в квадрат производится для каждой переменной отдельно.
(3) 2 + (4) 2
9 + 16
25
Обратите внимание, что этот последний ответ выше не соответствует ответу на предыдущую оценку. Это прямо демонстрирует тот факт, что показатели степени не распределяются при сложении так, как это происходит при умножении.
На следующем тесте, а также на выпускном экзамене следует ожидать как минимум упражнения, аналогичные двум предыдущим. Эта склонность пытаться распределять показатель степени (а не умножение) над сложением является распространенной ошибкой учащихся, и ваш преподаватель почти наверняка захочет напоминать вам — и часто! — о разнице между возведением суммы в квадрат и суммированием двух квадратов. Не путайте их!
В этом упражнении мне нужно использовать значения всех четырех переменных. Но мне нужно быть осторожным в своем размещении, потому что это выражение не использует переменные в алфавитном порядке.
(3)(−4) 3 − (−2)(4)
(3)(−64) − (−8)
−192 + 8
−184
Самые общий тип «выражения», который вам, вероятно, потребуется оценить, будет полиномом. Чтобы вычислить полином, вы берете этот полином и подставляете переменную (обычно x ) в любое число, которое они вам дали.
Какой пример вычисления многочлена?
Это мой первый многочлен для оценки, поэтому я снова начну с пустых скобок, показывающих, где нужно разместить значение переменной.
x 4 + 3 x 3 − x 2 + 6
( ) 4 + 3( ) 3 − ( ) 2 + 6
( −3) 4 + 3(−3) 3 − (−3) 2 + 6
81 + 3(−27) − (9) + 6
81 − 81 − 9 + 6
−3
Я рад, что научился использовать круглые скобки, чтобы сделать свои замены понятными. В этом случае эти скобки помогут мне отслеживать знаки «минус».
3(−2) 2 − 12(−2) + 4
3(4) + 24 + 4
12 + 24 + 4
40
Это другое. Мне дали уравнение с двумя переменными, но дали значение только одной из переменных. Я предполагаю, что они хотят, чтобы я подключил x и вычислил результирующее значение для y .
y = 4(−1) − 3
= −4 − 3 = −7
Тогда мой ответ будет уравнением:
y = −7
Примечание. В этом последнем упражнении выше мы подставляли значение одной из переменных и упрощали поиск значения другой переменной. Кроме того, часть, к которой мы подключались, была установлена равной имени, y . Из-за этого мы не просто вычисляли выражение; на самом деле мы оценивали полиномиальную функцию. Результат нашей операции plug-n-chug означает, что точка ( x , y ) = (−1, −7) находится на прямой y = 4 x — 3; то есть эта точка находится на графике полиномиальной функции.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении выражений для заданных значений переменных (или пропустите виджет и перейдите на следующую страницу). Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/evaluate.htm
Страница 2
Вычисление алгебраических выражений,… Пошаговое решение математических задач
3.1 Вычисление алгебраических выражений 6 Тот же набор правил для порядка операций с целыми числами, который обсуждался в
Разделе 1.2, также используется с целыми числами. Правила изложены здесь для удобства справки по
.
Правила порядка выполнения операций
1. Работайте с символами включения (круглые, квадратные или фигурные скобки), начиная с самой внутренней пары. 92 = 8 ÷ 4-9 показателей
= 2-9 деление
= -7 Вычитание
2. (7+8) ÷ 5*4-20
(7+8) ÷ 5*4-20 = 15 ÷ 5*4-20 Сложений
= 3*4-20 Разделение
= 12-20 Умножение
= -8 Вычитание
3. 4*5- (6*2-3)+4 ÷ 2
4*5-(6*2-3)+4÷2=4*5-(9)+4÷2 круглые скобки
=20-9+2 0083
= 13 вычитание и добавление
4. (-5-6)/11+3 (-5)
(-5-6)/11+3 (-5) =-11/11+3 (— 5) Дробная полоса является символом включения
= -1+(-15) Разделение и умножение
= -16 Дополнение
Практическая викторина
| Вопросы | Ответы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найти значение каждого выражения 92 не являются той же степенью х.
Числовая часть термина называется коэффициентом переменной или переменных в термине. Таким образом, в термине 8x,8 является коэффициентом x. Выражения с одинаковыми членами можно упростить, применив свойство дистрибутивности, обсуждавшееся в разделе 1. a(b+c)=ab+ac или ab+ac=a(b+c) или ba+ca=(b+c)a полезно, когда b и c являются числовыми коэффициентами. Например, 3x+5x=(3+5)x Коэффициенты складываются =8x Мы говорим, что 3x и 5x были объединены как слагаемые или что мы объединили 3x и 5x. Одинаковые члены можно комбинировать, добавляя (или вычитая) коэффициенты. Примеры Комбинируйте одинаковые термины, когда это возможно -7)+5(x+1)=4x-28+5x+5 Использовать распределительное свойство дважды. =4x+5x-28+5 92+2a 5. (x+3x)/2+x=(4x)/2+x Дробная черта — это символ включения, подобный скобкам. =2x+x=3x Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Решите похожую задачуВведите свою задачу 9092
3. Алгебра — это язык математики, и чтобы понимать математику, вы должны понимать язык. Мы хотим иметь возможность превращать английские фразы в их «алгебраические» эквиваленты и наоборот. Итак, если задача сформулирована на английском языке, мы можем перевести фразы в алгебраические символы и приступить к решению задачи по правилам, разработанным для алгебры. Следующие примеры иллюстрируют, как некоторые ключевые слова могут быть переведены в алгебраические символы. Примеры
Некоторые слова, например, выделенные жирным шрифтом в предыдущих примерах, являются ключами к операциям. Научитесь искать эти слова и слова из следующего списка.
Следует особо отметить слова «частное» и «разность». Как показано в задачах 3 и 6 практического теста, деление и вычитание выполняются со значениями в том порядке, в котором они даны в задаче. Например, разница между 3 и 5 равна 3-5=-2, а разница между 5 и 3 равна 5-3=2. 3.4 Решение уравнения Если уравнение содержит переменную, мы хотим найти значение (или значения) для переменной, которое даст истинное уравнение при замене переменной. Это значение (или значения) называется решением уравнения, и мы решили уравнение. Предположим, нам дано уравнение 2x-1 = x+3 , если мы заменим x = 4, то 2*4-1 = 7 и 4+3 = 7 SO 2*4-1 =4+3 и x=4 является решением Если мы подставим x=5, то 2*5-1=9 и 5+3=8 но 9!=8, * так что *! =5+3 и x=5 не является решением. Два уравнения эквивалентны, если они имеют абсолютно одинаковые решения. Например, 2x-1 = x+3 и x+1=5 эквивалентны, поскольку x=4 является решением каждого уравнения. Нам нужны некоторые процедуры, которые позволят нам шаг за шагом находить решения уравнений, содержащих переменные. Следующие две идеи являются основными. 1. Все, что делается с одной частью уравнения, должно быть сделано и с другой. 2. Цель состоит в том, чтобы найти простое уравнение, такое как x=4, которое эквивалентно исходному уравнению. В следующих примерах каждое уравнение решается поэтапно с объяснением каждого шага. Внимательно изучите каждый пример. Обратите внимание, что эквивалентные уравнения записываются одно под другим. Не пишите несколько уравнений в одной строке и не приравнивайте одно уравнение к другому уравнению. Примеры 1. x+7=12 Запишите уравнение. x+7-7=12-7 Добавить -7 к обеим сторонам x=5 Упрощение. 2. 2x-3=13 Запишите уравнение. 2x-3+3=13+3 Добавьте 3 к обеим сторонам. 2x=16 Упрощение. (2x)/2=16/2 Поделите обе части на 2, коэффициент при x. x=8 Упрощение. 3. 5x-1=-11 Запишите уравнение. 5x-1+1=-11+1 Добавьте +1 к обеим сторонам. 5x=-10 Упростить; теперь на одной стороне есть все термы с переменными и только термы с переменными. (5x)/5=-10/5 Поделите обе части на 5, коэффициент при x. x=-2 Упростите 4. 4x+1-x=13+x Запишите уравнение. 3x+1=13+x Упростить 3x+1-1=13+x-1 Добавить -1 к обеим сторонам. 3x=12+x Упростить 3x-x=12+x-x Добавить -x к обеим сторонам. 2x=12 Упрощение; теперь на одной стороне есть все термы с переменными и только термы с переменными. (2x)/2=12/2 Поделите обе части на 2, коэффициент при x. x=6 Упростить 5. (2x)/5+2=6 Запишите уравнение. (2x)/5+2-2=6-2 Добавьте -2 к обеим сторонам. (2x)/5 = 4 упростите 5*(2x)/5 = 4*5 Умножить обе стороны на 5. 2x = 20 Упрощение (2x)/2 = 20/2 Разделите обе стороны 2 x=10 Упрощение Давайте посмотрим, как наш решатель уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Решите похожую задачуВведите свою задачу Каждое решение можно проверить, подставив его в исходное уравнение. Если выражение, представляющее ненулевое число, (а) прибавить, (б) разделить или (в) умножить на обе части уравнения, новое уравнение будет эквивалентно исходному уравнению. 3.5 Формулы Формулы — это общие правила или принципы, сформулированные математически. Например, в бизнесе простые проценты — это произведение основного долга, процентной ставки и времени в годах. Таким же правилом математически является формула {Iota}=PRT. Другие формулы приведены ниже. 92 Площадь (A) круга равна произведению PI на квадрат радиуса (r). p=4s Периметр (p) квадрата в 4 раза больше длины одной стороны (s). A=1/2bh Площадь (A) треугольника равна половине произведения основания (b) и высоты (h). d=rt Пройденное расстояние равно произведению скорости (r) и времени (t). C=5/9(F-32) Температура в градусах Цельсия (C) равна 5/9 разницы между температурой по Фаренгейту (F) и 32, В последней формуле предположим, что F = 212°, температура кипения воды на уровне моря. C=5/9(212-32)=5/9(180)=100 Предположим, что вопрос поставлен наоборот. Если C = 20°, каково будет соответствующее значение F? Подстановка 20 вместо C и решение для F дает 20=5/9(F-32) 20*9/5=9/5*5/9(F-32) Умножьте обе части на 9/5, взаимный 5/9. 36 = F-32 68 = F Решение для F с точки зрения C может быть сделано следующим образом: C = 5/9 (F-32) 9/5*C = 9 /5*5/9(F-32) 9/5C=F-32 9/5C+32=F Формула для C: и решено для F равно F=9/5C+32 Цель здесь состоит в том, чтобы решить формулы для одной из переменных в терминах других переменных. То есть, используя методы решения уравнений, которые имеют только одну переменную, рассматривайте другие переменные как константы и находите нужную переменную. Примеры 1. Найти b. Решение: P = A+B+C P-A-C = A+B+C-A-C P-A-C = B 2. Приведенный P = 2L+2w Formul прямоугольник Найти l Решение: P=2l+2w P-2w=2wl0083 P-2W = 2L (P-W)/2 = (2L)/2 (P-2W)/2 = L или P = 2L+W P/2 = (2L+ 2w)/2 P/2=(2l)/2+(2w)/2 P/2=l+w P/2-w=l Оба ответа верны, поскольку P/2- w=P/2-(2w)/2=(P-2w)/2 3. Учитывая 3y-4x+9=0, найдите y. Решение: 3y-4x+9 = 0 3y-4x+9+4x-9 = 0+4x-9 3y = 4x-9 y = (4x-9)/3 или y=(4x)/3-9/3=4/3x-3 Любая из этих форм верна. Если у вас есть один ответ, а другой находится в ключе ответов, вы должны признать свой ответ правильным, но в другой форме. Давайте посмотрим, как наш решатель уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Решить похожую задачуВведите свою задачу 4. Учитывая V=T/(P-5), решите P. Решение: V=T/(P-5) V(P-5)=T/(P-5)(P-5) Умножьте обе части на P-5. V(P-5)=T (V(P-5))/V=T/V P-5=T/V P=T/V+5 3 900 задачи (Числа и последовательные целые числа) В разделе 3.3 мы обсуждали перевод английских фраз в алгебраические выражения. Фраза «8, добавленная к удвоенному числу» алгебраически переводится как 2x + 8. Как вы переводите «на 4 больше, чем число?» Если вы сказали x + 4, вы правы. Теперь цель состоит в том, чтобы перевести целое предложение в уравнение, а затем решить уравнение. Две приведенные выше фразы могут быть включены в предложение, подобное следующему: Алгебраически, 2x+8 = x+4 «Результат« переводится как = Решение, 2x+8 = x+4 2x+8-x = x+4-x x +8=4 x+8-8=4-8 x=-4 В этом разделе словесные задачи будут просто упражнениями на перевод предложений в уравнения и решение этих уравнений. Более сложные «прикладные» проблемы будут обсуждаться в последующих главах. Такие задачи будут включать геометрические формулы, расстояние, проценты, работу, неравенства и смешение. Примеры 1. Трижды сумма числа и 5 равна удвоенному числу плюс 5. Найдите число. Решение Пусть x : неизвестное число.
Число -10. 2. Если число уменьшить на 36, и результат будет на 76 меньше, чем удвоенное число, какое это будет число? Решение Пусть n = неизвестное число.
Число 40. Последовательные целые числа — это два целых числа, которые отличаются на 1, или второе целое число на 1 больше первого. Например, 21 и 22 — последовательные целые числа. -14 и -13 — последовательные целые числа. В общем случае, если n — одно целое число, то n + 1 — это следующее последовательное целое число. Примеры: последовательные целые числа 1. Найдите три последовательных целых числа таких, что сумма первого и третьего в 76 раз меньше второго. N+(n+2) = 3 (n+1) -76 2n+2 = 3n+3- 76 2n+2 = 3n-73 2n+2+73-2n = 3n-73+73-2n 75 = N 76 = N+1 77 = N+2 Три. последовательные целые числа равны 75, 76 и 77. 2. Три последовательных нечетных целых числа таковы, что их сумма равна -3. Что такое целые числа? let n = первое нечетное целое число n+(n+2)+(n+4) =-3 3n+6 =— 3 3n = -9 n = -3 N+2 = -1 N+4 =+1 Три последовательных нечетных целых числа составляют -3, -1 и +1. Разница между выражением и уравнением (со сравнительной таблицей) В математике вы, возможно, очень часто встречали термины выражение и уравнение. Однако, если оно не содержит знака равенства (=), то это просто выражение . Он содержит числа, переменные и операторы, которые используются для отображения значения чего-либо. Прочтите эту статью, чтобы понять основные различия между выражением и уравнением. Содержание: выражение и уравнение
Сравнительная таблица
Определение выражения В математике выражение определяется как фраза, которая объединяет числа (постоянные), буквы (переменные) или их комбинации, соединенные операторами (+, -, *, /), для представления ценность чего-либо. Выражение может быть арифметическим, алгебраическим, полиномиальным и аналитическим. Поскольку он не содержит знака равенства (=), он не показывает никакой связи. Следовательно, у него нет ничего похожего на левую или правую сторону. Выражение можно упростить, объединив одинаковые термины, или его можно вычислить, вставив значения вместо переменных, чтобы получить числовое значение. Примеры : 9x + 2, x – 9, 3p + 5, 4m + 10 Определение уравненияВ математике термин уравнение означает выражение равенства. Это предложение, в котором два выражения стоят равными друг другу. Чтобы удовлетворить уравнение, важно определить значение рассматриваемой переменной; это известно как решение или корень уравнения. Уравнение может быть условным или тождественным. Если уравнение условное , то равенство двух выражений верно для определенного значения вовлеченной переменной. Однако, если уравнение представляет собой identity , то равенство верно для всех значений, хранящихся в переменной. Существует четыре типа уравнений, которые обсуждаются ниже:
Основные различия между выражением и уравнениемПункты, приведенные ниже, обобщают важные различия между выражением и уравнением:
Заключение Таким образом, из приведенного выше объяснения становится ясно, что существует большая разница между этими двумя математическими понятиями. Выражение не раскрывает никакой связи, в отличие от уравнения. Уравнение содержит знак «равно», поэтому оно показывает решение или в конечном итоге представляет значение переменной. Примеры выраженийВ этой статье представлено множество примеров выражений в Access. Выражение — это комбинация математических или логических операторов, констант, функций, полей таблицы, элементов управления и свойств, результатом которой является одно значение. Вы можете использовать выражения в Access для вычисления значений, проверки данных и установки значения по умолчанию. В этой статье г.
|
|
Текстовые операции Значения в других элементах управления Операции с датами |
Заголовки и колонтитулы Подсчет, сумма и средние значения Условия только двух значений |
Арифметические операции Агрегатные функции SQL |
Все выражения запросов и фильтров
|
Текстовые операции Агрегатные функции SQL Соответствие текстовым значениям Сопоставьте шаблоны записей с лайком Обновить запросы |
Арифметические операции Найдите недостающие данные Критерии даты матча Сопоставьте строки с агрегатами SQL Операторы SQL |
Операции с датами Вычисляемые поля с подзапросами Поля с отсутствующими данными Сопоставьте поля с подзапросами |
Все табличные выражения
|
Значения поля по умолчанию |
Правила проверки полей |
Все выражения макроса
Формы и отчеты
Таблицы в этом разделе содержат примеры выражений, которые вычисляют значение в элементе управления, расположенном в форме или отчете. Чтобы создать вычисляемый элемент управления, введите выражение в свойство ControlSource элемента управления, а не в поле таблицы или запрос.
Примечание Вы также можете использовать выражения в форме или отчете при выделении данных с условным форматированием.
Текстовые операции
В выражениях в следующей таблице используются операторы & (амперсанд) и + (плюс) для объединения текстовых строк, встроенных функций для управления текстовой строкой или других операций с текстом для создания вычисляемого элемента управления.
|
Выражение |
г.
Результат |
|---|---|
|
=»Н/Д» |
Дисплеи Н/Д. |
|
=[Имя] & » » & [Фамилия] |
Отображает значения, находящиеся в полях таблицы с именами Имя и Фамилия. В этом примере оператор & используется для объединения поля «Имя», символа пробела (заключенного в кавычки) и поля «Фамилия». |
|
=Слева([ИмяПродукта], 1) |
Использует функцию Left для отображения первого символа значения поля или элемента управления с именем ProductName. |
|
=Правильно([КодАктива], 2) |
Использует функцию Right для отображения двух последних символов значения в поле или элементе управления с именем AssetCode. |
|
= Обрезать ([Адрес]) |
Использует функцию обрезки для отображения значения элемента управления Address, удаляя все начальные и конечные пробелы. |
|
=IIf(IsNull([Регион]), [Город] & » » & [Почтовый индекс], [Город] & » » & [Регион] & » » & [Почтовый индекс]) |
Использует функцию IIf для отображения значений элементов управления City и PostalCode, если значение в элементе управления Region равно null; в противном случае отображаются значения элементов управления City, Region и PostalCode, разделенные пробелами. |
|
=[Город] & (» » + [Регион]) & » » & [Почтовый индекс] |
Использует оператор + и распространение null для отображения значений элементов управления City и PostalCode, если значение в поле или элементе управления Region равно null; в противном случае отображаются значения полей или элементов управления City, Region и PostalCode, разделенные пробелами. Распространение null означает, что если какой-либо компонент выражения имеет значение null, все выражение также равно null. Оператор + поддерживает распространение null; оператор & не делает. |
Верх страницы
Верхние и нижние колонтитулы
Вы используете свойства Page и Pages для отображения или печати номеров страниц в формах или отчетах. Свойства Страница и Страница доступны только во время печати или предварительного просмотра, поэтому они не отображаются на странице свойств формы или отчета. Как правило, вы используете эти свойства, помещая текстовое поле в раздел верхнего или нижнего колонтитула формы или отчета, а затем используя выражение, подобное показанному в следующей таблице.
Дополнительные сведения об использовании верхних и нижних колонтитулов в формах и отчетах см. в статье Вставка номеров страниц в форму или отчет.
|
Выражение |
Результат |
|---|---|
|
=[Страница] |
1 |
|
=»Страница» и [Страница] |
Страница 1 |
|
=»Страница » & [Страница] & » из » & [Страницы] |
Страница 1 из 3 |
|
=[Страница] & » из » & [Страницы] & » Страницы» |
1 из 3 страниц |
|
=[Страница] & «/» & [Страницы] & «Страницы» |
1/3 страницы |
|
=[Страна/регион] & «-» & [Страница] |
Великобритания — 1 |
|
=Формат([Страница], «000») |
001 |
|
=»Напечатано: » & Дата() |
Напечатано: 31. |
Верх страницы
Арифметические операции
Вы можете использовать выражения для сложения, вычитания, умножения и деления значений в двух или более полях или элементах управления. Вы также можете использовать выражения для выполнения арифметических операций с датами. Например, предположим, что у вас есть поле таблицы Date/Time с именем RequiredDate. В поле или в элементе управления, привязанном к полю, выражение =[RequiredDate] — 2 возвращает значение даты/времени, равное двум дням до текущих значений в поле RequiredDate.
|
Выражение |
Результат |
|---|---|
|
=[Итог]+[Доставка] |
Сумма значений полей или элементов управления Subtotal и Freight. |
|
=[RequiredDate]-[ShippedDate] |
Интервал между значениями дат в полях или элементах управления RequiredDate и ShippedDate. |
|
=[Цена]*1,06 |
Произведение значения поля или элемента управления «Цена» и 1,06 (добавляет 6 процентов к значению «Цена»). |
|
=[Количество]*[Цена] |
Произведение значений полей или элементов управления «Количество» и «Цена». |
|
= [Всего сотрудников]/[Всего стран и регионов] |
Частное значений полей или элементов управления EmployeeTotal и CountryRegionTotal. |
Примечание Если в выражении используется арифметический оператор (+, -, * и /), а значение одного из элементов управления в выражении равно NULL, результатом всего выражения будет NULL — это известно как нулевое распространение. Если какие-либо записи в одном из элементов управления, которые вы используете в выражении, могут иметь нулевое значение, вы можете избежать распространения нулевого значения, преобразовав нулевое значение в ноль с помощью функции Nz — например, =Nz([Subtotal])+Nz ([Груз]).
Верх страницы
Значения в других элементах управления
Иногда вам нужно значение, которое существует где-то еще, например, в поле или элементе управления в другой форме или отчете. Вы можете использовать выражение для возврата значения из другого поля или элемента управления.
В следующей таблице перечислены примеры выражений, которые можно использовать в вычисляемых элементах управления в формах.
|
Выражение |
Результат |
|---|---|
|
=Формы![Заказы]![КодЗаказа] |
Значение элемента управления OrderID в форме Orders. |
|
=Формы![Заказы]![Подформа заказов].Форма![Итог заказа] |
Значение элемента управления OrderSubtotal в подчиненной форме с именем Orders Subform в форме Orders. |
|
=Forms![Заказы]![Подформа заказов]![ProductID].Column(2) |
Значение третьего столбца ProductID, списка из нескольких столбцов в подчиненной форме с именем «Подчиненная форма заказов» в форме «Заказы». (Обратите внимание, что 0 относится к первому столбцу, 1 — ко второму столбцу и т. д.) |
|
=Формы![Заказы]![Подформа заказов]![Цена] * 1,06 |
Произведение значения элемента управления «Цена» в подчиненной форме «Подчиненная форма заказов» в форме «Заказы» и 1,06 (добавляет 6 процентов к значению элемента управления «Цена»). |
|
=Родитель![ИдентификаторЗаказа] |
Значение элемента управления OrderID в основной или родительской форме текущей подчиненной формы. |
Выражения в следующей таблице показывают некоторые способы использования вычисляемых элементов управления в отчетах. Выражения ссылаются на свойство отчета.
|
Выражение |
Результат |
|---|---|
|
=Отчет![Счет-фактура]![IDЗаказа] |
Значение элемента управления «OrderID» в отчете «Счет». |
|
=Отчет![Сводка]![Сводный подотчет]![Всего по продажам] |
Значение элемента управления SalesTotal во вложенном отчете с именем Суммарный вложенный отчет в сводном отчете. |
|
=Родитель![ИдентификаторЗаказа] |
Значение элемента управления OrderID в основном или родительском отчете текущего вложенного отчета. |
Верх страницы
Подсчет, сумма и средние значения
Вы можете использовать тип функции, называемый агрегатной функцией, для вычисления значений для одного или нескольких полей или элементов управления. Например, вы можете рассчитать итоговую сумму группы для нижнего колонтитула группы в отчете или промежуточную сумму заказа для позиций в форме. Вы также можете подсчитать количество элементов в одном или нескольких полях или рассчитать среднее значение.
Выражения в следующей таблице показывают некоторые способы использования таких функций, как Avg, Count и Sum.
|
Выражение |
Описание |
|---|---|
|
=Среднее([Перевозка]) |
Использует функцию Avg для отображения среднего значения поля таблицы или элемента управления с именем «Freight». |
|
=Количество([ИдентификаторЗаказа]) |
Использует функцию Count для отображения количества записей в элементе управления OrderID. |
|
=Сумма([Продажи]) |
Функция «Сумма» используется для отображения суммы значений элемента управления «Продажи». |
|
=Сумма([Количество]*[Цена]) |
Функция «Сумма» используется для отображения суммы произведения значений элементов управления «Количество» и «Цена». |
|
=[Продажи]/Сумма([Продажи])*100 |
Отображает процент продаж, определяемый путем деления значения элемента управления «Продажи» на сумму всех значений элемента управления «Продажи». Если для свойства Format элемента управления установлено значение Percent, не включайте *100 в выражение. |
Дополнительные сведения об использовании агрегатных функций и суммировании значений в полях и столбцах см. в статьях Суммирование данных с помощью запроса, Подсчет данных с помощью запроса, Отображение итогов столбца в таблице с помощью строки итогов и Отображение итоговые значения столбца в таблице данных.
Верх страницы
агрегатные функции SQL
Вы используете тип функции, называемый функцией SQL или агрегатной функцией домена, когда вам нужно выборочно суммировать или подсчитывать значения. «Домен» состоит из одного или нескольких полей в одной или нескольких таблицах или одного или нескольких элементов управления в одной или нескольких формах или отчетах. Например, вы можете сопоставить значения в поле таблицы со значениями в элементе управления в форме.
|
Выражение |
Описание |
|---|---|
|
=DLookup(«[ContactName]», «[SupplierID]», «[SupplierID] = » & Forms(«SupplierID»)(«[SupplierID]»)) |
Использует функцию DLookup для возврата значения поля ContactName в таблице Suppliers, где значение поля SupplierID в таблице совпадает со значением элемента управления SupplierID в форме Suppliers. |
|
=DLookup(«[ContactName]», «[SupplierID]», «[SupplierID] = » & Forms![Новые поставщики]![SupplierID]) |
Использует функцию DLookup для возврата значения поля ContactName в таблице Suppliers, где значение поля SupplierID в таблице совпадает со значением элемента управления SupplierID в форме New Suppliers. |
|
=DSum(«[СуммаЗаказа]», «[Заказы]», «[КодКлиента] = ‘RATTC’») |
Использует функцию DSum для возврата суммы значений в поле OrderAmount в таблице Orders, где CustomerID — RATTC. |
|
=DCount(«[Выведено из эксплуатации]»,»[Активы]»,»[Выведено из эксплуатации]=Да») |
Использует функцию DCount для возврата количества значений «Да» в поле «Исключено» (поле «Да/Нет») в таблице «Активы». |
Верх страницы
Операции с датами
Отслеживание даты и времени является фундаментальной деятельностью базы данных. Например, вы можете рассчитать, сколько дней прошло с даты выставления счета, чтобы определить возраст вашей дебиторской задолженности. Вы можете форматировать дату и время различными способами, как показано в следующей таблице.
|
Выражение |
Описание |
|
=Дата() |
Использует функцию «Дата» для отображения текущей даты в формате мм-дд-гг, где мм — месяц (от 1 до 12), дд — день (от 1 до 31), а гг — две последние цифры числа. год (с 1980 по 2099 год). |
|
=Формат(Сейчас(), «ww») |
Использует функцию Format для отображения номера недели года для текущей даты, где ww представляет недели с 1 по 53. |
|
=ДатаЧасть(«гггг», [ДатаЗаказа]) |
Использует функцию DatePart для отображения четырехзначного года значения элемента управления OrderDate. |
|
=ДатаДобавить(«г», -10, [ОбещаннаяДата]) |
Использует функцию DateAdd для отображения даты за 10 дней до значения элемента управления PromisedDate. |
|
=DateDiff(«d», [ДатаЗаказа], [ДатаОтгрузки]) |
Использует функцию DateDiff для отображения разницы в количестве дней между значениями элементов управления OrderDate и ShippedDate. |
|
=[ДатаСчета] + 30 |
Использует арифметические операции с датами для вычисления даты через 30 дней после даты в поле InvoiceDate или элементе управления. |
Верх страницы
Условия только двух значений
Примеры выражений в следующей таблице используют функцию IIf для возврата одного из двух возможных значений. Вы передаете функции IIf три аргумента: Первый аргумент — это выражение, которое должно возвращать значение True или False. Второй аргумент — это значение, которое будет возвращено, если выражение истинно, а третий аргумент — это значение, которое будет возвращено, если выражение ложно.
|
Выражение |
Описание |
|---|---|
|
=IIf([Подтверждено] = «Да», «Заказ подтвержден», «Заказ не подтвержден») |
Использует функцию IIf (Немедленное если) для отображения сообщения «Заказ подтвержден», если значение элемента управления «Подтверждено» равно «Да»; в противном случае отображается сообщение «Заказ не подтвержден». |
|
=IIf(IsNull([Страна/регион]), » «, [Страна]) |
Использует функции IIf и IsNull для отображения пустой строки, если значение элемента управления Country/region равно null; в противном случае отображается значение элемента управления Страна/регион. |
|
=IIf(IsNull([Регион]), [Город] & » » & [Почтовый индекс], [Город] & » » & [Регион] & » » & [Почтовый индекс]) |
Использует функции IIf и IsNull для отображения значений элементов управления City и PostalCode, если значение в элементе управления Region равно null; в противном случае отображаются значения полей или элементов управления City, Region и PostalCode. |
|
=IIf(IsNull([RequiredDate]) или IsNull([ShippedDate]), «Проверить отсутствие даты», [RequiredDate] — [ShippedDate]) |
Использует функции IIf и IsNull для отображения сообщения «Проверить отсутствие даты», если результат вычитания ShippedDate из RequiredDate равен нулю; в противном случае отображается интервал между значениями дат элементов управления RequiredDate и ShippedDate. |
Верх страницы
Запросы и фильтры
В этом разделе содержатся примеры выражений, которые можно использовать для создания вычисляемого поля в запросе или для предоставления критериев запроса. Вычисляемое поле — это столбец в запросе, являющийся результатом выражения. Например, вы можете вычислить значение, объединить текстовые значения, такие как имя и фамилия, или отформатировать часть даты.
Вы используете критерии в запросе, чтобы ограничить количество записей, с которыми вы работаете. Например, вы можете использовать оператор «Между», чтобы указать начальную и конечную даты и ограничить результаты вашего запроса заказами, которые были отправлены между этими датами.
Ниже приведены примеры выражений для использования в запросах.
Текстовые операции
Выражения в следующей таблице используют операторы & и + для объединения текстовых строк, используют встроенные функции для работы с текстовой строкой или иным образом работают с текстом для создания вычисляемого поля.
|
Выражение |
Описание |
|---|---|
|
Полное имя: [Имя] & » » & [Фамилия] |
Создает поле FullName, в котором отображаются значения полей FirstName и LastName, разделенные пробелом. |
|
Address2: [Город] & » » & [Регион] & » » & [Почтовый индекс] |
Создает поле Address2, в котором отображаются значения полей City, Region и PostalCode, разделенные пробелами. |
|
ProductInitial: слева ([ProductName], 1) |
Создает поле с именем ProductInitial, а затем использует функцию Left для отображения в поле ProductInitial первого символа значения в поле ProductName. |
|
TypeCode: Right([AssetCode], 2) |
Создает поле с именем TypeCode, а затем использует функцию Right для отображения двух последних символов значений в поле AssetCode. |
|
Код города: Mid([Телефон],2,3) |
Создает поле с именем AreaCode, а затем использует функцию Mid для отображения трех символов, начиная со второго символа значения в поле Phone. |
|
ExtendedPrice: CCur([Сведения о заказе].[Цена за единицу]*[Количество]*(1-[Скидка])/100)*100 |
Присваивает вычисляемому полю имя ExtendedPrice и использует функцию CCur для расчета итоговых значений отдельных позиций с примененной скидкой. |
Верх страницы
Арифметические операции
Вы можете использовать выражения для сложения, вычитания, умножения и деления значений в двух или более полях или элементах управления. Вы также можете выполнять арифметические операции над датами. Например, предположим, что у вас есть поле даты/времени с именем RequiredDate. Выражение =[RequiredDate] — 2 возвращает значение даты/времени, равное двум дням до значения в поле RequiredDate.
|
Выражение |
Описание |
|---|---|
|
PrimeFreight: [Грузовые перевозки] * 1,1 |
Создает поле с именем PrimeFreight, а затем отображает стоимость перевозки плюс 10 процентов в поле. |
|
Сумма заказа: [Количество] * [Цена] |
Создает поле с именем OrderAmount, а затем отображает произведение значений в полях Quantity и UnitPrice. |
|
LeadTime: [RequiredDate] — [ShippedDate] |
Создает поле с именем LeadTime, а затем отображает разницу между значениями в полях RequiredDate и ShippedDate. |
|
Общий запас: [единиц в наличии]+[единиц в заказе] |
Создает поле с именем TotalStock, а затем отображает сумму значений в полях UnitsInStock и UnitsOnOrder. |
|
FreightPercentage: Sum([Freight])/Sum([Subtotal]) *100 |
Создает поле FreightPercentage, а затем отображает процент стоимости перевозки в каждой промежуточной сумме. Чтобы использовать это выражение, вы должны преобразовать свой запрос на выборку в итоговый запрос, потому что вам нужно использовать 9Строка 1973 Total в сетке дизайна, и вы должны установить для ячейки Total для этого поля значение Expression . Дополнительные сведения о создании итогового запроса см. в статье Суммирование данных с помощью запроса. Если для свойства Формат поля установлено значение Процент , не включайте *100. |
Дополнительные сведения об использовании агрегатных функций и суммировании значений в полях и столбцах см. в статьях Суммирование данных с помощью запроса, Подсчет данных с помощью запроса, Отображение итогов столбца в таблице с помощью строки итогов и Отображение итоговые значения столбца в таблице данных.
Верх страницы
Операции с датами
Почти все базы данных хранят и отслеживают дату и время. Вы работаете с датами и временем в Access, устанавливая поля даты и времени в своих таблицах на тип данных Дата/Время. Access может выполнять арифметические вычисления с датами; например, вы можете рассчитать, сколько дней прошло с даты выставления счета, чтобы определить возраст вашей дебиторской задолженности.
|
Выражение |
Описание |
|---|---|
|
LagTime: DateDiff(«d», [OrderDate], [ShippedDate]) |
Создает поле с именем LagTime, а затем использует функцию DateDiff для отображения количества дней между датой заказа и датой отгрузки. |
|
YearHired: DatePart(«yyyy»,[HireDate]) |
Создает поле с именем YearHired, а затем использует функцию DatePart для отображения года найма каждого сотрудника. |
|
Минустридцать: Дата( )- 30 |
Создает поле MinusThirty, а затем использует функцию Date для отображения даты за 30 дней до текущей даты. |
Верх страницы
агрегатные функции SQL
Выражения в следующей таблице используют функции SQL (язык структурированных запросов), которые объединяют или суммируют данные. Вы часто видите, что эти функции (например, Sum, Count и Avg) называются агрегатными функциями.
В дополнение к агрегатным функциям Access также предоставляет «доменные» агрегатные функции, которые можно использовать для выборочного суммирования или подсчета значений. Например, вы можете подсчитать только значения в определенном диапазоне или найти значение в другой таблице. Набор агрегатных функций домена включает функцию DSum, функцию DCount и функцию DAvg.
Для подсчета итогов часто требуется создать итоговый запрос. Например, для суммирования по группам необходимо использовать запрос «Итоги». Чтобы включить итоговый запрос из сетки дизайна запроса, нажмите Итого в меню Просмотр .
|
Выражение |
Описание |
|---|---|
|
Количество строк: количество (*) |
Создает поле с именем RowCount, а затем использует функцию Count для подсчета количества записей в запросе, включая записи с нулевыми (пустыми) полями. |
|
FreightPercentage: Sum([Freight])/Sum([Subtotal]) *100 |
Создает поле FreightPercentage, а затем вычисляет процент стоимости перевозки в каждой промежуточной сумме путем деления суммы значений в поле Freight на сумму значений в поле Subtotal. (В этом примере используется функция Sum.) Это выражение необходимо использовать с итоговым запросом. Если для свойства Формат поля установлено значение Процент , не включайте *100. Дополнительные сведения о создании итогового запроса см. в статье Суммирование данных с помощью запроса. |
|
AverageFreight: DAvg(«[Доставка]», «[Заказы]») |
Создает поле с именем AverageFreight, а затем использует функцию DAvg для расчета средней стоимости перевозки по всем заказам, объединенным в итоговом запросе. |
Верх страницы
Поля с отсутствующими данными
Показанные здесь выражения работают с полями с потенциально отсутствующей информацией, например с полями, содержащими нулевые (неизвестные или неопределенные) значения. Вы часто сталкиваетесь с нулевыми значениями, такими как неизвестная цена нового продукта или значение, которое коллега забыл добавить в заказ. Возможность находить и обрабатывать нулевые значения может быть важной частью операций с базой данных, и выражения в следующей таблице демонстрируют некоторые распространенные способы работы с нулевыми значениями.
|
Выражение |
Описание |
|---|---|
|
CurrentCountryRegion: IIf(IsNull([CountryRegion]), » «, [CountryRegion]) |
Создает поле с именем CurrentCountryRegion, а затем использует функции IIf и IsNull для отображения пустой строки в этом поле, когда поле CountryRegion содержит нулевое значение; в противном случае отображается содержимое поля CountryRegion. |
|
Время выполнения: IIf(IsNull([RequiredDate] — [ShippedDate]), «Проверить отсутствие даты», [RequiredDate] — [ShippedDate]) |
Создает поле с именем LeadTime, а затем использует функции IIf и IsNull для отображения сообщения «Проверить отсутствие даты», если значение поля RequiredDate или ShippedDate равно null; в противном случае отображается разница дат. |
|
SixMonthSales: Nz([Qtr1Sales]) + Nz([Qtr2Sales]) |
Создает поле с именем SixMonthSales, а затем отображает сумму значений в полях Qtr1Sales и Qtr2Sales, сначала используя функцию Nz для преобразования любых пустых значений в ноль. |
Верх страницы
Вычисляемые поля с подзапросами
Вы можете использовать вложенный запрос, также называемый подзапросом, для создания вычисляемого поля. Выражение в следующей таблице является одним из примеров вычисляемого поля, полученного в результате подзапроса.
|
Выражение |
Описание |
|---|---|
|
Cat: (ВЫБЕРИТЕ [CategoryName] FROM [Categories] WHERE [Products].[CategoryID]=[Categories].[CategoryID]) |
Создает поле с именем Cat, а затем отображает CategoryName, если CategoryID из таблицы Categories совпадает с CategoryID из таблицы Products. |
Верх страницы
Совпадение текстовых значений
Примеры выражений в этой таблице демонстрируют критерии, соответствующие целым или частичным текстовым значениям.
|
Поле |
Выражение |
Описание |
|---|---|---|
|
ШипСити |
«Лондон» |
Отображает заказы, отправленные в Лондон. |
|
ШипСити |
«Лондон» или «Хедж-Энд» |
Использует оператор Or для отображения заказов, отправленных в Лондон или Хедж-Энд. |
|
ShipCountryRegion |
В («Канада», «Великобритания») |
Использует оператор In для отображения заказов, отправленных в Канаду или Великобританию. |
|
ShipCountryRegion |
Не «США» |
Использует оператор Not для отображения заказов, отправленных в страны/регионы, отличные от США. |
|
Название продукта |
Не похоже на «С*» |
Использует оператор Not и подстановочный знак * для отображения продуктов, имена которых не начинаются с C. |
|
Название компании |
>=»Н» |
Отображает заказы, отправленные компаниям, названия которых начинаются с букв от N до Z. |
|
Код продукта |
Правильно([Код Продукта], 2)=»99″ |
Использует функцию Right для отображения заказов со значениями ProductCode, заканчивающимися на 99. |
|
Название корабля |
Нравится*» |
Отображает заказы, отправленные клиентам, имена которых начинаются с буквы S. |
Верх страницы
Критерии даты совпадения
Выражения в следующей таблице демонстрируют использование дат и связанных функций в выражениях критериев. Дополнительные сведения о вводе и использовании значений даты см. в статье Формат поля даты и времени.
|
Поле |
Выражение |
Описание |
|---|---|---|
|
Дата отправки |
#2/2/2017# |
Отображает заказы, отправленные 2 февраля 2017 г. |
|
Дата доставки |
Свидание() |
Отображает заказы, отправленные сегодня. |
|
ТребуемаяДата |
Между Date() и DateAdd(«m», 3, Date()) |
Использует оператор Between…And и функции DateAdd и Date для отображения заказов, требуемых между сегодняшней датой и тремя месяцами с сегодняшней даты. |
|
Дата заказа |
< Дата( ) – 30 |
Использует функцию Дата для отображения заказов старше 30 дней. |
|
Дата заказа |
Год([ДатаЗаказа])=2017 |
Использует функцию «Год» для отображения заказов с датами заказа в 2017 году. |
|
Дата заказа |
DatePart(«q», [ДатаЗаказа])=4 |
Использует функцию DatePart для отображения заказов на четвертый календарный квартал. |
|
Дата заказа |
DateSerial(Год ([ДатаЗаказа]), Месяц([ДатаЗаказа])+1, 1)-1 |
Использует функции DateSerial, Year и Month для отображения заказов на последний день каждого месяца. |
|
Дата заказа |
Год([ДатаЗаказа])= Год(Сейчас()) И Месяц([ДатаЗаказа])= Месяц(Сейчас()) |
Использует функции «Год» и «Месяц» и оператор «И» для отображения заказов на текущий год и месяц. |
|
Дата отправки |
Между 05.01.2017# и 10.01.2017# |
Использует оператор Between…And для отображения заказов, отгруженных не ранее 5 января 2017 г. и не позднее 10 января 2017 г. |
|
ТребуемаяДата |
Между Date() и DateAdd(«M», 3, Date()) |
Использует оператор Between. |
|
Дата рождения |
Месяц([ДатаРождения])=Месяц(Дата()) |
Использует функции «Месяц» и «Дата» для отображения сотрудников, у которых в этом месяце дни рождения. |
Верх страницы
Найти недостающие данные
Выражения в следующей таблице работают с полями, в которых потенциально может отсутствовать информация – те, которые могут содержать нулевое значение или строку нулевой длины. Нулевое значение представляет отсутствие информации; он вообще не представляет ноль или какое-либо значение. Access поддерживает эту идею отсутствия информации, потому что эта концепция жизненно важна для целостности базы данных. В реальном мире информация часто отсутствует, пусть даже временно (например, пока еще не определенная цена на новый продукт). Следовательно, база данных, которая моделирует объект реального мира, такой как бизнес, должна иметь возможность записывать информацию как отсутствующую. Вы можете использовать функцию IsNull, чтобы определить, содержит ли поле или элемент управления нулевое значение, и вы можете использовать функцию Nz, чтобы преобразовать нулевое значение в ноль.
|
Поле |
Выражение |
Описание |
|---|---|---|
|
ShipRegion |
Нулевой |
Отображает заказы для клиентов, поле ShipRegion которых пусто (отсутствует). |
|
ShipRegion |
не является нулевым |
Отображает заказы для клиентов, поле ShipRegion которых содержит значение. |
|
Факс |
«» |
Отображает заказы для клиентов, у которых нет факсимильного аппарата, обозначенного строковым значением нулевой длины в поле Факс вместо нулевого (отсутствующего) значения. |
Верх страницы
Совпадение с образцом записи с лайком
Оператор Like обеспечивает большую гибкость, когда вы пытаетесь сопоставить строки, соответствующие шаблону, поскольку вы можете использовать Like с подстановочными знаками и определять шаблоны для сопоставления Access. Например, подстановочный знак * (звездочка) соответствует последовательности символов любого типа и упрощает поиск всех имен, начинающихся с буквы. Например, вы используете выражение Like «S*», чтобы найти все имена, начинающиеся с буквы S. Дополнительные сведения см. в статье Оператор Like.
|
Поле |
Выражение |
Описание |
|---|---|---|
|
Название корабля |
Нравится*» |
Находит все записи в поле ShipName, начинающиеся с буквы S. |
|
Название корабля |
Как «*Импорт» |
Находит все записи в поле ShipName, которые заканчиваются словом «Импорт». |
|
Имя корабля |
Например, «[AD]*» |
Находит все записи в поле ShipName, начинающиеся с букв A, B, C или D. |
|
Название корабля |
Как «*ар*» |
Находит все записи в поле ShipName, содержащие последовательность букв «ar». |
|
Название корабля |
Нравится «Maison Dewe?» |
Находит все записи в поле ShipName, которые включают «Maison» в первой части значения и строку из пяти букв, в которой первые четыре буквы — «Dewe», а последняя буква неизвестна. |
|
Имя корабля |
Не похоже на «А*» |
Находит все записи в поле ShipName, которые не начинаются с буквы A. |
Верх страницы
Сопоставление строк с агрегатами SQL
Вы используете функцию агрегирования SQL или домена, когда вам нужно выборочно суммировать, подсчитывать или усреднять значения. Например, вы можете захотеть подсчитать только те значения, которые попадают в определенный диапазон или оцениваются как «Да». В других случаях может потребоваться найти значение в другой таблице, чтобы отобразить его. Примеры выражений в следующей таблице используют агрегатные функции предметной области для выполнения вычисления набора значений и использования результата в качестве критерия запроса.
|
Поле |
Выражение |
Описание |
|---|---|---|
|
Грузовые перевозки |
> (DStDev(«[Перевозка]», «Заказы») + DAvg(«[Перевозка]», «Заказы»)) |
Использует функции DStDev и DAvg для отображения всех заказов, для которых стоимость перевозки превысила среднее значение плюс стандартное отклонение стоимости перевозки. |
|
Количество |
> DAvg(«[Количество]», «[Детали заказа]») |
Использует функцию DAvg для отображения продуктов, заказанных в количествах, превышающих средний объем заказа. |
Верх страницы
Сопоставление полей с подзапросами
Вы используете подзапрос, также называемый вложенным запросом, для вычисления значения для использования в качестве критерия. Примеры выражений в следующей таблице сопоставляют строки на основе результатов, возвращенных подзапросом.
|
Поле |
Выражение |
Дисплеи |
|---|---|---|
|
Цена Единицы |
(ВЫБЕРИТЕ [UnitPrice] FROM [Products], WHERE [ProductName] = «Анисовый сироп») |
Товары, цена которых равна цене анисового сиропа. |
|
Цена Единицы |
>(ВЫБРАТЬ AVG([Цена за единицу]) ИЗ [Товары]) |
Товары, цена за единицу которых выше средней. |
|
Зарплата |
> ВСЕ (ВЫБЕРИТЕ [Зарплату] ИЗ [Сотрудников], ГДЕ ([Должность] НРАВИТСЯ «*Менеджер*») ИЛИ ([Должность] НРАВИТСЯ «*Вице-президент*»)) |
Заработная плата каждого торгового представителя, чья заработная плата выше, чем у всех сотрудников, имеющих в названии «Менеджер» или «Вице-президент». |
|
Сумма заказа: [Цена] * [Количество] |
> (ВЫБЕРИТЕ AVG([Цена] * [Количество]) ИЗ [Сведения о заказе]) |
Заказы с суммой, превышающей среднюю стоимость заказа. |
Верх страницы
Запросы на обновление
Вы используете запрос на обновление для изменения данных в одном или нескольких существующих полях в базе данных. Например, вы можете заменить значения или удалить их полностью. В этой таблице показаны некоторые способы использования выражений в запросах на обновление. Вы используете эти выражения в Обновление до строки в сетке дизайна запроса для поля, которое вы хотите обновить.
Дополнительные сведения о создании запросов на обновление см. в статье Создание и выполнение запроса на обновление.
|
Поле |
Выражение |
Результат |
|---|---|---|
|
Титул |
«Продавец» |
Изменяет текстовое значение на «Продавец». |
|
Начало проекта |
#8/10/17# |
Изменяет значение даты на 10 августа 17. |
|
Пенсионер |
Да |
Изменяет значение «Нет» в поле «Да/Нет» на «Да». |
|
Номер детали |
«PN» и [Номер детали] |
Добавляет PN в начало каждого указанного номера детали. |
|
Всего по строке |
[Цена] * [Количество] |
Вычисляет произведение цены за единицу и количества. |
|
Грузовые перевозки |
[Перевозка] * 1,5 |
Увеличивает стоимость перевозки на 50 процентов. |
|
Продажи |
DSum(«[Количество] * [Цена за единицу]», «Сведения о заказе», «[ProductID]=» и [ProductID]) |
Если значения ProductID в текущей таблице совпадают со значениями ProductID в таблице сведений о заказе, общие продажи обновляются на основе произведения Quantity и UnitPrice. |
|
Почтовый индекс корабля |
Правильно([ShipPostalCode], 5) |
Усекает крайние левые символы, оставляя пять крайних правых символов. |
|
Цена Единицы |
Nz([Цена за единицу]) |
Изменяет нулевое (неопределенное или неизвестное) значение на ноль (0) в поле UnitPrice. |
Верх страницы
Операторы SQL
Язык структурированных запросов, или SQL, — это язык запросов, который использует Access. Каждый запрос, создаваемый в режиме конструктора запросов, также может быть выражен с помощью SQL. Чтобы просмотреть оператор SQL для любого запроса, щелкните SQL View в меню View . В следующей таблице показаны примеры операторов SQL, в которых используется выражение.
|
Оператор SQL, использующий выражение |
Результат |
|---|---|
|
ВЫБЕРИТЕ [Имя],[Фамилия] ИЗ [Сотрудников], ГДЕ [Фамилия]=»Danseglio»; |
Отображает значения в полях Имя и Фамилия для сотрудников с фамилией Данселио. |
|
ВЫБЕРИТЕ [ProductID],[ProductName] FROM [Products], WHERE [CategoryID]=Forms![New Products]![CategoryID]; |
Отображает значения в полях ProductID и ProductName в таблице Products для записей, в которых значение CategoryID совпадает со значением CategoryID, указанным в открытой форме New Products. |
|
SELECT Avg([ExtendedPrice]) AS [Средняя расширенная цена] FROM [Расширенная информация о заказе] WHERE [ExtendedPrice]>1000; |
Вычисляет среднюю расширенную цену для ордеров, для которых значение в поле ExtendedPrice больше 1000, и отображает ее в поле с именем Средняя расширенная цена. |
|
ВЫБЕРИТЕ [CategoryID], Count([ProductID]) AS [CountOfProductID] FROM [Products] GROUP BY [CategoryID] HAVING Count([ProductID])>10; |
В поле с именем CountOfProductID отображается общее количество продуктов для категорий с более чем 10 продуктами. |
Верх страницы
Табличные выражения
Два наиболее распространенных способа использования выражений в таблицах — присвоение значения по умолчанию и создание правила проверки.
Значения поля по умолчанию
При разработке базы данных может потребоваться назначить значение по умолчанию для поля или элемента управления. Затем Access предоставляет значение по умолчанию при создании новой записи, содержащей поле, или при создании объекта, содержащего элемент управления. Выражения в следующей таблице представляют примеры значений по умолчанию для поля или элемента управления. Если элемент управления привязан к полю в таблице и поле имеет значение по умолчанию, значение по умолчанию элемента управления имеет приоритет.
|
Поле |
Выражение |
Значение поля по умолчанию |
|---|---|---|
|
Количество |
1 |
1 |
|
Район |
«МТ» |
МТ |
|
Регион |
«Нью-Йорк, штат Нью-Йорк» |
New York, NY (Обратите внимание, что вы должны заключить значение в кавычки, если оно содержит знаки препинания. |
|
Факс |
«» |
Строка нулевой длины, указывающая, что по умолчанию это поле должно быть пустым, а не содержать нулевое значение |
|
Дата заказа |
Свидание( ) |
Сегодняшняя дата |
|
Дата выполнения |
Дата() + 60 |
Дата на 60 дней вперед от сегодняшнего дня |
Верх страницы
Правила проверки полей
Вы можете создать правило проверки для поля или элемента управления с помощью выражения. Затем Access применяет правило при вводе данных в поле или элемент управления. Чтобы создать правило проверки, вы изменяете ValidationRule свойство поля или элемента управления. Также следует рассмотреть возможность установки свойства ValidationText , которое содержит текст, отображаемый Access при нарушении правила проверки. Если вы не зададите свойство ValidationText , Access отобразит сообщение об ошибке по умолчанию.
Примеры в следующей таблице демонстрируют выражения правил проверки для свойства ValidationRule и соответствующий текст для ValidationText свойство.
|
Свойство ValidationRule |
Свойство ValidationText |
|---|---|
|
<> 0 |
Введите ненулевое значение. |
|
0 или > 100 |
Значение должно быть либо 0, либо больше 100. |
|
Как «К???» |
Значение должно состоять из четырех символов, начиная с буквы K. |
|
< № 1/1/2017# |
Введите дату до 01.01.2017. |
|
>= 01. |
Дата должна быть в 2017 году. |
Дополнительные сведения о проверке данных см. в статье Создание правила проверки для проверки данных в поле.
Верх страницы
Макровыражения
В некоторых случаях вам может понадобиться выполнить действие или серию действий в макросе, только если выполняется определенное условие. Например, предположим, что вы хотите, чтобы действие выполнялось только тогда, когда значение текстового поля Счетчик равно 10. Вы используете выражение для определения условия в поле 9.1973 Условие столбец макроса:
[Счетчик]=10
Как и в случае свойства ValidationRule , выражение столбца Condition является условным выражением. Он должен разрешаться либо в значение True, либо в значение False. Действие происходит только тогда, когда условие истинно.
Совет Чтобы заставить Access временно игнорировать действие, введите False в качестве условия. Это может быть полезно, когда вы пытаетесь найти проблемы в макросе.
|
Используйте это выражение, чтобы выполнить действие |
Если |
|---|---|
|
[Город]=»Париж» |
Париж — значение города в поле формы, из которой был запущен макрос. |
|
DCount(«[OrderID]», «Заказы») > 35 |
В поле OrderID таблицы Orders содержится более 35 записей. |
|
DCount(«*», «[Детали заказа]», «[OrderID]=» & Формы![Заказы]![OrderID]) > 3 |
В таблице «Сведения о заказе» имеется более трех записей, для которых поле «Идентификатор заказа» в таблице совпадает с полем «Идентификатор заказа» в форме «Заказы». |
|
[Дата отправки] Между 2 февраля 2017 г. и 2 марта 2017 г. |
Значение поля ShippedDate в форме, из которой запускается макрос, не ранее 2 февраля 2017 г. и не позднее 2 марта 2017 г. |
|
Формы![Продукты]![ЕдиницыНа складе] < 5 |
Значение поля UnitsInStock в форме Products меньше 5. |
|
IsNull([Имя]) |
Значение FirstName в форме, из которой запускается макрос, равно null (не имеет значения). Это выражение эквивалентно выражению [FirstName] Is Null. |
|
[CountryRegion]=»UK» И Forms![Общие продажи]![Общие заказы] > 100 |
Значение в поле CountryRegion в форме, из которой запускается макрос, — UK, а значение поля TotalOrds в форме SalesTotals больше 100. |
|
[CountryRegion] In («Франция», «Италия», «Испания») And Len([Почтовый индекс])<>5 |
Значение в поле CountryRegion в форме, из которой запускается макрос, — Франция, Италия или Испания, а почтовый индекс не состоит из 5 символов. |
|
MsgBox(«Подтвердить изменения?»,1)=1 |
Вы нажимаете OK в диалоговом окне, которое отображает функция MsgBox. Если нажать Отмена в диалоговом окне, Access проигнорирует это действие. |
Верх страницы
Части выражения
Алгебраические выражения представляют собой комбинации
переменные
, числа и хотя бы одно арифметическое действие.
Например,
2
Икс
+
4
у
−
9
является алгебраическим выражением.
Срок:
Каждое выражение состоит из терминов.
Терм может быть числом со знаком, переменной или константой, умноженной на переменную или переменные.
Фактор:
Что-то, что умножается на что-то другое. Фактор может быть числом, переменной, термином или более длинным выражением. Например, выражение
7
Икс
(
у
+
3
)
имеет три фактора:
7
,
Икс
, а также
(
у
+
3
)
.
Коэффициент:
Числовой коэффициент выражения умножения, содержащего переменную. Рассмотрим выражение на рисунке выше,
2
Икс
+
4
у
−
9. В первый срок,
2
Икс
, коэффициент
2
: во второй срок,
4
у
, коэффициент
4
.
Постоянный:
Число, которое не может изменить свое значение. В выражении
2
Икс
+
4
у
−
9
, термин
9
является константой.
Нравятся условия:
Термины, содержащие одни и те же переменные, такие как
2
м
,
6
м
или же
3
Икс
у
а также
7
Икс
у
. Если выражение имеет более одного постоянного члена, они также похожи на термы.
|
|
|
|
|
|
|
|
|
|
Пример:
Определите термины, такие как термины, коэффициенты и константы в выражении.
9
м
−
5
н
+
2
+
м
−
7
Во-первых, мы можем переписать вычитания как сложения.
9
м
−
5
н
+
2
+
м
−
7
знак равно
9
м
+
(
−
5
н
)
+
2
+
м
+
(
−
7
)
Итак
условия
находятся
9
м
,
(
−
5
н
)
,
м
,
2
, а также
(
−
7
)
.
Нравятся условия
являются терминами, которые содержат одни и те же переменные.
9
м
а также
9м
являются парой
как термины
. Постоянные условия
2
а также
−
7
также как термины.
Коэффициенты
числовые части термина, содержащего переменную.
Итак, вот
коэффициенты
находятся
9
,
(
−
5
)
, а также
1
. (
1
коэффициент члена
м
.)
постоянный
термины — это термины без переменных, в этом случае
2
а также
−
7
.
Алгебраические выражения должны быть тщательно написаны и интерпретированы. Алгебраическое выражение
5
(
Икс
+
9
)
является
нет
эквивалентно алгебраическому выражению,
5
Икс
+
9.
См. разницу между двумя выражениями в таблице ниже.
|
Словосочетания |
Алгебраическое выражение |
| Пятикратная сумма числа и девяти |
5 |
| Девять более пяти раз число |
5 |
При записи выражений для неизвестных величин часто пользуются стандартными формулами.
No related posts.
ВИДЕО УРОК
Числа точные и приближённые.
В практической
деятельности люди постоянно имеют дело со значениями разных величин: длины,
площади, объема, массы, температуры и так далее.
Числа, встречающиеся
на практике, бывают двух видов. Одни дают истинное значение величины, другие –
только приблизительное. Первые называют точными, вторые – приближенными.
Точное значение
величины удается найти лишь в некоторых случаях.
ПРИМЕР:
Можно точно указать число вагонов железнодорожного
поезда.
Точно подсчитать, сколько учеников есть одновременно в
классе.
ПРИМЕР:
В книге 512 страниц, число 512 – точное.
В шестиугольнике 9 диагоналей, число
9 – точное.
В классе есть 29 учеников, число 29
– точное.
Однако по большей
части приходится иметь дело лишь с приближенными значениями величин.
Чаще всего удобно
пользоваться приближёнными числами вместо точных, тем более, что во многих
случаях точное число вообще найти невозможно. Числа, которые мы называем приближёнными, иначе говоря,
верными только приблизительно, но не совершенно точно, постоянно встречаются
нам в жизни на практике. Приближённые числа могут получаться, прежде всего, при
счёте предметов, если этих предметов слишком много и их почему – либо трудно
или даже нельзя подсчитать точно. Конечно, в результате счёта предметов могут
получаться и точные числа, если предметов не слишком много, если их число не
слишком быстро меняется и если их без затруднений можно подсчитывать.
ПРИМЕР:
Лишь приблизительно оценивают:
– количество зрителей телепередачи,
– количество перелетных птиц,
– количество деревьев в лесу.
ПРИМЕР:
Если же говорят, что расстояние от Москвы до Киева
равно 960 км, то здесь число 960 –
приближённое, так как с одной стороны, наши измерительные инструменты не
абсолютно точны, а с другой стороны, сами города имеют некоторую протяжённость.
Продавец взвесил на автоматических весах 50
г масла. Число 50 –
приближённое, так как весы нечувствительны к увеличению или уменьшению веса
на 0,5
г.
Приближенные
значения получаются в результате измерений.
Можно ли измерять длину рейки точно ? Нет.
Даже если услышите, что длина какой-то рейки равняется, например, 9,42783 м, не верьте этому. Ведь длину такой рейки с точностью до
сотой миллиметра нельзя измерять. Результат каждого измерения – приближенное
значение величины.
Невозможно, точно
измерять длину стержня. Ведь измерение мы проводим с помощью какого-то прибора
(линейки, штангенциркуля, микрометра, оптиметра (оптико-механический
измерительный прибор) и тому подобное), а точность измерения прибором всегда
ограничена. Кроме того, изготовляя прибор в заводских условиях, гарантируют
лишь ту или другую степень точности его изготовления. Наконец, выполняя
измерение, мы можем допускать ошибки, связанные с нашим опытом работы и личными
качествами.
Невозможно точно
измерять площадь земельного участка, температуру воздуха, скорость полета
самолета и так далее.
Приближенные значения получают при округлении истинных
значений величин.
Приближённые и
точные числа записываются при помощи десятичных дробей. Берётся только среднее
значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как
записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых
превосходит абсолютную погрешность числа.
Если же разряд цифры меньше абсолютной погрешности, она
называется сомнительной.
ПРИМЕР:
Для дроби 3,6714 с
погрешностью 0,002 верными
будут цифры 3, 6, 7, а сомнительными 1 и 4.
В записи приближённого числа оставляют только верные цифры. Дробь будет
выглядеть таким образом – 3,67.
ПРИМЕР:
Число 2,19563 в
расчете, который не нуждается высокой точности, можно округлить, заменив его
числом 2,196 или даже числом 2,20,
которые являются приближенными значениями числа
2,19563
с излишком.
Итак, в разных
случаях и в разных обстоятельствах счёт предметов может приводить и к точному и
к приближённому числу.
Границы значения величины.
Всякое измерение
(длины, веса и так далее) выполняется только приблизительно. Иногда, даже в тех
случаях, когда можно установить истинное значение величины, бывает достаточно
знать лишь её приближённое значение. Между истинной величиной предмета и
числом, полученным при измерении (или подсчёте), бывает некоторая, хотя бы и
небольшая разность.
ПРИМЕР:
Рассмотрим процесс определения массы детали с
помощью рычажных весов и набора гирь, наименьшая из которых имеет массу 1 г.

С помощью двух взвешиваний установили, что масса детали
больше 20 г, но меньше
30 г.

Обозначим массу детали в граммах через m,
тогда результат взвешивания можно записать в виде двойного неравенства:
20 < m < 30.
Заменив потом гирю 10 г гирей 5 г, и убедимся, что масса детали больше 25 г,

То есть
25 < m < 30.
Положив на чашу весов с гирьками еще 2 г, заметим, что масса
детали меньше чем 27 г.

25 < m < 27.
Заменив гирю
2 г гирей 1 г, и определим, что
масса детали больше 26 г.

26 < m
< 27.
Поскольку более мелких гирь нет, то процесс определения
массы на этом этапе закончим.
Взвешиваниями мы нашли приближенные значения массы детали
в граммах:
26 г – приближённое значение с
недостачей,
27 г – приближённое значение с излишком.
Другими словами, мы установили границы значения массы в
граммах. Число 26 – нижняя граница, число
27 –
верхняя граница.
Заметим, что когда бы наименьшая гиря была бы равна 2
г, то границами значения массы детали в граммах были бы числа 25 г и 27 г, то есть масса была бы определена менее точно.
Зная пределы
значения некоторой величины, можно оценить значение другой величины, которая
зависит от первой.
ПРИМЕР:
Пусть известны приближенные значения (в см) с недостачей и с излишком длины а стороны равностороннего треугольника:
5,4 ≤ а ≤ 5,5.
Надо найти пределы периметра Р.
РЕШЕНИЕ:
Периметр равностороннего треугольника вычисляется по
формуле:
Р = 3а.
Из условия, что а ≥ 5,4 выплывает, что 3а
≥ 16,2.
Из условия, что а ≤ 5,5 выплывает, что 3а
≤ 16,5.
Числа 16,2 и 16,5
– приближенные значения периметра (в см) с недостачей и излишком:
16,2 ≤ Р ≤ 16,5.
Записать решение можно и так:
5,4 ≤ а ≤ 5,5,
5,4 ∙ 3 ≤ 3а ≤ 5,5 ∙ 3,
то есть
16,2 ≤ Р ≤ 16,5.
ПРИМЕР:
Пусть известны границы какого-то числа х:
3 < х < 6.
Надо оценить значение выражения 1/х.
РЕШЕНИЕ:
Из условия задачи определяем, что х –
число положительное.
Поскольку х ˃ 3, то
1/х < 1/3.
Поскольку х < 6, то
1/х ˃ 1/6.
Выходит, что
1/6 < 1/х < 1/3.
Заменим границы значения выражения 1/х десятичными дробями. Число 1/6 можно заменить лишь меньшим числом (любым приближением
с недостачей), а число 1/3 –
лишь больше (приближением с излишком). Поскольку
1/6 =
0,166…
1/3 =
0,333… ,
то границами значения выражения 1/х могут быть десятичные дроби 0,1 и 0,4.
0,1 < 1/х < 0,4.
Заменив нижнюю границу
числом 0,1, а верхнюю – числом 0,4, мы
расширили промежуток, которому принадлежат значения выражения 1/х.

Если бы мы сделали иначе, округлив бесконечные десятичные
дроби
0,166… и 0,333…
по известным правилам округления, то получили бы, что
0,2 < 1/х < 0,3.
Но тогда неизвестное нам точное значение выражения 1/х могло бы очутиться вне полученных границах.
Способ записи приближённых чисел.
Приближённые
значения обычно записывают так, чтобы по записи можно было судить о точности
приближения.
ПРИМЕР:
На рулоне обоев написано, что его длина равна
18 ±
0,3 м.
Эта запись означает, что длина рулона равна 18
м с точностью до 0,3
м, то есть точное значение длины может отличаться от
приближённого значения, равного 18 м, не более чем на
0,3 м.
Другими словами длина рулона должна находиться между
18
– 0,3 = 17,7 м и
18
+ 0,3 = 18,3 м.
ПРИМЕР:
Если измеряя длину
х
некоторой рейки, выявили, что она больше чем 6,427
м и меньше чем 6,429
м, то записывают:
х = 6,428 ± 0,001 м.
Говорят, что значение длины рейки найдено с точностью
до
0,001 м (одного миллиметра).
ПРИМЕР:
При приближённых вычислениях отличают запись 2,4 от 2,40, запись 0,02 от 0,0200 и так далее.
Запись 2,4 означает,
что верны только цифры целых и десятых, истинное же значение числа может быть,
например, 2,43 или 2,38 (при отбрасывании цифры 8 происходит округление в сторону увеличения
предшествующей цифры).
Запись 2,40 означает,
что верны и сотые доли, истинное число может быть 2,403 или 2,398, но не 2,421 и
не 2,382.
То же отличие производится и для целых чисел. Запись 382 означает, что все цифры верны, если же за
последнюю цифру ручаться нельзя, то число округляется, но записывается не в
виде 380,
а в виде 38
∙ 10. Запись же 380 означает, что
последняя цифра (0) верна.
Если в числе 4720 верны лишь первые
две цифры, его нужно записать в виде 47 ∙ 102,
или это число можно также записать в виде
4,7 ∙
103 и так далее.
Значащими
цифрами называются все верные цифры числа, кроме нулей, стоящих впереди числа.
ПРИМЕР:
В числе
0,00385 три значащие цифры.
В числе
0,03085 четыре значащие цифры,
В числе
2500 – четыре,
В числе
2,5 ∙
103 – две.
Число
значащих цифр некоторого числа называется его значностью.
Через то, что мы не
можем выполнить бесконечного процесса деления, то мы должны прекратить деление
на каком-либо десятичном знаке, то есть выполнить приближенное деление. Мы
можем, например, прекратить деление на первом десятичном знаке, то есть
ограничиться десятыми частями; в случае потребности мы можем остановиться на
втором десятичном знаке, ограничиться сотыми частями, и так далее. В таких
случаях говорят о приближенном превращении обычных дробей в десятичные. В этих
случаях говорят, что мы округляем бесконечную десятичную дробь. Округление
делается с той точностью, которая нужна для решения данной задачи.
Вычисления с приближенными
данными.
Вычисления с
приближенными данными постоянно используется в практических задачах, при этом
результат вычислений обычно округляют. Результат действий с приближёнными
числами есть тоже приближённое число. Выполняя некоторые действия над точными числами,
можно так же получить приближённые числа.
При сложении и вычитании приближённых чисел в
результате следует сохранять столько десятичных знаков, сколько их в
приближённом данном с наименьшим числом десятичных знаков, то есть оставляют в
результате столько знаков после запятой, сколько их содержится в менее точном
данном числе.
ПРИМЕР:
Пусть
х ≈ 17,2 и у
≈ 8,407.
Найдём приближённое значение суммы х
и у.
РЕШЕНИЕ:
Имеем:
х +
у ≈ 25,607.
Из данных приближённых значений 17,2
и 8,407
менее точным является первое. Округлив результат по первому данному, то
есть до десятых, получим:
х + у ≈ 25,6.
ПРИМЕР:
Пусть
х ≈ 6,784 и
у ≈ 4,91.
Найдём приближённое значение разности х
и у.
РЕШЕНИЕ:
Имеем:
х –
у ≈ 1,874.
Из данных приближённых значений 6,784
и 4,91
менее точным является второе. Округлив результат по второму данному, то есть.
до сотых, получим:
х –
у ≈ 1,87.
ПРИМЕР:
Найдите разность приближенных значений
х = 1,52
± 0,01 и
у = 0,27
± 0,02.
РЕШЕНИЕ:
Данным приближенным значением отвечают двойные
неравенства
1,51 ≤ х ≤ 1,53 и
0,25 ≤ у ≤ 0,29.
Умножим все части последнего двойного неравенства на –1, получим
–0,29 ≤ –у ≤ –0,25.
Прибавив это двойное неравенство к первому, получим
1,22 ≤ х – у ≤ 1,28, или
х – у = 1,25
± 0,03.
Несколько иначе
поступают при умножении и делении приближённых значений. Здесь округление
производится с учётом относительной точности данных. В
этом случае находят произведение или частное приближённых значений, и результат
округляют по менее точному данному, имея ввиду относительную точность. Для
этого исходные данные и полученный результат записывают в стандартном виде
а × 10n,
и множитель а результата округляют, оставляя в нём столько
знаков после запятой, сколько их имеет соответствующий множитель в менее точном
данном.
ПРИМЕР:
Пусть
х ≈ 0,86 и
у ≈ 27,1.
Найдём приближённое значение произведения х и у.
РЕШЕНИЕ:
Перемножив 0,86 и 27,1, получим:
ху ≈
23,306.
Запишем данные числа и результат в стандартном виде:
0,86 = 8,6 × 10-1;
27,1 = 2,71 × 101;
23,306 = 2,3306 × 101.
В множителе 8,6 одна цифра после запятой, а в множителе 2,71
две цифры после запятой. Округлим число 2,2306 по первому данному, то есть до десятых.
Получим:
ху ≈ 2,3 × 101 = 23.
ПРИМЕР:
Пусть
х ≈ 60,2 и
у ≈ 80,1.
Найдём приближённое значение произведения х и у.
РЕШЕНИЕ:
Известно, что все выписанные цифры верны, так что
истинные величины могут отличаться от приближённых лишь сотыми, тысячными и так
далее долями.
В произведении получаем
4822,02. Здесь
могут быть неверными не только цифры сотых и десятых, но и цифры единиц.
Пусть, например, сомножители получены округлением точных
чисел 60,23 и 80,14.
Тогда точное произведение будет 4826,8322, так что цифра единиц в приближённом произведении (2)
отличается от точной цифры (6) на 4 единицы.
ПРИМЕР:
Пусть
х ≈ 563,2 и
у ≈ 32.
Найдём приближённое значение частного х и у.
РЕШЕНИЕ:
Разделив 563,2 на 32, получим:
х :
у ≈ 17,6.
Запишем данные числа и результат в стандартном виде:
563,2 = 5,632 × 102;
32 = 3,2 × 10;
17,6 = 1,76 × 10.
Из этой записи видно, что число 1,76
следует округлить по второму данному, то есть до десятых. Получим:
х :
у ≈ 1,8 × 10
≈ 18.
При умножении и делении приближённых чисел нужно в
результатах сохранять столько значащих цифр, сколько их было в приближённом
данном с наименьшим числом значащих цифр.
Таким образом, при
сложении, вычитании, умножении и делении приближённых значений результат
округляется по менее точному данному. При этом при сложении и вычитании данные
числа записываются в десятичных дробях и менее точное данное определяется по
абсолютной точности, а при умножении и делении данные числа записываются в
стандартном виде и менее точное данное определяется по относительной точности.
Теория приближённых
вычислений позволяет:
– зная степень точности данных, оценить степень
точности результатов ещё до выполнения действий;
– брать данные с надлежащей степенью точности,
достаточной для обеспечения требуемой точности результата, но не слишком
большой, чтобы избавить вычислителя от бесполезных расчётов;
– рационализировать сам процесс вычисления,
освободив его от тех выкладок, которые не окажут влияния на точные цифры
результата.

