Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.
На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.
Содержание
- 1 Общие понятия о системах координат в геодезии
- 2 Исходные данные для расчетов
- 3 Уравнивание измерений
- 4 Вычисление дирекционных углов вершин
- 5 Решение прямой и обратной геодезической задачи
- 5.1 Создавайте будущее вместе с нами
- 6 Приращение координат и их увязка
- 7 Как вычислить координаты точек хода
- 8 Нанесение точек на план и его оформление
Общие понятия о системах координат в геодезии
Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.
Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:
- Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
- Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.
Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.
Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.
Исходные данные для расчетов
Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.
По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:
– горизонтальные углы пунктов;
– измеренное расстояние между ними;
– координаты пункта ГГС или опорной сети;
– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.
Уравнивание измерений
Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:
(f_{beta}=sum beta _{изм}-sum beta_{теор})
где:
(sum beta _{изм}=beta _{1}+beta _{2}+…beta _{n}) – сумма углов пунктов;
(sum beta _{теор}) – теоретическая сумма, определяемая выражением:
(sum beta _{теор}=180^{circ}cdot (n-2))
(n) – количество углов.
Вычисленная невязка допустима, если соответствует требованию:
(beta _{испр}=pm 1,5sqrt{n})
Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:
(beta _{испр}=beta _{изм}+delta _{beta })
(delta _{beta }) – поправка.

Правильность уравнивания подтверждается следующим условием:
(sum beta _{теор}=beta _{испр})
Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:
для левых углов:
(sum beta _{теор}=alpha _{кон}-alpha _{нач}+ncdot 180^{circ})
правых:
(sum beta _{теор}=alpha _{нач}-alpha _{кон}+ncdot 180^{circ})
Для упрощения дальнейших вычислений поправки могут быть распределены с целью округления десятых долей минут в углах до целых минут.
Вычисление дирекционных углов вершин
В геодезии за дирекционный угол ((alpha )) принимают угол, который начинают отсчитывать от северного направления осевого меридиана и до заданной стороны. Он измеряется от 0 до 360°. Вычислить его значение для правой стороны хода можно по формуле ниже:
(alpha _{n}=alpha _{n-1}+eta )
(eta=180^{circ} -beta _{пр.испр})
(a _{n}=alpha _{n-1}+180^{circ}-beta _{пр.испр})
Для левой стороны это выражение будет иметь такой вид:
(alpha _{n}=alpha _{n-1}+eta )
(eta=beta _{лев.исп.}-180^{circ} )
(a _{n}=alpha _{n-1}-180^{circ}+beta _{лев.исп.})
где:
(alpha _{n-1}) – дирекционный угол предыдущей стороны, а (n) – последующей;
(beta _{пр.исп.}) – значение правого исправленного угла между сторонами отрезка, а (beta _{лев.исп.})– левой стороны.

Вычисления выполнены верно при равенстве заданного α и начальной стороны теодолитного хода. Если дирекционный угол больше 360° или имеет отрицательное значение, то это говорит об ошибке в расчетах.
После дирекционных углов необходимо найти румбы – острые углы, отсчитываемые от 0 до 90°. Они берут свое начало от ближайшего окончания осевого меридиана до ориентирной линии.
| Четверть румба | Название четверти | Пределы изменения α | Формула румба | Знаки приращения | |
| ΔХ | ΔУ | ||||
| I | С.В. (северо-восток) | 0° – 90° | r = α | + | + |
| II | Ю.В. (юго-восток) | 90°-180° | r = 180° – α | – | + |
| III | Ю.З. (юго-запад) | 180°-270° | r = α – 180° | – | – |
| IV | С.З. (северо-запад) | 270°-360° | r = 360° – °α | + | – |
Таблица 1. Связь дирекционного угла и румба
Вычисление румбов и их знаков приращений зависит от четверти геодезических прямоугольных координат, в которой находится линия ориентирования.
Решение прямой и обратной геодезической задачи
Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
где:
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
(d)–расстояния между соседними пунктами.
(alpha ) – значение дирекционного угла.
Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:
(X_{2}=X_{1}+Delta X)
(Y_{2}=Y_{1}+Delta Y)
(X_{2}=X_{1}+d_{1-2}cdot cosalpha _{1-2})
(Y_{2}=Y_{1}+d_{1-2}cdot sinalpha _{1-2})

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:
(Delta X=X_{2}-X_{1})
(Delta Y=Y_{2}-Y_{1})
определяется румб линии (r_{1-2}):
(tgr=frac{Delta Y}{Delta X})
из этого выходит, что:
(r=arctgfrac|{Delta Y}{Delta X}|)
По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:
(d=frac{Delta X}{cosalpha })
(d=frac{Delta Y}{sinalpha })
(d=sqrt{Delta X^2+Delta Y^2})
Приращение координат и их увязка
Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор};sum Delta X_{теор}=0)
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор};sum Delta Y_{теор}=0)
(sum Delta X_{выч},sum Delta Y_{выч}) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;
(sum Delta X_{теор},sum Delta Y_{теор}) – теоретические суммы приращений.
Если невязки не находятся в допуске, необходимы повторные расчеты, чтобы определить ошибку и устранить ее. В противном случае проводятся повторные измерения на участке.

Вследствие влияния погрешностей на ход, он будет разомкнут на величину , которая представляет собой абсолютную невязку в его периметре. По этому причине проверяется соответствие условию допустимости его невязок.
- Абсолютное значение:
(f_{p}=sqrt{f_{x}^2+f_{y}^2})
- Относительное
(f_{отн}=frac{f_{абс}}{P})
P – периметр хода, полученный суммированием всех его сторон.
Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению (|f_{отн}|leq |f_{доп}|) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:
(delta _{x_{i}}=-frac{f_{x}d_{i}}{P});(delta _Delta {y_{i}}=-frac{f_{y}d_{i}}{P})
(delta _{x_{i}},delta _{y_{i}})– значения поправок в приращениях.
Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.
Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор}; sum Delta X_{теор}=x_{B}-x_{A})
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор}; sum Delta Y_{теор}=y_{B}-y_{A})
Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.
Как вычислить координаты точек хода
Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.

Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:
(X_{n}=X_{n-1}+Delta X _{n-1(испр)})
(Y_{n}=Y_{n-1}+Delta Y _{n-1(испр)})
(X_{n-1},Y_{n-1}) – координатные значения предыдущего пункта
(Delta X_{теор}=x_{B}-x_{A},Delta Y_{теор}=y_{B}-y_{A}) – исправленные приращения.
В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.
Нанесение точек на план и его оформление
После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:
- Создание координатной сетки. Ход необходимо равномерно отобразить на плане, поэтому сначала определяют середину листа. Через весь лист проводят два диагональных отрезка, от которых и будет строиться сетка, состоящая из отрезков по 10 см. Допускается погрешность не более 0,2 мм. Определить их количество можно по формуле:
(N_{X}=(x_{max}-x_{min})/200)
(N_{Y}=(y_{max}-y_{min})/200)
(x_{max},y_{max}) – наибольшие значения координат, увеличенные до большего значения, которое кратное 200.
(x_{min},y_{min}) – наименьшее значение, но уменьшенное и кратное 200.
200 – длина стороны квадрата в метрах , которая в плане равна 10 см.

- Обозначение точек на плане. Лучше всего подходят для нанесения координат пунктов на план циркуль и масштабная линейка. Соседние вершины должны иметь такое же расстояние и дирекционный угол, как записано в ведомости.
- Нанесение ситуации на план. Участки снимаемой местности в процессе полевых работ отображают на специальном схематическом бланке – абрисе. В дальнейшем их используют для переноса контуров, линий и вершин точек. Ситуация изображается на планах и картах специальными обозначениями – условными знаками.
- Оформление плана в соответствии с требованиями. Все топографические материалы должны строго соответствовать нормативным документам. В частности, нужно выдерживать заданные очертания и их размеры. Должны присутствовать пояснительные надписи, легенда, а также указан масштаб.
Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.
Теодолитный ход – это геодезическое построение в виде ломаной линии, вершины которой закрепляются на местности, и на них измеряются горизонтальные углы βi между сторонами хода и длины сторон Si. Закрепленные на местности точки называют точками теодолитного хода.
Построение теодолитного хода состоит из двух этапов. Это:
1. Построение ломаной линии на местности и осуществление полевых работ;
2. Математическое уравнивание хода и выполнение камеральной обработки полученных результатов.
Оба этапа выполняются строго по установленному регламенту с соблюдением норм и правил. Точность построения и обработки результатов обеспечивает правильность работы и последующую безопасность строительства или осуществления любой другой деятельности на местности. Теодолитный ход относиться к геодезическим работам цены на которые на сегодняшний день очень вариативные.
Основные виды теодолитного хода.
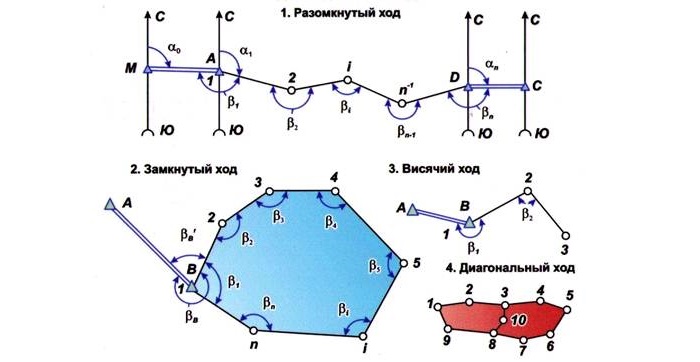
Теодолитный ход – это разомкнутая или замкнутая ломаная линия. В зависимости от формы построения, различают несколько видов ходов:
Разомкнутый теодолитный ход, опирающийся на два пункта с известными координатами и два дирекционных угла. Разомкнутый ход можно охарактеризовать как простую линию. Проект трассы или любого другого продолжительного участка невозможен без разомкнутой линии. Опора у нее на известные точки. В отличие от замкнутого, начало и конец располагаются в разных точках.
Разомкнутый теодолитный ход, опирающийся на один исходный пункт и один дирекционный угол – такой ход еще называют висячим. Висячий ход используют редко, потому что для его вычисления потребуется специальная формула. Суть его такова, что он имеет только начало в определенной точке координат. Конец нужно вычислять.
Замкнутый ход по своей сути является многоугольной фигурой и опирается только на один базовый пункт с установленными координатами и дирекционным углом. Вершинами стороны выступают точки, закрепленными на местности, а отрезками – расстояние между ними. Его чаще всего создают для съемки стройплощадок, жилых зданий, промышленных сооружений или земельных участков.
Диагональный (прокладывают внутри других ходов). Если необходимо заснять ровный участок, вроде строительной площадки, лучшим выбором будет полигон. На объектах вытянутого типа, вроде автодорог, принято использовать разомкнутый ход, а висячий – для съемки закрытой местности, вроде глухих улиц
Порядок выполнения работ
Как и другие геодезические мероприятия, эта процедура проводится с предварительной подготовкой для получения точных метрических данных. Немаловажную роль играет также их математическая обработка. Сами работы выполняются по принципу от общего к частному и состоят из следующих этапов:
1. Рекогносцировка местности. Оценка снимаемой территории, изучение ее особенностей. На этом этапе определяется местоположение снимаемых точек.
2. Полевая съемка. Работы непосредственно уже на местности. Выполнение линейных и угловых измерений, составление абрисов, предварительные расчеты и внесение изменений при необходимости.
3. Камеральная обработка. Завершающий этап работ, который заключается в вычислении координат замкнутого теодолитного хода и последующего составления плана и технического отсчета.
Рекогносцировка и полевые измерения выполняются непосредственно на объекте и являются наиболее трудоемкими и затратными мероприятиями. Тем не менее, от качества их проведения зависит дальнейший результат.
Обработка данных проводится уже в помещении. Сегодня она осуществляется при помощи специального программного обеспечения, хотя и ручные расчеты все также остаются актуальными и могут быть использованы геодезистом в целях проверки.
Обработка данных
Обработка результатов измерений замкнутого теодолитного хода позволит оценить качество проделанной работы и внести исправления в полученные геометрические величины. Чтобы убедится в том, что угловые и линейные измерения находятся в допуске, еще во время полевых работ выполняют первичные расчеты.
Для вычисления значений координат точек замкнутого хода используют такие данные: – координаты исходного пункта;
– исходный дирекционный угол;
– горизонтальные углы;
– длины сторон.
Уравнивание
При начале расчетов определяют теоретическую сумму углов , а потом увязывают их, распределяя между ними угловую невязку.
∑βтеор=180∘⋅(n−2)
n- количество точек полигона
fβ=∑βизм−180∘⋅(n−2)
∑βизм – значение измеренных угловых величин;
Для получения fβ, необходимо рассчитать разность между βизм, в которой присутствуют погрешности, и ∑βтеор.
В уравнивании fβ выступает как показатель точности проведенных измерительных работ, а ее значение не должно быть выше предельной величины, определяемой из следующей формулы:
fβ1=1,5tn−−√
t-точность измерительного устройства,
n – количество углов.
Уравнивание заканчивается равномерным распределением полученной невязки между угловыми величинами.
Определение дирекционных углов
При известном значении дирекционного угла (α) одной стороны и горизонтального (β) можно определить значение следующей стороны:
αn+1=αn+η
η=180∘−βпр
βпр – значение правого по ходу угла, из чего следует:
αn+1=αn+180∘−βпр
Для левого (βлев) эти знаки будут противоположными:
αn+1=αn−180∘+βлев
Поскольку значение дирекционного угла не может быть больше, чем 360∘, то из него, соответственно, отнимают 360∘. В случае с отрицательным углом, необходимо к предыдущему α добавить 180∘ и отнять значение βиспр.
Вычисление румбов
У румбов и дирекционных углов существует взаимосвязь, а определяют их по четвертям, которые носят название четырех сторон света. Как видно из табл.1. расчёты проводят согласно установленной схеме.
Таблица 1. Расчеты румба в зависимости от пределов дирекционного угла.
Приращения координат
Для приращений координат в замкнутом ходе применяют формулы, использующиеся при решении прямой геодезической задачи. Ее суть состоит в том, что по известным значениям координат исходного пункта, дирекционного угла и горизонтального приложения можно определить координаты следующего. Исходя из этого, формула приращения значений будет иметь следующий вид:
ΔX=d⋅cosα
ΔY=d⋅sinα
d-горизонтальное проложение;
α-горизонтальный угол.
Для полигона, который имеет вид замкнутой геометрической фигуры, теоретическая сумма приращений будет равняться нулю для обеих координатных осей:
∑ΔXтеор=0
∑ΔYтеор=0
Линейная невязка и невязка приращения значений координат
Несмотря на вышесказанное, случайные погрешности не позволяют алгебраическим суммам выйти в ноль, поэтому они будут равняться другим невязкам приращений координат:
fx∑ni=1ΔX1
fy∑ni=1ΔY1
Переменные fx и fy – проекции линейной невязки fp на координатной оси, которую можно рассчитать по формуле:
fp=f2x+f2y−−−−−−√
При этом fp, не должно быть боле, чем 1/2000 от доли периметра полигона, а распределения fx и fy проводится следующим образом:
δXi=−fxPdi
δYi=−fyPdi
В этих формулах δXi и δYi – поправки приращения координат.
і- номера точек;
После приращений и внесения поправок в данные измерений, проводят расчет их исправленных значений.
Вычисление координат
Когда будут произведены увязки приращений точек полигона, следует определение координат, которое осуществляют с использованием следующих формул:
Xпос=Xпр+ΔXисп
Yпос=Yпр+ΔYисп
Значения Xпос Yпос – координаты последующих пунктов, Xпр и Yпр – предыдущих.
ΔXисп и ΔYисп – исправленные приращения между этими двумя значениями.
Если координаты первой и последней точки совпадают, то обработку можно считать завершённой.
На основе полученных координат и составленных во время полевых измерений абрисов в дальнейшем составляется план теодолитного хода.
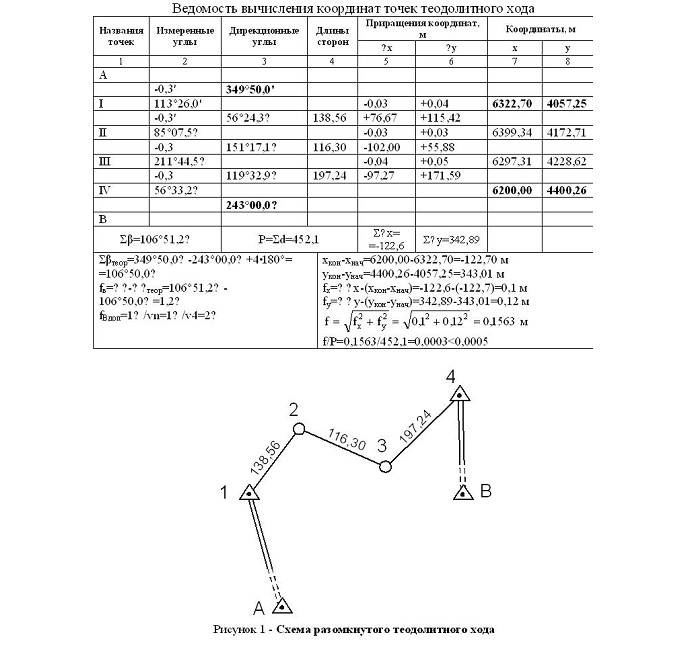
Исходными данными для выполнения работы являются :
измеренные, правые по ходу, горизонтальные углы (графа 2.табл. № 1,приложение 2);
горизонтальные проложения сторон (графа 2.табл. № 1, приложение 2) – эти данные для всех вариантов одинаковы.
Значения координат «х» и «у» первой вершины и дирекционного угла стороны 1-2 индивидуальны и, в зависимости от варианта, берутся по таблице № 1 приложения 1; заносятся в табл. № 1 в графы : 4, 12, 13, в строчки, отмеченные звездочками.
1.2 Вычисление координат вершин замкнутого теодолитного хода
Уравнивание измеренных углов
Измерения горизонтальных углов сопровождаются неизбежными ошибками (невязками).
Угловая невязка вычисляется по формуле:
|
fβ = Σ βизм – Σ β теор |
(1), |
Σ β изм = β1 + β 2+ … + βn – сумма измеренных горизонтальных углов,
Σ β теор – теоретическая сумма внутренних углов замкнутого
|
теодолитного хода, определяется по формуле: |
|
|
Σ β теор = 180˚ (n – 2) |
(2) |
|
n – количество измеренных углов. |
|
|
Полученную невязку сравнивают с допустимой : |
|
|
f β доп = ± 1,5´ √ n. |
(3) |
Если полученная невязка не превышает допустимую, то ее разбрасывают с обратным знаком на все измеренные углы, не дробя при этом менее чем на 0,1‘.
Вписывают полученные поправки (δ β ) над значениями углов (графа 2 таблицы 2). С учетом поправок и их знака вычисляют исправленные углы:
|
βиспр= βизм + δβ. |
( 4) |
||
|
Контролем правильного |
уравнивания |
измеренных |
|
|
горизонтальных |
углов служит равенство суммы исправленных |
||
|
горизонтальных |
углов теоретической сумме. |
5
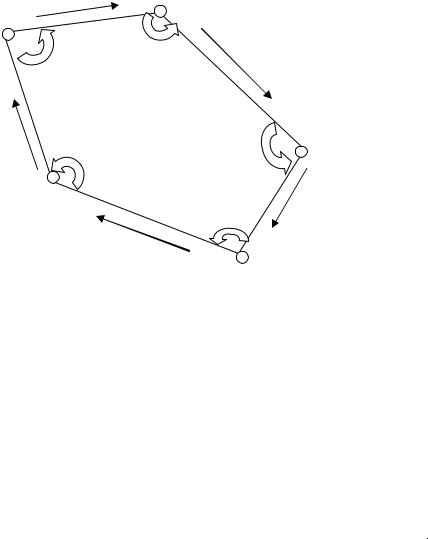
Пример: для построения плана был проложен замкнутый теодолитный ход в виде пятиугольника (рис. 1), в котором были измерены правые по ходу горизонтальные углы. Результаты измерений приведены в табл. 1.
Б
А
В
Д
Г
Рис. 1. Замкнутый теодолитный ход Точки А, Б, В, Г, Д – станции замкнутого теодолитного хода и
вершины горизонтальных правых по ходу углов. Стрелками показано направление хода.
Таблица 1. Результаты измерения и исправления горизонтальных углов
|
Номер вершины |
Горизонтальные углы, |
|
|
теодолитного хода |
измеренные |
исправленные |
|
А |
+ 0,3′ |
|
|
76° 11,3′ |
76° 11,6′ |
|
|
Б |
+ 0,4′ |
|
|
113° 49,1′ |
113° 49,5′ |
|
|
В |
+ 0,3′ |
|
|
101° 05,2′ |
101° 05,5′ |
|
|
Г |
+ 0,3′ |
|
|
98° 17,4′ |
98° 17,7′ |
|
|
Д |
+ 0,4′ |
|
|
150° 35,3′ |
150° 35,7′ |
|
|
Сумма углов |
539° 58.3′ |
540° |
Теоретическую сумму внутренних углов пятиугольника (которым является наш замкнутый теодолитный ход) вычисляем согласно формулы 2: 180°(5 – 2) = 540°.
Определяем угловую невязку: 539° 58.3′ – 540° = – 1,7′.
6
Вычисляем допустимую невязку: ± 1,5′ 5 = ± 3,35′
Т. к. полученная невязка меньше допустимой по абсолютной величине, распределяем ее на все измеренные углы с обратным знаком, т. е. с плюсом; причем к большим углам прибавим большие поправки.
Проверяем сумму исправленных углов, она равна 540°.
Вычисление дирекционных углов сторон теодолитного хода
Дирекционный угол (α ) – это угол, отсчитываемый от северного направления осевого меридиана до рассматриваемой стороны по ходу часовой стрелки. Он изменяется от 0˚ до 360˚.
Вычисление дирекционных углов сторон теодолитного хода выполняют по формуле:
|
αn = α n-1 + 180˚ – β прав.испр. |
(5), |
где α n-1 – дирекционный угол предыдущей стороны, α n– дирекционный угол последующей стороны,
β прав.испр. – правый исправленный угол между рассматриваемыми сторонами.
Вычисление дирекционных углов ведется в столбик, при этом следует помнить, что в одном градусе – 60 минут.
Контролем верного вычисления дирекционных углов служит равенство заданного дирекционного угла и вычисленного начальной стороны теодолитного хода.
Осевые меридианы
В
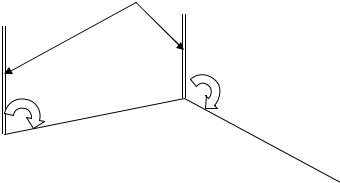
Рис. 2. Схема дирекционных углов сторон АБ и БВ
7
Пример: дирекционный угол стороны А-Б равен : 79° 58′.
Дирекционный угол стороны Б-В : 79° 58′ + 180° – 113° 49,5′ = 146° 08,5′ Дирекционный угол стороны В-Г: 146° 08,5′ + 180° – 101° 05,5′ = 225° 03′ Дирекционный угол стороны Г-Д: 225° 03′ + 180° – 98° 17,7′ = 306° 45,3′ Дирекционный угол стороны Д-А: 306° 45,3′ + 180° – 150° 35,7′ = 336° 9,6′ Дирекционный угол стороны А-Б: 336° 09,6′ + 180° – 76° 11,6′ = 439° 58′.
Если значения вычисленных дирекционных углов больше 360°, перед занесением результатов в таблицу, вычитаем 360°.
Например: дирекционный угол стороны А-Б: 439° 58′ – 360° = 79° 58′.
Определение румбов и знаков приращений координат
Румб – это острый угол, отсчитываемый от ближайшего окончания осевого меридиана до ориентируемой линии.
Вычисление румбов осуществляется в зависимости от того, в какой четверти геодезических прямоугольных координат находится ориентируемая линия.
Таблица 2. Значения румбов
|
Четверть |
Пределы |
Название |
Формула |
Знаки приращений |
|
|
изменения |
румба |
расчета румба |
координат |
||
|
дирекционных |
ΔX |
ΔY |
|||
|
углов |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0° – 90˚ |
С.В. |
r = α |
+ |
+ |
|
11 |
90˚ – 180˚ |
Ю.В. |
r= 180˚ -α |
– |
+ |
|
111 |
180˚ – 270˚ |
Ю.З. |
r= α – 180˚ |
– |
– |
|
1V |
270˚ – 360˚ |
С.З. |
r= 360˚ – α |
+ |
– |
Знаки приращений координат определяются также по положению рассматриваемой стороны, т.е. в зависимости от того, в какой четверти геодезических прямоугольных координат находится конкретная сторона теодолитного хода.
Пользуясь таблицей 2 или рисунком 3, определить значения румбов, их название относительно сторон света, знаки приращений координат; результаты занести в соответствующие графы таблицы 1 Приложения 2.
Например: Дирекционный угол стороны Б-В : 146° 08,5′, следовательно она находится во второй четверти.
|
Название румба |
Ю.В. |
|
|
Значение |
180˚ – 146° 08,5′ = 33° 51,5′. |
|
|
Знаки приращений координат: |
||
|
для |
X «минус» |
|
|
для |
Y «плюс». |
|
|
8 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.
На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.
Общие понятия о системах координат в геодезии
Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.
Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:
- Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
- Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.
Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.
Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.
Расчёт на онлайн-калькуляторе
Существуют сервисы, позволяющие решать геометрические задачи координатным методом без утомительных самостоятельных вычислений. Сам расчёт обычно занимает не более трёх секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться услугами таких сайтов сможет любой пользователь интернета, даже не имеющий представления о геометрии. Всё, что от него требуется — это подключение к сети и веб-обозреватель с поддержкой Flash-технологии.
Пользователю необходимо ввести условие задания, при этом система будет сама направлять действия и в случае каких-либо ошибок укажет на них, а затем нажать кнопку «Рассчитать». Привлекательность таких сайтов состоит ещё и в том, что ответ будет содержать объяснения с необходимыми формулами и рисунками.
Исходные данные для расчетов
Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.
По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:
– горизонтальные углы пунктов;
– измеренное расстояние между ними;
– координаты пункта ГГС или опорной сети;
– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.
Уравнивание измерений
Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:
(f_{beta}=sum beta _{изм}-sum beta_{теор})
где:
(sum beta _{изм}=beta _{1}+beta _{2}+…beta _{n}) – сумма углов пунктов;
(sum beta _{теор}) – теоретическая сумма, определяемая выражением:
(sum beta _{теор}=180^{circ}cdot (n-2))
(n) – количество углов.
Вычисленная невязка допустима, если соответствует требованию:
(beta _{испр}=pm 1,5sqrt{n})
Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:
(beta _{испр}=beta _{изм}+delta _{beta })
(delta _{beta }) – поправка.

Правильность уравнивания подтверждается следующим условием:
(sum beta _{теор}=beta _{испр})
Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:
Решение прямой и обратной геодезической задачи
Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
где:
(d)–расстояния между соседними пунктами.
(alpha ) – значение дирекционного угла.
Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:
(X_{2}=X_{1}+Delta X)
(Y_{2}=Y_{1}+Delta Y)
(X_{2}=X_{1}+d_{1-2}cdot cosalpha _{1-2})
(Y_{2}=Y_{1}+d_{1-2}cdot sinalpha _{1-2})

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:
(Delta X=X_{2}-X_{1})
(Delta Y=Y_{2}-Y_{1})
определяется румб линии (r_{1-2}):
(tgr=frac{Delta Y}{Delta X})
из этого выходит, что:
(r=arctgfrac|{Delta Y}{Delta X}|)
По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:
(d=frac{Delta X}{cosalpha })
(d=frac{Delta Y}{sinalpha })
(d=sqrt{Delta X^2+Delta Y^2})
Нахождение угла
Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:
- записать уравнения плоскостей;
- составить векторы нормали;
- вычислить значение косинуса угла между поверхностями.

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.
Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:
{A + 0 +C + 1 = 0;
{0 + 0 + C + 1 = 0;
{A + B + 0 + 1 = 0.

Из второго равенства можно определить C. Подставив найденное C в первое равенство, можно выразить A, а после найти B. Таким образом, решением системы будет A = 0, B = -1, C = -1. Вектор нормали, соответственно, будет: N1 (0; -1; -1).
Чтобы составить уравнение второй плоскости, нужно найти координаты лишь С1. Исходя из условия, они будут равны С1 (0; 1; 1), а A и D уже известны. Подставляя данные в уравнение Ax+By+Cz+1 = 0, опять составляют систему и находят её коэффициенты. После решения второй матрицы, например, методом разложения, можно записать координаты второго вектора: N2 (-½; ½; -½).
Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2½ * ¾½) = 1 / (6½/2) = 2/6½ = 6½ / 3. Соответственно, угол равен: α = arccos = 6½ / 3.
Приращение координат и их увязка
Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор};sum Delta X_{теор}=0)
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор};sum Delta Y_{теор}=0)
Как вычислить координаты точек хода
Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.

Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:
(X_{n}=X_{n-1}+Delta X _{n-1(испр)})
(Y_{n}=Y_{n-1}+Delta Y _{n-1(испр)})
(X_{n-1},Y_{n-1}) – координатные значения предыдущего пункта
(Delta X_{теор}=x_{B}-x_{A},Delta Y_{теор}=y_{B}-y_{A}) – исправленные приращения.
В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.
Скалярное произведение
Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.
Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB2 = OA2 + OB2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a|2 + |b|2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a|2 + |b|2 — |a — b|2) /2. Подставив координаты в формулу, получим следующее: a*b = (x12 + y12 + x22 + y22 — (x1-x2)2 + (y1-y2)2) /2 = x1*x2 + y1*y2. Равенство доказано.
Теодолитный ход – это одна из самых важных частей работы в геодезии. Часто это понятие переплетается с деятельностью инженеров и включается в различные работы.
Многие геодезисты годами обучаются тому, чтобы правильно и с первого раза прокладывать верную схему данных ходов. Также часто употребляют этот термин, как ломаное построение.
Определение и назначение теодолитных ходов
Теодолитный ход – это определенная линия, которая выполнена в ломаной последовательности. Нередко его используют для того, чтобы вычислить координаты определенной местности.

Более опытные геодезисты знают огромное количество таких систем. Нужны они также для того, чтобы точно отобразить нужную местность, определить углы на карте крупного масштаба или на специальных планах участка.
Само теодолитное построение отображается на плане или карте системой точек, которые закреплены на полотне. Благодаря им измеряется необходимый угол.
Основные виды теодолитных ходов
Опытные эксперты выделают несколько типовых схем ломаного построения:
-
замкнутый;
-
висячий;
-
разомкнутый.

Замкнутый ход представляет собой многоугольную фигуру, которая имеет начало и конец в одной только точке. Само название говорит о построении этой линии. Замкнутая фигура это и есть система такого вида. Чаще всего нужна такая линия для того, чтобы создать контур на любой местности.
Висячий ход используют редко, потому что для его вычисления потребуется специальная формула. Суть его такова, что он имеет только начало в определенной точке координат. Конец нужно вычислять.
Разомкнутый ход можно охарактеризовать как простую линию. Проект трассы или любого другого продолжительного участка невозможен без разомкнутой линии. Опора у нее на известные точки. В отличие от замкнутого, начало и конец располагаются в разных точках.
Схема теодолитного хода
Каждый путь имеет определенную схему, по которой можно определить его вид и назначение, положение. Как говорилось ранее, каждая линия имеет свои отличительные признаки.
Замкнутая схема напоминает собой закрытую фигуру. Для того, чтобы огородить любой участок, нужно именно это построение.
Необходима только одна известная относительная точка, чтобы сделать замкнутое пространство. Так как линия состоит из множества координат, то нахождение углов не является проблемой. Схема напоминает многоугольник.
Висячий ход нужен для тех участков, которые еще находятся в проекте. Эта схема имеет единственную координату, так как конца у нее нет. Конец у данной линии свободен.
Разомкнутый план удобен тем, что координаты известны. Остается только вычислить необходимые углы по координатам.
Начало и конец на данной линии лежат на геодезических обоснованиях. Эта фигура любима многими геодезистами-новичками, которые только пришли в это дело, для них есть допустимая минимальная погрешность.
Обработка результатов измерений
Мало знать точки, может произойти невязка. Для качественного выполнения полевой работы необходимо знать углы, с помощью которых строится то или иное пространство.
Для начала составляют проект, от которого будут отталкиваться на местности, часто это делается онлайн. Вычисление координат геодезических обоснований – важный шаг в работе.
Чтобы качественно обработать полученные результаты измерений, необходимо:
-
Составить таблицу с полученными углами.
-
Выписать точки начала и конца.
-
С помощью различных формул вычисляется сумма углов, а также длина. Расчет оформляется на отдельном полотне.
-
Далее необходимо вычислить теоретическую сумму для того, чтобы составить верное построение. Для каждого построения свои формулы.
Составление плана
Качественное построение системы предполагает собой точную ведомость всех необходимых данных. Недостаточно знать примерный чертеж или точки. Различаются виды планов, для которых присутствует своя система.
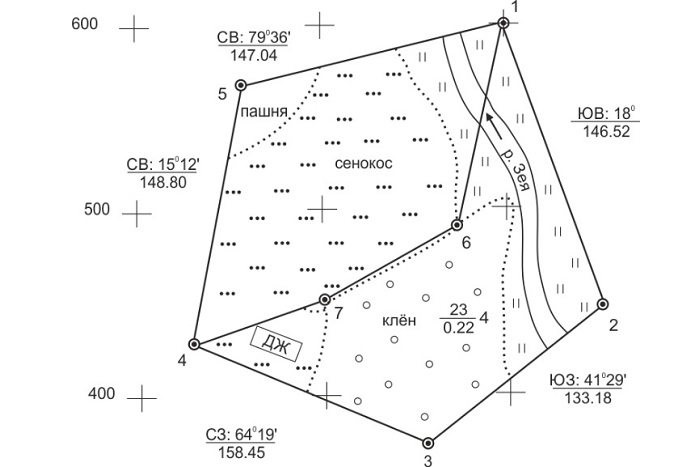
Теодолитная съемка нужна для того, чтобы составить план. Необходима такая последовательность действий:
-
создание сетки координат;
-
нанесение координат с предельной точностью;
-
отображение местной ситуации;
-
оформление по критериям.
Заключение
Построение системы и точное знание каждого угла поможет с высокой точностью наметить необходимые построение. Геодезисты больше всего времени тратят на то, чтобы составить точный план.
Ошибки в расчетах могут привести к трате времени или потере проекта. Выполнение всех пунктов последовательности приведёт к отличной и законченной работе.
