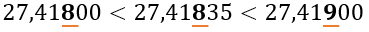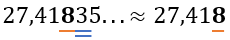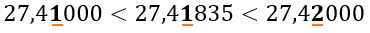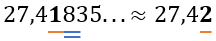Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
— Который час?
— Какой вес?
— Сколько стоит?
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
Если число c < х < d, тогда с — это приближенное значение x с недостатком. А d — это приближенное значение x с избытком.
Чтобы округлить дробную часть десятичной дроби, пользуйтесь следующими правилами:
- Подчеркните цифру округляемого разряда.
- Отделите все цифры, стоящие справа.
- Если справа от цифры, которую нужно округлить, стоит 0, 1, 2, 3 или 4 — цифра остается без изменений. Отбросьте все цифры справа от цифры округляемого разряда.
- Если справа от цифры округляемого разряда стоит 5, 6, 7, 8 или 9 — к цифре округляемого разряда прибавляем один. Отбросьте все цифры справа.
Приближенное значение записывается после вот такого знака: ≈
Еще одно правило округления, которое нужно запомнить
Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число.
Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Примеры округления десятичной дроби
Давайте разберем несколько примеров округления дробной части десятичных дробей.
Пример 1. Округлите дробь 56,786 до сотых.
Цифра, которую нужно округлить, — 8. Обращайтесь к таблице с подсказками названия разрядов, чтобы верно определять нужную цифру.
Справа от цифры округляемого разряда цифра 6.
Смотрим на пункт 4. Прибавляем: 8 + 1 = 9.
Ответ. 56,786 ≈ 56,79.
Пример 2. Округлите дробь 0,647 до десятых.
Округляемая цифра — 6.
Справа — 4.
Смотрим пункт 3. Значит, цифра 6 остается неизменной.
Ответ: 0,647 ≈ 0,6.
Пример 3. Округлите дробь 23,98 до разряда единиц в целой части.
Цифра, которую нужно округлить, — 3.
Первая цифра после запятой — 9. Значит, нужно прибавить: 3 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Ответ: 23,98 ≈ 24.
Пример 4. Округлите дробь 3,286 до десятых.
Цифра, которую нужно округлить, — 2.
Справа от — 8.
Согласно правилу, прибавляем: 2 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Ответ: 3,286 ≈ 3,3.
Пример 5. Округлите дробь 45,387 до сотых.
Цифра сотых — 8.
Справа — 7.
Прибавляем: 8 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Ответ: 45,387 ≈ 45,39.
Округление дробей
Если у нас есть длинная десятичная дробь, например: 27,41835… то вряд ли у нас получится полностью её записать. Для того чтобы запись таких дробей была возможной, используют округление по математическому правилу.
Округление до разряда – замена числа этого разряда на приближенное значение с отбрасыванием последующих разрядов.
ОКРУГЛЕНИЕ В МЕНЬШУЮ СТОРОНУ:
Если нам нужно округлить такое число, например до тысячных, это значит, что тысячная доля будет последней цифрой округленной дроби, то есть:
Посмотрим на следующую цифру после неё. Если она равно 0, 1, 2, 3 или 4, то тысячная доля не изменится, то есть округлится в меньшую сторону, а следующие разряды мы отбросим:
ОКРУГЛЕНИЕ В БОЛЬШУЮ СТОРОНУ:
Если нам нужно округлить такое число, например до сотых, это значит, что сотая доля будет последней цифрой округленной дроби, то есть:
Посмотрим на следующее число после нее. Если оно равно 5, 6, 7, 8 или 9, то сотая доля увеличится на один, то есть округлится в большую сторону, а следующие разряды мы отбросим:
В данной публикации мы рассмотрим, каким образом можно округлить десятичные дроби до разных разрядов дробной (десятых, сотых, тысячных и т.д.) и целой (единиц, десятков, сотен и т.д.) частей. Также разберем примеры для лучшего понимания и закрепления материала.
-
Правила округления десятичной дроби
-
Округление дробной части
- Округление до целого числа
- Особый случай: последняя цифра – ноль
-
Округление дробной части
Правила округления десятичной дроби
Десятичную дробь можно округлить:
- до целого числа с точностью до единиц, десятков, сотен и т.д.;
- до определенного разряда дробной части: десятых, сотых, тысячных, десятитысячных и т.д.
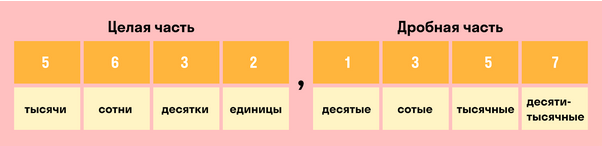
Но, прежде чем перейти к правилам округления, давайте еще раз вспомним, из чего состоит десятичная дробь. В качестве примера – от тысяч до десятитысячных:

Округление дробной части
Итак, чтобы выполнить округление десятичной дроби, придерживаемся следующего плана действий:
- Отмечаем разряд, до которого следует округлить дробь. Его можно отделить от следом идущих цифр разделительной линией.
- Далее возможно два варианта (согласно правилам округления чисел):
- если после выбранного разряда идут цифры 0, 1, 2, 3 или 4, то цифру этого разряда мы оставляем той же, а все остальные цифры после линии убираем.
- если после выбранного разряда стоят цифры 5, 6, 7, 8 или 9, то к цифре этого разряда прибавляем единицу и, как в пункте выше, все цифры с правой стороны от линии убираем.
Пример 1: округлим 12,624 до десятых.

Пример 2: округлим 5,176 до сотых.

Округление до целого числа
Если десятичную дробь требуется округлить до целого числа (до единиц), смотрим на цифру, которая идет сразу же после запятой (разряд – десятые). Если это 5, 6, 7, 8 или 9, то к единицам в целой части прибавляем число 1, а всю дробную часть отбрасываем. В остальных случаях просто убираем дробную часть без каких-либо изменений целой части.
Примеры округления десятичных дробей до целого числа:
- 2,15 ≈ 2;
- 4,64 ≈ 5;
- 7,063 ≈ 7;
- 12,814 ≈ 13.
Примечание: Если дробь требуется округлить до целого числа большего разряда, чем единицы (десятки, сотни, тысячи и т.д.), отбрасываем дробную часть, затем округляем полученный результат согласно правилам округления натуральных чисел.
Пример 1: выполним округление до десятков числа 156,71:
![]()
Пример 2: выполним округление до сотен числа 8134,145:
![]()
Особый случай: последняя цифра – ноль
Если в результате округления десятичной дроби последней цифрой в дробной части остается 0, его нельзя убирать. Это нужно для того, чтобы наглядно было понято, до какого разряда было выполнено округление.
Примеры округления с нулем на конце
- 5,01 ≈ 5,0 (до десятых);
- 3,199 ≈ 3,20 (до сотых).
Остановимся подробнее на втором примере. Т.к. в следующем разряде после сотых стоит цифра 9, значит по правилам округления к сотым мы прибавляем единицу: 9 + 1 = 10. Следовательно, в разряде сотых мы пишем ноль, а единицу прибавляем к десятым (1 + 1 = 2).

Различные простые математические процедуры, такие как округление, помогут вам легко выполнять вычисления. Десятичное округление – один из эффективных подходов к быстрому выполнению вычислений при использовании сложных чисел. Понимание того, как округлять десятичные числа, может помочь вам в выполнении как личных, так и профессиональных задач при работе с измерениями.
В этой статье мы дадим определение округления и объясним, как округлять десятичные числа.
Что такое округление?
Округление – это процесс уменьшения числа до более простой формы, чтобы оно стало более удобным для быстрых вычислений. Хотя округление является частью базовой математики, это также навык для взрослых, которые хотят делать оценки и сравнения при работе с измерениями, такими как время или деньги.
При округлении целых чисел одинарные цифры представляют единицы единицы, двойные цифры образуют группы по 10, тройные цифры – группы по 100, четверные цифры – группы по 1 000 и так далее. Округление преобразует числа в ближайшую группу из 10, 100, 1,000 или других значений места. Например, округление 74 до ближайших десятков дает 70, а округление 2650 до ближайших 100 дает 2700.
Правило округления
Правило округления гласит, что если справа от значения знака места, которое вы округляете, находится число больше четырех, то вы должны округлять в большую сторону. Это означает увеличение его значения на 1, чтобы учесть все последующие числа. В приведенном выше примере при округлении 2650 до ближайших 100 нужно обратить внимание на цифры 6 и 5. Поскольку 5, которое занимает место десятка рядом с 6 в значении 100, больше, чем 4, вы округляете 6 до 7. В результате вы получите 2700.
Если число рядом со значением места, которое вы хотите округлить, равно четырем или меньше, вы округляете вниз, сохраняя его значение и усекая все последующие числа. В приведенном примере округление 74 до ближайшего десятка дает 70, потому что цифра 4 на месте единицы рядом с 7 на месте десятка меньше 5.
Округление десятичных дробей
Округление может стать более сложным при работе с десятичными дробями. Первое значение после запятой представляет десятую часть единицы, второе – сотую часть единицы, третье – тысячную часть единицы. Эти значения мест уменьшаются с каждым дополнительным числом после десятичных знаков.
Как округлить десятичные числа
Используйте следующие шаги в качестве руководства для быстрого и простого округления десятичных значений:
1. Определите, насколько точным должно быть значение
Чтобы округлить десятичное значение, учитывайте степень точности, которая требуется для конкретного вычисления. Например, вы можете захотеть использовать больше десятичных знаков при округлении времени в лабораторном эксперименте, чем при оценке расстояния до дома. В зависимости от цели вычислений, например, при сложении значений цен, принято округлять десятичные числа до сотых долей. APA рекомендует два знака после запятой, а Европейская ассоциация научных редакторов рекомендует от двух до трех эффективных цифр.
2. Определите значение места для округления
Определите, до какого знака места вы хотите округлить десятичную дробь. Если вы вычисляете десятичные числа, например, для объединения цен, округление до ближайшего сотого значения будет наиболее целесообразным. Также, если вы хотите округлить цены до ближайшего целого доллара, посмотрите на значение, стоящее на первом месте слева от десятичной дроби.
Пример 1
Например, если вы хотите округлить 76.289, определите значение места каждой цифры и определите наиболее подходящее место для вашей оценки:
-
Округление до ближайшей единицы: В числе 76.289, цифра, на которой вы хотите сосредоточиться, это 6.
-
Округление до ближайшей сотой: При округлении 76.289 до ближайшей сотой, вы хотите сосредоточиться на числе 8.
3. Определите, хотите ли вы округлить вниз или вверх
После определения значения места, до которого вы хотите округлить, вы можете использовать исходное число, чтобы определить, в большую или меньшую сторону округлять. Используйте правило округления.
Пример 2
Исходя из предыдущего примера, 76.289, вот как округлить эту десятичную дробь до ближайших сотых, десятых и единичных значений:
-
Ближайшая сотая: посмотрите на 9, которая следует за 8 в числе 76.289. Поскольку 9 больше четырех, то 8 в сотой степени увеличивается до 9, в результате получается 76.29 в качестве окончательной оценки.
-
Ближайшая десятая: При округлении 76.289 до ближайшей десятой, посмотрите на 8 справа от 2. Поскольку 8 больше четырех, 2 на десятом месте увеличивается до 3, в результате получается число 76.3.
-
Ближайшая единица: В числе 76.287, округляйте 6, глядя на 2. Поскольку 2 меньше четырех, 6 остается неизменным, что дает 76.
Важность понимания того, как округлять десятичные числа
Понимание того, как быстро округлять десятичные числа, является эффективным навыком по многим причинам. Рассмотрим следующие преимущества понимания того, как округлять десятичные дроби:
1. Это применимо к повседневным ситуациям
При покупке топлива, покупке продуктов или расчете чаевых в ресторане округление десятичных дробей поможет вам легко выполнить многие основные вычисления. Например, при сложении расходов на продукты или другие товары вы можете округлить до ближайшего целого доллара, чтобы получить представление о том, сколько денег вам нужно для покрытия расходов.
Ежегодное заполнение декларации о доходах также может потребовать понимания того, как округлять десятичные числа, особенно если вы пытаетесь получить представление о том, что ожидаете получить или задолжать перед подачей декларации. В декларации о подоходном налоге можно округлить центы до долларов. Округляйте суммы меньше 50 центов и больше 50 центов до ближайшего доллара. Например, при округлении $2.49 превращается в $2 и $3.57 превращается в $4.
2. Позволяет быстро оценивать
Округление десятичных дробей ускоряет принятие решений на основе данных. Это может облегчить выполнение длительных вычислений и понимание их результатов. Например, при работе с несколькими десятичными знаками, как в числе 11.3478076 проще округлить до ближайшей десятой или целого числа. Это может помочь людям быстро выполнять математические операции и легче понимать свои вычисления.
3. Поддерживает финансовые и бухгалтерские процессы
Большинство отраслей промышленности полагаются на финансовые процессы для отслеживания и записи важных бухгалтерских документов, данных и налоговой информации. Когда люди, работающие в сфере бухгалтерского учета и финансов, имеют дело с десятичными значениями, выходящими за пределы сотого знака, они часто используют десятичное округление, чтобы упростить процесс и сделать свои вычисления более легкими для просмотра и понимания. Это может облегчить понимание финансовой информации и принятие решений на основе данных для частных лиц и организаций.
4. Это упрощает научные и технические вычисления
Округление десятичных дробей также является распространенной функцией в технических и научных отраслях. Округление десятичных дробей может помочь вам сделать более быстрые оценки при работе с длинными цепочками чисел. Например, люди в медицинской сфере, такие как врачи или доктора, медсестры и фармацевты, полагаются на сильные вычислительные навыки для интерпретации, оценки и применения десятичных измерений. В таких технических областях, как наука, статистика и информационные технологии, часто требуется применение математики, включая десятичные операции.
Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным. Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».
Приближённые значения
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета.
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:
![]()
Читается как «приближённо (приблизительно) равно».
Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:
![]()
На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:
![]()
На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:
![]()
На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
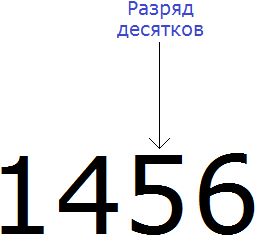
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
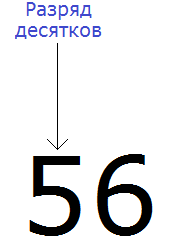
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
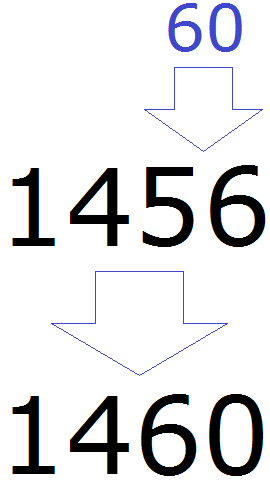
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Первое правило округления
В предыдущих примерах мы видели, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами.
Первое правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Например, округлим число 123 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать самó задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.
Видим, что в разряде десятков нахóдится двойка. Значит сохраняемой цифрой является цифра 2
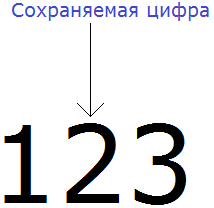
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой.
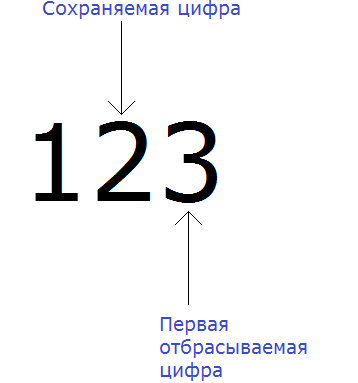
Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):
123 ≈ 120
Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.
Теперь попробуем округлить то же самое число 123, но уже до разряда сотен.
Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:
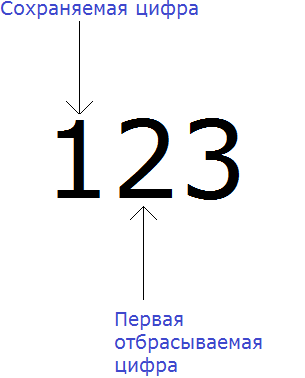
Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:
123 ≈ 100
Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.
Пример 3. Округлить число 1234 до разряда десятков.
Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:
1234 ≈ 1230
Пример 4. Округлить число 1234 до разряда сотен.
Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1200
Пример 3. Округлить число 1234 до разряда тысяч.
Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1000
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.
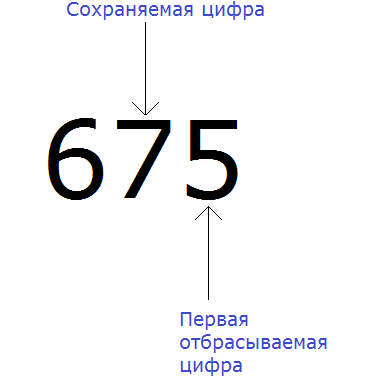
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:
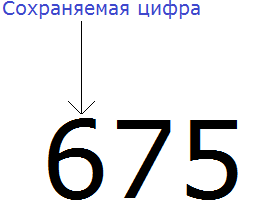
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
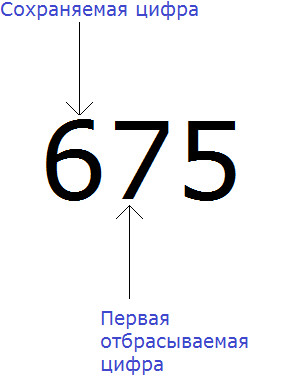
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3. Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4. Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5. Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6. Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
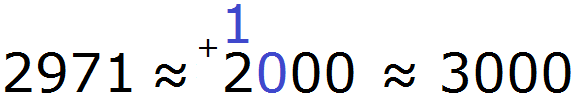
2971 ≈ 3000
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых. Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.
Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже