Определенный интеграл. Площадь криволинейной трапеции
- Теорема о площади криволинейной трапеции
- Формула Ньютона-Лейбница
- Геометрический смысл теоремы Лагранжа о среднем
- Площадь плоской фигуры, ограниченной двумя кривыми
- Примеры
п.1. Теорема о площади криволинейной трапеции
Фигуру, ограниченную прямыми (x=a, x=b), осью абсцисс (y=0) и графиком функции (y=f(x)) называют криволинейной трапецией.

Теорема
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b], равна (F(b)-F(a)), где (F(x)) – первообразная функции (f(x)) на [a;b].

Доказательство:
Выберем на интервале (xin [a;b]). Площадь соответствующей криволинейной трапеции (S(x)) является функцией от (x). Дадим переменной (x) приращение (triangle x).
Площадь криволинейной трапеции на интервале (left[a;x+triangle xright]) равна сумме
(S(x+triangle x)=S(x)+S(triangle x)). Откуда приращение площади: $$ triangle S=S(triangle x)=S(x+triangle x)-S(x) $$ По теореме о среднем (см. ниже в этом параграфе) между (x) и (x+triangle x) всегда найдется такое (t), что приращение площади равно произведению: $$ triangle S=f(t)cdot (x+triangle x-x)=f(t)cdot triangle x $$ Если (triangle xrightarrow 0), то (trightarrow x), и в пределе получаем: begin{gather*} S'(x)=lim_{triangle xrightarrow 0}frac{triangle S}{triangle x}=lim_{triangle xrightarrow 0} frac{f(t)cdot triangle x}{triangle x}=lim_{triangle xrightarrow 0}f(t)=f(x) end{gather*} Т.е. (S(x)) является первообразной для (f(x)) на [a;b]. В общем виде: $$ S(x)=F(x)+C $$ Найдем C. В точке a: $$ S(a)=0=F(a)+CRightarrow C=-F(a) $$ Тогда вся площадь: $$ S=S(b)=F(b)+C=F(b)-F(a) $$ Что и требовалось доказать.
п.2. Формула Ньютона-Лейбница
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b] записывают в виде определенного интеграла: $$ S=int_{a}^{b}f(x)dx $$ По формуле Ньютона-Лейбница определенный интеграл равен: $$ int_{a}^{b}f(x)dx=F(x)|_a^b=F(a)-F(b) $$
Например:
Найдем площадь фигуры, ограниченной осью абсцисс и графиком функции $$ y=3-2x-x^2 $$
 |
Построим график (см. §28 справочника для 8 класса). Это парабола. (alt 0) – ветки вниз. Координаты вершины: begin{gather*} x_0=-frac{b}{2a}=-frac{-2}{2cdot (-1)}=-1,\ y_0=3+2-1=4 end{gather*} Точки пересечения с осью OX: begin{gather*} 3-2x-x^2=0Rightarrow x^2+2x-3=0\ (x+3)(x-1)=0Rightarrow left[ begin{array}{l} x=-3,\ x=1 end{array} right. end{gather*} Точка пересечения с осью OY: $$ x=0, y=3 $$ |
Необходимо найти площадь заштрихованной фигуры.
Функция: (f(x)=3-2x-x^2)
Пределы интегрирования: (a=-3, b=1) begin{gather*} S=int_{-3}^{1}(3-2x-x^2)dx=left(3x-2cdotfrac{x^2}{2}-frac{x^3}{3}right)|_{1}^{-3}=left(3x-x^2-frac{x^3}{3}right)|_{1}^{-3}=\ =left(3-cdot 1-1^2-frac{1^3}{3}right)-left(3cdot(-3)-(-3)^2-frac{(-3)^3}{3}right)=2-frac13+9=10frac23 end{gather*} Ответ: (10frac23)
п.3. Геометрический смысл теоремы Лагранжа о среднем
Теорема Лагранжа о среднем
Если функция (F(x)) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), то существует такая точка (muin(a;b)), что $$ F(b)-F(a)=F'(mu)(a-b) $$ Пусть (F'(x)=f(x)), т.е. функция (F(x)) является первообразной для (f(x)). Тогда: $$ F(b)-F(a)=int_{a}^{b}f(x)dx=f(mu)(b-a) $$

Геометрический смысл теоремы Лагранжа о среднем в интегральной форме заключается в том, что площадь криволинейной трапеции равна площади прямоугольника с основанием (d=b-a) и высотой (h=f(mu)), где (aleqmuleq b).
Теорема о среднем используется при доказательстве многих формул, связанных с использованием определенных интегралов (центра тяжести тела, площади поверхности и т.д.).
п.4. Площадь плоской фигуры, ограниченной двумя кривыми
Площадь плоской фигуры, ограниченной прямыми (x=a, x=b, alt b) и кривыми (y=f(x), y=g(x)), причем (f(x)geq g(x)) для любого (xin [a;b]), равна: $$ S=int_{a}^{b}(f(x)-g(x))dx $$
Например:
Найдем площадь фигуры, ограниченной двумя параболами (y=x^2) и (y=4x-x^2).
Найдем точки пересечения парабол: $$ x^2=4x-x^2Rightarrow 2x^2-4x=0Rightarrow 2x(x-2)=0Rightarrow left[ begin{array}{l} x=0\ x=2 end{array} right. $$ Строим графики.
Необходимо найти площадь заштрихованной фигуры.
Функция сверху: (f(x)=4x-x^2)
Функция снизу: (g(x)=x^2)
Пределы интегрирования: (a=0, b=2) begin{gather*} S=int_{0}^{2}left((4x-x^2)-x^2right)dx=int_{0}^{2}(4x-2x^2)dx=left(4cdotfrac{x^2}{2}-2cdotfrac{x^3}{3}right)|_0^2=\ =left(2x^2-frac23 x^3right)|_0^2=2cdot 2^2-frac23cdot 2^3-0=8-frac{16}{3}=frac83=2frac23 end{gather*} Ответ: (2frac23)
п.5. Примеры
Пример 1. Найдите определенный интеграл:
a) (int_{-2}^{3}x^2dx) $$ int_{-2}^{3}x^2dx=frac{x^3}{3}|_{-2}^{3}=frac{3^3}{3}-frac{(-2)^3}{3}=9-frac83=frac{19}{3}=6frac13 $$
б) (int_{0}^{fracpi 3}sinxdx) $$ int_{0}^{fracpi 3}sinxdx=(-cosx)|_{0}^{fracpi 3}=-cosfracpi 3+cos0=-frac12+1=frac12 $$
в) (int_{1}^{2}left(e^x+frac 1xright)dx) $$ int_{1}^{2}left(e^x+frac 1xright)dx=(e^x+ln|x|)|_{1}^{2}=e^2+ln 2-e^1-underbrace{ln 1}_{=0}=e(e-1)+ln 2 $$
г) (int_{2}^{3}(2x-1)^2 dx) begin{gather*} int_{2}^{3}(2x-1)^2 dx=frac12cdotfrac{(2x-3)^3}{3}|_{2}^{3}=frac16((2cdot 3-1)^3)-(2cdot 2-1)^3)=frac{5^3-3^3}{6}=\ =frac{125-27}{6}=frac{98}{6}=frac{49}{3}=16frac13 end{gather*}
д) (int_{1}^{3}frac{dx}{3x-2}) begin{gather*} int_{1}^{3}frac{dx}{3x-2}=frac13cdot ln|3x-2| |_{1}^{3}=frac13left(ln 7-underbrace{ln 1}_{=0}right)=frac{ln 7}{3} end{gather*}
e) (int_{-1}^{4}frac{dx}{sqrt{3x+4}}) begin{gather*} int_{-1}^{4}frac{dx}{sqrt{3x+4}}=frac13cdotfrac{(3x+4)^{-frac12+1}}{-frac12+1}|_{-1}^{4}=frac23sqrt{3x+4}|_{-1}^{4}=\ =frac23left(sqrt{3cdot 4+4}-sqrt{3cdot(-1)+4}right)=frac23(4-1)=2 end{gather*}
Пример 2. Найдите площадь фигуры под кривой на заданном интервале:
a) (f(x)=x^3+3, xinleft[-1;1right]) $$ S=int_{-1}^{1}(x^3+3)dx=left(frac{x^4}{4}+3xright)|_{-1}^{1}=frac14+3-left(frac14-3right)=6 $$
$$ S=int_{-1}^{1}(x^3+3)dx=left(frac{x^4}{4}+3xright)|_{-1}^{1}=frac14+3-left(frac14-3right)=6 $$
б) (f(x)=sin2x, xinleft[0;fracpi 2right]) $$ S=int_{0}^{fracpi 2}sin2xdx=-frac12cos2x|_{0}^{fracpi 2}=-frac12left(cosleft(2cdotfracpi 2right)-cos0right)=-frac12(-1-1)=1 $$
$$ S=int_{0}^{fracpi 2}sin2xdx=-frac12cos2x|_{0}^{fracpi 2}=-frac12left(cosleft(2cdotfracpi 2right)-cos0right)=-frac12(-1-1)=1 $$
в) (f(x)=frac4x+3, xinleft[2;6right])
(f(x)=frac4x+3) – гипербола с асимптотами (x=0, y=3)
Площадь под кривой: begin{gather*} S=int_{2}^{6}left(frac4x+3right)dx=(4cdot ln|x|+3x)|_{2}^{6}=(4ln 6+18)-(4ln 2+6)=\ =4(ln 6-ln 2)+12=4lnfrac62+12=4ln 3+12=4(ln 3+3) end{gather*}
г) (f(x)=frac{1}{sqrt{x}}, xinleft[1;4right]) $$ S=int_{1}^{4}frac{dx}{sqrt{x}}=frac{x^{-frac12+1}}{-frac12+1}|_{1}^{4}=2sqrt{x}|_{1}^{4}=2(sqrt{4}-sqrt{1})=2 $$
$$ S=int_{1}^{4}frac{dx}{sqrt{x}}=frac{x^{-frac12+1}}{-frac12+1}|_{1}^{4}=2sqrt{x}|_{1}^{4}=2(sqrt{4}-sqrt{1})=2 $$
Пример 3. Найдите площадь фигуры, ограниченной линиями:
a) (y=x-2, y=x^2-4x+2)
Найдем точки пересечения прямой и параболы: $$ x-2=x^2-4x+2Rightarrow x^2-5x+4=0Rightarrow (x-1)(x-4)=0Rightarrow left[ begin{array}{l} x=1,\ x=4 end{array} right. $$ 
Функция сверху: (f(x)=x-2)
Функция снизу: (g(x)=x^2-4x+2)
Пределы интегрирования: (a=1, b=4) begin{gather*} S=int_{1}^{4}left((x-2)-(x^2-4x+2)right)dx=int_{1}^{4}(-x^2+5x-4)dx=\ =left(-frac{x^3}{3}+frac{5x^2}{2}-4xright)|_{1}^{4}=left(-frac{64}{3}+5cdotfrac{16}{2}-4cdot 4right)-left(-frac13+frac52-4right)=\ =-frac{63}{3}+24+1,5=4,5 end{gather*} Ответ: 4,5
б) (y=e^{frac x2}, y=frac1x, x=2, x=3)
Функция сверху: (f(x)=e^{x/2})
Функция снизу: (g(x)=frac1x)
Пределы интегрирования: (a=2, b=3) begin{gather*} S=int_{2}^{3}left(e^{x/2}-frac1xright)dx=(2e^{x/2}-ln|x|)|_{2}^{3}=left(2e^{frac32}-ln 3right)-(2e-ln 2)=\ =2e^{frac32}-2e-ln 3+ln 2=2e(sqrt{e}-1)+lnfrac23 end{gather*} Ответ: (2e(sqrt{e}-1)+lnfrac23)
в*) (y=3-x^2, y=1+|x|)
Найдем точки пересечения ломаной и параболы: begin{gather*} 3-x^2=1+|x|Rightarrow x^2+|x|-2=0Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ x^2+x-2=0 end{cases} \ begin{cases} xlt 0\ x^2-x-2=0 end{cases} end{array} right. Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ (x+2)(x-1)=0 end{cases} \ begin{cases} xlt 0\ (x-2)(x+1)=0 end{cases} end{array} right. Rightarrow \ left[ begin{array}{l} begin{cases} xgeq 0\ left[ begin{array}{l} x=-2\ x=1 end{array} right. end{cases} \ begin{cases} xlt 0\ left[ begin{array}{l} x=2\ x=-1 end{array} right. end{cases} end{array} right. Rightarrow left[ begin{array}{l} x=1\ x=-1 end{array} right. end{gather*} 
Функция сверху: (f(x)=3-x^2)
Функция снизу: (g(x)=1+|x|)
Пределы интегрирования: (a=-1, b=1)
Чтобы не раскрывать модуль под интегралом, заметим, что площади на интервалах [-1;0] и [0;1] равны, т.к. обе функции четные и симметричные относительно оси OY. Поэтому можно рассматривать только положительные (xinleft[0;1right]), найти для них интеграл (площадь) и умножить на 2: begin{gather*} S=2int_{0}^{1}left((3-x^2)-(1+x)right)dx=2int_{0}^{1}(-x^2-x+2)dx=2left(-frac{x^3}{3}-frac{x^2}{2}+2xright)|_{0}^{1}=\ =2left(-frac13-frac12+2right)-0=frac73=2frac13 end{gather*} Ответ: (2frac13)
г*) (y=3sinx, y=cosx, x=-frac{5pi}{4}, x=fracpi 4)
На отрезке (left[-frac{5pi}{4};-frac{3pi}{4}right]) синус над косинусом, далее на (left[-frac{3pi}{4};frac{pi}{4}right]) – косинус над синусом.
Площадь фигуры, закрашенной голубым, в два раза больше площади фигуры, закрашенной сиреневым. Поэтому общая площадь будет равна трем площадям, закрашенным сиреневым: begin{gather*} S=3int_{-frac{5pi}{4}}^{-frac{3pi}{4}}(sinx-cosx)dx=3(-cosx-sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}} end{gather*} Прибавим полный период, он одинаков для обеих функций:
(-frac{3pi}{4}+2pi=frac{5pi}{4}; -frac{5pi}{4}+2pi=frac{3pi}{4}) begin{gather*} -3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3left(cosleft(frac{5pi}{4}right)+sinleft(frac{5pi}{4}right)-cosleft(frac{3pi}{4}right)-sinleft(frac{3pi}{4}right)right)=\ =-3left(-frac{sqrt{2}}{2}-frac{sqrt{2}}{2}+frac{sqrt{2}}{2}-frac{sqrt{2}}{2}right)=3sqrt{2} end{gather*} Ответ: (3sqrt{2})
Пример 4*. Пусть (S(k)) – это площадь фигуры, образованной параболой (y=x^2+2x-3) и прямой (y=kx+1). Найдите (S(-1)) и вычислите наименьшее значение (S(k)).
1) Найдем (S(-1)).
(k=-1, y=-x+1 )
 |
Точки пересечения прямой и параболы: begin{gather*} -x+1=x^2+2x-3\ x^2+3x-4=0\ (x+4)(x-1)=0Rightarrow left[ begin{array}{l} x=-4,\ x=1 end{array} right. end{gather*} Функция сверху: (y=-x+1) Функция снизу: (y=x^2+2x-3) Пределы интегрирования: (a=-4, b=1) |
begin{gather*} S(-1)=int_{-4}^{1}left((-x+1)-(x^2+2x-3)right)dx=int_{-4}^{1}(-x-3x+4)dx=\ =left(-frac{x^3}{3}-frac{3x^2}{2}+4xright)|_{-4}^{1}=left(-frac13-frac32+4right)-left(frac{64}{3}-24-16right)=-21frac23+42frac12=20frac56 end{gather*}
2) Решаем в общем виде.
Все прямые (y=kx+1) проходят через точку (0;1) и при образовании фигуры находятся над параболой.
Точки пересечения прямой и параболы: begin{gather*} kx+1=x^2+2x-3Rightarrow x^2+(2-k)x-4=0\ D=(2-k)^2-4cdot (-4)=(k-2)^2+16gt 0 end{gather*} Дискриминант (Dgt 0) при всех (k). Точки пересечения (пределы интегрирования): $$ x_{1,2}=frac{-(2-k)pmsqrt{D}}{2}=frac{k-2pmsqrt{D}}{2} $$ Разность корней: $$ x_2-x_1=sqrt{D}=sqrt{(k-2)^2+16} $$ Минимальное значение разности корней будет при (k=2).
Площадь: begin{gather*} S(k)=int_{x_1}^{x_2}left((kx+1)-(x^2+2x-3)right)dx=int_{x_1}^{x_2}(-x^2+(k-2)x+4)dx=\ =left(-frac{x^3}{3}+frac{(k-2)x^2}{2}+4xright)|_{x_1}^{x_2}=-frac13(x_2^3-x_1^3)+frac{k-2}{2}(x_2^2-x_1^2)+4(x_2-x_1) end{gather*}
 |
begin{gather*} S(k)_{min}=S(2)\ x_{1,2}=pm 2\ S(2)=-frac13cdot(2^3+2^3)+0+4sqrt{16}=\ =-frac{16}{3}+16=frac{32}{3}=10frac23 end{gather*} |
Ответ: 1) (S(-1)=20frac56); 2) (S(k)_{min}=S(2)=10frac23)
Пример 5*. Фигура ограничена линиями (y=(x+3)^2, y=0, x=0). Под каким углом к оси OX надо провести прямые через точку (0;9), чтобы они разбивали фигуру на три равновеликие части?
 |
Площадь криволинейной трапеции AOB: begin{gather*} S_0=int_{-3}^{0}(x+3)^2dx=frac{(x+3)^3}{3}|_{-3}^{0}=\ =9-0=9 end{gather*} Площадь каждой части: (S_i=frac13 S_0=3) Точки (C(x_1; 0)) и (D(x_2; 0)) c (-3lt x_1lt x_2lt 0) такие, что прямые AC и AD отсекают по 1/3 от фигуры. Площадь прямоугольного треугольника (triangle AOD): begin{gather*} S_3=frac12|x_2|cdot 9=3Rightarrow |x_2|=frac69=frac23Rightarrow\ x_2=-frac23 end{gather*} Площадь прямоугольного треугольника (triangle AOC): begin{gather*} S_2+S_3=frac12|x_1|cdot 9=6Rightarrow |x_1|=frac{12}{9}=frac43Rightarrow\ x_1=-frac43 end{gather*} |
Находим углы соответствующих прямых.
Для (x_1: tgalpha=frac{9}{|x_1|}=frac{9}{4/3}=frac{27}{4}, alpha=arctgfrac{27}{4})
Для (x_x: tgbeta=frac{9}{|x_2|}=frac{9}{2/3}=frac{27}{2}, beta=arctgfrac{27}{2})
Ответ: (arctgfrac{27}{4}) и (arctgfrac{27}{2})
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S(G)=∫abf(x)dx для непрерывной и неотрицательной функции y=f(x) на отрезке [a;b],
S(G)=-∫abf(x)dx для непрерывной и неположительной функции y=f(x) на отрезке [a;b].
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y=f(x) или x=g(y).
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Пусть функции y=f1(x) и y=f2(x) определены и непрерывны на отрезке [a;b], причем f1(x)≤f2(x) для любого значения x из [a;b]. Тогда формула для вычисления площади фигуры G, ограниченной линиями x=a, x=b, y=f1(x) и y=f2(x) будет иметь вид S(G)=∫abf2(x)-f1(x)dx.
Похожая формула будет применима для площади фигуры, ограниченной линиями y=c, y=d, x=g1(y) и x=g2(y): S(G)=∫cd(g2(y)-g1(y)dy.
Разберем три случая, для которых формула будет справедлива.
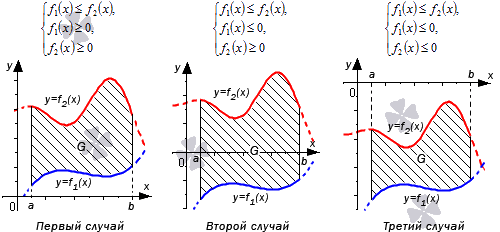
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G1 равна площади фигуры G2. Это значит, что
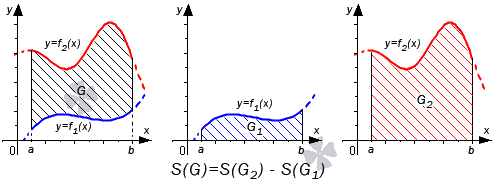
Поэтому, S(G)=S(G2)-S(G1)=∫abf2(x)dx-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx.
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
Во втором случае справедливо равенство: S(G)=S(G2)+S(G1)=∫abf2(x)dx+-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx
Графическая иллюстрация будет иметь вид:
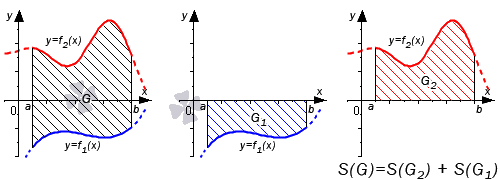
Если обе функции неположительные, получаем: S(G)=S(G2)-S(G1)=-∫abf2(x)dx–∫abf1(x)dx=∫ab(f2(x)-f1(x))dx . Графическая иллюстрация будет иметь вид:
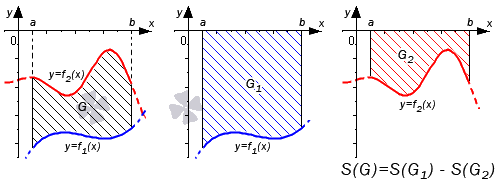
Перейдем к рассмотрению общего случая, когда y=f1(x) и y=f2(x) пересекают ось Ox.
Точки пересечения мы обозначим как xi, i=1, 2,…, n-1. Эти точки разбивают отрезок [a; b] на n частей xi-1; xi, i=1, 2,…, n, где α=x0<x1<x2<…<xn-1<xn=b. Фигуру G можно представить объединением фигур Gi, i=1, 2,…, n. Очевидно, что на своем интервале Gi попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S(Gi)=∫xi-1xi(f2(x)-f1(x))dx, i=1, 2,…, n
Следовательно,
S(G)=∑i=1nS(Gi)=∑i=1n∫xixif2(x)-f1(x))dx==∫x0xn(f2(x)-f(x))dx=∫abf2(x)-f1(x)dx
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
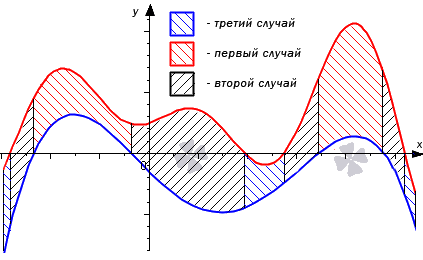
Формулу S(G)=∫abf2(x)-f1(x)dx можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y=f(x) и x=g(y).
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
Необходимо определить площадь фигуры, которая ограничена параболой y=-x2+6x-5 и прямыми линиями y=-13x-12, x=1, x=4.
Решение
Изобразим линии на графике в декартовой системе координат.
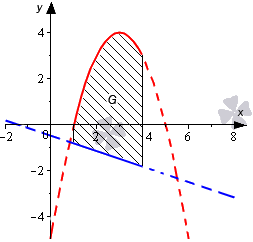
На отрезке [1;4] график параболы y=-x2+6x-5 расположен выше прямой y=-13x-12. В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S(G)=∫14-x2+6x-5–13x-12dx==∫14-x2+193x-92dx=-13×3+196×2-92×14==-13·43+196·42-92·4–13·13+196·12-92·1==-643+1523-18+13-196+92=13
Ответ: S(G)=13
Рассмотрим более сложный пример.
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x+2, y=x, x=7.
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x=7. Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
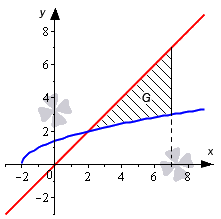
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y=x и полу параболы y=x+2. Для нахождения абсциссы используем равенства:
y=x+2ОДЗ: x≥-2×2=x+22×2-x-2=0D=(-1)2-4·1·(-2)=9×1=1+92=2∈ОДЗx2=1-92=-1∉ОДЗ
Получается, что абсциссой точки пересечения является x=2.
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y=x+2 , y=x пересекаются в точке (2;2), поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [2;7] график функции y=x расположен выше графика функции y=x+2 . Применим формулу для вычисления площади:
S(G)=∫27(x-x+2)dx=x22-23·(x+2)3227==722-23·(7+2)32-222-23·2+232==492-18-2+163=596
Ответ: S(G)=596
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y=1x и y=-x2+4x-2.
Решение
Нанесем линии на график.
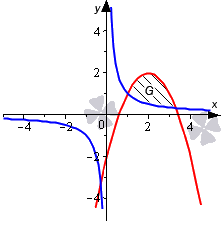
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1x и -x2+4x-2. При условии, что x не равно нулю, равенство 1x=-x2+4x-2становится эквивалентным уравнению третьей степени -x3+4×2-2x-1=0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х=1: -13+4·12-2·1-1=0.
Разделив выражение -x3+4×2-2x-1 на двучлен x-1, получаем: -x3+4×2-2x-1⇔-(x-1)(x2-3x-1)=0
Оставшиеся корни мы можем найти из уравнения x2-3x-1=0:
x2-3x-1=0D=(-3)2-4·1·(-1)=13×1=3+132≈3.3 ; x2=3-132≈-0.3
Мы нашли интервал x∈1; 3+132, на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S(G)=∫13+132-x2+4x-2-1xdx=-x33+2×2-2x-ln x13+132==-3+13233+2·3+1322-2·3+132-ln3+132—133+2·12-2·1-ln 1=7+133-ln3+132
Ответ: S(G)=7+133-ln3+132
Необходимо вычислить площадь фигуры, которая ограничена кривыми y=x3, y=-log2x+1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y=-log2x+1 из графика y=log2x, если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у=0.
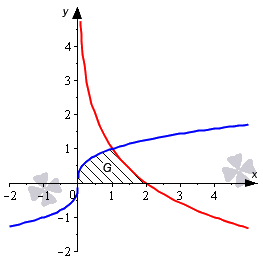
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y=x3 и y=0 пересекаются в точке (0;0). Так получается потому, что х=0 является единственным действительным корнем уравнения x3=0.
x=2 является единственным корнем уравнения -log2x+1=0, поэтому графики функций y=-log2x+1 и y=0 пересекаются в точке (2;0).
x=1 является единственным корнем уравнения x3=-log2x+1. В связи с этим графики функций y=x3 и y=-log2x+1 пересекаются в точке (1;1). Последнее утверждение может быть неочевидным, но уравнение x3=-log2x+1 не может иметь более одного корня, так как функция y=x3 является строго возрастающей, а функция y=-log2x+1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x∈0; 1, а вторая ниже красной линии на отрезке x∈1;2. Это значит, что площадь будет равна S(G)=∫01x3dx+∫12(-log2x+1)dx.
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x∈0; 2, а вторая между красной и синей линиями на отрезке x∈1; 2. Это позволяет нам найти площадь следующим образом:
S(G)=∫02x3dx-∫12×3-(-log2x+1)dx
В этом случае для нахождения площади придется использовать формулу вида S(G)=∫cd(g2(y)-g1(y))dy. Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y.
Разрешим уравнения y=x3 и -log2x+1 относительно x:
y=x3⇒x=y3y=-log2x+1⇒log2x=1-y⇒x=21-y
Получим искомую площадь:
S(G)=∫01(21-y-y3)dy=-21-yln 2-y4401==-21-1ln 2-144–21-0ln 2-044=-1ln 2-14+2ln 2=1ln 2-14
Ответ: S(G)=1ln 2-14
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x, y=23x-3, y=-12x+4.
Решение
Красной линией нанесем на график линию, заданную функцией y=x. Синим цветом нанесем линию y=-12x+4, черным цветом обозначим линию y=23x-3.
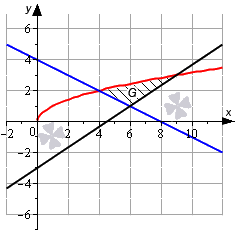
Отметим точки пересечения.
Найдем точки пересечения графиков функций y=x и y=-12x+4 :
x=-12x+4ОДЗ: x≥0x=-12x+42⇒x=14×2-4x+16⇔x2-20x+64=0D=(-20)2-4·1·64=144×1=20+1442=16; x2=20-1442=4Проверка:x1=16=4, -12×1+4=-12·16+4=-4⇒x1=16 не является решением уравненияx2=4=2, -12×2+4=-12·4+4=2⇒x2=4 является решением уравниния ⇒(4; 2) точка пересечения y=x и y=-12x+4
Найдем точку пересечения графиков функций y=x и y=23x-3:
x=23x-3ОДЗ: x≥0x=23x-32⇔x=49×2-4x+9⇔4×2-45x+81=0D=(-45)2-4·4·81=729×1=45+7298=9, x245-7298=94Проверка:x1=9=3, 23×1-3=23·9-3=3⇒x1=9 является решением уравнения ⇒(9; 3) точка пересечания y=x и y=23x-3×2=94=32, 23×1-3=23·94-3=-32⇒x2=94 не является решением уравнения
Найдем точку пересечения линий y=-12x+4 и y=23x-3:
-12x+4=23x-3⇔-3x+24=4x-18⇔7x=42⇔x=6-12·6+4=23·6-3=1⇒(6; 1) точка пересечения y=-12x+4 и y=23x-3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
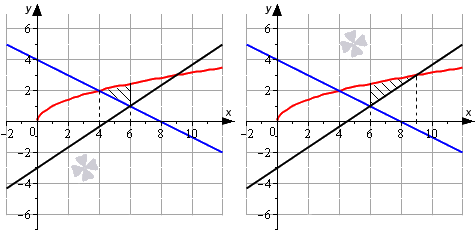
Тогда площадь фигуры равна:
S(G)=∫46x–12x+4dx+∫69x-23x-3dx==23×32+x24-4×46+23×32-x23+3×69==23·632+624-4·6-23·432+424-4·4++23·932-923+3·9-23·632-623+3·6==-253+46+-46+12=113
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
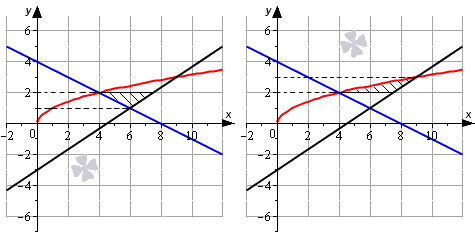
Тогда решим уравнение линии относительно x, а только после этого применим формулу вычисления площади фигуры.
y=x⇒x=y2 красная линияy=23x-3⇒x=32y+92 черная линияy=-12x+4⇒x=-2y+8 синяя линия
Таким образом, площадь равна:
S(G)=∫1232y+92–2y+8dy+∫2332y+92-y2dy==∫1272y-72dy+∫2332y+92-y2dy==74y2-74y12+-y33+3y24+92y23=74·22-74·2-74·12-74·1++-333+3·324+92·3–233+3·224+92·2==74+2312=113
Как видите, значения совпадают.
Ответ: S(G)=113
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
- Примеры с решением
Рассмотрим функцию  , которая непрерывна на отрезке
, которая непрерывна на отрезке  и принимает на этом промежутке неотрицательные значения. Фигуру, ограниченную графиком функции
и принимает на этом промежутке неотрицательные значения. Фигуру, ограниченную графиком функции  и прямыми
и прямыми  ,
,  и
и  , называют криволинейной трапецией.
, называют криволинейной трапецией.
На рисунке 26.1 приведены примеры криволинейных трапеций.

Рассмотрим теорему, которая позволяет вычислять площади криволинейных трапеций.
Теорема 26.1.
Площадь  криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции  и прямыми
и прямыми  ,
,  и
и 
 , можно вычислить по формуле
, можно вычислить по формуле

где  — любая первообразная функции
— любая первообразная функции  на отрезке
на отрезке  .
.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Доказательство. Рассмотрим функцию  , где
, где  , которая определена таким правилом.
, которая определена таким правилом.
Если  , то
, то  ; если
; если  , то
, то  — это площадь криволинейной трапеции, показанной штриховкой на рисунке 26.2.
— это площадь криволинейной трапеции, показанной штриховкой на рисунке 26.2.
Докажем, что  для всех
для всех  .
.
Пусть  — произвольная точка отрезка
— произвольная точка отрезка  и
и  — приращение аргумента в точке
— приращение аргумента в точке  , Ограничимся рассмотрением случая, когда
, Ограничимся рассмотрением случая, когда  (случай, когда
(случай, когда  , рассматривают аналогично).
, рассматривают аналогично).
Имеем: 
Получаем, что  — это площадь криволинейной трапеции, заштрихованной на рисунке 26.3.
— это площадь криволинейной трапеции, заштрихованной на рисунке 26.3.

На отрезке  как на стороне построим прямоугольник, площадь которого равна
как на стороне построим прямоугольник, площадь которого равна  (рис. 26.4). Длины сторон этого прямоугольника равны
(рис. 26.4). Длины сторон этого прямоугольника равны  и
и  , где
, где  — некоторая точка промежутка
— некоторая точка промежутка  . Тогда
. Тогда  Отсюда
Отсюда 
Если  , то
, то  .
.
Возможно вам будут полезны данные страницы:
Поскольку функция  непрерывна в точке
непрерывна в точке  , то
, то  . Отсюда, если
. Отсюда, если  , то
, то 
Имеем

Поскольку  — произвольная точка области определения функции
— произвольная точка области определения функции  , то для любого
, то для любого  выполняется равенство
выполняется равенство  . Получили, что функция
. Получили, что функция  является одной из первообразных функции
является одной из первообразных функции  на отрезке
на отрезке  .
.
Пусть  — некоторая первообразная функции
— некоторая первообразная функции  на отрезке
на отрезке  . Тогда по основному свойству первообразной можно записать
. Тогда по основному свойству первообразной можно записать

где  — некоторое число.
— некоторое число.
Имеем:

По определению функции  искомая площадь
искомая площадь  криволинейной трапеции равна
криволинейной трапеции равна  . Следовательно,
. Следовательно,

Примеры с решением
Пример 1.
Найдите площадь  фигуры, ограниченной графиком функции
фигуры, ограниченной графиком функции  и прямыми
и прямыми  ,
,  и
и 
Решение:
На рисунке 26.5 изображена криволинейная трапеция, площадь которой требуется найти.

Одной из первообразных функции  на отрезке
на отрезке  является функция
является функция  Тогда
Тогда

Пример 2.
Найдите площадь  фигуры, ограниченной графиком функции
фигуры, ограниченной графиком функции  и прямой
и прямой  .
.
Решение:
График функции  пересекает прямую
пересекает прямую  в точках
в точках  и
и  (рис. 26.6). Тогда фигура, площадь которой требуется найти, является криволинейной трапецией, ограниченной графиком функции
(рис. 26.6). Тогда фигура, площадь которой требуется найти, является криволинейной трапецией, ограниченной графиком функции  и прямыми
и прямыми 


Одной из первообразных функции  на отрезке
на отрезке  является функция
является функция  Тогда
Тогда
Определение. Пусть
— первообразная функции
на промежутке
, числа
и
, где
, принадлежат промежутку
. Разность
называют определенным интегралом функции
на отрезке
.
Определенный интеграл функции  на отрезке
на отрезке  обозначают
обозначают  (читают: «интеграл от
(читают: «интеграл от  до
до  эф от икс де икс»). Следовательно,
эф от икс де икс»). Следовательно,


где  — произвольная первообразная функции
— произвольная первообразная функции  на промежутке
на промежутке  .
.
Например, функция  является первообразной функции
является первообразной функции  на промежутке
на промежутке  . Тогда для произвольных чисел
. Тогда для произвольных чисел  и
и  , где
, где  , можно записать:
, можно записать:

Заметим, что значение разности  не зависит от того, какую именно первообразную функции
не зависит от того, какую именно первообразную функции  выбрали. Действительно, каждую первообразную
выбрали. Действительно, каждую первообразную  функции
функции  на промежутке
на промежутке  можно представить в виде
можно представить в виде  , где
, где  — некоторая постоянная. Тогда
— некоторая постоянная. Тогда

Равенство (1) называют формулой Ньютона—Лейбница. Следовательно, для вычисления определенного интеграла  по формуле Ньютона-Лейбница надо:
по формуле Ньютона-Лейбница надо:
- найти любую первообразную
 функции
функции  на отрезке
на отрезке  ;
; - вычислить значение первообразной
 в точках
в точках  и
и  ;
; - найти разность
 .
.
При вычислении определенных интегралов разность  обозначают
обозначают 
Используя такое обозначение, вычислим, например,  Имеем:
Имеем:

Пример 3.
Вычислите 
Решение:
Имеем:

Если функция  имеет первообразную
имеет первообразную  на отрезке
на отрезке  и
и  , то из формулы Ньютона-Лейбница следует такое свойство определенного интеграла:
, то из формулы Ньютона-Лейбница следует такое свойство определенного интеграла:

Действительно,

Если каждая из функций  и
и  имеет первообразную на отрезке
имеет первообразную на отрезке  , то, используя теоремы 25.1 и 25.2, можно доказать (сделайте это самостоятельно) такие свойства определенного интеграла:
, то, используя теоремы 25.1 и 25.2, можно доказать (сделайте это самостоятельно) такие свойства определенного интеграла:

-
 где
где  — некоторое число.
— некоторое число.
Формула Ньютона-Лейбница позволяет установить связь между определенным интегралом и площадью  криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции  и прямыми
и прямыми  ,
,  и
и  (
( ).
).
Используя теорему 26.1, можно записать:

Заметим, что в этой формуле рассматриваются непрерывные функции  , которые на отрезке
, которые на отрезке  принимают только неотрицательные значения. Однако определенный интеграл можно использовать для вычисления площадей более сложных фигур.
принимают только неотрицательные значения. Однако определенный интеграл можно использовать для вычисления площадей более сложных фигур.
Рассмотрим непрерывные на отрезке  функции
функции  и
и  такие, что для всех
такие, что для всех  выполняется неравенство
выполняется неравенство 
Покажем, как найти площадь
фигуры
, ограниченной графиками функций
и
и прямыми
и
(рис. 26.7).
Перенесем фигуру  вверх на
вверх на  единиц так, чтобы полученная фигура
единиц так, чтобы полученная фигура  находилась выше оси абсцисс (рис. 26.8). Фигура
находилась выше оси абсцисс (рис. 26.8). Фигура  ограничена графиками функций
ограничена графиками функций  и
и  и прямыми
и прямыми  ,
,  .
.

Поскольку фигуры  и
и  имеют равные площади, то искомая площадь
имеют равные площади, то искомая площадь  равна разности
равна разности 
где  — площадь криволинейной трапеции, ограниченной графиком функции
— площадь криволинейной трапеции, ограниченной графиком функции  и прямыми
и прямыми  ,
,  и
и  (рис. 26.9, а);
(рис. 26.9, а);
 — площадь криволинейной трапеции, ограниченной графиком функции
— площадь криволинейной трапеции, ограниченной графиком функции  и прямыми
и прямыми  ,
,  и
и  (рис. 26.9, б).
(рис. 26.9, б).

Таким образом, используя свойства определенного интеграла, можем записать:

Следовательно, если функции  и
и  непрерывны на отрезке
непрерывны на отрезке  и для всех
и для всех  выполняется неравенство
выполняется неравенство  то площадь
то площадь  фигуры, ограниченной графиками функций
фигуры, ограниченной графиками функций  и
и  и прямыми
и прямыми  и
и  , можно вычислить по формуле
, можно вычислить по формуле

Пример 4.
Найдите площадь  фигуры, ограниченной графиками функций
фигуры, ограниченной графиками функций  и
и 
Решение:
На рисунке 26.10 изображена фигура, площадь которой требуется найти.

Решив уравнение  , устанавливаем, что графики функций
, устанавливаем, что графики функций  и
и  пересекаются в двух точках с абсциссами
пересекаются в двух точках с абсциссами  и
и  .
.
Тогда искомая площадь




Лекции:
- Экспонента, натуральные логарифмы и гиперболические функции
- Непрерывная случайная величина
- Математическое ожидание и дисперсия случайной величины
- Исследование функции: пример решения
- Понятие функции. Теория пределов
- Элементарные функции комплексного переменного. Дробно-рациональные функции
- Равномерная сходимость функционального ряда
- Критерий Сильвестра
- Преобразования в пространстве и на плоскости
- Площадь поверхности подобных фигур
План урока:
Криволинейная трапеция и понятие определенного интеграла
Формула Ньютона-Лейбница
Задачи, связанные с определенным интегралом
Криволинейная трапеция и понятие определенного интеграла
Построим на плоскости график произвольной функции у(х), который полностью располагается выше горизонтальной оси Ох. Далее проведем две вертикальные линии, пересекающие ось Ох в некоторых точках a и b. В результате мы получим интересную фигуру, которая на рисунке показана штриховкой:

Особенностью этой фигуры является то, что одна из ее сторон (верхняя) – это не прямая линия, а какая-то произвольная кривая. Условно будем считать эту фигуру четырехугольником, ведь у нее действительно четыре угла и четыре стороны. Две из них (вертикальные красные линии), очевидно, параллельны друг другу. Две другие стороны (кривую линию и участок оси Ох) параллельными назвать никак нельзя.
Напомним, что в геометрии четырехугольник, у которого две стороны параллельны друг другу, а две другие не параллельны, называют трапецией. Поэтому полученную нами фигуру мы также назовем трапецией. Но так как одна из ее сторон кривая, то мы будем использовать термин «криволинейная трапеция», чтобы отличать ее от трапеции «настоящей».

У каждой плоской фигуры есть площадь, и криволинейная трапеция – не исключение. Но как ее подсчитать? Есть приближенный способ подсчета. Разобьем отрезок [a; b] на несколько более мелких отрезков, и построим на каждом из них прямоугольник:

Обозначим площадь первого прямоугольника как S1, площадь второго прямоугольника – как S2 и т. д. Мы строим прямоугольники таким образом, что их левая сторона в точности равна значению функции в соответствующей точке. Обозначим те точки, на которых стоят стороны прямоугольника, как х1, х2, х3 и т. д. Тогда значения функции в этих точках будут соответственно равны у(х1), у(х2) и т. д.:
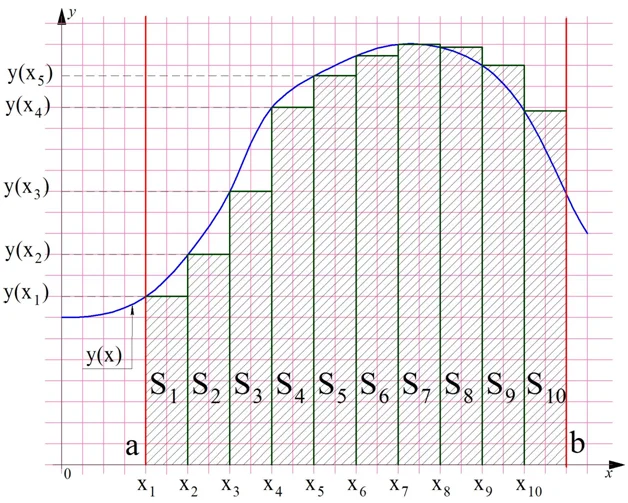
Площадь каждого полученного прямоугольника подсчитать несложно – она равна произведению его высоты на ширину. Мы организовали разбиение на прямоугольники таким образом, что ширина у них одинакова. Обозначим ее как ∆х. Тогда площадь каждого отдельного прямоугольника равна

Тогда общая площадь криволинейной трапеции приближенно будет равна сумме площадей всех треугольников:

где n – это количество прямоугольников (на рисунках мы выбрали n = 10).
Ясно, что чем больше число n, тем более точное приближение мы получим. Например, если разбить трапецию уже не на 10, а на 20 прямоугольников, то получим такую картинку:
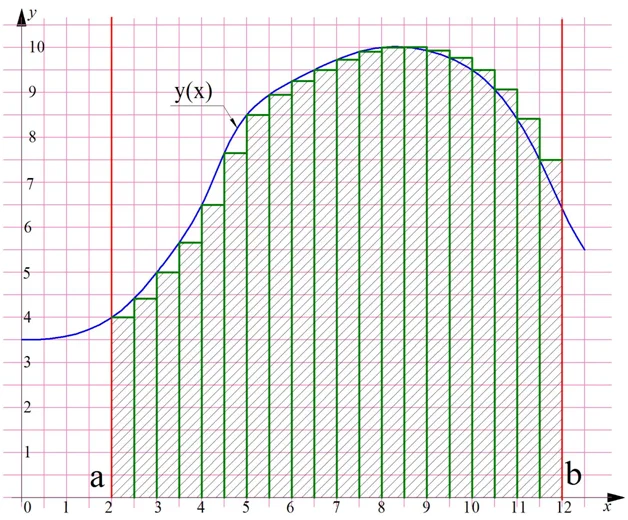
Обратите внимание, что ширина каждого прямоугольника, то есть величина ∆х, уменьшилась.
При росте числа n ошибка при оценке площади трапеции будет уменьшаться и стремится к нулю. Поэтому в предельном случае, когда n стремится к бесконечности, в формуле (1) вместо знака приближенного равенства «≈» можно поставить знак «=». При этом величина ∆х также будет стремится к нулю, то есть становится бесконечно малой. В математике для таких величин вместо символа ∆ принято использовать букву d, то есть вместо ∆х мы напишем dx. С учетом всего этого формула (1) примет вид:

В правой части стоит сумма бесконечного числа слагаемых. У нее есть специальное название – определенный интеграл. Ясно, что величина этой суммы, то есть площадь трапеции, зависят от чисел а и b (боковых границ трапеции). Поэтому обозначение интеграла выглядит так:

Обозначение очень похоже на неопределенный интеграл. Единственное отличие – это появление чисел а и b, которые определяют боковые границы трапеции. Число b называют верхним пределом интегрирования, а число a– нижним пределом интегрирования. Дадим более строгое определение понятию определенного интеграла.

Геометрический смысл определенного интеграла заключается в том, что он равен площади криволинейной трапеции, ограниченной графиком функции у(х) и вертикальными прямыми, проходящими через точки а и b.

Формула Ньютона-Лейбница
Изначально мы хотели научиться вычислять площадь криволинейной трапеции, однако пока что мы лишь придумали, как ее обозначать – через определенный интеграл. Но как вычислить значение его значение? Оказывается, определенный интеграл очень тесно связан с неопределенным интегралом, и эта связь описывается формулой Ньютона-Лейбница.
Ещё раз построим криволинейную трапецию, а ее площадь обозначим как S. Пусть ее левая граница совпадает с осью Оу, а правая будет равна некоторому значению х0. Дело в том, что нас будет интересовать зависимость площади трапеции от значения ее правой границы, то есть некоторая функция S(x). Обозначим площадь получившейся трапеции как S(x0):

Теперь сдвинем правую границу вправо на величину ∆х. В итоге получим новую трапецию, площадь которой можно записать как S(x0 + ∆x). При этом ее площадь увеличилась на некоторую величину ∆S:

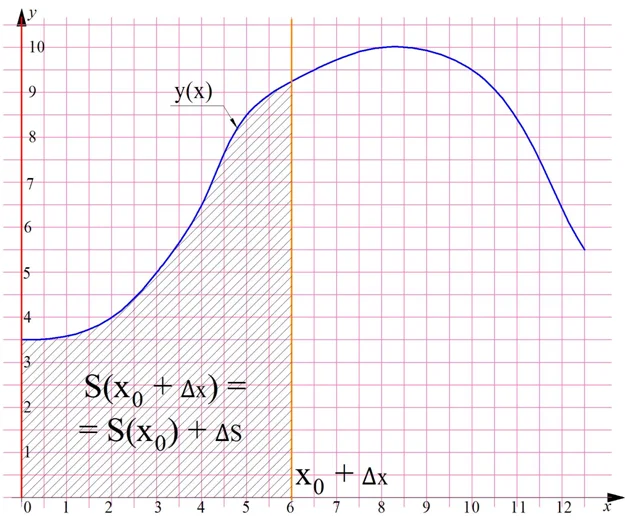
Получается, что мы дали некоторое приращение аргумента ∆х, и получили приращение функции ∆S. Мы уже выполняли похожие действия в рамках предыдущих уроков, изучая понятие производной.
Итак, мы можем записать, что
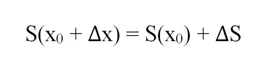
Оценим величину ∆S. Если заменить соответствующую площадь прямоугольником, то его площадь окажется равной произведению ширины прямоугольника (она равна ∆x) на высоту, которая равна у(х0):

Поделим обе части равенства (2) на величину ∆х и получим:

А теперь устремим величину ∆х к нулю. В результате в равенство (2), а значит, и (3) будет становиться все более точным. В итоге мы можем написать, что

Хорошо подумайте, что мы получили. Вспомните определение производной. Оказывается, в левой части равенства (4) стоит не что иное, как производная функции S! То есть мы можем написать, что

Получается, что производная функции S на равна значению функции у(х). А это значит, что она является ее первообразной:

Здесь F(x) – первообразная функции у(х), а F(x0) – конкретное значение этой первообразной в точке х0.
Теперь рассмотрим более привычную криволинейную трапецию, у которой правой и левой границей являются числа а и b:
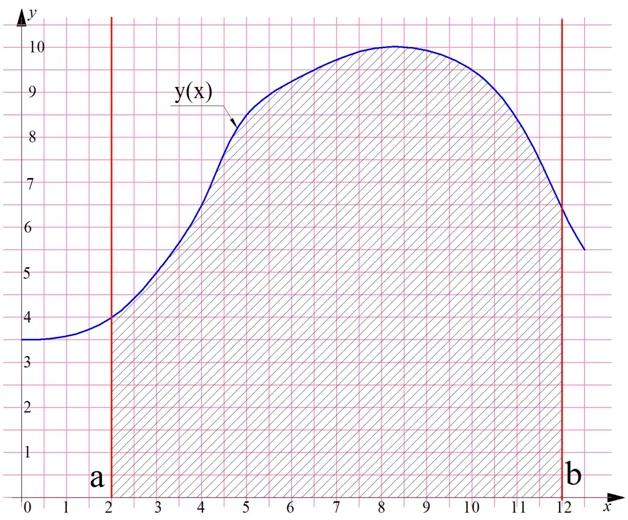
Как найти ее площадь? С помощью формулы (5) мы можем найти две площади:

Из рисунков очевидно, что площадь интересующей нас трапеции равна разности величин S(b) и S(a):

Эту площадь мы и обозначаем определенным интегралом. То есть можно записать, что

Таким образом, чтобы найти площадь криволинейной трапеции, необходимо проинтегрировать функцию у(х), а потом в полученную первообразную подставить числа а и b вычесть один результат из другого.
Для примера вычислим площадь криволинейной трапеции, ограниченной линией у = х2 и вертикальными прямыми х = 1 и х = 3.

Сначала находим первообразную функции у = х2, взяв от нее интеграл (неопределенный):

Отметим, что в обоих случаях речь идет об одной и той же первообразной, поэтому значения констант С у них одинаковы. Теперь вычитаем из F(3) величину F(1):

Константы интегрирования сократились. Для простоты решение записывают в несколько более короткой форме. Сначала сразу после определенного интеграла пишут первообразную (то есть находят неопределенный интеграл), причем без константы интегрирования

Далее ставят вертикальную черту и пишут пределы интегрирования, которые надо подставить в первообразную:
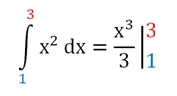
Потом ставят знак равно и подставляют в первообразную верхнее и нижнее число, после чего выполняют оставшиеся арифметические действия:

Задание. Вычислите

Задание. Найдите площадь фигуры, ограниченной полуволной синусоиды и осью Ох.
Решение. Сначала построим схематичный график у = sinx, чтобы понять, что именно нам надо вычислить:

Теперь ясно, что надо произвести вычисление определенного интеграла синуса на отрезке [0; π]:

Итак, мы теперь знаем и про определенный, и про неопределенный интеграл. Хотя они и очень похожи, между ними есть большая разница, и ее важно понимать. Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции. Формула Ньютона-Лейбница как раз и показывает ту связь, которая есть между двумя этими различными понятиями.
Может ли определенный интеграл быть отрицательным числом? Кажется, что нет, ведь площадь фигур не бывает отрицательной. Но не всё так просто. Рассмотрим случай, когда график функции является не верхней, а нижней границей трапеции. Например, пусть трапеция образована функцией

Просто надо найти определенный интеграл:

Получили отрицательное значение. Дело в том, что фигура располагается под осью Ох. Из-за этого ее площадь получается со знаком минус.
Рассмотрим ещё один пример. Найдем интеграл косинуса на промежутке от 0 до 2π:

Получился ноль. Посмотрим на графике, какую же площадь мы посчитали:
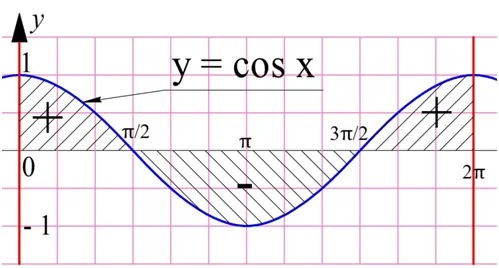
Оказывается, график на отрезке дважды пересекает ось Ох. В результате получается сразу три криволинейных трапеции. Две из них расположены выше оси Ох, а потому из площади считаются со знаком «+». Третья трапеция лежит ниже оси Ох, а потому ее площадь считается со знаком «–». То, что интеграл оказался равным нулю, означает, что площадь нижней трапеции в точности равна сумме площадей двух верхних фигур, поэтому в сумме они и дали ноль.
Отметим важное свойство определенного интеграла:

Проиллюстрируем это правило графически. Каждый из этих интегралов равен площади соответствующих криволинейных трапеций:

Задачи, связанные с определенным интегралом
Определенный интеграл помогает находить и площади более сложных фигур, которые получаются при пересечении нескольких различных графиков.
Рассмотрим задачу на интеграл. Пусть требуется найти площадь фигуры, полученной при пересечении параболы


Сначала найдем точки пересечения графиков. Для этого приравняем функции:

Корнями этого квадратного уравнения являются числа 1 и 4. Именно в этих точках и пересекаются графики (это и так видно из графика). Площадь интересующей нас фигуры можно получить вычитанием из одной криволинейной трапеции другой:

Величины S1и S2 можно вычислить через определенный интеграл. Обратите внимание, что найденные нами корни являются пределами интегрирования:
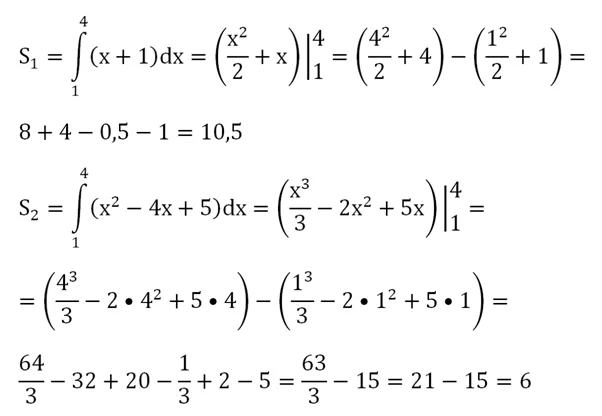
Тогда искомая нами площадь составит

Ошибочно думать, что определенные интегралы нужны только для расчета площадей. С их помощью можно и решать ряд физических задач. Пусть известен закон изменения скорости тела v(t). Можно доказать, что путь, пройденный этим телом за период времени с t1по t2, будет равен интегралу

Задание. Самолет разгоняется, однако из-за сопротивления воздуха он набирает скорость не равномерно. Скорость самолета в момент времени t может быть вычислена по формуле

Определите, какое расстояние пролетит самолет в период времени между 16-ой и 25-ой секундой разгона.
Решение. Задача сводится к простому вычислению интеграла:

Ответ: 610 метров.
Этот пример показывает важную зависимость между скоростью тела и путем, который она преодолевает. Если есть график изменения скорости тела, то площадь под этим графиком равна тому пути, которое проходит тело:
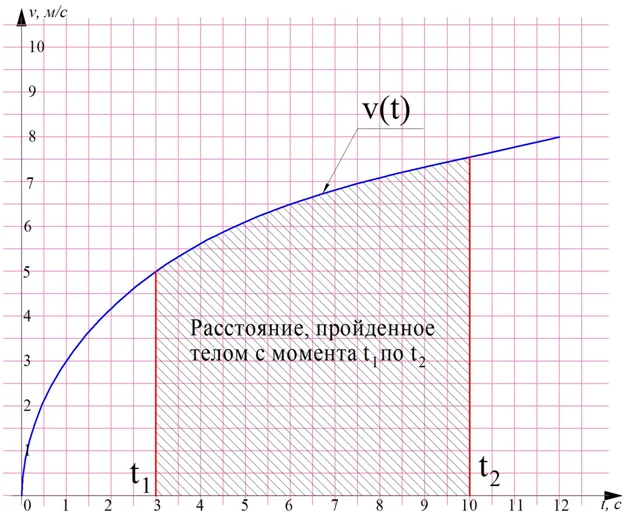
Действительно, если тело двигается равномерно (то есть с постоянной скоростью), то путь, пройденный им, может быть вычислен по известной формуле

Но если построить для такого случая график v(t), то он будет выглядеть как горизонтальная прямая линия. Тогдафигура под графиком окажется прямоугольником, чья площадь равна произведению длины и ширины:

Заметим, что зависимость между путем, скоростью временем носит линейный характер, и именно поэтому здесь может быть использован неопределенный интеграл. Но ведь в физике очень много линейных зависимостей! И во всех этих случаях интегралы играют огромную роль!
Рассмотрим задачу. Есть пружина, которая изначально находится в нерастянутом состоянии. Потом человек начинает медленно и с постоянной скоростью, растягивать пружину, увеличивая ее длину на 0,5 метра. Жесткость пружины (ее коэффициент упругости) равна 100 Н/м. Какую работу совершил человек при растягивании пружины?
Из средней школы известна следующая формула для вычисления работы:
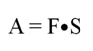
где F– сама сила, а S– путь, пройденный телом под действием этой силы. Легко заметить, что эта формула похожа на ранее рассмотренную зависимость пути от скорости и времени (они обе являются линейными). Сначала рассмотрим простой случай, когда сила остается неизменной. Тогда можно построить график F(S). Окажется, что площадь под графиком как раз равна работе, совершенной силой:

Случай с пружиной сложнее, ведь сила при растяжении пружины не остается неизменной. Чем сильнее растянута пружина, с тем большей силой ее приходится тянуть. Известен закон Гука, связывающий удлинение пружины с силой ее натяжения:

где k – коэффициент жесткости пружины, а x– ее удлинение. По смыслу задачи максимальное удлинение известно и равно 0,5 м. Можно нарисовать такой график зависимости силы натяжения пружины от ее удлинения (он будет выглядеть как прямая линия, так как эта зависимость является прямой пропорциональностью):

И в данном случае работа также будет равна площади под графиком функции, то есть ее можно посчитать с помощью определенного интеграла! В качестве пределов интегрирования надо взять крайние значения удлинения пружины (это 0 и 0,5 м), а качестве интегрируемой функции – F(t), которая равна

Существует и много других примеров приложений определенного интеграла. С его помощью можно находить объемы сложных фигур (конуса, пирамиды, тел вращения), определять центр масс тел сложной формы. Следует отметить и использование интегралов в механике при решении задач, в которых сила действует не на конкретную точку, а на площадь (задачи на распределенную нагрузку). В качестве примера можно привести расчет прочности крыши, на которой лежит слой снега.Но для их рассмотрения необходим более высокий уровень математических и физических знаний, который можно получить уже в рамках не среднего, а высшего образования.
Алгебра и начала математического анализа, 11 класс
Урок №23.Площадь криволинейной трапеции. Интеграл и его свойства.
Перечень вопросов, рассматриваемых в теме
1) Нахождение определенного интеграла
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница

Формула Ньютона – Лейбница
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции


формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).
Примеры и разбор решения заданий тренировочного модуля
№1.Найти площадь криволинейной трапеции, изображенной на рисунке

Решение
Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.

Ответ: 
№2. Вычислить определенный интеграл:
Решение: Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) – F(а), это и будет ответ.

№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) – F(а), это и будет ответ.

