Понятие “Множество” в математике и
информатике играет очень важную роль. В
математике существует целая теория множеств.
Первое знакомство с данной темой может быть у
учащихся как в начальной школе, если у них есть
курс информатики, так и у учащихся 5-6 классов,
которые раньше не изучали информатику. Данный
материал подготовлен для учащихся 5-6 классов.
Теме “Множества” желательно посвятить как
минимум 2 урока. Материал может быть полезен и для
преподавания информатики в начальной школе.
В курсе А.В. Горячева “Информатика в играх и
задачах”, рассчитанного на учащихся начальной
школы, тема “Множества” рассматривается и во 2
классе, и в 3 и в 4 классах. Естественно, что эта
тема прорабатывается с детьми не один урок, а
задания постепенно усложняются.
1. На первом уроке по теме “Множества” важно
сразу же дать четкие определения тех терминов,
которые потом будут использоваться в самых
различных заданиях. Урок основан на
использовании презентации (см.
Приложение 1).
Множество произошло от слова “много”. Но в
математике понятие “множество” используется
более широко.
Множество может объединять любое
количество предметов, чисел, существ. Каждый
предмет множества называется элементом
множества.
Множество, которое не содержит элементов,
называется пустым.
Множество может иметь подмножества.
Множества могут пересекаться, не
пересекаться, объединяться.
Равными называются множества, состоящие из одинакового
числа одинаковых элементов.
(Желательно, чтобы эти определения были
записаны учащимися в тетрадь, чтобы потом они
могли к ним вернуться.)
Эти определения необходимо закрепить на
простейших примерах, например: множество
животных имеет несколько подмножеств: рыбы,
птицы, звери, насекомые – и они не пересекаются.
Если же мы возьмем множество морских животных,
то оно будет пересекаться с множеством птиц и
множеством зверей (приводятся несколько
примеров). В качестве пустого множества можно
дать такой пример: в яркий солнечный день на небе
нет облаков, поэтому в этот день множество
облаков (такое множество естественно существует)
– пустое, а в другой день оно уже не будет пустым.
Этот пример используется в тетради А.В. Горячева
“Информатика в играх и задачах” 3 класс, часть 2.
Можно привести и другие примеры, когда какое-то
множество в конкретной ситуации будет пустым.
Также для удобства выполнения различных
заданий необходимо ввести систему обозначения
множеств (геометрические фигуры), подчеркнув,
что это только условное обозначение, но оно очень
удобно. Элементы множеств обозначаются точками.
Для закрепления понятия “элементы множества”
учащимся предлагается следующее задание 1 (приложение 2) (его можно давать
как домашнее задание, которое вклеивается в
тетрадь).
2. Далее вводятся понятия, связанные с
использованием логических связок в названиях
множеств.
В названиях множеств и высказываниях могут
употребляться логические связки: “и”, “не”,
“или” и их комбинация: “не … и”, “не …
или”. “не … и не …”
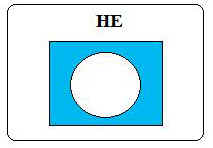
Если в названии множества есть связка “не”,
то его элементы находятся за пределами фигуры,
обозначающей это множество.
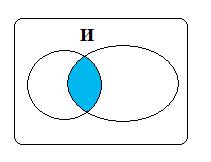
Если в названии множества есть связка “и”,
то его элементы находятся на пересечении фигур,
обозначающих множества.
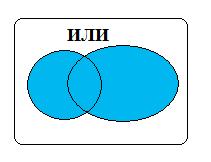
Если в названии множества есть связка “или”,
то это означает, что его элементы находятся в
нескольких фигурах.
Эти схемы также необходимо закрепить с
учащимися на разных примерах, включенных в
задания в тетради (курс Горячева для начальной
школы), а также на тех, где они сами приводят
примеры различных множеств. Для закрепления
понятий пересечения и объединения множеств
учащимся предлагается дополнительное задание 2.
3. На следующем(их) уроке(ах) следует продолжить
подробный разбор заданий, например, включив
задания на пересечение трех множеств. (Желательно
также, чтобы эти схемы были зарисованы учащимися
в тетрадях).
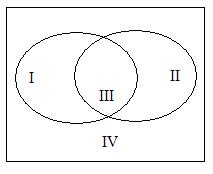
При пересечении 2-х множеств образуется IV
области: 2 области без пересечения, одна область
пересечения множеств и одна область, лежащая за
пределами выделенных множеств.
При пересечении 3-х множеств образуется VIII
областей: 3 области без пересечения, 4 области
пересечения множеств и 1 область, лежащая за
пределами выделенных множеств.
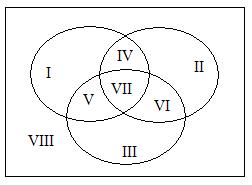
Обозначение множеств:
При пересечении двух множеств
закрашивается вся область пересечения этих
множеств. При объединении двух множеств
закрашиваются оба множества. При пересечении
трех множеств закрашивается общая часть всех
трех множеств. При отрицании всех трех
множеств закрашивается область, не включающая в
себя сами множества.
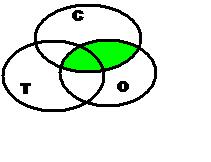
Данные схемы сделаны для задания, когда надо
распределить слова, в состав которых входят
буквы “С”, “Т” и “О”. Набор слов должен
включать слова только с “Т”, только с “С”,
только с “О”, а также одновременно с двумя и
тремя буквами. Два-три слова должны быть без букв
“С”, “Т”, “О”. (Например: рельсы, купе,
проводник, скорость, колесо, электровоз, тамбур,
вагон, сумка, место, шпалы, поезд, машинист, билет,
состав, дверь, станция).
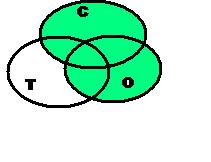
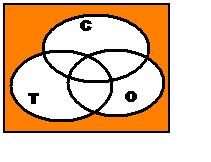
В курсе информатики А.В. Горячева в тетради 2
класса есть аналогичное задание на множества
“Круглые”, “Желтые”, “Шары”.
Закрепление теоретического материала должно
сопровождаться решением задач. Простейшие
задачи, например, “Про коз и коров”, “Фиалки и
подруги”, “Газеты и журналы” могут быть
использованы даже во 2 классе (см. приложение
4). Для более сильных учеников и для более
старших классов, соответственно, можно подобрать
задачи нужного уровня, а можно также
использовать какие-то задачи и для проведения
конкурсов, КВНов, школьных олимпиад, недели
математики и информатики. Подобные задачи удобно
решать, используя схему множеств и обозначая
элементы просто точками (если числа малые) или
указывая число элементов в соответствующей
области (в пересечении, без пересечения).
Задачи собраны из самых различных источников,
включая журнал “1 сентября. Информатика”, сайт
Малого Мехмата МГУ и другие сайты, посвященные
решению логических задач.
- Приложение 1. Презентация
“Множества” - Приложение 2. Задание 1.
- Приложение 3. Задание 2.
- Приложение 4. Дополнительные
задачи.
Список литературы.
- Горячев А.В., Горина К.И., Суворова Н.И.
“Информатика в играх и задачах” 2 кл., в 2-х ч. - Горячев А.В., Горина К.И., Суворова Н.И.
“Информатика в играх и задачах” 3 кл., в 2-х ч. - Горячев А.В., Горина К.И., Суворова Н.И.
“Информатика в играх и задачах” 4 кл., в 2-х ч. - Горячев А.В., Горина К.И., Суворова Н.И.
Методические рекомендации для учителя. 2 кл.. - Горячев А.В., Горина К.И., Суворова Н.И.
Методические рекомендации для учителя. 3 кл.. - Горячев А.В., Горина К.И., Суворова Н.И.
Методические рекомендации для учителя. 4 кл. - Горячев А.В., Суворова Н.И. Информатика. Логика и
алгоритмы. 3 кл. - Горячев А.В., Суворова Н.И. Информатика. Логика и
алгоритмы. 4 кл. - Журнал “1 сентября. Информатика”. Сайт https://inf.1sept.ru/
- Фестиваль “Открытый урок”. Сайт https://urok.1sept.ru/ раздел
“Информатика”. - Малый Мехмат МГУ. Сайт http://mmmf.msu.ru/.
- Сайт Логические задачи и головоломки http://www.smekalka.pp.ru/.
- Сайт Логические задачи, головоломки, загадки,
тесты – Лого-рай http://logo-rai.ru/
Множество — это коллекция, которая реализует основные математические операции над множествами: пересечения (intersection), объединение (union), разность (difference) и симметрическая разность (symmetric difference). Каждый из алгоритмов мы разберем в соответствующем разделе.
Также смотрите другие материалы этой серии: бинарное дерево, стеки и очереди, динамический массив, связный список, оценка сложности алгоритма и сортировка.
Множество
В математике множества — это коллекции объектов, у которых есть что-то общее. Например, мы можем объявить множество четных положительных целых чисел:
[2, 4, 6, 8, 10, ...]
Или множество нечетных положительных целых:
[1, 3, 5, 7, 9, ...]
В этих двух множествах нет общих элементов. Давайте теперь посмотрим на множество делителей числа 100:
[1, 2, 4, 5, 10, 20, 25, 50, 100]
Теперь мы можем узнать, какие делители числа 100 — нечетные, просто глядя на множество нечетных чисел и на множество делителей и выбирая те из чисел, которые присутствуют в обоих. Мы также можем ответить на вопрос: «Какие нечетные числа не являются делителями ста?» или «Какие положительные целые, четные или нечетные, не являются делителями ста?».
На первый взгляд это кажется не очень полезным, но это искусственный пример. Предположим, что у нас есть множество всех работников предприятия и множество работников, прошедших ежемесячную проверку. Тогда мы с легкостью сможем ответить на вопрос: «Кто из работников не прошел проверку?».
Мы также можем добавить различные множества и построить более сложный запрос, например: «Кто из штатных работников отдела продаж, имеющих корпоративную кредитную карточку, не прошел обязательный курс повышения квалификации?».
Класс Set
Класс Set реализует интерфейс IEnumerable и принимает аргумент типа, который является наследником IComparable, так как для работы алгоритмов нужна проверка элементов на равенство.
Элементы нашего множества будут храниться в экземпляре стандартного класса .NET List, но на практике для хранения обычно используются древовидные структуры, например, двоичное дерево поиска. Выбор внутреннего представления будет влиять на сложность алгоритмов работы с множеством. К примеру, при использовании списка метод Contains будет выполняться за O(n) времени, в то время как множество, реализованное с помощью дерева, будет работать в среднем за O(log n) времени.
Кроме методов для работы с множеством класс Set также имеет конструктор, который принимает IEnumerable с начальными элементами.
public class Set : IEnumerable
where T: IComparable
{
private readonly List _items = new List();
public Set()
{
}
public Set(IEnumerable items)
{
AddRange(items);
}
public void Add(T item);
public void AddRange(IEnumerable items);
public bool Remove(T item);
public bool Contains(T item);
public int Count
{
get;
}
public Set Union(Set other);
public Set Intersection(Set other);
public Set Difference(Set other);
public Set SymmetricDifference(Set other);
public IEnumerator GetEnumerator();
System.Collections.IEnumerator
System.Collections.IEnumerable.GetEnumerator();
}
Метод Add
- Поведение: Добавляет элементы в множество. Если элемент уже присутствует в множестве, бросается исключение
InvalidOperationException. - Сложность: O(n)
При реализации метода Add необходимо решить, будем ли мы разрешать дублирующиеся элементы. К примеру, если у нас есть мнжество:
[1, 2, 3, 4]
Если пользователь попытается добавить число 3, в результате получится:
[1, 2, 3, 3, 4]
В некоторых случаях это допустимо, но в нашей реализации мы не будем поддерживать дубликаты. Если представить, например, множество студентов колледжа, было бы нелогичным добавлять в него одного и того же студента дважды. На самом деле, попытка добавить элемент, который уже присутствует — скорее всего ошибка, и наша реализация класса Set воспринимает ее именно так.
Метод Add использует метод Contains, который будет рассмотрен далее.
public void Add(T item)
{
if (Contains(item))
{
throw new InvalidOperationException(
"Item already exists in Set"
);
}
_items.Add(item);
}
Метод AddRange
- Поведение: Добавляет несколько элементов в множество. Если какой-либо из добавляемых элементов присутствует в множестве, или в добавляемых элементах есть дублирующиеся, выбрасывается исключение
InvalidOperationException. - Сложность: O(m·n), где m — количество вставляемых элементов и n — количество элементов множества.
public void AddRange(IEnumerable items)
{
foreach (T item in items)
{
Add(item);
}
}
Метод Remove
- Поведение: Удаляет указанный элемент из множества и возвращает
true. В случае, если элемента нет, возвращаетfalse. - Сложность: O(n)
public bool Remove(T item)
{
return _items.Remove(item);
}
Метод Contains
- Поведение: Возвращает
true, если множество содержит указанный элемент. В противном случае возвращаетfalse. - Сложность: O(n)
public bool Contains(T item)
{
return _items.Contains(item);
}
Метод Count
- Поведение: Возвращает количество элементов множества или 0, если множество пусто.
- Сложность: O(1)
public int Count
{
get
{
return _items.Count;
}
}
Метод GetEnumerator
- Поведение: Возвращает итератор для перебора элементов множества.
- Сложность: Получение итератора — O(1), обход элементов множества — O(n).
public IEnumerator GetEnumerator()
{
return _items.GetEnumerator();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return _items.GetEnumerator();
}
Алгоритмы
Метод Union
- Поведение: Возвращает множество, полученное операцией объединения его с указанным.
- Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.
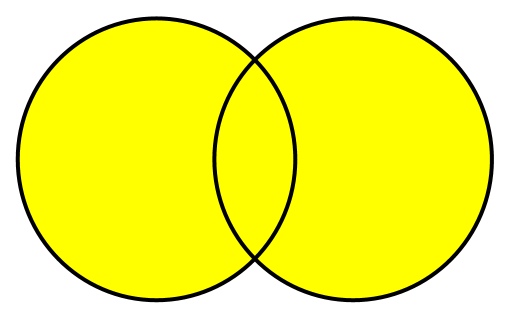
Объединение множеств — это множество, которое содержит элементы, присутствующие хотя бы в одном из двух.
Например, есть два множества (выделены красным):
При операции объединения выбираются элементы обоих множеств. Если элемент присутствует в обоих множествах, берется только одна его копия. Объединение двух множеств показано желтым цветом.
Такая диаграмма, наглядно показывающая операции над множествами, называется диаграммой Венна.
Другой пример с использованием множеств целых чисел:
[1, 2, 3, 4] union [3, 4, 5, 6] = [1, 2, 3, 4, 5, 6]
public Set Union(Set other)
{
Set result = new Set(_items);
foreach (T item in other._items)
{
if (!Contains(item))
{
result.Add(item);
}
}
return result;
}
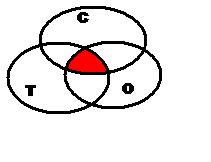
Метод Intersection
- Поведение: Возвращает множество, полученное операцией пересечения его с указанным.
- Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.
Пересечение множеств содержит только те элементы, которые есть в обоих множествах. Используя диаграмму Венна, пересечение можно изобразить так:
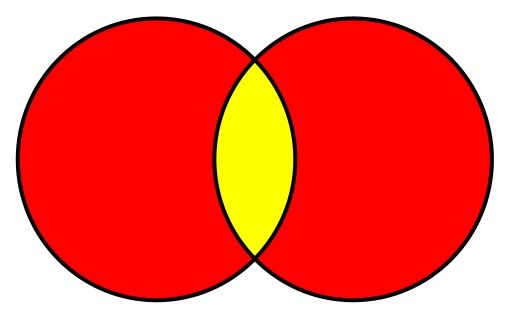
Или, используя целые числа:
[1, 2, 3, 4] intersect [3, 4, 5, 6] = [3, 4]
public Set Intersection(Set other)
{
Set result = new Set();
foreach (T item in _items)
{
if (other._items.Contains(item))
{
result.Add(item);
}
}
return result;
}
Метод Difference
- Поведение: Возвращает множество, являющееся разностью текущего с указанным.
- Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.
Разность множеств — это все элементы, которые содержатся в одном множестве (том, у которого вызывается метод), но не содержатся в другом (том, которое передается аргументом). Диаграмма Венна для разности множеств будет выглядеть так:
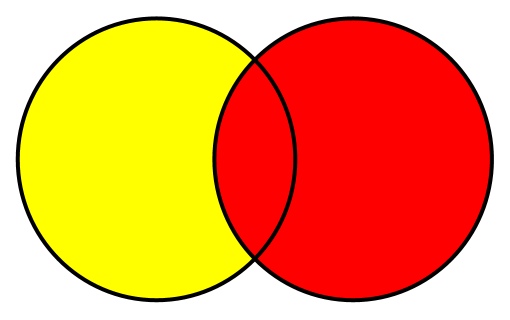
Или, используя целые числа:
[1, 2, 3, 4] difference [3, 4, 5, 6] = [1, 2]
public Set Difference(Set other)
{
Set result = new Set(_items);
foreach (T item in other._items)
{
result.Remove(item);
}
return result;
}
Метод Symmetric Difference
- Поведение: Возвращает множество, являющееся симметрической разностью текущего с указанным.
- Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.
Симметрическая разность — это все элементы, которые содержатся только в одном из рассматриваемых множеств. Диаграмма Венна для симметрической разности будет выглядеть так:
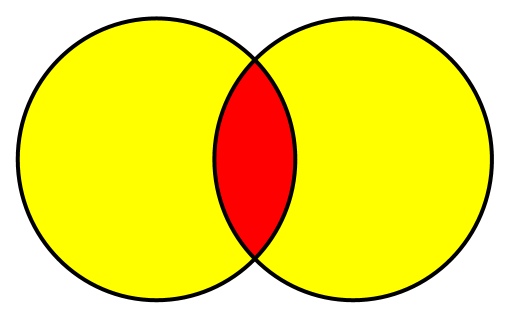
Или, используя целые числа:
[1, 2, 3, 4] symmetric difference [3, 4, 5, 6] = [1, 2, 5, 6]
Вы, возможно, заметили, что симметрическая разность — это «пересечение наоборот». Учитывая это, давайте попробуем найти ее, используя уже имеющиеся операции.
Итак, мы хотим получить множество, которое содержит все элементы из двух множеств, за исключением тех, которые есть в обоих. Другими словами, мы хотим получить разность объединения двух множеств и их пересечения.
Или, если рассматривать по шагам:
[1, 2, 3, 4] union [3, 4, 5, 6] = [1, 2, 3, 4, 5, 6] [1, 2, 3, 4] intersection [3, 4, 5, 6] = [3, 4] [1, 2, 3, 4, 5, 6] set difference [3, 4] = [1, 2, 5, 6]
Что дает нам нужный результат: [1, 2, 5, 6].
public Set SymmetricDifference(Set other)
{
Set union = Union(other);
Set intersection = Intersection(other);
return union.Difference(intersection);
}
Метод IsSubset
Вы, возможно, интересуетесь, почему мы не добавили метод IsSubset, который проверяет, содержится ли одно множество целиком в другом. Например:
[1, 2, 3] is subset [0, 1, 2, 3, 4, 5] = true
В то время, как:
[1, 2, 3] is subset [0, 1, 2] = false
Дело в том, что эту проверку можно провести, используя имещиеся методы. К примеру:
[1, 2, 3] difference [0, 1, 2, 3, 4, 5] = []
Пустое множество в результате говорит нам о том, что все элементы первого множества содержатся во втором, а значит, первое является подмножеством второго. Другой способ проверить это:
[1, 2, 3] intersection [0, 1, 2, 3, 4, 5] = [1, 2, 3]
Если в результате мы получим множество с таким же количеством элементов, что и изначальное, значит, оно является подмножеством второго.
В общем случае, конечно, класс Set может иметь метод IsSubset (который может быть реализован более эффективно). Однако стоит помнить, что это уже не какая-то новая возможность, а просто другое применение существующих.
Продолжение следует
На этом все, а в следующий раз мы перейдем к заключительной теме этого цикла статей — алгоритмам сортировки.
Перевод статьи «The Set Collection»

Множественный тип данных
Множество в языке Паскаль – это ограниченный набор различных элементов одного (базового) типа , которые рассматриваются как единое целое.

Базовый тип
- это совокупность значений, из которых могут быть образованы множества. В качестве базового типа может быть использован любой тип, кроме вещественного.
Значение переменной множественного типа может содержать любое количество различных элементов базового типа – от нуля элементов (пустое множество) до всех возможных значений базового типа (всего может быть не более 256 различных элементов).

Описание
- В разделе описания типов:
Type = set of ;
Var : ;
- В разделе описания переменных:
Var : set of ;
- Пример :
Type mnog_char = set of char;
Var mn1: mnog_char;
mn2: set of char;
mn3: set of ‘A’..’Z’;
s1: set of byte;
s2: set of 1000 .. 1200;
![Формирование множеств В программе элементы множества задаются в квадратных скобках, через запятую. Если элементы идут подряд друг за другом, то можно использовать диапазон. Пример: Type digit = set of 1..5; Var s: digit; Переменная s может принимать значения, состоящие из любой совокупности целых чисел от 1 до 5: [ ] – пустое множество; [1], [2], [3], [4], [5] - одноэлементные множества; [1,2],…[4,5] – двухэлементные; [1, 2, 3] – трехэлементное; [1, 2, 3, 4],… [2, 3, 4, 5] – четырехэлементные; [1, 2, 3, 4, 5] – полное множество (взяты все элементы базового типа)](https://fsd.multiurok.ru/html/2017/02/20/s_58ab30d245526/img3.jpg)
Формирование множеств
В программе элементы множества задаются в квадратных скобках, через запятую. Если элементы идут подряд друг за другом, то можно использовать диапазон.
- Пример:
Type digit = set of 1..5;
Var s: digit;
Переменная s может принимать значения, состоящие из любой совокупности целых чисел от 1 до 5:
[ ] – пустое множество;
[1], [2], [3], [4], [5] – одноэлементные множества;
[1,2],…[4,5] – двухэлементные; [1, 2, 3] – трехэлементное;
[1, 2, 3, 4],… [2, 3, 4, 5] – четырехэлементные;
[1, 2, 3, 4, 5] – полное множество (взяты все элементы базового типа)
![Операции над множествами Объединением двух множеств называется множество элементов, принадлежащих обоим множествам. Знак операции – « + ». Примеры: [‘A’, ’F’] + [‘B’, ’D’] = [‘A’,’F’,‘B’, ’D’]; [1..3, 5, 7, 11] + [3..8,10, 12, 15..20] = [1..8, 10..12, 15..20]; A1:=[‘a’, .. ‘z’]; A1:= A1 + [‘A’]; - к множеству A1 добавляем элемент. Тогда A1 = [‘A’, ‘a’ .. ‘z’]; А + В В А](https://fsd.multiurok.ru/html/2017/02/20/s_58ab30d245526/img4.jpg)
Операции над множествами
- Объединением двух множеств называется множество элементов, принадлежащих обоим множествам. Знак операции – « + ».
- Примеры:
- [‘A’, ’F’] + [‘B’, ’D’] = [‘A’,’F’,‘B’, ’D’];
- [1..3, 5, 7, 11] + [3..8,10, 12, 15..20] = [1..8, 10..12, 15..20];
- A1:=[‘a’, .. ‘z’]; A1:= A1 + [‘A’]; – к множеству A1 добавляем элемент. Тогда A1 = [‘A’, ‘a’ .. ‘z’];
А + В
В
А
![Операции над множествами Пересечением двух множеств называется множество элементов, принадлежащих одновременно и первому, и второму множеству, т.е. это общие элементы. Знак операции – « * ». Примеры: [‘A’, ’F’] * [‘B’, ’D’] =[ ] – так как общих элементов нет ; [1..3, 5, 7, 11] * [3..8,10, 12, 15..20] = [ 3, 5, 7 ]; S1:=[1 .. 5, 9]; S2:= [3 .. 7, 12]; S:= S1 * S2; то результат выполнения S =[3 .. 5];](https://fsd.multiurok.ru/html/2017/02/20/s_58ab30d245526/img5.jpg)
Операции над множествами
Пересечением двух множеств называется множество элементов, принадлежащих одновременно и первому, и второму множеству, т.е. это общие элементы. Знак операции – « * ».
- Примеры:
- [‘A’, ’F’] * [‘B’, ’D’] =[ ] – так как общих элементов нет ;
- [1..3, 5, 7, 11] * [3..8,10, 12, 15..20] = [ 3, 5, 7 ];
- S1:=[1 .. 5, 9]; S2:= [3 .. 7, 12]; S:= S1 * S2;
то результат выполнения S =[3 .. 5];
![Операции над множествами Вычитанием двух множеств называется множество, состоящее из тех элементов первого множества, которые не являются элементами второго множества. Знак операции – « - ». Примеры: [‘A’, ’F’] - [‘B’, ’D’] =[‘A’, ‘F’ ] – так как общих элементов нет ; [1..3, 5, 7, 11] - [3..8,10, 12, 15..20] = [1 .. 2, 11]; S1:=[1 .. 5, 9]; S2:= [3 .. 7, 12]; S:= S1 - S2; то результат выполнения S =[1 .. 2, 9];](https://fsd.multiurok.ru/html/2017/02/20/s_58ab30d245526/img6.jpg)
Операции над множествами
Вычитанием двух множеств называется множество, состоящее из тех элементов первого множества, которые не являются элементами второго множества. Знак операции – « – ».
- Примеры:
- [‘A’, ’F’] – [‘B’, ’D’] =[‘A’, ‘F’ ] – так как общих элементов нет ;
- [1..3, 5, 7, 11] – [3..8,10, 12, 15..20] = [1 .. 2, 11];
- S1:=[1 .. 5, 9]; S2:= [3 .. 7, 12]; S:= S1 – S2;
то результат выполнения S =[1 .. 2, 9];
 true , т.к 5 принадлежит [3 .. 7]; ‘ a’ in [‘A’ ..’Z’] = false , т.к. маленькой латинской буквы ‘a’ нет среди больших латинских букв. Примечание. Оператор вида: if (ch=‘a’) or (ch=‘b’) or (ch=‘x’) or (ch=‘y’) then s; может быть переписан в компактной наглядной форме: if ch in [‘a’,’b’,’x’,’y’] then s; ” width=”640″
true , т.к 5 принадлежит [3 .. 7]; ‘ a’ in [‘A’ ..’Z’] = false , т.к. маленькой латинской буквы ‘a’ нет среди больших латинских букв. Примечание. Оператор вида: if (ch=‘a’) or (ch=‘b’) or (ch=‘x’) or (ch=‘y’) then s; может быть переписан в компактной наглядной форме: if ch in [‘a’,’b’,’x’,’y’] then s; ” width=”640″
Операция определения принадлежности элемента множеству
in – служебное слово. Логическая операция имеет результат true , если значение входит в множество и false в противном случае.
- Примеры:
5 in [3 .. 7] = true , т.к 5 принадлежит [3 .. 7];
‘ a’ in [‘A’ ..’Z’] = false , т.к. маленькой латинской буквы ‘a’ нет среди больших латинских букв.
Примечание. Оператор вида:
if (ch=‘a’) or (ch=‘b’) or (ch=‘x’) or (ch=‘y’) then s;
может быть переписан в компактной наглядной форме: if ch in [‘a’,’b’,’x’,’y’] then s;
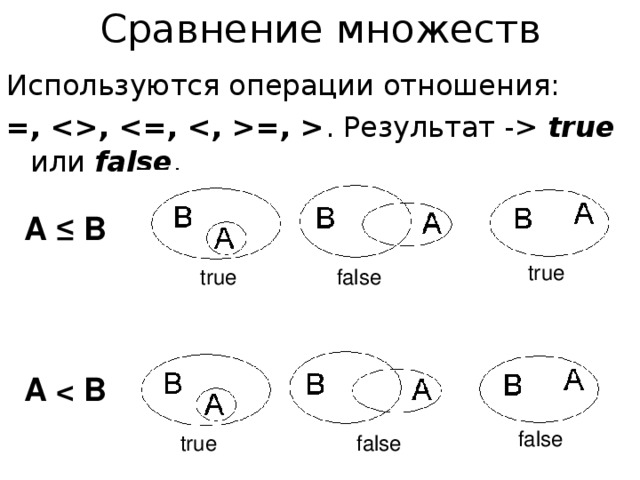 . Результат – true или false . A ≤ B true true false A false true false ” width=”640″
. Результат – true или false . A ≤ B true true false A false true false ” width=”640″
Сравнение множеств
Используются операции отношения:
= , , =, . Результат – true или false .
A ≤ B
true
true
false
A
false
true
false

- Пример
Составить программу выделения из множества целых чисел от 1 до 30 следующих множеств:
- множества чисел кратных 2;
- множества чисел кратных 3;
- множества чисел кратных 6;
- множества чисел кратных 2 или 3;
Вопросы:
- Сколько множеств надо описать? Какого они типа?
- Какое первоначальное значение множеств?
- Как формируются множества?
- Как осуществить вывод сформированных множеств?
- 4 множества типа byte
- – пустое множество
- Первые два – перебором всех чисел данного промежутка и занесением необходимых, третье и четвертое – из первых двух путем применения операций пересечения и объединения
- Вывод делается только поэлементно, поэтому удобно составить процедуру, которой передается множество, элементы которого и будут выдаваться на экран. Для этого в разделе типов надо создать тип множества и его использовать в дальнейшем.

program Ex1;
const n=30;
type mn=set of 1..n;
var n2,n3,n6,n23: mn; {n2 – множество чисел кратных 2, } { n3 – кратных 3}
k:integer; { n6 – кратных 6, n23 – кратных 2 или 3}
procedure Print(m:mn);
var i:integer;
Begin
for i:=1 to n do If i in m then write(i:3);
writeln;
end;
![begin n2:=[ ]; n3:=[ ]; {начальное значение множества} for k:=1 to n do { формирование n2 и n3} begin if k mod 2=0 then n2:=n2+[k]; if k mod 3=0 then n3:=n3+[k] end; n6:=n2*n3;{числа кратные 6, это те, которые кратны и 2, и 3 ,} { поэтому это пересечение двух первых множеств} n23:=n2+n3; {а числа кратные 2 или 3 – это объединение этих же множеств} writeln(‘числа, кратные 2'); print(n2); writeln(' числа, кратные 3'); print(n3); writeln(' числа, кратные 6'); print(n6); writeln(' числа, кратные 2 или 3'); print(n23); readln; end.](https://fsd.multiurok.ru/html/2017/02/20/s_58ab30d245526/img11.jpg)
begin
n2:=[ ]; n3:=[ ]; {начальное значение множества}
for k:=1 to n do { формирование n2 и n3}
begin
if k mod 2=0 then n2:=n2+[k];
if k mod 3=0 then n3:=n3+[k]
end;
n6:=n2*n3;{числа кратные 6, это те, которые кратны и 2, и 3 ,} { поэтому это пересечение двух первых множеств}
n23:=n2+n3; {а числа кратные 2 или 3 – это объединение этих же множеств}
writeln(‘числа, кратные 2′); print(n2);
writeln(‘ числа, кратные 3’); print(n3);
writeln(‘ числа, кратные 6’); print(n6);
writeln(‘ числа, кратные 2 или 3’); print(n23);
readln;
end.

Задание.
Изменить программу так, чтобы результатом ее работы являлось множество чисел, делящихся на 3, но не делящихся на 2.

Задача.
Дано натуральное число n .составить программу, печатающую все цифры, не входящие в десятичную запись данного натурального числа в порядке возрастания.
![program ex3; type mn=set of 0..9; var s:mn; n:longint; l,k:integer; begin write(‘Введите число N '); readln(n); s:=[ ]; { формирование множества цифр десятичной записи числа n } while n0 do begin k:=n mod 10; n:=n div 10; if not (k in s) then s:=s+[k]; end; { вывод цифр в порядке возрастания} for k:=0 to 9 do if not (k in s) then write(k:2); writeln; readln end.](https://fsd.multiurok.ru/html/2017/02/20/s_58ab30d245526/img14.jpg)
program ex3;
type mn=set of 0..9;
var s:mn; n:longint; l,k:integer;
begin
write(‘Введите число N ‘); readln(n);
s:=[ ]; { формирование множества цифр десятичной записи числа n }
while n0 do
begin
k:=n mod 10; n:=n div 10;
if not (k in s) then s:=s+[k];
end;
{ вывод цифр в порядке возрастания}
for k:=0 to 9 do
if not (k in s) then write(k:2);
writeln;
readln
end.

Другие задачи
Множества
Понятие множества в языке ПАСКАЛЬ основывается на математическом
представлении о множествах: это ограниченная совокупность различных
элементов. Для построения конкретного множественного типа используется
перечисляемый или интервальный тип данных. Тип элементов, составляющих
множество, называется базовым типом.
например:
type M= Set of B;
typeM= Set of 'A'..'D';
var
MS : M;
прямо в разделе описания переменных:
varC : Set of 0..7;
квадратные скобки последовательности элементов или интервалов базового
типа, разделенных запятыми, например:
['A', 'C'] [0, 2, 7] [3, 7, 11..14].
ножества данного множества, а также пустое подмножество. Если базовый
тип, на котором строится множество, имеет К элементов, то число подм-
ножеств, входящих в это множество, равно 2 в степени К. Пусть имеется
переменная Р интервального типа:
varP : 1..3;
Эта переменная может принимать три различных значения – либо 1,
либо 2, либо 3. Переменная Т множественного типа
varT : Set of 1..3;
может принимать восемь различных значений:
[ ] [1,2][1] [1,3]
[2] [2,3]
[3] [1,2,3]
вида [T], где T – переменная базового типа.
присваивания(:=), объединения(+), пересечения(*) и вычитания(-):
['A','B'] + ['A','D'] даст ['A','B','D']['A'] * ['A','B','C'] даст ['A']
['A','B','C'] - ['A','B'] даст ['C'].
типа.
нетождественность (<>), содержится в (<=), содержит (>=). Результат
выполнения этих операций имеет логический тип, например:
['A','B'] = ['A','C'] даст FALSE['A','B'] <> ['A','C'] даст TRUE
['B'] <= ['B','C'] даст TRUE
['C','D'] >= ['A'] даст FALSE.
языке ПАСКАЛЬ используется операция
in
проверяющая принадлежность элемента базового типа, стоящего слева
от знака операции, множеству, стоящему справа от знака операции.
Результат выполнения этой операции – булевский. Операция проверки
принадлежности элемента множеству часто используется вместо операций
отношения, например:
A in ['A', 'B'] даст TRUE,2 in [1, 3, 6] даст FALSE.
При использовании в программах данных множественного типа
выполнение операций происходит над битовыми строками данных. Каждому
значению множественного типа в памяти ЭВМ соответствует один двоичный
разряд. Например, множество
['A','B','C','D']
представлено в памяти ЭВМ битовой строкой
1 1 1 1.
Подмножества этого множества представлены строками:
['A','B','D'] 1 1 0 1['B','C'] 0 1 1 0
['D'] 0 0 0 1
да – вывода.
количество элементов базового типа, на котором строится множество,
ограничено. В TURBO PASCAL количество базовых элементов не должно
превышать 256.
типизированных констант:
const seLit: Set of 'A'..'D'= [];
экран дисплея наборы случайных чисел для игры в “Спортлото 5 из 36”.
из пяти псевдослучайных чисел. К этим числам предъявляются два требования:
- числа должны находиться в диапазоне 1..36;
- числа не должны повторяться.
Program Lotto;
var
nb, k: Set of 1..36;
kol, l, i, n: Integer;
begin
Randomize;
WriteLn('ВВЕДИ kol');
ReadLn(kol);
nb:=[1..36];
for i:=1 to kol do
begin
k:=[];
for l:=1 to 5 do
begin
repeat
n:=Random(36)
until (n in nb) and not (n in k);
k:=k+[n];
Write(n:4)
end;
WriteLn
end
end.
Программирование с использованием множеств
Общие сведения
различных элементов одного типа. В отличие от массивов к элементам
множества нет прямого доступа (по индексам этих элементов, как в
массивах). Поэтому ввод-вывод множеств производится с использованием
операций объединения (при вводе) и проверки принадлежности (при выводе).
Под мощностью множества понимают количество элементов, содержащихся в
данном множестве.
описания и использования переменных типа множество, типизированных
констант типа множество, переменных, заданных перечислением, изучить
допустимые операции над переменными этих типов.
Пример
Пример1: Дан текст. Определить каких букв больше – гласных или согласных.
Этапы решения задачи: 1. Составим блок схему программы



Опишем подробнее блок “Подсчитываем количество гласных и согласных букв”


Рассмотрим блок “Печатаем соответствующее сообщение”


Запишем блок-схему целиком


2. Переведем алгоритм на язык Паскаль
program example1;
const
glasn=['а','е','и','о','у','ы','э','ю','я'];
soglas=['б','в','г','д','ж','з','й','л','м',
'н','р','к','п','с','т','ф','х','ц','ч','ш','щ'];
var
st: string;
g,s,i:integer;
begin
write('Введите строку> '); readln(st);
g:=0; s:=0;
for i:= 1 to length(st) do
if st[i] in glasn then inc(g) else if st[i] in soglas then inc(s);
if g> s then writeln('Гласных больше')
else if g< s then writeln('Согласных больше')
else writeln('Согласных и гласных букв поровну');
readln;
end.
Контрольные вопросы
- Что такое множество, как оно описывается в языке Pascal?
- Как определить новый тип данных с использованием перечисления?
- Как описываются типизированные константы типа множество?
- Как осуществляется ввод-вывод значений переменных типа множество?
- Какие типы данных используются в качестве базовых при объявлении типа множество?
- Какие операции определены над множествами?
- Какие операции допустимы над переменными, заданными перечислением?
- Чем похожи и чем отличаются множества и массивы?
- Какое значение у выражений: а) x in [x]; б) [ ] <= [x,y,z]; в) [x]<>[x,x,x]
Задания
Гласные буквы – а,е,и,о,у,ы,э,ю,я (ё обычно не входит в литерный тип);
согласные – все остальные буквы, кроме ь, ъ;
звонкие согласные – б,в,г,д,ж,з,й,л,м,н,р;
глухие согласные – к,п,с,т,ф,х,ц,ч,ш,щ.
- Дан текст из строчных латинских букв, за которым следует точка. Напечатать:
– первые вхождения букв в текст, сохраняя их взаимный исходный порядок;
– все буквы, входящие в текст не менее двух раз;
– все буквы, входящие в текст по одному разу.
Дана непустая последовательность слов из строчных русских букв;
между соседними словами – запятая, за последним словом – точка.
Напечатать в алфавитном порядке: - все гласные буквы, которые входят в каждое слово;
все согласные буквы, которые не входят ни в одно слово; - все звонкие согласные буквы, которые входят хотя бы в одно слово;
все глухие согласные буквы, которые не входят хотя бы в одно слово; - все согласные буквы, которые входят только в одно слово;
все глухие согласные буквы, которые не входят только в одно слово; - все звонкие согласные буквы, которые входят более чем в одно слово;
все гласные буквы, которые не входят более чем в одно слово; - все звонкие согласные буквы, которые входят в каждое нечетное слово и не входят ни в одно четное слово;
все глухие согласные буквы, которые входят в каждое нечетное слово и не входят хотя бы в одно четное слово. - Имеются три множества символьного типа, которые заданы своими конструкторами:
Y1=[‘A’,’B’,’D’,’R’,’H’]
Y2=[‘R’,’A’,’H’,’D’]
Y3=[‘A’,’R’].
Сформировать новое множество .
Предусмотреть формирование исходных множеств с клавиатуры. - Подсчитать общее количество цифр и знаков ‘+’, ‘-‘, и ‘*’, входящих в строку s.
- Подсчитать количество различных (значащих) цифр в десятичной
записи натурального числа n и напечатать в возрастающем порядке все
цифры, не входящие в десятичную запись натурального числа n. - Вычислить сумму тех элементов матрицы A, номера строк и
столбцов которых принадлежат соответственно непустым множествам S1 и S2
типа Nom.
Cons n=10;
Type Nomer= 1..n;
Матрица = Array[Nomer,Nomer] of Real;
Nom = Set of Номер;
Задачи повышенной сложности
- Дан текст, являющийся русскими словами. Выполнить разделение каждого его слова на части для переноса.
Далее правила переноса русских слов.
a) Две идущие подряд гласные можно разделить, если первой из них
предшествует согласная, а за второй идет хотя бы одна буква (буква й при
этом рассматривается вместе с предшествующей гласной как единое целое).b) Две идущие подряд согласные можно разделить, если первой из них
предшествует гласная, а в той части слова, которая идет за второй
согласной, имеется хотя бы одна гласная (буквы ъ, ь вместе с
предшествующей согласной рассматриваются как единое целое).
c) Если не удается применить пункты a, b, то следует попытаться
разбить слова так, чтобы первая часть содержала более чем одну букву и
оканчивалась на гласную, а вторая содержала хотя бы одну гласную.
Вероятность правильного разбиения увеличивается, если предварительно
воспользоваться хотя бы неполным списком приставок, содержащих гласные, и
попытаться, прежде всего, выделить из слова такую приставку. - Написать программу раздачи карт при игре в дурака, количество игроков задается с клавиатуры.
- Для произвольного символьного множества сгенерировать все подмножества
Сегодня на уроке мы познакомимся с таким понятием, как множество
и с числом элементов множества.
Ребята, на уроках информатики вы уже научились описывать состав
объектов, выделять их отличительные признаки, отвечать на
вопросы «Что это такое?» и «Кто это такой?». Также
научились отвечать на вопрос «Как это делается?» с помощью
составления алгоритма. Но существуют и другие вопросы, на которые
нужно уметь отвечать. Например, как определить относится ли объект к данной
группе? А чтобы узнать, как ответить на этот вопрос, давайте для начала
отгадаем загадки.
Он любит мёд
Зимой он спит
Весной хороший аппетит!
Это медведь.
Крепко сбит да невысок,
На носу – крепкий рог,
Кто его дразнить посмеет –
Того он на свой рог подденет.
Носорог.
Он один сидит на ветке,
Зорок глаз и когти цепки,
Всех в два счёта б поборол,
Потому что он – …
Орёл.
Гнездо своё он в поле
вьёт,
Где тянутся растения.
Его и песни, и полет
Вошли в стихотворения!
Это жаворонок.
Симпатичен, сер, усат,
Его хвостик полосат.
Пищу грязной не грызёт —
Моет всё в воде …
Енот.
Днём спит, ночью летает,
Ухает, людей пугает.
В темноте горят глаза –
Всем мышам она гроза.
Это Сова.
Он хвостатый и усатый,
И, конечно, полосатый.
̶ Рррр, ̶ рычит, ̶ мне не до игр.
Кто же это, дети? …
Тигр.
Эта птица всем знакома ̶
Важно ходит возле дома
Кар-Кар-Кар вдруг закричит,
И спокойно улетит.
Ворона.
Он других не обижает.
Ест траву, в лесу гуляет,
Но ветвистыми рогами
Может справиться с волками!
Это олень.
По велению волшебной палочки объекты все распределились вот так!
И получилось две группы. Как мы разделили объекты? По
общему признаку. В одной группе у нас находятся животные, а в
другой птицы.
А теперь посмотрите – из первых букв можно сложить слово. Какое?
Слово “Множество“. И это очень важное слово для нашего
урока!
Под множеством понимают объединение объектов на
основе каких-то общих свойств или признаков.
Чтобы узнать принадлежит объект данному множеству или нет,
достаточно выделить характерный признак, по которому точно можно
определить, что этот объект можно включить в данное множество.
Другой же предмет, у которого этот признак отсутствует, включать в это
множество нельзя.
Глядя на две наши группы, можно сказать, что у нас есть два
множества: множество животных и множество птиц.
Какие объекты входят в эти множества?
В первое множество входят: медведь, енот, олень,
носорог, тигр.
Во второе множество: орёл, жаворонок, сова, ворона.
Объекты, которые принадлежат множеству, называются элементами
множества.
Как вы думаете, от какого слова произошло название «множество»?
Много.
А сколько это много? Точно мы сказать не можем.
Во множестве может быть любое количество элементов, даже один
элемент. Может быть бесконечно большое число
элементов, например, множество чисел. А также может быть и такое, что во
множестве не будет ни одного элемента. Такое множество называется
пустым. Например, множество чисел, которые делятся на ноль. Мы
знаем, что нет таких чисел, которые бы делились на ноль, ведь на ноль делить
нельзя.
Множества могут быть самыми разными: детей, гуляющих в парке,
множество сказок Пушкина, множество учащихся, занимающихся танцами, множество
страниц в книге и т.д.
А сколько всего элементов в наших множествах? Во множестве
животных пять, а во множестве птиц четыре.
А как нам отмечать объекты во множестве, не рисовать
же рисунки всё время? А отмечать объекты мы будем точками.
И так в нашем множестве животных пять объектов, значит, ставим
пять точек: раз, два, три, четыре, пять.
Как можно показать, что они вместе составляют одно множество?
Обвести их.
Теперь тоже самое делаем для множества птиц. Ставим четыре точки и
обводим их.
Итак, ребята у нас получилось множество животных, в которое входит
пять элементов и множество птиц, в это множество входят четыре элемента.
А сейчас я предлагаю вам построить пирамиду множеств.
На первом этаже будут жить четыре элемента, на втором – три, на
третьем – два. На четвёртом этаже будет жить один элемент, а на чердаке – никто
не будет жить. Давайте посмотрим какие это множества, и разместим их по этажам,
так, чтобы на каждом этаже находилось множество с соответствующим
количеством элементов.
Итак! Согласные в слове «пирамида». Сколько согласных в слове
«пирамида»? Четыре. Значит, это множество разместим на этаж, где
будут жить четыре элемента.
Крылья у птицы. У птицы два крыла, значит, помещаем туда, где два
элемента.
Ученики шестнадцатого класса. Шестнадцатого класса? Хм, это пустое
множество, нет в школе 16 класса. Помещаем на чердак.
Зимние месяцы. Их три. Помещаем на второй этаж.
Гласные в слове «торт». В этом слове одна гласная – это буква о.
Помещаем на четвёртый этаж.
Множества расставлены по своим местам. И пирамида готова!
Но, несмотря на то, что на чердаке находится пустое множество, там
не так уж и пусто. Оказывается, там лежала записка.
А я очень любопытная и мне хочется её прочитать. Надеюсь, вы не
против…
«Это письмо множества. Если вы его нашли, то обязаны выполнить
одно очень важное задание. Выбрасывать это письмо или не выполнять задание
нельзя. Если вы его всё-таки выбросите, то получать вам по информатике только
двойки!!!» Я не хочу получать по информатике двойки, как и вы, надеюсь, поэтому
будем выполнять.
А вот и само задание!
«Необходимо, разместить объекты во множества. Но будьте
очень внимательны. Всё не так просто, как вам может показаться».
Для начала давайте прочитаем названия элементов множеств:
сосна, яблоня, ель, вишня, дуб, ромашка.
А теперь прочитаем названия множеств: деревья, плодовые
деревья, растения.
Какой фигурой обозначено множество плодовых деревьев? Кругом.
Какие элементы войдут в это множество? Яблоня, вишня.
Перенесём название элементов в круг.
А теперь запишем элементы множества деревьев.
Сосна, яблоня, ель, вишня, дуб. Впишем их в квадрат.
А как получилось, что яблоня и вишня входят в оба множества?
Яблоня и вишня, это – плодовые деревья. Все плодовые деревья
входят и во множество деревьев.
Какое множество больше: плодовых деревьев или всех деревьев?
Множества деревьев больше, так как в него входят все плодовые
деревья и остальные деревья тоже.
По велению волшебной полочки получилось следующее.
Оказывается, если ВСЕ элементы одного множества входят в другое
более крупное множество, то первое является подмножеством второго.
Значит, во множестве деревьев есть подмножество плодовые деревья.
Однако есть ещё одно множество – растений. Назовём его элементы.
Это все элементы в списке: сосна, яблоня, ель, вишня, дуб, ромашка. Они все
растения.
Ребята, получается, что это множество ещё больше: в
него входят все элементы, из предыдущих множеств и ещё ромашка.
Впишем эти элементы в прямоугольник.
По велению нашей волшебной палочки произошло следующее.
Рассмотрите, что получилось. Есть большое множество
растений, в которое входят ромашка и подмножество Деревья. А в подмножество
Деревья входит подмножество Плодовые деревья.
Ребята, сегодня вы узнали, что такое множество.
Множество – это объединение
объектов на основе каких-то общих свойств или признаков.
Сколько же элементов может быть во множестве? Сколько угодно. И
один, и два, и бесконечно много, и даже ни одного. Такое множество
называется пустым.
А так же вы узнали, что есть множество, которое входит в другое
множество и оно называется подмножеством.
Я надеюсь, что урок для вас был и полезным, и интересным.
