Научите меня находить разность во времени. Чё там на что умножать нужно? См. внутри
Валерия
Мастер
(1409),
закрыт
11 лет назад
Вот, например
Найдите разность 16 ч 26 мин – 9 ч 52 мин.
Я ответ знаю, а как до него быстро не знаю.
Просто подробно объясните плиз
Дополнен 11 лет назад
Вот, например
Найдите разность 16 ч 26 мин – 9 ч 52 мин.
Я ответ знаю, а как до него быстро добраться не знаю.
Просто подробно объясните плиз
нголаллпрлп арпалнгоп
Ученик
(160)
11 лет назад
переводи все в минуты так проще к примеру 16 надо умножить на 60 =960 и +26 это ролучится 986. и так же 9умножим на 60 получим 540 +52 равно 592. а потом считай уже. итог 986-592=394. Переводим обратно в часы 394 делить на 60 равно 6 часов 56 минут. всё 🙂
Alexa_Gri
Знаток
(397)
11 лет назад
Можно просто перевести часы в минуты и посчитать, а потом обратно. Не самый быстрый, но самый простой способ. =) А можно только один час, если необходимо, перевести в минуты и посчитать.
16 ч 26 минут = 15 ч 86 минут
15 ч 86 мин – 9 ч 52 мин = 6 ч 34 мин
Светило науки – 12239 ответов – 139185 раз оказано помощи
а) Определение разницы во времени между часовыми зонами России.Определить поясное время в Якутске, если в Москве 9 часов.(Для начала определяем разницу в поясах 8-2=6 часов.Теперь определяем поясное время, учитывая при этом, что к востоку время увеличивается, а к западу уменьшается:9+6=15 часов.Ответ:поясное время в Якутске равно 15 часов).
б) Расчет разницы во времени по элементам градусный сетки.Определить местное время в Магадане, если в Москве 5 часов.(Для начала определяем долготу этих городов:Москва 37 долгота, Магадан 150 долгота; затем находим разницу в градусах между городами: 150-37=113;теперь находим разницу во времени: 113х4=452 минуты или 7 часов 32 мин.;и наконец находим местное время:5 ч+7 ч 32 мин=12 ч 32 мин.Ответ:местное время в Магадане 12 ч 32 мин.).
в) Расчёт продолжительности светового дня.Рассчитать продолжительность светового дня в Харькове 16 апреля, если восход солнца в 5 ч.30 мин , а закат в 19 ч 30 мин.( Находим разницу между закатом и восходом: 19 ч 30 мин-5 ч.30 мин=14 часов.Ответ: продолжительность светового дня в Харькове 16 апреля составляет 14 часов).
г) Определение высоты полуденного солнца. Определить высоту полуденного солнца в Каире в день летнего солнцестояния.(Находим широту Каира – 30°.Теперь находим высоту по формуле: 90°-(30° с.ш.-23,5° с.ш.(Южный тропик))=83,5°.Ответ:высота полуденного солнца в Каире составляет 83,5°).
Привет,
ребята!
Вы
знаете, я собираюсь в путешествие. Мне придётся ехать на автобусе и на поезде.
И чтобы никуда не опаздывать, мне необходимо точно знать время отъезда,
время приезда и время, которое я буду находиться в пути.
Время
отъезда можно назвать началом движения, время в пути – его продолжительностью,
а время приезда – окончанием движения.
Из
замка я поеду в Город геометрических фигур. Автобус отправляется в восемь часов
утра. Мне сказали, что до Города геометрических фигур надо ехать шесть часов. Когда
же я буду на месте?
Для
решения этой задачи воспользуюсь часами со стрелками.
Так,
время отправления или начало, – восемь часов, время в пути, или
продолжительность, – шесть часов. Раз, два, три, четыре, пять, шесть. Это будет
два часа дня. Но на вокзалах называют время в двадцатичетырёхчасовом
формате. И чтобы перевести два часа в двадцатичетырёхчасовой счёт, к
числу два надо прибавить двенадцать.
2
+ 12 = 14 (ч)
Ответ:
автобус прибывает в 14 ч.
Хотя,
эту задачу можно было бы решить и без циферблата часов. Если известно время
начала какого-то действия и его продолжительность, то для того, чтобы узнать
время окончания действия, два известных числа надо сложить. Автобус
отправляется в восемь часов и находится в пути шесть часов. Складываем эти
числа. Время прибытия – четырнадцать часов.
8
+ 6 = 14 (ч)
Ответ:
автобус прибывает в 14 ч.
А
вот если бы было известно время начала и окончания движения? И узнать
надо было бы время в пути, то есть продолжительность движения.
Каким
действием его надо было бы находить?
Давайте
я вам это продемонстрирую не на циферблате часов, а на числовом луче.
Вот
на нем время отправления, вот время прибытия. А разница между этими числами и
есть время в пути. Вы слышите слово «разница»? Какое родственное математическое
слово вы знаете? Разность. А разность, как и разницу, мы находим действием
вычитания. Из времени окончания движения вычитаем время его начала.
14
– 8 = 6 (ч)
Ответ:
автобус находился в пути 6 ч.
Ну
и представим себе ещё одну обратную ситуацию, в которой известно время окончания
движения и его продолжительность, а узнать надо время начала движения.
Вот
часы, которые показывают время прибытия автобуса. Для того, чтобы они показали
время отправления, надо чтобы стрелки двигались назад, в прошлое. А если показать
это на числовом луче, то становится понятно, что опять выполняется действие
вычитание.
Вот
мы с вами решили три задачи, в одной из которых надо было узнать время
окончания движения, во второй – продолжительность движения и в третьей – время
начала движения. И теперь можно составить памятку – как решать такие
задачи. Только сначала я хочу вам сказать, что так можно находить время не
только в задачах про движущиеся объекты, но и про любые совершаемые действия или
события – про учёбу, работу, отдых. Поэтому я буду использовать именно слово
событие. Итак:
Если
известно время начала и продолжительности какого-либо события, то время
его окончания находим сложением.
Если
известно время начала и окончания какого-либо события, то его продолжительность
находим вычитанием.
Если
известно время окончания какого-либо события и его продолжительность, то время
его начала находим вычитанием.
Получились
формулы для решения взаимообратных задач на нахождение начала,
продолжительности или окончания действия или события. Обратите внимание на то,
что только время окончания действия находится сложением, а его
продолжительность и время начала – вычитанием.
Ну,
что же, теперь надо составить план дальнейшего путешествия. Надеюсь, вы мне
поможете.
В
Город геометрических фигур я приеду в четырнадцать часов, а далее мне предстоит
поездом доехать до Города уравнений. Поезд отправляется в двадцать часов
пятнадцать минут. Сколько времени я могу погулять по городу?
Помогите мне, пожалуйста, это узнать.
Так
как в этой задаче надо было узнать продолжительность события, то
я находила его вычитанием.
20
ч 15 мин – 14 ч = 6 ч 15 мин
Ответ:
Решалочка будет находиться в Городе
геометрических
фигур 6 ч 15 мин.
Итак,
после прогулки я отправлюсь на поезде в Город уравнений. Как вы знаете – время
отправления – двадцать часов пятнадцать минут, и в дороге я буду находиться три
часа 40 минут. Во сколько я приеду в Город уравнений?
Узнайте, ребята!
Вы
так решали?
20
ч 15 мин + 3 ч 40 мин = 23 ч 55 мин
Ответ:
поезд прибудет в 23 ч 55 мин.
Ведь
узнать надо было время окончания движения, поэтому решать надо
было действием сложения.
Да,
поздновато приеду. Но там я пробуду несколько дней, хорошо отдохну с друзьями. Однако
в следующее воскресенье в пятнадцать часов сорок пять минут я должна быть дома.
Из города уравнений в замок я поеду уже на автомобиле. Посчитайте, ребята, во сколько
я должна выехать, если автомобиль доезжает до замка за пять часов тридцать
минут, а дома, как вы знаете, я должна быть в пятнадцать сорок пять.
Давайте
сверим наши результаты.
Я
надеюсь, вы все так решили, ведь время начала движения надо
находить вычитанием.
15
ч 45 мин – 5 ч 30 мин = 10 ч 15 мин
Ответ:
автомобиль должен выехать в 10 ч 15 мин.
Сегодня
мы с вами рассмотрели лишь некоторые случаи задач на нахождение начала,
окончания и продолжительности действия. Таким способом они решаются в
тех случаях, если действие происходит в течение одних суток. Если же действие
продолжается по истечении суток, то есть после двенадцати ночи, то такие задачи
надо будет решать уже не одним, а несколькими действиями. Но об этом мы
поговорим не сегодня, а в другой раз. Ведь время нашей встречи уже истекло. Однако,
прежде, чем попрощаться, я ещё раз хочу напомнить вам, как находить время
начала, окончания и продолжительности действия.
Эта
памятка поможет вам в дальнейшем и при решении более трудных задач.
А
теперь я говорю вам до свидания, ребята!
ВИДЕОУРОК
Задачи на время могут
быть трёх видов:
– на вычисление длительности или длины определённого
периода, если даны его начало и конец;
– на вычисление конца периода, если даны начало и длительность
его;
– на вычисление начала периода, если известны его конец
и длительность.
Полезно изображать эти
задачи схемой в виде горизонтальных отрезков.

На такой схеме обязательно фигурирует
точка О – момент начала отсчёта времени. Чтобы правильно и уверенно
решать задачи на время, надо какому-нибудь фиксированному моменту времени
ставить в соответствие промежуток времени, при этом устанавливаем некоторый
момент, от которого отсчитываем время, например, начало нашей эры, начало года,
начало месяца, начало суток и т. д.. Также необходимо знать как складывать и отнимать
именованные числа, которые выражают время.
Чтобы правильно и уверенно
решать задачи на время, нужно помнить следующее:
– любому фиксированному моменту времени (на схеме – определенной точке, например
точке А, ставить в
соответствие промежуток времени, отрезок ОА), при этом установлен определенный момент,
от которого отсчитываем время, например начало нашей эры, начало года, начало
месяца, начало суток и другие;
– добавлять и вычитать именуемые числа, выражающие
время.
Задачи на вычисление
длительности или длины определённого периода, если даны его начало и конец.
ПРИМЕР:
Запишите 4 часа 16
мин в минутах.
РЕШЕНИЕ:
4 час 16
мин = 4 ∙ 60 мин +
16 мин =
= 240 мин +
16 мин = 256 мин.
ПРИМЕР:
Какую часть минуты составляют 23 сек ?
РЕШЕНИЕ:
23 сек = 23/60 мин.
ПРИМЕР:
Выполните умножение:
3 суток 18 час ∙ 6.
РЕШЕНИЕ:
Имеем:
3 суток 18 час ∙ 6 =
= 18 суток 108 час =
= 22 суток 12 час.
При решении примера было использовано распределительное
свойство умножения относительно сложения:
3 доби 18 год ∙ 6 = (3 доби + 18 год) ∙ 6 =
= 3 суток ∙ 6 + 18 час
∙ 6 = 18 суток
+ 108 час =
= 18 суток + 96 час
+ 12 час =
= 18 суток + 4 суток
+ 12 час = 22 суток 12
час
ЗАДАЧА:
Предположим, что сейчас 18
часов 16
декабря 1962 года. Сколько лет, месяцев, суток и часов прошло с
начала нашей эры до настоящего момента.
ВІДПОВІДЬ:
От начала нашей эры до данного в задаче момента времени
прошло
1961
год 11
месяцев 15
суток и 18
часов.
ЗАДАЧА:
А. С. Пушкин родился
26 мая 1799 г.
Сколько времени прошло со дня его рождения до
18 декабря 1962 г.
РЕШЕНИЕ:
Такие задачи можно решать двумя способами.
ПЕРВЫЙ СПОСОБ.
Пусть отрезок
ОА изображает
промежуток времени от начала нашей эры (точка О) до дня рождения А. С. Пушкина,
то есть период времени, который равен 1798 годам, 4 месяцам, 25 дням (для простоты вычислений считаем, что
А. С. Пушкин родился в 0 часов 26 мая).Пусть, отрезок ОВ изображает промежуток времени от начала нашей
эры до сегодняшнего дня, то есть период времени, который равен 1961 году,
11 месяцам, 18 дням (для простоты вычислений считаем, что сутки 18 декабря
закончены, то есть имеем 2400 часа 18 декабря).
Тогда период времени
АВ определим как разность
периодов ОВ и ОА,
то есть:
АВ = ОВ – ОА.
Поэтому имеем:

Если мы будем считать соответствующие сутки не законченными
(общий случай), то тогда в рассмотренной
задаче в уменьшаемом будет 17 суток,
а в вычитаемом 24.
ВТОРОЙ СПОСОБ
Рассмотрим отрезок
АВ как сумму трёх отрезков:
АС + СD + DВ, где
АС – период времени от момента рождения до конца XVIII
ст.;
СD – период времени, который определяет XIX
ст.;
DВ – период времени от начала XX
ст. до сегодняшнего дня.
Месяцы считаем
по 30 суток.
Тогда имеем:
АС равно 5 суток (30 – 25), 7 месяцев (12 – 5), 1 год (1800 – 1799);
СD – 100 лет;
DВ – 61 год 11 месяцев 18 суток.
А весь период АВ равен:
(1 год + 7 месяцев
+ 5 суток) +
100 лет + (61 год + 11 месяцев
+ 18 суток) =
163 года 6 месяцев 23 дня.
Задачи на вычисление конца
периода, если известно начало и длительность его.
Решение задач на сложение
именуемых чисел особого труда не составляет. Сложнее здесь случаи перехода
через разрядную единицу.
ПРИМЕР:
Выполнить
действия, если 1 месяц = 30 суткам:

ПРИМЕР:
Найти
сумму:
7 мин 44 сек + 5 мин 38 сек.
РЕШЕНИЕ:
Учитывая, что 1 мин = 60
сек, имеем:
7 мин 44 сек + 5 мин 38 сек
=
= 7 мин
+ 44 сек + 5 мин
+ 38 сек
=
= (7 мин + 5 мин) + (44 сек + 38 сек)
=
= 12 мин +
82 сек = 12 мин
+ 60 сек + 22 сек =
= 12 мин +
1 мин + 22 сек = 13 мин
+ 22 сек.
ЗАДАЧА:
Определить час, число месяца, месяц и год, если с начала
нашей эры прошло
1940 лет + 5 месяцев + 21 день + 4 час.
ВІДПОВІДЬ:
1941
год,
22 июня,
4 часа.
ЗАДАЧА:
Какое число, месяц и год наступили, когда с начала нашей
эры прошло 1961 год 6 месяцев 15 суток ?
РЕШЕНИЕ:
Размышляем так: полностью прошел 1961 год; кроме этого,
прошло еще несколько месяцев следующего года. Итак, длится 1962
год. Полностью прошло 6 месяцев 1962; кроме этого прошло еще несколько дней
следующего, седьмого месяца;
следовательно, длится июль месяц. Далее в условии сказано, что полностью прошло
15
суток; следовательно, наступили шестнадцатые сутки, то есть продолжается 16 июля.
ОТВЕТ: 16 июля 1962 года;
Задачи на вычисление начала
периода, если известны его конец и длительность.
Решение задач на
вычитание именуемых чисел особого труда не составляет. Сложнее здесь случаи
перехода через разрядную единицу.
ПРИМЕР:
Выполнить действия, если 1 месяц
= 30 дням:

ПРИМЕР:
9 час 8
мин – 2 час
26 мин.
= 6 час 42
мин.
При вычислениях были использованы правила вычитания суммы
из числа и вычитания числа из суммы.
= 6 час +
42 мин
= 6 час 42 мин.
35 час 17 мин – 15 час 35
мин.
= 19 час 42
мин.
43 мин 15 сек – 13 мин
48 сек.
= 29 мин 27 сек.
6 час 26 мин – 5 мин 17 сек.
= 6 час
20 мин 43
сек.
Известная ученая-математик С. В. Ковалевская умерла 10
февраля 1891
г., когда ей было 41 год и 25 дней
от рождения. Вычислить дату ее рождения.
До дня смерти С. В. Ковалевской прошло
с начала нашей эры, а прожила она 41 год и 25 дней. Чтобы вычислить
дату ее рождения, достаточно отнять от первого составленного именуемого числа
второе, тогда будем иметь:

Итак, на день рождения С. В. Ковалевской прошло полностью
1849 и несколько дней следующего года; значит, она
родилась в 1850 году. На день рождения еще не прошел полностью ни один месяц; следовательно,
она родилась в январе. Прошло полностью 14 дней; значит, она родилась 15
января.
С. В.
Ковалевская родилась 15 января 1850 года.
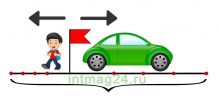 Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
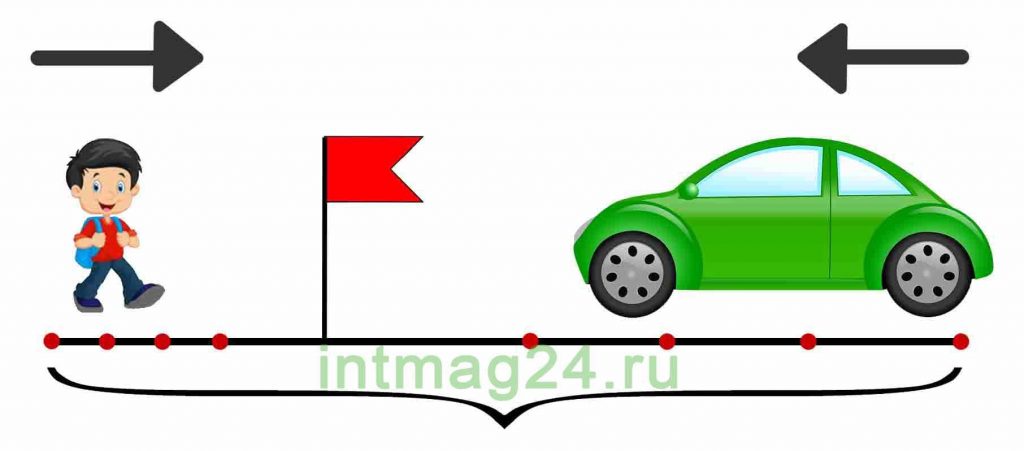
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
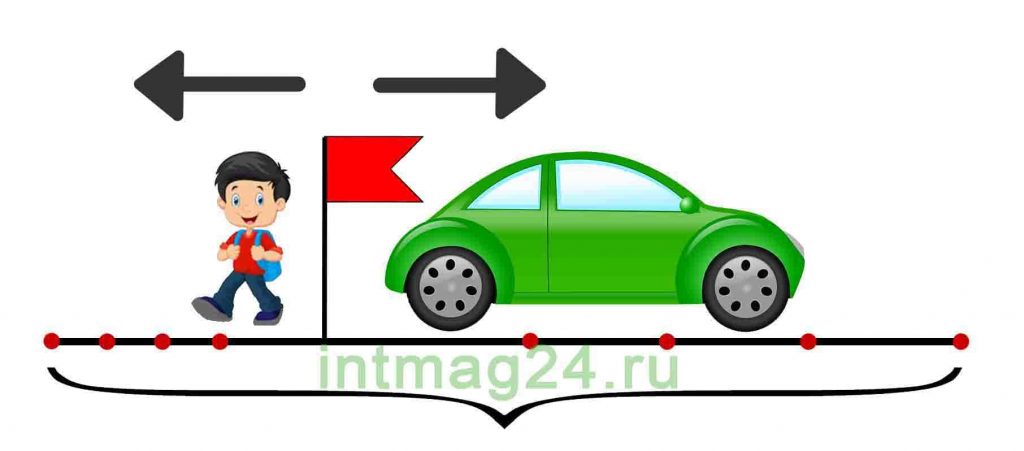
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.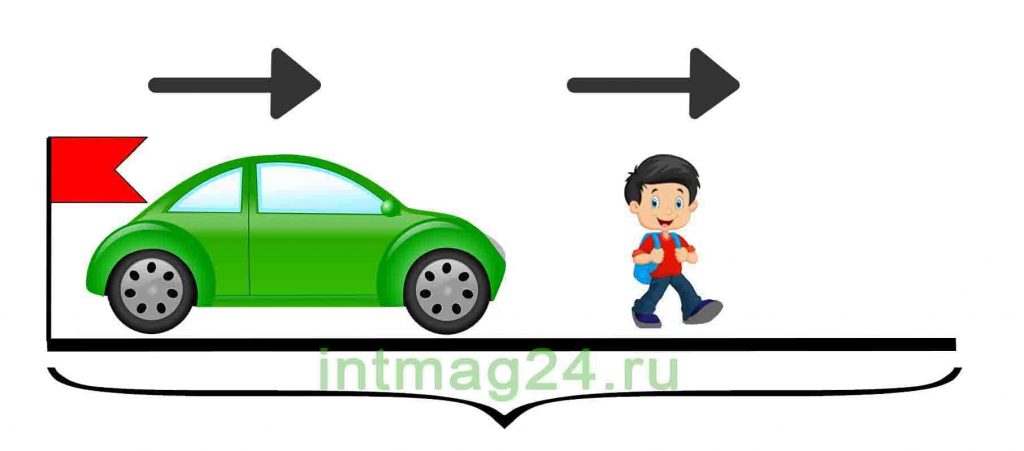
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
