Петров Дмитрий
Оракул
(63357)
5 лет назад
А что ее искать? Ее слышно. И чем модулируется? микрофон или тональный сигнал.. Берешь в руки щуп осциллоскопа… и тыкаешь куды надо.. все просто. В одном случае – синусоида, в другом – спектр.
А вообще —скачай и прочитай . Желательно от корки до корки.
publ.lib.ru/ARCHIVES/S/SVOREN’_Rudol’f_Anatol’evich/_Svoren’_R.A..html
Destino
Искусственный Интеллект
(312221)
5 лет назад
Очень просто – настроить на эту частоту рабиоприёмник и наслаждаться радиопередачей…
виктор носковОракул (88323)
5 лет назад
настроить на “частоту модуляции” ?
Destino
Искусственный Интеллект
(312221)
Частота модуляции у амплитудной модуляции совпадает с несущей частотой. Если вы не в курсе, в АМ-радио всё просто: есть сигнал – единица, нет сигнала – 0…
Частотная
модуляции (ЧМ) – это изменение
частоты переносчика (несущей)
пропорционально мгновенному значению
сообщения. На рис. 5.1,дпоказано, что при увеличении
мгновенных значений сообщения частота
несущей увеличивается, а при отрицательной
полуволне сообщения – уменьшается, при
этом амплитуда модулированного сигнала
остаётся постоянной. Еслиω– угловая частота модулированного
колебания (сигнала),ω0– среднее значение угловой частоты
переносчика и – угловая частота
сообщения, то можно записать
ω=ω0
+ mчcost,
(5.9)
где
mч
=ω/
(5.10)
– коэффициент
частотного отклонения, или глубина
частотной модуляции; ω– девиация угловой частоты, или
максимальное отклонение частоты
переносчика (в одну сторону) от исходного
значения.
Девиация
частоты зависит от амплитуды модулирующего
сообщения (см. рис. 5.1, д). При увеличении
амплитуды сообщения частота переносчикаFω0возрастает, при уменьшении (отрицательная
полуволна сообщения на рис. 5.1,а)
– снижается. Девиация частоты и индекс
модуляции связаны соотношениемFдев=
тчF.
На
рис. 5.7, в–д представлен спектр
при частотной модуляции. Строго говоря,
спектр частот при ЧМ бесконечно велик,
и для точного воспроизведения передаваемого
сообщения нужна бесконечно большая
ширина полосы. Однако боковые частоты
высших порядков имеют ничтожную
интенсивность и ими можно пренебречь.
Полоса частот при ЧМ может быть приближенно
определена из выражения
FЧМ
=2Fmin(mч+
1)=2(F
max
+ Fдев).
(5.12)
В
телеизмерении оптимальное значение тч
зависит от требуемой точности
передачи. Так, для систем ТИ с погрешностью
δ = 1% оптимальный индекс частотной
модуляциитч.опт=5.
Для точных систем ТИ (δ=0,1 %)тч.опт=15.
-
Частотная манипуляция.
При
манипуляции видеоимпульсами (см. рис.
5.3, а) частота переносчика принимает
только два значения (см. рис. 5.3,г).
Спектр частот представлен на рис. 5.4,д.
Ширина
полосы частот канала связи при передаче
определяется допустимым временем
установления сигнала на выходе входного
фильтра приемника и девиацией частоты
(частоты f1согласно рис. 5.3,г, на котором
переходный процесс установления частоты
не показан). Однако искажения, вносимые
входным фильтром при ЧМ, несколько
больше, чем при АМ. Поэтому для частотной
манипуляции, считая, что ΔF/(2Fдев)
=1,4, имеем:
ΔFч
min=(1,7
÷3)/τ. (5.13)
-
Реализация частотной модуляции.
Существуют
прямые и косвенные методы реализации
частотной модуляции. При прямых методах
частотная модуляция осуществляется
непосредственным изменением частоты
задающего генератора. Наиболее
распространенным косвенным методом
является использование фазового
модулятора для изменения фазы колебаний
по закону частотной модуляции.
При
прямых методах частота генератора
изменяется путем изменения индуктивности
катушки или емкости конденсатора,
подключаемых параллельно катушке или
конденсатору колебательного контура
генератора. Прямые методы, несмотря на
простоту, не могут обеспечить достаточной
стабильности частоты генератора. Поэтому
в модуляторах, основанных на этом
принципе, в случае необходимости
дополнительно применяют автоматическую
подстройку частоты. В телемеханике, как
правило, используют прямые методы
частотной модуляции.
Демодуляция
частотно-модулированных колебаний.
Для этой цели частотно-модулированные
колебания превращают сначала в колебания,
модулированные по фазе или по амплитуде,
из которых затем выделяется передаваемое
сообщение. Поэтому различают
частотно-амплитудные или частотно-фазовые
(либо просто фазовые) детекторы. В
телемеханике в большинстве случаев
применяют частотно-амплитудные детекторы.
Простейший
частотно-амплитудный детектор состоит
из обычного колебательного контура
(расстроенного относительно основной
частоты приходящего сигнала) и амплитудного
детектора. При изменении частоты сигнала
значение напряжения на контуре изменяется.
Однако из-за криволинейности ветвей
резонансной кривой колебательного
контура такие детекторы дают значительные
нелинейные искажения.
Более
совершенным частотно-амплитудным
детектором является частотный
дискриминатор, выполняемый с двумя
вторичными расстроенными контурами
(рис. 5.5, а).
Если,
например, модулированные по частоте
колебания, подаваемые на вход, лежат в
полосе 1100 ÷ 1000 Гц, то контур К1
настраивается на частоту 1050 Гц,
контурК2 – на частоту
1100 Гц и контурК3 – на
частоту 1000 Гц (рис. 5.5,б).
Контур
К1 является
широкополосным, пропускающим частоты,
на которые настраиваются контурыК2
иК3. Напряжения, снимаемые
с контуровК2,К3,
детектируются, и с резисторовR1,R2 снимается напряжение,
зависящее от частоты сигнала.
Когда
на вход подается частота 1100 Гц, с резистора
R1можно снять напряжениеU2,
которое больше напряженияU3(на резистореR2) при прохождении
частоты, например, 1070 Гц.
Диоды
Д1 иД2
включены таким образом, что напряжениеUвыхна
выходе дискриминатора равно разности
напряжений:Uвых=U2
– U3. Поэтому резонансную кривую
контураК3 можно
изобразить в другой полярности (пунктир
на рис. 5.11,б) по отношению к
кривой контураК2.
Если
сложить резонансные кривые контуров
К2 иК3, то
получится результирующая кривая
дискриминатора, представляющая собой
зависимость напряжения на выходе от
частоты входного сигнала (рис. 5.11,в). На значительном участке эта
характеристика линейна.

Рис.
5.5. Демодуляция
частотно-модулированного сигнала:
схема
частотного дискриминатора (а) и его
характеристики (б, в)
Сравнение
амплитудной (АМ) и частотной (ЧМ) модуляций
показывает, что:
1)
техническая реализация АМ проще, чем
ЧМ;
2)
полоса частот при АМ значительно меньше,
чем при ЧМ;
3)
помехоустойчивость ЧМ значительно выше
АМ. Это объясняется тем, что помехи
воздействуют в первую очередь на
амплитуду сигнала (см. рис. 5.1, e),
что при ЧМ не имеет существенного
значения, так как в ЧМ-приемниках обычно
применяют двустороннее ограничение
сигнала (см. пунктир на рис. 5.1,е). В
то же время при АМ изменение амплитуды
сообщения вызывает изменение амплитуды
переносчика, и такое ограничение,
срезающее помехи, применять нельзя;
4)
при ограниченной пиковой мощности
передатчика средняя мощность АМ-сигнала
оказывается меньше мощности ЧМ-сигнала.
Это следует из рис. 5.1, ж, на
котором изображена немодулированная
несущая с максимальной амплитудой. При
ЧМ амплитуда несущей не изменяется, а
при АМ ее необходимо уменьшать до
значенияА (пунктир), что снижает
среднюю мощность сигнала.
Из-за
меньшей помехоустойчивости АМ как
самостоятельный вид модуляции в
телемеханике находит ограниченное
применение и используется в основном
как промежуточный вид модуляции при
двойных модуляциях, о которых будет
сказано далее. Большое применение нашла
амплитудная демодуляция как промежуточный
этап при частотной или фазовой демодуляции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
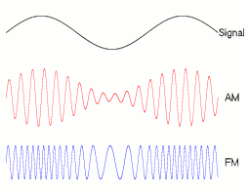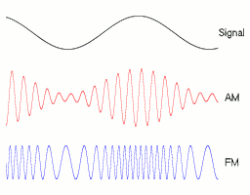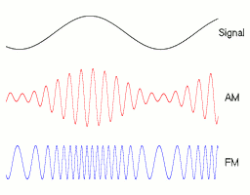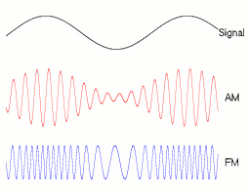
A signal may be carried by an AM or FM radio wave.

FM has better noise (RFI) rejection than AM, as shown in this dramatic New York publicity demonstration by General Electric in 1940. The radio has both AM and FM receivers. With a million-volt electric arc as a source of interference behind it, the AM receiver produced only a roar of static, while the FM receiver clearly reproduced a music program from Armstrong’s experimental FM transmitter W2XMN in New Jersey.
Frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. The technology is used in telecommunications, radio broadcasting, signal processing, and computing.
In analog frequency modulation, such as radio broadcasting, of an audio signal representing voice or music, the instantaneous frequency deviation, i.e. the difference between the frequency of the carrier and its center frequency, has a functional relation to the modulating signal amplitude.
Digital data can be encoded and transmitted with a type of frequency modulation known as frequency-shift keying (FSK), in which the instantaneous frequency of the carrier is shifted among a set of frequencies. The frequencies may represent digits, such as ‘0’ and ‘1’. FSK is widely used in computer modems, such as fax modems, telephone caller ID systems, garage door openers, and other low-frequency transmissions.[1] Radioteletype also uses FSK.[2]
Frequency modulation is widely used for FM radio broadcasting. It is also used in telemetry, radar, seismic prospecting, and monitoring newborns for seizures via EEG,[3] two-way radio systems, sound synthesis, magnetic tape-recording systems and some video-transmission systems. In radio transmission, an advantage of frequency modulation is that it has a larger signal-to-noise ratio and therefore rejects radio frequency interference better than an equal power amplitude modulation (AM) signal. For this reason, most music is broadcast over FM radio.
However, under severe enough multipath conditions it performs much more poorly than AM, with distinct high frequency noise artifacts that are audible with lower volumes and less complex tones.[citation needed] With high enough volume and carrier deviation audio distortion starts to occur that otherwise wouldn’t be present without multipath or with an AM signal.[citation needed]
Frequency modulation and phase modulation are the two complementary principal methods of angle modulation; phase modulation is often used as an intermediate step to achieve frequency modulation. These methods contrast with amplitude modulation, in which the amplitude of the carrier wave varies, while the frequency and phase remain constant.
Theory[edit]
If the information to be transmitted (i.e., the baseband signal) is 

where 


In this equation, 

It is important to realize that this process of integrating the instantaneous frequency to create an instantaneous phase is quite different from what the term “frequency modulation” naively implies, namely directly adding the modulating signal to the carrier frequency
which would result in a modulated signal that has spurious local minima and maxima that do not correspond to those of the carrier.
While most of the energy of the signal is contained within fc ± fΔ, it can be shown by Fourier analysis that a wider range of frequencies is required to precisely represent an FM signal. The frequency spectrum of an actual FM signal has components extending infinitely, although their amplitude decreases and higher-order components are often neglected in practical design problems.[5]
Sinusoidal baseband signal[edit]
Mathematically, a baseband modulating signal may be approximated by a sinusoidal continuous wave signal with a frequency fm. This method is also named as single-tone modulation. The integral of such a signal is:
In this case, the expression for y(t) above simplifies to:
where the amplitude 

The harmonic distribution of a sine wave carrier modulated by such a sinusoidal signal can be represented with Bessel functions; this provides the basis for a mathematical understanding of frequency modulation in the frequency domain.
Modulation index[edit]
As in other modulation systems, the modulation index indicates by how much the modulated variable varies around its unmodulated level. It relates to variations in the carrier frequency:
where 

If 


For digital modulation systems, for example binary frequency shift keying (BFSK), where a binary signal modulates the carrier, the modulation index is given by:
where 




If 



With a tone-modulated FM wave, if the modulation frequency is held constant and the modulation index is increased, the (non-negligible) bandwidth of the FM signal increases but the spacing between spectra remains the same; some spectral components decrease in strength as others increase. If the frequency deviation is held constant and the modulation frequency increased, the spacing between spectra increases.
Frequency modulation can be classified as narrowband if the change in the carrier frequency is about the same as the signal frequency, or as wideband if the change in the carrier frequency is much higher (modulation index > 1) than the signal frequency.[7] For example, narrowband FM (NFM) is used for two-way radio systems such as Family Radio Service, in which the carrier is allowed to deviate only 2.5 kHz above and below the center frequency with speech signals of no more than 3.5 kHz bandwidth. Wideband FM is used for FM broadcasting, in which music and speech are transmitted with up to 75 kHz deviation from the center frequency and carry audio with up to a 20 kHz bandwidth and subcarriers up to 92 kHz.
Bessel functions[edit]

Frequency spectrum and waterfall plot of a 146.52 MHz carrier, frequency modulated by a 1,000 Hz sinusoid. The modulation index has been adjusted to around 2.4, so the carrier frequency has small amplitude. Several strong sidebands are apparent; in principle an infinite number are produced in FM but the higher-order sidebands are of negligible magnitude.
For the case of a carrier modulated by a single sine wave, the resulting frequency spectrum can be calculated using Bessel functions of the first kind, as a function of the sideband number and the modulation index. The carrier and sideband amplitudes are illustrated for different modulation indices of FM signals. For particular values of the modulation index, the carrier amplitude becomes zero and all the signal power is in the sidebands.[5]
Since the sidebands are on both sides of the carrier, their count is doubled, and then multiplied by the modulating frequency to find the bandwidth. For example, 3 kHz deviation modulated by a 2.2 kHz audio tone produces a modulation index of 1.36. Suppose that we limit ourselves to only those sidebands that have a relative amplitude of at least 0.01. Then, examining the chart shows this modulation index will produce three sidebands. These three sidebands, when doubled, gives us (6 × 2.2 kHz) or a 13.2 kHz required bandwidth.
| Modulation index |
Sideband amplitude | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Carrier | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 0.00 | 1.00 | ||||||||||||||||
| 0.25 | 0.98 | 0.12 | |||||||||||||||
| 0.5 | 0.94 | 0.24 | 0.03 | ||||||||||||||
| 1.0 | 0.77 | 0.44 | 0.11 | 0.02 | |||||||||||||
| 1.5 | 0.51 | 0.56 | 0.23 | 0.06 | 0.01 | ||||||||||||
| 2.0 | 0.22 | 0.58 | 0.35 | 0.13 | 0.03 | ||||||||||||
| 2.40483 | 0.00 | 0.52 | 0.43 | 0.20 | 0.06 | 0.02 | |||||||||||
| 2.5 | −0.05 | 0.50 | 0.45 | 0.22 | 0.07 | 0.02 | 0.01 | ||||||||||
| 3.0 | −0.26 | 0.34 | 0.49 | 0.31 | 0.13 | 0.04 | 0.01 | ||||||||||
| 4.0 | −0.40 | −0.07 | 0.36 | 0.43 | 0.28 | 0.13 | 0.05 | 0.02 | |||||||||
| 5.0 | −0.18 | −0.33 | 0.05 | 0.36 | 0.39 | 0.26 | 0.13 | 0.05 | 0.02 | ||||||||
| 5.52008 | 0.00 | −0.34 | −0.13 | 0.25 | 0.40 | 0.32 | 0.19 | 0.09 | 0.03 | 0.01 | |||||||
| 6.0 | 0.15 | −0.28 | −0.24 | 0.11 | 0.36 | 0.36 | 0.25 | 0.13 | 0.06 | 0.02 | |||||||
| 7.0 | 0.30 | 0.00 | −0.30 | −0.17 | 0.16 | 0.35 | 0.34 | 0.23 | 0.13 | 0.06 | 0.02 | ||||||
| 8.0 | 0.17 | 0.23 | −0.11 | −0.29 | −0.10 | 0.19 | 0.34 | 0.32 | 0.22 | 0.13 | 0.06 | 0.03 | |||||
| 8.65373 | 0.00 | 0.27 | 0.06 | −0.24 | −0.23 | 0.03 | 0.26 | 0.34 | 0.28 | 0.18 | 0.10 | 0.05 | 0.02 | ||||
| 9.0 | −0.09 | 0.25 | 0.14 | −0.18 | −0.27 | −0.06 | 0.20 | 0.33 | 0.31 | 0.21 | 0.12 | 0.06 | 0.03 | 0.01 | |||
| 10.0 | −0.25 | 0.04 | 0.25 | 0.06 | −0.22 | −0.23 | −0.01 | 0.22 | 0.32 | 0.29 | 0.21 | 0.12 | 0.06 | 0.03 | 0.01 | ||
| 12.0 | 0.05 | −0.22 | −0.08 | 0.20 | 0.18 | −0.07 | −0.24 | −0.17 | 0.05 | 0.23 | 0.30 | 0.27 | 0.20 | 0.12 | 0.07 | 0.03 | 0.01 |
Carson’s rule[edit]
A rule of thumb, Carson’s rule states that nearly all (≈98 percent) of the power of a frequency-modulated signal lies within a bandwidth 
where 




Condition for application of Carson’s rule is only sinusoidal signals. For non-sinusoidal signals:
where W is the highest frequency in the modulating signal but non-sinusoidal in nature and D is the Deviation ratio which the ratio of frequency deviation to highest frequency of modulating non-sinusoidal signal.
Noise reduction[edit]
FM provides improved signal-to-noise ratio (SNR), as compared for example with AM. Compared with an optimum AM scheme, FM typically has poorer SNR below a certain signal level called the noise threshold, but above a higher level – the full improvement or full quieting threshold – the SNR is much improved over AM. The improvement depends on modulation level and deviation. For typical voice communications channels, improvements are typically 5–15 dB. FM broadcasting using wider deviation can achieve even greater improvements. Additional techniques, such as pre-emphasis of higher audio frequencies with corresponding de-emphasis in the receiver, are generally used to improve overall SNR in FM circuits. Since FM signals have constant amplitude, FM receivers normally have limiters that remove AM noise, further improving SNR.[8][9]
Implementation[edit]
Modulation[edit]
FM signals can be generated using either direct or indirect frequency modulation:
- Direct FM modulation can be achieved by directly feeding the message into the input of a voltage-controlled oscillator.
- For indirect FM modulation, the message signal is integrated to generate a phase-modulated signal. This is used to modulate a crystal-controlled oscillator, and the result is passed through a frequency multiplier to produce an FM signal. In this modulation, narrowband FM is generated leading to wideband FM later and hence the modulation is known as indirect FM modulation.[10]
Demodulation[edit]

Many FM detector circuits exist. A common method for recovering the information signal is through a Foster–Seeley discriminator or ratio detector. A phase-locked loop can be used as an FM demodulator. Slope detection demodulates an FM signal by using a tuned circuit which has its resonant frequency slightly offset from the carrier. As the frequency rises and falls the tuned circuit provides a changing amplitude of response, converting FM to AM. AM receivers may detect some FM transmissions by this means, although it does not provide an efficient means of detection for FM broadcasts. In Software-Defined Radio implementations the demodulation may be carried out by using the Hilbert transform (implemented as a filter) to recover the instantaneous phase, and thereafter differentiating this phase (using another filter) to recover the instantaneous frequency. Alternatively, a complex mixer followed by a bandpass filter may be used to translate the signal to baseband, and then proceeding as before.
Applications[edit]
Doppler effect[edit]
When an echolocating bat approaches a target, its outgoing sounds return as echoes, which are Doppler-shifted upward in frequency. In certain species of bats, which produce constant frequency (CF) echolocation calls, the bats compensate for the Doppler shift by lowering their call frequency as they approach a target. This keeps the returning echo in the same frequency range of the normal echolocation call. This dynamic frequency modulation is called the Doppler Shift Compensation (DSC), and was discovered by Hans Schnitzler in 1968
Magnetic tape storage[edit]
FM is also used at intermediate frequencies by analog VCR systems (including VHS) to record the luminance (black and white) portions of the video signal. Commonly, the chrominance component is recorded as a conventional AM signal, using the higher-frequency FM signal as bias. FM is the only feasible method of recording the luminance (“black-and-white”) component of video to (and retrieving video from) magnetic tape without distortion; video signals have a large range of frequency components – from a few hertz to several megahertz, too wide for equalizers to work with due to electronic noise below −60 dB. FM also keeps the tape at saturation level, acting as a form of noise reduction; a limiter can mask variations in playback output, and the FM capture effect removes print-through and pre-echo. A continuous pilot-tone, if added to the signal – as was done on V2000 and many Hi-band formats – can keep mechanical jitter under control and assist timebase correction.
These FM systems are unusual, in that they have a ratio of carrier to maximum modulation frequency of less than two; contrast this with FM audio broadcasting, where the ratio is around 10,000. Consider, for example, a 6-MHz carrier modulated at a 3.5-MHz rate; by Bessel analysis, the first sidebands are on 9.5 and 2.5 MHz and the second sidebands are on 13 MHz and −1 MHz. The result is a reversed-phase sideband on +1 MHz; on demodulation, this results in unwanted output at 6 – 1 = 5 MHz. The system must be designed so that this unwanted output is reduced to an acceptable level.[11]
Sound[edit]
FM is also used at audio frequencies to synthesize sound. This technique, known as FM synthesis, was popularized by early digital synthesizers and became a standard feature in several generations of personal computer sound cards.
Radio[edit]

An American FM radio transmitter in Buffalo, NY at WEDG
Edwin Howard Armstrong (1890–1954) was an American electrical engineer who invented wideband frequency modulation (FM) radio.[12]
He patented the regenerative circuit in 1914, the superheterodyne receiver in 1918 and the super-regenerative circuit in 1922.[13] Armstrong presented his paper, “A Method of Reducing Disturbances in Radio Signaling by a System of Frequency Modulation”, (which first described FM radio) before the New York section of the Institute of Radio Engineers on November 6, 1935. The paper was published in 1936.[14]
As the name implies, wideband FM (WFM) requires a wider signal bandwidth than amplitude modulation by an equivalent modulating signal; this also makes the signal more robust against noise and interference. Frequency modulation is also more robust against signal-amplitude-fading phenomena. As a result, FM was chosen as the modulation standard for high frequency, high fidelity radio transmission, hence the term “FM radio” (although for many years the BBC called it “VHF radio” because commercial FM broadcasting uses part of the VHF band—the FM broadcast band). FM receivers employ a special detector for FM signals and exhibit a phenomenon known as the capture effect, in which the tuner “captures” the stronger of two stations on the same frequency while rejecting the other (compare this with a similar situation on an AM receiver, where both stations can be heard simultaneously). However, frequency drift or a lack of selectivity may cause one station to be overtaken by another on an adjacent channel. Frequency drift was a problem in early (or inexpensive) receivers; inadequate selectivity may affect any tuner.
An FM signal can also be used to carry a stereo signal; this is done with multiplexing and demultiplexing before and after the FM process. The FM modulation and demodulation process is identical in stereo and monaural processes. A high-efficiency radio-frequency switching amplifier can be used to transmit FM signals (and other constant-amplitude signals). For a given signal strength (measured at the receiver antenna), switching amplifiers use less battery power and typically cost less than a linear amplifier. This gives FM another advantage over other modulation methods requiring linear amplifiers, such as AM and QAM.
FM is commonly used at VHF radio frequencies for high-fidelity broadcasts of music and speech. Analog TV sound is also broadcast using FM. Narrowband FM is used for voice communications in commercial and amateur radio settings. In broadcast services, where audio fidelity is important, wideband FM is generally used. In two-way radio, narrowband FM (NBFM) is used to conserve bandwidth for land mobile, marine mobile and other radio services.
There are reports that on October 5, 1924, Professor Mikhail A. Bonch-Bruevich, during a scientific and technical conversation in the Nizhny Novgorod Radio Laboratory, reported about his new method of telephony, based on a change in the period of oscillations. Demonstration of frequency modulation was carried out on the laboratory model.[15]
See also[edit]
- Amplitude modulation
- Continuous-wave frequency-modulated radar
- Chirp
- FM broadcasting
- FM stereo
- FM-UWB (FM and Ultra Wideband)
- History of radio
- Modulation, for a list of other modulation techniques
References[edit]
- ^ Gibilisco, Stan (2002). Teach yourself electricity and electronics. McGraw-Hill Professional. p. 477. ISBN 978-0-07-137730-0.
morse-code frequency-shift-keying sent-using-fsk.
- ^ Rutledge, David B. (1999). The Electronics of Radio. Cambridge University Press. p. 310. ISBN 978-0-521-64645-1.
- ^ B. Boashash, editor, Time-Frequency Signal Analysis and Processing – A Comprehensive Reference, Elsevier Science, Oxford, 2003; ISBN 0-08-044335-4
- ^ Faruque, Saleh (2017). Radio Frequency Modulation Made Easy (PDF). Springer Cham. pp. 33–37. ISBN 978-3-319-41200-9.
- ^ a b T.G. Thomas, S. C. Sekhar Communication Theory, Tata-McGraw Hill 2005, ISBN 0-07-059091-5 page 136
- ^ Der, Lawrence. “Frequency Modulation (FM) Tutorial” (PDF). Silicon Laboratories. S2CID 48672999. Archived from the original (PDF) on 2014-10-21. Retrieved 17 October 2019.
- ^ Lathi, B. P. (1968). Communication Systems, p. 214–217. New York: John Wiley and Sons, ISBN 0-471-51832-8.
- ^ H. P. Westman, ed. (1970). Reference Data for Radio Engineers (Fifth ed.). Howard W. Sams & Co. pp. 21–11.
- ^ Alan Bloom (2010). “Chapter 8. Modulation”. In H. Ward Silver; Mark J. Wilson (eds.). The ARRL Handbook for Radio Communications. American Radio Relay League. p. 8.7. ISBN 978-0-87259-146-2.
- ^ Haykin, Simon [Ed]. (2001). Communication Systems, 4th ed.
- ^ : “FM Systems Of Exceptional Bandwidth” Proc. IEEE vol 112, no. 9, p. 1664, September 1965
- ^ A. Michael Noll (2001). Principles of modern communications technology. Artech House. p. 104. ISBN 978-1-58053-284-6.
- ^ US 1342885
- ^ Armstrong, E. H. (May 1936). “A Method of Reducing Disturbances in Radio Signaling by a System of Frequency Modulation”. Proceedings of the IRE. IRE. 24 (5): 689–740. doi:10.1109/JRPROC.1936.227383. S2CID 43628076.
- ^ Ф. Лбов. Новая система радиофона // «Радиолюбитель». — 1924. — № 6. — С. 86.
Further reading[edit]
- Carlson, A. Bruce (2001). Communication Systems. Science/Engineering/Math (4th ed.). McGraw-Hill. ISBN 0-07-011127-8, ISBN 978-0-07-011127-1.
- Frost, Gary L. (2010). Early FM Radio: Incremental technology in twentieth-century America. Baltimore, MD: Johns Hopkins University Press. ISBN 978-0-8018-9440-4, ISBN 978-0-8018-9440-4.
- Seymour, Ken (1996). “Frequency Modulation”. The Electronics Handbook (1st ed.). CRC Press. pp. 1188–1200. ISBN 0-8493-8345-5. (2nd ed., 2005)
External links[edit]
- Analog Modulation online interactive demonstration using Python in Google Colab Platform, by C Foh.
4.2.1. Помехоустойчивость частотной модуляции
4.2.2. Методы осуществления частотной модуляции
4.2.2.1. Косвенные методы частотной модуляции
4.2.2.2. Прямые методы частотной модуляции
4.2.3. Особенности построения высокочастотного тракта передатчиков с частотной модуляцией
При частотной модуляции по периодическому закону изменяется частота колебаний w:
w = w0 + DwcosWt ,
где ![]() амплитуда отклонения частоты от некоторого среднего значения, носящая название девиации частоты, она пропорциональна амплитуде модулирующего сигнала низкой частоты Uмод:
амплитуда отклонения частоты от некоторого среднего значения, носящая название девиации частоты, она пропорциональна амплитуде модулирующего сигнала низкой частоты Uмод:
![]() (4.6)
(4.6)
Можно показать, что мгновенное значение тока высокой частоты при частотной модуляции определяется выражением:
![]() , (4.7)
, (4.7)
где ![]() индекс частотной модуляции:
индекс частотной модуляции:
![]() (4.8)
(4.8)
Легко видеть, что выражения для колебаний, модулированных по фазе формула (4.1) и по частоте формула (4.7) идентичны. Это можно было предвидеть, исходя из физических соображений. Однако, между колебаниями, модулированными по фазе и по частоте есть существенная разница: индекс фазовой модуляции ![]() (4.3) не зависит от модулирующей частоты F, тогда как индекс частотной модуляции
(4.3) не зависит от модулирующей частоты F, тогда как индекс частотной модуляции ![]() (4.8) от нее зависит. Отсюда следует, что если изменить частоту F модулирующего напряжения при его неизменной амплитуде
(4.8) от нее зависит. Отсюда следует, что если изменить частоту F модулирующего напряжения при его неизменной амплитуде![]() , то изменится индекс частотной модуляции
, то изменится индекс частотной модуляции ![]() . Это приведет к изменению амплитуд всех составляющих спектра и , что самое важное, к изменению их числа n. Что касается ширины спектра, то нетрудно показать, что она остается постоянной. Если учитывать только те составляющие спектра, амплитуды которых больше 15% от амплитуды сигнала без модуляции (при этом сохраняются составляющие спектра, мощность которых больше 2% мощности без модуляции) то подставляя (4.8) в (4.3), получим, что полоса частот, занимаемая спектром, равна:
. Это приведет к изменению амплитуд всех составляющих спектра и , что самое важное, к изменению их числа n. Что касается ширины спектра, то нетрудно показать, что она остается постоянной. Если учитывать только те составляющие спектра, амплитуды которых больше 15% от амплитуды сигнала без модуляции (при этом сохраняются составляющие спектра, мощность которых больше 2% мощности без модуляции) то подставляя (4.8) в (4.3), получим, что полоса частот, занимаемая спектром, равна:
![]() (4.9)
(4.9)
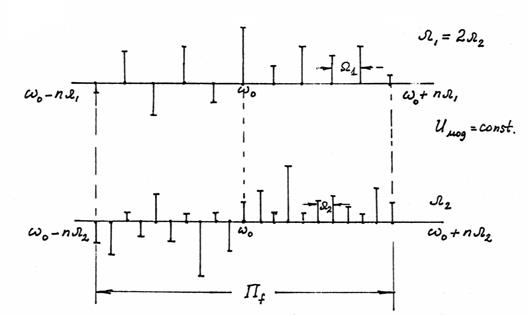
Рис.4.3
В самом деле, допустим, что Df= 50 кГц, a F = 50 Гц; при этом ![]() , а ширина полосы Пf=2×103×50=100кГц. Спектр содержит по 1000 составляющих слева и справа от средней частоты
, а ширина полосы Пf=2×103×50=100кГц. Спектр содержит по 1000 составляющих слева и справа от средней частоты ![]() , расстояние между соседними составляющими спектра по оси частот равно 50 Гц. Если F = 10 кГц, то
, расстояние между соседними составляющими спектра по оси частот равно 50 Гц. Если F = 10 кГц, то ![]() , и ширина полосы Пf=2×5×10×103=100кГц. В этом случае спектр содержит всего по 5 составляющих слева и справа от частоты f0 , но расстояние между соседними составляющими спектра по оси частот равно 10 кГц. Таким образом, ширина спектра колебаний, модулированных по частоте, при неизменной амплитуде модулирующего напряжения остается постоянной, меняется лишь структура спектра число боковых частот и амплитуды боковых частот и средней частоты
, и ширина полосы Пf=2×5×10×103=100кГц. В этом случае спектр содержит всего по 5 составляющих слева и справа от частоты f0 , но расстояние между соседними составляющими спектра по оси частот равно 10 кГц. Таким образом, ширина спектра колебаний, модулированных по частоте, при неизменной амплитуде модулирующего напряжения остается постоянной, меняется лишь структура спектра число боковых частот и амплитуды боковых частот и средней частоты ![]() (рис.4.3 ).
(рис.4.3 ).
Следует отметить, что при малом индексе частотной модуляции, когда ![]() , полоса частот, занимаемая сигналом, определяется наивысшей частотой модуляции Fmax , а не девиацией частоты Df . Индекс
, полоса частот, занимаемая сигналом, определяется наивысшей частотой модуляции Fmax , а не девиацией частоты Df . Индекс ![]() соответствует узкополосной частотной модуляции, при этом ширина полосы , занимаемой сигналом, равна Пfузк=2Fmax, то есть такая же как при амплитудной модуляции.
соответствует узкополосной частотной модуляции, при этом ширина полосы , занимаемой сигналом, равна Пfузк=2Fmax, то есть такая же как при амплитудной модуляции.
В заключение следует отметить, что при высококачественном радиовещании необходимо передавать составляющие спектра, амплитуда которых больше 0,01 амплитуды колебаний без модуляции. При этом ширина спектра модулированного по частоте сигнала определяется эмпирической формулой Манаева:
![]()
В России девиация частоты при высококачественном радиовещании принята равной Df =50 кГц, тогда при Fmin=50Гц полоса частот, занимаемая радиосигналом Пfmin=103кГц, а при Fmax=15кГц Пfmax=183кГц (таблица 4.1), то есть при изменении модулирующей частоты в 300 раз полоса частот, занимаемая модулированным по частоте сигналом, увеличивается приблизительно на 80%, то есть менее, чем вдвое. На практике для передачи сигнала с частотной модуляцией при высококачественном радиовещании отводится канал шириной 250кГц, т.е. он во много раз шире полосы сигнала с амплитудной модуляцией. По этой причине частотная модуляция используется в диапазоне УКВ.
Таблица 4.1
| ∆f=50кГц | ||
| F,Гц | φ1, радиан | П,кГц |
| 50 | 1000 | 103 |
| 100 | 500 | 105 |
| 1000 | 50 | 118 |
| 3000 | 16,6 | 130 |
| 5000 | 10 | 142 |
| 10000 | 5 | 165 |
| 15000 | 3,33 | 183 |
4.2.1. Помехоустойчивость частотной модуляции
Большим достоинством частотной модуляции, наряду с её высокими экономическими показателями, является высокая помехоустойчивость. Причину этого можно пояснить следующим образом. Как известно, блок-схема приемника ЧМ сигнала всегда содержит ограничитель и частотный детектор. Предположим, что на вход частотного детектора поступают синусоидальное напряжение сигнала Uc вектор ОА (рис 4.4), и меньшее по амплитуде синусоидальное напряжение помехи Uп вектор АВ.
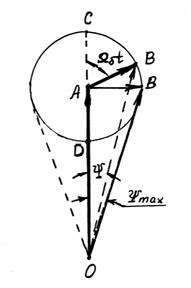
Рис.4.4
Обозначим отношение Uс/Uп=p. Если предположить, что плоскость рисунка вращается с угловой скоростью вектора ОА, то этот вектор будет неподвижным, а вектор помехи АВ, частота которой отличается от частоты сигнала, будет вращаться вокруг неподвижного вектора ОА c угловой частотой Wб, равной разности угловых частот сигнала и помехи, т.е. Wб=wсwп. При этом происходит изменение длины результирующего вектора ОВ от OD до OC и изменение его фазы в пределах угла ±Y. Если напряжение сигнала по крайней мере вдвое больше напряжения помехи, т.е. угол Y£300, то максимальный угол отклонения результирующего вектора приблизительно равен:
Ymax=аrctg (АВ/ОА)»АВ/ОА=Uп/Uс =1/р
Точно такой же максимальный угол отклонения результирующего вектора Ymax будет и на выходе ограничителя. Изменение амплитуды будет устранено ограничителем. При р>2 можно считать, что угол отклонения Y результирующего вектора от исходного положения будет изменяться во времени по синусоидальному закону:
Y»YmaxsinWбt
Таким образом, на входе частотного детектора появляется обусловленная напряжением помехи паразитная фазовая модуляция, которая согласно (4.2) сопровождается частотной модуляцией с индексом Dwп=WбY=Wб/р,
т.е. в результате действия помехи на выходе ограничителя появляются колебания, модулированные по частоте с девиацией Df=Fб/р, где Fб=fcfп. Если полезный сигнал промодулирован по частоте с девиацией Dfc, то отношение сигнал/помеха на выходе частотного детектора будет равно:
![]()
![]() (4.10)
(4.10)
Из (4.10) следует, что если девиация частоты сигнала с частотной модуляцией равна 50кГц, а разность между частотами сигнала и помехи составляет 1кГц, то на выходе частотного детектора отношение сигнал/помеха в 50 раз больше, чем на выходе ограничителя. При этом больше подавляются помехи с частотами, близкими к средней частоте f0, которые в меньшей степени подавляются системой контуров приемника.
На практике на входе частотного детектора приемника может действовать напряжение помех сложной формы. Анализ показывает, что выигрыш (Q) в отношении сигнал/помеха, т.е. в помехоустойчивости, при частотной модуляции по сравнению с амплитудной модуляцией для гладких или флуктуационных помех составляет Qф=1.73j1fmax, а для импульсных Qи=2j1fmax, где j1fmax =![]() . Здесь j1fmax индекс частотной модуляции при наивысшей модулирующей частоте Fmax. Для обеспечения помехоустойчивости ЧМ передатчика требуется, чтобы величина j1fmax =23. В настоящее время в России при высококачественном радиовещании принята девиация частоты Dfс=50 кГц при наивысшей модулирующей частоте Fв=15кГц, при этом индекс модуляции j1fmax»3,3.
. Здесь j1fmax индекс частотной модуляции при наивысшей модулирующей частоте Fmax. Для обеспечения помехоустойчивости ЧМ передатчика требуется, чтобы величина j1fmax =23. В настоящее время в России при высококачественном радиовещании принята девиация частоты Dfс=50 кГц при наивысшей модулирующей частоте Fв=15кГц, при этом индекс модуляции j1fmax»3,3.
4.2.2. Методы осуществления частотной модуляции
В радиопередающих устройствах широко применяются два метода частотной модуляции: косвенный и прямой.
4.2.2.1. Косвенные методы частотной модуляции
При косвенном методе колебания, модулированные по частоте, получают в результате фазовой модуляции интегральной функцией модулирующего сигнала (рис.4.5а). В самом деле, в схеме, показанной на рис.4.5а, при ![]()
![]() , где
, где ![]() самая низкая модулирующая частота , напряжение UвхW ,действующее на входе фазового модулятора, равно:
самая низкая модулирующая частота , напряжение UвхW ,действующее на входе фазового модулятора, равно:
![]()
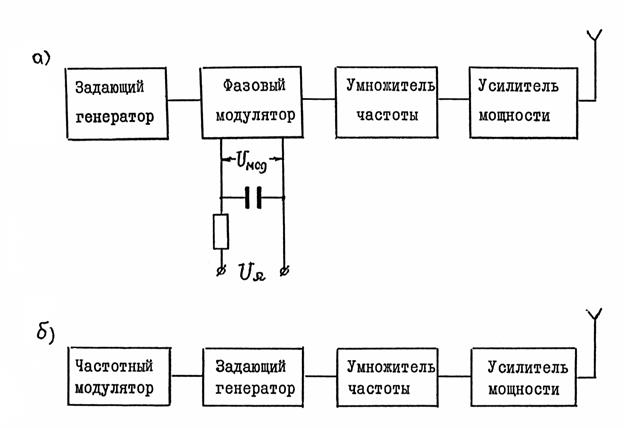
Рис.4.5
При этом фазовая модуляция будет иметь индекс ![]() , который обратно пропорционален модулирующей частоте, то есть на выходе фазового модулятора будут колебания с частотной модуляцией. Основным достоинством косвенных методов частотной модуляции является возможность обеспечения сколь угодно высокой стабильности средней частоты
, который обратно пропорционален модулирующей частоте, то есть на выходе фазового модулятора будут колебания с частотной модуляцией. Основным достоинством косвенных методов частотной модуляции является возможность обеспечения сколь угодно высокой стабильности средней частоты ![]() , поскольку модуляция осуществляется в одном из промежуточных каскадов возбудителя, а не в автогенераторе. К недостаткам косвенных методов следует отнести значительные трудности, возникающие при необходимости осуществления глубокой (широкополосной) частотной модуляции.
, поскольку модуляция осуществляется в одном из промежуточных каскадов возбудителя, а не в автогенераторе. К недостаткам косвенных методов следует отнести значительные трудности, возникающие при необходимости осуществления глубокой (широкополосной) частотной модуляции.
4.2.2.2. Прямые методы частотной модуляции
При прямых методах частотной модуляции модулирующим напряжением звуковой частоты воздействуют через частотный модулятор непосредственно на задающий автогенератор, изменяя его частоту (рис.4.5б).
Частотные модуляторы представляют собой управляемые реактивные сопротивления, величина которых изменяется по закону низкочастотного модулирующего сигнала. Основными требованиями, предъявляемыми к частотным модуляторам, являются: безынерционность (время переходных процессов должно быть намного меньше периода наивысшей модулирующей частоты); линейность модуляционной характеристики ![]() ; максимально возможная девиация частоты
; максимально возможная девиация частоты ![]() , не ухудшающая стабильности средней частоты
, не ухудшающая стабильности средней частоты ![]() ; постоянство девиации частоты по диапазону; минимальный уровень паразитной амплитудной модуляции (ПАМ) и др. В качестве частотных модуляторов используют реактивные лампы и диоды, транзисторы, варикапы и др.
; постоянство девиации частоты по диапазону; минимальный уровень паразитной амплитудной модуляции (ПАМ) и др. В качестве частотных модуляторов используют реактивные лампы и диоды, транзисторы, варикапы и др.
Методы поддержания стабильности средней частоты
Основным недостатком прямых методов частотной модуляции является низкая стабильность средней частоты: при осуществлении модуляции частота задающего автогенератора под воздействием частотного модулятора должна изменяться в сравнительно широких пределах и, вместе с тем, средняя частота ![]() должна иметь высокую стабильность. Для удовлетворения этих противоречивых требований используются специальные методы поддержания стабильности средней частоты схемы с автоматической подстройкой частоты (АПЧ), интерполяционный метод, описанный в 2.2.7, и др.
должна иметь высокую стабильность. Для удовлетворения этих противоречивых требований используются специальные методы поддержания стабильности средней частоты схемы с автоматической подстройкой частоты (АПЧ), интерполяционный метод, описанный в 2.2.7, и др.
При использовании интерполяционного метода (рис.2.18) диапазонным (интерполяционным) генератором является генератор с частотной модуляцией. Для обеспечения высокой стабильности средней частоты интерполяционное число N= fкв /fc должно быть как можно больше (здесь fкв частота кварцевого генератора, fc средняя частота генератора с частотной модуляцией). Величину N ограничивают возможности селектора. Обычно N £ 20. На рис.4.6а показана простейшая структурная схема осуществления автоматической подстройки средней частоты в передатчике с ЧМ. В этой схеме напряжение с выхода ЧМ Генератора, работающего на частоте fг, поступает на дискриминатор, колебательная система которого настроена на эту же частоту. При изменении частоты генератора относительно частоты дискриминатора на выходе последнего появляется напряжение, закон изменения которого соответствует закону изменения частоты генератора. Это напряжение поступает на частотный модулятор, управляющий частотой генератора. Если бы схема рис.4.6а не содержала корректирующего четырехполюсника, выполненного в виде потенциометра RC, частотная модуляция была бы невозможна, поскольку из-за АПЧ происходила бы демодуляция сигнала.
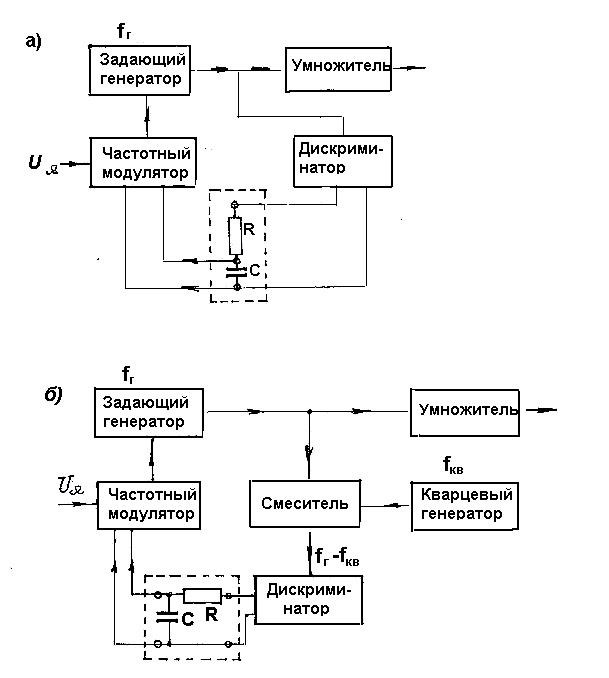
Рис.4.6
Благодаря корректирующему четырехполюснику параметры которого должны удовлетворять неравенству:
![]() << R ,
<< R ,
где Wн самая низкая модулирующая звуковая частота, напряжение, появляющееся на выходе дискриминатора из-за частотной модуляции, не поступает на вход частотного модулятора. Изменения частоты из-за нестабильности генератора очень медленные, поэтому здесь дискриминатор на процесс модуляции не влияет. Так как в схеме рис.4.6а колебательные системы генератора и дискриминатора настроены на одну и ту же частоту, то если раньше, без АПЧ, нестабильность частоты определялась колебательным контуром генератора, то теперь она в такой же степени определяется контуром дискриминатора. От этого недостатка свободна схема, приведенная на рис.4.6б, где дискриминатор работает на значительно более низкой частоте, поскольку его колебательный контур настроен на разностную частоту (fг fкв), при этом, как было показано ранее (см.2.5.1), эталонность контура намного выше. Схема АПЧ с кварцевым гетеродином существенно повышает стабильность средней частоты ЧМ генератора, поэтому она получила широкое распространение.
Частотные модуляторы на реактивных лампах
В качестве частотных модуляторов используют реактивные лампы, представляющие собой реактивный двухполюсник, сопротивление которого носит чисто реактивный характер и зависит от величины модулирующего напряжения, приложенного к управляющей сетке лампы. Все схемы реактивных лампы построены так, что колебательный контур модулируемого генератора подключен к потенциометру, состоящему из двух сопротивлений Z1 и Z2, включенных последовательно между анодом и катодом реактивной лампы, одно из них всегда активное, а другое реактивное (рис.4.7а), причем Z1 >> Z2. Напряжение со всего потенциометра Uп подается на анод реактивной лампы, а с его части с сопротивления Z2 на ее управляющую сетку. Сопротивление ![]() потенциометра равно:
потенциометра равно:
![]() .
.
Здесь Sср средняя крутизна: Sср= ![]() , где Uупр = Ug DUк, но при малой проницаемости D, а в качестве реактивных ламп используют всегда многоэлектродные лампы, Sср @
, где Uупр = Ug DUк, но при малой проницаемости D, а в качестве реактивных ламп используют всегда многоэлектродные лампы, Sср @ ![]() . Поско0льку Sср=S×a1( 1 соsq ) (см.1.6 ), а
. Поско0льку Sср=S×a1( 1 соsq ) (см.1.6 ), а 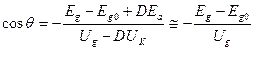 , то при изменении напряжения смещения Еg на управляющей сетке реактивной лампы изменяется средняя крутизна Sср, а следовательно и величина сопротивления Z.
, то при изменении напряжения смещения Еg на управляющей сетке реактивной лампы изменяется средняя крутизна Sср, а следовательно и величина сопротивления Z.
На рис.4.7б приведены варианты схем потенциометра и соответствующие им векторные диаграммы. Сопротивление Z будет чисто реактивным при условии, что фазовый сдвиг Y между напряжением Uа= Uп и током Iа1 равен 900.
Можно показать, что относительное изменение частоты генератора при использовании реактивной лампы определяется формулой:
![]() ,
,
где р коэффициент связи реактивной лампы с колебательным контуром генератора, r характеристическое сопротивление его колебательного контура, n=![]() , Емод – модулирующее напряжение низкой частоты на управляющей сетке реактивной лампы. Таким образом, линейная зависимость
, Емод – модулирующее напряжение низкой частоты на управляющей сетке реактивной лампы. Таким образом, линейная зависимость ![]() возможна при условии, что производная
возможна при условии, что производная ![]() при изменении Емод постоянна. Возможны два режима работы реактивной лампы: в режиме колебаний класса А и класса В.
при изменении Емод постоянна. Возможны два режима работы реактивной лампы: в режиме колебаний класса А и класса В.
При работе в режиме колебаний класса А амплитуда переменного напряжения на управляющей сетке реактивной лампы должна быть мала, для этого Z1 должно быть значительно больше Z2 (обычно n ³10 ). При q=1800Sср=S крутизне статической характеристики лампы.
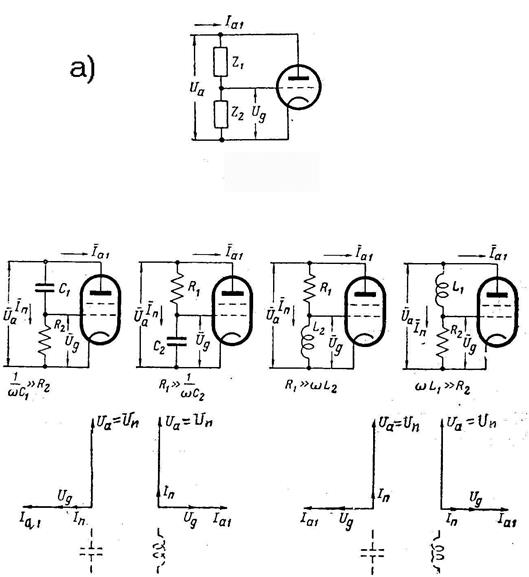
б)
Рис.4.7
Известно, что производная ![]() постоянна при S£ 0,5Smax, поэтому рабочая точка лампы должна быть при значении Еg, которому соответствует крутизна S’=0,25Smax, при этом DS = 0,25Smax, и максимальное значение относительного отклонения частоты равно:
постоянна при S£ 0,5Smax, поэтому рабочая точка лампы должна быть при значении Еg, которому соответствует крутизна S’=0,25Smax, при этом DS = 0,25Smax, и максимальное значение относительного отклонения частоты равно:
![]() .
.
При работе реактивной лампы в режиме колебаний класса В допускают меньшую величину n ради увеличения девиации частоты. Величина средней крутизны Sср= S / ai (q). Как известно (см.1.7.2 ), величина 1/ai (q) изменяется линейно при 600 < q <1200. Если рабочая точка выбрана при q=900 , то
DSср= 0,5×S[ 1/ ai (1200) 1/ ai (600) ] » 0,3×S,
при этом
![]() .
.
(ai (1200) = 0,807, ai (600) = 0,2 ).
Эта величина больше, чем при работе реактивной лампы в режиме колебаний класса А, поскольку здесь меньше значение n.
Выше предполагалось, что фазовый сдвиг Y между напряжением Uа=Uп и током Ia1 равен 900, в действительности Y ¹ 900. Это объясняется рядом причин.
Во-первых, потенциометр, составленный из двух сопротивлений, реактивного и активного, не может обеспечить фазовый сдвиг между напряжением Uа и током Iа1 равный точно 900.
Во-вторых, не учитывался ток потенциометра: сопротивление потенциометра Zаб было принято равным отношению ![]() , тогда как в действительности оно определяется отношением
, тогда как в действительности оно определяется отношением ![]() , где Iп ток потенциометра, который может вызвать дополнительный фазовый сдвиг.
, где Iп ток потенциометра, который может вызвать дополнительный фазовый сдвиг.
В-третьих, не была учтена реакция анода.
При Y ¹ 900 реактивная лампа вносит в колебательный контур генератора не только реактивное сопротивление, но и активное, в результате при модуляции изменяется не только частота колебаний, но и их амплитуда, т.е. появляется ПАМ. При работе реактивной лампы в режиме колебаний класса А, где Z1 >> Z2, уровень ПАМ меньше. Можно показать, что требуемую величину n определяет неравенство n>10Q×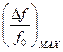 , где Q – добротность контура генератора. Так, при Q»100 и
, где Q – добротность контура генератора. Так, при Q»100 и 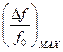 @ 0,02 n>20. Кроме того, для обеспечения Y=900, в качестве реактивных ламп используют пентоды, обладающие малой проницаемостью D (порядка 103), поэтому реакция анода незначительна. Реактивные лампы должны работать без сеточных токов.
@ 0,02 n>20. Кроме того, для обеспечения Y=900, в качестве реактивных ламп используют пентоды, обладающие малой проницаемостью D (порядка 103), поэтому реакция анода незначительна. Реактивные лампы должны работать без сеточных токов.
Меньший уровень ПАМ создают двухтактные схемы реактивных ламп, в которых одна лампа представляет собой емкостное сопротивление, а другая индуктивное, при этом достигается удвоенная девиация частоты: при увеличении реактивного сопротивления одной из ламп реактивное сопротивление другой уменьшается. Если активное сопротивление, вносимое в контур генератора первой лампой увеличивается, то активное сопротивление, вносимое второй уменьшается, при этом результирующее активное сопротивление, вносимое в контур, сохраняется приблизительно постоянным.
Для обеспечения постоянства девиации в диапазоне рабочих частот передатчика используют реактивные лампы с усложненными схемами потенциометра.
Частотные модуляторы на варикапах
В настоящее время в качестве частотных модуляторов используют варикапы полупроводниковые диоды, у которых барьерная емкость Сб запертого p-n-перехода зависит от напряжения, действующего на переходе, и определяется формулой:
Сб = Cб0 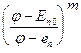 , (4.11)
, (4.11)
где j @ 0,5В контактная разность потенциалов: еп – запирающее напряжение на переходе (eп<0); Еп0 произвольное начальное смещение; Сб0 емкость перехода в рабочей точке при еп=Еп0; m@1/3 для плавного перехода, m @ 1/2 для резкого и m@1 для сверхрезкого. Обычно на практике применяют диоды с m@1/2. Значения Еп0 и Сб0 (рабочая точка) определяются перед началом расчета по реальной вольтфарадной характеристике варикапа. В режиме закрытого p-n-перехода барьерная емкость Сб является емкостью варикапа и можно принять, что емкость Сб является управляющей. Достоинствами варикапов являются малые габариты и вес, малая мощность, расходуемой на питание, а также простота схем. Главным их недостатком является недостаточная линейность модуляционной характеристики. Коэффициент гармоник kf клирфактор, характеризующий содержание гармоник, не должен превышать допустимого значения от 0,01 до 0,1 (последняя цифра для портативных радиостанций индивидуального пользования и т.п.). Как известно, клирфактор определяется формулой:
kf=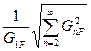 ,
,
где G1F – амплитуда первой гармоники модулирующей частоты, а GnF – амплитуды n ее гармоник. Появление этих гармоник обусловлено нелинейностью вольтфарадной характеристики варикапа. Если под действием модулирующего напряжения емкость варикапа изменяется с частотой F, то с такой же частотой изменяется и средняя частота f0. Однако, из-за нелинейности вольтфарадной характеристики варикапа в спектре функции Cу(t), а следовательно и f0(t), появляются высшие гармоники частоты F, что и приводит к появлению высших гармоник этой частоты на выходе частотного детектора.
Варикап подключают к контуру автогенератора по одной из схем, приведенных на рис.4.8 (или по какой-либо иной), и на него подается модулирующее напряжение низкой частоты. Частота колебаний автогенератора w близка к собственной частоте его колебательного контура wк, которая зависит от управляющего напряжения еу на p-n-переходе варикапа, т.е. w@wк(еу). При безынерционной связи частоты w от еу функция w(еу) – алгебраическая, она носит название статической модуляционной характеристики (СМХ). При проектировании автогенераторов, управляемых по частоте, кроме расчёта энергетического режима генератора и параметров его колебательного контура, необходимо выбрать тип варикапа, а также схему его подключения к контуру, при этом требуется, чтобы полученная СМХ обеспечивала максимальную девиацию частоты при заданной нелинейности и допустимом уровне паразитной амплитудной модуляции (ПАМ). Управляющее напряжение на p-n-переходе варикапа равно eу= Еу0+DEу, где DEу= UW cоsWt его переменная составляющая, а Еу0 постоянное напряжение на переходе в рабочей точке. Девиация частоты автогенератора Dw=wк(еу)wо(еу0), где wк текущее значение частоты. Тогда Dw=D(еу). Частотный модулятор представляет собой ёмкость Су=Суо+DСу(DEу), где Суо барьерная ёмкость при eу= Еу0. Величину Суо учитывают при расчёте частоты wо=wк(Еу0), а отклонение ёмкости DСу определяет девиацию Dw . Относительное значение девиации yf определяется формулой:
yf =![]()
![]() , (4.12)
, (4.12)
где
ωк= ![]() =
= ![]()
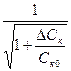 =
= 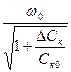 ,
,![]()
![]() , (4.13),
, (4.13),
Lк – контурная индуктивность
a) 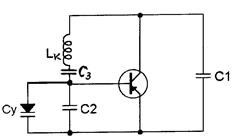 б)
б)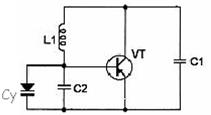
Рис.4.8
В результате несложных преобразований схему колебательного контура автогенератора рис.4.8а можно представить эквивалентной схемой рис.4.9в (этой схемой может быть представлена практически любая схема автогенератора с варикапом, в том числе и схема Клаппа (рис.4.8б). Здесь емкость варикапа (управителя) равна Су=Су0+∆Су, где Су0 емкость варикапа в рабочей точке, т.е. при напряжении на переходе равном Еу0. Полная емкость контура при напряжении на переходе равном Еу0 равна:
Ск0 =![]() =
= ![]() .
.
Здесь
С20=С2 + Су0,
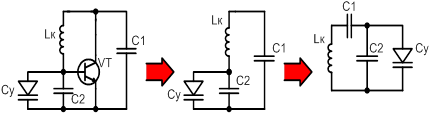
а) б) в)
Рис. 4.9
Емкость контура при напряжении на переходе Еу =Е у0+∆Еу равна
Ск1= ![]() ,
,
где
С21= С2+ Су0+ ∆Су .
В (4.13) ω0 резонансная частота контура при Еу= Еу0, а ωк – при
Еу= Еу0+∆Еу.
![]() , (4.14)
, (4.14)
где согласно (4.13):
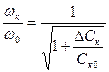 … (4.15)
… (4.15)
Вводя обозначения:
р0= ![]()
![]()
и (4.16)
р1 = ![]() ,
,
где р0 представляют собой коэффициент подключения варикапа к управляемой емкости С2, а р1 –коэффициент включения управляемой емкости С2 в колебательный контур автогенератора получим, что в (4.15):
![]() =
=![]() =
=![]() =
= ![]() 1 (4.17)
1 (4.17)
Тогда согласно (4.14):
yf = ![]()
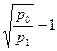 , (4.18)
, (4.18)
а отклонение частоты равно:
∆f= yff0 = f0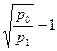 . (4.19)
. (4.19)
Формула (4.19) представляет собой зависимость отклонения частоты ∆f от модулирующего напряжения, т.е. СМХ, поскольку величина р1определяется зависимостью Супр, от управляющего напряжения Еупр, т.е. вольтфарадной характеристикой варикапа.
При изменении рабочей точки, т.е. при изменении значений Еу0 и Су0, емкость контура С1 необходимо изменить для сохранения величины поляной емкости контура Ск0 и, соответственно, частоты автоколебаний f0.
При проектировании управляемых по частоте автогенераторов необходимо найти максимальное отклонение частоты, которое можно получить при заданном варикапе и заданной амплитуде напряжения на контуре автогенератора Uк, так как кроме управляющего напряжения низкой частоты к варикапу приложено также переменное напряжение высокой частоты, величина которого зависит от схемы подключения варикапа к контуру автогенератора. Таким образом, напряжение на р-n-переходе uп представляет собой сумму постоянного напряжения E0 напряжения на переходе в рабочей точке (Eу0<0), модулирующего напряжения с частотой W и амплитудой UW и высокочастотного напряжения с частотой w и амплитудой U (рис.4.10):
uп= Eу0 + UW cоsWt + Ucoswt (4.20)
Пределы изменения напряжения uп на переходе ограничены. Чтобы частотная модуляция не сопровождалась недопустимым уровнем ПАМ, мгновенное значение uп не должно быть отпирающим, т.е. оно должно быть всегда отрицательным. При uп > 0 диод отпирается, при этом его емкость в основном определяется диффузионной емкостью, которую шунтирует малое сопротивление проводящего перехода. С другой стороны, напряжение uп по абсолютной величине не должно превышать пробивного напряжения eпд, в противном случае произойдет лавинное нарастание тока через диод. Эти условия удовлетворяются при выполнении неравенств:
E0 + UW + Uw £ 0 | E0 UW Uw | £ епд ![]() (4.21) Если рабочая точка Е0 выбрана в центре рабочего участка характеристики варикапа, то пределы изменения управляющего напряжения симметричны относительно Е0 и согласно (4.21): UWmax = 0,5|e пд| Umax
(4.21) Если рабочая точка Е0 выбрана в центре рабочего участка характеристики варикапа, то пределы изменения управляющего напряжения симметричны относительно Е0 и согласно (4.21): UWmax = 0,5|e пд| Umax
Наибольшая величина Dw может быть достигнута при оптимальном значении коэффициента включения варикапа в контур при DСу=0.
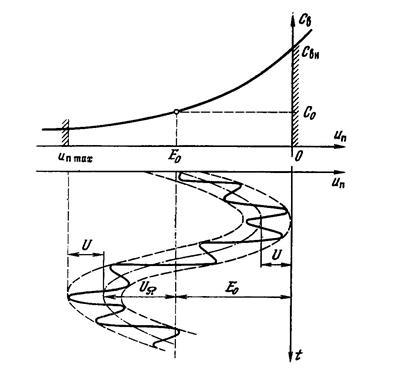
Рис.4.10
Существование этого оптимума можно ожидать исходя из следующих соображений. Амплитуда высокочастотного напряжения U на варикапе пропорциональна коэффициенту его включения в контур, р2, и амплитуде напряжения на контуре автогенератора Uк (на контурной катушке индуктивности Lк (рис.4.8 и 4.9в)):
U=p2Uк . (4.22)
При малых значениях р2 и ограниченных пределах изменении емкости DСу отклонение частоты Dw от значения w0 будет мало. Согласно (4.22) стремление увеличить Dw за счет увеличения р2 приводит к росту высокочастотного напряжения U на рn переходе. из-за ограничения (4.21) увеличение амплитуды U приводит к уменьшению допустимых изменений амплитуды низкочастотного напряжения UW на переходе (рис.4.10), а значит и к уменьшению допустимых значений DС. Расчеты максимальной девиации частоты подтверждают существование оптимального значения коэффициента р2. Величина р2опт может быть рассчитана по одной из двух формул [2]:
р2опт = ![]() при | eпд | £ 3Uк (4.23)
при | eпд | £ 3Uк (4.23)
1 при |eпд| ³ 3Uк ![]()
![]()
Максимально возможная девиация частоты зависит от значений двух отношений: Су0/Ск0 и епд/Uк. Желательно, чтобы величина (Су0 /Ск0) ®1. Что касается отношения епд /Uк, то его величина зависит от характеристик варикапа и транзистора. В маломощном автогенераторе, когда значения Uк и Uпmax максимальное напряжение на переходе соизмеримы, девиация частоты больше.
При расчете автогенератора обычно задаются величиной полной емкости контура Ск0(пФ), которую принимают равной (14)l(м), где λ длина волны. Значение емкости С1 (в схемах рис.4.8) определяется коэффициентом включения колебательного контура автогенератора в выходную цепь транзистора, р:
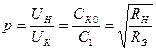
Здесь UН амплитуда напряжения первой гармоники на нагрузке транзистора, т.е. между коллектором и эмиттером; Uк амплитуда напряжения первой гармоники на колебательном контуре автогенераторе, т.е. на контурной катушке индуктивности Lк; RЭ =Qr эквивалентное сопротивление колебательного контура автогенератора, Q его добротность, а r = w0L=![]() его характеристическое сопротивление на резонансной частоте. Режим автогенератора должен быть таким, чтобы амплитуда переменного напряжения на варикапе была мала, так как при этом увеличивается допустимая амплитуда управляющего напряжения низкой частоты.
его характеристическое сопротивление на резонансной частоте. Режим автогенератора должен быть таким, чтобы амплитуда переменного напряжения на варикапе была мала, так как при этом увеличивается допустимая амплитуда управляющего напряжения низкой частоты.
Недостатком автогенераторов, управляемых одним варикапом, является зависимость частоты автоколебаний от амплитуды высокочастотных колебаний на варикапе, обусловленная тем, что амплитуда первой гармоники тока через варикап является нелинейной функцией амплитуды U высокочастотного напряжения [3]. Барьерная емкость варикапа Сб при U > 0 оказывается несколько большей чем при U®0. При расчете СМХ этим можно пренебречь, однако зависимость емкости варикапа от амплитуды высокочастотного напряжения на переходе увеличивает нестабильность средней частоты автогенератора. Увеличение средней емкости варикапа с ростом амплитуды высокочастотного напряжения можно объяснить тем, что приращение этой емкости, вызванное «отпирающей» полуволной u(t) = Ucoswt, преобладает над ее уменьшением, вызванным «запирающей» полуволной (рис.4.10). Расчеты показывают, что при U << (φ E0) проводимость варикапа с резким pnпереходом определяется емкостью Сб (4.11).
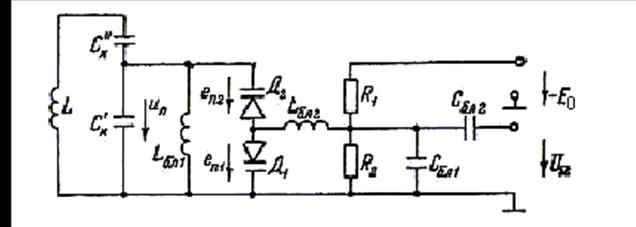
Рис.4.11
При амплитуде U близкой E0 проводимость варикапа возрастает, что эквивалентно увеличению общей емкости контура автогенератора, что приводит к понижению частоты автоколебаний, которая, таким образом, зависит от амплитуды U. Для ослабления этого влияния используют схему частотного модулятора на двух варикапах, включенных последовательно навстречу друг другу (рис.4.11). По низкочастотному управляющему напряжению варикапы включены параллельно, поэтому зависимости емкостей обоих варикапов от Е0 будут одинаковыми, они определяются (4.11) при еп=Е0. Переменная высокочастотная составляющая напряжения действует на варикапы поразному. Увеличение переменного напряжения на контуре вызывает увеличение заряда, накопленного в Д1, и уменьшение заряда в Д2. Соответственно меняются и емкости диодов. Количественно эти изменения таковы, что по отношению к переменному напряжению встречно включенные диоды с резким переходом ведут себя как постоянная емкость.
Частотная модуляция кварцевого генератора
Прямой метод частотной модуляции автогенератора на кварце осуществим лишь при небольшой девиации частоты: ![]() » (1,5 ¸2 )104. Его основное преимущество высокая стабильность средней частоты сигнала. В качестве частотного модулятора здесь также используют варикапы. Большей частью используют схемы автогенераторов с кварцем, работающем при частоте последовательного резонанса. Простейшая схема такого генератора, построенного по схеме Клаппа, изображена на рис.4.12а, а колебательная система автогенератора с включенными в нее емкостью варикапа и эквивалентной схемой кварцевого резонатора на рис.4.12б. На этой схеме приняты следующие обозначения: Cкв, Lкв, rкв и С0кв эквивалентные параметры кварцевого резонатора; Сп емкость варикапа, управляемого напряжением; L1, С1 и С3 индуктивность и емкости колебательной системы генератора, включающие в себя емкости рnпереходов транзистора.
» (1,5 ¸2 )104. Его основное преимущество высокая стабильность средней частоты сигнала. В качестве частотного модулятора здесь также используют варикапы. Большей частью используют схемы автогенераторов с кварцем, работающем при частоте последовательного резонанса. Простейшая схема такого генератора, построенного по схеме Клаппа, изображена на рис.4.12а, а колебательная система автогенератора с включенными в нее емкостью варикапа и эквивалентной схемой кварцевого резонатора на рис.4.12б. На этой схеме приняты следующие обозначения: Cкв, Lкв, rкв и С0кв эквивалентные параметры кварцевого резонатора; Сп емкость варикапа, управляемого напряжением; L1, С1 и С3 индуктивность и емкости колебательной системы генератора, включающие в себя емкости рnпереходов транзистора.
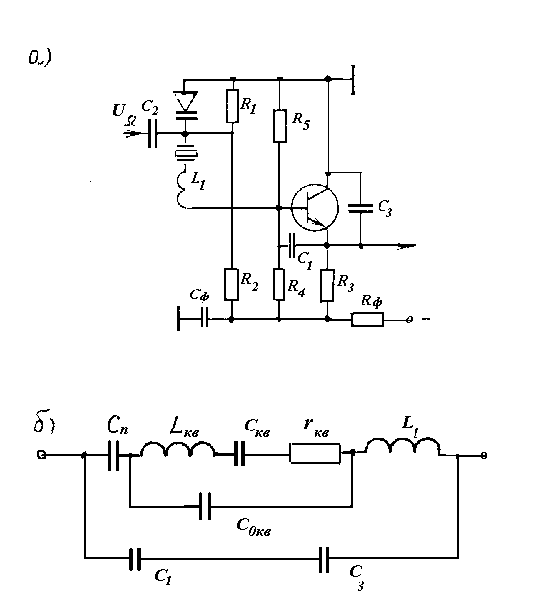
Рис.4.12
При частоте автоколебаний wг, близкой к частоте последовательного резонанса кварца, емкостью С0кв можно пренебречь, тогда согласно рис.4.12б частота автоколебаний равна:
wг=w1кв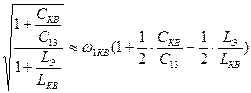 ,
,
где С13 = ![]() суммарная емкость колебательного контура (без кварца),
суммарная емкость колебательного контура (без кварца),
w1кв=![]() частота последовательного резонанса кварцевого резонатора; Lэ = L1(1
частота последовательного резонанса кварцевого резонатора; Lэ = L1(1 ![]()
![]() эквивалентная индуктивность цепи, составленной из последовательно включенных индуктивности L1 и емкости варикапа Сп. Частота автоколебаний равна:
эквивалентная индуктивность цепи, составленной из последовательно включенных индуктивности L1 и емкости варикапа Сп. Частота автоколебаний равна:
wг =wг0+ Dw ,
где wг0 частота автоколебаний при отсутствии модулирующего сигнала:
wг0 =w1кв (1+![]() ,
,
wг частота автоколебаний под действием поданного на варикап модулирующего напряжения низкой частоты. Отклонение частоты Dw рассчитывают на основании изложенных выше соображений, полученных при анализе частотной модуляции автогенератора с параметрической стабилизацией.
4.2.3. Особенности построения высокочастотного тракта передатчиков с частотной модуляцией
Построение высокочастотного тракта передатчиков с амплитудной и с частотной (как и с фазовой) модуляциями отличаются весьма существенно. Частотная модуляция осуществляется всегда на малом уровне мощности, а высокочастотный тракт, помимо каскадов усиления, всегда содержит умножители частоты. Здесь умножение частоты необходимо по следующим причинам. Вопервых, как было показано выше, ЧМпередатчики работают в диапазоне УКВ, поэтому умножители используют для увеличения частоты fг колебаний, создаваемых задающим генератором, до требуемой величины f0раб; вовторых, при умножении частоты происходит и умножение девиации Df; и, наконец, при наличии на входе умножителя паразитной амплитудной модуляции (ПАМ) ЧМсигнала умножитель, при соответствующем выборе его режима, в значительной степени ее подавляет. Угол отсечки умножителя должен быть немного больше оптимального qopt (cм.1.9.1): q > qopt. Напряжение смещения Еg на сетке лампы умножителя всегда постоянно и поскольку q < 900, то ÷ Eg÷ >÷![]() ÷ (рис.4.13). Амплитуда nой гармоники анодного тока равна Ian= aniamax, где an коэффициент разложения n ой гармоники анодного тока, iamax максимальное значение импульса анодного тока. Если амплитуда напряжения возбуждения Ugm из-за ПАМ возрастает, то при этом возрастают и iamax, и угол отсечки q; последнее, согласно рис.1.3, приводит к уменьшению коэффициента an, и амплитуда n –ой гармоники анодного тока Ian= aniamax меняется мало (или вообще не меняется). При уменьшении Ugm и iamax, и угол отсечки q уменьшаются, но в этом случае, как видно из рис.1.3, коэффициент an увеличивается, и в результате изменение амплитуды nой гармоники анодного тока Ian= aniamax невелико. Требуемая величина угла отсечки q умножителя подбирается в процессе регулировки передатчика.
÷ (рис.4.13). Амплитуда nой гармоники анодного тока равна Ian= aniamax, где an коэффициент разложения n ой гармоники анодного тока, iamax максимальное значение импульса анодного тока. Если амплитуда напряжения возбуждения Ugm из-за ПАМ возрастает, то при этом возрастают и iamax, и угол отсечки q; последнее, согласно рис.1.3, приводит к уменьшению коэффициента an, и амплитуда n –ой гармоники анодного тока Ian= aniamax меняется мало (или вообще не меняется). При уменьшении Ugm и iamax, и угол отсечки q уменьшаются, но в этом случае, как видно из рис.1.3, коэффициент an увеличивается, и в результате изменение амплитуды nой гармоники анодного тока Ian= aniamax невелико. Требуемая величина угла отсечки q умножителя подбирается в процессе регулировки передатчика.
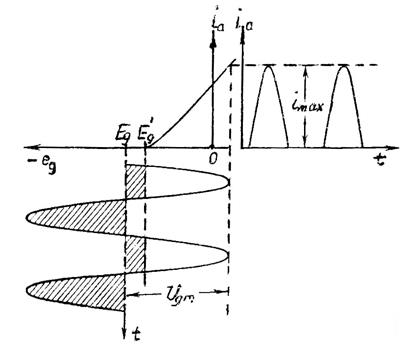
Рис.4.13
Каскады, следующие после умножителей частоты, являются усилителями радиосигнала, они подобны аналогичным каскадам высокочастотного тракта передатчиков с амплитудной модуляцией того же диапазона частот. Различия состоят в том, что, вопервых, режимы ламп высокочастотного тракта при модуляции не изменяются (если нет ПАМ) и, вовторых, колебательные системы усилительных каскадов высокочастотного тракта передатчиков с частотной модуляцией должны пропускать без искажений намного более широкую полосу частот, чем при амплитудной модуляции.
Общие сведения о модуляции
Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.
В результате модуляции сигналы переносятся в область более высоких частот.
Использование модуляции позволяет:
- согласовать параметры сигнала с параметрами линии;
- повысить помехоустойчивость сигналов;
- увеличить дальность передачи сигналов;
- организовать многоканальные системы передачи (МСП с ЧРК).
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:
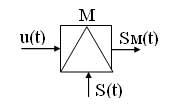
Рисунок 1 – Условное графическое обозначение модулятора
При модуляции на вход модулятора подаются сигналы:
u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);
S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w0 или f0);
Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.
В качестве несущего сигнала может использоваться:
- гармоническое колебание, при этом модуляция называется аналоговой или непрерывной;
- периодическая последовательность импульсов, при этом модуляция называется импульсной;
- постоянный ток, при этом модуляция называется шумоподобной.
Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.
1. Виды аналоговой модуляции:
- амплитудная модуляция (АМ), происходит изменение амплитуды несущего колебания;
- частотная модуляция (ЧМ), происходит изменение частоты несущего колебания;
- фазовая модуляция (ФМ), происходит изменение фазы несущего колебания.
2. Виды импульсной модуляции:
- амплитудно-импульсная модуляция (АИМ), происходит изменение амплитуды импульсов несущего сигнала;
- частотно-импульсная модуляция (ЧИМ), происходит изменение частоты следования импульсов несущего сигнала;
- Фазо-импульсная модуляция (ФИМ), происходит изменение фазы импульсов несущего сигнала;
- Широтно-импульсная модуляция (ШИМ), происходит изменение длительности импульсов несущего сигнала.
Амплитудная модуляция
Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала
u(t)=Umu sin? t (1)
на несущее колебание
S(t)=Um sin(?0t+?) (2)
происходит изменение амплитуды несущего сигнала по закону:
Uам(t)=Um+аам Umu sin? t (3)
где аам — коэффициент пропорциональности амплитудной модуляции.
Подставив (3) в математическую модель (2) получим:
Sам(t)=(Um+аам Umu sin? t) sin(?0t+?). (4)
Вынесем Um за скобки:
Sам(t)=Um(1+аам Umu/Um sin? t) sin(?0t+?) (5)
Отношение аам Umu/Um = mам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом mам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:
Sам(t)=Um(1+mам sin? t) sin(?0t+?). (6)
Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:
Sам(t)=(Um+аам u(t)) sin(?0t+?). (7)
Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.
Sам(t)=Um(1+mам sin? t) sin(?0t+?)= Um sin(?0t+?)+
+mамUm/2 sin((?0 — ?) t+j) — mамUm/2 sin((?0 +?)t+j). (8)
Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?0—? называется нижней боковой составляющей, а на частоте ?0 + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).
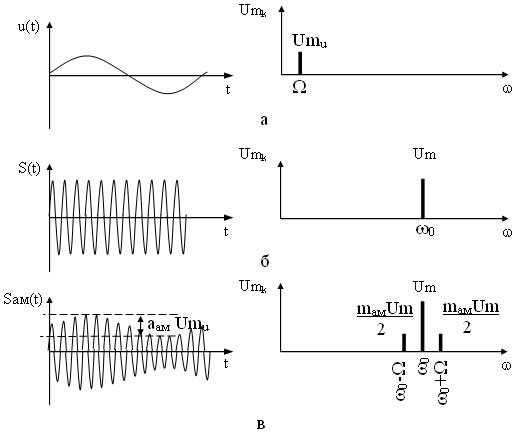
Рисунок 2 – Временные и спектральные диаграммы модулирующего (а), несущего (б) и ампдтудно-модулированного (в) сигналов
Ширина спектра для данного сигнала будет определятся
D?ам=(?0+?)—(?0—?)=2? (9)
Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).
Составляющие в диапазоне частот (?0 — ?max) ? (?0 — ?min) образуют нижнюю боковую полосу (НБП), а составляющие в диапазоне частот (?0 + ?min) ? (?0 + ?max) образуют верхнюю боковую полосу (ВБП)
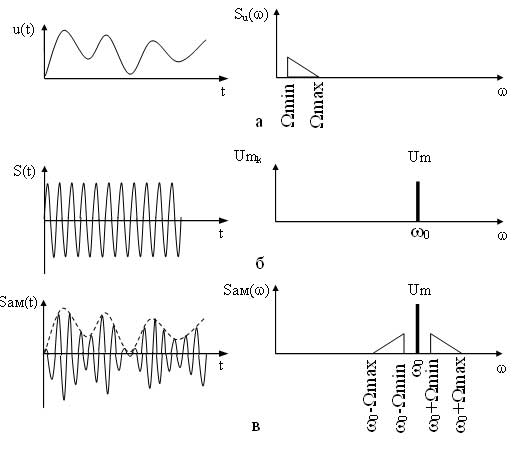
Рисунок 3 – Временные и спектральные диаграммы сигналов при случайном модулирующем сигнале
Ширина спектра для данного сигнала будет определятся
D?ам=(?0+? max) — (?0 — ? min)=2? max (10)
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах mам. Как видно при mам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,
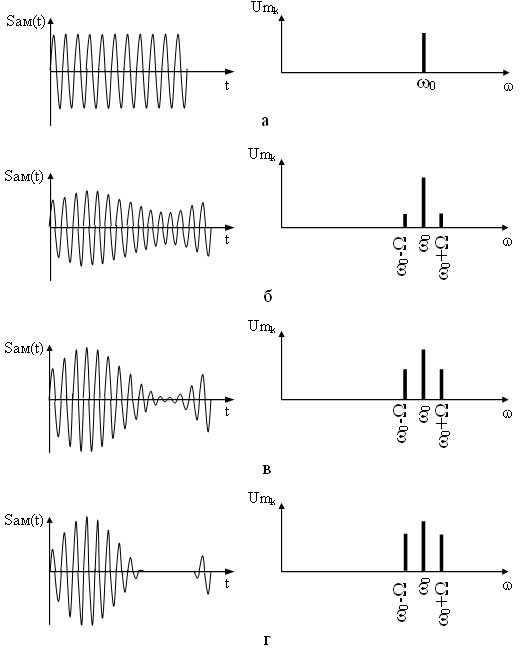
Рисунок 4 – Временные и спектральные диаграммы АМ сигналов при различных mам: а) при mам=0, б) при mам=0,5, в) при mам=1, г) при mам>1
а), при индексе модуляции mам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0<mам<1 (рисунок 4б). При mам>1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).
Основными достоинствами амплитудной модуляции являются:
- узкая ширина спектра АМ сигнала;
- простота получения модулированных сигналов.
Недостатками этой модуляции являются:
- низкая помехоустойчивость (т. к. при воздействии помехи на сигнал искажается его форма — огибающая, которая и содержит передаваемое сообщение);
- неэффективное использование мощности передатчика (т. к. наибольшая часть энергии модулированного сигнала содержится в составляющей несущего сигнала до 64%, а на информационные боковые полосы приходится по 18%).
Амплитудная модуляция нашла широкое применение:
- в системах телевизионного вещания (для передачи телевизионных сигналов);
- в системах звукового радиовещания и радиосвязи на длинных и средних волнах;
- в системе трехпрограммного проводного вещания.
Балансная и однополосная модуляция
Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.
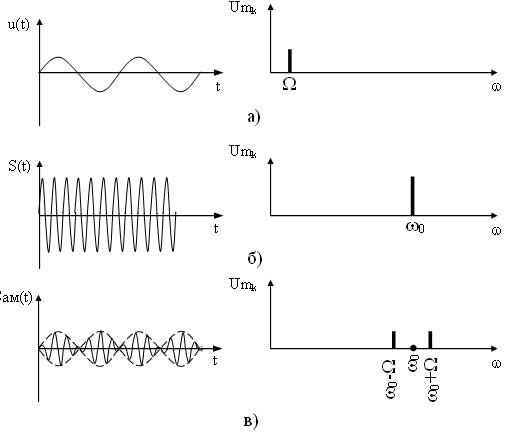
Рисунок 5 – Временные и спектральные диаграммы модулирующего (а), несущего (б) и балансно-модулированного (в) сигналов
Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.
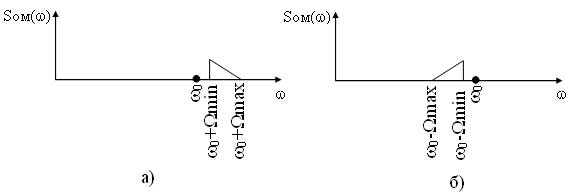
Рисунок 6 – Спектральные диаграммы однополосно-модулированных сигналов: а) с верхней боковой полосой (ВБП), б) с нижней боковой полосой (НБП)
Частотная модуляция
Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала
u(t) = Umu sin? t
на несущее колебание
S(t) = Um sin(?0t+?)
происходит изменение частоты несущего сигнала по закону:
wчм(t) = ?0+ачм Umu sin? t (9)
где ачм — коэффициент пропорциональности частотной модуляции.
Поскольку значение sin ?t может изменятся в диапазоне от -1 до 1, то наибольшее отклонение частоты ЧМ сигнала от частоты несущего сигнала составляет
??m= ачм Umu (10)
Величина Dwm называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.
Значение ?чм(t) непосредственно подставить в S(t) нельзя, т. к. аргумент синуса ?t+j является мгновенной фазой сигнала ?(t) которая связана с частотой выражением
?=d?(t)/dt (11)
Отсюда следует что, чтобы определить ?чм(t) необходимо проинтегрировать ?чм(t)
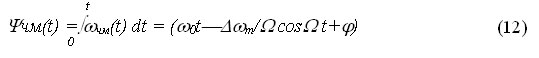
Причем в выражении (12) ? является начальной фазой несущего сигнала.
Отношение
Мчм = ??m/? (13)
называется индексом частотной модуляции.
Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:
Sчм(t)=Um sin(?0t — Мчм cos? t+?) (14)
Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.
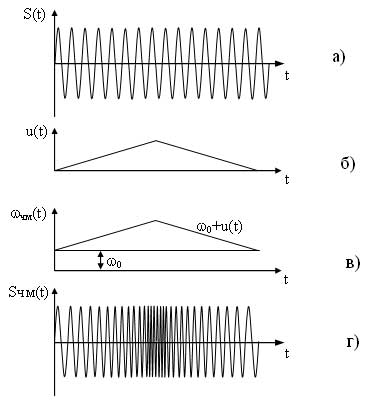
Рисунок 7 – Формирование ЧМ сигнала
Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим
Sчм(t)= Um J0(Mчм) sin(?0t+?) —
—Um J1(Mчм) {cos[(?0 — ? )t+j]+ cos[(?0+?)t+?]} —
— Um J2(Mчм) {sin[(?0 — 2?)t+j]+ sin[(?0+2?)t+?]}+
+ Um J3(Mчм) {cos[(?0 — 3?)t+j]+ cos[(?0+3?)t+?]} —
— Um J4(Mчм) {sin[(?0 — 4?)t+j]+ sin[(?0+4?)t+?]} —… (15)
где Jk(Mчм) — коэффициенты пропорциональности.
Jk(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как
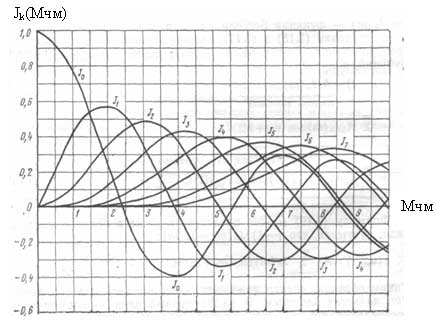
Рисунок 8 – Функции Бесселя
видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты Jk(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J0, J1, J2, J3, J4) Их значение при заданном индексе будет равно: J0=0,21; J1=0,58; J2=0,36; J3=0,12; J4=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J0) и по четыре составляющих в каждой боковой полосе (Um J1; Um J2; Um J3; Um J4).
Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J0(Мчм) будет равно нулю (в месте пересечения функции J0 с осью Мчм), например Мчм=2,4.
Поскольку увеличение составляющих приводит к увеличению ширины спектра ЧМ сигнала, то значит, ширина спектра зависит от Мчм (рисунок 9). Как видно из рисунка, при Мчм ?0,5 ширина спектра ЧМ сигнала соответствует ширине спектра АМ сигнала и в этом случае частотная модуляция является узкополосной, при увеличении Мчм ширина спектра увеличивается, и модуляция в этом случае является широкополосной. Для ЧМ сигнала ширина спектра определяется
D?чм=2(1+Мчм)? (16)
Достоинством частотной модуляции являются:
- высокая помехоустойчивость;
- более эффективное использование мощности передатчика;
- сравнительная простота получения модулированных сигналов.
Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.
Частотная модуляция используется:
- в системах телевизионного вещания (для передачи сигналов звукового сопровождения);
- системах спутникового теле- и радиовещания;
- системах высококачественного стереофонического вещания (FM диапазон);
- радиорелейных линиях (РРЛ);
- сотовой телефонной связи.
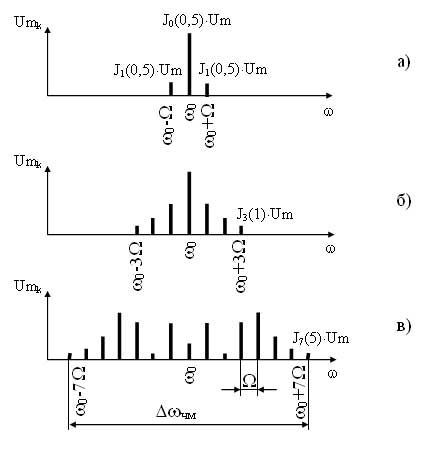
Рисунок 9 – Спектры ЧМ сигнала при гармоническом модулирующем сигнале и при различных индексах Мчм: а) при Мчм=0,5, б) при Мчм=1, в) при Мчм=5
Фазовая модуляция
Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала
u(t) = Umu sin? t
на несущее колебание
S(t) = Um sin(?0t+?)
происходит изменение мгновенной фазы несущего сигнала по закону:
?фм(t) = ?0t+?+афм Umu sin? t (17)
где афм — коэффициент пропорциональности частотной модуляции.
Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:
Sфм(t) = Um sin(?0t+афм Umu sin? t+?) (18)
Произведение афм Umu=Djm называется индексом фазовой модуляции или девиацией фазы.
Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:
?фм(t)=d?фм(t)/dt=w0+афмUmu? cos ? t (19)
Произведение афмUmu?=??m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.
Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.
При разложении математической модели ФМ сигнала на гармонические составляющие получится такой же ряд, как и при частотной модуляции (15), с той лишь разницей, что коэффициенты Jk будут зависеть от индекса фазовой модуляции ??m (Jk(??m)). Определятся эти коэффициенты будут аналогично, как и при ЧМ, т. е. по функциям Бесселя, с той лишь разницей, что по оси абсцисс необходимо заменить Мчм на ??m. Поскольку спектр ФМ сигнала строится аналогично спектру ЧМ сигнала, то для него характерны те же выводы что и для ЧМ сигнала (пункт 1.4).
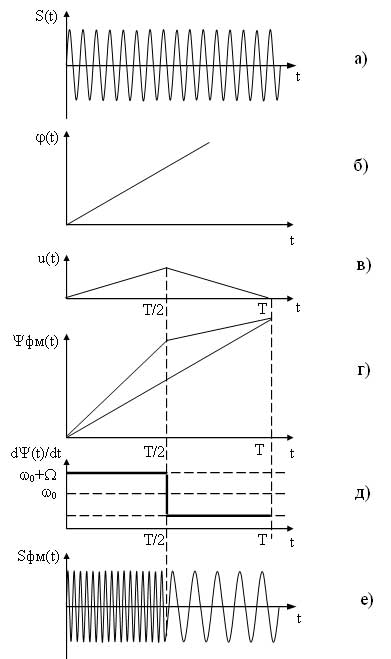
Рисунок 10 – Формирование ФМ сигнала
Ширина спектра ФМ сигнала определяется выражением:
??фм=2(1+?jm)? (20).
Достоинствами фазовой модуляции являются:
- высокая помехоустойчивость;
- более эффективное использование мощности передатчика.
- недостатками фазовой модуляции являются:
- большая ширина спектра;
- сравнительная трудность получения модулированных сигналов и их детектирование
Дискретная двоичная модуляция (манипуляция гармонической несущей)
Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.
Различают четыре вида манипуляции:
- амплитудную манипуляцию (АМн или АМТ);
- частотную манипуляцию (ЧМн или ЧМТ);
- фазовую манипуляцию (ФМн или ФМТ);
- относительно-фазовую манипуляцию (ОФМн или ОФМ).
Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.
При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая SАМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).
При частотной манипуляции используются две частоты ?1 и ?2. При наличии импульса в модулирующем сигнале (посылке) используется более высокая частота ?2, при отсутствии импульса (активной паузе) используется более низкая частота w1 соответствующая немодулированной несущей (рисунок 11, г)). Спектр частотно-манипулированного сигнала SЧМн(t) имеет две полосы возле частот ?1 и ?2.
При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).
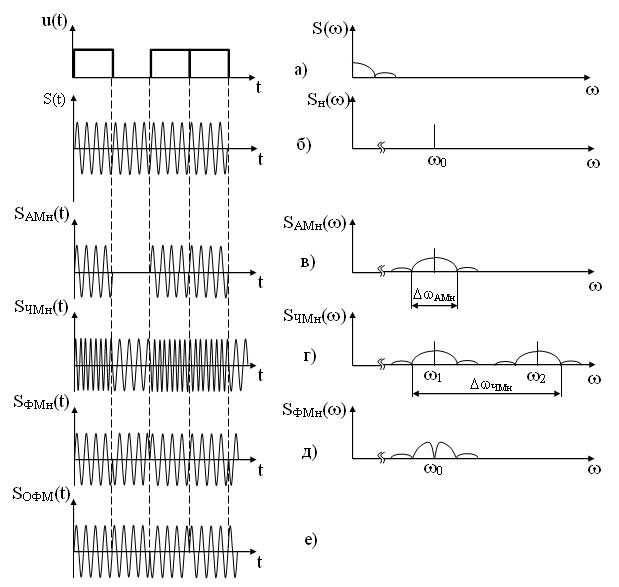
Рисунок 11 – Временные и спектральные диаграммы модулированных сигналов различных видов дискретной двоичной модуляции
При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).
Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.
В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).
Импульсная модуляция
Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.
Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:
- амплитудно-импульсная модуляция (АИМ); происходит изменение амплитуды импульсов несущего сигнала;
- частотно-импульсная модуляция (ЧИМ), происходит изменение частоты следования импульсов несущего сигнала;
- фазо-импульсная модуляция (ФИМ), происходит изменение фазы импульсов несущего сигнала;
- широтно-импульсная модуляция (ШИМ), происходит изменение длительности импульсов несущего сигнала.
Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.
При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).
При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).
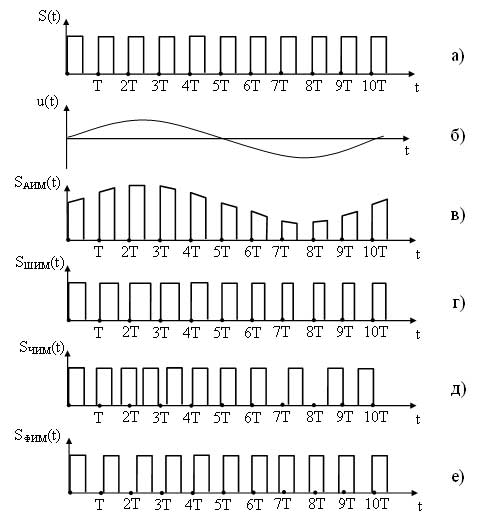
Рисунок 12 – Временные диаграммы сигналов при импульсной модуляции
При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).
При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.
Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.
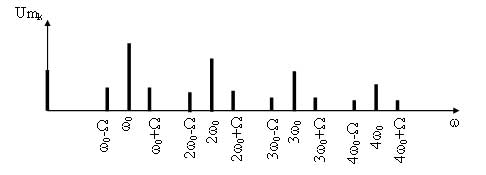
Рисунок 13 – Спектр импульсно-модулированного сигнала
Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.
Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f0 =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.
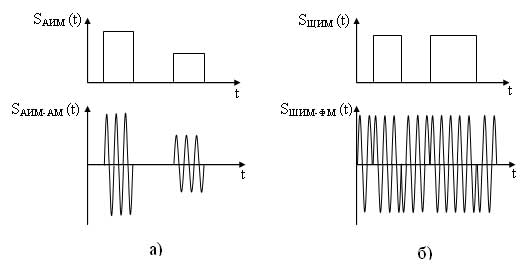
Рисунок 14 – Временные диаграммы сигналов при импульсной повторной модуляции
![{displaystyle {begin{aligned}y(t)&=A_{c}cos left(2pi int _{0}^{t}f(tau )dtau right)\&=A_{c}cos left(2pi int _{0}^{t}left[f_{c}+f_{Delta }x_{m}(tau )right]dtau right)\&=A_{c}cos left(2pi f_{c}t+2pi f_{Delta }int _{0}^{t}x_{m}(tau )dtau right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a85546c0eab3462755f52bf3808a8b9f5083b38)
![{displaystyle {begin{aligned}y(t)&=A_{c}cos left(2pi left[f_{c}+f_{Delta }x_{m}(t)right]tright)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e21e0bf408a5afae4268fde1d3ec3d0ca150c3)






