Сегодня разберем одно из сложных заданий ОГЭ на знание функций и их свойств. Для решения задания нужно будет знать, как график параболы зависит от ее коэффициентов, а также уметь решать уравнения графическим методом.
Мы уже разбирали другие задания из 22-го номера ОГЭ, вы можете ознакомиться с ними по следующим ссылкам:
Задание №22 из ОГЭ. Как найти точку пересечения двух прямых, если нет уравнения?
Разбор №22 из пробного ОГЭ по математике
Текст сегодняшнего задания представлен на картинке:
Теперь, удобнее всего, превратить это уравнение во что-то более простое. Для этого, сделаем так, чтобы и слева и справа от знака равно, располагались функции, графики которых строить довольно легко. Чтобы это осуществить, перенесем модуль в правую сторону:
Теперь, наше задание свелось к тому, чтобы найти количество точек пересечения графиков двух функций:
График модуля строить довольно легко. Он выглядит так:
А вот с квадратичной функцией немного сложнее, т.к. она зависит от параметра а. Исследуем ее коэффициенты и опишем, как они влияют на график:
- Коэффициент при старшей степени равен единице, т.е. он больше нуля. Следовательно, ветви направлены вверх.
- Коэффициент при переменной х. Такого слагаемого в нашем случае вообще нет. Т.е. коэффициент при нем равняется нулю. Это значит, что парабола не смещена ни влево ни вправо. Ее центр лежит точно посередине, на оси ординат.
- Свободный член. В данном случае, это и есть наш параметр. Он отвечает за то, насколько выше или ниже оси абсцисс лежит вершина параболы.
Таким образом, в зависимости от параметра а, мы будем получать семейство парабол такого вида:
Посмотрим на общий чертеж обеих функций: семейства парабол и модуля:
Этот чертеж можно описать следующим так: при достаточно больших значениях параметра а, парабола лежит выше графика модуля и не имеет с ним общих точек. При уменьшении параметра, парабола смещается ниже и у графиков появляются точки пересечения.
Тогда, по мере того, как вершина параболы будет снижаться, возникнут такие случаи взаимного расположения графиков:
Значение параметра а в двух последних случаях легко найти. Т.к. вершина параболы, в четвертом случае, должна находиться в начале координат, то а=0. Следовательно, для 5-го графика – a<0.
С первыми тремя случаями все не так очевидно. Нам нужно понять, в каком случае ветви параболы касаются графика модуля? Так как и модуль и парабола, симметричны, относительно оси ординат, то будем рассматривать только правую половину графиков:
Для этого случая, значения иксов – неотрицательные, тогда после раскрытия модуля, знак подмодульного выражения не меняется. Т.к. на графике – одна общая точки, то, получившееся квадратное уравнение будет иметь один корень:
Квадратное уравнение имеет один корень только в том случае, когда его дискриминант равен нулю. Вычислим дискриминант, приравняем его к нулю и найдем значение параметра а:
Таким образом, при а=1/4 уравнение имеет два корня. Если а>1/4, то уравнение не имеет корней. Если a принадлежит интервалу от 0 до 1/4 – то уравнение имеет 4 корня. Если а<0 – уравнение имеет 2 корня.
Если Вам понравилась статья – ставьте лайки и подписывайтесь на канал.
Помните – ОГЭ близко. Чтобы лучше к нему подготовиться – читайте разборы других заданий на моем канале.
сколько точек пересечения имеют функции? Объясните пожалуйста как рашать? у=3х+1 и у=3х^2
Правильнее сказать: сколько точек пересечения имеют
ГРАФИКИ функций.
3x+1=3x^2, 3x^2-3x-1=0, два корня, а это и означает, что
две точки пересечения.
Приравниваешь уравнения 3х+1=3х^2, у тебя получается уравнение квадратное. Узнаешь сколько корней оно содержит, столько и пересечений. Честно дискриминант не оч помню.
Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики
Существует определенный класс задач по дисциплине «Алгебра и начало анализа», в которых нужно найти точки пересечения графиков функций без их построения. Решать такие задания довольно просто, когда известна определенная методика нахождения координат по оси абсцисс и ординат. Однако для этого необходимо научиться правильно находить корни уравнений различных типов.

Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Классификация уравнений
Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:
Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S — коэффициенты при неизвестных, а U — свободный член.
Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S — коэффициенты при переменных, а U — константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).
Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 .
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.
Иными словами, в выражении (t+2)^2=0 для упрощения можно разделить обе части на (t+2) при условии, что t не равно -2, т. к. [(t+2)^2]/(t+2)=0/(t+2).
Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.
Разложение на множители
Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:
В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы «p+r)^2=p^2+2pr+r^2» нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.
Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:
Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).
Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д
![]()
Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта “Образование”.
Сколько точек пересечения имеют график уравнения х – 3у = 1 и 6 – 2х = 3?
Математика | 5 – 9 классы
Сколько точек пересечения имеют график уравнения х – 3у = 1 и 6 – 2х = 3.

Необходимо решить систему
x – 3y = 1 3y = x – 1 = 3 / 2 – 1 = 1 / 2 y = 1 / 6
6 – 2x = 3 2x = 3 x = 3 / 2.

Не выполняя построения графика функции у = х + 6, найдите координаты точек пересечения графика с осями координат?
Не выполняя построения графика функции у = х + 6, найдите координаты точек пересечения графика с осями координат.

Постройте графики функций у = – 3x и у = x + 4?
Постройте графики функций у = – 3x и у = x + 4.
Укажите координаты точек пересечения этих графиков.

Найдите координаты точек пересечения графика линейного уравнения у = – 4х и у = 2х + 6?
Найдите координаты точек пересечения графика линейного уравнения у = – 4х и у = 2х + 6.

Построите график функции?
Построите график функции.
Найдите координаты точек пересечения графика с осями координат : у = 0, 5х – 2.

Сколько точек пересечения имеют окружность и луч?
Сколько точек пересечения имеют окружность и луч?

Найдите координаты точек пересечения с осями координат графика функции у = 8х – 8?
Найдите координаты точек пересечения с осями координат графика функции у = 8х – 8.

Сколько точек пересечения имеют графики функций у = корень из х и у = – х – 1?
Сколько точек пересечения имеют графики функций у = корень из х и у = – х – 1.

Не выполняя построение графика функции, найдите координаты точек пересечения графика с осями координат у = х – 3?
Не выполняя построение графика функции, найдите координаты точек пересечения графика с осями координат у = х – 3.

Найдите координаты точек пересечение с осью ox прямых являющихся графиками уравнения x + y = 8?
Найдите координаты точек пересечение с осью ox прямых являющихся графиками уравнения x + y = 8.

Сколько точек пересечения имеют?
Сколько точек пересечения имеют.
Графики y = 5x и y = 10 / x.
На этой странице находится ответ на вопрос Сколько точек пересечения имеют график уравнения х – 3у = 1 и 6 – 2х = 3?, из категории Математика, соответствующий программе для 5 – 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Lg100 = 2 lg10 = 1 3x – 11 = 100 3x = 111 x = 37 37 – 27 = 10 2 + 1 = 3.

1)78дм 2) 89мм 3) 8см 3мм 4) 5дм 6см 5)1м 2дм 6)4дм 7см 7)33см.

, т. к 5% это 0, 05 то : 15000÷1, 05 = 14286 сумма должна пролежать второй год. Т. к. Процент сложный, то : 14286÷1, 05 = 13606 сумма которую необходимо положить на 2 года под 5%. Ответ : 13606 Проверка : 13606 под 5% = 14286 за 1 год 14286 под 5%..
[spoiler title=”источники:”]
http://kupuk.net/uroki/algebra/kak-naiti-tochki-peresecheniia-grafikov-fynkcii-algoritmy-i-primery-pravila-i-metodiki/
http://matematika.my-dict.ru/q/2583440_skolko-tocek-peresecenia-imeut-grafik-uravnenia/
[/spoiler]
Точки пересечения графиков функций
В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.
График функции (y = f(x)) является множеством точек ((x; y)), координаты которых связаны соотношением (y = f(x).)
Равенство (y = f(x)) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.
Как найти координаты, примеры решения
Существует несколько способов решения подобных задач:
- Поиск точек пересечения графиков функций заключается в приравнивании обеих функций друг к другу. При этом все члены с х переносят в левую сторону, а оставшиеся – в правую. Затем остается найти корни уравнения, которое получилось после преобразований.
- Второй метод состоит в записи системы уравнения для ее последующего решения с помощью подстановки одной функции в другую.
- Третий способ подразумевает построение графиков функций, чтобы определить точки их пересечения визуально.
В качестве примера можно рассмотреть две линейные функции:
(f(x) = k_1 x+m_1)
(g(x) = k_2 x + m_2)
Данные функции являются прямыми. Их можно графически изобразить, если принять какие-либо два значения (x_1) и (x_2) и найти (f(x_1)) и ((x_2)). Далее действия необходимо повторить с функцией (g(x)). Затем достаточно легко определить визуально координаты точки пересечения рассматриваемых функций.
Важно отметить, что для линейных функций характерна лишь одна точка пересечения только в том случае, когда (k_1 neq k_2). В противном случае (k_1=k_2), а функции будут параллельными друг другу, в связи с тем, что k является коэффициентом угла наклона. При( k_1 neq k_2) и (m_1=m_2) точка пересечения будет соответствовать (M(0;m)). Данная закономерность упрощает решение многих подобных задач.
Задача № 1
Имеются функции: (f(x) = 2x-5)
(g(x)=x+3)
Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.
Решение
В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:
(k_1 = 2)
(k_2 = 1)
Заметим, что:
(k_1 neq k_2)
По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:
(f(x)=g(x))
(2x-5 = x+3)
Необходимо перенести члены с x в левую часть, а остальные – в правую:
(2x – x = 3+5)
(x = 8)
В результате удалось найти x=8, что соответствует абсциссе точки пересечения графиков. Требуется определить ординату y с помощью подстановки x = 8 в любое из уравнений – в (f(x)), либо в (g(x)):
(f(8) = 2cdot 8 – 5 = 16 – 5 = 11)
Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.
Ответ: M (8;11)
Задача № 2
Записаны две функции: (f(x)=2x-1)
(g(x) = 2x-4.)
Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.
Решение
Угловые коэффициенты:
(k_1 = k_2 = 2)
Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.
Ответ: графики функций параллельны, точки пересечения отсутствуют.
Задача № 3
Требуется определить координаты точки, в которой пересекаются графики следующих функций: (f(x)=x^2-2x+1)
(g(x)=x^2+1)
Решение
В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:
(x^2-2x+1=x^2+1)
Далее необходимо разнести в разные стороны уравнения члены с x и без него:
(x^2-2x-x^2=1-1)
(-2x=0)
(x=0)
Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить (x = 0) в какое-либо из двух начальных уравнений. К примеру:
(f(0)=0^2-2cdot 0 + 1 = 1)
M (0;1) является точкой, в которой пересекаются графики функций.
Ответ: M (0;1)
Приравнивание функций друг к другу и нахождение корней
Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.
Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:
- раскрытие скобок, приведение подобных коэффициентов;
- перенос членов с неизвестными в одну сторону, а с известными – в другую;
- математические преобразования;
- определение корня.
Квадратные уравнения решают с помощью одного из способов:
- разложение на множители;
- выделение полного квадрата;
- поиск дискриминанта;
- теорема Виета.
В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.
Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:
((-S)^2-4PU)
В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.
Квадратные уравнения решают таким образом:
- выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
- выбор наиболее оптимального способа решения и его реализация;
- проверка корней с помощью их подстановки в начальное выражение.
Примечание
Распространенной ошибкой является пренебрежение проверкой результатов решения. Некорректные действия могут привести к образованию ложных корней.
Существует несколько методик решения тождеств кубического и биквадратного типов:
- понижение степени, то есть разложение на множители;
- замена переменной.
Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:
- выполнение математических преобразований;
- выражение переменной через другую;
- решение квадратного или линейного уравнения;
- подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
- вычисление искомых корней;
- проверка;
- исключение ложных решений;
- запись ответа.
Путем составления системы уравнений
Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:
Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.
Порядок действий при решении системы уравнений можно рассмотреть на примере:
Решение будет иметь следующий вид:
Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.
Решение системы представляет сбой единственную пару чисел:
Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).
В процессе решения линейной системы можно столкнуться с разными ситуациями:
- система обладает единственным решением, прямые пересекаются;
- решения системы отсутствуют. прямые параллельны;
- система обладает бесчисленным множеством решений, прямые совпадают.
При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.
В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:
Решение имеет следующий вид:
График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).
Ответ: (0; 1); (-1; 0).
Можно решить систему графическим способом:
В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).
Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).
В качестве еще одного примера можно решить следующую систему:
Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.
Далее необходимо построить график функции:
График будет являться ломанной:
Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:
При помещении обоих графиков в одну систему координат получится следующая ситуация:
Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)
Нахождение через графическое построений функций
Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:
(f1(x)=f2(x))
Решение данного уравнения будет являться искомой точкой.
Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.
В общем случае двух линейных функций можно предположить, что:
(y1=k1x+b1)
(y2=k2x+b2)
Для поиска точки пересечения графиков необходимо решить уравнение:
(y1=y2 или k1x+b1=k2x+b2)
После преобразований получится, что:
(k1x-k2x=b2-b1.)
Далее нужно выразить x:
(x=(b2-b1)/(k1-k2).)
При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:
(((b2-b1)/(k1-k2); k1(b2-b1)/(k1-k2)+b2))
График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.
С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке:
В данном случае при х=0 ((y=a*0+b)) функция равна b. Таким образом, график пересекает ось ординат (ось Y) в точке (0,b). Когда пересекается ось абсцисс (ось Х) функция равна 0, то есть (y=f(x)=0). Для того чтобы определить х, следует решить уравнение (f(x)=0). В случае линейной функции получаем уравнение (ax+b=0), откуда и находим (x=-b/a). В результате можно сделать вывод, что ось Х пересекается в точке ((-b/a,0).)
При наличии квадратичной зависимости y от х, уравнение (f(x)=0) обладает двумя корнями. Таким образом, ось абсцисс пересекается два раза. В случае периодической зависимости y от х, например, (y=sin(x)), график функции обладает бесконечным количеством точек пересечения с осью Х. Проверить корректность расчета координат точек, в которых пересекаются графики функций, можно с помощью подстановки найденных значений х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
$$ ax^2+bx+c = a(x+ frac{b}{2a})^2-frac{D}{4a}, D = b^2-4ac $$
Мы получаем:
- ось симметрии $x = -frac{b}{2a}$
- вершину параболы на оси симметрии $(–frac{b}{2a}; -frac{D}{4a})$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c).
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$, парабола имеет две точки пересечения с $x_1,2 = frac{-b pm sqrt{D}}{2a}$ на оси OX.
Если D = 0, парабола имеет одну точку пересечения $x_0 = -frac{b}{2a}$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX
|
$a gt 0$ |
$a lt 0$ |
|
|
$D gt 0$ |
 |
 |
|
$x_(1,2) = frac{-b pm sqrt{D}}{2a}$ |
||
|
D = 0 |
 |
 |
|
$x_0 = -frac{b}{2a}$ |
||
|
$ D lt 0 $ |
 |
 |
|
${ varnothing }$-нет пересечений |
Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.

Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
$$ Ax^2+Bx+C = 0 $$
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
A = B = C = 0
$ a_1 = a_2, b_1 = b_2, $
$ c_1 = c_2 $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$

$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+bx+c_1$
$ y = ax^2+bx+c_2 $
У них общая ось симметрии
$ x = -frac{b}{2a}$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет

$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c$
$ y = ax^2+b_2 x+c $
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
(0;c)

$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c_1$
$ y = ax^2+b_2 x+c_2 $
Абсцисса точки пересечения
$ x = – frac{C}{B} = -frac{c_1-c_2}{b_1-b_2}$
Одна точка пересечения (касание)

$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c$
$ y = a_2 x^2+bx+c $
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)

$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c_1$
$ y = a_2 x^2+bx+c_2 $
Не пересекаются, если
$- frac{c_1-c_2}{a_1-a_2} lt 0 $
Две точки пересечения

Если
$- frac{c_1-c_2}{a_1-a_2} gt 0 $
Пересекаются в двух точках
$$ x_{1,2} = pm sqrt{-frac{c_1-c_2}{a_1-a_2}} $$
Две точки пересечения

$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
$ x_1 = 0 $
$$x_2 = -frac{b_1-b_2}{a_1-a_2}$$
Две точки пересечения,
одна из которых (0;c)

$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Все параметры парабол разные
Ищем дискриминант:
$$ D = B^2-4AC $$
Если $D gt 0$
Две точки пересечения
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} $$
Две точки пересечения

Если D = 0
Одна точка пересечения (касание)
$$ x_0 = -frac{B}{2A} $$
Одна точка пересечения
(касание)

Если $D lt 0$
Точек пересечения нет
Точек пересечения нет

Внимание!
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
$а) y = 3x^2+2x-1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -1end{array} right.}$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{3} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ – две точки пересечения
$б) y = -4x^2-3x+1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{4} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ – две точки пересечения
$в) y = 5x^2-2x+1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ 5x^2-2x+1 = 0 $$
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
$ г) y = -x^2+4x-4 $

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -4end{array} right.}$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow {left{ begin{array}{c} x = 2 \ y = 0 end{array} right.}$$ – одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
По условию
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1

$$x_1 = 0, x_2 = -frac{B}{A} = -2$$
$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x+1 end{array} right.} Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x_1 = 0 \ y_1 = 1end{array} right.} \ {left{ begin{array}{c} x_2 = -2 \ y_2 = -1 end{array} right.} end{array} right.$$
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$

Например, k = 4
$$ D = 4k = 16 = 4^2 $$
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} = frac{-2 pm 4}{2} = left[ begin{array}{cc} x_1 = -3\ x_2 = 1 end{array} right. $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$

$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x end{array} right.} $$
$$ x_0 = frac{-B}{2A} = -1 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$

Например, k = -1
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Координаты вершин:
$$ left( -frac{b_1}{2a_1}, – frac{D_1}{4a_1} right), left(- frac{b_2}{2a_2},- frac{D_2}{4a_2} right) $$
По условию:
$$ {left{ begin{array}{c} -frac{b_1}{2a_1} = -frac{b_2}{2a_2} \ -frac{D_1}{4a_1} = -frac{D_2}{4a_2} end{array} right.} Rightarrow {left{ begin{array}{c} frac{b_1}{a_1} = frac{b_2}{2a_2} \ frac{D_1}{a_1} = frac{D_2}{a_2} end{array} right.} $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac{x^2}{2}-3x+1$.
Координаты вершины:
$$ x_0 = – frac{b}{2a} = – frac{-3}{2 cdot frac{1}{2}} = 3, D = b^2-4ac = 3^2-4 cdot frac{1}{2} cdot 1 = 7 $$
$$ y_0 = – frac{D}{4a} = – frac{7}{4 cdot frac{1}{2}} = -3,5 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
$$ {left{ begin{array}{c} frac{b}{a} = frac{-3}{1/2} = -6 \ frac{D}{a} = frac{7}{1/2} = 14 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = 14a end{array} right.} $$
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ {left{ begin{array}{c} a = 1 \ b = -6a = -6 \ D = 14a = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ b^2-4ac = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ 36-4c = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ c = frac{36-14}{4} = 5,5 end{array} right.}$$
$$ y = x^2-6x+5,5 $$
$$ {left{ begin{array}{c} a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ c = – frac{1,44+2,8}{0,8} = -5,3 end{array} right.} $$
$$ y = -0,2x^2+1,2x-5,3 $$
Параболы
$$ y = frac{x^2}{2}-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)

Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac{x^2}{3}-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac{b}{2a} = -frac{-2}{2 cdot frac{1}{3}} = 3, D = b^2-4ac = 2^2-4 cdot frac{1}{3} cdot 5 = – frac{8}{3} $$
$$ y_0 = – frac{D}{4a} = – frac{-8/3}{4 cdot 1/3} = 2 $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
$$ {left{ begin{array}{c} frac{b}{a} = frac{-2}{1/3} = -6 \ frac{D}{a} = frac{-frac{8}{3}}{frac{1}{3}} = -8 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = b^2-4a underbrace{c}_{text{= 0 }} = b^2 = -8a end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ b^2 = -8a end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} b = frac{-8a}{-6a} = frac{4}{3} \ a = -frac{b}{6} = -frac{2}{9} end{array} right.} $$
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
$$ y = -frac{2}{9} x^2+ frac{4}{3} x $$

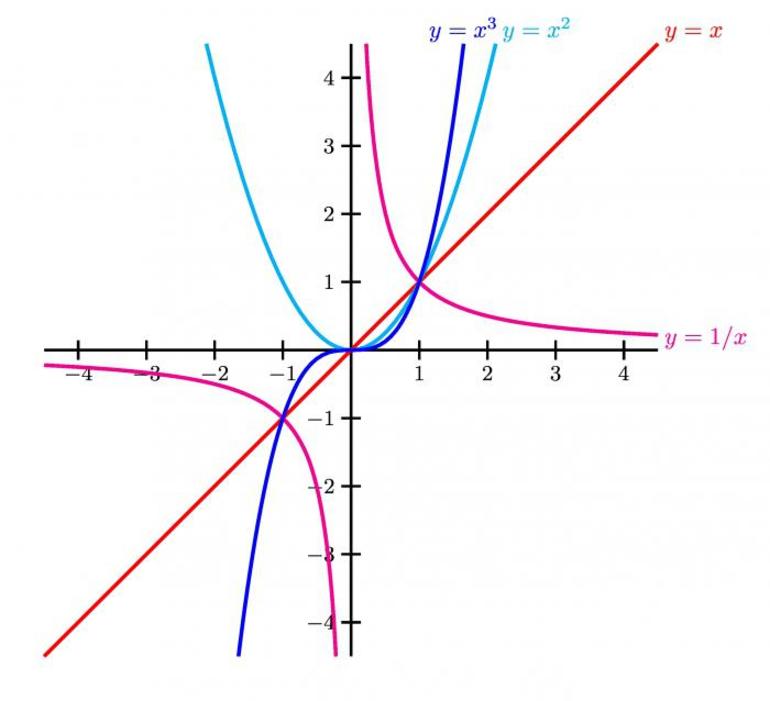
Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Классификация уравнений
Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:
- Линейные.
- Квадратные.
- Кубические.
- Биквадратные.
Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S – коэффициенты при неизвестных, а U – свободный член.
Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S – коэффициенты при переменных, а U – константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).
Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II – III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 {R(t)=0 и S(t)=0}.
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

- Правильное раскрытие скобок с учетом алгебраической операции и знаков.
- Упрощение выражения (приведение подобных величин).
- Перенос элементов в любые части равенства с противоположным знаком.
- Возможность прибавлять или вычитать эквивалентные величины.
- Деление и умножение на любые эквивалентные значения, не превращающие тождества в пустое множество.
Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.
Иными словами, в выражении (t+2)^2=0 для упрощения можно разделить обе части на (t+2) при условии, что t не равно -2, т. к. [(t+2)^2]/(t+2)=0/(t+2).
Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.
Разложение на множители
Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:
- Квадрат суммы и разности: (p+r)^2=p^2+2pr+r^2 и (p-r)^2=p^2-2pr+r^2 соответственно.
- Разность квадратов: p^2-r^2=(p-r)(p+r).
В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы “p+r)^2=p^2+2pr+r^2” нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.
Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные – в другую сторону. Методика решения имеет следующий вид:
- Раскрыть скобки и привести подобные коэффициенты.
- Выполнить перенос известных в одну, а неизвестных – в другую часть равенства.
- Произвести необходимые математические преобразования.
- Найти корень.
Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

- Разложить на множители.
- Выделить полный квадрат.
- Найти дискриминант.
- По теореме Виета.
Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).
Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.
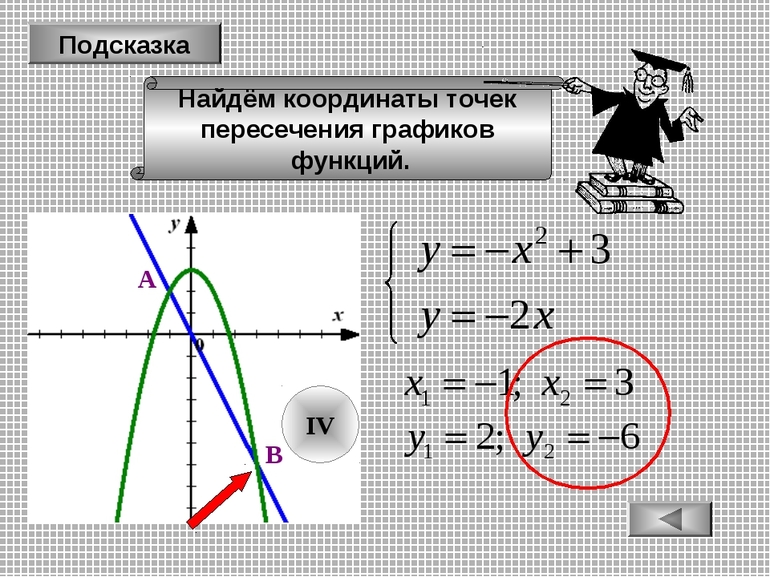
Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д<0, искомое тождество с неизвестными вообще не имеет решений. Определить значение корней возможно по таким соотношениям: t1=[-S-(Д)^(1/2)]/2P и t2=[-S+(Д)^(1/2)]/2P, где t1 и t2 – точки пересечения с осью абсцисс.
Если коэффициент при второй степени (P) эквивалентен 1, то дискриминант можно не высчитывать, а воспользоваться сокращенным вариантом решения – теоремой Виета. Суть ее заключается в подборе корней по таким формулам: t1+t2=-S и t1*t2=U. Иногда для реализации этой методики нужно сократить обе части на коэффициент Р. Алгоритм решения квадратных уравнений имеет следующий вид:
- Выполнить при необходимости различные алгебраические преобразования (раскрыть скобки и привести подобные слагаемые).
- Выбрать один из способов решения и реализовать его.
- Проверить корни, подставив их в исходное выражение.
Следует отметить, что распространенная ошибка новичков – отсутствие проверки. В результате неправильных действий образуются ложные корни, а оценка на контрольной, зачете или экзамене существенно снижается.
Кубические и биквадратные
Решение тождеств кубического и биквадратного типов с неизвестными осуществляется двумя способами. К ним относятся:
- Понижение степени (разложение на множители).
- Замена переменной.
В первом случае необходимо выполнить преобразования, которые позволят применить одну из формул сокращенного умножения. Однако этот метод применяется довольно редко, поскольку математики отдают предпочтение второму способу. Для его реализации вводится дополнительная переменная, обладающая более низкой степенью и существенно упрощающая выражение. Алгоритм имеет такой вид:
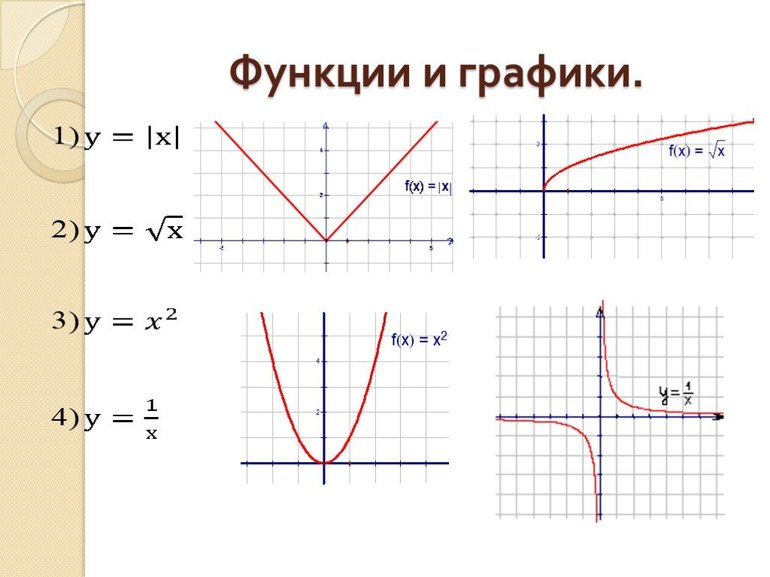
- Выполняются необходимые математические преобразования.
- Выражается переменная через другую.
- Решается квадратное или линейное уравнение.
- Промежуточные корни, полученные в третьем пункте алгоритма, подставляются во второй.
- Вычисляются искомые корни.
- Осуществляется проверка.
- Отсеиваются ложные решения, и записывается ответ.
Для проверки рекомендуется воспользоваться онлайн-приложениями, позволяющими вычислить корни, а также построить графики функций. Кроме того, для кубического многочлена Pt 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:
- Уравнение требуется разделить на P.
- Осуществить замену: t=m-(S/(3P)). При этом получается тождество вида m^3 +km+l=0.
- Найти значение коэффициентов по формулам: k=[2S 3 -9PSU+27(P 2 )V] / (27P 3 ) и l=[(3PU-S 2 )/(3P 2 )]. Подставить их во второй пункт и найти промежуточные корни, при помощи которых найти основные значения переменных.
Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.
Пример решения
Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:

- Приравнять уравнения: 2t+7=t-1.
- Перенести переменные влево, а константы – вправо: 2t-t=-1-7.
- Привести подобные коэффициенты: t=-8.
- Найти координаты второй составляющей: z=-8-1=-9.
- Искомая точка пересечения: (-8;-9).
В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.
