Содержание:
- Определение и формула кинетической энергии
- Кинетическая энергия материальной точки и тела
- Единицы измерения кинетической энергии
- Теорема Кенига
- Примеры решения задач
Определение и формула кинетической энергии
Определение
Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.
Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.
Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.
Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:
$$A^{prime}=E_{k 2}-E_{k 1}(1)$$
Кинетическая энергия материальной точки и тела
Кинетическая энергия материальной точки равна:
$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.
Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ – плотность участка, m–масса всего рассматриваемого тела, V – объем тела.
В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.
При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$
где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$
$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.
Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
[Ek]=Дж (джоуль),
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 107 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$
где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$
где Jc – момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
Примеры решения задач
Пример
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?
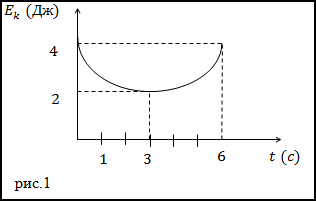
Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:
$$A^{prime}=Delta E_{k}(1.1)$$
Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:
$A^{prime}=2-4=-2$ (Дж)
Ответ. A’=-2 Дж.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?
Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:
$$E_{k}=frac{m v^{2}}{2}(2.1)$$
Но по условию задачи:
$$E_{k}=alpha s^{2}(2.2)$$
Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:
$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$
Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:
$$bar{F}=m bar{a}(2.4)$$
где
$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$
При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:
$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$
Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:
$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$
Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:
$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$
Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$
Читать дальше: Формула массы тела.
Энергия – важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.
Что такое энергия?
Энергия в физике – это способность тела совершать работу.
Кинетическая энергия
Что такое кинетическая энергия?
Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A.
Работа всех сил, действующих на тело, равна работе равнодействующей силы.
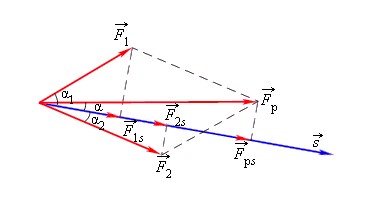
Fр→=F1→+F2→
A=F1·s·cosα1+F2·s·cosα2=Fрcosα.
Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины.
Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:
A=Fs=F·v22-v122a=ma·v22-v122a
A=mv22-mv122=mv222-mv122.
Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела.
Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости. Вот как выглядит формула кинетической энергии:
EK=mv22.
Кинетическая энергия – это энергия движения тела. При нулевой скорости она равна нулю.
Теорема о кинетической энергии
Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.
Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.
A=EK2-EK1.
Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.
A=mv22=EK.
Чтобы остановить тело, нужно совершить работу
A=-mv22=-EK
Потенциальная энергия
Что будет означать или обозначать кинетическая энергия?
Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.
Формула потенциальной энергии:
E пот = m * g * h
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.
Примеры консервативных сил: сила тяжести, сила упругости.
Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.
Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2.
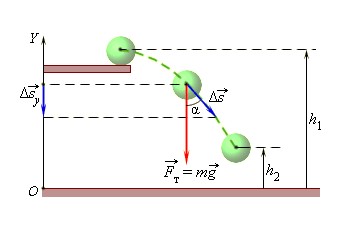
При этом сила тяжести совершила работу, равную
A=-mg(h2-h1)=-(mgh2-mgh1).
Эта работа равна изменению величины mgh, взятому с противоположным знаком.
Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.
Потенциальная энергия – часть полной механической энергии системы, с нахождением в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему. Механическая энергия – это сумма потенциальной и кинетической энергий, которые есть в компонентах механической системы.
Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины (пружинной энергии) и т.д.
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
A=-(EП2-EП1).
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.
При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
EП=-GmMr.
Здесь G – гравитационная постоянная, M – масса Земли.
Потенциальная энергия пружины
Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами.
При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна
Aупр=-A=-kx22.
Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.
Данная тема будет посвящена решению задач на расчет
кинетической энергии тела и применение теоремы о кинетической энергии.
Задача 1. Тело массой 10 кг движется вдоль оси Оx
под действием постоянной силы. На рисунке приведен график зависимости проекции
скорости тела на эту ось от времени. Определите кинетическую энергию тела в
момент времени 4 с.
Задача 2. Какую работу совершают силы сопротивления при
остановке автомобиля массой 3 т, движущегося со скоростью 54 км/ч?
Задача 3. На тело массой 2,5 кг действует сила 5 H в течение 3
с. Определите кинетическую энергию тела в этот момент времени, если его
начальная скорость равна нулю.
Задача 4. Тело массой 12 кг ударяется абсолютно неупруго о тело
меньшей массы. Если тело меньшей массы до удара покоилось, а доля потерянной
кинетической энергии после удара составила 14%, то какова масса меньшего тела?
Задача
5. На горизонтальном участке пути
длиной 500 м скорость поезда возрастает с 15 м/с до 20 м/с. Локомотив развивает
постоянную силу тяги 4 ∙ 106 Н. Определите массу поезда, если
коэффициент трения между колесами и рельсами равен 0,07.
«Вам знакомо выражение
«Выше головы не
прыгнешь»?
Это заблуждение.
Человек может все!»
Никола Тесла
Энергия сама по себе – физическая величина, которая характеризует способность тела совершать работу. А если в момент совершения работы тело будет двигаться, то это уже будет кинетическая энергия.
Примеры кинетической энергии окружают нас повсюду: едущие по дороге автомобили, проходящие мимо люди, летающие птицы. Все они совершают какую-то работу и при этом двигаются. То есть, кинетическая энергия – это та энергия, которая создается движущимся телом.
Кинетическая энергия может передаваться от одного объекта к другому. Например, на гидроэлектростанции поток воды, обладающий кинетической энергией, передает ее лопастям турбины, заставляя их двигаться. Это запускает генератор, и вырабатывается электричество. Передаваясь между объектами, кинетическая энергия может преобразовываться в другие виды энергии. Так спортсмен при беге преобразовывает свою химическую энергию, которую он получил от пищи, в кинетическую, энергию движущегося тела. Не будет пищи – станет меньше сил на бег (если, конечно, он не бежит за булочкой).
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
Разделяют три типа кинетической энергии:
- Поступательная. Это энергия, возникающая при движении тел по связанной с ними прямой, параллельной самой себе. Это может быть машина на дороге, брошенный мяч или бегущий кот.
- Вращательная. Логично, что она появляется в процессе вращательного движения. Пример: Земля вращается вокруг Солнца.
- Колебательная. Энергия присуща телам в процессе колебательного движения. Например, движение маятника или камертона.
Для измерения кинетической энергии используют джоули.
Формула
Мы уже выяснили, что кинетическая энергия – это энергия тел в движении. Но как узнать, чему она равна? Проведем мыслительный эксперимент. Представьте, вы берете легкий пластмассовый шарик, примерно 20-30 гр., встаете перед окном и кидаете шарик в стекло. Шарик просто отскочит от стекла. А теперь берем большой камень, который весит в 100 раз больше этого шарика и кидаем его в стекло так, чтобы он летел с такой же скоростью. Шансов что обычное стекло уцелеет после такой встречи с камнем очень мало, только если это стекло бронированное. То есть мы видим, чем больше масса тела, тем больше будет его энергия. А теперь представим себе 2 одинаковые машины. Одна еде со скоростью 20 км/ч, а другая 120 км/ч. Как думаете, какая из них получит больше повреждений при встрече со стеной? Та, что движется быстрее. Делаем вывод: чем больше скорость, тем больше энергия движения. Таким образом, мы получаем, что для того, чтобы рассчитать, чему равна кинетическая энергия E, нам надо знать какой массой m обладает тело и с какой скоростью v оно двигается. Если нам известны эти показатели, то они подставляются в формулу:
И заметьте, что от увеличения массы тела в 2 раза, его энергия увеличиться тоже в 2 раза, а от увеличения скорости в 2 раза, энергия увеличится в 4.
Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!
Пример решения задачи
Чему будет равна кинетическая энергия 4-х килограммового кота, бегущего по комнате со скоростью 5 м/с?
Решение: E=(4кг x (5м/с)^2)/2=(4кг х 25м/с)/2=50 Дж
Спасибо, что прочитали статью. Не забывайте про подписку на канал, а также рекомендую почитать канал наших друзей:
https://zen.yandex.ru/fgbnuac — последние научные достижения и лучшие образовательные практики.
Хорошего дня и не болейте.
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая |
|
| ‹♦› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная |
|
| Химическая | ||
| Ядерная | ||
 |
Гравитационная | |
 |
Вакуума | |
| Гипотетические: | ||
 |
Тёмная | |
| См. также: Закон сохранения энергии |
Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как
где индекс 



Упрощённо, кинетическая энергия — это работа, которую необходимо совершить, чтобы тело массой 



История и этимология понятия[править | править код]
Прилагательное «кинетический» происходит от греческого слова κίνησις (kinesis, «движение»). Дихотомия между кинетической энергией и потенциальной энергией восходит к аристотелевским концепциям потенциальности и актуальности[en][5] .
Принцип классической механики, согласно которому E ∝ mv2/2, был впервые разработан Готфридом Лейбницем и Иоганном Бернулли, описавшими кинетическую энергию как живую силу (лат. vis viva)[6]. Вильгельм Гравезанд из Нидерландов предоставил экспериментальные доказательства этой связи. Сбрасывая грузы с разной высоты на глиняный блок, он определил, что глубина их проникновения пропорциональна квадрату скорости удара. Эмили дю Шатле осознала значение данного эксперимента и опубликовала объяснение[7].
Понятия «кинетическая энергия» и «работа» в их нынешнем научном значении восходят к середине XIX века. В 1829 году Гаспар-Гюстав Кориолис опубликовал статью Du Calcul de l’Effet des Machines, в которой излагалась математика того, что по сути является кинетической энергией. Создание и введение в оборот самого термина «кинетическая энергия» приписывают Уильяму Томсону (лорду Кельвину) c 1849—1851 гг.[8][9]. Ренкин, который ввел термин «потенциальная энергия» в 1853 году[10], позже цитировал У. Томсона и П. Тэйта с заменой слова «кинетическая» на «фактическая»[11].
Кинетическая энергия в классической механике[править | править код]
Случай одной материальной точки[править | править код]
По определению, кинетической энергией материальной точки массой 
,
при этом предполагается, что скорость точки 


Если 





Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина 
Случай абсолютно твёрдого тела[править | править код]
При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:
Здесь 



Кинетическая энергия в гидродинамике[править | править код]
В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа 


где по повторяющемуся индексу 
Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса[13]. Если, в согласии с методом Рейнольдса, представить 

где 





Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.
Кинетическая энергия в квантовой механике[править | править код]
В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (

где 


Кинетическая энергия в релятивистской механике[править | править код]
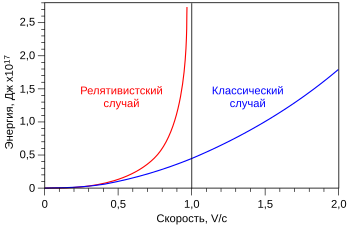
Зависимости кинетической энергии от скорости в классическом и релятивистском случаях для массы в 1 кг
Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как:
- где
— масса материальной точки,
— скорость движения в выбранной инерциальной системе отсчёта,
— скорость света в вакууме (
— энергия покоя).
Кинетическая энергия в этой формуле может быть разложена в ряд Маклорена по степеням 
При скоростях много меньших скорости света (


Как и в классическом случае, имеет место соотношение 


Релятивистское соотношение между кинетической энергией и импульсом p записывается в виде
Разложив это выражение по степеням 
первый член которого равен нерелятивистскому выражению кинетической энергии через импульс, а последующие члены — релятивистские поправки к этому выражению, которые малы при 
Свойства кинетической энергии[править | править код]
- Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему[1].
- Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки и направления её скорости, а зависит лишь от модуля скорости или от квадрата её скорости[1].
- Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
- Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии[15][16].
Физический смысл кинетической энергии[править | править код]
Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии[2]:
Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения 
Соотношение кинетической и внутренней энергии[править | править код]
Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.
То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.
См. также[править | править код]
- Теорема о кинетической энергии системы
- Потенциальная энергия
- Закон сохранения энергии
- Хаос
- Энтальпия
- Негэнтропия
- Термодинамика
- Парадокс кинетической энергии
Примечания[править | править код]
- ↑ 1 2 3 4 Айзерман, 1980, с. 49.
- ↑ 1 2 Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва, Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
- ↑ Brenner, Joseph. Logic in Reality. — illustrated. — Springer Science & Business Media, 2008. — P. 93. — ISBN 978-1-4020-8375-4. Архивная копия от 25 января 2020 на Wayback Machine Extract of page 93 Архивировано 4 августа 2020 года.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
- ↑ Judith P. Zinsser. Emilie Du Châtelet : daring genius of the Enlightenment. — New York: Penguin Books, 2007. — viii, 376 pages, 16 unnumbered pages of plates с. — ISBN 0-14-311268-6, 978-0-14-311268-6.
- ↑ Crosbie Smith. Energy and empire : a biographical study of Lord Kelvin. — Cambridge [Cambridgeshire]: Cambridge University Press, 1989. — xxvi, 866 pages с. — ISBN 0-521-26173-2, 978-0-521-26173-9. Архивировано 25 января 2022 года.
- ↑ John Theodore Merz. A history of European thought in the nineteenth century. — Gloucester, Mass.: Peter Smith, 1976. — 4 volumes с. — ISBN 0-8446-2579-5, 978-0-8446-2579-9.
- ↑ William John Macquorn Rankine. XVIII. On the general law of the transformation of energy // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1853-02. — Т. 5, вып. 30. — С. 106–117. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786445308647205.
- ↑ W.J. Macquorn Rankine. XIII. On the phrase “Potential energy,” and on the definitions of physical quantities // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1867-02. — Т. 33, вып. 221. — С. 88–92. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786446708639753.
- ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245. Архивировано 23 августа 2017 года.
- ↑ 1 2 Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
- ↑ Блохинцев Д. И. Основы квантовой механики Архивная копия от 15 февраля 2022 на Wayback Machine, 5-е изд. Наука, 1976. — 664 с., см. § 26.
- ↑ Айзерман, 1980, с. 54.
- ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» Архивная копия от 1 января 2015 на Wayback Machine // УФН, 59, с. 325—362, (1956)
Литература[править | править код]
- Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.
- Фриш С. Э. Курс общей физики. В 3-х тт. Т.1. Физические основы механики. Молекулярная физика. Колебания и волны. 13-е изд. — СПб.: Лань, 2010. — 480 с. — ISBN 978-5-8114-0663-0.
- Сивухин Д. В. Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.










