ПРИЛОЖЕНИЕ 7
Рекомендуемое
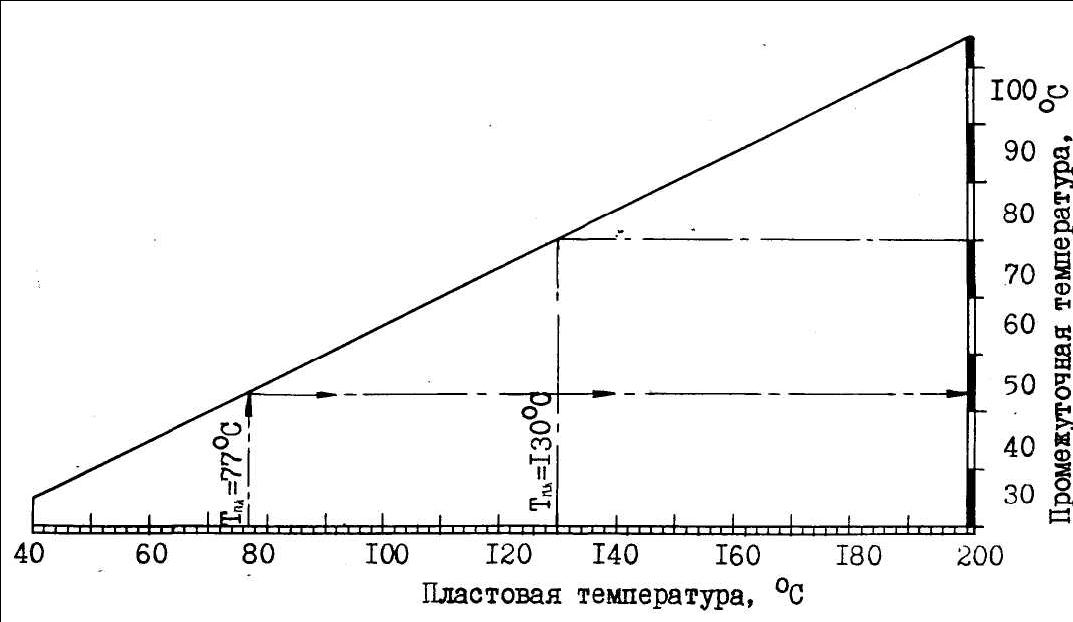
График для нахождения промежуточной температуры
Правило нахождения промежуточной температуры
Для нахождения промежуточной температуры по п. 2.2.6 на горизонтальной шкале откладывают значение пластовой температуры и восстанавливают перпендикуляр до пересечения с наклонной линией графика. Из точки пересечения проводят горизонтальную линию до пересечения с вертикальной шкалой, на которой читают значение промежуточной температуры.
Пример 1. Пластовая температура 77 °C. По графику находят промежуточную температуру 50 °С. Следовательно температуры эксперимента будут: 20, 50 и 77 °С.
Пример 2. Пластовая температура 130 °С. По графику находят промежуточную температуру на границе 70 и 80 °С. Следовательно, температуры эксперимента будут: 20, 80 и 130 °С.
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Числовые ряды. Необходимый признак сходимости. Признак Даламбера
1 ставка
Высшая математика. Помогите пожалуйста, очень нужно!
1 ставка
(Вопрос по химии) Пять способов получения 2,8-диметилнонан.
1 ставка
Опрос по теме "Влияние маркетинговых "уловок" на московскую молодёжь"
1 ставка
Что за глупый вопрос. Универ
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Ксения
Ученик
(176),
закрыт
9 лет назад
Лучший ответ
Любовь Орлова
Гений
(50391)
9 лет назад
Промежуточную температуру можно определить графическим способом:
показания температуры на графике увеличь в 10 раз и подставь свои значения.

Остальные ответы
Похожие вопросы
Промежуточная температура
Cтраница 2
Для промежуточных температур коэффициент Т определяется методом интерполяции.
[16]
Вычисление промежуточных температур позволяет построить график изменения температуры рабочей среды вдоль поверхности.
[17]
Для промежуточных температур коэффициент Т находится интерполяцией.
[18]
Для промежуточных температур, не указанных в таблицах, потери давления определяются интерполированием.
[19]
Значения промежуточных температур вычисляются, как и в случае плоской стенки, по формулам ( 96), в которые надо вставить соответствующие термические сопротивления.
[21]
Для промежуточных температур коэффициент Т определяется методом интерполяции.
[23]
Для промежуточных температур допускаемое напряжение определяется линейной интерполяцией ближайших значений с округлением до 0 5 МПа в меньшую сторону.
[24]
Для промежуточных температур стенки величина допускаемого напряжения определяется интерполяцией между ближайшими значениями с округлением до 0 05 кгс / мм в меньшую сторону.
[25]
Для промежуточных температур значения коэффициентов xNa и pNa получают линейной интерполяцией.
[26]
Для промежуточных температур значения ав находятся интерполяцией.
[27]
Измерение промежуточных температур продуктов сгорания часто затруднено, поэтому из теплового баланса по известным конечным температурам определяют промежуточные.
[28]
Для промежуточных температур значения ав находятся интерполяцией.
[29]
Заменив промежуточную температуру уходящей нагреваемой среды / конечным ее значением К.
[30]
Страницы:
1
2
3
4
Как вы думаете, что быстрее нагревается на плите: литр воды в кастрюльке или же сама кастрюлька массой 1 килограмм? Масса тел одинакова, можно предположить, что нагревание будет происходить с одинаковой скоростью.
А не тут-то было! Можете проделать эксперимент – поставьте пустую кастрюльку на огонь на несколько секунд, только не спалите, и запомните, до какой температуры она нагрелась. А потом налейте в кастрюлю воды ровно такого же веса, как и вес кастрюли. По идее, вода должна нагреться до такой же температуры, что и пустая кастрюля за вдвое большее время, так как в данном случае нагреваются они обе – и вода, и кастрюля.
Однако, даже если вы выждете втрое большее время, то убедитесь, что вода нагрелась все равно меньше. Воде потребуется почти в десять раз большее время, чтобы нагреться до такой же температуры, что и кастрюля того же веса. Почему это происходит? Что мешает воде нагреваться? Почему мы должны тратить лишний газ на подогрев воды при приготовлении пищи? Потому что существует физическая величина, называемая удельной теплоемкостью вещества.
Эта величина показывает, какое количество теплоты надо передать телу массой один килограмм, чтобы его температура увеличилась на один градус Цельсия. Измеряется в Дж/(кг * ˚С). Существует эта величина не по собственной прихоти, а по причине разности свойств различных веществ.
Удельная теплоемкость воды примерно в десять раз выше удельной теплоемкости железа, поэтому кастрюля нагреется в десять раз быстрее воды в ней. Любопытно, что удельная теплоемкость льда в два раза меньше теплоемкости воды. Поэтому лед будет нагреваться в два раза быстрее воды. Растопить лед проще, чем нагреть воду. Как ни странно звучит, но это факт.
Обозначается удельная теплоемкость буквой c и применяется в формуле для расчета количества теплоты:
где Q – это количество теплоты,
c – удельная теплоемкость,
m – масса тела,
t2 и t1 – соответственно, конечная и начальная температуры тела.
По этой формуле можно рассчитать количество тепла, которое нам необходимо, чтобы нагреть конкретное тело до определенной температуры. Удельную теплоемкость различных веществ можно найти из соответствующих таблиц.
А что насчет удельной теплоемкости газов? Тут все запутанней. С твердыми веществами и жидкостями дело обстоит намного проще. Их удельная теплоемкость – величина постоянная, известная, легко рассчитываемая. А что касается удельной теплоемкости газов, то величина эта очень различна в разных ситуациях. Возьмем для примера воздух. Удельная теплоемкость воздуха зависит от состава, влажности, атмосферного давления.
При этом, при увеличении температуры, газ увеличивается в объеме, и нам надо ввести еще одно значение – постоянного или переменного объема, что тоже повлияет на теплоемкость. Поэтому при расчетах количества теплоты для воздуха и других газов пользуются специальными графиками величин удельной теплоемкости газов в зависимости от различных факторов и условий.
Предыдущая тема: Количество теплоты: формула, расчет
Следующая тема:   Энергия топлива: удельная теплота сгорания + ПРИМЕРЫ
Все неприличные комментарии будут удаляться.
все для проектирования
Формула расчета конечной температуры воды после смещения холодной и горячей:
где: Тс — температура смещенной воды, град.
М1 — масса холодной воды, кг
М2 — масса горячей воды, кг
Т1 — температура холодной воды, град.
Т2 — температура горячей воды, град.
Пример 1:
холодная вода 10 литров температурой 5 град смешивается с горячей водой 8 литров 60 градусов.
Необходимо определить конечную температуру воды. Подставляем все значения в формулу 1:
Формула расчета количество холодной и горячей воды в зависимости от температуры:
Бывает задача стоит в обратном направлении. Когда наоборот известно какую температуру необходимо иметь на выходе и общий вес воды, но не известна масса холодной и горячей воды. Тогда из формула 1 выводим новую формулу:
Пример 2:
из циркуляционного душа воды выходит температурой 36 градусов и объемом 40 литров. Необходимо определить количество холодной и горячей воды.
Как правило холодная вода имеет расчетную температуру 5 градусов. Горячая вода — 60 градусов.
Подставляем значения в формулу 2 и 3:
М1=(36*40-60*40)/(5-60)=17,45 литров холодной воды
М2=40-17,45=22,55 литров горячей воды
Удачного Вам дня! И успешных проектов!
Выше конечной целью теплового расчете являлось определение поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это — так называемый поверочный расчет.
При решении такой задачи известными являются следующие величины: поверхность нагрева F, коэффициент теплопередачи k, водяные эквиваленты W1 и W2 и начальные температуры t1’ и t2’, а искомыми: конечные температуры t1” и t2” и количество переданного тепла Q.
В приближенных расчетах можно исходить из следующих представлений. Количество тепла, отдаваемое горячей жидкостью, равно:
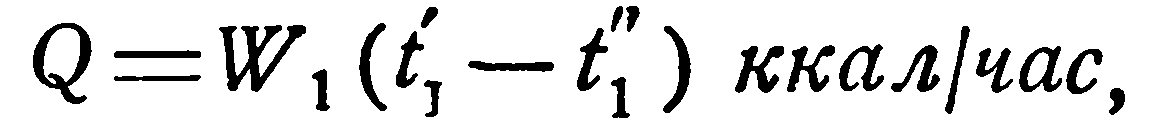 (2.13)
(2.13)
откуда конечная температура ее t1” определяется соотношением:
 (a)
(a)
Соответственно для холодной жидкости имеем:
 (2.14)
(2.14)
 (b)
(b)
Если принять, что температуры рабочих жидкостей меняются по линейному закону, то
 (с)
(с)
Вместо неизвестных t1” и t2” подставим их значения из уравнений (а) и (b), тогда получим:
 (d)
(d)
Произведя дальнейшее преобразование, имеем:
 (e)
(e)
откуда окончательно получаем:
 (2.15)
(2.15)
Зная количество переданного тепла Q, очень просто формулам (а) и (b) определить и конечные температуры рабочих жидкостей t1” и t2”.
Приведенная схема расчета, хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока ниже приводится вывод более точных формул.
1. Прямоток. Выше было показано, что температурный напор изменяется по экспоненциальному закону:
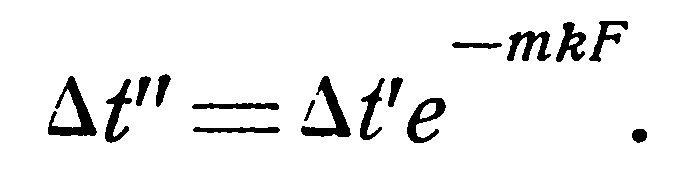 (2.16)
(2.16)
Имея в виду, что

и, что в конце поверхности нагрева Δt” = t1’ – t2’, то, подставляя эти значения в уравнение (19), последнее можно представить в следующем виде:
 (2.17)
(2.17)
Однако, это уравнение дает лишь разности температур. Чтобы отсюда получить конечные температуры в отдельности, необходимо обе части равенства вычесть из единицы:
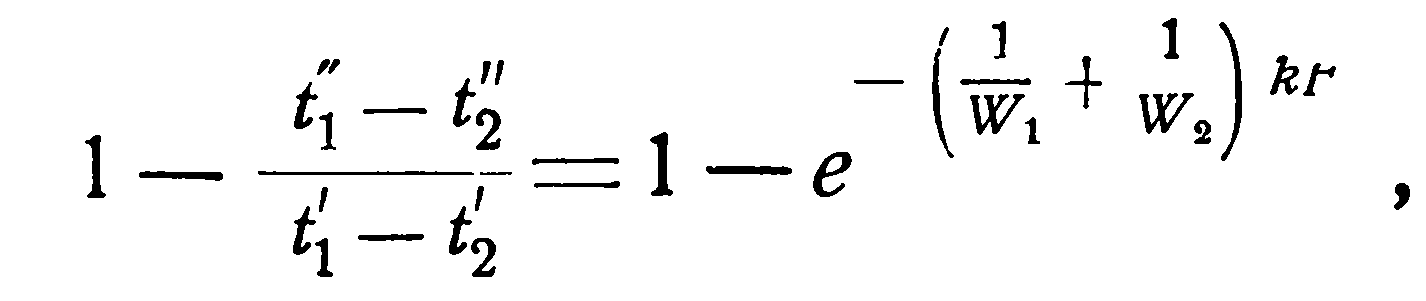 (2.18)
(2.18)
 (2.19)
(2.19)
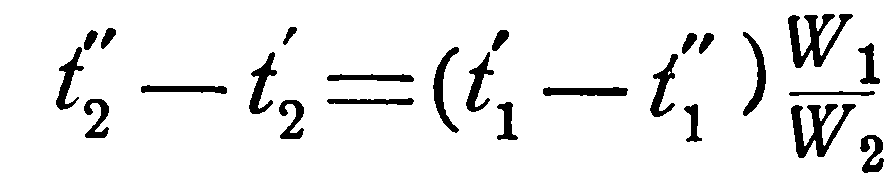
[см. разд.2.1 уравнение (2.5)].
то, подставляя это значение в левую часть уравнения (2.19), получаем:
 (2.20)
(2.20)
Последнее уравнение, показывает, что изменение температуры горячей жидкости δt1 равно некоторой доле П располагаемого начального температурного напора, t1’ – t2’; эта доля зависит только от двух безразмерных параметров 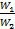 и
и  .
.
Аналогичным образом из уравнения (2.19) можно получить выражение и для изменения температуры холодной жидкости, а именно:
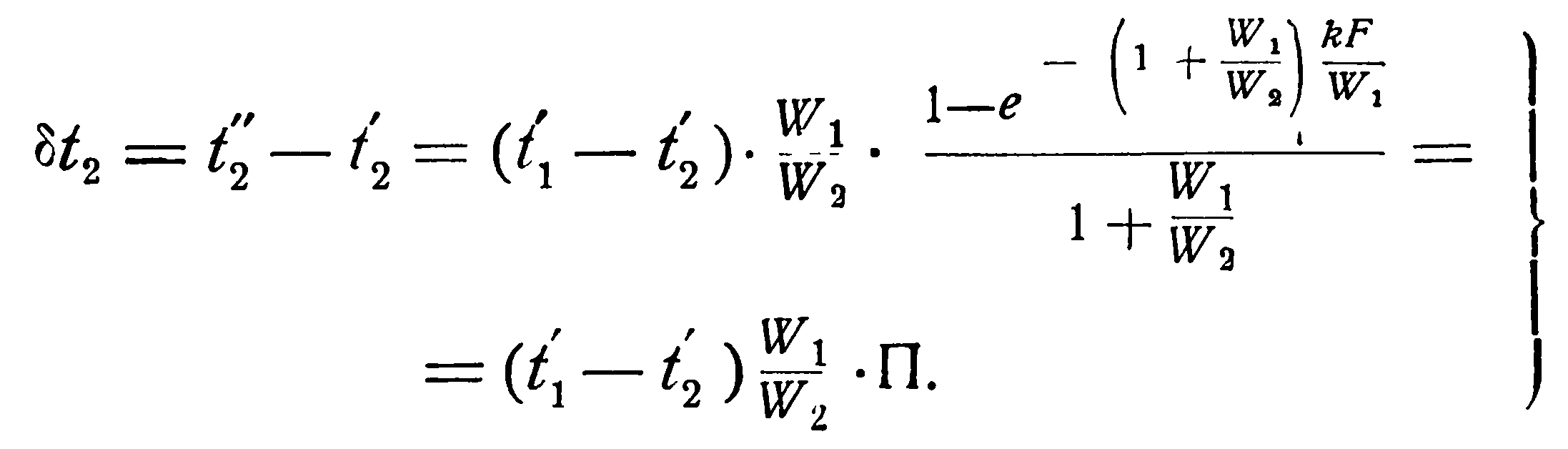 (2.21)
(2.21)
Определив изменения температур рабочих жидкостей и зная их начальные температуры, легко определить конечные:
 (2.22)
(2.22)
Расход тепла определяется путем умножения водяного эквивалента жидкости на изменение ее температуры:
 (2.23)
(2.23)
Значение функции  приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение Fx.
приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение Fx.
Пример 2.2. Имеется водяной холодильник с поверхностью нагрева F=8 м 2 . Определить конечные температуры жидкостей и часовое количество передаваемого тепла Q, если заданы следующие величины: V1= 0,25 м 3 /час, γ1 = 1100 кг/м 3 , cp1 = 0,727 ккал/кг °С и t1’ = 120 °С Для охлаждения в распоряжении имеется 1000 л воды в час при температуре t2’ = 10 °С. Кроме того, известно значение коэффициента теплопередачи k = 30 ккал/м 2 час °С.
Соответствующее значение функции П находим из рис.2.5:

Рис. 2.5.  — вспомогательная функция для расчета конечной температуры при прямотоке
— вспомогательная функция для расчета конечной температуры при прямотоке
Изменение (понижение) температуры горячей жидкости согласно уравнению (2.20) равно:

Следовательно, конечная температура ее равна:

Количество переданного тепла в час определится по уравнению (2.23)

Изменение температуры холодной жидкости определяется по уравнению (2.21). Но его можно также определить и из соотношения Q = W2 (t2” — t2’), откуда

2. Противоток. Для противотока расчетные формулы выводятся так же, как и для прямотока. Окончательно они имеют следующий вид:
 (2.24)
(2.24)
 (2.25)
(2.25)
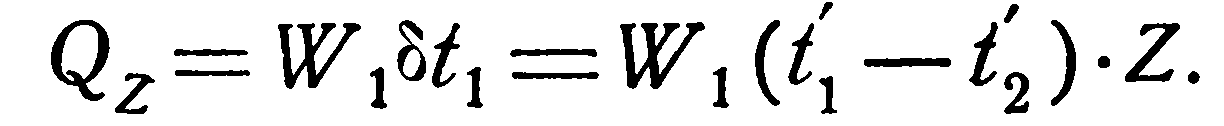 (2.26)
(2.26)
В частном случае, когда  формулы
формулы
(2.24) – (2.26) принимают вид:
 (2.27)
(2.27)
 (2.28)
(2.28)
 (2.29)
(2.29)
Значение функции 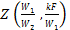 приведено на рис. 2.6.
приведено на рис. 2.6.

Рис. 2.6.  — вспомогательная функция для расчета конечной температуры при противотоке
— вспомогательная функция для расчета конечной температуры при противотоке
Для расчета промежуточных значений температуры рабочих жидкостей и количества переданного тепла в формулах (2.23) – (2.29) в числителе значение F заменяется на Fx, а в знаменателе остается значение полной поверхности F.
Пример 2.3. Если взять тот же теплообменник, который был рассмотрен в условиях прямотока, и допустить, что условия теплопередачи остаются без изменения (k = 30 ккал/м 2 час °С), то получим следующие соотношения:

Из рис. 2.6 находим значение функции Z:
Изменение температуры горячей жидкости равно [уравнение (2.24)]:

Конечная температура ее:
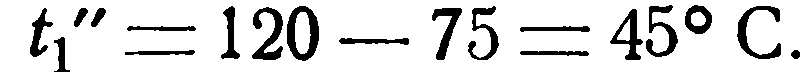
Изменение температуры холодной жидкости [уравнение (2.25)];

Конечная температура ее:

Количество переданного тепла в час [уравнение (2.26)]:

Таким образом, в случае противотока в теплообменнике происходит более глубокое охлаждение горячей жидкости.
3. Сравнение прямотока с противотоком. Чтобы выявить преимущество одной схемы перед другой, достаточно сравнить количество передаваемого тепла при прямотоке и противотоке при равенстве прочих условий. Для этого необходимо уравнение (2.23) разделить на уравнение (2.26). В результате этого действия мы получаем новую функцию тех же двух безразмерных аргументов
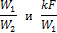
характер изменения которой графически показан на рис. 2.7.

Рис. 2.7.  -сравнение прямотока с противотоком
-сравнение прямотока с противотоком
Из рисунка следует, что схемы можно считать равноценными в том случае, если водяные эквиваленты обеих жидкостей значительно отличаются один от другого (при  и при
и при 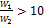 ) или если значение параметра
) или если значение параметра  — мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку
— мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку 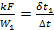 , то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.
, то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.
При конденсации и кипении температура жидкости постоянна. Это означает, что водяной эквивалент такой жидкости бесконечно велик. В этом случае прямоток и противоток равнозначны, и уравнения (2.23) и (2.26) становятся тождественными. Конечная температура той жидкости, для которой водяной эквивалент имеет конечное значение, определяется следующим образом.
При конденсации паров;

 (2.30)
(2.30)
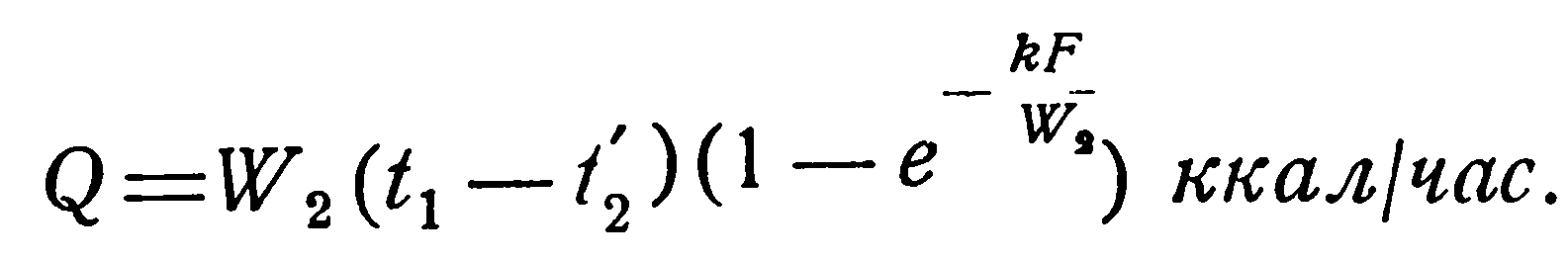 (2.31)
(2.31)
При кипении жидкостей:

 (2.32)
(2.32)
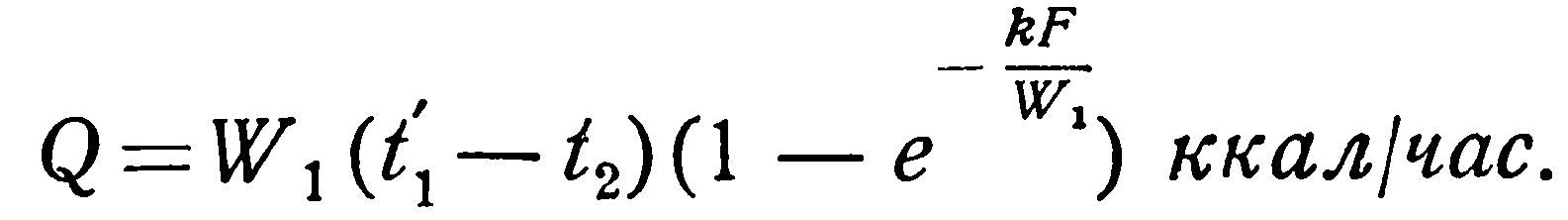 (2.33)
(2.33)
Вместо t1 и t2 в уравнения (2.30) – (2.33) можно подставить температуру стенки, значение которой при этом также постоянно. Значения функции  находятся из таблиц показательных функций.
находятся из таблиц показательных функций.
В случае перекрестного тока конечные температуры рабочих жидкостей находятся между конечными температурами для прямотока и противотока. Поэтому в приближенных расчетах можно пользоваться методом расчета одной из указанных схем. Если одна из жидкостей движется навстречу другой зигзагообразно (смешанный ток), то расчет может быть произведен, как для противотока.
4. Влияние тепловых потерь и проницаемости стенок.Все вышеприведенные формулы справедливы для случая, когда тепловые потери во внешнюю среду равны нулю. В действительности они всегда имеются. Более или менее точно учесть их влияние, вообще говоря, возможно, однако расчетные формулы при этом становятся громоздкими. Поэтому для учета влияния тепловых потерь в практике обычно применяется приближенный метод, который состоит в следующем.
Тепловые потери со стороны горячей жидкости вызывают более сильное падение ее .температуры. Это равносильно случаю, когда теплоотдающая жидкость в аппарате без потерь в окружающую среду имела бы меньшее значение водяного эквивалента. Поэтому влияние потерь в окружающую среду можно учесть, изменив водяной эквивалент теплоотдающей жидкости в тепловом аппарате таким образом, чтобы в последнем происходило такое же понижение температуры, как и при потоке с действительным водяным числом при наличии тепловых потерь. Внешние тепловые потери со стороны холодной жидкости оказывают обратное влияние, они уменьшают повышение температуры жидкости, что приводит к кажущемуся увеличению ее водяного эквивалента.
Наличие присоса наружного холодного воздуха оказывает такое же влияние, как и внешняя потеря тепла. Присосанный вездух на горячей стороне понижает температуру горячей жидкости (газа) точно так же, как если бы теплообменный аппарат был абсолютно непроницаем, но жидкость имела меньшее значение водяного эквивалента. Присос вездуха на холодной стороне понижает температуру холодной жидкости, что равносильно увеличению значения водяного эквивалента.
Если потеря тепла составляет р% к общему количеству передаваемого тепла, то вместо действительного значения водяного эквивалента W в расчетные формулы следует подставить значение W’ которое определяется следующим образом:
 (2.34)
(2.34)
Знак минус (-) берется для горячей, а знак плюс (+) для холодной жидкости.
При таком способе учета внешних тепловых потерь все приведенные выше формулы для расчета конечных температур можно применять без какого-либо их изменения.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

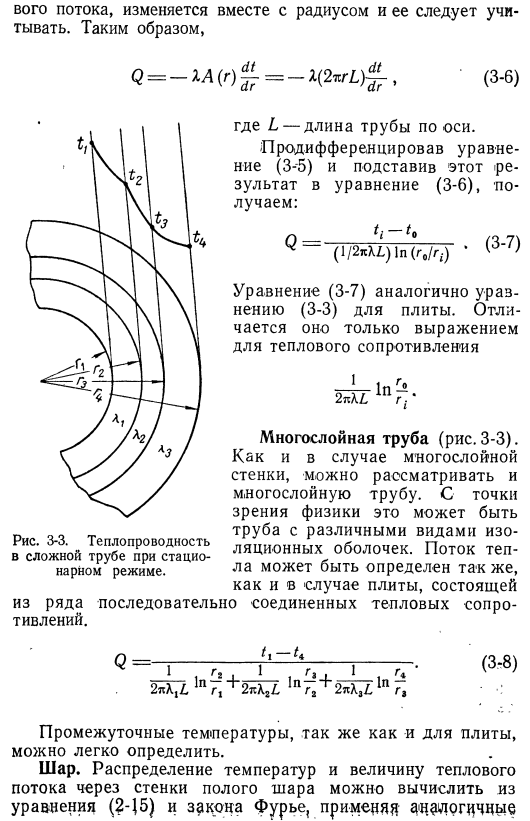



Решения простейших уравнений теплопроводности для условий стационарного режима
- Теплопроводность в стационарном состоянии Режим Для тел простой формы, таких как стенки, полые трубы и полые шары, уравнение теплопроводности значительно упрощается, если тепло постоянно распространяется в 1 измерении. * Плоские стенки (пластины); в плоской стенке(рис.3-1) с постоянной теплопроводностью толщиной I и бесконечной длиной другого измерения тепловой поток в этой области фактически равен 1 измерению.
Поэтому такие объекты удобно отображать в ортогональной системе координат. Если на стенке нет источника тепла, а тепловой поток стационарный и 1-мерный, то формула (2-13) принимает вид: (3-1) Решение: Т = Cₜx-C₂. Константы C и C₂ могут быть вычислены из граничных условий, определяющих температуры поверхности x = 0 и x = 1.Используйте эти условия для получения уравнения распределения температуры стенки. Тепловой поток через стенку можно получить из закона теплопроводности Фурье. Г_ _ Г ^ 2 / ЛЯ.• (3-3).
Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой.
Людмила Фирмаль
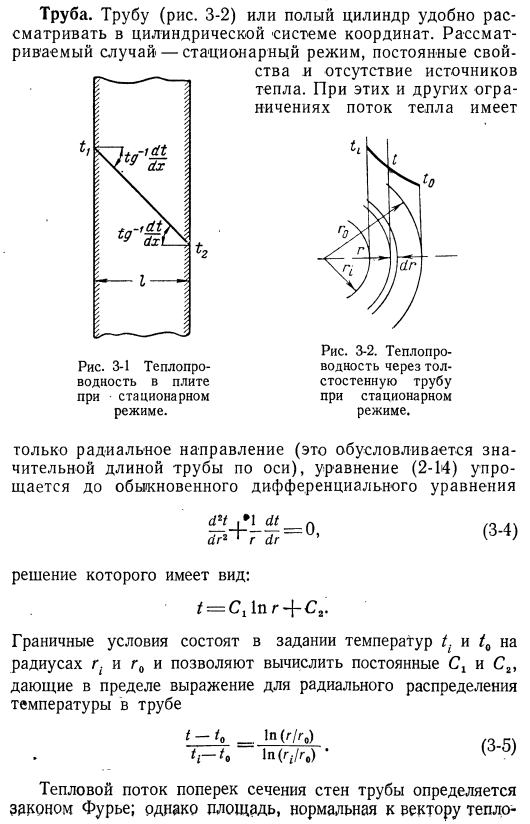
Поэтому и здесь уместно отметить совпадение в виде совпадения с обычным законом Ома (3-3). / Термин / LD соответствует электрическому сопротивлению, поэтому его называют термическим сопротивлением или термическим сопротивлением. The pipe. It удобно рассматривать полый цилиндр с трубой (рис. 3-2) или цилиндрическую систему координат. Рассматриваемый случай является стационарным режимом и является постоянным Рис. 3-1 * теплопроводность печи в стационарном режиме. уств и отсутствие источника тепла. При этих и других ограничениях тепловой поток составляет Рисунок 3-2.
- Теплопроводность толстостенных труб в стационарном режиме. Только в радиальном направлении(это зависит от важной длины трубы вдоль оси) формула (2-14) упрощается до обычных дифференциальных уравнений а Г2* /•доктор—» 1 (3-4) Форма его решения выглядит следующим образом: =₁₁1пг -} — ^ 2. Граничное условие находится в настройке температуры. Радиуса R и R/и пневмония Т-ТП(Фо) tᵢ-tlnln(РЗ / r₀) ’ Тепловой поток по сечению стенки трубы определяется законом Фурье. Однако площадь перпендикулярна теплу Поток, в зависимости от радиуса, должен быть учтен. Подобный этому М = — м (р) г.=- я(2wL)Дж Рисунок 3-3.
Теплопроводность сложной трубы в стационарном режиме. Где L — длина оси трубы. Если мы дифференцируем уравнение (3-5) и подставим этот результат в уравнение (3-6), то: ГВ (1/2 «Л1) 1П(г,/ г;) * ⁽3′ ⁷ ⁾ Формула (3-7) аналогична формуле плиты (3-3).Отличается только формула термического сопротивления Многослойные трубы(рис. 3-3); так же как и многослойные стенки, можно рассматривать многослойные трубы. С точки зрения физики, это будет труба с различными типами изолирующих оболочек. Тепловой поток можно определить так же, как и в случае с плитой От серии сопротивления жары соединенных последовательно.
Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой.
Людмила Фирмаль
Также, как плита, промежуточную температуру можно легко определить. Мяч. Можно ли рассчитать распределение температуры и величину теплового потока через стенку полого шара по уравнению (2-J5) и закону Фурье? Аналогичное приложение Такие предположения, как в случае с плитами и трубами. Распределение температуры получается таким образом Мы найдем тепловой поток отсюда. Н.—__ В. (1 / 4nL) [(1 / год)-(1 /год)] ’ (3-10) Формулу составного шара можно легко найти таким же образом, как из Формулы (3-10) в Формулу (3-8).
Смотрите также:
- Предмет теплотехника

